Abstract
The net reclassification improvement (NRI) is a widely used metric used to assess the relative ability of 2 risk models to distinguish between low- and high-risk individuals. However, the validity and usefulness of the NRI have been questioned. Criticism of the NRI focuses on its use comparing nested risk models, whereas in practice it is often used to compare nonnested risk models derived from distinct data sources. In this study, we evaluated the performance of the NRI in a nonnested context by using it to compare competing cardiovascular risk-prediction models. We explored the NRI’s sensitivity to variations in risk categories and to the calibration of the compared models. We found that the NRI was very sensitive to changes in the definition of risk categories, especially when at least 1 model was miscalibrated. To address these shortcomings, we describe a novel alternative to the usual NRI that uses percentiles of risk instead of cutoffs based on absolute risk. This percentile-based NRI demonstrates the relative ability of 2 models to rank patient risk. It displays more stable behavior, and we recommend its use when there are no established risk categories or when models are miscalibrated.
Keywords: discrimination, electronic health data, model comparison, net reclassification improvement, reclassification, risk assessment
The ability of a risk model to discriminate individuals who experience an event of interest from those who do not experience the event of interest is important in practice. For example, studies of cardiovascular disease (CVD) have shown that targeting those with high absolute CVD risk instead of those with single risk factors above goal can minimize unnecessary treatment and is more than twice as effective in reducing death from cardiovascular outcomes (1, 2). In many settings, including CVD, multiple risk-prediction models are available, and investigators must determine which model performs better (3, 4).
One popular metric for assessing the discrimination ability of a risk-prediction model is the concordance index or C-index. However, the C-index has been criticized as being relatively insensitive to changes in absolute risk estimates and therefore having little power to detect modest but potentially meaningful differences between risk models (5, 6). As an alternative, Pencina et al. (5) proposed the net reclassification improvement (NRI). Given a set of predefined risk categories, the NRI assesses 2 models’ relative ability to discriminate between events and nonevents by quantifying the agreement between “upward” and “downward” risk reclassifications and event status.
Using the NRI to assess model discrimination, either as an alternative or as a supplement to the C-index, has become popular since its publication (7). A search on PubMed yielded 1,347 papers with the phrase “net reclassification improvement” or “net reclassification index” in the title or abstract through December 2016, including 278 in 2016 alone.
Despite its popularity, the NRI has been criticized in several recent papers (7–13). The main criticisms are that the NRI varies substantially depending on choice in risk cutoffs, is unstable when used to compare miscalibrated models, and is challenging to interpret. Additional criticisms include the possibility of noninformative model changes appearing useful and potentially problematic confidence intervals. Assessment of variation in risk cutoffs is limited to 2–3 categories, which is not always consistent with risk category definitions used in practice (8, 9, 12). Because the NRI is commonly used to evaluate the improvement when one biomarker is added to a model, virtually all published criticism focuses on its use in comparing nested models (9, 11, 12). However, the NRI is also frequently used to compare nonnested models, in particular models developed using different data sets (14–18). Although some have recommended against the use of the NRI for making nonnested comparisons (15), few studies have provided real-world evidence demonstrating the performance of the NRI in this context.
In this analysis, we used electronic health data to investigate the performance of the categorical NRI and the continuous NRI in a practical setting and to compare 2 nonnested models for cardiovascular risk, the Framingham Risk Score (FRS) and the Pooled Cohort Equations (PCE). We have assessed the sensitivity of the NRI to variations in the number and placement of risk cutoffs and to miscalibration of models. In addition, we propose a novel adaptation of the NRI using percentiles of risk as an alternative to standard categories of risk based on absolute cutoffs and have assessed its performance in comparison to the traditional NRI.
METHODS
Data source and inclusion criteria
Data were collected for this study from a large health-care delivery and insurance organization based in the upper Midwestern United States. The data were extracted from a virtual data warehouse that captured patient information between January 1, 2001, and December 31, 2011. Patients were excluded from our analysis to be consistent with the target population for the cardiovascular risk models evaluated, leading to a final analytical data set of 84,116 patients. The full inclusion and exclusion criteria are described in Web Appendix 1 (available at https://academic.oup.com/aje). Data from half of the patients were used to refit the risk-prediction models, as described below, and data from the remaining half were used as a test set to evaluate model performance. Characteristics of this population are tabulated in Web Table 1.
Cardiovascular risk models
The FRS is among the most commonly used risk models for predicting CVD outcomes (19). The PCE are one alternative, recently developed by the American College of Cardiology and the American Heart Association (4). The PCE involve more interaction terms and are more complex than the FRS; it is important to note that these are separately developed, nonnested models predicting risk for different sets of cardiovascular events. Event definitions and rates for both risk models are included in Web Appendix 1. To compensate for these differences, the analyses presented here are based on the time to CVD events and event indicator used for the PCE.
Risk factors used in the calculation of FRS and PCE cardiovascular-risk estimates were obtained from the data as described in Wolfson et al. (20). The FRS and PCE predict cardiovascular risk over a 10-year period; however, the median follow-up time for patients in our data set under the PCE event definition was 4.3 years. Therefore, both risk models were adapted to predict 5-year CVD risk. The scaled 5-year version of FRS, which we refer to as “original FRS,” was calculated by combining the published coefficients for the Framingham lipid model and 5-year baseline survival probabilities obtained directly from the creators of FRS (19) (R. B. D’Agostino, Boston University, personal communication, 2012). The scaled version of the PCE, which we refer to as “original PCE,” was computed using the formulas in Muntner et al. (21). We also estimated locally customized versions using the available electronic health data; we refer to these as the “refitted FRS” and the “refitted PCE.”
Calibration for these models was assessed using a Hosmer-Lemeshow goodness-of-fit statistic modified for censored outcomes (22). C-index values were calculated using Harrell’s C-index (23). We computed the NRI comparing each pair of the 4 different cardiovascular risk models. In particular, comparing the original PCE with the original FRS allows us to assess whether a new alternative model has better discriminative ability than an old model. We expect the original FRS model to be miscalibrated, given the use of the PCE event definition when fitting the model; this allows for a comparison of models where at least 1 model is known to be miscalibrated. Investigators may be interested in whether or not model performance improves if the model is fitted to the specific population; we examined this by comparing the original with the refitted model for both FRS and PCE. Finally, we also compared the refitted PCE with the refitted FRS, where we expect 2 well-fitting models based on different model structures.
Net reclassification improvement
Because the primary outcome of the study is a time-to-event outcome, we used an extension of the traditional NRI developed by Pencina et al. (24) for time-to-event data with censored observations. The formula for the censored NRI for comparing model 1 versus model 2 is given below:
Up-classification or down-classification occurs when model 2 categorizes an individual to a higher or lower risk category, respectively, compared with model 1. Kaplan-Meier estimates were used to estimate the probability of an event (), the probability of an event given up-classification (), and the probability of an event given down-classification (). In the absence of censoring, we could simply use the number of participants who are up- or down-classified and experience an event. However, due to censoring, we use the Kaplan-Meier estimate to find . is the number of individuals up-classified, and is the number of individuals down-classified. Standard clinical risk cutoffs for cardiovascular risk classification reference a 10-year risk of CVD. Because our data refer to a 5-year follow-up period, we approximated 5-year risk categories by cutting the original risk categories in half to be 0%–2.5%, 2.5%–5%, 5%–7.5%, 7.5%–10%, and 10%–100%. The continuous NRI was computed similarly, but all changes in risk prediction were considered without using risk categories. The event NRI (first term in above formula) is positive when model 2 correctly up-classifies more events; similarly, the nonevent NRI (second term above) is positive when model 2 correctly down-classifies more nonevents. The 95% confidence intervals were computed using 1,000 bootstrap samples.
Percentile-based NRI
As an alternative to using absolute risk to form the categories for the NRI, we propose using percentiles of risk. By using percentiles of risk rather than absolute risk to form the cutoffs for the categorical NRI, we allow for generalizability of the NRI to applications in which a standard choice in cutoffs is not available. In addition, the percentile NRI is invariant to monotone transformations of the risk predictions.
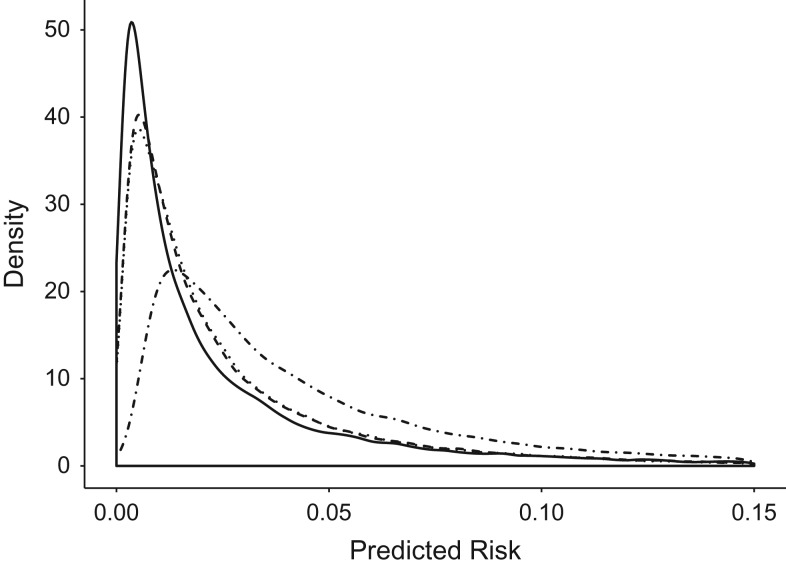
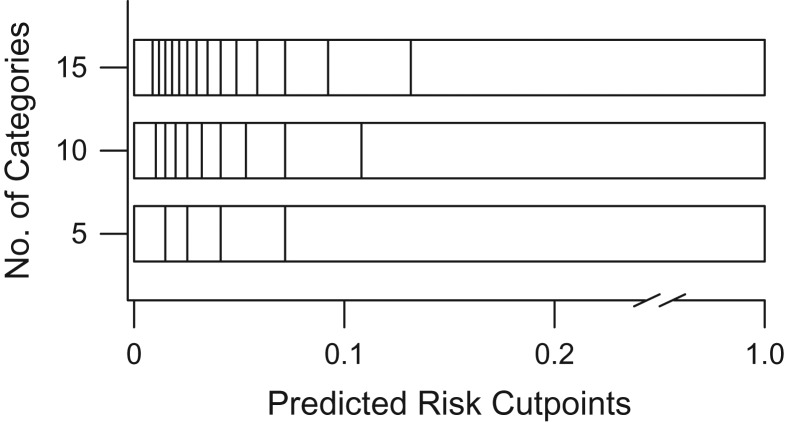
To implement the percentile-based NRI, we divided the predicted risk for each model into quantiles based on evenly spaced fractions. Reclassification was considered across quantiles of risk based on the estimated risks. For example, comparing 2 models, if a patient falls into the first decile of estimated risk for model 1 and the second decile of estimated risk for model 2, we consider this an up-classification of the patient. Due to the skewed distribution of risk predictions in our data (Figure 1), we saw more cutoffs concentrated in the lower end of the absolute risk prediction range (Figure 2). By evenly spacing the risk categories across estimated risk percentiles, we see unevenly spaced categories across the corresponding values of absolute risk. It is important to note that the cutoffs are determined separately for each model and will vary based on the distribution of risk predictions for that model. For example, an individual could have identical absolute risk predictions from both model 1 and model 2, yet fall into different categories of risk for the 2 models, leading to an up-classification or down-classification by this metric. We used R (R Foundation for Statistical Computing, Vienna, Austria) to implement the percentile-based NRI; code is available in Web Appendix 2.
Figure 1.
Distribution of predicted risk for original Framingham Risk Score (FRS) model (dotted and dashed line), original Pooled Cohort Equations (PCE) model (solid line), refitted FRS model (dotted line), and refitted PCE model (dashed line), using electronic health data from HealthPartners, 2001–2011.
Figure 2.
Quantiles based on evenly spaced fractions yield risk cutoff values for use in calculation of the net reclassification improvement (NRI), using electronic health data from HealthPartners, 2001–2011. The number of categories indicates how many quantiles were used. Cutpoints are displayed at the level of absolute risk corresponding to the quantiles.
Scenarios for evaluating the performance of the NRI
The performance of the NRI has been criticized for inconsistency when changes are made to the risk cutoffs. While previous investigations have been limited to 2–3 risk categories, we investigate more cutoffs, as is often seen in practice (8, 9, 12). We investigated the impact of increasing the number of cutoffs in 2 ways. First, we added additional evenly spaced categories to the upper end of the standard risk cutoffs until the interval of risk from 0%–100% was covered entirely by categories of size 2.5%. We compared these values with the continuous NRI. Second, we maintained the upper limit of 10% as the highest risk boundary and increased the number of categories (i.e., decreased the length of each category within the range). We compared this with a modified continuous NRI in which all subjects with greater than 10% risk were treated as if their risk was 10%, in order to limit the continuous NRI to the same range considered for the categorical risk cutoffs in this method.
We also examined how the NRI changes in response to the location of risk cutoffs. In the context of cardiovascular risk prediction, the standard (adapted to 5-year risk) NRI is based on 4 evenly spaced categories from 0%–10% predicted risk. We adjusted the upper limit of the range of risk from 10% in increments of 2.5%, evenly spacing 4 categories across the new range. Additionally, we addressed the impact of altering a single category in the standard clinical cutoffs. One at a time, we divided each of the categories in half to be 2 risk categories of length 1.25% while the other categories were maintained at the standard 2.5% length. Figures displaying the location of risk category cutoffs used in assessment of the NRI under the described scenarios are displayed in Web Appendix 3.
Finally, we assessed the impact of increasing the number of categories on the percentile-based NRI. We cut the estimated risk distributions into a varying number of categories based on evenly spaced quantiles and considered the impact on the NRI. We compared the impact of variations in the number of categories on the NRI when absolute risks versus percentiles were used to form risk categories.
RESULTS
Risk predictions, model calibration, and conventional NRI
On average, the original FRS predicted higher cardiovascular risk (median, 0.0322) than the other models (original PCE median, 0.0126; refitted FRS median, 0.0163; refitted PCE median, 0.0160). Distributions of risk predictions for all 4 models are displayed in Figure 1. The original FRS model was substantially miscalibrated (calibration statistic: 453.2) due to consistent overestimation of risk. The original PCE model was somewhat miscalibrated (calibration statistic: 43.7). The refitted FRS and refitted PCE models were both relatively well calibrated (refitted FRS calibration statistic: 9.3; refitted PCE calibration statistic: 17.4). All calibration statistics refer to an approximate distribution with 8 degrees of freedom. C-index values indicated similar discrimination across models (original FRS: 0.742, refitted FRS: 0.748, original PCE: 0.747, refitted PCE: 0.746).
The categorical NRI estimates under the standard 5-year risk categories are displayed in Web Table 2. The confidence interval for the overall NRI crosses zero for some comparisons, which indicates little difference in the discriminative ability of the 2 models. Where significant, the NRI statistic suggests that the original FRS model better discriminates cardiovascular risk than do the refitted FRS model and the original PCE model.
Sensitivity of the NRI to the number of risk categories
Table 1 summarizes the result of increasing the number of categories by adding additional 2.5% risk categories to the upper end of the risk cutoffs. For most model comparisons, the magnitude of the NRI increased substantially with the number of risk categories. For the comparison of refitted FRS versus original FRS, adding 1 additional category more than doubled the magnitude of the NRI. We observed a similar pattern for the comparison between the original PCE and the original FRS, both largely due to changes in event reclassification. We observed changes of a smaller magnitude when comparing the refitted PCE with the original PCE and insignificant changes when comparing the refitted PCE with the refitted FRS, where both models are well calibrated. The original FRS as calculated here was most likely to classify a patient’s cardiovascular risk above 10%, so adding additional categories increases event reclassification in that range more than for other models. Across all model comparisons, the continuous NRI value was quite different and often the opposite sign from the categorical NRI with many categories.
Table 1.
Additional Categories Based on Extending Range of Risk Categories for Overall Net Reclassification Improvement of Cardiovascular Risk-Prediction Model Comparisons, Using Electronic Health Data From HealthPartners, 2001–2011
| No. of Categories | Refitted FRS vs. Original FRS | Refitted PCE vs. Original PCE | Original PCE vs. Original FRS | Refitted PCE vs. Refitted FRS | ||||
|---|---|---|---|---|---|---|---|---|
| NRI | 95% CI | NRI | 95% CI | NRI | 95% CI | NRI | 95% CI | |
| 5a | −0.042 | −0.072, −0.001 | −0.006 | −0.042, 0.027 | −0.044 | −0.081, −0.008 | −0.006 | −0.037, 0.029 |
| 6 | −0.097 | −0.142, −0.055 | −0.027 | −0.069, 0.005 | −0.081 | −0.126, −0.046 | −0.007 | −0.038, 0.028 |
| 7 | −0.122 | −0.153, −0.081 | −0.047 | −0.077, −0.008 | −0.094 | −0.142, −0.050 | −0.002 | −0.029, 0.034 |
| 10 | −0.147 | −0.190, −0.103 | −0.062 | − 0.099, − 0.020 | −0.125 | −0.164, −0.087 | 0.002 | −0.033, 0.044 |
| 15 | −0.157 | −0.200, −0.120 | −0.069 | −0.108, −0.031 | −0.138 | −0.174, −0.087 | −0.006 | −0.037, 0.035 |
| 25 | −0.159 | −0.189, −0.126 | −0.068 | −0.116, −0.026 | −0.143 | −0.186, −0.103 | −0.006 | −0.036, 0.027 |
| Continuous | 0.116 | 0.077, 0.160 | −0.429 | −0.500, −0.349 | 0.107 | 0.075, 0.143 | 0.198 | 0.125, 0.270 |
Abbreviations: CI, confidence interval; FRS, Framingham Risk Score; NRI, net reclassification improvement; PCE, Pooled Cohort Equations.
a Indicates use of standard categories: 0%–2.5%, 2.5%–5%, 5%–7.5%, 7.5%–10%, and 10%–100%.
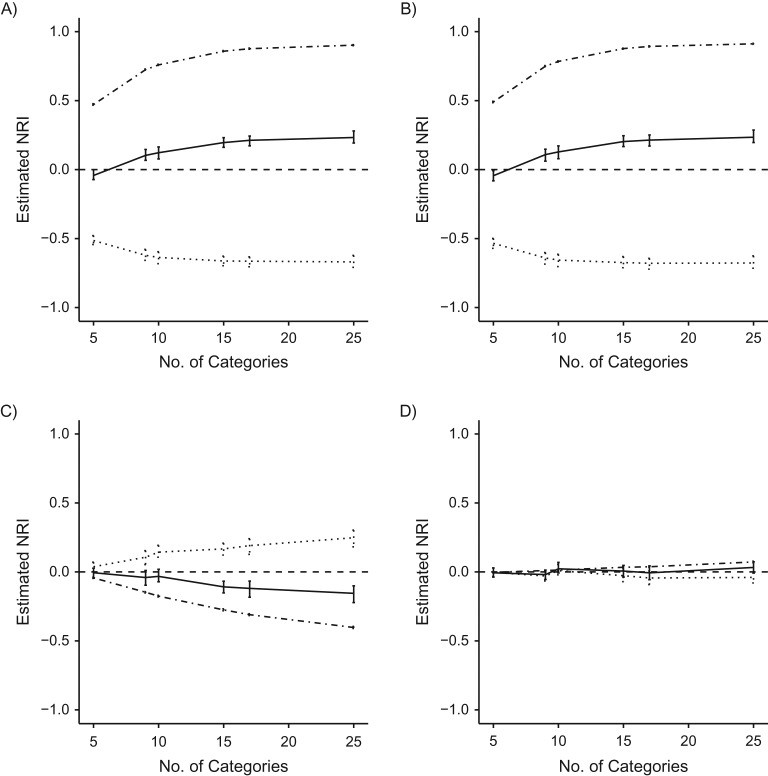
Results of increasing the number of categories by maintaining an upper limit for the highest cutoff at 10% and shrinking the size of the categories within that range are displayed in Figure 3 and Web Table 3. Comparing the refitted FRS to the original FRS, the NRI steadily increases as the number of categories increases, from −0.042 for the 5-category NRI to 0.233 when the 10% range is covered by categories of size 0.1%. Importantly, 95% confidence intervals for both values exclude zero, indicating that depending on the number of “internal” categories, we would draw different conclusions on the discriminative ability of the models. As the number of risk categories increases, the results contradict both the finding with fewer risk categories and the results in Table 1, where categories were increased using a different method. We compared the categorical NRI with a modified continuous NRI; as the number of categories increased, the categorical NRI approached the modified continuous NRI.
Figure 3.
Changing number of categories within 10% range of risk for estimated net reclassification improvement (NRI) for different model comparisons, using electronic health data from HealthPartners, 2001–2011. Nonevent NRI (dashed and dotted line), event NRI (dotted line), and overall NRI (solid line) are reported separately. A) Refitted Framingham Risk Score (FRS) versus original FRS; B) original Pooled Cohort Equations (PCE) versus original FRS; C) refitted PCE versus original PCE; D) refitted PCE versus refitted FRS. Bars: 95% confidence intervals.
Varying range of risk categories
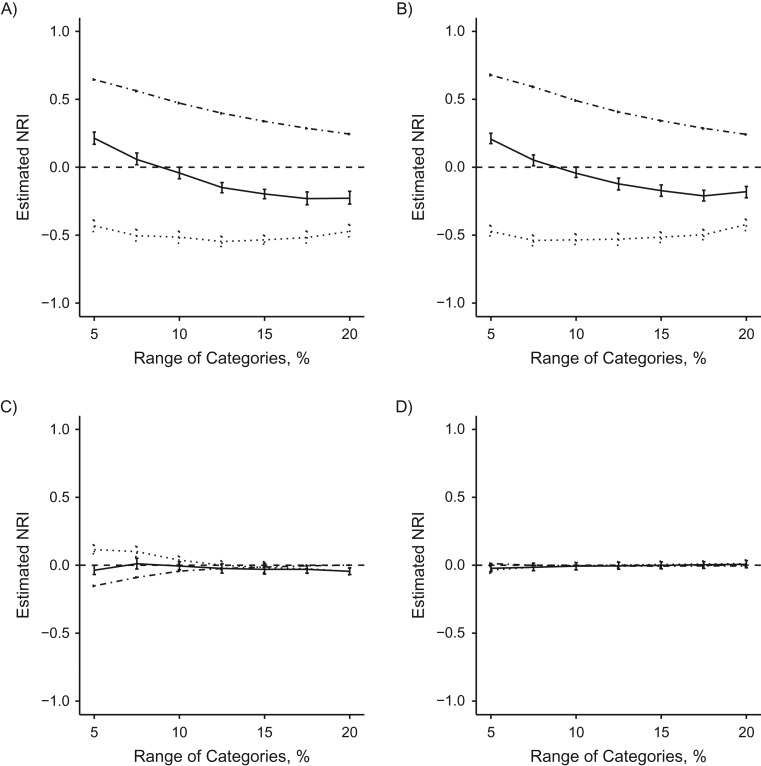
We also examined changes to the NRI when the number of categories remains constant while the range of the risk cutoffs is changed. The results of these changes are displayed in Figure 4 and Web Table 4. When the range of the risk categories was decreased from the standard 10%, the NRI indicated that the refitted FRS model better discriminated compared with the original FRS model. However, if the range of risk was increased, the opposite interpretation was observed. Increasing the range of risk cutoffs from 10% to 12.5%, a relatively small shift, caused large changes in the NRI. Model comparisons that included the original FRS, the most miscalibrated model, yielded the largest shifts in the NRI.
Figure 4.
Changing range of 4 evenly spaced risk categories for estimated net reclassification improvement (NRI) for different model comparisons, using electronic health data from HealthPartners, 2001–2011. Nonevent NRI (dashed and dotted line), event NRI (dotted line), and overall NRI (solid line) are reported separately. A) Refitted Framingham Risk Score (FRS) versus original FRS; B) original Pooled Cohort Equations (PCE) versus original FRS; C) refitted PCE versus original PCE; D) refitted PCE versus refitted FRS. Bars: 95% confidence intervals.
Minor changes to categories
We assessed the impact of minor changes to the risk categories on the NRI by individually cutting each of the standard categories in half while keeping the rest of the categories standard (Table 2). The original NRI value comparing the refitted and original FRS was −0.042; after cutting the first category in half, the NRI jumped to 0.115. Less substantial changes were seen when changes were made to other categories, likely due to the lower number of subjects that fall into those risk categories. Similar changes were seen comparing the refitted PCE and original FRS with the original PCE.
Table 2.
One Standard Category Modified at a Time for Overall Net Reclassification Improvement of Cardiovascular Risk-Prediction Model Comparisons, Using Electronic Health Data From HealthPartners, 2001–2011
| Modified Category | Refitted FRS vs. Original FRS | Refitted PCE vs. Original PCE | Original PCE vs. Original FRS | Refitted PCE vs. Refitted FRS | ||||
|---|---|---|---|---|---|---|---|---|
| NRI | 95% CI | NRI | 95% CI | NRI | 95% CI | NRI | 95% CI | |
| Nonea | −0.042 | −0.083, 0.001 | −0.006 | −0.034, 0.026 | −0.044 | −0.081, −0.008 | −0.006 | −0.032, 0.026 |
| 1.25%–2.5% | 0.115 | 0.078, 0.149 | −0.044 | −0.085, −0.008 | 0.117 | 0.068, 0.158 | −0.003 | −0.040, 0.030 |
| 3.75%–5% | −0.053 | −0.094, −0.010 | 0.002 | −0.040, 0.035 | −0.051 | −0.098, −0.004 | −0.010 | −0.037, 0.025 |
| 6.25%–7.5% | −0.045 | −0.079, −0.011 | 0.002 | −0.043, 0.034 | −0.044 | −0.078, −0.011 | −0.015 | −0.051, 0.019 |
| 8.75%–10% | −0.041 | −0.081, 0.005 | −0.019 | −0.050, 0.018 | −0.046 | −0.090, −0.004 | −0.010 | −0.031, 0.016 |
Abbreviations: CI, confidence interval; FRS, Framingham Risk Score; NRI, net reclassification improvement; PCE, Pooled Cohort Equations.
a Indicates use of standard categories: 0%–2.5%, 2.5%–5%, 5%–7.5%, 7.5%–10%, and 10%–100%.
Percentile-based NRI
A comparison of changes in the original NRI and the percentile NRI as the number of categories increases is displayed in Table 3. Using percentiles of risk distribution as opposed to absolute risk cutoffs led to more stable NRI predictions as the number of categories increased. In addition, the NRI was generally smaller than the standard NRI calculated using absolute risk categories. When comparing the refitted PCE and the refitted FRS, both well-calibrated models, changes were relatively small and none were statistically significant, as indicated by the confidence intervals. This leads to the interpretation that the 2 models are equally good at ranking the risk of patients.
Table 3.
Comparison of Original and Percentile-Based Net Reclassification Improvement for Cardiovascular Risk-Prediction Model Comparisons as Number of Categories Increases, Using Electronic Health Data From HealthPartners, 2001–2011
| No. of Categories | Original | Percentile | ||
|---|---|---|---|---|
| NRI | 95% CI | NRI | 95% CI | |
| Refitted FRS vs. Original FRS | ||||
| 5 | −0.042 | −0.072, −0.001 | 0.020 | −0.018, 0.045 |
| 10 | 0.122 | 0.077, 0.164 | 0.025 | −0.018, 0.067 |
| 15 | 0.196 | 0.161, 0.232 | 0.033 | −0.025, 0.085 |
| Refitted PCE vs. Original PCE | ||||
| 5 | −0.006 | −0.042, 0.027 | 0.015 | −0.012, 0.05 |
| 10 | −0.032 | −0.071, 0.019 | 0.008 | −0.028, 0.040 |
| 15 | −0.108 | −0.152, −0.068 | −0.024 | −0.082, 0.023 |
| Original PCE vs. Original FRS | ||||
| 5 | −0.044 | −0.081, −0.008 | 0.000 | −0.041, 0.033 |
| 10 | 0.128 | 0.079, 0.172 | 0.026 | −0.029, 0.075 |
| 15 | 0.203 | 0.167, 0.245 | 0.064 | 0.011, 0.106 |
| Refitted PCE vs. Refitted FRS | ||||
| 5 | −0.006 | −0.037, 0.029 | −0.009 | −0.029, 0.009 |
| 10 | 0.023 | −0.008, 0.069 | 0.015 | −0.015, 0.044 |
| 15 | 0.006 | −0.037, 0.047 | −0.010 | −0.049, 0.030 |
Abbreviations: CI, confidence interval; FRS, Framingham Risk Score; NRI, net reclassification improvement; PCE, Pooled Cohort Equations.
Additional categories were also added to the percentile-based NRI in the 85%–100% range, focusing on NRI performance in assessing reclassification in the riskiest 15% of patients. The increase in number of categories in the riskiest 15% led to overall small changes in the NRI, indicating that there was not a large increase in reclassification for high-risk patients as compared with the overall subject group. Results are displayed in Web Appendix 5.
DISCUSSION
Our results showed that the categorical NRI has serious shortcomings for comparing nonnested risk-prediction models. The NRI is highly sensitive to changes in the number of risk categories and the location of risk categories with respect to the absolute risk distribution. As a result, small changes in how risk is categorized can lead to opposing, statistically significant conclusions about which risk model is better at discrimination. The results of the continuous NRI often contradict those of the categorical NRI, adding doubt to the use of either. In addition, because the magnitude of the NRI does not directly correspond to a clinical scale, the degree of impact of the results can be difficult to assess.
Our results indicated that criticisms of the NRI in a nested context also apply to nonnested models. Mihaescu et al. (8) demonstrated that the NRI is sensitive to changes in the choice of risk cutoff when there are only 2 risk categories. The fact that the NRI gives different results when a single risk cutoff is varied is neither surprising nor inherently a bad feature. The predictive ability of a model may vary over the range of possible predictions, and the discriminative ability of a model may change as our definition of “high risk” changes. Our analysis more comprehensively assessed the impact of changing risk cutoffs in settings where multiple categories are used, a more realistic scenario in practice. The results indicated that even minor modification to one of multiple “internal” categories can alter the value of the NRI drastically. When at least 1 model was miscalibrated, as was the case for the original FRS model in our analysis, we found that changes to the cutoffs caused more extreme changes to the NRI. In addition, we found that when comparing the miscalibrated original FRS with the refitted FRS, the NRI yielded results indicating better performance by the original FRS, a concerning result given that after internal validation we expected the model performance to improve. Pepe et al. (11) have previously shown that in theoretical situations, large values of the NRI can be due in part to overfitting caused by poorly fitting risk models. We demonstrate here that similar outcomes are seen using real-world data; poorly fitting risk models can cause dramatic variation in values of the NRI. This is particularly relevant in the context of cardiovascular health, as several risk-prediction models have been shown to be systematically miscalibrated (25, 26).
The continuous NRI yielded results inconsistent with the categorical NRI; the 2 metrics often reported the opposite conclusion. By changing the number of categories used for the NRI in 2 different ways, we demonstrated that the categorical NRI approaches the continuous NRI as expected when the size of the categories is gradually decreased. In models with miscalibration, this occurs more rapidly. This supports previous research indicating that the continuous NRI may not be a good choice for analysis when models are miscalibrated (13).
We proposed the use of percentiles of the estimated risk distributions instead of absolute risk values to determine categories for use in calculating the NRI. The use of percentiles led to more stable NRI estimates that were much less sensitive to variation in the number of risk categories, even for comparisons involving miscalibrated models. Percentile-based risk cutoffs allow for more informative capturing of the up-classification and down-classification occurring between 2 risk-prediction models; an arbitrary choice in cutoffs of absolute risk may be too narrow or too wide to appropriately capture the difference. As demonstrated by our results, this is particularly applicable for miscalibrated models that may have skewed estimated risk distributions. Additional categories were also added in the 15% of patients with the highest CVD risk, a group medical professions may be especially concerned with; reclassification was found to be minimal for all models. It is important to note that accurate assessment of cardiovascular risk in intermediate-risk patients is especially important from both the population health and preventive medicine perspectives.
We assessed the performance of the time-to-event NRI in the specific context of comparing cardiovascular risk-prediction models using electronic health data. However, based on previous research and the wide variety of scenarios we considered, we believe that similar results would be found for the “classical” NRI with fully observed outcomes and when applying the NRI to risk prediction in a different clinical context. The time frame of our data limits us to studying a 5-year risk prediction, compared with the typical 10-year risk prediction.
The behavior of the NRI is often unstable in certain circumstances, and it should not be used as the sole tool for evaluation of model discrimination. In addition, it is important that model discrimination be assessed in conjunction with model calibration. When used with clinically relevant categories, the results of the NRI can be a valuable addition to analysis, consistent with prior recommendations (27). However, in many medical contexts, when a moderate number of risk categories (5 or more) is used, it is unlikely that each cutoff is clinically actionable. We have shown that even small changes to these internal cutoffs can lead to large differences in the NRI, indicating that the NRI should be used with caution. In these scenarios, the percentile-based NRI offers improved stability across differing choice in categories. In addition, because the percentile-based NRI is invariant to monotone transformations, it is a valuable tool in assessing discrimination when one or more models are miscalibrated. The percentile-based NRI should, therefore, be used in situations where 2 competing models predict slightly different health outcomes (as seen in the FRS and PCE). The percentile-based NRI illustrates the relative ability of 2 models to rank patient risk. The percentile-based NRI offers the same benefits in interpreting the relative discriminative ability between 2 models as the standard NRI, with improved stability in situations that are common when working in real-world situations.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Division of Biostatistics, School of Public Health, University of Minnesota, Minneapolis, Minnesota (Shannon B. McKearnan, Julian Wolfson, David M. Vock); and HealthPartners Institute, Minneapolis, Minnesota (Gabriela Vazquez-Benitez, Patrick J. O’Connor).
This work was funded by National Cancer Institute, National Institutes of Health (grants R01-CA214825 and R01-CA225190).
Conflict of interest: none declared.
Abbreviations
- CI
confidence interval
- FRS
Framingham Risk Score
- NRI
net reclassification improvement
- PCE
Pooled Cohort Equations
REFERENCES
- 1. Marshall T. Evaluating national guidelines for prevention of cardiovascular disease in primary care. J Eval Clin Pract. 2005;11(5):452–461. [DOI] [PubMed] [Google Scholar]
- 2. Manuel DG. Effectiveness and efficiency of different guidelines on statin treatment for preventing deaths from coronary heart disease: modelling study. BMJ. 2006;332(7555):1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Wilson PW, D’Agostino RB, Levy D, et al. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97(18):1837–1847. [DOI] [PubMed] [Google Scholar]
- 4. Goff DC Jr, Lloyd-Jones DM, Bennett G, et al. 2013 ACC/AHA guideline on the assessment of cardiovascular risk: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. J Am Coll Cardiol. 2014;63(25 Pt B):2935–2959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Pencina MJ, D’agostino RB Sr, D’agostino RB Jr, et al. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Stat Med. 2008;27(2):157–172. [DOI] [PubMed] [Google Scholar]
- 6. Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143(1):29–36. [DOI] [PubMed] [Google Scholar]
- 7. Leening MJ, Vedder MM, Witteman JC, et al. Net reclassification improvement: computation, interpretation, and controversies: a literature review and clinician’s guide. Ann Intern Med. 2014;160(2):122–131. [DOI] [PubMed] [Google Scholar]
- 8. Mihaescu R, van Zitteren M, van Hoek M, et al. Improvement of risk prediction by genomic profiling: reclassification measures versus the area under the receiver operating characteristic curve. Am J Epidemiol. 2010;172(3):353–361. [DOI] [PubMed] [Google Scholar]
- 9. Mühlenbruch K, Heraclides A, Steyerberg EW, et al. Assessing improvement in disease prediction using net reclassification improvement: impact of risk cut-offs and number of risk categories. Eur J Epidemiol. 2013;28(1):25–33. [DOI] [PubMed] [Google Scholar]
- 10. Kerr KF, Wang Z, Janes H, et al. Net reclassification indices for evaluating risk prediction instruments: a critical review. Epidemiology. 2014;25(1):114–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Pepe MS, Fan J, Feng Z, et al. The net reclassification index (NRI): a misleading measure of prediction improvement even with independent test data sets. Stat Biosci. 2015;7(2):282–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Cook NR, Paynter NP. Performance of reclassification statistics in comparing risk prediction models. Biom J. 2011;53(2):237–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Hilden J, Gerds TA. A note on the evaluation of novel biomarkers: do not rely on integrated discrimination improvement and net reclassification index. Stat Med. 2014;33(19):3405–3414. [DOI] [PubMed] [Google Scholar]
- 14. Pencina MJ, D’Agostino RB, Demler OV. Novel metrics for evaluating improvement in discrimination: net reclassification and integrated discrimination improvement for normal variables and nested models. Stat Med. 2012;31(2):101–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Siontis GC, Tzoulaki I, Siontis KC, et al. Comparisons of established risk prediction models for cardiovascular disease: systematic review. BMJ. 2012;344:e3318. [DOI] [PubMed] [Google Scholar]
- 16. Palmerini T, Caixeta A, Genereux P, et al. Comparison of clinical and angiographic prognostic risk scores in patients with acute coronary syndromes: analysis from the Acute Catheterization and Urgent Intervention Triage Strategy (ACUITY) trial. Am Heart J. 2012;163(3):383–391, 391.e1–5. [DOI] [PubMed] [Google Scholar]
- 17. Heng DY, Xie W, Regan MM, et al. External validation and comparison with other models of the International Metastatic Renal-Cell Carcinoma Database Consortium prognostic model: a population-based study. Lancet Oncol. 2013;14(2):141–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Chia YC, Lim HM, Ching SM. Validation of the pooled cohort risk score in an Asian population—a retrospective cohort study. BMC Cardiovasc Disord. 2014;14:163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. D’Agostino RB Sr, Vasan RS, Pencina MJ, et al. General cardiovascular risk profile for use in primary care: the Framingham Heart Study. Circulation. 2008;117(6):743–753. [DOI] [PubMed] [Google Scholar]
- 20. Wolfson J, Vock DM, Bandyopadhyay S, et al. Use and customization of risk scores for predicting cardiovascular events using electronic health record data. J Am Heart Assoc. 2017;6(4):e003670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Muntner P, Colantonio LD, Cushman M, et al. Validation of the atherosclerotic cardiovascular disease Pooled Cohort risk equations. JAMA. 2014;311(14):1406–1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. D’Agostino RB, Nam B-H. Evaluation of the performance of survival analysis models: discrimination and calibration measures. Handb Stat. 2003;23:1–25. [Google Scholar]
- 23. Harrell FE Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med. 1996;15(4):361–387. [DOI] [PubMed] [Google Scholar]
- 24. Pencina MJ, D’Agostino RB Sr, Steyerberg EW, et al. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat Med. 2011;30(1):11–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. DeFilippis AP, Young R, Carrubba CJ, et al. An analysis of calibration and discrimination among multiple cardiovascular risk scores in a modern multiethnic cohort. Ann Intern Med. 2015;162(4):266–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Blaha MJ. The critical importance of risk score calibration: time for transformative approach to risk score validation? J Am Coll Cardiol. 2016;67(18):2131–2134. [DOI] [PubMed] [Google Scholar]
- 27. Pencina MJ, D’Agostino RB, Pencina KM, et al. Interpreting incremental value of markers added to risk prediction models. Am J Epidemiol. 2012;176(6):473–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.