Universal Pre-Ejection Period Estimation Using Seismocardiography: Quantifying the Effects of Sensor Placement and Regression Algorithms

Abstract

Seismocardiography (SCG), the measurement of local chest vibrations due to the heart and blood movement, is a non-invasive technique to assess cardiac contractility via systolic time intervals such as the pre-ejection period (PEP). Recent studies show that SCG signals measured before and after exercise can effectively classify compensated and decompensated heart failure (HF) patients through PEP estimation. However, the morphology of the SCG signal varies from person to person and sensor placement making it difficult to automatically estimate PEP from SCG and electrocardiogram signals using a global model. In this proof-of-concept study, we address this problem by extracting a set of timing features from SCG signals measured from multiple positions on the upper body. We then test global regression models that combine all the detected features to identify the most accurate model for PEP estimation obtained from the best performing regressor and the best sensor location or combination of locations. Our results show that ensemble regression using XGBoost with a combination of sensors placed on the sternum and below the left clavicle provide the best RMSE = 11.6 ± 0.4 ms across all subjects. We also show that placing the sensor below the left or right clavicle rather than the conventional placement on the sternum results in more accurate PEP estimates.

I. Introduction

Heart failure (HF) is a disorder where the heart is unable to supply sufficient blood to the tissues and organs [1], and it affects nearly 6 million Americans [2], [3]. The annual health care costs for HF in the United States are almost $31 billion [4]. Nearly half of the overall costs associated with HF are due to hospitalizations, and thus there has been great interest in developing novel methods for monitoring patients with HF at home to potentially reduce hospitalizations and improve the quality of life and care for the patients.

Our group is investigating the use of wearable seismocardiogram (SCG) sensing as a means for extracting systolic time intervals in the context of activity for monitoring patients with HF at home. Specifically, we recently found that changes in the pre-ejection period (PEP) following a six-minute walk test (6MWT) exercise were significantly lower in decompensated versus compensated patients, thus indicating that the changes in PEP following exercise provide information related to the clinical state of patients with HF [5]. The PEP is the time elapsed between the electrical depolarization of the ventricular muscle and the ensuing opening of the aortic valve [6], and is a surrogate measure of cardiac contractility [7]. We posited that congested (i.e., decompensated) patients would have reduced myocardial reserve as compared to compensated patients, and thus would not be able to modulate PEP (i.e., contractility) sufficiently in response to the exercise stressor.

While these results in patients with HF were promising, an important limitation of SCG signals remains: SCG waveforms vary significantly from person to person which makes it difficult to accurately detect the “AO” (aortic valve opening) point, and thus extract an absolute measure of PEP (i.e., the R-AO interval). Figure 1 shows three example SCG waveforms from different subjects with simultaneously obtained impedance cardiogram (ICG) signals. Note that, while the standard approach based on the existing literature is to denote the AO point as the second main peak of the SCG signal following the R-wave of the electrocardiogram (ECG), this point does not occur concurrently with the “reference-standard” aortic valve opening point from the ICG signal (the B-point). For patients with HF, even greater variability is observed in the shape of the SCG waveform from person to person, thus motivating the need for improved methods for universal PEP estimation from SCG waveforms.

Fig. 1.

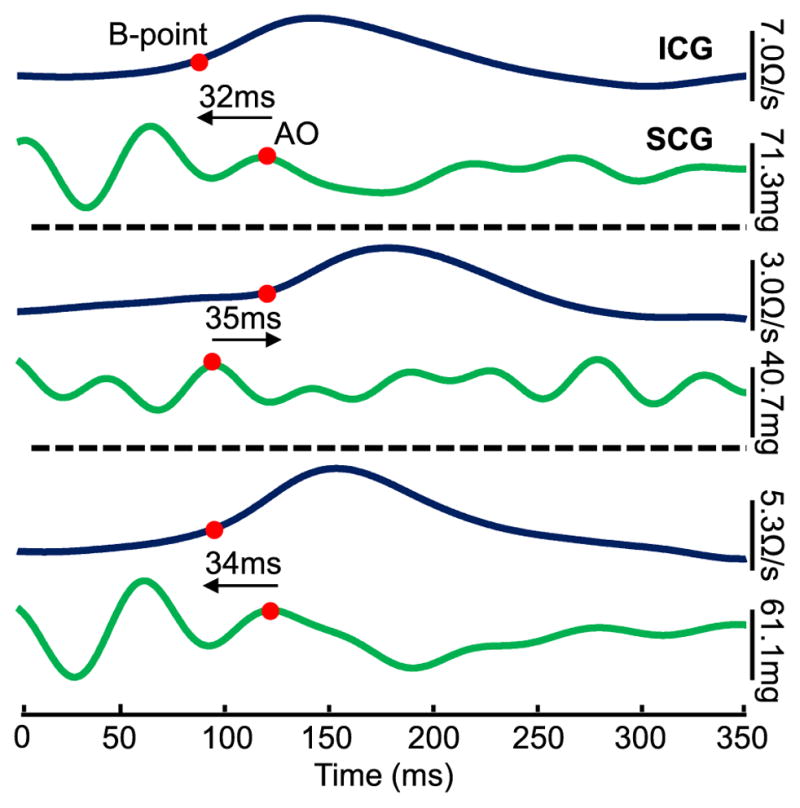
ICG and dorsoventral SCG ensemble averaged traces (n = 5 heartbeats) obtained with the sensor on the sternum for three different subjects. The ICG B-points and SCG AO-points are marked with red circles, and there is a substantial time difference between the two corresponding points for the three subjects: in two cases the ICG B-point occurs first, and in the third case the SCG AO-point occurs first.

In this proof-of-concept study, we set forth a novel approach to detecting the AO point from SCG recordings. Rather than searching for a single peak in the signal that corresponds to the aortic valve opening, we extracted multiple timing features from the SCG signal and combined all the detected features to create a universal regression model that predicts the relationship with the B-point in the ICG, across all subjects. We also quantified the effects of sensor location on the quality of PEP estimation to provide data-driven recommendations on optimal placement for minimizing PEP estimation error.

II. Methods

A. Protocol

The study was conducted under a protocol reviewed and approved by the Georgia Institute of Technology Institutional Review Board (IRB). All subjects provided written consent before experimentation. Data were collected from 10 healthy subjects, 5 males and 5 females (demographics: 23±3.3 years, 168.1±10.4 cm, 64.1±11.8 kg).

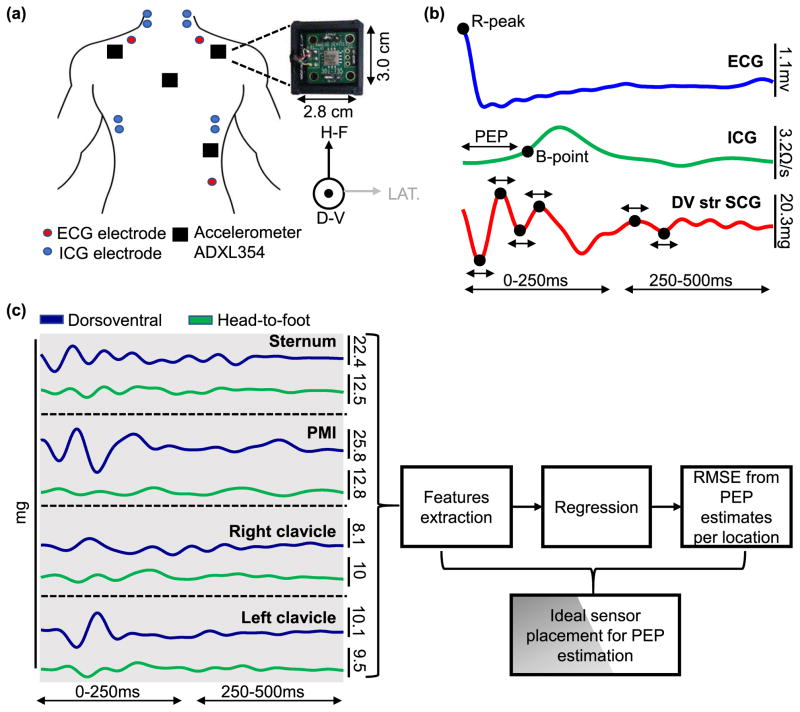
The experiment was divided into three parts with 15-minute breaks in between the parts. In each part of the experiment, the subject was asked to stand still for one minute, then perform a stepping exercise for one minute, to modulate changes in the subject’s physiological state (PEP decreases by approximately 30% and heart rate increases by approximately 60%), then stand still for five minutes (recovery). In part I, four accelerometers were placed on the subject: one on each of the mid-sternum (Str), point of maximum impulse (PMI), below the left clavicle (LC) and below the right clavicle (RC). In part II, two accelerometers were coupled with a rigid plastic mold that was placed on the sternum such that the sensors were on the upper sternum (US) and lower sternum (LS). Finally, in part III, one accelerometer was placed on a flexible silicone sheet which was placed on the sternum such that the accelerometer was on the mid-sternum (FStr). We also measured electrocardiogram (ECG) signals, whose R-peaks were used as timing references for beat segmentation, and ICG signals, whose B-points were used as the reference standard timing for aortic valve opening. Figure 2(a) shows the placement of the electrodes and accelerometers in part I of the experiment. The purpose of part I of the experiment was to determine the location or combination of locations for SCG that provide the best PEP estimates. Parts II and III in combination with the sternum-placed accelerometer from part I are used to determine the best interfacing method of the sensors with the body.

Fig. 2.

(a) The experimental setup for Part I of the experiment. Four ADXL354 Accelerometers are placed on the subject, one each at the mid-sternum, below the left and right clavicle, and at the point of maximal impulse. ICG and ECG signals are collected simultaneously. (b) Five beat ensemble averaged traces of ECG, ICG and mid-sternum dorsoventral SCG heartbeats. The ECG R-peak is used as a reference point for beat segmentation, the B-point of the ICG is used to detect aortic valve opening and the R-B interval is used as the ground truth PEP. Peak timing locations and width are extracted from the SCG signal as shown. (c) After extracting the features from the head-to-foot and dorsoventral axes of the SCG signals from all locations, a regression model is used to obtain PEP estimates from the features obtained from a single location, multiple combination of locations, one axis, and both axes. RMSE between the ground truth PEP and every estimate is calculated and the optimal location/ combination of location and axes is determined.

B. Hardware

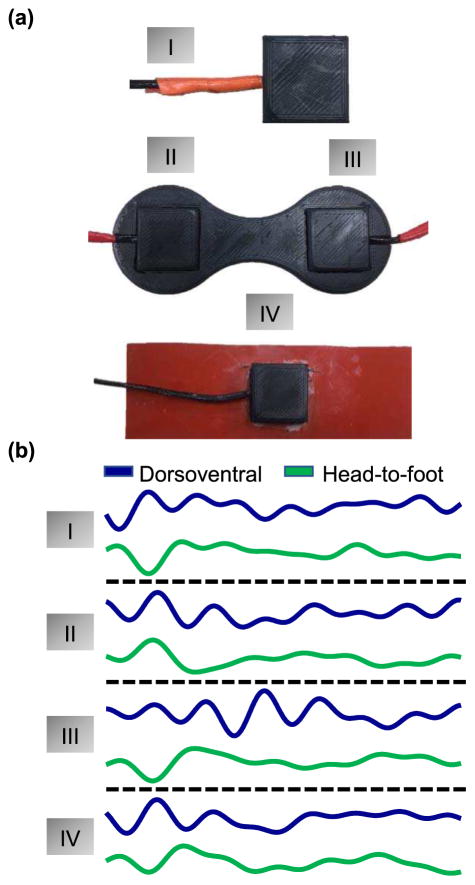
To measure SCG signals, ADXL354 low noise(approximately 0.7 mg_pp total noise for the measurement bandwidth used in this paper), low drift, low power 3-axis accelerometers were used. The accelerometers were placed in a plastic case 2.8 cm wide and 3 cm long (shown in Figure 2(a)). The outputs of the accelerometers were connected to the data acquisition system (MP150, BIOPAC System, Inc. Goleta, CA). For part II of the experiment, two of the ADXL354 accelerometers in the plastic casing were placed in a custom-made rigid acrylonitrile butadiene styrene(ABS) plastic mold that is 12.7 cm long with a 5.1 cm spacing between the accelerometers. For part III of the experiment, one of the accelerometers in the plastic casing was placed on a silicone rubber sheet with durometer of 50A (Shore Hardness Scale) and dimensions of 15.2 cm length, 5.1 cm width and 0.16 cm thickness. The different interfaces are shown in figure 3 (a).

Fig. 3.

(a) Different methods of interfacing the ADXL354 accelerometer with the sternum. (b) SCG signals obtained from each of the different interfacing materials.

To measure ECG and ICG, BN-EL50 and BN-NICO wireless modules (BIOPAC System, Inc. Goleta, CA) were used respectively then transmitted wirelessly into the MP150. All signals were sampled at 2 kHz.

C. Data Processing

The SCG, ICG and ECG signals were filtered with finite impulse response (FIR) Kaiser window band-pass filters (cutoff frequencies: 0.8–30 Hz for SCG, 0.8–35 Hz for the ICG and 0.8–40 Hz for the ECG) [8]. These cutoff frequencies preserve the waveform shape sufficiently to detect the necessary features while removing out-of-band noise. For each subject, the R-peaks in the ECG signal were detected as described in [9] and the minimum R-R interval was calculated. The R-peak timings were used as fiducial points to segment the remaining signals into heartbeats with a window length equal to the minimum R-R interval. The extracted heartbeats for each signal were then averaged together to obtain ensemble averages with reduced noise.

D. Feature Extraction

Every five beats from each of the SCG and ICG signals were averaged together to reduce the noise, and an overlap of four beats between consecutive ensemble averages was used to maximize the number of ensembles. This made up a total of 6084 ensemble averages across all 10 subjects.

The B-point (inflection point) of the ICG, which is the first derivative of the impedance time function (dz/dt), was extracted by detecting the maximum peak of the second derivative of the impedance time function [10]. The B-point is then used as the reference standard aortic valve opening, and the R-B interval was calculated for every ensemble average to obtain the ground truth PEP.

The following features were extracted from the z-axis (dorsoventral) and x-axis (head-to-foot) SCG ensemble averages from every location for all subjects: first and second maxima locations (0–250 ms), first and second maxima width (0–250 ms), first and second minima location (0–250 ms), first and second minima width (0–250 ms), first maximum location (250–500 ms), first maximum width (250–500 ms), first minimum location (250–500 ms), first minimum width (250–500 ms). Thus, a total of 12 features per axis for each sensor placement were extracted. We picked timing features from the early portion of the signal (0–250 ms) in order to captures events related to the aortic valve opening. Rather than calculating only the R-AO interval, we explored a number of peaks timings and widths as these timings might also be related to cardiac mechanics. Additionally, although it is the timing features from the systolic portion of the signals that are related to PEP, we decided to explore the diastolic portion as well by adding peak timings and widths from the later portion of the signals (250–500 ms). The features are illustrated in Figure 2(b).

E. Regression Model

To estimate the PEP using the features extracted from the SCG signals, we trained a regression model. For every accelerometer placement, M features extracted from N ensemble averages were placed in an N × M matrix X while the corresponding PEP values are placed in an N ×1 vector y_PEP. These were then used to train a regression model which learns the relationship between X and y_PEP. The learned model can then be used to estimate PEP for new heartbeats, given the features extracted from the SCG signals.

Many previous studies that utilize SCG signals to estimate hemodynamic parameters use linear regression to relate the SCG features to the estimated parameter [11]–[14]. However, it is possible that the relationship between PEP and SCG features is not necessary linear, as is often the case in real data sets [15]. Therefore, rather than using only linear techniques, we chose to exploit recent advances in the field of machine learning:specifically, in this work, we used Extreme Gradient Boosting (XGBoost) regression which is a relatively new algorithm that has recently gained popularity as it is a computationally efficient implementation of a powerful ensemble learning technique [16]. XGBoost is an implementation of the gradient boosting machine learning algorithm [17]. This falls under a category of learning algorithms called ensemble methods, which combines multitudes of estimators to predict a variable rather than using a single estimator [18]. We used the XGBoost library for Python to implement XGBoost [16]. It trains many regression trees iteratively, where new models predict the residual errors of previous ones and are then added together.

Specifically, let x be a vector containing all features extracted from one ensemble in our dataset. Let h (x) denote a regression tree, which partitions the feature space into pieces and assigns a constant to each partition [19]. XGBoost trains many regression trees h_m (x) in a consecutive manner, and adds them up such that the cumulative model f_m (x) at iteration m is:

$$f_m(\mathbf{x})=f_{m-1}(\mathbf{x})+\upsilon h_m(\mathbf{x})$$ (1)

h_m (x) is trained to predict the error residuals between f_m (x) and the target variable. The hyperparameter υ is referred to as the learning rate and has the effect of shrinking the contribution of each individual tree h_m (x), thus reducing the risk of overfitting [17]. Each regression tree is trained on a randomly sampled subset of the ensembles (rows of X) and features (columns of X). This introduces two hyper-parameters which are the factors by which the rows and columns of X are sampled.

Furthermore, while training the regression tree h_m (x), the weights assigned to each partition of the feature space are L₂ regularized using a regularization hyper-parameter λ. Row and column subsampling as well as regularization has been reported to increase model accuracy and decrease overfitting [16]–[19]. The final regression model f_Mb(x) emerges after M_b stages of iteratively applying equation (1), where M_b is referred to as the number of boosting rounds.

We used XGBoost regression to estimate PEP using SCG signals from different sensor locations. PEP results from different sensor locations were compared using a variation of the repeated cross-validation model assessment method discussed in [20].

Given that our dataset consists of 10 subjects, we first randomly paired these subjects into five groups. We then performed cross-validation by leaving one group (two subjects) out at each fold. At each fold of the cross-validation, we trained an XGBoost regressor on the data from all subjects except the ones that were left out. We predicted PEP for the left-out subjects and repeated this four more times to have PEP predictions for all ensembles from all subjects. We then calculated the root mean squared error (RMSE) between the estimated and ground truth PEPs. The entire process was repeated 50 times with a new random pairing of subjects each time. We calculated the cross-validation RMSE as the average of the RMSE scores from 50 repetitions. This approach was repeated for different SCG sensor locations and compared the resulting RMSE scores. We also combined pairs/ multiple combinations of sensor locations in order to explore which combination of two locations yields better PEP estimates. This was performed by combining features from a pair/ multiple sensor locations and running the cross-validation procedure for different pairs/ combinations of locations. We repeated this procedure using features only from the z-axis (dorsoventral), and both z+x axes combined (dorsoventral + head-to-foot). Single and multiple sensor comparisons were supported using statistical analysis of the cross-validation results which are described below in Section II.K. Using this approach, a global model was trained rather than multiple subject-specific models.

We performed this cross-validation procedure rather than using a leave one subject out cross-validation (LOSO-CV) to minimize the risk of overfitting the model to the dataset [21]. In LOSO-CV, only one subject is left out at each fold. Therefore, the training sets at each fold do not differ significantly. Leaving more subjects out leads to more variety in the training sets at each fold, and thus improves the generalizability of the resultant regression model. Additionally, there are many ways in which subjects can be grouped into pairs for leave two subjects out cross-validation. To mitigate dependency on this grouping, we repeat the cross-validation 50 times with different pairing at each repetition.

F. SCG Sensor Location Comparison

To compare different SCG sensor locations, we trained XGBoost regressors on SCG features acquired from the different locations on the body. We assessed the ability of a sensor location in estimating PEP by calculating the RMSE between the estimated PEP values (P Ê P)_i and the ground truth PEP acquired from the ICG signals (P E P_i ):

$$\mathit{RMSE}=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left({(P\widehat{E}P)}_i-PE{P}_i\right)}^2}$$ (2)

where N is the number of ensembles. Figure 2(c) shows a high-level block diagram of the process.

All XGBoost regressors trained for sensor location and axis comparison have the following hyper-parameter settings: learning rate=0.1, number of boosting rounds=200, column sampling factor=0.5, row sampling factor=0.5, regularization parameter (λ) = 1. These parameters were selected heuristically and the sensitivity of our results to them is analyzed in section III.D.

G. Rigid vs. Flexible Interfacing Material Between the SCG Sensor and Sternum

To compare different methods of interfacing the SCG sensor to the sternum, we calculated the cross-validation RMSE scores by repeating the procedure explained in Section II.E on signals acquired by placing the accelerometer (1) directly on the sternum; (2) placing two accelerometers on the upper and lower sternum using a rigid custom sensor housing; and (3) placing flexible material between the accelerometer and the skin. The process was repeated using only the z axis of the sensors and combining both z+x axes. For the rigid custom housing, we compared PEP estimates obtained using only the accelerometer placed on the upper sternum, only the lower sternum and combining both locations. Comparisons of different sensor interfacing methods were supported using statistical analysis as explain in section II.K. The SCG signals obtained from the different interfaces are shown in Figure 3(b).

H. Feature Importance Evaluation

While evaluating different SCG sensor locations and interfacing methods, we trained XGBoost regressors using many features acquired from one or multiple sensors and axes as shown in Figure 2(b)). However, only a portion of these features is relevant. The XGBoost regressor (like any other gradient boosting tree) trains regression trees which can be used to rank the features according to importance. Typically, the deep nodes of a tree divide using less important features while the main (first) node divides on the most important feature. The importance of features obtained from all trees are averaged resulting in the final relative feature importance scores, which can then be used to rank the features. Mathematical details of the feature importance scoring and ranking are explained in detail in [19].

To evaluate which features generated from the SCG signals were more relevant in estimating PEP, we trained an XGBoost regressor on the pair of sensor combination and axis that gave the best PEP estimates (left clavicle + sternum, z-axis). All data from every subject were used to train the regressor and the resulting model was used to generate relative feature importance scores as described above. It should be noted that no testing set is required to score feature importance as we are not evaluating generalizability of the model for this portion of the study.

I. Comparing Different Regression Techniques

We hypothesized that XGBoost regression would perform better than linear regression models as well as other non-linear regression models. To address our hypothesis, we compared results obtained using SCG sensors (z-axis only) placed on the left clavicle and sternum (sensor placement combination with lowest cross-validated RMSE) and XGBoost regression to the same sensor placement combination (same feature set) but using simple multiple linear regression. This method uses ordinary least squares [19] and is the regressor of choice for previous related work [11]–[14].

An extension of ordinary least squares regression is Ridge regression which penalizes regression coefficients by utilizing L₂ regularization to reduce overfitting [22]. This regression model is still linear but the L₂ regularization results in some coefficients to shrink, where the amount of shrinkage is controlled by a parameter α_ridge. Setting α_ridge = 0 is identical to ordinary least squares regression and coefficients are more heavily shrunk as α_ridge is increased. We assessed the performance of this regression technique as well on our dataset by training Ridge Regression models with α_ridge ranging from 10⁻³ to 10² logarithmically, keeping the feature and data set the same as explained above.

Another variant of ordinary least squares regression is Lasso Regression which uses L₁ regularization to shrink regression coefficients via a regularization parameter α_Lasso [23]. Compared to Ridge Regression (which utilizes L₂ regularization), Lasso tends to produce sparser linear models where many coefficients can be reduced to zero, which results in a form of feature selection. We also trained Lasso regressors on the same dataset varying α_lasso logarithmically from 10⁻³ to 10².

XGBoost is an ensemble method combining many base estimators [16]. Ensemble methods using regression tree estimators can fit complicated non-linear functions robustly, which might result in better estimations compared to linear models such as ordinary, Ridge, or Lasso regression. We compared XGBoost to two other ensemble regression methods: random forest regression and Extra-Trees regression.

Random forest regression like XGBoost trains many regression trees but unlike gradient boosting, each trained tree is independent. Trees are trained on a sample drawn with replacement and on a random subset of features [24]. Extra-Trees regression is similar to random forest regression but adds more randomness to the model.

While Random forest tree nodes are divided using the most discriminative threshold, in Extra Trees, a subset of thresholds is chosen for each feature and the best combination of these random splits are chosen [25]. We assessed the performance of Random forest and Extra-Trees regression on our dataset where regressors contain 200 trees and column sampling factor is chosen as 0.5 similar to XGBoost model parameters. Each tree was trained on a subset of features consisting of $\sqrt{n_{\text{features}}}$ features.

All these regression methods were implemented using scikit-learn library for Python [26]. We compared the cross-validated RMSE resulting from the different regression models using the cross-validation procedure explained in Section II.E. The features and dataset were kept the same and only the regression technique was altered.

J. Evaluating the Effect of XGBoost Hyperparameters

Our choice of XGBoost hyperparameters as explained in Section II.E was heuristic; however, variations of these parameters may alter results. An algorithm can be considered robust if changes in hyper-parameters do not alter the results greatly. Contrarily, if small perturbations in parameters cause large variations in results, the algorithm might not generalize well due to sensitive dependence on the choice of parameters.

We evaluated the dependence of results on the learning rate by varying this parameter on a logarithmic grid of 50 points ranging from 10⁻² to 10⁰. We evaluated the cross-validated RMSE as explained in Section II.E on the feature set derived from the SCG signals acquired from the left clavicle and sternum (z-axis), for each of 50 different learning rates, keeping everything else constant. We repeated this for 50 column sampling factor values on a linear grid from 0.1 to 1.0, 50 row sampling factor values on the same grid, and 50 regularization parameters (λ) on a logarithmic grid ranging from 10⁻² to 10¹. While varying each parameter, we set all other parameters constant at the values described in Section II.E.

K. Statistical Analysis

We performed statistical analysis on the cross-validated RMSE results to compare various SCG sensor locations. We performed leave two subjects out cross-validation 50 times and calculated RMSE for each repetition. In each of the 50 repetitions, the subjects were randomly paired, and this process was repeated for different sensor locations and combinations of locations. The random seed was fixed so that in the j^th repetition, the subjects were paired in the same way for all sensor locations/combinations. RMSE results from the 50 repetitions were compared using multiple comparison statistical testing for different locations and combinations. The Friedman Test was used to detect if any differences exist. For post-hoc testing, Wilcoxon signed rank test was performed on pairs of sensor locations / combinations to be compared. Benjamini-Hochberg correction for multiple comparison was performed on the p-value from the post-hoc testing. These statistical tests and the reasons they should be used to compare machine learning models are discussed in detail in [27]. A similar procedure was followed to compare different sensor interfacing methods statistically. P-values below 0.05 were considered statistically significant.

III. Results

A. Comparison of Different Sensor Locations

Results comparing RMSE in milliseconds (ms) from the SCG signals obtained from accelerometers placed on sternum, PMI, below the left clavicle and below the right clavicle, and every combination of these accelerometers for both the dorsoventral (z-axis) and the head-to-foot combined with the dorsoventral axis (z+x) are shown in Table I. Statistically significant differences exist in these results according to Friedman test (P<0.05). To investigate where the significance exists, Wilcoxon signed rank test was performed on the different pairs of locations/combination of locations.

TABLE I.

RMSE (MS) for PEP Estimates From SCG Signals Measured From Sensors Placed in Different Locations (Str, PMI, LC, RC)

Location	z-axis RMSE	z+x axes RMSE
Str	16.4±0.7	16.3±0.6
PMI	17.1±0.6	17.5±0.6
LC	13.4±0.4	12.4±0.5
RC	13.2±0.4	13.4±0.4
Str+PMI	14.6±0.5	15.3±0.6
Str+LC	11.6±0.4	12.0±0.6
Str+RC	13.6±0.6	14.1±0.5
PMI+LC	13.1±0.5	12.6±0.5
PMI+RC	13.0±0.3	13.8±0.5
LC+RC	12.0±0.5	12.4±0.5
Str+PMI+RC	13.3±0.4	13.7±0.5
Str+PMI+LC	12.0±0.4	11.9±0.3
Str+RC+LC	12.0±0.4	12.4±0.5
siliPMI+RC+LC	12.2±0.5	12.8±0.5
Str+PMI+LC+RC	11.8±0.4	12.4±0.4

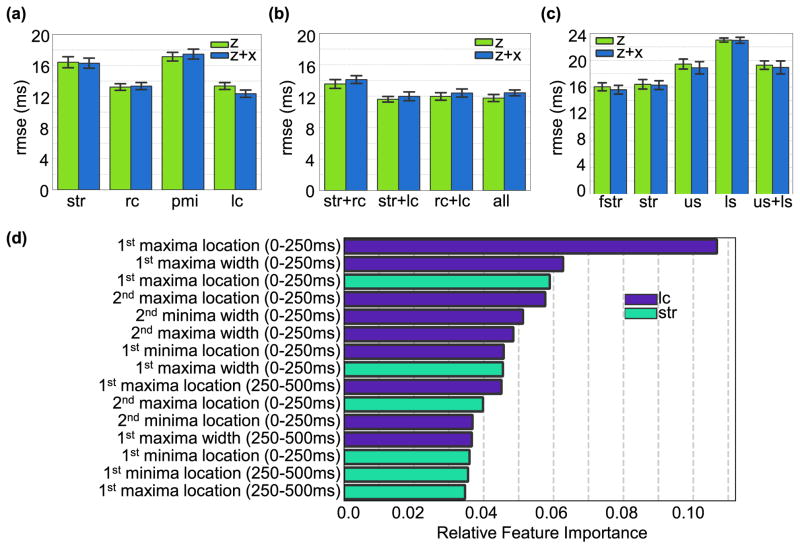
When comparing single locations, results showed that the z-axis of the signals from the sensors placed below the left and right clavicle provided the least RMSE in PEP estimates with 13.4±0.4 ms and 13.2±0.4ms respectively (Figure 4(a), P<0.05 according to the Wlicoxon signed rank test comparing RC and LC to sternum and PMI). Additionally, features from head-to-foot SCG did not add substantial information to dorsoventral SCG features for all the signals except LC SCG, whose RMSE improves from 13.4±0.4ms to 12.4±0.5ms by combining the dorsoventral and head-to-foot features (P<0.05 according to Wilcoxon signed rank).

Fig. 4.

(a). RMSE from PEP estimated from features obtained from accelerometers placed on the sternum (Str), below the right clavicle (RC), point of maximal impulse (PMI), and below the left clavicle (LC)for both the dorsoventral axis (z-axis) and head-to-foot and dorsoventral axes combined (z+x axes). (b) RMSE from PEP estimated from features obtained from the best performing combination of accelerometer locations. It can be observed that adding more sensors does not substantially reduce the error obtained using one sensor below the left or right clavicle. (c) RMSE from PEP estimated from accelerometers placed on the sternum with different interfacing techniques: in the middle of a silicone rubber sheet placed along on the sternum (fstr), directly on the sternum (Str), and two accelerometers coupled by a rigid plastic mold and placed on the upper sternum (US) and lower sternum (LS). (d) Ranking of best 15 features obtained from the combination of sensors and axis that rendered the lowest RMSE (Str+LC axis z).

When combining features from signals from multiple locations, the best performing combination was the dorsoventral SCG from the sternum and LC with RMSE=11.6±0.4ms (P<0.05 with every single location and combination except the combination of all sensors z-axis, Wilcoxon signed rank). Adding features from other locations and axes to the z-axis of these two locations did not improve the estimation (Figure(4(b)). This best combination of signals (sternum+LC z-axis) was used in the feature importance analysis as described in Section II.H. The results show that the timing of the first maximum of the dorsoventral LC SCG signal (0–250 ms) is the most important feature used in the XGBoost trees. Out of the top 15 features, nine features belonged to the LC SCG signals and six belonged to the sternum SCG signal. The top 15 features are shown in Figure 4(d).

B. Comparison of Different Sensor Interfacing Materials

Results comparing RMSE in ms from SCG signals obtained from accelerometers placed on the sternum directly (Str), using a flexible silicone rubber sheet (FStr), and using a rigid plastic mold coupling two accelerometers on upper and lower sternum (US and LS) are shown in Figure 4(c). Statistically significant differences exist in these results according to Friedman test (P<0.05). To investigate where the significance exists, Wilcoxon signed rank test was performed on the different pairs of interfacing methods.

Placing the accelerometer on the flexible silicone rubber sheet rather than directly on the sternum did not reduce the accuracy of the PEP estimates obtained from the SCG signals compared to placing the accelerometer directly on the sternum and even slightly improved it (16.0±0.6 ms vs. 16.4±0.7 ms respectively for the z-axis, P<0.05, Wilcoxon signed rank test; and 15.6±0.6 ms vs. 16.3±0.6 ms respectively for the z+x axes, P<0.05, Wilcoxon signed rank test). On the other hand, coupling the accelerometers using a rigid mold significantly reduced the accuracy of the PEP estimates obtained from these signals even when features from both accelerometers placed on the upper and lower sternum were combined (P<0.05 when compared to str and fstr, Wilcoxon singed rank test).

C. Comparison of Different Regressors

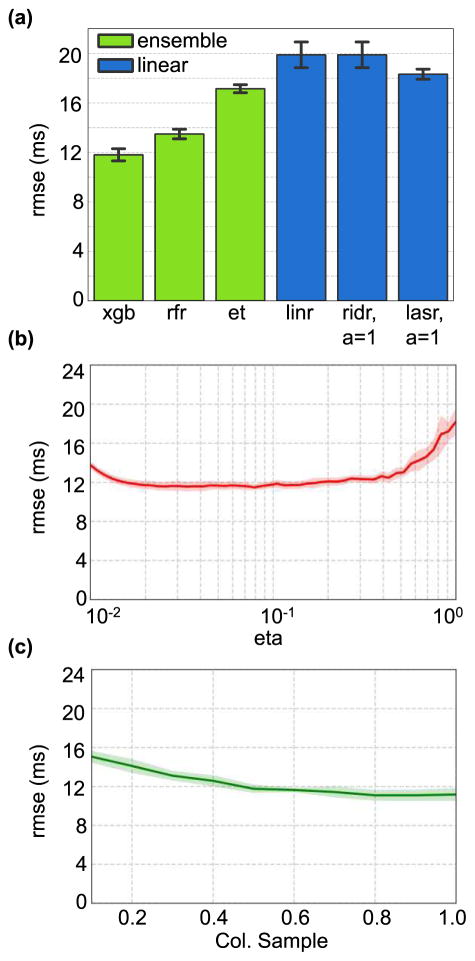
When different regression techniques were compared keeping the feature set the same, it was observed that XGBoost produced the lowest RMSE as expected (Figure 5(a), P<0.05 according to Friedman test and P<0.05 when comparing XGBoost to all other regressors, Wilcoxon singed rank test). Compared to XGBoost, ordinary least squares regression resulted in an RMSE that was 8ms higher. Introduction of L₂ regularization via Ridge regression does not improve linear regression results. Figure 5(a) shows results only for α_ridge = 1, but results did not alter substantially for the range of α_ridge values tested. L₁ regularization via Lasso regression improves linear regression RMSE results by around 2ms (P<0.05, Wilcoxon singed rank test), however, this is still substantially greater error than corresponding results using XGBoost.

Fig. 5.

(a). Comparing RMSE for PEP estimates obtained using ensemble regression models vs. linear regression models on features obtained from SCG signals that performed best with XGBoost (i.e., LC+sternum z-axis). (b) RMSE for PEP estimates obtained using XGBoost on features obtained from LC+sternum z-axis while varying the learning rate parameter (c) RMSE for PEP estimates obtained using XGBoost on features obtained from LC+sternum z-axis while varying the column sample parameter. The shaded regions in parts (b) and (c) indicate the standard deviation since the cross-validation is repeated 50 times.

In Figure 5(a), ensemble learning methods have been highlighted in green while linear methods are shown in blue. As hypothesized, ensemble methods produce lower RMSE when compared to generalized linear methods. Out of the ensemble methods, we find that random forest regression performs better than Extra-Trees regression (P<0.05, Wilcoxon signed rank test), while XGBoost maintains the best performance.

D. Effect of XGBoost Hyperparameters

Figure 5(b) shows the variation in cross-validated RMSE as the learning rate is varied. The variations in RMSE for learning rates in the range 2×10⁻² to 4×10⁻¹ is minimal. However, learning rate must not be increased or decreased too much, as values above 0.4 and below 2×10⁻² lead to deterioration in RMSE.

Figure 5(c) shows the effect of varying the column sampling factor on the RMSE. It can be seen that for values between 0.4 and 1.0, the variation in RMSE is minimal but for values below 0.4, RMSE deteriorates.

We also investigated the effect of varying the row sampling factor and the regularization parameter on RMSE as discussed in Section II. J. Varying these parameters within the ranges explained in Section II.J lead to nearly no changes in RMSE (<1 ms change in RMSE).

IV. Discussion

Our universal regression model showed, for the first time, that SCG signals collected from below the left or right clavicle provide better PEP estimates than those collected from the sternum. This suggests that SCG signals obtained from below the left or right clavicle are more representative of entire body displacement than SCG signals obtained from the sternum. Additionally, when examining the top features from the best combination of signals (sternum+LC), most top features were from LC SCG rather than from sternum SCG, which can be attributed to the fact that LC performs better than the sternum in terms of PEP estimation error for our dataset. Although we are more interested in how PEP changes in response to activity than in obtaining absolute values of PEP, according to the findings in [5], our assumption is that the better accuracy we can obtain in absolute PEP measurements, the better we can track its changes.

Beyond providing insight into sensor placement, the regression models differentiated the effects of different interfacing methods. Finding that SCG obtained from placing the sensor on a silicone rubber sheet performs as well, and even slightly better, in PEP estimation than SCG obtained from placing the sensor in direct contact with the skin could be an indication that the sensor can be worn over a thin layer of clothing(tightly fitted over the body to ensure good coupling of the sensor to the skin) without affecting the measurements. This is an important finding that supports the practicality of a wearable SCG device, and warrants further investigation.

Furthermore, we demonstrated in this paper that the relation between the extracted features and PEP is better characterized by non-linear models rather than linear ones. Ensemble methods, were shown to model non-linear relationships between the predictors and PEP well [18]. Ensemble methods also attempt to perform automatic feature selection by picking random subsets of the whole feature set which might be more effective than intrinsic feature selection using L1 or L2 regularization [19], [24]. In general, ensemble learners produce powerful estimators as they combine a diverse set of models. Each regression tree in the ensemble is built by randomly subsampling instances and features. A committee of these models is robust (reduced variance) and generalizes well [23].

From the examined linear regression methods, introducing L1 regularization via Lasso regression slightly improved the linear regression while L2 regularization via Ridge regression did not. This can be attributed to the fact that there is a large number of features and L1 regularization produces better intrinsic feature selection (via shrinkage) than anL2 penalty. On the other hand, from the examined ensemble regression methods, Extra-Trees regression performing worse than random forest regression can be linked to the increased randomness in determining tree node division thresholds in Extra-Trees which might account for the degradation in performance. Finally, XGBoost performed best possibly because each tree in the ensemble is iteratively trained according to the prediction errors of previous trees, whereas the other methods train independent trees. XGBoost also regularizes each tree in the ensemble to improve generalization and reduce overfitting, which is not performed in random forests or Extra-Trees.

A drawback of XGBoost compared to the other techniques considered is the abundance of hyperparameters to tune. However, the performance was found to be robust to changes in hyperparameters as variations in the regularization parameter row sampling factor, and in learning rate even by an order of magnitude caused infinitesimal variation in RMSE. Large values of the learning rate mean that each tree in the gradient boosting ensemble contribute more to the model which reduces the regularization effect, rendering the trained model more prone to overfitting. On the other hand, as the learning rate is decreased, each tree’s contribution decreases and in the extreme of a null learning rate, the consecutive trees do not contribute to the mode at all, meaning the gradient boosting is no longer performed. Therefore, a learning rate value > 0.4 or <2×10⁻² resulted in deterioration in RMSE. Finally, when varying the column sampling factor, values below 0.4 worsened the RMSE, because as the column sampling factor decreases, increasingly smaller subsets of the features space are used to train each tree in the ensemble.

In general, our method was robust to changes in hyperparameters, and thus we did not perform any hyperparameter tuning. While hyperparameter tuning via extensive grid search or random search can likely lead to improvement in RMSE, this approach would also be very time consuming and computationally expensive. Robustness to variations in the hyperparameters also means that the gains due to tuning might be relatively small compared to gains due to better sensor positioning.

V. Conclusion and Future Work

In this paper, we developed universal regression models to estimate PEP from SCG signals measured from multiple locations and compared the outputs of the resulting regression models by calculating the RMSE between the estimated PEP values with the ground truth PEP values obtained from ICG. We demonstrated that ensemble regression models provide significantly more accurate PEP estimates than linear regression models. Additionally, in our dataset, we showed, for the first time, that placing an accelerometer below the right or left clavicle results in better PEP estimates than placing the accelerometer on the sternum, which is the common placement in the SCG literature. Finally, we showed that placing the sensor on a flexible silicone rubber sheet rather than directly on the skin does not reduce the accuracy of the measurements which suggests that the wearable SCG sensing device can be placed over a thin layer of clothing without deteriorating its performance.

Future work should include analyzing SCG signals obtained from placing the sensor on different fabrics to verify that the SCG wearable device can be placed over clothes. More subjects should be included in future studies to be able to leave more subjects out during the model training, and hyperparameter tuning should be performed to minimize RMSE. Additionally, these subjects should include both healthy subjects as well as patients with various cardiovascular diseases. Finally, the same approach used in this paper can be used to estimate other cardiac parameters such as left ventricular ejection time which, with PEP, can provide us with a measure of changes in cardiac performance.

Biographies

Hazar Ashouri received her B.E. in electrical and computer engineering from the American University of Beirut, Lebanon, in 2013, and the M.S. and Ph.D. degrees in electrical and computer engineering from the Georgia Institute of Technology, Atlanta, GA, USA in 2016 and 2017, respectively.

She is currently a Postdoctoral Researcher in Inan Research Lab, Department of Electrical and Computer Engineering, Georgia Institute of Technology. Her research interests include cardiomechanical signals, non-invasive physiological sensing and modulation, signal processing, and machine learning.

Sinan Hersek received the B.S. in electrical and electronics engineering from Bilkent University Ankara, Turkey, in 2013, and the M.S. and Ph.D. degrees in electrical and computer engineering from the Georgia Instititue of Technology, Atlanta, GA, USA, in 2015 and 2017, respectively.

During his senior undergraduate year, he worked on developing digitally controlled, efficient, on-coil power amplifiers for MRI systems in the National Magnetic Resonance Research Center, Bilkent University. The same year he worked as a Part-Time Engineer with ASELSAN (Turkish Military Electronic Industries, Ankara, Turkey), in the radar and electronic warfare systems business sector. He is currently a Postdoctoral Researcher in the Gerogia Institute of Technology, Department of Electrical and Computer Engineering. His research interests include analog electronics, embedded systems, wearable device design, signal processing, and machine learning.

Omer T. Inan (S’06, M’09, SM’15) received the B.S., M.S., and Ph.D. degrees in electrical engineering from Stanford University, Stanford, CA, in 2004, 2005, and 2009, respectively.

He joined ALZA Corporation (A Johnson and Johnson Company) in 2006, where he designed micropower circuits for iontophoretic drug delivery. In 2007, he joined Countryman Associates, Inc., Menlo Park, CA where he was Chief Engineer, involved in designing and developing high-end professional audio circuits and systems. From 2009–2013, he was also a Visiting Scholar in the Department of Electrical Engineering, Stanford University. Since 2013, Dr. Inan is an Assistant Professor of Electrical and Computer Engineering at the Georgia Institute of Technology. He is also an Adjunct Assistant Professor in the Wallace H. Coulter Department of Biomedical Engineering. His research focuses on non-invasive physiologic sensing and modulation for human health and performance, including for chronic disease management, acute musculoskeletal injury recovery, and pediatric care.

Dr. Inan is an Associate Editor of the IEEE Journal of Biomedical and Health Informatics, Associate Editor for the IEEE Engineering in Medicine and Biology Conference and the IEEE Biomedical and Health Informatics Conference, Invited Member of the IEEE Technical Committee on Translational Engineering for Healthcare Innovation and the IEEE Technical Committee on Cardiopulmonary Systems, and Technical Program Committee Member or Track Chair for several other major international biomedical engineering conferences. He has published more than 100 technical articles in peer-reviewed international journals and conferences, and has multiple issued patents. Dr. Inan received the Gerald J. Lieberman Fellowship in 2008-’09 for outstanding scholarship, the Lockheed Dean’s Excellence in Teaching Award in 2016, and the Sigma Xi Young Faculty Award in 2017. He was a National Collegiate Athletic Association (NCAA) All-American in the discus throw for three consecutive years (2001–2003).