Coordination of receptor tyrosine kinase signaling and interfacial tension dynamics drive radial intercalation and tube elongation

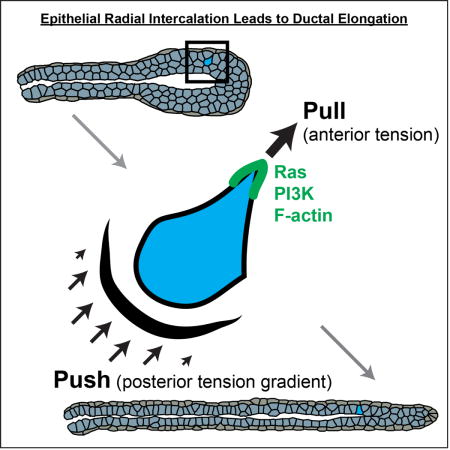
SUMMARY

We sought to understand how cells collectively elongate epithelial tubes. We first used 3D culture and biosensor imaging to demonstrate that epithelial cells enrich Ras activity, PIP3, and F-actin to their leading edges during migration within tissues. PIP3 enrichment coincided with, and could enrich despite inhibition of, F-actin dynamics, revealing a conserved migratory logic compared to single cells. We discovered that migratory cells can intercalate into the basal tissue surface and contribute to tube elongation. We then connected molecular activities to subcellular mechanics using force inference analysis. Migration and transient intercalation required specific and similar anterior-posterior ratios of interfacial tension. Permanent intercalations were distinguished by their capture at the boundary through time-varying tension dynamics. Finally, we integrated our experimental and computational data to generate a finite element model of tube elongation. Our model revealed that intercalation, interfacial tension dynamics, and high basal stress are together sufficient for mammary morphogenesis.

eTOC blurb

Neumann et al. demonstrate that the spatial asymmetries and molecular logic of migration are conserved between epithelial cells within mammalian tissues and single cells on flat substrates. Force inference techniques and finite element modeling further define a set of mechanical properties and cell behaviors, including radial intercalation, that elongate tubes.

INTRODUCTION

Epithelial tubes are a fundamental building block of metazoan organs and their diverse structures enable respiration, secretion, and absorption. The anatomy of epithelial tissues is well defined and many genes have been identified as required for their morphogenesis (Andrew and Ewald, 2010; Costantini and Kopan, 2010; McNally and Martin, 2011). Yet, it has remained challenging to connect molecular activities to cell behaviors to tissue organization. A major barrier has been the relative inaccessibility of mammalian epithelial organs during development. While intravital imaging has been achieved in multiple organs (Masedunskas et al., 2011; Scheele et al., 2017), both real-time analysis and mechanical manipulations remain challenging in vivo compared to 2D culture. In response, organoid and whole organ culture techniques have been developed across organs to enable cellular and molecular analysis of epithelial development (Shamir and Ewald, 2014).

We focus on the mammary gland due to its large scale of tube elongation, postnatal development, and iterative cycles of branching (Sternlicht, 2006; Sternlicht et al., 2006). The first epithelial tubes in the mammary gland sprout from an embryonic placode and elaborate subtly during fetal development to form a rudimentary network (Hogg et al., 1983). These initial structures are apico-basally polarized, connected by extensive junctions, and composed of an inner layer of luminal epithelial cells and an outer layer of contractile myoepithelial cells. Rising steroid hormone levels at the onset of puberty induce the formation of a stratified terminal end bud (TEB) at the end of each duct (Hinck and Silberstein, 2005; Williams and Daniel, 1983). The TEB is the major site of proliferation (Hinck and Silberstein, 2005), its cells have few junctions and reduced polarity (Ewald et al., 2012), and morphologies within the end bud are consistent with motility (Ewald et al., 2008; Huebner et al., 2016; Paine et al., 2016). Yet, it remains unclear how cells within the TEB accomplish elongation or how its multiple luminal epithelial layers resolve to a single layer to polarize the tissue (Ewald et al., 2012).

Paradigms for motile cellular systems emerged from study of isolated cells migrating on rigid substrates (Lauffenburger and Horwitz, 1996). The model for chemotaxis that emerges from the study of Dictyostelium leads from signaling to the cytoskeleton to force generation to migration (Artemenko et al., 2014; Shi et al., 2013). Specifically, molecular asymmetries in PI3K activity lead to actin polymerization, extension of a leading edge, and directional migration (Zhu and Nelson, 2013). This model has been extended to mammalian neutrophils (Devreotes and Horwitz, 2015) but it is was unclear whether the migration of cells within an epithelium followed a similar logic.

The mechanical environment a cell encounters as it migrates between other cells within a tissue is quite different from that encountered by a cell migrating over a 2D surface. Accordingly, we sought to understand how these mechanical constraints regulated cell migration. Conventional mechanical perturbations, such as optical tweezers or pipette pulling, are difficult to deploy within a tissue that is itself embedded within a thick extracellular matrix gel. We therefore used force inference techniques from civil engineering to acquire information on the mechanical relationships among cells in the tissue, based on 3D images of cell-cell interfaces. We previously demonstrated that cell movements within tissues are regulated by tensions at cell and tissue interfaces (Brodland, 2002, 2004; Chen and Brodland, 2000).

In the present study, the observed cell movements and inferred mechanical relationships were used to inform finite element (FE) models. These models were then applied to test the plausibility of different cellular mechanisms of elongation. Our overarching goal was to determine how cells collaborate to elongate epithelial tubes. We first tested whether cell motility within a tissue utilized similar molecular asymmetries and followed a similar logic as migrations of individual cells over 2D surfaces. We next asked how migration within a tissue was regulated mechanically and leveraged these analyses to demonstrate that intercalation can couple cell migration to tissue elongation. Finally, we used FE modeling to test the sufficiency of distinct cell behaviors and properties to drive mammary morphogenesis. The experiments, force inference analysis, and FE modeling proceeded in an iterative fashion, with data informing modeling choices and modeling results driving the design of new experiments.

RESULTS

Epithelial Cells Display a Migratory Molecular Polarity as they Move within Tissues

The major polarity axis in quiescent simple epithelia is apico-basal, typified by apical enrichment of Par3 and basolateral enrichment of Scribble (Ewald et al., 2012; Huang and Muthuswamy, 2010). Single cells migrating on top of 2D substrates instead organize a front-rear polarity axis, typified by localization of Ras, PIP3, and F-actin to the leading edge (Devreotes and Horwitz, 2015). We previously developed techniques to label and image individual cells within branching organoids (Ewald et al., 2012; Huebner et al., 2016). It was clear that apico-basal polarity was greatly reduced in the stratified region of a mammary end bud (Ewald et al., 2012) and both cytoplasmic and membrane deformations suggesting cell migration within the tissue (Huebner et al., 2016). However, it was not known whether these deformations were accompanied by front-rear asymmetries in Ras, PI3K, and F-actin or whether they required these pathways for motility (Figure 1A).

Figure 1. Migratory epithelial protrusions enrich Ras activity, PI3K activity, and F-actin polymerization.

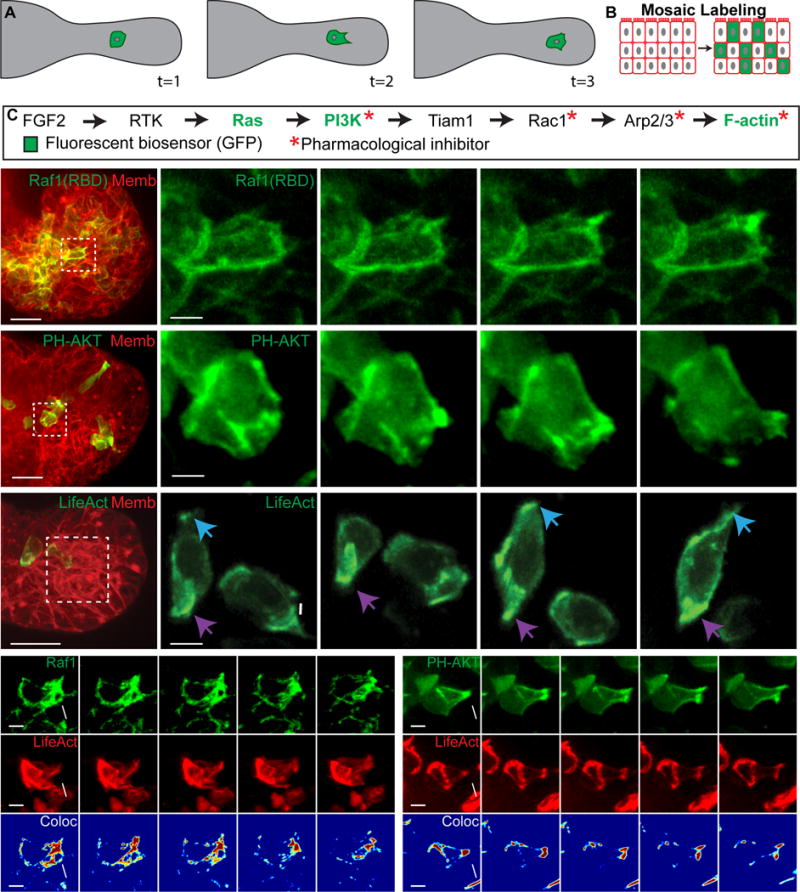
(A) Schematic of cell migration within an organoid branch.

(B) Organoids are labeled mosaically with GFP biosensors.

(C) Receptor tyrosine kinase pathway indicating biosensors and inhibitors used.

(D–H) 3D confocal projections of cells migrating within organoid branches (0.137 μm Gaussian blur, all channels).

(D) A migratory cell enriches Ras activity to a new protrusion (white arrow) (Raf1(RBD)-GFP, green; membrane, red). N=210 cells,16 orgs, r=3. Scale, 20 μm (5 μm inset).

(E) A migratory cell enriches PI3K activity to a new protrusion (PH-Akt-GFP, green; membrane, red). N=150 cells, 10 orgs, r=3. Scale, 20 μm (5 μm inset).

(F) Migratory cells enrich F-actin to new protrusions (white and blue arrows) and display posterior enrichment of F-actin (purple arrows) (LifeAct-GFP, green; membrane, red). N=176 cells from 73 orgs, r=4. Scale, 20 μm (5 μm inset).

(G) A migratory cell enriches (H) Ras activity and (H′) F-actin within a protrusion (Raf1(RBD)-GFP, green; LifeAct-RFP, red). (H″) Colocalization channel of Raf1(RBD) and LifeAct (Jet look up table). N=74 cells, 19 orgs, r=3. Scale, 5 μm.

(H) An intercalating cell enriches (G) PIP3 and (G′) F-actin within a protrusion (PH-Akt-GFP, green; LifeAct-RFP, red). (G″) Colocalization channel of PH-Akt and LifeAct (Jet look up table). N=10 cells, 25 orgs, r=3. Scale, 5 μm. See also Movie S1.

To study the molecular dynamics of cell migration during branching morphogenesis, we adapted protocols to enable delivery and imaging of genetically encoded biosensors for signaling activity and cytoskeletal dynamics. Biosensors were delivered mosaically to enable high contrast imaging of cellular protrusions (Figure 1B). Mammary branching is induced by receptor tyrosine kinases signaling (Sternlicht et al., 2006), with FGF2 serving as the model ligand in our assay. We assayed molecular activity at key nodes of this pathway using fluorescent biosensors (Figure 1C). Ras activity was visualized using a fusion protein of GFP and the Ras binding domain (RBD) of Raf1, which specifically binds GTP-bound Ras. 3D volumes were collected in organoids mosaically expressing Raf1(RBD)-GFP and ubiquitously expressing a red fluorescent membrane label (membrane tdTomato). We observed sustained Ras activity enrichment to protrusions during migration (minutes to hours; Figure 1D). Ras activity was specifically enriched in anterior protrusions relative to lateral surfaces of the cell (Figure S1B).

PIP3 enrichment is also a key molecular component of a migratory cell front. We therefore anticipated that phosphoinositide 3-kinase (PI3K) activity would enrich to epithelial protrusions and selected a biosensor that localizes to regions of PIP3 enrichment (pleckstrin homology domain (PH) of AKT fused to GFP; PH-AKT-GFP). We specifically observed PIP3 biosensor accumulation in the protrusions of migratory cells (Figure 1E,S1D). PI3K activity was dynamic over minutes and membrane enrichment persisted for an hour or more. We next tested the requirement for PI3K activity and observed a dose-dependent block of branching in the presence of LY-294002 (Figure 2A,B). To test the functional connection between PI3K, migration, and protrusion formation, we imaged the PIP3 biosensor before and after LY-294002 inhibition. This led to a cytosolic localization of the PIP3 biosensor (Figure 2E, +2.2h), in addition to reduced mean cell speed, and rate of protrusions (Figures 2C,D; Figures S2F,G).

Figure 2. Branching morphogenesis and protrusions require PI3K activity and actin polymerization.

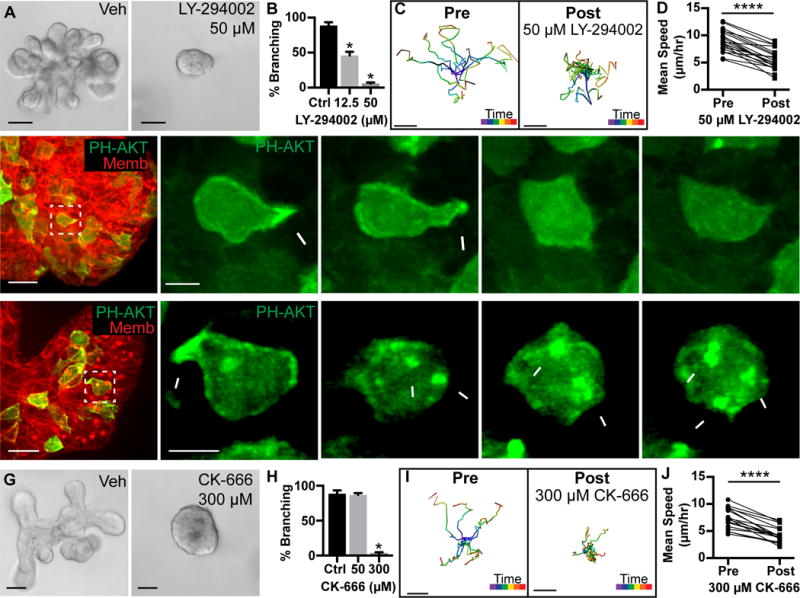
(A) Organoids treated with vehicle or 50 μM PI3K inhibitor (LY-294002) from Day 0. Scale, 50 μm.

(B) Quantification of branched organoids treated at Day 0 with vehicle (87.1±2.5%, 403 orgs), 12.5 μM LY-294002 (46.1±5.2%, 530 orgs), and 50 μM LY-294002 (6.1±1.3%, 514 orgs) (r=4; mean ± SD). Mann-Whitney test, p<0.05.

(C) Tracks of cell migration pre-and post-treatment with 50 μM LY-294002. Scale, 10 μm. Track color codes time (purple, start; red, end).

(D) Quantification of paired mean cell speed (μm/hour) pre-and post-treatment with 50 μM LY-294002. N=20 cells, 3 orgs, r=3. Wilcoxon matched-pairs test, p<0.0001.

(E–F) 3D confocal projections of cell migration (0.137 μm Gaussian blur, all channels).

(E) A migratory cell enriches PIP3 and generates a protrusion (white arrowhead; PH-Akt-GFP, green; membrane, red). PI3K inhibition (50 μM LY-294002) resulted in loss of PIP3 biosensor from the membrane. N=696 cells, 44 orgs, r=3. Scale, 20 μm (5 μm inset).

(F) A migratory cell enriches PIP3 and generates a protrusion (white arrowhead; PH-Akt-GFP, green). Jasplakinolide, Latrunculin A, and Y27632 (JLY) treatment induced retraction of protrusions and cell rounding. Dynamic membrane enrichment of PIP3 continued (white arrows), but did not lead to protrusions. N>1,000 cells, 65 orgs, r=4. Scale, 20 μm (5 μm inset). See also Movie S2.

(G) Organoids were treated with vehicle or 300 μM Arp2/3 inhibitor (CK-666) from Day 0. Scale, 50 μm.

(H) Quantification of percent branching in organoids treated from Day 0 with vehicle (88.7±4.8%, 403 orgs), 50 μM CK-666 (87.1±2.5%, 522 orgs), or 300 μM CK-666 (2.9±1.9%, 425 orgs) (r=4; mean ± SD). Mann-Whitney test, p<0.05.

(I) Tracks of cell migration pre-and post-treatment with 300 μM CK-666. Scale, 10 μm. Track color codes time (purple, start; red, end).

(J) Quantification of paired mean cell speed (μm/hour) pre-and post-treatment with 300 μM CK-666. N=18 cells, 10 orgs, r=3. Wilcoxon matched-pairs test, p<0.0001.

For localized Ras and PI3K activity to alter cell shape, they must lead to the generation of F-actin rich protrusions. Consistent with this concept, we observed enrichment of F-actin to both the anterior protrusions and the posterior surface of migratory cells (Figure 1F), using the LifeAct biosensor (Riedl et al., 2008). F-actin specifically enriched in protrusions relative to lateral surfaces (Figure S1F). We next tested the requirement for Arp2/3 mediated actin branching and observed viable organoids that failed to initiate new ducts (Figure 2G,H and S2A–E). Inhibition of Arp2/3 also reduced mean cell speed and rate of protrusions (Figure 2I,J; Figure S2H,I).

Taken together, the recruitment of Ras, PI3K, and actin polymerization to the cell anterior reveal that the molecular features of the migration front, first defined in single cells, are conserved during epithelial migration within a tissue. Furthermore, the dependence on PI3K activity and Arp2/3 for protrusions and migration suggest that the molecular requirements are similar for migration within epithelial tissues and of single cells on flat substrates (Devreotes and Horwitz, 2015; Nelson, 2009).

Conserved Molecular Logic of Migration Between Single Cells and Tissues

Molecular models of directed cell migration based on Dictyostelium discoideum predict that Ras activity promotes actin polymerization and should therefore colocalize with F-actin within protrusions. To test this, we mosaically co-infected organoids with Ras activity and F-actin biosensors. Both Ras activity (Figure 1G) and actin polymerization (Figure 1G′) enrich within protrusions (Figure 1G″). Interestingly, these enrichments are sustained for minutes to hours in epithelial cells, vs. seconds to a minute in neutrophils, suggesting that the same molecular systems are used, albeit on a very different time scale (Wang et al., 2014). Chemotaxis models further predict that PI3K activity leads to actin polymerization and that PI3K enrichment can occur in the absence of actin dynamics. To test this model in migratory epithelial cells, we mosaically co-infected organoids with the PIP3 and F-actin biosensors. We found that both PIP3 (Figure 1H) and actin polymerization (Figure 1H′) concurrently enrich within protrusions (Figure 1H″; Movie S1). We next tested the functional relationship between PI3K and F-actin by using a cocktail of inhibitors targeting actin depolymerization (Jasplakinolide), polymerization (Latrunculin A), and contractility (Y27632), termed ‘JLY’. This drug combination disconnects the PI3K signaling axis from its ability to influence or respond to actin dynamics (Peng et al., 2011; Wang et al., 2014). Following addition of JLY, cells arrested their actin dynamics and failed to extend new protrusions. However, they continued to enrich PI3K activity to focal regions of the plasma membrane (Figure 2F; Movie S2). Together, these data suggest that PI3K signaling leads to F-actin polymerization and migratory cell dynamics.

Migrating Cells Display High Anterior and Posterior Tensions

Migration within an epithelial tissue necessarily involves displacement of surrounding cells and as such it represents a distinct mechanical challenge compared to migration on a surface. We therefore next sought to connect the observed spatial asymmetries in molecular activities to force generation. To determine the mechanical forces associated with cell migration within tissues, we used our recently developed 3D Cellular Force Inference Toolkit (CellFIT-3D) to analyze relative interfacial tensions (Veldhuis et al., 2017) (see STAR Methods for details). Geometric information is extracted from 3D confocal images to construct a mesh that defines the shapes and intersections of the plasma membranes (Figure 3A). The angles between cellular junctions are determined (Figure 3B), then Young’s equations are generated and solved to infer relative tension values. Migrating cells displayed high tension in anterior protrusions and a posteriorly increasing perimeter tension gradient (referred to as posterior tension gradient) (Figure 3C,D). The high anterior protrusion tension causes the sides of the cell to frame to a narrow anterior and the posterior tension gradient causes the posterior of the cell to become curved into a teardrop shape. Importantly, our CellFIT analyses yielded consistent tension relationships when applied to cells in culture (Figure 3C–E) and to in vivo mammary epithelial cells (Figure S5A–C).

Figure 3. Anterior protrusions and posterior tension gradients can drive migration.

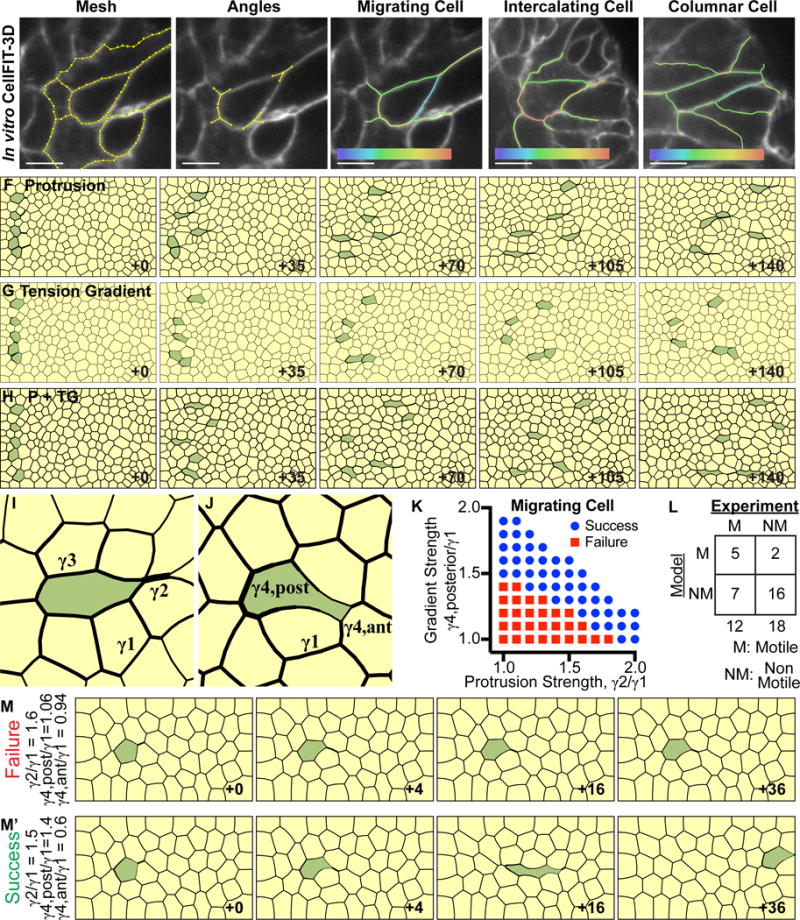
(A) CellFIT-3D was applied to confocal z-stacks of membrane labeled organoids (tdTomato, white) to generate a mesh. Membranes were segmented using a watershed filter to reconstruct 3D cell shape (CellFIT-3D segments, yellow). Scale, 5 μm.

(B) Curvilinear triple junctions (where three cells meet) were reconstructed using vectors to define angles (triple junction vector diagrams, yellow).

(C) Migrating cells often display a teardrop shape. CellFIT-3D analysis revealed high interfacial tension in the anterior protrusion and a gradient of tension increasing towards the posterior. Relative tension: low (violet) to high (red).

(D) Intercalating cells also exhibit high interfacial tension in the anterior protrusion and a gradient of tension increasing towards the posterior. Relative tension: low (violet) to high (red).

(E) Columnar epithelial cells display modestly higher anterior and posterior tensions, relative to lateral tensions. Relative tension scale: low (violet) to high (red).

(F–H) Finite element models (FEM) were generated to test the efficacy of anterior protrusions and posterior tension gradients. Cells migrated successfully in all scenarios. Line width indicates relative tension strength. The FE models are reported using a dimensionless time parameter defined by Equation 12 (Wayne Brodland and Veldhuis, 2003); which accounts for model characteristics such as average tension magnitude and mesh density, and allows for time comparison between models.

(F) Five cells were selected to extend rightward anterior protrusions at 2× tension strength relative to field tension.

(G) Five cells were selected to generate a posterior tension gradient of 0.4-1.6× tension strength relative to field tension.

(H) Five cells were selected to, in combination, extend rightward anterior protrusions at 1.5× and generate a posterior tension gradient of 0.7-1.3× tension strength relative to field tension.

(I) Characteristic shape of protrusion-only driven migration (green). γ1 indicates the field tension magnitude, γ2 indicates the anterior protrusion tension magnitude, and γ3 indicates the perimeter interfacial tension magnitude.

(J) Characteristic shape of posterior gradient-only driven migration (green). γ1 indicates field tension magnitude, γ4, posterior indicates the maximum posterior perimeter tension magnitude, and γ4, anterior indicates the minimum anterior perimeter tension magnitude.

(K) Protrusion strength and gradient strength were varied across FEM simulations to define the mechanical characteristics of successfully migrating cells. Success was defined as ≥4 cell diameters. Tension magnitudes are defined as in (I–J).

(L) CellFIT-3D was used to define the relative strength of anterior protrusions and posterior tension gradients in 30 cells. The criteria defined in (K) were used to predict migration. Blinded predictions correctly identified 16/18 non-migratory and 5/12 migratory cells (two-tailed Fischer’s exact test for contingency tables, p=0.0837). See related Supplemental Figure S5G.

(M)Example of a failed cell migration (green). Protrusion and maximum gradient strengths are 1.6× and 1.06× field strength, respectively. (M′) Example of a successful cell migration (green). Protrusion and maximum gradient strengths are 1.5× and 1.4× field strength, respectively.

Epithelial Cells Can Migrate within Tissues Using Anterior Protrusions and a Posterior Tension Gradient

Our force inference analysis suggested two potential ‘engines’ for migration within tissues: anterior protrusions and posterior tension gradients. Our biosensor imaging revealed F-actin accumulation in both regions and so either could be sites of actomyosin force generation. We utilized our imaging data to inform the selection of parameters and mechanisms for a FE model (discussed in STAR Methods). We then applied this FE model to distinguish the relative advantages of anterior protrusions, posterior tension gradients, or a combination. A field of cells was generated within which interfacial membrane tensions were varied in a random fashion (±15%). To initiate the simulation, 5 cells were selected to extend an anterior, forward reaching protrusion with a 2× tension strength (Figure 3F). Protrusion-only cells migrated successfully past neighboring cells. We next tested migration based solely on a posterior tension gradient. A similar field of cells was generated and then 5 cells were selected to generate a posterior tension gradient (Figure 3G). Cells with a posterior tension gradient also migrated successfully, revealing that either engine is individually sufficient for migration through our computational tissue models. Finally, the combination of the two mechanisms migrated successfully and generated cell shapes more consistent with our experimental observations (Figure 3H).

Specific Ratios of Anterior Protrusion and Posterior Tension Gradient Strength Are Required for Successful Cell Migration

We next conducted a parametric analysis of the relative contribution of these mechanisms. Inside a tissue, a migrating cell must extend between cells at its anterior end and release from cells at its posterior end. There are three key parameters for protrusions – average field interfacial tension strength (γ1), anterior protrusion tension strength (γ2), and perimeter tension strength (γ3) (Figure 3I). There are three key parameters for posterior tension gradients – average field interfacial tension strength (γ1), minimum anterior perimeter tension strength (γ4, anterior), and maximum posterior perimeter tension strength (γ4, posterior) (Figure 3J). The ratio between γ2/γ1 and γ4, post/γ1 can be varied and simulated using FEM. We defined successful migration as greater than 4 cell lengths of movement. The simulations revealed a sharp boundary defining successful migration (Figure 3K), with a range of effective strategies, including protrusion-only (data point (1.8,1)), tension gradient-only mechanism (data point (1,1.5)), or combined utilization of protrusions and a tension gradient (intermediate data points) (Figure 3K). Cells with ratios outside these values were stationary (Figure 3K,M), while those within these values migrated (Figure 3K,M′).

Cells using only protrusions (γ2/γ1≥1.9× field tension strength), can pull through anterior cells and release from posterior cells, without tension gradients. The migrating cell anterior edges and the edges of the cells being pulled on by the protrusion are concave and frame to a single point; creating a mirror effect (Figure 3I, γ2). Adding a tension gradient alleviates the pulling and releasing imbalance, and reduces the required protrusion strength to successfully migrate. Increasing the perimeter tension of the migrating cell (Figure 3I, γ3) would also alleviate the pulling and releasing imbalance. Cells using only posterior tension gradient, (γ4, post/γ1≥1.5× field tension strength) can migrate without a protrusion. This migrating cell is pulled between anterior cells because of a reduction in anterior perimeter tension and releases from posterior cells because of an increase in posterior perimeter tension. Different parameter combinations yield variations in cell shape. However, successfully migrating cells typically exhibit a teardrop shape.

CellFIT-3D was next used to define the relative strength of anterior protrusions and posterior tension gradients in 30 cells that were either motile (M) or non-motile (NM) from elongating organoids. The criteria defined in Figure 3K were used to predict whether the cell would migrate. Blinded predictions correctly identified the migratory outcome in 21/30 cells (Figure 3L and S5G; p=0.0837, ns). Analysis of subcategories revealed high accuracy in predicting immotility (16/18 cells) relative to migration (5/12). We interpret this discrepancy as suggesting that the interfacial tension relationships identified here are necessary but not sufficient for migration.

Radial Intercalation Couples Cell Migration to Tissue Elongation

For a duct to elongate, the tissue’s surface area must expand. If a migratory internal cell inserts into the most superficial cell layer, this radial intercalation directly increases tissue surface area. We therefore examined the dynamics of migration as epithelial cells moved between layers. Based on extensive work in model systems (Keller et al., 1989; Shih and Keller, 1992; Walck-Shannon and Hardin, 2014), we hypothesized that radial intercalation could thin the epithelial multilayer, expand the tissue surface, and directly elongate the tube (Walck-Shannon and Hardin, 2014).

The elongating branch displays characteristic proximal-distal differences in cell behavior, with cells near the tip displaying higher speeds and coordinated protrusive activity in the direction of elongation (Huebner et al., 2016). Accordingly, we spatially segmented our analysis (Figure 4A) and observed radial intercalation to contact the basal surface in all four regions, with a majority in the front or middle (Figure 4B,D–D′; Movie S3). We observed the same characteristic teardrop cell morphology in intercalating cells that we had seen during internal migrations (Figures 4D′, +1.2h; E, +1.0h). Additionally, radial intercalation was observed to resolve a multilayer to a bilayer with a single luminal layer (Figure S4A,A′). As luminal cells radially intercalate they make direct contact with the myoepithelium but remain luminal in character (Figure 4E and S4B–B″). Interestingly, we observed transient intercalations, which eventually release from the basal surface (Figure 4F). Intercalating cells exhibited a range of mean basal residence times. We classified intercalating cells as permanent or transient based on a residence of greater than 12 hours (see STAR Methods and Figure 4C). We next applied CellFIT-3D to intercalation and columnar organization (Figure 3D–E). Intercalating cells displayed high tension in anterior protrusions and a posterior tension gradient, consistent with migratory cells (Figure 3D). Non-motile columnar cells displayed low perimeter tension laterally and intermediate tensions anteriorly and posteriorly (Figure 3E). The relatively higher anterior and posterior tensions cause the anterior and posterior of the cell to shorten and the sides of the cell to lengthen into a columnar shape. These data establish that migrations within the epithelium can lead to intercalation at the basal surface. These intercalations can then contribute to tube elongation and thin a multilayered epithelium back to a bilayered epithelium after morphogenesis.

Figure 4. Radial intercalation occurs during duct elongation.

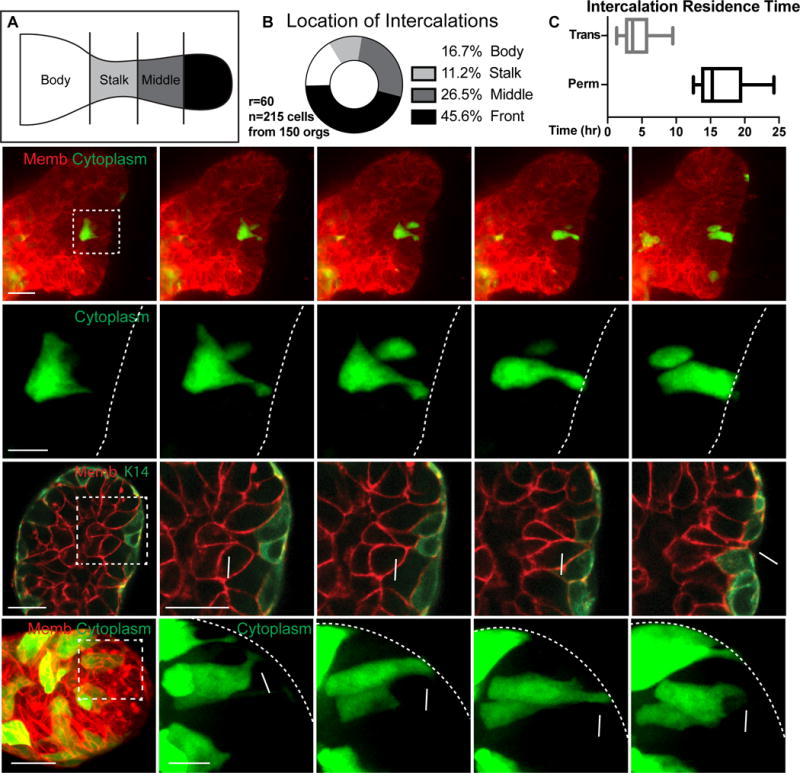
(A) Branches were divided into body, stalk, middle, and front regions.

(B) Intercalations were quantified within body (36, 16.7%), stalk (24, 11.2%), middle (57, 26.5%) or front (98, 45.6%) regions. (215 cells, 150 orgs, r=60). A lower boundary of the rate of permanent intercalations was calculated to be 0.078 per hour (n=39, r=3). This rate is expected to be an undercount due to the stochastic mosaic nature of the labeling.

(C) Basal residence time for intercalations (hours; box and whiskers, Q1::Median::Q3), showing permanent (13.6::15.3::19.7hr, N=13 cells from 11 orgs, r=6) and transient (2.5::3.7::5.9hr, N=16 cells, 12 orgs, r=5).

(D) (D′) 3D confocal projections of a cell migrating, intercalating, and transitioning to columnar morphology (membrane, tdTomato, red; cytoplasm, GFP, green). Scale, 20 μm (10 μm inset). See also Movie S3.

(E) A single plane showing a luminal cell (star) intercalating to contact the myoepithelium (membrane, tdTomato, red; myoepithelium, K14-actin-GFP, green). Scale, 20 μm (10 μm inset).

(F) 3D confocal projections of a transient intercalation, with a cell migrating, intercalating, and exiting the basal surface (membrane, tdTomato, red; cytoplasm, GFP, green). Scale, 20 μm (10 μm inset).

An alternate mechanism for transitioning from a multilayer to a bilayer is cavitation, in which interior cells die (Figure S3A) (Mailleux et al., 2007). To test this concept, we analyzed the distribution of apoptotic cells using cleaved caspase 3 (CC3). We did not detect internal enrichment of apoptotic cells (Figure S3B), nor were CC3 levels significantly different over time (Figures S3B,C). Therefore, neither the location nor timing of apoptosis were consistent with cavitation (Paine et al., 2016). We next tested the requirement for apoptosis using caspase-3, caspase-9, or pan-caspase inhibitors. Each inhibitor reduced apoptosis (Figure S3F) and every organoid examined had a lumen and polarized architecture (Figures S3D,E). Our data therefore favor the concept that intercalation is the primary mechanism for resolving the multilayered epithelium back to a bilayer (Figure S4A,A′).

Epithelial Cells Enrich Migratory Molecular Markers in Protrusions During Radial Intercalation

Having established that epithelial cells utilize conserved molecular programs to migrate within tissues and that radial intercalation can drive tube elongation, we next assayed molecular asymmetries during radial intercalation. First, we observed Ras activity specifically enrich in anterior protrusions during intercalation (Figure 5A,S1C; Movie S4). Ras activity was dynamic and membrane enrichment persisted over hours. Second, we observed PIP3 biosensor accumulation specifically in anterior protrusions during intercalation (Figure 5B, arrows, S1E; Movie S5). PI3K activity was dynamic and membrane enrichment lasted for an hour or more, with distinct localization patterns to Ras. Finally, F-actin specifically accumulates in anterior protrusions during intercalation (Figure 5C,S1G; Movie S6). F-actin polymerization was dynamic and enrichment lasted for an hour or more, with distinct localization patterns to the other biosensors. When intercalating cells reached the basal tissue surface, Ras activity, PI3K localization, and F-actin enrichment all dissipated as the cell assumed a columnar epithelial shape (Figure S1C,E,G). These dynamics are consistent with a transition from migratory front-rear to stationary apico-basal polarity (Nelson, 2009) and with the known absence of ECM directed protrusions in these cells (Ewald et al., 2008).

Figure 5. Intercalating epithelium enrich Ras activity, PI3K activity, and F-actin polymerization in protrusions.

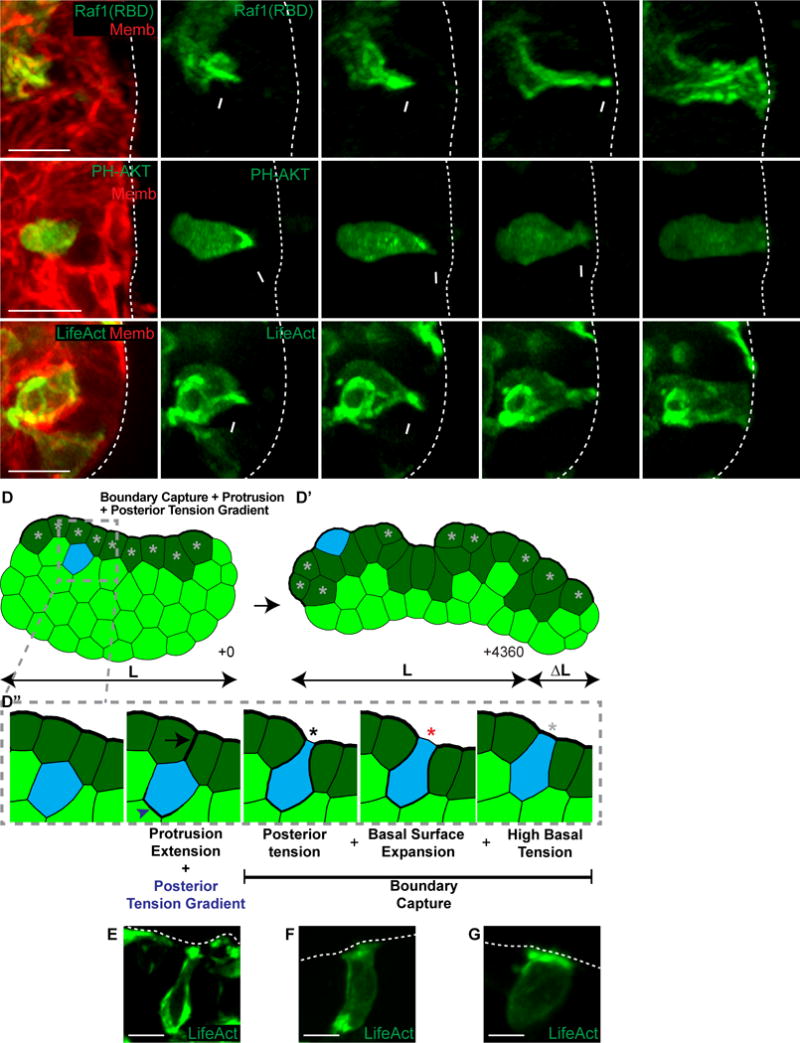
(A–C) 3D confocal projections of intercalation (0.137 μm Gaussian blur, all channels).

(A) An intercalating cell enriches Ras activity to its anterior membranes (Raf1(RBD)-GFP, green; membrane, red). N=10 cells, 28 orgs, r=4. Scale, 10 μm. See also Movie S4.

(B) An intercalating cell enriches PIP3 to its anterior protrusion (PH-Akt-GFP, green; membrane, red). N=30, 131 orgs, r=6. Scale bar=10 μm. See also Movie S5.

(C) An intercalating cell enriches F-actin to its anterior protrusion (LifeAct-GFP, green; membrane, red). N=26, 73 orgs, r=4. Scale, 10 μm. See also Movie S6.

(D) A FEM was generated of a tissue with high basal surface tension (dark green cells) to test candidate intercalation mechanisms. Cells were randomly chosen to intercalate towards the basal surface using high anterior protrusion tension and a posterior tension gradient. (D′) The combined intercalation mechanism was sufficient for elongation. (D″) Intercalating cells generated an anterior protrusion (black arrow) and a posterior tension gradient (blue arrowhead) towards the basal high tension line (+1). Cells were captured at the basal surface through a combination of posterior tension and focal disruption of the high basal tissue tension (+3, black star). The basal surface of the intercalating cell then expanded (+4, red star). Intercalation was made permanent when high basal tension was restored (+12, light gray star). Line width indicates relative tension strength. See also Movie S7.

(E–G) 3D confocal projections of intercalation (LifeAct-GFP, green; 0.137 μm Gaussian blur). Scale, 10 μm.

(E) F-actin anterior enrichments and rear gradients, consistent with (D″) +1.

(F) Loss of anterior F-actin enrichments with high posterior tension, consistent with (D″) +3 and +4.

(G) High basal F-actin enrichment upon intercalation completion, consistent with (D″) +12.

Combining Anterior Protrusions and a Time-Varying Posterior Tension Gradient is Sufficient for Radial Intercalation

Next, we wanted to determine the specific mechanical requirements for radial intercalation in silico. We were particularly interested to determine whether the teardrop shape of intercalating cells had a similar physical explanation as that observed in migrating epithelial cells. Our initial simulations modeled the dynamics of migration deep within a tissue. We then extended our model to include the mechanical constraints faced at the edge. A field of cells was generated with no horizontal constraints and high basal tension (Figure 5D, Movie S7). We encoded two populations of cells – the first population (light green) is interior and the second population (dark green) is touching the basal surface. Interfacial tension at the basal surface is equal to 1.5, while all other interfacial tensions are equal to 1. From this starting configuration, we randomly selected light green cells to both protrude and have a posterior tension gradient (Figure 5D″, +1). We modeled these properties because we experimentally observed intercalating cells enrich F-actin to protrusions and to the cell posterior (Figure 5E). If an intercalating cell extended to the basal surface, a time-varying mechanism was triggered to expand the basal surface via decreased anterior and increased posterior perimeter tensions (Figure 5D″, +3-4) and establish stable boundary capture via decreased posterior and increased anterior perimeter tensions (Figure 5D″, +12). The boundary capture mechanism was included in our FEM because we experimentally observed intercalating cells lose anterior F-actin but retain high posterior tension as they transitioned to columnar shape (Figure 5F). Our FEM found further experimental support in our observation of high basal F-actin enrichment upon intercalation completion (Figure 5G). Intercalations across the tissue in the FEM were sufficient to reduce the number of cell layers and increase length (Figure 5D′). However, simulated intercalations were sometimes transient, consistent with our experimental observations (Figure 4F).

Specific Ratios of Anterior Protrusion and Posterior Tension Gradient Strength Are Required for Radial Intercalation

To understand the mechanical properties that enable successful intercalation, we conducted a parametric analysis and defined the interfacial tension ratios compatible with boundary contact (Figure 6A–B). Having defined the core engines of intercalation in a generic tissue (Figure 5D″), we built an in silico TEB by wrapping the epithelium around a lumen (Figure 6A). The outer luminal layer is non-migratory (green) and the interior cells are capable of intercalation (yellow). These cells were iterated through time steps with specified protrusion strengths (P), specified posterior tension gradients (T), and boundary capture mechanism (Bc). Boundary contact could occur with varying reliance on protrusions vs. posterior tension (Figure 6B). Cells that fail to contact the boundary recede into the tissue interior (Figure 6A), while successful cells reach the boundary, stabilize their location, and remain at the surface (Figure 6A′). Intercalation success was characterized by: (1) the ability to pull between anterior cells to contact the basal surface, (2) the ability to release from posterior cells to transition to a columnar cell, and (3) persistent incorporation into the basal surface. These criteria can be accomplished with different combinations of protrusion and posterior tension gradient strengths (Figure 3K) but predominantly require the boundary capture mechanism (Figure 5D″). Both protrusions (Figure S5E) and posterior tension gradients (Figure S5F) are individually sufficient for contacting the basal surface, but typically fail to establish permanent contact without the boundary capture mechanism. Intercalating cells therefore exhibit similar mechanical properties as cells migrating through tissues, with the additional constraint of remaining persistently at the basal surface.

Figure 6. Transient and permanent intercalations are distinguished at the basal tissue surface.

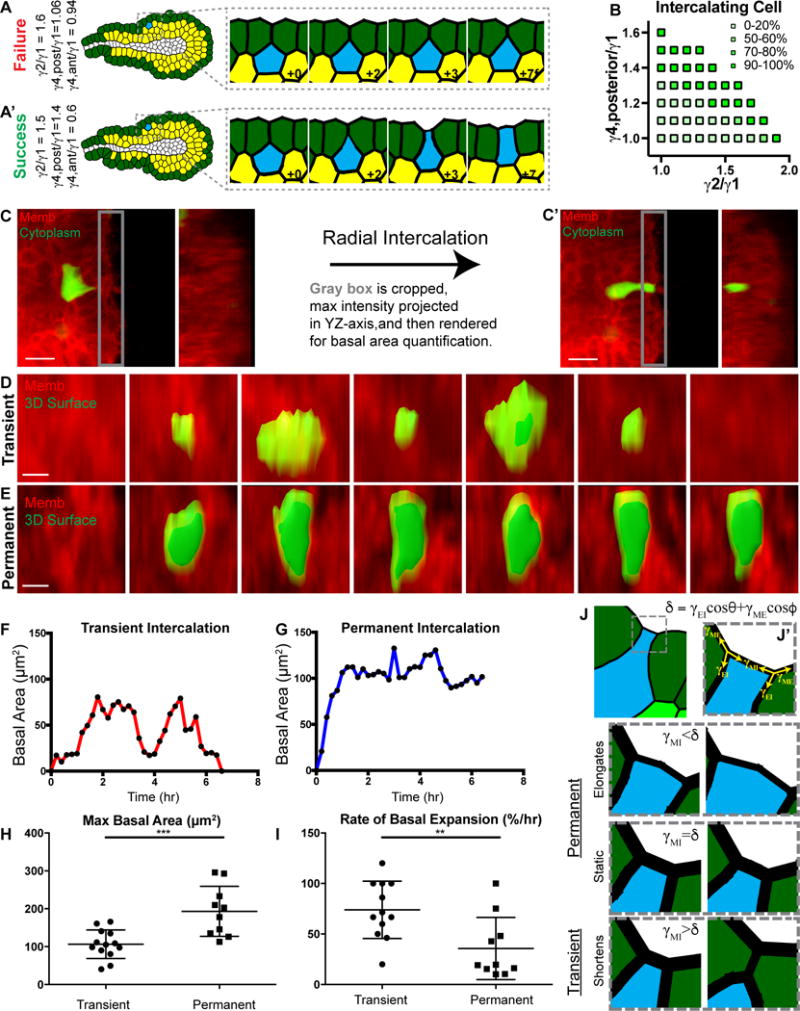
(A) A tissue field was wrapped around a lumen to form a 2D stratified epithelium modeling a 3D mammary end bud. Example of a cell failing to contact the basal surface (blue), with protrusion strength of 1.6× and posterior gradient strength of 1.06× field strength. (A′) Example of a successful intercalation (blue), with protrusion strength of 1.5× and posterior gradient strength of 1.4× field strength.

(B) Protrusion strength and gradient strength were varied across FEM simulations to define the mechanical characteristics of successful boundary contact, within the context of the in silico TEB model from (A). Tension magnitudes are defined as in (Figures 3I–J).

(C) Quantification of basal area dynamics (C) prior to and (C′) after radial intercalation. The YZ maximum intensity projection displays the cell’s basal area in green.

(D) YZ-axis projection showing membrane (tdTomato, red) and 3D surface rendering (green) of basal area during (D) transient and

(E) permanent intercalation.

(F) Quantification of basal area (μm², from D) during transient and

(G) permanent (μm², from E) intercalation.

(H) Quantification of the maximum basal area (μm², mean ± SD) during intercalation for transient (106.5 ± 37.8μm²) and permanent (193.2 ± 66.1μm²). N=22 cells, 19 orgs, r=11. Mann-Whitney test, p<0.001.

(I) Quantification of the rate of basal expansion (%/hour, mean ±S D) during intercalation for transient (73.9 ± 28.4%/hr) and permanent (35.7 ± 30.7%/hr). N=22 cells, 19 orgs, r=11. Mann-Whitney test, p<0.01.

(J) A FEM was generated of a tissue with high basal surface tension (dark green cells) to test candidate mechanisms for basal area of an intercalating cell. A cell (blue) was captured at the basal surface through a combination of posterior cell tension and focal disruption of the high basal tissue tension. (J′) Principle tension components (γ_MI, γ_EI, γ_ME, yellow arrows) acting at the two intercellular junctions. M, Matrix; I, Intercalating cell; E, Epithelial cell. Angles θ and ϕ are the angles γ_EI and γ_ME, respectively, make with the action line of γ_MI as illustrated in Figure S5D. The intercalated cell basal surface could then undergo 1 of 3 conditions:

(K) γ_MI<γ_EIcosθ+γ_MEcosϕ results in expansion of the basal surface (+0.75), a permanent intercalation.

(L) γ_MI=γ_EIcosθ+γ_MEcosϕ results in stasis of the basal surface (+0.75), a permanent intercalation.

(M) γ_MI>γ_EIcosθ+γ_MEcosϕ results in contraction of the basal surface (+0.75), a transient intercalation.

Transient and Permanent Radial Intercalations Display Different Physical Properties at the Basal Surface

The critical feature that enables radial intercalation to contribute to tube elongation is permanent incorporation into the most basal cell layer, as these cells can then increase tissue surface area. We therefore sought to determine if there were aspects of cell shape, dynamics, or mechanics that distinguish transient and permanent intercalations. We first characterized the basal surface dynamics during intercalation. The ‘basal surface’ was defined as up to 5 μm from the tissue-ECM interface (Figure 6C, gray box). This region was cropped and projected orthogonal to the imaging plane to visualize and quantify the basal area of the intercalating cell as a function of time (Figure 6C′, YZ panel). Transiently intercalating cells approached the tissue surface rapidly and typically oscillated in and out of contact before receding to the interior (Figures 6D,F). Permanently intercalating cells were morphologically similar on approach but exhibited a slower and more persistent increase in basal area (Figures 6E,G,I). Furthermore, the maximum basal area obtained was greater in permanent intercalations (Figure 6H).

To further understand the properties distinguishing transient and permanent intercalations, we constructed a FEM of a teardrop shaped cell that has nascently intercalated (Figure 6J; like Figure 5D″, +3). We identified the elongation or shortening of the basal surface to be a function of tensions acting at cellular junctions (Figure 6J′; γ_MI, γ_EI, γ_ME; see also Figure S5D). At this stage, the basal surface can either undergo elongation, remain static, or shorten. The initial two settings could be classified as permanent intercalations, as the cell remained at the basal surface. The final situation that undergoes basal surface contraction would be classified as a transient intercalation. When γ_MI<γ_EIcosθ+γ_MEcosϕ, the basal surface expands and the cell permanently intercalates once the equilibrium condition has been reached (Figure 6K, +0.75). When γ_MI=γ_EIcosθ+γ_MEcosϕ, the basal surface remains at equilibrium and the cell permanently intercalates (Figure 6L, +0.75). In the final condition, when γ_MI>γ_EIcosθ+γ_MEcosϕ, the basal surface contracts, the cell transiently intercalates and retreats to the interior (Figure 6M, +0.75). A reduction in γ_MI, θ, or ϕ (Figures 6J′ and S5D) can satisfy the basal expansion and equilibrium conditions. This explains that an insignificant number of intercalating in silico cells were able to establish permanent basal capture without the prescribed boundary capture mechanism. The boundary capture mechanism greatly improves the probability of satisfying the permanent intercalation conditions.

A Combination of Radial Intercalation, Cell Migration, Proliferation, and Basal Stress is Sufficient for Tube Elongation In Silico

Having established that this combined mechanism for radial intercalation was plausible, we next encoded cell migration, proliferation, and radial intercalation within the stratified region of an in silico TEB (Figure 7A; Movie S8A). The randomly chosen intercalating cells were given protrusion strengths (P) and posterior tension gradients (TG) from a normal distribution determined from Fig 6B, and the boundary capture mechanism (Bc). Surprisingly, the tissue did not elongate, instead forming clusters of small buds (Figure 7A″). This disorganized morphology is not consistent with the smooth tissue surface observed on elongating branches in culture and in vivo (Ewald et al., 2008).

Figure 7. Mammary tubes can elongate using radial intercalation, anterior protrusions, posterior tension gradients, and high basal stress.

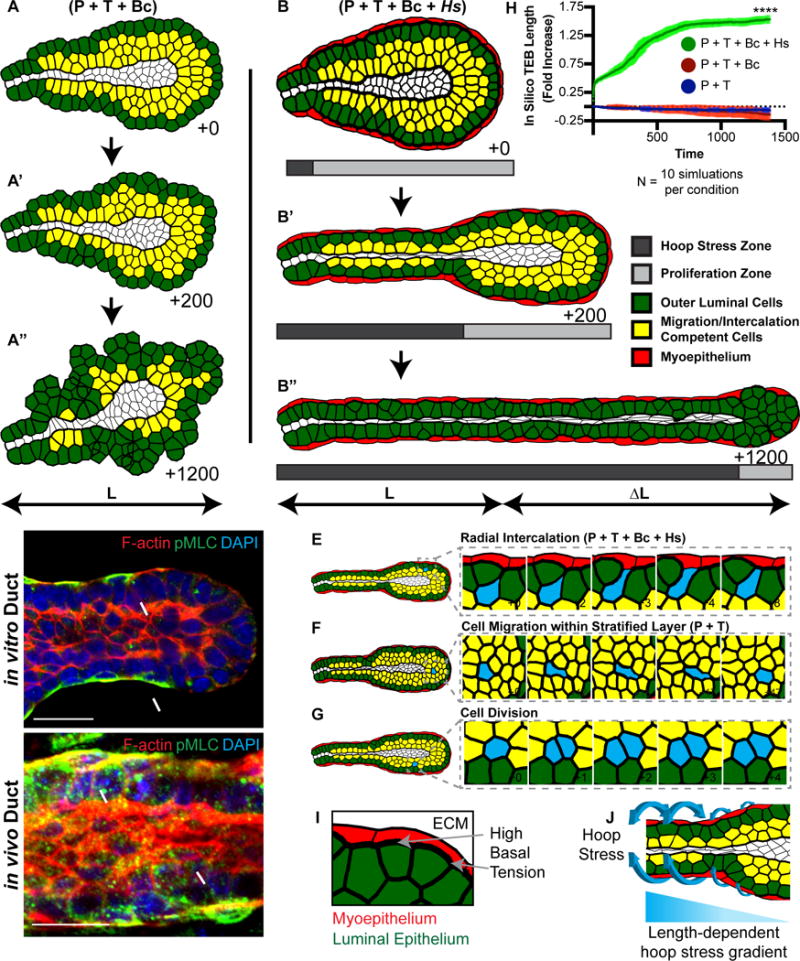
(A) A FEM of a terminal end (TEB) testing the combination of anterior protrusion (P), posterior tension gradient (T), and boundary capture mechanism (Bc) driven intercalation. Interior cells could migrate and divide and a subset were randomly chosen to intercalate (yellow), with normally distributed protrusion and tension gradient strengths, directed towards the basal most luminal cell layer (green cells). The lumen does not affect cellular tensions. These mechanisms resulted in disorganized growth and not efficient elongation. See also Movie S8.

(B) The FEM from (A) was extended to include high basal tension and in-plane stress applied towards the organoid center-line (hoop stress), to model the function of the contractile myoepithelium (red). The region in which the hoop stress (dark gray) was applied or cell proliferation (light gray) occurred varied over time (B′ and B″). The combination of anterior protrusions (P), posterior tension gradients (T), boundary capture mechanism (Bc), and high basal hoop stress (Hs) was sufficient to drive efficient elongation. See also Movie S8.

(C) A confocal image of an organoid branch showing F-actin (Phalloidin, red), phosphomyosin light chain (pMLC, green), and nuclei (DAPI, blue). Scale, 20 μm. Representative of 49 orgs, r=3.

(D) A confocal image of an in vivo 8-week old mammary duct showing F-actin (Phalloidin, red), pMLC (green), and nuclei (DAPI, blue). Scale, 20 μm. Representative of 32 ducts, r=4.

(E) An interior cell (blue) intercalating via the mechanisms identified in (B).

(F) An interior cell (blue) migrating in the tissue via the mechanisms identified in (B).

(G) An example of cell proliferation (blue) in the proliferation zone.

(H) Representative results of in silico TEB fold increase from FEM simulations using the following conditions: blue, protrusions + posterior tension gradient; red, protrusions + posterior tension gradient + boundary capture mechanism; and, green, protrusions + posterior tension gradient + boundary capture mechanism + hoop stress. T-test, p<0.0001.

(I) Schematic demonstrating the high basal tension (thick black line, gray arrows) between the two layers of the myoepithelium (red) and luminal epithelium (green).

(J) Schematic demonstrating the circumferential hoop stress applied in 3D (blue arrows). A time-varying length-dependent hoop stress gradient is applied during elongation of the in silico TEB.

A smooth surface at the edge of a 2D tissue requires high tension at the boundary (Brodland, 2004). The surface in our simulation is the edge of a 3D cylinder and high tissue tension at this interface represents 3D stress composed of circumferential (or hoop stress) and axial stress. We therefore sought evidence for high tension at this boundary in order to identify an experimental correlate for this feature before including it in the FE model. Given the importance of actin dynamics, we stained for phosphomyosin light chain (pMLC). We observed enriched pMLC staining at the basal surface of myoepithelial cells both in vitro and in vivo (Figures 7C,D). This staining had a threshold appearance, with high levels at the trailing duct and typically undetectable levels at the front (Figure 7C). To model this 3D myoepithelial influence (Figure 7B, red cells) in a 2D plane, we added basal tension (Figure 7I, thick basal line) and an inward radial force (Hs) to the in silico TEB (Figure 7J) to represent the axial and circumferential hoop stress components of the 3D basal stress, respectively. The exact relationship between the axial and circumferential hoop stress components of the 3D basal stress inferred from the actomyosin staining is currently unknown. Therefore, we modeled the mechanical influence of each stress component on the epithelial tube to test the significance of 3D basal stress in branch elongation and polarization. Cells in the stratified layer (yellow) in this new model are capable of radial intercalation (Figure 7E), cell migration (Figure 7F), and cell division (Figure 7G, corresponding to Figure 7G–G″, Proliferation Zone, light gray). As the duct elongates, the hoop stress in the model concurrently advanced forward with the thinning duct (Figure 7B–B″, Hoop Stress Zone, dark gray; Movie S8B). The addition of these hoop stress and basal tension enabled the in silico TEB to elongate and eventually resolve to a bilayer, while maintaining plausible cell and tissue morphologies (Figure 7A vs. 7B).

We next tested whether the rate of intercalation would influence the developmental trajectory or the final morphology of the epithelium. We generated a series of FEMs, similar to Fig 7B, in which we varied the time interval between selection of interior cells to have intercalation tension parameters normally distributed from Fig 6B (Figure S6). Decreasing the rate of intercalation in this way reduced the rate of tube elongation, but did not alter the intermediate or final morphologies of the epithelium. This computational result emphasizes the capacity of radial intercalations, whether rare or frequent, to drive tube elongation. Finally, three conditions were simulated 10 times: protrusions combined with a rear tension gradient (P+T, Figure 7H, blue), with the addition of boundary capture mechanism (P+T+Bc, Figure 7H, red), and finally, combined with hoop stress (P+T+Bc+Hs, Figure 7H, green). P+T cannot elongate because it predominantly fails at intercalation without Bc. P+T+Bc shortens because its intercalations produce a lumpy tissue surface. P+T+Bc+Hs was uniquely capable of elongating the in silico TEB while transitioning from a multilayer to a bilayer.

DISCUSSION

We sought to define the cellular, molecular, and mechanical principles regulating mammary epithelial tube elongation. We first utilized molecular biosensors to demonstrate that epithelial cells migrating within tissues utilized a conserved molecular logic first defined during single cell migration on 2D surfaces. Specifically, we observed localization of Ras activity, PI3K activity, and actin polymerization to leading protrusions of both migratory and intercalating cells. Both Arp2/3 and PI3K activity were required for protrusions and for tissue elongation. Consistent with molecular models of chemotaxis in single cells, PI3K activity temporally coincided with actin polymerization and PI3K dynamics occurred spontaneously in the absence of F-actin dynamics (Devreotes and Horwitz, 2015). We next utilized force inference analysis and FE modeling to identify conserved mechanical features regulating migration within tissues. Cells migrating within mammary organoids and in silico epithelia organize into a teardrop cell shape defined by posterior tension gradients and a single anterior protrusion that served as dual engines for migration within the tissue. We next discovered that migratory epithelial cells utilize radial intercalation to extend tube length and to resolve to a bilayer.

These experimental data were then used to develop FE models of epithelial morphogenesis, with the intent of testing the relative plausibility of different cellular mechanisms as drivers of tube elongation. We sought to recapitulate mammary ductal elongation in silico. Our starting point was the observation of cell migration within the multilayered epithelium, anterior-posterior tension gradients within migratory cells, and intercalation to the basal surface. Surprisingly, these cell behaviors produced a disorganized tissue and did not support elongation. Instead, elongation required 3D basal tensile stress, which we modeled in 2D as axial tension and circumferential hoop stress at the basal surface. The incorporated basal tensile stress smoothed the basal surface and contributed to elongation by promoting the capture of intercalating cells. Future studies should develop methods to manipulate these tensions and stresses experimentally, as current techniques are underdeveloped for 3D tissues. The critical role of basal tensile stress in our simulations finds experimental support in the disorganized morphology that results from genetic disruption of basal tensions in vivo by overexpression of p190-B Rho-GAP (Vargo-Gogola et al., 2006).

The term branching morphogenesis suggests the possibility of common mechanisms in organ formation, despite known differences in adult structure and function. For example, tube shape in the mammalian lung is regulated by mitotic spindle orientation angle (Tang et al., 2011), while new branches initiate in the avian lung without proliferation (Kim et al., 2013). There are therefore distinct ways to build a similar tube. We speculate that common themes emerge at the level of cell behaviors, conceived as modules, and combined in distinct ways to generate tubes with different properties. Our recent work has shown the importance of the MAPK, and now the PI3K, pathway in regulating cell migration during branching, consistent with previous studies in other epithelial systems (Chi et al., 2009; Hoshi et al., 2012; Zhu and Nelson, 2013). Our modular cell behavior hypothesis is also supported by modeling work demonstrating that modulation of either matrix elasticity or proliferation rate induces changes in branching pattern (Varner and Nelson, 2014).

From this perspective, we propose that the key cell behavior in mammary branching is radial intercalation. Intercalation is a common morphogenetic mechanism (Keller et al., 1989; Shih and Keller, 1992; Walck-Shannon and Hardin, 2014) and contributes to organ morphogenesis in amphibian (Szabo et al., 2016) and mammalian systems (Heller et al., 2014). Recent work in the Xenopus mucociliary epithelium revealed that radial intercalation increases surface area and patterns the tissue (Sedzinski et al., 2016). In the mammary epithelium, we have shown that intercalation both increases surface area during elongation and allows the tissue to transition back to a polarized bilayered organization when morphogenesis is complete. To achieve these goals, the intercalating cell must remain at the basal surface. Our experimental and computational work suggests that permanently intercalating cells are distinguished by their behavior and mechanical properties at the basal surface. The molecular mechanisms responsible for these differences remain unknown. A plausible candidate would be hemidesmosomal adhesion to the basement membrane (Runswick et al., 2001), however this hypothesis requires experimental validation.

Our ability to understand the mechanical constraints on cell migration within tissues was critically enabled by an iterative dialogue between experiment, computational analysis, and FE modeling. We observed an unusual tear-drop shape in migrating cells, used CellFIT-3D to reveal high anterior protrusive tensions and a time-varying posterior tension gradient, and applied FE modeling to reveal the contribution of these mechanisms to stable intercalation. Similarly, iterative computational and experimental work elucidated the contributions of proliferation and apoptosis to mammary elongation in vivo (Paine et al., 2016). Multidisciplinary studies of this kind will enable a quantitative understanding of the physical principles of cell migration through tissues that pattern organs (Cai et al., 2016; Sedzinski et al., 2016; Szabo et al., 2016).

STAR METHODS

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies or Fluorophores
Phospho-Myosin Light Chain 2 (Ser19)	Cell Signaling Technology	#3671S; RRID: AB_330428
Cleaved Caspase-3 (Asp175) (D3E9)	Cell Signaling Technology	#9579S; RRID: AB_10897512
Goat anti-Rabbit IgG, Alexa Fluor Plus 488	ThermoFisher	Cat. No. A32731; RRID: AB_2633280
BODIPY 558/568 Phalloidin	ThermoFisher	Cat. No. B3475
DAPI	ThermoFisher	Cat. No. D3571
Calcein Green	ThermoFisher	C3100MP
Bacterial and Virus Strains
eGFP Adenovirus	Vector Biolabs	Cat. No. 1060
CFP Adenovirus	Vector Biolabs	Cat. No. 1766
LifeAct GFP Adenovirus	Ibidi	Cat. No. 60121
LifeAct RFP Adenovirus	Ibidi	Cat. No. 60122
Lentivirus Raf1-(RBD)-GFP	Devreotes Lab, AddGene
Lentivirus PH-Akt-GFP	Devreotes Lab, AddGene	#51465
Biological Samples
Chemicals, Peptides, and Recombinant Proteins
LY-294002	Sigma	L9908
CK-666	Sigma	SML0006
Jasplakinolide	Tocris	Cat. No. 2792
Latrunculin A	Tocris	Cat. No. 3973
Y-27632	Calbiochem	Cat. No. 688000
FGF2	Sigma	F0291
Insulin	Sigma	I9278
Gentamicin	ThermoFisher	15750
Trypsin	ThermoFisher	27250-018
Collagenase	Sigma	C2139
FBS	Sigma	F0926
DMEM/F-12	ThermoFisher	10565-018
D-PBS	ThermoFisher	14040-133
Penicillin-Streptomycin	Sigma	P4333
ITS	ThermoFisher	51500-056
Matrigel, Growth Factor Reduced, ~9 mg/mL	Corning	354230
Collagen-I, Rat Tail	Corning	354236
DNase	Sigma	D4263
Critical Commercial Assays
Experimental Models: Organisms/Strains
Mouse: FVB/NJ	The Jackson Laboratory	Stock No: 001800; RRID: IMSR_JAX:001800
Mouse:FVB, Gt(ROSA26)ACTB-tdTomato-EGFP	Andrew Ewald Laboratory	Stock No: 007576; RRID: IMSR_JAX:007576
Mouse: FVB, Tg(KRT14-EGFP/Actb)50Efu; Gt(ROSA26)ACTB-tdTomato-EGFP	Andrew Ewald Laboratory	MGI: 4421514
Software and Algorithms
CellFIT-3D
Imaris, version 8.4		www.imaris.com
Fiji, version 2.0.0-rc-43/1.51j		https://fiji.sc/
Prism 7		https://www.graphpad.com/scientific-software/prism/
Matlab, R2017a		https://www.mathworks.com/
Micromanager, version 1.4		https://micro-manager.org/
Other
ViroMag	OZ Bioscience	#RL400200
24-well glass bottom plates	Greiner Bio-One	662892
96-well low adherent plates	ThermoFisher	174907
Immersion medium Immersol W 2010	Zeiss	444969

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information about experiments, modeling, and requests for reagents may be directed to, and fulfilled by, the Lead Contact, Andrew Ewald (andrew.ewald@jhmi.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Mice

Mouse husbandry and experimental procedures were conducted in accordance with protocols approved by the JHU Medicine Institutional Animal Care and Use Committee. A transgenic mouse line expressing tdTomato (FVB strain) was used to label cell membranes and acquired from the Jackson Laboratories (Muzumdar et al., 2007) (Jackson Laboratory, #007676). A transgenic mouse line expressing K14-actin-GFP/mTmG (Vaezi et al., 2002) was used to follow the myoepithelial population in relation to the luminal population. FVB/n mice (Jackson Laboratory) were used for inhibitor experiments.

METHOD DETAILS

Mouse Genotyping

Fluorescent mice were visually genotyped by observing the presence of either RFP or GFP expression on 1 mm tail-clippings from 3-week pups on an epifluorescence microscope.

Three-Dimensional Mammary Gland Organotypic Culture

We performed 3D primary mammary organotypic culture, as previously described (Ewald et al., 2008; Nguyen-Ngoc et al., 2015). Briefly, mammary glands (#3, 4, and 5) are harvested from 8-12 wk old mice, mechanically minced with #10 blade scalpel, and shaken at 150 RPMs for 60 min at 37°C in collagenase solution, composed of DMEM-F12 (Gibco, #10565-018), 2 mg/mL collagenase (Sigma, C2139), 2 mg/mL trypsin (Gibco, 27250-018), 5% heat-inactivated FBS (Sigma, F0926), 5 μg/mL insulin (Sigma, I9278), and 50 μg/mL gentamicin (Gibco, 15750). Digested glands are centrifuged at 423g to separate the stroma and adipose (supernatant) from the epithelium (pellet), which is then treated with 2 U/μL DNase (Sigma, D4263). Next, organoids are filtered through a 100μm nylon filter (Corning, CLS431752) to remove nerve bundles, followed by four differential centrifugations (3 sec, 423g) to removed enzymes, single cells, and enrich for organoids, each of which is an intact, heterotypic cell cluster (approximately 100 μm in diameter) composed of several hundred cells. Organoids were then embedded in a 3D matrix composed of equal parts Matrigel (Corning, 354230, ~9.0 mg/mL) and fibrillar rat tail collagen-I (Corning, 354236) at 1-2 orgs/μL in 24-well coverslip-bottomed plates (Greiner Bio-One, 662892) over a 37°C heating block. Gels were polymerized for 30 min in an incubator at 37°C and then cultured in organoid medium, composed of DMEM-F12, 1% insulin-transferrin-selenium (Gibco, 51500-056) and 1% penicillin-streptomycin (Sigma, P4333). Branching morphogenesis was induced by the addition of 2.5 nM FGF2 (Sigma, F0291). Branching was scored as organoids with three or more elongated buds.

Infection of Mammary Organoids

Adeno-GFP (Vector BioLabs, Cat. No. 1060) or Adeno-LifeAct-GFP or -RFP (Ibidi, Cat. No. 60121 and 60122) were added after organoid isolation, prior to suspension in ECM. Isolated organoids were centrifuged in an Eppendorf tube at 520 g for 10 min. The supernatant was removed and organoids were resuspended in 100 μl DMEM-F12 (Gibco). Adenovirus was added at 5000-10,000 plaque-forming units per organoid to achieve gene expression in ~50 percent of cells. Organoids were incubated with virus for 1 h at 37°C and then washed twice with DMEM-F12 and suspended in ECM for plating. Lentiviruses encoding Raf1-(RBD)-GFP (Bondeva et al., 2002; Sasaki et al., 2004; Taylor and Shalloway, 1996) and PH-Akt-GFP (Addgene #51465) (Varnai and Balla, 1998) mixed at 100,000 PFUs with 3 μL of Viromag (OZ Bioscience, #RL400200) into 50 μL of DMEM-F12 and incubated for 30 min at RT. Organoids were plated at 1,500 orgs per well in a 96-well non-adherent plate (Thermo, #174907) and allowed to gravity settle for 30 min. Lentivirus was then mixed with organoids and incubated on top of a magnetic plate (OZ Bioscience, #MF10000) for 90 min and then incubated overnight at 37°C. Organoids are then washed twice with DMEM-F12, suspended in ECM, and plated.

Pharmacological Inhibitors

Pharmacological inhibitors were used at the indicated doses. Unless otherwise noted, inhibitors were dissolved using DMSO and DMSO was used as vehicle control at 1/1000. Caspase inhibitors (Enzo Life Sciences) were added at 2 μM on day 0 in culture and changed every 3 days until fixation and imaging at day 10. Inhibitors include pan-caspase inhibitor (ALX-260-138), caspase-3 inhibitor (ALX-260-141), caspase-9 inhibitor (ALX-260-145), and scrambled negative control (ALX-260-148). The Arp2/3 complex inhibitor CK-666 (Sigma, SML0006) and PI3K inhibitor LY-294002 (Sigma, L9908) were added on day 0 in culture, then fixed and imaged at day 7. Actin turnover was inhibited using a combination of 8 μM Jasplakinolide (Tocris, 2792) to decrease actin disassembly, 1.25 μM Latrunculin A (Tocris, 3973) to decrease assembly of actin, and 10 μM Y-27632 (Calbiochem, 688000) to decrease ROCK activity, termed ‘JLY’ (Peng et al., 2011). For confocal time-lapse imaging, images were acquired for 4-6 hours, at which point either the described concentration of either LY-294002, CK-666, or JLY was added and imaging resumed.

Immunofluorescence

Organoids grown in 3D with 1:1 ratio of Matrigel to fibrillar collagen-I were fixed in 4% paraformaldehyde for 12 min, rinsed three times in PBS for 10 min, and then prepared for immunofluorescence (IF). For antibody staining, samples were permeabilized with 0.5% Triton X-100 for 45 min and then blocked for 3 h at room temperature (RT) with 10% FBS/0.1% Triton X-100, incubated with primary antibodies overnight at 4°C in 1% FBS/0.1% Triton X-100, and rinsed three times in 10% FBS/0.1% Triton X-100 three times for 10 min. Incubation with secondary antibodies was conducted in 1% FBS/0.1% Triton X-100 overnight at 4°C or for 2 h at RT. Gel s were rinsed three times in PBS for 10 min. F-Actin was stained with Alexa Fluor Phalloidin-561 (1:100; Invitrogen), and nuclei were stained with DAPI (1:1,000; D3571; Invitrogen). Immunofluorescence staining for each antibody was performed at least three independent times for a minimum of 10–15 organoids. Primary antibodies used were rabbit cleaved caspase-3 (1:500; Cell Signaling Technology, #9579) and rabbit phospho-myosin light chain 2 (1:500; Cell Signaling Technology, #3671). Secondary antibodies used were all Alexa Fluor–conjugated antibodies (1:200; Invitrogen).

Confocal Fluorescence Microscopy

Confocal imaging was performed on a spinning-disk confocal microscope (Solamere Technology Group Inc.) with a iXon3 885 EM-CCD camera (Andor), as previously described (Ewald et al., 2011; Ewald, 2013). An LD C-Apochromat 40×/1.1 W Korr objective lens (Carl Zeiss) was used for high magnification single and time-lapse image acquisition, with water and Immersol (Carl Zeiss) used as the imaging mediums, respectively. Acquisition of both single and time-lapse images was performed using a combination of μManager (Edelstein et al., 2010) and Piper (Stanford Photonics, Inc.). For time-lapse imaging, images were collected at 1 to 15-min intervals for 1 to 24 hours with 0.5-2 μm z-steps for 1-3 channels (excitation at 488 nm, 561 nm, and 641 nm), and temperature was maintained at 37°C and CO₂ at 5%.

Differential Interference Contrast (DIC) Microscopy

Differential interference contrast images of mammary organoids were conducted using an LD Plan-Neofluar 20×/0.4 Korr Ph2 objective lens and a Cell Observer system with an AxioObserver Z1 and an AxioCam MRM camera (Carl Zeiss). In general, 3D mammary cultures were fixed with 4% PFA for 12 min and washed 3 times for 10 min with PBS prior to imaging. The images were acquired with organoids in PBS. AxioVision (Carl Zeiss) was used to acquire images, place scale bars, and export individual TIFFs. Fiji was used to adjust levels on entire images to maximize image clarity.

QUANTIFICATION AND STATISTICAL ANALYSIS

Figure legends describe the statistical test and the associated parameters used to analyze the data. Asterisks indicate statistical significance as explained in each figure legend (*, p < 0.05; **, p < 0.01; ***, p < 0.001; ****, p < 0.0001). The following statistical tests were performed: Wilcoxon, Mann-Whitney, and ANOVA.

Analysis of Mammary Organoids

Imaris 8 (Bitplane) was used to analyze time-lapse movies, place scale bars, adjust levels and gamma for each channel on entire images to maximize image clarity, and export individual TIFFs. Additional adjustments for brightness, contrast, and levels, if necessary, were done using Adobe Photoshop. A minimal 0.137 μm Gaussian image filter was applied across the entire image field, where appropriate, to maximize image clarity. Images were cropped using the clipping mask function within Adobe Illustrator.

Figures 1G,H: Colocalization images were produced using the ‘Coloc’ function within Imaris by visual inspection of the 2D histogram. The results were then converted to a new colocalization channel and the jet look up table was used for visual clarity.

Figures 2A,B,G,H: the number of branched organoids was counted using a 10× objective per well per condition, with 2 technical replicates.

Figures 2C,I: Cells were tracked using the ‘Spots’ function within Imaris. Representative tracks from multiple organoids and biological replicates were imported into a single Imaris scene. The Tracks Function ‘Translate Tracks’ was used to have pre-inhibitor and then post-inhibitor treated organoids originate from a common origin.

Figure 4B: organoid branches were divided into body, stalk, middle, and front. Middle and front regions were primarily stratified, the stalk was a connector region, and the body is the main organoid. Each intercalation event was assigned to a region manually using Imaris 8.

Figure 4C: Basal residence time for intercalations was classified in the following way – Transient intercalations were quantified from movies of least 12 hours in length and could track the cell for a minimum of 6 hours. Permanent intercalations were quantified from movies of minimum 24 hours in length, could track the cell for a minimum of 16 hours, and the cell remained at the basal surface for a minimum of 12 hours.

Figures 6C–I: To quantify the basal surface area, organoid were rotated in Imaris, such that the cell can be cropped and then MIP orthogonally in either the YZ or XZ plane. 5 μm section was chosen to characterize the ‘basal surface’ for MIP. The surface was then rendered in the appropriate cytoplasmic marker channel (either eGFP or CFP). The data was then quantified over time. The maximum basal area was the maximum size (in μm²) of the basal surface area. The rate of basal expansion is the maximum basal area reached divided by the number of hours to reach that maximum.

Supplemental Figure S1: The ‘Standardized Biosensor Enrichment Ratio’ is defined by a 2 μm by 2 μm square within Fiji. The ROI is then placed over the appropriate enrichment (identified by eye) of the biosensor. The mean value is measured within Fiji for both the biosensor and the membrane marker (membrane tdTomato) – this is called ‘region 1’. Then a region with a clearly identifiable membrane marker (in the membrane tdTomato channel) is chosen within a maximum of 4 z-stacks above or below the protrusion within that same cell and the ratio of biosensor to membrane is then obtained – this is called ‘region 2’. Then a ratio of region 1 divided by region 2 is obtained – this is defined as the standardized biosensor enrichment ratio. It was applied for 7 different conditions on two types of cells. The first type of cell is an intercalating cell. The ‘protrusion’ is identified first and the ratio analysis is performed. Then a region prior to the protrusion forms is chosen as the ‘pre-protrusion’. The ratio analysis is performed on this. The same analysis is then performed on the region after the protrusion occurs called the ‘basal expansion’ and then once the cell completes intercalation, this ratio analysis is performed on the ‘columnar’ shape. The second type of cell is a migrating cell. The same analysis, as above, is performed by identifying a ‘protrusion’, then a ‘pre-protrusion’, followed by a ‘post-protrusion’. This analysis was performed for the three molecular biosensors used in the article.

Supplemental Figures S2A–D: Viability of organoids treated with CK-666 was assessed using Calcein green AM (ThermoFisher, C3100MP). 2.5 μM Calcein green (dissolved in DMSO) was incubated for 1 hour at 37C with organoids, washed 3 × 20min with DMEM/F12 at 37C, then incubated for 30 min. The organoids were then quantified and imaged using DIC and epifluorescence.

Supplemental Figure S2: Organoids pre and post treated with indicated inhibitors were exported from Imaris to Fiji, z-projected, thresholded for cells of interest, selected images were then placed into a hyperstack and the Fiji plugin “Temporal-Color_code.ijm” was used to create a color-coded time series projection.

Supplemental Figures S3C and S3F: nuclei were quantified in the DAPI channel using ‘Spots’ in Imaris 8. Parameters were: ‘Estimated XY Diameter’ = 5 μm, ‘Background Subtraction’ on, and ‘Quality’ metric >25. Analyses were conducted uniformly across all z-stacks. CC3⁺ spots were manually counted for each z-stack and the %CC3⁺ cells were calculated per branch.

Supplemental Figure S4A: Computational rendering of images was performed using the ‘Surfaces’ function within Imaris 8 and applied to regions of interests – intercalating cells (green), basally located cells (light gray, white), lumen (dark gray), and organoid branch (red).

Supplemental Figure S4B: Confocal movies with three labels were acquired: K14-actin-GFP (representing the myoepithelial population), membrane tdTomato (the luminal population), and infected the organoids with a cytoplasmic marker (adenoviral delivered cytoplasmic cyan fluorescent protein, CFP). We acquired movies during active elongation (from day 4 to day 7) to observe radial intercalations. Of the luminal cells that undergo radial intercalation, they were observed throughout each movie for potential expression of GFP, indicating a conversion to the K14, myoepithelial fate. A 0.5 μm Gaussian blur was applied to the cyan channel.

Interfacial Tensions

The computational modeling follows the Differential Interfacial Tension Hypothesis (DITH) in assuming the specific tensions acting along each cell-cell interface arise from contractile cytoskeletal systems within the cell and along the membrane (Brodland, 2002). These contractions are reduced by the contact forces produced by any adhesion systems, in accordance with Eqn [1] (Chen and Brodland, 2000).

$${\mathrm{\gamma }}^{\text{AB}}={\mathrm{F}}_{\text{MF}}^{\mathrm{A}}+{\mathrm{F}}_{\text{MF}}^{\mathrm{B}}+{\mathrm{F}}_{\text{Mem}}^{\mathrm{A}}+{\mathrm{F}}_{\text{Mem}}^{\mathrm{B}}+{\mathrm{F}}_{\text{Other}}^{\text{AB}}-{\mathrm{F}}_{\text{Adh}}^{\text{AB}}$$ [1]

where γ^AB is the net interfacial tension along the interface between cells A and B, ${\mathrm{F}}_{\text{MF}}^{\mathrm{A}}$ and ${\mathrm{F}}_{\text{MF}}^{\mathrm{B}}$ are the tensions produced along the edges of cells A and B, respectively, by cortical actomyosin. ${\mathrm{F}}_{\text{Mem}}^{\mathrm{A}}$ and ${\mathrm{F}}_{\text{Mem}}^{\mathrm{B}}$ are the membrane tensions in cells A and B due to tension in the plasma membrane and any associated protein networks, ${\mathrm{F}}_{\text{Other}}^{\text{AB}}$ is the tension from any other contractile systems along that interface, and ${\mathrm{F}}_{\text{Adh}}^{\text{AB}}$ is the strength of the adhesion force between cells A and B. The reason that adhesion forces reduce the cortical tensions, and do so by the same amount as their strength (when appropriate units are used), is that they tend to increase the size of the contacting area by the amount of the area in which new adhesions are allowed to form. The other forces tend to reduce this area. In the case of an interface between a cell A and medium M, Equation [1] simplifies to

$${\mathrm{\gamma }}^{\text{AM}}={\mathrm{F}}_{\text{MF}}^{\mathrm{A}}+{\mathrm{F}}_{\text{Mem}}^{\mathrm{A}}+{\mathrm{F}}_{\text{Other}}^{\text{AM}}-{\mathrm{F}}_{\text{Adh}}^{\text{AM}}$$ [2]

where ${\mathrm{F}}_{\text{Adh}}^{\text{AM}}$ represents molecular forces associated with affinity between the cell surface and the medium.

Finite Element Modeling (FEM)

Computational models were implemented using custom FE code, with each cell modeled individually, and each of its edges modeled as a polyline to approximate the curvature of cell-cell interfaces (Perrone et al., 2016) and assigned tension values specific to the simulation. The lumen was maintained by volume-filling virtual elements that contributed insignificant additional tensions. Modeling individual cells and interfaces allows for each element to be described by rigorous mathematical equations derived from physics, quantitative biology, mechanics. The resulting equations are cast into matrix form and assembled in such a way that interactions between the pieces can be accurately modeled. Complex coupling and non-linear interactions can be handled with relative ease and precision if appropriate iterative solvers are used (Brodland, 2004; Chen and Brodland, 2000).

The interfacial tensions, acting tangent to cell-cell interfaces, cause local displacements at cell junctions which lead to cell motions and tissue rearrangements (Brodland, 2002). In this study, the forces in the cells were resolved into two primary types, active tensions γ along each cell-cell or cell-medium boundary, and a passive viscosity μ in the interior of each cell. As noted in equations 1 and 2, these interfacial tensions arise from a variety of cortical forces, and as noted elsewhere, the viscosity was assumed to represent the response of the cytoplasm, organelles, and filamentous networks (Brodland et al., 2007; Chen and Brodland, 2000).

For each time increment in the simulations, the vector sum of the interfacial tensions framing into each three-cell junction (triple junction) is calculated and placed into a system of matrix equations that also involve the corresponding contributions from the viscous dashpot systems (Brodland et al., 2007; Chen and Brodland, 2000). Solving the system of equations yields the incremental triple junction displacements occurring during each time increment, such that the viscous forces induced by cytoplasm deformation just balance any imbalanced interfacial tension forces. The locations of the triple junctions are updated and the mathematical procedure is repeated for the next time increment. Algorithms for cell rearrangement (Chen and Brodland, 2000) and polyline segment refinement (Perrone et al., 2016) are utilized.

Finite element models have a number of features of particular interest in the study of biological systems, such as the interactions between multiple cells each with its own time-varying characteristics. One of these features is the ability of the FE model to predict how those cells would interact with each other, and in appropriately-designed models, to show the motions of the cells, the nature of their interfaces and even the contact angles that form at their triple junctions (Brodland, 2004; Perrone et al., 2016). Another feature is that the properties of single cells or groups of cells can be specified arbitrarily by the user, and the values of those properties adjusted precisely and to any degree desired. This feature allows the user to test hypotheses about the forces that could drive particular cell motions, and in particular to eliminate from consideration mechanisms that do not in fact generate observed patterns of motion (Brodland, 2002). The user can also modulate any particular property at will, to test the sensitivity of the system to individual parameters.

In this study, custom C++ code was written so that the model could represent the generation and contraction of protrusions, linearly varying tension gradients, and mechanical responses to changes in neighbors or contact surfaces. One might wish for a 3D model (Brodland, 2004), but until the curvilinear interfaces made possible by 2D polyline representations are available in 3D, it is necessary to choose between 3D models with simplified faces and polyline 2D models. Membrane flexibility is crucial to cell rearrangements of the kind of interest here (Perrone et al., 2016), and so we chose to use a 2D polyline model of a longitudinal section of the duct. One might argue that only one side of the duct needs to be modeled since that side could be rotated about the long axis of the duct to generate its full axisymmetric geometry. We chose instead to model both sides so that consistency between two simultaneous simulations could be assessed and so that any inherent mechanical instabilities that might exist in the system would be more likely to manifest.

The FE models are reported using a dimensionless time parameter defined by Equation 12 (Wayne Brodland and Veldhuis, 2003); which accounts for model characteristics such as average tension magnitude and mesh density, and allows for time comparison between models.

Cellular Force Inference Toolkit in Three Dimensions (CellFIT-3D)

Finite element studies of cells carried out over the last several decades showed that the structures they form, as well as their shapes and contact angles depend on the relative strengths of the tensions γ that act along each cell-cell or cell-medium interface (Brodland, 2004; Perrone et al., 2016). In contrast, μ the effective viscosity of the cytoplasm and the scaling of the tensions γ affect the rate at which reshaping occurs. Even relatively subtle changes in the ratios of the tensions γ can affect the geometries and contact angles produced, and this observation initiated a quest to determine whether tension ratios could be inferred from cell geometries. CellFIT makes it possible to not only infer these tensions, but to obtain estimates of their precision (Brodland et al., 2014; Veldhuis et al., 2017).

Maps of cell edge tensions were created using CellFIT-3D (Veldhuis et al., 2017). This technique assumes that cell-cell interfacial tensions are the primary drivers of motion and it constructs and solves force-balance equations at the curvilinear triple junctions (triple edges) where three cells meet. The cell of interest and its immediate neighbors were segmented using a watershed algorithm (Mashburn et al., 2012) and segmented outlines in successive sections were grouped by cell and used to reconstruct triple edges. Cell boundaries in confocal images may seem well defined; however, noise, gaps, and other anomalies become apparent at the pixel level. To reduce any errors introduced by poorly defined edges and to eliminate unnecessary effort, a minimal neighborhood around the cell of interest was digitized. Planes were constructed normal to spline-based approximations of curvilinear edges and geometric projection techniques were used to reconstruct the dihedral angles of cells in these planes (Brodland et al., 2014). Manual angular adjustments were made, as needed. Cell boundaries were assumed to be curved and local curve fitting was used to obtain best approximations of these angles in each plane. Data from multiple planes along each triple edge were used to optimize angle measurements and confirm reliability. Angle measurements at triple edges gave rise to a pair of equilibrium equations that relate the relative tensions in the three faces that meet there. The tensions acting along these faces were assumed to be isotropic and constant over that face, and so the pairs of equations arising from the various edges along the perimeter of any one face can be related to each other, and used to produce a master set of simultaneous equations. These equations were overdetermined and were solved in a least-squares sense to optimize solution accuracy, verify the mutual compatibility of the various dihedral angle equations, assess the power of the available equations to offer a trustworthy solution and estimate the accuracy of the tension calculated for each cellular face (Veldhuis et al., 2017). The constraints of the system of equations were modified from previous iterations where the mean of the interfacial tension magnitudes equals one. To measure local changes in tension strength along anterior protrusions and the posterior end of a migrating cell, other interfacial tensions in the observed patch of cells were set to have magnitudes of one.

DATA AND SOFTWARE AVAILABILITY

No novel gene sequences, protein sequences, structures, or microarray data were generated in this study. Comprehensive methods were provided for each technique used in the study; further information regarding protocols will be made available upon request to the corresponding author (AJE). All molecular reagents, animal models, and image analysis / 3D visualization software are commercially available, as indicated in the Resource Table.

Supplementary Material

1

Movie S1, Related to Figure 1G. Epithelial cells concurrently enrich PI3K activity and polymerized actin in protrusions during intercalation.

3D confocal projection of an intercalating cell concurrently enriching PI3K activity and polymerized actin to its anterior membranes. PI3K activity (PH-Akt-GFP, green); F-actin (LifeAct-RFP, red). Scale = 10 μm; Timescale = hh:mm.

Movie S2, Related to Figure 2F. Epithelial cells fail to initiate protrusions following treatment with ‘JLY’ to inhibit actin dynamics.

3D confocal projection of organoids treated with a combination of Jasplakinolide, Latrunculin A, and Y-27634 (termed ‘JLY’) to inhibit actin dynamics. The organoid is imaged briefly, followed by addition of JLY and additional imaging. The cells round up and continue to focally enrich PI3K activity, but fail to generate protrusions. PI3K activity (PH-Akt-GFP, green); membranes (tdTomato, red). Scale = 20 μm; Timescale = hh:mm.

Movie S3, Related to Figure 4D. Epithelial cells undergo radial intercalation.

3D confocal projection of a cell migrating, intercalating, and transitioning to columnar morphology during branch elongation. Membranes (tdTomato, red); cytoplasm (GFP, green). Scale = 20 μm; Timescale = hh:mm:ss.

Movie S4, Related to Figure 5A. Epithelial cells enrich Ras activity in protrusions during intercalation.

3D confocal projection of an intercalating cell enriching Ras activity to its anterior membranes. Ras activity (Raf1(RBD)-GFP, green); membranes (tdTomato, red). Scale = 20 μm; Timescale = hh:mm.

Movie S5, Related to Figure 5B. Epithelial cells enrich PI3K activity in protrusions during intercalation.

3D confocal projection of an intercalating cell enriching PI3K activity to its anterior membranes during intercalation. PI3K activity (PH-Akt-GFP, green); membranes (tdTomato, red). Scale = 5 μm; Timescale = hh:mm.

Movie S6, Related to Figure 5C. Epithelial cells enrich polymerized actin in protrusions during intercalation.

3D confocal projection of an intercalating cell enriching F-actin to its anterior membranes. F-actin (LifeAct-GFP, green); membranes (tdTomato, red). Scale = 10 μm; Timescale = hh:mm.

Movie S7, Related to Figure 5D. Radial intercalation can elongate a field of cells using a combination of anterior protrusion, posterior tension gradient, and boundary capture mechanism, within a finite element model.

This movie shows a finite element model (FEM) of a successful tissue elongation through radial intercalation using a combination method of anterior protrusions, posterior tension gradient, and boundary capture mechanism. Cells were randomly chosen (light green) to intercalate towards the high-tension surface (line width indicates relative tension strength). Cells in permanent contact with the high-tension surface were colored dark green and cells that temporarily contact were colored olive green. Movie dimensions: 960 × 540 pixels and 48 frames/sec.

Movie S8, Related to Figure 7A,B. In silico terminal ends buds with hoop stress can elongate using radial intercalation, within a finite element model.

These movies show a finite element model (FEM) of an in silico terminal end bud (TEB) with (A) radial intercalation driven by a combination method of anterior protrusions, posterior tension gradient, and boundary capture mechanism. The tissue fails to elongate and instead forms disorganized buds on the surface. (B) With the addition of high basal tension and in-plane stress applied towards the organoid center-line (hoop stress), the tissue elongates successfully and restores bilayered organization over most of the tube length. The high basal tension was functionally encoded by the myoepithelium (red). Cells were randomly chosen to intercalate (yellow), with random protrusion and tension gradient strengths, towards the basal surface. Outer luminal cells or cells that transition to contact the basal surface were colored dark green. The lumen was modeled using multiple, non-contributory elements (white). Cells within the stratified layer were modeled to migrate and divide. The in silico TEB in (B) was modeled to have the same initial condition and shape as (A), but with added hoop stress. The hoop stress was initiated at t=0, resulting in large initial shape alterations. Movie dimensions: (A) 640 × 476 pixels and 64 frames/sec and (B) 640 × 260 pixels and 64 frames/sec.

Highlights.

• Cells in epithelial tissues display a similar migratory logic as single cells

• Migration through tissues requires specific interfacial tension ratios

• Intercalation at the tissue surface couples migration to tube elongation

• Molecular signaling coordinates with cell and tissue mechanics to elongate tubes