Developing a Reference of Normal Lung Sounds in Healthy Peruvian Children

Abstract

Purpose

Lung auscultation has long been a standard of care for the diagnosis of respiratory diseases. Recent advances in electronic auscultation and signal processing have yet to find clinical acceptance; however, computerized lung sound analysis may be ideal for pediatric populations in settings, where skilled healthcare providers are commonly unavailable. We described features of normal lung sounds in young children using a novel signal processing approach to lay a foundation for identifying pathologic respiratory sounds.

Methods

186 healthy children with normal pulmonary exams and without respiratory complaints were enrolled at a tertiary care hospital in Lima, Peru. Lung sounds were recorded at eight thoracic sites using a digital stethoscope. 151 (81 %) of the recordings were eligible for further analysis. Heavy-crying segments were automatically rejected and features extracted from spectral and temporal signal representations contributed to profiling of lung sounds.

Results

Mean age, height, and weight among study participants were 2.2 years (SD 1.4), 84.7 cm (SD 13.2), and 12.0 kg (SD 3.6), respectively; and, 47 % were boys. We identified ten distinct spectral and spectro-temporal signal parameters and most demonstrated linear relationships with age, height, and weight, while no differences with genders were noted. Older children had a faster decaying spectrum than younger ones. Features like spectral peak width, lower-frequency Mel-frequency cepstral coefficients, and spectro-temporal modulations also showed variations with recording site.

Conclusions

Lung sound extracted features varied significantly with child characteristics and lung site. A comparison with adult studies revealed differences in the extracted features for children. While sound-reduction techniques will improve analysis, we offer a novel, reproducible tool for sound analysis in real-world environments.

Introduction

Since the invention of the stethoscope by Laennec in 1819, few advances have been made in the field of auscultation. More recently, electronic stethoscopes and digital signal processing have grown in popularity but have yet to find clinical acceptance [1–7]. Acoustic information captured by clinical auscultation is limited by frequency attenuation due to the stethoscope, ambient noise interference, interobserver variability and subjectivity in differentiating subtle sound patterns [8–10].

Computerized technologies come as a natural adjunct to aid in the diagnosis of respiratory disease and may be ideal for a pediatric population, especially in settings where skilled healthcare workers are unavailable. Electronic auscultation and automated analysis are advantageous for a number of reasons. They provide standardized methods for sound acquisition and enable continuous monitoring and analysis, which allows for a deeper understanding of the mechanisms that produce adventitious respiratory sounds. Finally automated interpretation of auscultatory findings may offer diagnostic potential for use by community health workers or other first line providers in low resource settings.

Existing approaches in the literature use techniques to capture spectral and temporal details of adventitious sounds like wheezes and crackles, employing frequency analysis [3, 11], time–frequency and wavelet analysis [7, 11–13], image processing methods [14], or comparison with reference signals. In most studies, however, auscultation recordings have been limited to adults and acquired in a controlled, near-ideal environment, where ambient noise was limited. In this study, we aimed to obtain better insight into the signal characteristics of lung sounds in healthy children without respiratory complaints recorded in a noisy hospital environment. We present an alternative signal-processing scheme and describe features of normal lung sounds in healthy children. By characterizing normal lung sounds in healthy children, our group aims to utilize these features to better differentiate pathologic sounds associated with respiratory disease in children.

Methods

Study Design

We enrolled 186 children without respiratory complaints from outpatient clinics at the Instituto Nacional de Salud del Niño in Lima, Peru between January and November 2012. Inclusion criteria were: (1) age 2–59 months, (2) no active respiratory complaint, and (3) normal respiratory exam performed by a skilled physician. Exclusion criteria were: (1) history of chronic lung disease excluding asthma, (2) significant cardiac disease, and (3) acute respiratory illness within the past month. We obtained informed consent from parents in the Emergency Department (ED) or outpatient clinics, where testing was performed in a single visit. Detailed methods are described in detail elsewhere [15]. The study was approved by the ethics committees of the Instituto Nacional de Salud del Niño and A.B. PRISMA in Lima, Peru, and the Johns Hopkins School of Medicine in Baltimore, USA.

Electronic Auscultation

We recorded lung sounds at 44.1 kHz using a digital stethoscope (ThinkLabs ds32a, Centennial, Colorado, USA) and a standard MP3 recorder at each of the following eight thoracic sites for 10 s: left and right anterior superior (AS), right and left antero-lateral inferior (AI), right and left posterior superior (PS), and left and right posterior inferior (PI). The ThinkLabs stethoscope contains a diaphragm, behind which is a metal plate that allows conversion of sound to an electronic signal at the level of the patient. Lung sounds were obtained as in most clinical settings, with the diaphragm in contact with the skin of the patient. The examiner adjusted the pressure applied to the diaphragm based on the cleanliness of sound he/she appreciated through the earpieces and the cooperation of the patient.

We obtained lung sounds recordings when the child was breathing normally without being asked to take deep breaths. Although not ideal for sound quality, deep breathing was not expected of infants and young children in real-world clinical settings for a few reasons. Developmentally, following simple commands occurs around age of 18 months, and realistically, sick, irritable children often refuse or are unable to breathe deeply due to tachypnea. All children were supine or upright and often were held by a parent during sound recording.

Computerized Lung Sound Analysis

Acquired signals were low-pass filtered using a fourth order Butterworth filter at 1 kHz cutoff, down-sampled to 2 kHz, and normalized to have zero mean and unit variance (Fig. 1). This was done because 91 % of the total signal energy was found in frequencies below 1 kHz. Sounds were processed into short-time 2-s segments using a rectangular window with 50 % overlap.

Fig. 1.

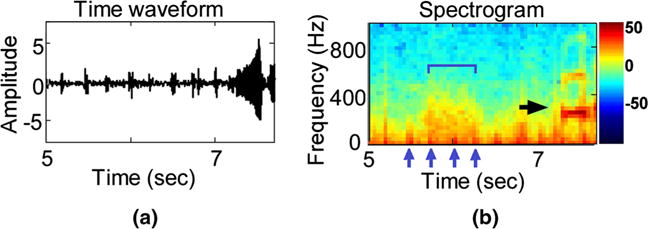
Recording excerpt of one study subject. Top the time waveform. Bottom the corresponding spectrogram representation, calculated on a 64 ms Hanning window with 50 % overlap. A processing window of 2-s duration is marked within the black margins. The two arrows indicate recorded noise, in the form of stethoscope movement (short burst of energy at 4.9 s) and cry (longer duration interval starting at 7.2 s). The color bar is shown in decibels (db)

Noise Segment Removal

We excluded segments judged as either non-informative or contaminated with noise from our analyses. We defined non-informative segments as intervals whose amplitude was less than 20 % of the average signal’s amplitude, typically corresponding to silent segments; and, segments contaminated with noise as those characterized with irregular high frequency contents in the range of 200–500 Hz, which corresponds with children’s crying [16–18]. Increased energy in the power spectrum was defined relative to a uniform threshold and set to 1E–07, to ensure that no false positives were produced during exclusion. (see Fig. 2a for an example of a crying interval.) The power spectrum was obtained using a 2¹⁴-point Fast Fourier Transform [25] and was further smoothed by a low-pass fifth order Butterworth filter at 20 Hz to better capture regions of increased frequency contents. The above criterion was developed considering the current sample of healthy children. Extension of this approach to children with respiratory disease will require caution and further refinement to account for any abnormal sounds with overlapping spectral components.

Fig. 2.

a Power spectrum computed from the 2-s window marked in Fig. 1 bottom, and a power spectrum of an interval containing crying (dashed line). The peak width feature (PW) is marked. Inset shows the logarithmic spectrum (dashed line) and the corresponding regression line (solid line). The slope of the regression line (SL) is −11.26 dB/octave and is marked together with an octave interval. b The average subject profile of the power spectrum, as calculated using a short-time FFT, smoothed with a Butterworth low-pass filter. The dashed lines depict variations among different subjects. c Schematic representation for the extraction of the Spectral shape profile. Spectrogram information was processed for each time index and passed through a bank of 31 filters varying from narrowband (ex. top filter shown), capturing the peaky contents, to broadband (ex. bottom filter shown) capturing the smooth contents. For display purposes, spectrogram was computed on a 64 ms Hanning window with 50 % overlap. d The average profile for the spectral shape over all subjects. Dashed lines depict the variation among subjects, and the vertical bold line indicates the separation of contents below and above 1 cycle/octave. e Schematic representation for the extraction of the temporal modulation profile. Spectrogram information was processed along each frequency band and passed through a bank of 23 filters varying from high/fast rates (filters shown on the left) to low/slow rates (filters shown on the right), for both positive phase-downward direction (+) and negative phase-upward direction (−), capturing the changes of the frequency content along time. For display purposes spectrogram was computed on a 64 ms Hanning window with 50 % overlap. f The average profile for the temporal modulations over all subjects. Dashed lines depict the variation among subjects. Notice the strong energy around the region of −1 Hz and 2 Hz

Biostatistical Methods

We extracted ten unique parameters from the spectral and spectro-temporal representations of recordings from individual children (Table 1). The spectral analysis captures information about the frequency content of the recorded signal such as slow or fast variations in the signal and includes parameters such as peak width (PW), the spectrum slope (SL), power of regression line (PLN), and power ratio (PR). These features highlight energy concentration along frequency regions and were extracted from the smoothed power spectrum described above. In addition, Mel-frequency cepstral coefficients (MFCC) features were extracted. They encode information about the chest shape and resonances of lung sounds. Finally, more complete joint time–frequency parameters were extracted, including spectral shape and temporal modulations, to give a better representation of the dynamic changes (or modulations) in the frequency content of lung sounds. Preliminary analysis revealed linear associations between spectral/spectro-temporal signals and basic clinical information. We, therefore, used multivariable linear regression to model each of the spectral and spectro-temporal parameters as a function of age, weight, height, and gender, and determined goodness-of-fit with the coefficient of determination (see Online Supplement). A complete analysis was also performed for each auscultation site by combining both left and right recoded signals from AS, AI, PS, and PI sites. We conducted one-way ANOVA to determine if there were differences among thoracic sites. We used Matlab (www.mathworks.com) and R (www.r-project.org) for analyses.

Table 1.

Spectral and spectro-temporal parameters

Peak width (PW)	The peak width of the smoothed power spectrum, P. The peak of the spectrum was identified in the range of 0–200 Hz. Its width was measured at 75 % of the corresponding height (Fig. 2a)
Spectrum slope (SL)	The slope of the linear regression line, fit to spectrum P in logarithmic axes. The power spectrum, when plotted in dB as 20 log (P/Pmin) with Pmin = 5 E–05, was previously shown to decrease exponentially with frequency for contents higher than 75 Hz [19]. SL is measured in dB/octave, where an octave represents the interval needed to double the frequency (Fig. 2a inset)
Power of regression line (PLN)	The power of the area under the regression line
Power ratio (PR)	The power ratio is defined as PR = 1 – I1 – Espectrm/EregressionI, where Espectrm is the area under the logarithmic spectrum and Eregression is the area under the regression line. These areas are computed using trapezoidal integration method. A power ratio value close to 1 means that the logarithmic spectrum follows the regression line closely [19]
Mel-frequency cepstral coefficient (MFCC)	Mel-frequency cepstral coefficients encode information about the peak energies or resonances of a sound signal and are indirectly related to the impulse response of the system used to produce the sound. In our study, we can consider the chest as a solid system and the resulting MFCC coefficients as indicators of its impulse response. As the lung sound signal is recorded after traveling through various chest chambers, different chest formations are expected to yield variations in the MFCCs (see Online Supplement A). MFCC sequences can be calculated using filters centered at various frequencies. For the current study, three coefficients (MFCC1, MFCC2, MFCC3) were kept for each subject by averaging over all short-time extracted MFCCs, corresponding to filters centered at frequencies {56, 116, 181} Hz respectively
Spectral shape (scales)	Scales estimate how broad or narrow the spectral profile is. These spectral modulations reflect how contents vary along frequency and were calculated from the auditory spectrogram, modeling the cochlear representation of sounds, calculated over 8 ms window. The auditory spectrogram was filtered using 31 Gabor-shape seed filters, logarithmically spaced, and varying from wideband to narrowband: 0–8 cycles/octave (c/o) [26, 27]. The response, produced for each scale and time index, was averaged over time to yield the scale profile. Low scale values (<1 c/o) corresponded to a very smooth spectral profile with peaks that spread over more than 1 octave; high scale values corresponded to a peaky spectrum with number of tips to troughs in the spectrum greater than 1 in each octave. Figure 2c shows a schematic representation
Temporal modulations (rates)	Rates capture how fast or slow the frequency contents change with time and in which phase (direction), positive or negative. These temporal modulations were calculated from the auditory spectrogram using 23 exponential filters, constructed of varying velocities ∈ [0, 64] Hz for both directions [26, 27]. Rates were computed for each frequency band of the spectrogram, and results were averaged to yield one rate profile per subject. Figure 2e shows a schematic representation

Results

Patient and Sound Recording Characteristics

A total of 186 children were enrolled into the study. Mean age, height, and weight among study participants were 2.2 years (±1.4), 84.7 cm (±13.2), and 12.0 kg (±3.6), respectively. A total of 27 % were infants (2–12 months), 44 % were aged 1–2 years, and 30 % were aged 3–5 years. We used 151 sound recordings (71 girls and 80 boys) out of 186 in our analysis. We excluded 21 (11 %) complete sound recordings because of technical difficulties during the recording process and 14 complete sound recordings (8 %) because of missing child data. The recordings were mostly comprised normal airflow and heart beat sounds. A total of 11,721 two-second segments (50 % overlap) were available for analyses in the 151 children; however, after noise removal, 348 (3 %) segments were found to be either non-informative or noisy (Fig. 2a) and were not included in the analyses. For example, crying intervals were easily visualized through the spectral characteristics of the time waveforms due to their distinct patterns (Fig. 1).

Spectral Characteristics, Spectral Shape, and Temporal Modulation

In Fig. 2, we summarize the feature extraction process for the average power spectrum, spectral shape, and temporal modulation (panels a, c, and e), and the average profiles for these features (panels b, d, and f). As expected, lung sounds were found in the lower frequency range. For example, the average spectrum profile shows that most of the energy contents were concentrated in the lower frequencies (i.e., below 500 Hz) and the MFCC₁ contained resonances mostly at frequencies close to 56 Hz. Our analyses also revealed that the spectral shape profile was mostly smooth over the frequency axis, i.e., 70 % of the frequency contents of lung sounds were concentrated among scales less than 1 cycle per octave. The smoothness was not a feature of the inherent background noise. In fact, if we exclude some of the heavily noise-contaminated sounds, the average spectrum profile looked even smoother. This suggests that auscultation signals were strongly broadband and at any given time they varied smoothly along the frequency axis. The average temporal modulation profile showed high-energy contents around −1 Hz (i.e., upward deflection) and 2 Hz (i.e., downward deflection), suggesting a slow change in energy contents along the time axis.

Average population values for all spectral and spectro-temporal parameters are presented in the first column of Table 2; however, our analyses of 109 sounds with annotations of auscultation site (72 % of total data) revealed that spectral and spectro-temporal characteristics indeed varied across auscultation sites (Table 2). The proportion of sounds that were excluded from analyses because they were either non-informative or contaminated with noise was similar across auscultation sites, and ranged from 1.4 % to 4.9 %. Specifically, we identified a wider power spectrum and a lower energy of MFCC₁ in anterior versus posterior sites. Furthermore, the scale profile was increased in anterior sites versus posterior sites, especially in the AS which can be indicative of the prominent energy peaks due to heart rate. Finally, the upward rate profile was increased in posterior versus anterior sites, but this difference was not significant.

Table 2.

Mean spectral and spectro-temporal parameters by auscultation site, and corresponding one-way analysis of variance

	Mean (5 and 95 % percentiles)					ANOVA
	Overall	Anterior superior	Anterior-lateral inferior	Posterior superior	Posterior inferior	P value
Respiratory rate (breaths/min)	26.2 [21.5, 38.9]
Heart rate (beats/min)	112.5 [90.0, 143.9]
MFCC1	4.9 [4.2, 5.4]	4.7 [3.8, 5.7]	4.7 [3.9, 5.6]	5.2 [4.0, 6.1]	5.1 [3.7, 6.2]	<0.001
MFCC2	0.1 [−0.4, 0.6]	0.08 [−0.5, 0.5]	0.1 [−0.5, 0.6]	0.2 [−0.6, 0.8]	0.2 [−0.4, 0.8]	0.17
MFCC3	1.1 [0.8, 1.4]	1.0 [0.6, 1.3]	1.0 [0.7, 1.4]	1.1 [0.7, 1.5]	1.1 [0.7, 1.5]	<0.001
Spectral width (PW)	158.3 [93.9, 237.2]	174.9 [91.2, 260.1]	168.0 [84.5, 250.1]	139.3 [77.9, 232.0]	138.1 [71.8, 199.8]	<0.001
Spectral slope (SL)	−10.1 [−11.1, −8.1]	−10.4 [−13.0, −8.1]	−10.4 [−12.1, −8.8]	−10.7 [−12.6, −0.03]	−10.6 [−12.8, −7.6]	0.18
Power ratio (PR)	0.993 [0.980, 1.00]	0.991 [0.975, 0.999]	0.992 [0.977, 0.999]	0.991 [0.981, 0.999]	0.991 [0.976,0.999]	0.85
Power of regression line(PLN)	9,729.6 [6,473.1, 12,135.4]	10,234.0 [6,011.8, 15,494.7]	10,382.5 [6,692.4, 14,396.8]	10,921.6 [5,786.2, 14,795.6]	10,524.8 [4,251.8, 15,314.3]	0.30
Scales1 × IE—3	94.6 [78.0, 110.1]	99.2 [73.5, 122.2]	95.8 [67.5, 119.2]	90.5 [57.1, 123.1]	90.9 [53.6, 122.5]	0.002
${\text{Rates}}_1^{+}\times 1\mathrm{E}-3$	19.0 [12.7, 24.2]	16.2 [6.9, 24.9]	16.2 [8.3, 23.3]	17.6 [10.1, 25.3]	17.7 [10.3, 24.9]	0.02
${\text{Rates}}_1^{-}\times 1\mathrm{E}-3$	10.9 [7.8, 13.5]	9.0[4.2, 12.7]	8.9 [5.1, 12.2]	9.8 [6.1, 13.7]	9.8 [6.0, 13.0]	0.004

Effect of Child Characteristics on Spectral and Spectro-Temporal Signal Parameters

In Fig. 3, we show the relationship between spectral/spectro-temporal signal parameters and specific child characteristics. While most of the signal features revealed linear relationships with age, height, and weight for the particular study population, no significant relation was found with gender. We did not find differences when data were analyzed using either Z-scores instead of raw anthropometry data or if non-parametric tests were used (see Online Supplement). Trends of the regression lines for age, height, and weight were similar across parameters. In other words for RR, HR, PW, and SL parameters, lower distribution values were found for subjects of lower age, height, and weight, while older kids yielded higher distribution values for MFCCs, PR, PLN, and Rates-parameters. A detailed display of the regression coefficients can be found in Table 3 and in the Online Supplement.

Fig. 3.

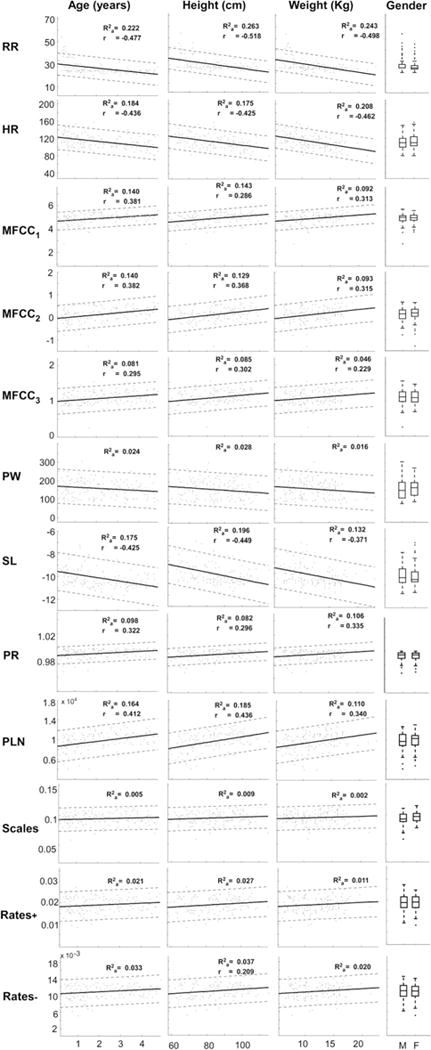
Linear fit (solid line) for each feature (rows, y axis) with respect to patient characteristics (columns, x axis). Point-wise prediction bounds (see Online Supplement) with 95 % confidence level are also shown with dashed lines. Inset $R_a^2$, the adjusted coefficient of determination of the quadratic fit; r, the linear correlation coefficient, displayed only if a significant correlation (P value <0.01) was achieved. Gender column: boxplots for boys (M) and girls (F). HR: heart rate, RR: respiratory rate, MFCC_1,2,3: Mel-frequency cepstrum coefficients for filters centered at 56, 116, and 181 Hz, respectively, PW: spectrum peak width, SL: slope of regression line fit of the logarithmic spectrum, PR: power ratio of the total calculated power versus the power of the regression line, PLN: total power of the regression line

Table 3.

Spectral and spectro-temporal parameters as a function of age, gender, weight, and height as extracted using the complete recordings

	Fitted regression line	Lower/upper limits of normal (±1.64 σ)
Respiratory rate	44.97 + 0.46 × age – 0.196 × height – 0.260 × weight	±37.00
Heart rate	118.63 − 3.45 × age + 0.277 × height – 1.842 × weight	+320.54
MFCC1	3.97 + 0.050 × age + 0.013 × height – 0.024 × weight	±0.23
MFCC2	−0.24 + 0.074 × age + 0.004 × height – 0.009 × weight	±0.14
MFCC3	0.69 + 0.015 × age + 0.006 × height – 0.013 × weight	±0.05
Spectral width (PW)	220.64 – 0.67 × age − 0.892 × height + 1.23 × weight	±3,588.45
Spectral slope (SL)	−7.11 – 0.013 × age − 0.043 × height + 0.05 × weight	±1.15
Power ratio (PR)	0.99 + 0.002 × age − 0.000023 × height – 0.000041 × weight	+5.93 × 10−5
Power of regression line (PLN)	3844.61 + 30.72 × age + 89.11 × height – 144.06 × weight	+3.96 × 106

Discussion

Our results provide a novel method of analysis and characterization of normal lung sounds in children. By extracting spectral and spectro-temporal signals in recordings of lung sounds, we were able to identify ten unique parameters that characterize both static and dynamic features of normal breathing in healthy children. With these parameters, we provide a range of normal lung sounds in children ≤5 years of age taken in real-world noisy environments. With this information, we offer simple, reproducible equations that account for age, height, and weight that allow for comparison with pathologic sounds in future studies.

While age, height, and weight were shown to influence normal sounds in children, no significant relation was found between the extracted features and gender information in this age range. Age was also correlated strongly with both heart rate and respiratory rate in our study, as would be expected. MFCC coefficients, or measurements of chest formation, were also strongly associated with age, particularly low-frequency filter MFCCs, which showed higher spectral envelope power for older children.

Comparing results with previously published work on adult subjects [19, 20], the spectral slope in our study was found to be shallower. This could be a result of additional noise in our dataset or intrinsic to age itself. Broader spectrum peaks and shallower slopes were observed in signal segments containing more noise, which tend to manifest mostly at higher frequencies and broaden the spectral profile; however, this might also be unique to young age. More research and improved noise-cancelation techniques will allow clarification of this discrepancy. With regard to different lung fields, our results differed from those of Boersma, who found the spectral slope varied among site locations [19]. While this was not consistent with our study, peak width, MFCC coefficients, and the spectral modulations varied significantly with site locations, particularly when respect to front versus back sites. This may be partially due to the finding that children were more likely to be agitated when the stethoscope was out of their visual range, possibly altering variable analysis.

The spectral shape profile portrayed interesting information about HR and RR in pediatric subjects. In the temporal profile, two distinctive peaks were observed: one with negative and one with positive phase. The envelope of the HR cycle has been shown to have a strong positive peak followed by a weaker negative one [21–23], while the breathing cycle has been reported to have a strong negative peak (at the end of expiration phase) followed by a strong positive peak (beginning of inspiration phase) [24, 25]. This would suggest that the observed peak at +2 Hz is likely a result of HR, as it was strong and non-variable across individual subjects. In contrast, content at −1 Hz was weaker and more variable, which is indicative of uncontrolled pediatric respirations.

Perhaps the greatest challenge and limitation of this study was also one of the most innovative aspects, analyzing sounds from noisy children in a noisy environment. Literature to date do not account for the above factors. Instead, most studies involve adults in controlled sound environments with specific instructions for respiration rate and depth of breathing. Our study was designed to promote analysis of a vulnerable population in a real-world environment. We used minimal noise-cancelation techniques for this analysis. We opted to simply remove excessively low or high-energy segments that are outside the range of known lung sound frequency. While our results contain variable information, we have shown trends with a range of data points that can be considered within normal. In addition, we were able to identify simple linear relationships and equations among extracted features and patient information that will allow for subsequent comparison with adventitious lung sounds.

Future work will include improved sound acquisition and sound processing techniques. Our group has been developing a device composed on electret pressure microphone arrays, inverted large area electret microphones, piezoelectric, and pseudo-piezoelectric transducers designed to achieve a uniform sensitivity over the entire area of the chest. With improved coupling to the body to reduce leaks from the outside and echo-canceling techniques to further mitigate environmental noise, we will improve the quality of sound before signal processing occurs.

This study has successfully presented a thorough characterization of control cases in pediatric auscultation, and described the inherent challenges and the way those challenges may affect the profiles of lung sounds of a subject. Future work by our group will focus on two crucial areas: noise reduction techniques and identifying abnormal lung sounds using our knowledge of what is normal. Further noise modification techniques will be required for analyzing and automating pathologic sounds, as wheezing has been shown to elicit similar peaks in the power spectrum [19]. Nonetheless, electronic auscultation will likely benefit from using additional clinical information to avoid misinterpretation of pathologic versus normal sounds. We aim to then utilize the information gained from this study to compare these sound parameters with those of children with respiratory diseases to better understand how disease processes affect their spectral profiles. Our eventual goal is to create an automated algorithm for the diagnosis of respiratory disease in children, particularly where trained ears are not readily available.