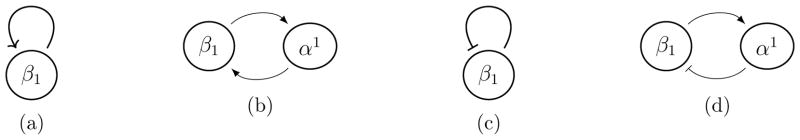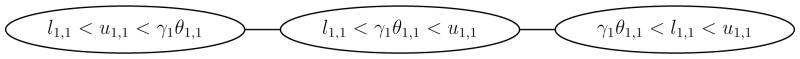Global dynamics for switching systems and their extensions by linear differential equations

Abstract

Switching systems use piecewise constant nonlinearities to model gene regulatory networks. This choice provides advantages in the analysis of behavior and allows the global description of dynamics in terms of Morse graphs associated to nodes of a parameter graph. The parameter graph captures spatial characteristics of a decomposition of parameter space into domains with identical Morse graphs. However, there are many cellular processes that do not exhibit threshold-like behavior and thus are not well described by a switching system. We consider a class of extensions of switching systems formed by a mixture of switching interactions and chains of variables governed by linear differential equations. We show that the parameter graphs associated to the switching system and any of its extensions are identical. For each parameter graph node, there is an order-preserving map from the Morse graph of the switching system to the Morse graph of any of its extensions. We provide counterexamples that show why possible stronger relationships between the Morse graphs are not valid.

1 Introduction

While the last twenty years have brought unprecedented advances in experimental techniques allowing us to gather data on many cellular processes, the development of methods to combine this data into informative models is lagging behind [2, 33, 32]. Models of dynamic cellular processes based on ordinary differential equations require a choice of nonlinearities, parameters and initial conditions, and most of these are difficult to measure experimentally. Moreover, since the nonlinearities of multi-scale cellular processes are by necessity phenomenological, the measurement of the parameters depends on the model with which the data is interpreted. Changing the model leads to re-interpretation of the measurements, and often the need to remeasure all the parameters in the new model.

In this situation it is important to develop methods that compare the outcomes of models of different acuity and at different scales. It also calls for new approaches to modeling, which de-emphasizes comparison of individual trajectories of dynamical models with data. Instead, we should look for global coarse structures in dynamical systems, that are robust under perturbations, can be refined when more information becomes available, and that are computable.

Switching systems, also known as Glass systems, were developed [23, 24, 12, 6, 2] as an attempt to combine the advantages of ordinary differential equation models with Boolean rules, that are often used to represent the logic of gene regulation [3, 9, 8]. These models have the form

$${\stackrel{.}{y}}_j=-{\gamma }_j{y}_j+M_j({\sigma }_i(y_i))$$ (1)

where σ_i(y_i) are piecewise constant functions whose values represent expression of the gene y_i in its “on” state and its “off” state, and M_j is a multi-linear function that prescribes how different inputs into gene j are combined.

The piecewise constant character of σ_i has its advantages and disadvantages. The disadvantages are mostly mathematical, and involve difficulties with interpreting the interaction of trajectories with thresholds, which are places where variables switch between the on state and the off state. Many papers have been devoted to making sense of continuation of solutions in switching systems [36, 31, 13, 1, 7]. A key biological objection to switching models is that in the majority of the cellular networks it is not reasonable to assume that all variables are switch-like in their behavior. For instance, while (1) can be a reasonable model for a network of mutually regulating proteins, including mRNA concentration for one of the proteins as an additional variable brings up a modeling difficulty since the rate of protein production usually depends linearly on the concentration of its mRNA. Such interaction cannot be modeled in a switching system. To address this challenge, in this paper we consider systems of the form

$$\begin{gathered} {\stackrel{.}{x}}^1=-a^1{x}^1+b^1{y}_i \\ {\stackrel{.}{x}}^k=-a^k{x}^k+b^k{x}^{k-1},k=2,3,\dots ,n, \\ {\stackrel{.}{y}}_j=-{\gamma }_j{y}_j+M_j({\sigma }_i(x^n)) \end{gathered}$$ (2)

and compare their dynamics to that of system (1). Here a direct influence from variable y_i on variable y_j in (1) is mediated in (2) by a chain of variables y_i → x¹ → x² → … → xⁿ → y_j that depend linearly on the previous variable in the chain. The nonlinear interaction is in the dependence of y_j on xⁿ which is mediated by a piecewise constant (i.e. switching) function.

The advantages of model (1) have been recognized since its inception [24, 25]. In each domain bounded by thresholds in the phase space the equations (1) are decoupled and linear. Their readily computable solutions can be organized in a state transition diagram (STD) which is a graph whose vertices are these domains and whose directed edges unambiguously represent flow between the domains [25, 18, 35]. The state transition diagram combinatorializes the dynamics of (1), and there are several results on the correspondence between paths in STD and invariant sets of (1) [25, 14, 15]. Another interesting approach that uses decomposition of phase space into rectangles in the context of multi-affine vector fields to address questions of control of trajectories into specific region is discussed in [5, 26, 27, 28].

The recent results in [11] have gone a step further. A Morse graph collects strongly connected components of the STD as vertices, and edges represent reachability between these components. This is a coarse version of a fundamental concept of a Morse decomposition of a dynamical system [10] and represents a summary of global dynamics of (1). In [21] it is shown that the Morse graph of (1) provides information about a Morse decomposition of nearby smooth perturbations of (1). Since Morse graphs are readily computable, the system (1) can now be viewed as a computational tool to compute coarse descriptions of the global dynamics of smooth systems.

The second insight that has come from changing the perspective from considering trajectories to looking at Morse graphs, is that Morse graphs are locally constant in the parameter space of (1). Furthermore, the boundaries of the constancy regions are given by readily computable inequalities in parameters [11, 31]. We represent each region as a node of a parameter graph and connect two nodes by an edge when they share a codimension 1 boundary in the parameter space. The parameter graph, together with a Morse graph attached to each of its nodes, form a DSGRN database [29, 11]. This database encodes global dynamics over the parameter space of the system (1). As such, it can be readily searched for particular dynamic signatures (stable equilibria, periodic patterns), and their robustness in the parameter space can be readily assessed [4].

In this paper we study the relationship between the Morse graphs and the parameter graphs of the switching system (1) and the corresponding extended system (2). The motivation comes from several sources. In [20], the correspondence between the dynamics of a network of proteins and a network with included mRNA for each protein is studied. The additional equations for mRNA are linear. The authors assumed arbitrary monotone nonlinearities and showed that while there is a correspondence between the equilibria in the two systems, their stability can differ.

In a series of papers, Edwards and collaborators [16, 30] studied the same question in the context of switching system (1) with appended linear equations, or appended switching equations [17]. The key insight that we take from [16, 30] is that there is a natural way to define domain boundaries in the new linear variables and use these new domains to define a state transition diagram for the extended system. In a generalization of the approach in [16, 30], each interaction in the switching system (1), corresponds in the extended system (2) to a chain of new variables, each depending on the previous one in a linear fashion. We call any such system an chain linear extension (or simply an extension) of (1).

Our central result is that the parameter graph of the original system (1) and any of its extensions are the same. Since the parameter graph tracks the changes in the Morse graphs and is therefore an analog of a bifurcation diagram in classical theory of dynamical systems, this shows that the structure of changes in dynamics in parameter space is the same. While the parameter graphs of the two systems are the same, this does not necessarily imply that the Morse graphs describing the phase space dynamics at the same parameter node are the same. In fact, since the dimension of the phase space of the switching system and its extension can be vastly different, we would expect the dynamics of the extension to be richer, and hence the Morse graphs larger.

We prove two positive results about the relationship between the Morse graphs of the two systems. We first show that each fixed point attractor in the Morse graph of the switching system corresponds to a unique fixed point attractor in the Morse graph of the extended system. Second, for every node of the parameter graph, we construct an order preserving map φ that maps the Morse graph (viewed as a partially ordered set) of the switching system into the Morse graph of its extension.

We close our results by three examples that show that φ is not injective in general and that in general there is no surjection from the Morse graph of the switching system onto the Morse graph of its extension. While these examples rule out certain natural stronger relationships between the corresponding Morse graphs of the two systems, there is a possibility that there exists a stronger relationship between a Morse graph computed from a properly formulated extension of the state transition graph of the switching system and the Morse graph of its chain linear extension. Switching systems with variables that affect their own dynamics, i.e. self-feedback, always contain pairs of neighboring domains where flows in both either point toward, or away, from their common boundary. These boundaries are known as black (white) walls and present mathematical challenges to extending the solutions entering these walls. In our perspective of global dynamics, the Morse graphs of the switching systems do not reflect the potential existence of invariant sets in these walls. However, there will be Morse nodes in a Morse graph for any smooth system that is a small perturbation of a switching system, that correspond to these invariant sets. We conjecture that there is a surjection from any Morse graph that captures invariant sets of nearby smooth approximations of the switching system to a coarsened Morse graph of the extended system (2).

2 Chain linear extension of the switching system

This paper relies on concepts developed in [11] for switching systems. In this section, as we recall these concepts, we generalize them to the extended system (2).

2.1 Network and equations

Definition 2.1

A regulatory network RN = (V,E) is a directed graph with N distinct network nodes V = {β₁, β₂, …, β_N} and signed edges E ⊂ V ×V × {→, ⊣}. Edges of sign → represent positive regulation or activation and those of sign ⊣ represent negative regulation or repression. We will use the notation (β_i, β_j) ∈ E to describe a directed edge from β_i to β_j of either sign, and β_i → β_j or β_i ⊣ β_j to denote signed directed edges. We require that at most one edge exists from β_i to β_j.

Let

$$\begin{gathered} S({\beta }_i):=\{{\beta }_j\mid ({\beta }_j,{\beta }_i)\in E\} \\ T({\beta }_i):=\{{\beta }_j\mid ({\beta }_i,{\beta }_j)\in E\} \end{gathered}$$

be the sources and targets of β_i, respectively.

Definition 2.2

Let RN = (V,E) be a regulatory network. Then an extension of RN is a directed annotated graph EX = (V ∪ X, E_X). The vertex set X and the edge set E_X are constructed in the following way. To edge (β_i, β_j) ∈ E we associate a set of nodes X_j,i, disjoint from V (X_j,i = ∅ is permitted). Each nonempty set X_j,i admits a linear ordering of its vertices $X_{j,i}:=\{{\alpha }_{j,i}^1,\dots ,{\alpha }_{j,i}^{n_{j,i}}\}$. Then a chain from β_i to β_j is a subgraph G_j,i = (X_j,i ∪ {β_i, β_j}, C_j,i) where the set of edges C_j,i ⊂ (X_j,i ∪ {β_i})×(X_j,i ∪ {β_j}) × {→, ⊣} is

$$\begin{gathered} C_{j,i}:=\{({\beta }_i,{\alpha }_{j,i}^1),({\alpha }_{j,i}^1,{\alpha }_{j,i}^2),\dots ,({\alpha }_{j,i}^k,{\alpha }_{j,i}^{k+1}),\dots ,({\alpha }_{j,i}^{n_{j,i}},{\beta }_j)\}\text{if}{X}_{j,i}\ne \varnothing ,\text{or} \\ {C}_{j,i}:=\{({\beta }_i,{\beta }_j)\}\text{if}{X}_{j,i}=\varnothing , \end{gathered}$$

and the signs of the edges may take either value in {→, ⊣}. We require that X_j,i and X_t,s are disjoint for each (β_i, β_j) ≠ (β_s, β_t) in E. Then we define

$$X:=\underset{({\beta }_i,{\beta }_j)\in E}{\cup }{X}_{j,i},E_X:=\underset{({\beta }_i,{\beta }_j)\in E}{\cup }{C}_{j,i}.$$

We refer to ${\alpha }_{j,i}^k\in X_{j,i}$ as the k^th intermediary between β_i and β_j. We define a canonical extension of RN to be an extension that fulfills the additional conditions:

1. The vertex set X is nonempty.

2. X_i,i is nonempty whenever (β_i, β_i) ∈ E,

3. if X_j,i is nonempty with n_j,i > 0 elements, then

   1. ${\beta }_i\to {\alpha }_{j,i}^1\in C_{j,i}$ and

   2. for k = 1, 2, …, n_j,i − 1, ${\alpha }_{j,i}^k\to {\alpha }_{j,i}^{k+1}\in C_{j,i}$,

   3. if β_i → β_j ∈ E, then ${\alpha }_{j,i}^{n_{j,i}}\to {\beta }_j\in C_{j,i}$

   4. if β_i ⊣ β_j ∈ E, then ${\alpha }_{j,i}^{n_{j,i}}⊣{\beta }_j\in C_{j,i}$.

Whenever we will be considering a single chain and the context is clear, we will simplify the notation from ${\alpha }_{j,i}^k$ to α^k to improve readability.

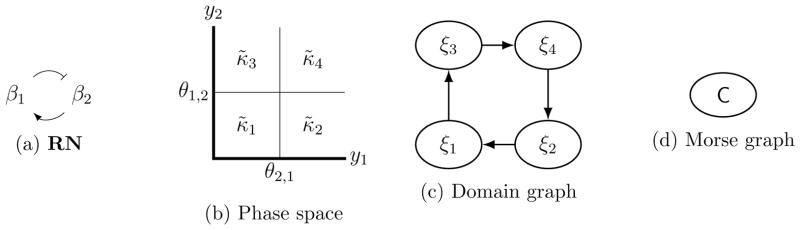
As we introduce new concepts, we will illustrate them on a pair of simple networks in Figure 1.

Figure 1.

(a) RN for positive self-loop, (b) Canonical extended network EX for (a), (c) RN for negative self-loop and (d) Canonical extended network EX for (c).

Definition 2.3

A switching system associated to RN is a set of ordinary differential equations in variables V′:= {y_j | j = 1, …, N}, with piecewise constant nonlinearities of the form

$$\begin{gathered} {\stackrel{.}{y}}_j=-{\gamma }_j{y}_j+{\stackrel{\sim }{\mathrm{\Lambda }}}_j(y) \\ {\stackrel{\sim }{\mathrm{\Lambda }}}_j=M_j\circ {\stackrel{\sim }{\sigma }}_j \\ {\stackrel{\sim }{\sigma }}_j=(\stackrel{\sim }{\sigma }(y_j,y_1;{\theta }_{j,1}),\stackrel{\sim }{\sigma }(y_j,y_2;{\theta }_{j,2}),\dots ,\stackrel{\sim }{\sigma }(y_j,y_N;{\theta }_{j,N})). \end{gathered}$$ (3)

Here γ_j is a decay rate, M_j is a multilinear function, and θ_j,i are regulatory thresholds. The functions σ̃(y_j, y_i; θ_j,i) are step functions of the form

$$\stackrel{\sim }{\sigma }(y_j,y_i;{\theta }_{j,i})=\{\begin{array}{cc}{l}_{j,i}& \text{if}{\beta }_i\to {\beta }_j\in E\text{and}{y}_i<{\theta }_{j,i}\\ & \text{or}{\beta }_i⊣{\beta }_j\in E\text{and}{y}_i>{\theta }_{j,i}\\ u_{j,i}& \text{if}{\beta }_i\to {\beta }_j\in E\text{and}{y}_i>{\theta }_{j,i}\\ & \text{or}{\beta }_i⊣{\beta }_j\in E\text{and}{y}_i<{\theta }_{j,i}\\ \text{undefined}& \text{if}({\beta }_i,{\beta }_j)\notin E\end{array}$$ (4)

We will say that θ_j,i exists if and only if (β_i, β_j) ∈ E. In order for the step function σ̃ to correspond to positive or negative regulation, we require that l_j,i ≤ u_j,i for every (β_i, β_j) ∈ E, with l_j,i = u_j,i being the degenerate case. We also assume strictly positive parameters, so that 0 < γ_i, l_j,i, u_j,i, θ_j,i for all i, j.

In an abuse of notation we define

$$\begin{gathered} S(y_i):=\{y_j\mid ({\beta }_j,{\beta }_i)\in E\} \\ T(y_i):=\{y_j\mid ({\beta }_i,{\beta }_j)\in E\} \end{gathered}$$

to be the sources and targets of variable y_i, respectively. It should be clear from the context whether we work with nodes of the graph, or the corresponding variables.

We now define an analog of the switching system (3), in which we introduce intermediate variables x that are governed by linear equations.

Definition 2.4

The extended system associated to EX is a set of ordinary differential equations in variables V′ ∪ X′, where $X^{\prime }:=\{x_{j,i}^k\mid {\alpha }_{j,i}^k\in X\}$. The equations take the form

$$\begin{gathered} {\stackrel{.}{y}}_i=-{\gamma }_i{y}_i+{\mathrm{\Lambda }}_i(y,x),i=1,2,\dots ,N \\ {\stackrel{.}{\overrightarrow{x}}}_i=A_i{\overrightarrow{x}}_i+{\overrightarrow{b}}_i,i\in \mathcal{I}\subseteq \{1,2,\dots ,N\} \end{gathered}$$ (5)

where ℐ:= {i | X_j,i ≠ = ∅ for some y_j ∈ T(y_i)}. The matrix A_i is block diagonal and x⃗_i and b⃗_i are block vectors, each containing a unique block A_j,i, x⃗_j,i, and b⃗_j,i, respectively, for each y_j ∈ T(y_i). In particular, if C_j,i is a chain {(β_i, α¹), (α¹, α²), …, (αⁿ, β_j)} ⊂ E_X, these blocks take the form

$$\begin{gathered} A_{j,i}=\left[\begin{array}{ccccc}-a^1& 0& 0& \cdots & 0\\ b^2& -a^2& 0& \cdots & 0\\ 0& b^3& -a^3& \cdots & 0\\ ⋮& ⋮& \ddots & \ddots & ⋮\\ 0& 0& 0& b^n& -a^n\end{array}\right] \\ {\overrightarrow{x}}_{j,i}=\left[\begin{array}{c}{x}^1\\ x^2\\ ⋮\\ x^n\end{array}\right],{\overrightarrow{b}}_{j,i}=\left[\begin{array}{c}{b}^1{y}_i\\ 0\\ ⋮\\ 0\end{array}\right] \end{gathered}$$

where we have written x^k, a^k, and b^k in lieu of $x_{j,i}^k,a_{j,i}^k$, and $b_{j,i}^k$ for brevity. In non-matrix form, this becomes

$${\stackrel{.}{y}}_i=-{\gamma }_i{y}_i+{\mathrm{\Lambda }}_i(y,x)$$ (6)

$${\stackrel{.}{x}}^1=-a^1{x}^1+b^1{y}_i$$ (7)

$${\stackrel{.}{x}}^k=-a^k{x}^k+b^k{x}^{k-1},k=2,3,\dots ,n$$ (8)

The function Λ_i:= M_i ∘ σ_i, where M_i is the same multilinear function as in the switching system in (3), and σ_i, defined in Definition 2.7, is a step function similar to σ̃_i in (4). The new parameters $a^k(=a_{j,i}^k)$ and $b^k(=b_{j,i}^k)$ denote a decay rate and a production rate for $x^k(=x_{j,i}^k)$ and are strictly positive. We take

$$a_{j,i}=\{a_{j,i}^k\mid k=1,\dots ,n_{j,i}\},b_{j,i}=\{b_{j,i}^k\mid k=1,\dots ,n_{j,i}\}.$$ (9)

Note that a_j,i = b_j,i = ∅ whenever X_j,i = ∅.

For the examples in Figure 1 both single loop RN networks give rise to a single differential equation

$${\stackrel{.}{y}}_1=-{\gamma }_1{y}_1+{\stackrel{\sim }{\mathrm{\Lambda }}}_1(y_1),$$

the only difference between the positive and negative self-loop is reflected in the function ${\stackrel{\sim }{\mathrm{\Lambda }}}_1^{\pm }$:

$${\stackrel{\sim }{\mathrm{\Lambda }}}_1^{+}(y_1)=\{\begin{array}{ll}{l}_{1,1}\hfill & \text{if}{y}_1<{\theta }_{1,1}\hfill \\ u_{1,1}\hfill & \text{if}{y}_1>{\theta }_{1,1}\hfill \end{array}{\stackrel{\sim }{\mathrm{\Lambda }}}_1^{-}(y_1)=\{\begin{array}{ll}{u}_{1,1}\hfill & \text{if}{y}_1<{\theta }_{1,1}\hfill \\ l_{1,1}\hfill & \text{if}{y}_1>{\theta }_{1,1}\hfill \end{array}$$

The extended system for EX in both cases has the form

$$\begin{gathered} {\stackrel{.}{y}}_1=-{\gamma }_1{y}_1+{\mathrm{\Lambda }}_1^{\pm }(y_1,x^1) \\ {\stackrel{.}{x}}^1=-a^1{x}^1+b^1{y}_1 \end{gathered}$$

We describe functions ${\mathrm{\Lambda }}_1^{\pm }(y_1,x^1)$ below in Definition 2.7.

2.2 Parameters

A parameter of the switching system (3) is z:= (l, u, θ, γ), where l = {l_j,i}, u = {u_j,i}, and θ = {θ_j,i} are indexed by edges (β_i, β_j) ∈ E in RN, and γ = {γ_i} is indexed by nodes β_i ∈ V, or equivalently y_i ∈ V′. The parameter z is an element of (0,∞)^D where D = |V | + 3|E| = N + 3|E|.

An extended parameter or a parameter for EX is a tuple h = (z, a, b) = (l, u, θ, γ, a, b) ∈ (0, ∞)^D′, where a and b are vectors of length |X| (a is the union of sets a_j,i and b is the union of sets b_j,i in (9)). Moreover z = π(h), where π is the projection from ℝ^D′ to ℝ^D. The new parameter length D′ is then

$$D^{\prime }=D+2\mid X\mid =N+3\mid E\mid +2\mid X\mid .$$

2.3 Phase space

The phase space of a switching system admits a natural decomposition into domains.

Definition 2.5

Fix a parameter z = (l, u, θ, γ) for the switching system (3). We will use the convention that for each y_s ∈ V′, θ_−∞,s = 0 and θ_∞,s = ∞. Let θ_vs,s and θ_ws,s be consecutive threshold values. Then a domain is a subset of the phase space (0,∞)^N of the switching system at z, given by

$$\stackrel{\sim }{\kappa }:=\prod _{s=1}^N({\theta }_{v_s,s},{\theta }_{w_s,s}).$$

We denote the collection of domains in (0, ∞)^N by 𝒦(z).

A face of κ̃ is a subset of the boundary of κ̃ given by

$$\stackrel{\sim }{\tau }:=\prod _{s=1}^{i-1}({\theta }_{v_s,s},{\theta }_{w_s,s})\times \{{\theta }_{m_i,i}\}\times \prod _{s=i+1}^N({\theta }_{v_s,s},{\theta }_{w_s,s}),m_i\notin \{\pm \infty \}$$

on which y_i = θ_mi,i is constant.

Let τ̃ be a face of κ̃ on which y_i = θ_mi,i. The pair (τ̃, κ̃) is called a wall. We say that τ̃ is a left face (right face) of κ̃ if y_i > θ_mi,i (y_i < θ_mi,i) everywhere in κ̃. We say the sign of the wall (τ̃, κ̃) is 1, sgn(τ̃, κ̃) = 1, if τ̃ is a left face of κ̃. Similarly, sgn(τ̃, κ̃) = −1 when τ̃ is a right face of κ̃.

We would like to define domains for the extended system. A naive solution would be to define them as products κ̃ × (0, ∞)^|X| for each κ̃ ∈ 𝒦(z). However, the key ingredient in describing the dynamics in terms of a partition of phase space has been the fact that the solutions to (3) cross each face τ̃ in one direction. This is not true under extended flow for extended walls (τ̃ × (0, ∞)^|X|, κ̃ × (0, ∞)^|X|). To resolve this problem we follow [16, 30] and define new domain boundaries in the x variables to further partition phase space. The choice of these values is not arbitrary, as shall be demonstrated later in Theorem 2.15. We give a geometric reason for their definition in Appendix A.

Definition 2.6

Consider a chain C_j,i = {(β_i, α¹), (α¹, α²), …, (αⁿ, β_j)} ∈ E_X, where X_j,i ≠ ∅. Fix a parameter h = (l, u, θ, γ, a, b) ∈ (0,∞)^D′. Define values ϑ^k associated to edges in C_j,i as follows.

1. Let ϑ⁰:= θ_j,i be associated to the edge (β_i, α¹) ∈ C_j,i.

2. For k = 1, 2, …, n, let ${\vartheta }^k=\frac{b^k}{a^k}{\vartheta }^{k-1}$ be associated to edge (α^k, α^k+1) or (αⁿ, β_j) when k = n.

Because the values ϑ^k are defined recursively, we can rewrite ϑ^k associated to edges in C_j,i in terms of the threshold θ_j,i:

$${\vartheta }^k=\left(\prod _{\ell =1}^k\frac{b^{\ell }}{a^{\ell }}\right){\theta }_{j,i},k=1,2,\dots ,n.$$ (10)

When dealing with multiple chains, we denote the value associated to the edge ( ${\alpha }_{j,i}^k,{\alpha }_{j,i}^{k+1}$) by the triple indexing scheme ${\vartheta }_{j,i}^k$. If X_j,i = ∅, then we say these thresholds ${\vartheta }_{j,i}^k$ do not exist.

We now explicitly define the vector of step functions σ_j = (σ_j,1, …, σ_j,N) associated to variable y_j ∈ V′, which is based on Definition 2.3 for the step function in the switching system.

Definition 2.7

Let C_j,i ⊂ E_X be a chain from β_i to β_j and y_i, y_j the associated variables. If X_j,i = ∅, then

$${\sigma }_{j,i}:=\stackrel{\sim }{\sigma }(y_j,y_i;{\theta }_{j,i}),$$

referring back to the step function in (4). If X_j,i is nonempty, denote the last intermediate variable by xⁿ with associated value ϑⁿ. Then

$${\sigma }_{j,i}:=\stackrel{\sim }{\sigma }(y_j,x^n;{\vartheta }^n).$$

In other words, the number and form of the step functions in the extended system is the same as the original switching system, except that the inputs into the step function will change in each chain.

Since the value ϑⁿ plays a role of a threshold in the function σ_j,i we will refer to the values ϑⁿ also as thresholds. However, we want to emphasize that they are constructed with the sole purpose of defining domains for the extended system, and do not have the same role in the dynamics of system (5) as thresholds θ_j,i have in the dynamics of (3).

According to Definition 2.7 the extended systems for the positive (left) and negative (right) self loop have the form

$$\begin{array}{ll}{\stackrel{.}{y}}_1=-{\gamma }_1{y}_1+\{\begin{array}{ll}{l}_{1,1}\hfill & \text{if}{x}^1<{\vartheta }^1\hfill \\ u_{1,1}\hfill & \text{if}{x}^1>{\vartheta }^1\hfill \end{array}\hfill & {\stackrel{.}{y}}_1=-{\gamma }_1{y}_1+\{\begin{array}{ll}{u}_{1,1}\hfill & \text{if}{x}^1<{\vartheta }^1\hfill \\ l_{1,1}\hfill & \text{if}{x}^1>{\vartheta }^1\hfill \end{array}\hfill \\ {\stackrel{.}{x}}^1=-a^1{x}^1+b^1{y}_1\hfill & {\stackrel{.}{x}}^1=-a^1{x}^1+b^1{y}_1\hfill \end{array}$$

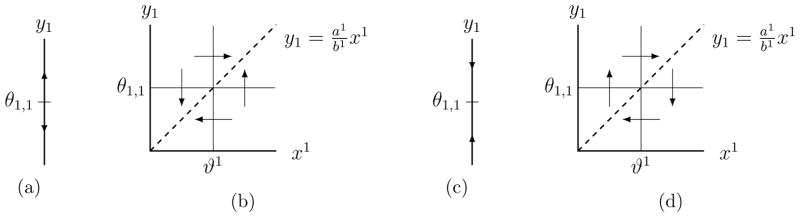
where ${\vartheta }^1=\frac{b^1}{a^1}{\theta }_{1,1}$. The phase space of these extended systems is depicted in Figures 2b and 2d.

Figure 2.

Phase space for (a) the positive self-loop RN in Figure 1a; (b) the positive feedback extension EX in Figure 1b; (c) the negative self loop RN in Figure 1c; and (d) the negative feedback extension EX in Figure 1d, when for all systems parameters satisfy l_1,1 < γ₁θ_1,1 < u_1,1. The arrows represent direction of transversal flow on the interior of each face. In the extended systems (b) and (d), the vertical arrows are determined by the switching function ${\mathrm{\Lambda }}_1^{\pm }$, and the horizontal arrows are a consequence of the fact that $y_1=\frac{a^1}{b^1}{x}^1$ is a nullcline of the second, linear equation.

Definition 2.8

Let RN be a regulatory network and EX an extension of RN. Let the associated switching and extended systems be parameterized with z = (l, u, θ, γ) and h = (z, a, b), respectively. For a domain κ̃ ∈ 𝒦(z) of the switching system, we define an extended domain κ ∈ 𝒦 (h) to be a choice

$$\kappa :=\stackrel{\sim }{\kappa }\times \prod _{s\in \mathcal{I}}\mathrm{\Xi }(y_s)$$

where recall from Definition 2.4 that ℐ = {i | X_j,i ≠ ∅ for some y_j ∈ T(y_i)}. Here each Ξ(y_s) is a product

$$\mathrm{\Xi }(y_s)=\prod _{t\in \mathcal{J}(s)}\prod _{\ell =1}^{n_{t,s}}({\vartheta }_{v_t,s}^{\ell },{\vartheta }_{w_t,s}^{\ell })$$

where 𝒥 (s):= {t | y_t ∈ T(y_s) and X_t,s ≠ ∅} and for each t ∈ 𝒥(s) either (v_t, w_t) = (−∞, t) or (t, ∞). Note that Ξ(y_s) represents the values of all of the chain variables $x_{t,s}^{\ell }$ in each chain with initial vertex β_s. As in the switching system, we will use the convention that for each $x_{t,s}^{\ell }\in X^{\prime },{\vartheta }_{-\infty ,s}^{\ell }=0$ and ${\vartheta }_{\infty ,s}^{\ell }=\infty$. We illustrate this on Figure 2. In both cases the phase space of the switching system contains two domains (0, θ_1,1) and (θ_1,1, ∞), which share the face {θ_1,1} on which y₁ is constant. The phase spaces of both extensions contain four domains, which are Cartesian products of both domain of the switching system with both (0, ϑ¹) and (ϑ¹, ∞). Both of (0, ϑ¹) and (ϑ¹, ∞) are themselves products of the form Π_s∈ℐ Ξ(y_s) with ℐ = {1}, 𝒥(1) = {1}, and n_1,1 = 1.

Let τ̃ be a face of the domain κ̃. A y-face of an extended domain κ is given by

$${\tau }_y:=\stackrel{\sim }{\tau }\times \prod _{s\in \mathcal{I}}\mathrm{\Xi }(y_s)$$

Clearly this is a subset of one of the y-hyperplanes bounding κ. In Figure 2 each extended domain has a y-face equal to either {θ_1,1} × (0, ϑ¹) or {θ_1,1} × (ϑ¹, ∞). An x-face of the extended domain κ is

$${\tau }_x:=\stackrel{\sim }{\kappa }\prod _{\begin{array}{c}s\in \mathcal{I},\\ s\ne i\end{array}}\mathrm{\Xi }(y_s)\times \prod _{\begin{array}{l}t\in \mathcal{J}(s),\\ t\ne j\end{array}}\prod _{\ell =1}^{n_{t,i}}({\vartheta }_{v_t,i}^{\ell },{\vartheta }_{w_t,i}^{\ell })\times \mathrm{\Upsilon }(i,j,k)$$

where

$$\mathrm{\Upsilon }(i,j,k)=\prod _{\ell =1}^{k-1}({\vartheta }_{v_j,i}^{\ell },{\vartheta }_{w_j,i}^{\ell })\times \{{\vartheta }_{j,i}^k\}\times \prod _{\ell =k+1}^{n_{j,i}}({\vartheta }_{v_j,i}^{\ell },{\vartheta }_{w_j,i}^{\ell }).$$

Note that the last index k in ϒ(i, j, k) is the index of the variable $x_{i,j}^k$ which is at threshold. Therefore τ_x is a subset of the hyperplane { $x_{j,i}^k={\vartheta }_{j,i}^k$}. In Figure 2, each extended domain κ has an x-face equal to κ × (0, ϑ¹) or κ × (ϑ¹, ∞).

We use the terms left and right x-faces and y-faces analogously to Definition 2.5, and (τ_x, κ), (τ_y, κ) will denote x-walls and y-walls, respectively. As before, we say that sgn(τ, κ) = 1 if τ is a left x- or y-face of κ and that sgn(τ, κ) = −1 if τ is a right x- or y-face of κ.

2.4 Generic parameters

The following corollary is an immediate consequence of the definition of domains and the piecewise constant form of Λ̃_i.

Corollary 2.9

Fix a domain κ̃. Then the values Λ̃_i(p), i = 1, …, N are constant over p ∈ κ̃.

We denote these constants

$${\stackrel{\sim }{\mathrm{\Lambda }}}_i(\stackrel{\sim }{\kappa }):={\stackrel{\sim }{\mathrm{\Lambda }}}_i(p)\text{for}\text{any}p\in \stackrel{\sim }{\kappa }.$$

Definition 2.10

The parameter space Z̄ associated to RN is the set of all (l, u, θ, γ) ∈ ℝ^D such that 0 < γ_i,0 < θ_j,i and 0 < l_j,i ≤ u_j,i. A parameter z = (l, u, θ, γ) ∈ Z̄ is regular if, in addition,

1. all of these inequalities are strict,

2. for each y_i ∈ V′, the thresholds {θ_j,i} are distinct, and

3. for any κ̃ ∈ 𝒦(z), −γ_iθ_j,i + Λ̃_i(κ̃) ≠ 0 for each hyperplane {y_i = θ_j,i} bordering κ̃.

We denote the set of regular parameters of RN by Z.

Remark 2.11

Note that at any parameter z ∈ Z̄, the range of Λ̃_i is a finite set for each y_i ∈ V′. As a consequence, the property that −γ_iθ_j,i + Λ̃_i(κ̃) ≠ 0 is generic.

The following fact will be important in proofs in future sections.

Corollary 2.12

Let z ∈ Z. Let κ̃, κ̃′ be two domains separated by a face τ̃ on which y_i = θ_j,i with i ≠ j. Then Λ̃_i(κ̃) = Λ̃_i(κ̃′) = Λ̃_i(p) for any p ∈ τ̃.

Proof

Since the thresholds of y_i are distinct, the threshold θ_j,i is associated to the unique edge (β_i, β_j) ∈ E. Therefore, only the switching function associated to y_j may change across τ̃: Λ̃_j(κ̃) ≠ Λ̃_j(κ̃′). Since i ≠ j, Λ̃_i is constant across τ̃.

Definition 2.13

We define the parameter space H̄ associated to an extended system to be the set of all h = (z, a, b) ∈ ℝ^|D′| such that z ∈ Z̄ and $0<a_{j,i}^k$ and $0<b_{j,i}^k$ for all $x_{j,i}^k\in X$. A parameter h = (z, a, b) ∈ H̄ is regular if z ∈ Z̄ is regular. We denote the set of regular parameters by H.

Note as in Remark 2.11 for the switching system that H is generic in H̄.

2.5 Wall-labeling function

We now explain how to assign a uniform direction of flow across each face in the phase space of a canonical extension at a regular parameter.

Lemma 2.14

Let EX be a canonical extension of RN with extended system (5) and regular parameter h = (z, a, b). Let κ, κ′ ∈ 𝒦(h) be extended domains such that there exists τ_y ⊂ {y_i = θ_j,i} with (τ_y, κ) a left y-face and (τ_y, κ′) a right y-face. Then,

$${\mathrm{\Lambda }}_i(\kappa )={\mathrm{\Lambda }}_i(p)={\mathrm{\Lambda }}_i({\kappa }^{\prime })\mathit{for}\mathit{all}p\in {\tau }_y.$$ (11)

Proof

First consider an edge (β_i, β_j) ∈ E such that X_j,i = ∅. From Definition 2.8, we know that there exists a fixed $\widehat{\mathrm{\Xi }}:={\displaystyle \prod _{s=1}^N}\mathrm{\Xi }(y_s)$ such that

$$\kappa =\stackrel{\sim }{\kappa }\times \widehat{\mathrm{\Xi }},{\kappa }^{\prime }={\stackrel{\sim }{\kappa }}^{\prime }\times \widehat{\mathrm{\Xi }},{\tau }_y=\stackrel{\sim }{\tau }\times \widehat{\mathrm{\Xi }}$$

for some domains κ̃, κ̃′ ∈ 𝒦(z) that share the face τ̃. Since i ≠ j in a canonical extension when X_j,i = ∅ and since z is regular by Definition 2.13 then Corollary 2.12 tells us

$${\stackrel{\sim }{\mathrm{\Lambda }}}_i(\stackrel{\sim }{\kappa })={\stackrel{\sim }{\mathrm{\Lambda }}}_i(p)={\stackrel{\sim }{\mathrm{\Lambda }}}_i({\stackrel{\sim }{\kappa }}^{\prime })\text{for}\text{all}p\in \stackrel{\sim }{\tau }.$$ (12)

We note that Λ̃_i(κ̃) is not guaranteed to equal Λ_i(κ). However, in Ξ̂, there are no $x_{i,s}^k$ at threshold. In other words, y_i cannot be regulated by any y_ℓ or $x_{i,s}^k$ on κ ∪ τ_y ∪ κ′. Therefore (12) implies (11).

Now we consider an edge (β_i, β_j) ∈ E with X_j,i ≠ ∅ with a corresponding chain C_j,i = {(β_i, α¹), (α¹, α²), …, (αⁿ, β_j)}. Then on τ_y where y_i = θ_j,i, only the variable x¹ is regulated because h is regular; in particular we use condition (2) of Definition 2.10. Therefore Λ_s(κ) = Λ_s(p) = Λ_s(κ′) for all p ∈ τ_y and for all s = 1, …, N, a stronger result than required.

Theorem 2.15

Let EX be a canonical extension where the associated extended system has a regular parameter h = (z, a, b) ∈ H. Let τ be a face on which μ ∈ V′ ∪ X′ is constant. Then sgn(μ̇) is constant and nonzero on τ.

Proof

Let μ ∈ V′, so that μ = y_i and μ|_τ = θ_j,i for some i, j. Let κ be such that (τ, κ) is a wall. Combining Lemma 2.14 with (6) evaluated on τ, we have

$${\stackrel{.}{\mu }\mid }_{\tau }=-{\gamma }_i{\theta }_{j,i}+{\mathrm{\Lambda }}_i(\kappa ).$$

In other words, μ̇|_τ exists and is constant. Since h ∈ H, γ_iθ_j,i ≠ Λ_i(κ) and so μ̇ is also nonzero on τ.

Now let μ ∈ X′, so that $\mu =x_{j,i}^k$ and ${\mu \mid }_{\tau }={\vartheta }_{j,i}^k$ for some i, j, k. If k = 1, then from (7) evaluated on τ,

$$sgn{(\stackrel{.}{\mu })\mid }_{\tau }=sgn(-a_{j,i}^1{\vartheta }_{j,i}^1+b_{j,i}^1{y}_i)\Rightarrow sgn{(\stackrel{.}{\mu })\mid }_{\tau }=sgn(y_i-{\theta }_{j,i}),$$

using Definition 2.6. We have τ ∩{y_i = θ_j,i} = ∅ by Definition 2.8, which states that exactly one variable is at threshold on each face. Thus y_i remains strictly on one side of θ_j,i on τ, so that sgn(μ̇) = sgn(y_i − − θ_j,i) is constant and nonzero on τ.

If k > 1, then from (8) evaluated on τ,

$$sgn{(\stackrel{.}{\mu })\mid }_{\tau }=sgn(-a_{j,i}^k{\vartheta }_{j,i}^k+b_{j,i}^k{x}^{k-1})\Rightarrow sgn{(\stackrel{.}{\mu })\mid }_{\tau }=sgn(x_{j,i}^{k-1}-{\vartheta }_{j,i}^{k-1}).$$

Similarly, $\tau \cap \{x_{j,i}^{k-1}={\vartheta }_{j,i}^{k-1}\}=\varnothing$ implies that sgn(μ̇) is constant and nonzero on τ.

Theorem 2.15 allows us to introduce a well-defined wall labeling scheme that indicates a direction of flow on either side of each face.

Definition 2.16

Let z ∈ Z̄ and let 𝒲(z) be the set of walls in the phase space associated to z. Then the wall-labeling function ℓ̃: 𝒲(z) → {−1, 0, 1} is

$$\stackrel{\sim }{\ell }(\stackrel{\sim }{\tau },\stackrel{\sim }{\kappa }):=sgn(\stackrel{\sim }{\tau },\stackrel{\sim }{\kappa })·sgn(-{\gamma }_i{\theta }_{j,i}+{\stackrel{\sim }{\mathrm{\Lambda }}}_i(\stackrel{\sim }{\kappa })),$$

where τ̃ ⊂ {y_i = θ_j,i}.

Definition 2.17

Let h ∈ H for the extended system of a canonical extension EX and let 𝒲(h) be the set of walls in phase space. We define the wall-labeling function ℓ: 𝒲(h) → {−1, 0, 1} by

$$\ell (\tau ,\kappa ):=sgn(\tau ,\kappa )·sgn{(\stackrel{.}{\mu })\mid }_{\tau },$$

where μ is constant on τ and

$$sgn{(\stackrel{.}{\mu })\mid }_{\tau }=\{\begin{array}{ll}sgn(-{\gamma }_i{\theta }_{j,i}+{\mathrm{\Lambda }}_i(\kappa ))\hfill & \text{if}\mu =y_i\text{and}\tau \subset \{y_i={\theta }_{j,i}\}\hfill \\ sgn{(y_i-{\theta }_{j,i})\mid }_{\tau }\hfill & \text{if}\mu =x_{j,i}^1\text{and}\tau \subset \{x_{j,i}^1={\vartheta }_{j,i}^1\}\hfill \\ sgn{(x_{j,i}^{k-1}-{\vartheta }_{j,i}^{k-1})\mid }_{\tau }\hfill & \text{if}\mu =x_{j,i}^k\text{and}k>1\text{and}\tau \subset \{x_{j,i}^k={\vartheta }_{j,i}^k\}\hfill \end{array}$$

A wall (τ, κ) is an outgoing wall if ℓ(τ, κ) = −1, an incoming wall if ℓ(τ, κ) = 1, and a tangential wall if ℓ(τ, κ) = 0. A domain κ is an attracting domain if every (τ, κ) is an incoming wall.

Observe that Definition 2.17 for an extended system reduces to Definition 2.16 for a switching system, when X_j,i = ∅ for all (β_i, β_j) ∈ E.

Remark 2.18

Note that Definitions 2.10 and 2.16 imply that there are no tangential walls for any regular parameter z ∈ Z in the switching system. Theorem 2.15 says that sgn(μ̇)|_τ ≠ 0 for h ∈ H a regular parameter and EX a canonical extension, so there are no tangential walls in the extended system either.

A canonical extension has an important additional property that every face is an outgoing wall on one side and an incoming wall on the other, as we now prove. Existence of white and black walls in the switching system shows that this result is not true for the switching system.

Corollary 2.19

Let h ∈ H be a regular parameter for the extended system of a canonical extension EX. Then for any x- or y-face τ between adjacent domains κ, κ′ ∈ 𝒦(h), we have that

$$\ell (\tau ,\kappa )·\ell (\tau ,{\kappa }^{\prime })=-1.$$

Proof

Let μ ∈ V ∪ X be constant on τ. If (τ, κ) is a right face, it is necessary that (τ, κ′) is a left face, so that sgn(τ, κ) = −sgn(τ, κ′). Since sgn(μ̇) is constant and nonzero on τ by Theorem 2.15, we have that ℓ(τ, κ) · ℓ(τ, κ′) = −1.

The consequence of Corollary 2.19 is that flow is transverse across all faces in a canonical extension, as can be seen in phase space in Figures 2b and 2d.

2.6 Domain graph and Morse graph

We now construct graphs that represent the coarse dynamics of (3) and (5). We first build a state transition diagram, which we call a domain graph, and take the strongly connected components (recurrent components) as a Morse decomposition to build a Morse graph.

Definition 2.20

For each parameter z ∈ Z, we construct a domain graph (𝒱, ℰ_z) with vertex set 𝒱 which is in one-to-one correspondence with the domains 𝒦(z) via a bijection f_z: 𝒦(z) → 𝒱. The edges (u, v) ∈ ℰ_z are defined via a multivalued map

$${\mathcal{F}}_z:\mathcal{V}\rightrightarrows \mathcal{V}$$

where v ∈ ℱ_z(u) if and only if there is a directed edge u → v in the domain graph, (u, v) ∈ ℰ_z. The map ℱ_z is defined as follows

1. if u = v, then v ∈ ℱ_z(u) if and only if $\stackrel{\sim }{\kappa }=f_z^{-1}(u)$ is attracting, or

2. if u ≠ v, then v ∈ ℱ_z(u) if and only if there exists a face τ̃ such that (τ̃, $f_z^{-1}(u)$) is an outgoing wall and (τ̃, $f_z^{-1}(v)$) is an incoming wall.

Using the wall-labeling function ℓ, we can now construct a domain graph associated to the extended system analogous to the domain graph (𝒱, ℰ_z) for the switching system of Definition 2.20.

Definition 2.21

Recall that there is a bijection f_z: 𝒦(z) → 𝒱 between the set of domains 𝒦(z) and the vertices 𝒱 of the domain graph for the switching system. Each extended domain κ ∈ 𝒦(h) has the form

$$\kappa :=\stackrel{\sim }{\kappa }\times \prod _{s=1}^N\mathrm{\Xi }(y_s)$$

for some κ̃ ∈ 𝒦(z), where h = (z, a, b). We define a set of vertices for the domain graph of the extended system as

$$\mathfrak{X}:=\mathcal{V}\times {\{-1,1\}}^{\mid X\mid }.$$

Then there is bijection f_h: 𝒦(h) → 𝔛 defined by

$$f_h(\kappa )=(f_z(\stackrel{\sim }{\kappa }),D)$$

where D ∈ {−1, 1}^|X| satisfies

$$\begin{gathered} D(i,j,k)=-1\text{if}{x}_{j,i}^k<{\vartheta }_{j,i}^k\text{on}\kappa \\ D(i,j,k)=+1\text{if}{x}_{j,i}^k>{\vartheta }_{j,i}^k\text{on}\kappa . \end{gathered}$$

We define the domain graph (𝔛, ℰ_h) induced by the wall-labeling ℓ at the regular parameter h ∈ H via a multivalued map

$${\mathcal{F}}_h:\mathfrak{X}\rightrightarrows \mathfrak{X},$$

where an edge from u ∈ 𝔛 to v ∈ 𝔛 exists, (u, v) ∈ ℰ_h, if and only if v ∈ ℱ_h(u). To define the multivalued map ℱ_h, we let κ, κ′ ∈ 𝒦(h) and (ξ, D):= f_h(κ), (ξ′, D′):= f_h(κ′) respectively. We say (ξ, D) ∈ ℱ_h((ξ′, D′)) if and only if one of the following holds:

• κ = κ′ is an attracting extended domain, or

• κ ≠ κ′ and there exists a y- or x-face τ such that ℓ(τ, κ) = 1 and ℓ(τ, κ′) = −1.

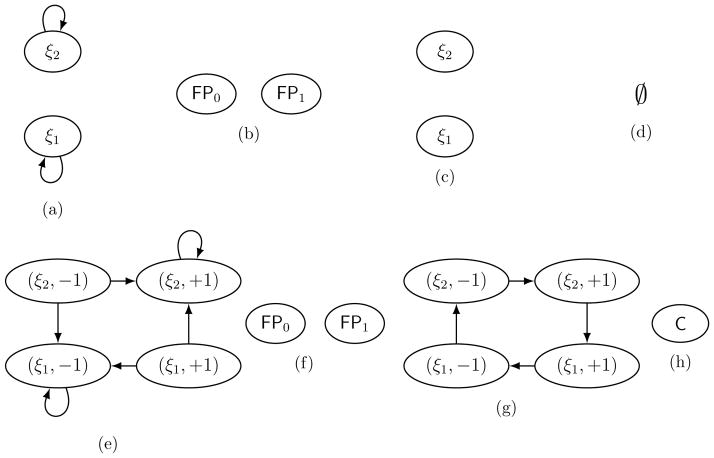
Figure 3(a) and (c) show domain graphs for extended systems in Figure 2.

Figure 3.

Domain graphs and Morse graphs for the phase spaces in Figure 2. (a), (b) Domain and Morse graphs for the switching phase space in Figure 2a for the positive self-loop in Figure 1a. (c), (d) Domain and (empty) Morse graphs for the switching phase space in Figure 2c for the negative self-loop in Figure 1c. (e), (f) Domain and Morse graphs for the extended phase space in Figure 2b for the positive feedback in Figure 1b. (g), (h) Domain and Morse graphs for the extended phase space in Figure 2d for the positive feedback in Figure 1d. In all cases, ξ₁ is the domain graph node corresponding to the switching domain where y₁ < θ₁,₁, and ξ₂ corresponds to y₁ > θ₁,₁.

Definition 2.22

A recurrent component of a directed graph 𝒢 is a maximal subgraph 𝒞 of 𝒢 such that for any vertices u, v ∈ 𝒞, there exists a nonempty path in 𝒞 from u to v.

We refer to a recurrent component of (𝒱, ℰ_z) as a Morse set of (𝒱, ℰ_z). Consider the collection of all Morse sets of (𝒱, ℰ_z). Observe that there exists a partial order on (𝒱, ℰ_z) arising from the reachability relation on (𝒱, ℰ_z). We define an indexing set P for the elements of (𝒱, ℰ_z), respecting this partial order. In particular, for any p, q ∈ P, q ≤ p if and only if there exists a path in (𝒱, ℰ_z) from an element of 𝒞_p to an element of 𝒞_q. The collection of Morse sets of (𝒱, ℰ_z) together with this partial order is called a Morse decomposition of (𝒱, ℰ_z), which we denote by (MD((𝒱, ℰ_z)),≤), or when the order is clear, by MD((𝒱, ℰ_z)).

The Morse graph of (𝒱, ℰ_z), denoted MG((𝒱, ℰ_z)), is the Hasse diagram of the poset (MD((𝒱, ℰ_z)),≤). For this reason we also call the elements of MD((𝒱, ℰ_z)) Morse nodes of (𝒱, ℰ_z).

Using the map ℱ_h, we define the Morse decomposition and Morse graph of (𝔛, ℰ_h), MD((𝔛, ℰ_h)) and MG((𝔛, ℰ_h)) respectively, exactly as in Definition 2.22 by replacing (𝒱, ℰ_z) by (𝔛, ℰ_h).

The Morse graph is a compact representation of the dynamics in phase space. The nodes of the graph represent the recurrent-like dynamics and the directed edges represent the gradient-like dynamics. Figures 3f and 3h show Morse graphs for the extended phase spaces in Figures 2b and 2d. The labels on these nodes are explained in Definition 4.1.

2.7 Combinatorial parameter graph

2.7.1 Switching system

For each parameter z ∈ Z, there is a Morse graph representing the coarse dynamics of the switching system (3). Furthermore, there is a finite partition of the parameter space z ∈ Z into semi-algebraic sets such that within each component the Morse graph is constant [11]. This decomposition can be represented in the form of a geometric parameter graph and its combinatorial representation, a combinatorial parameter graph.

For clarity of presentation, we reproduce the construction of the latter from [11].

Definition 2.23

Define the input combinations of β_j ∈ V to be the Cartesian product

$${ln}_j:=\prod _{{\beta }_i\in S({\beta }_j)}\{\text{off},\text{on}\}.$$

Define the valuation function v_j: In_j → ℝ^|S(β_j)| via

$$v_{j,i}(A)=\{\begin{array}{ll}{l}_{j,i}\hfill & \text{whenever}{A}_i=\text{off}\hfill \\ u_{j,i}\hfill & \text{whenever}{A}_i=\text{on}\hfill \\ \text{undefined}\hfill & \text{otherwise.}\hfill \end{array}$$

Now define the output combinations of the node β_j to be the set

$${\text{Out}}_j:=\{i\mid ({\beta }_j,{\beta }_i)\in E\}.$$

Definition 2.24

A logic parameter is a function

$$L:\coprod _{i=1}^N({In}_i\times {\text{Out}}_i)\to \{-1,1\}.$$

We denote the restriction of L onto In_i ×Out_i as L_i. An order parameter O is a collection of total orderings O_i of Out_i for each y_i ∈ V. A combinatorial parameter is a pair ϕ = (L,O) where L is a logic parameter and O is an order parameter. We denote the collection of combinatorial parameters as Φ. The combinatorial assignment function ω: Z → Φ is given by ω(z):= (L,O) where O = O(z) is the total order of thresholds given by z and

$$L_i(A,B)=sgn(M_i\circ v_i(A)-{\gamma }_i{\theta }_{B,i})\text{for}\text{all}1\le i\le N,$$ (13)

where M_i is the multilinear function from (3). For all z ∈ Z, we say that ω(z) is the combinatorial parameter associated to the parameter z. A combinatorial parameter ϕ ∈ Φ is realizable in Z if there exists z ∈ Z such that ϕ = ω(z).

We impose an adjacency relation between combinatorial parameters to arrange them into a graph.

Definition 2.25

Let ϕ = (L,O) and ϕ′ = (L′,O′) be two distinct combinatorial parameters in Φ. Denote the domain of the logic parameters by $\mathcal{D}:=\coprod _{i=1}^N({In}_i\times {\text{Out}}_i)$. Then ϕ and ϕ′ are adjacent if and only if one of the following holds.

1. O = O′ and there exists d ∈ 𝒟 such that L and L′ are equal on all of 𝒟 except at d.

2. L = L′, $O_i=O_i^{\prime }$ for i = 1, 2, …, i^* − 1, i^* + 1, …, N and the total orders O_i^* and $O_{i^{\ast }}^{\prime }$ differ only by a single swap of the ordering of consecutive thresholds.

The combinatorial parameter graph CPG_Z is the undirected graph on the realizable combinatorial parameters with an edge between two parameter nodes ϕ and ϕ′ if and only if they are adjacent.

We now show that given a combinatorial parameter ϕ = (L,O), every z in its preimage ω⁻¹(ϕ) is associated to the same domain graph and Morse graph. We start by defining a vector-valued indicator function χ̃_j: (0,∞)^N → In_j such that the i^th component of χ̃_j is given by

$$\stackrel{\sim }{\chi }(y_j,y_i;{\theta }_{j,i})=\{\begin{array}{ll}\text{off}\hfill & \text{if}{\beta }_i\to {\beta }_j\text{and}{y}_i<{\theta }_{j,i}\text{or}\text{if}{\beta }_i⊣{\beta }_j\text{and}{y}_i>{\theta }_{j,i}\hfill \\ \text{on}\hfill & \text{if}{\beta }_i\to {\beta }_j\text{and}{y}_i>{\theta }_{j,i}\text{or}\text{if}{\beta }_i⊣{\beta }_j\text{and}{y}_i<{\theta }_{j,i}\hfill \\ \text{undefined}\hfill & \text{otherwise}\hfill \end{array}$$ (14)

Note that with this definition, we have

$${\stackrel{\sim }{\sigma }}_j=v_j\circ {\stackrel{\sim }{\chi }}_j.$$

So the valuation function v_j uses binary inputs provided by χ̃_j to define the values of σ̃_j. The binary inputs describe the relative position of y_i with respect to the thresholds θ_j,i. Notice that χ̃_i is constant across a domain κ̃, so that χ̃_i(κ̃) is well-defined, and we can associate to each κ̃ and i the value

$$L_i({\stackrel{\sim }{\chi }}_i(\stackrel{\sim }{\kappa }),j)=sgn({\stackrel{\sim }{\mathrm{\Lambda }}}_i(\stackrel{\sim }{\kappa })-{\gamma }_i{\theta }_{j,i})$$ (15)

Definition 2.26

For z ∈ Z with ω(z) = ϕ and (τ̃, κ̃) ∈ 𝒲(z) with τ̃ ⊂ {y_i = θ_j,i}, define the combinatorial wall labeling ℒ̃: 𝒲(z) → {−1, 0, 1} for ϕ by

$$\stackrel{\sim }{\mathcal{L}}(\stackrel{\sim }{\tau },\stackrel{\sim }{\kappa })=sgn(\stackrel{\sim }{\tau },\stackrel{\sim }{\kappa })·L_i({\stackrel{\sim }{\chi }}_i(\stackrel{\sim }{\kappa }),j).$$

With this definition, the following is immediate:

Theorem 2.27

Let z ∈ Z with ω(z) = ϕ and (τ̃, κ̃) ∈ 𝒲(z) with τ̃ ⊂ {y_i = θ_j,i}. Then ℓ̃(τ̃, κ̃) = ℒ̃(τ̃, κ̃). That is, the wall-labeling functions for a parameter and its associated combinatorial parameter are identical over phase space.

2.7.2 Extended system

We define a combinatorial parameter graph for EX in a way analogous to that of RN. The results of this section are a consequence of an observation that the parameters a and b in h = (z, a, b) do not affect the combinatorial parameter associated to z. This is because every $x_{j,i}^k$ has only a single threshold ${\vartheta }_{j,i}^k$ and no associated values $l_{j,i}^k$ and $u_{j,i}^k$.

Note that In_i and v_i only depend on the number of sources of the node β_i, and Out_i only depends on the number of targets of β_i. Therefore In_i, Out_i and v_i are the same in the original and the extended system for every β_i. It follows that the set of combinatorial parameters Φ is the same in the original and the extended system.

Definition 2.28

We define the combinatorial assignment function ψ: H → Φ for EX by

$$\psi :=\omega \circ \pi$$ (16)

where π: H → Z is the projection (z, a, b) ↦ z, and ω: Z → Φ is the combinatorial assignment function for the original system. Again we say a combinatorial parameter ϕ is realizable in H if there exists h ∈ H such that ϕ = ψ(h).

The combinatorial parameter graph for EX, denoted CPG_H (as opposed to CPG_Z), is the undirected graph on the combinatorial parameters realizable in EX with an edge between two combinatorial parameters ϕ, ϕ′ ∈ Φ if and only if ϕ and ϕ′ are adjacent as in Definition 2.25.

Lemma 2.29

A combinatorial parameter ϕ ∈ Φ is realizable in Z if and only if it is realizable in H.

Proof

Let ϕ ∈ Φ be realizable in Z. Then there exists z ∈ Z such that ϕ = ω(z). Let h:= (z, 1, 1), by which we mean that we set $a_{j,i}^k=b_{j,i}^k=1$ for all i, j, k where X_j,i ≠ ∅. Clearly, h ∈ H is regular. By (16),

$$\psi (h)=\omega (z)=\varphi .$$

Therefore ϕ is realizable in H.

Let ϕ ∈ Φ be realizable in H. Then there exists h = (l, u, θ, γ, a, b) such that ϕ = ψ(h). Let z:= (l, u, θ, γ). By Definition 2.13, z is regular. By (16),

$$\omega (z)=\omega \circ \pi (h)=\psi (h)=\varphi \in \mathrm{\Phi }.$$

Therefore ϕ is realizable in Z.

Theorem 2.30

CPG_Z and CPG_H are isomorphic.

Proof

Recall that CPG_Z and CPG_H are undirected graphs on the same realizable subset of Φ by Lemma 2.29. The rules of adjacency are identical and depend only on the combinatorial parameter (see Definition 2.25).

We illustrate Theorem 2.30 on our running examples in Figure 1: the combinatorial parameter graphs are identical for the switching systems and their canonical extensions in Figure 1. This parameter graph is depicted in Figure 4. All three combinatorial parameters in Figure 4 are realizable. For example, if we take γ₁ = 1, l_1,1 = 2 and u_1,1 = 4, then the choices θ_1,1 = 5, θ_1,1 = 3, and θ_1,1 = 1 define regular realizations of the combinatorial parameters for vertices from left to right in Figure 4.

Figure 4.

Combinatorial parameter graph for all networks in Figure 1.

The phase spaces in Figure 2 and the domain and Morse graphs in Figure 3 correspond to the middle combinatorial parameter in Figure 4.

Remark 2.31

We emphasize that although the combinatorial parameter graphs are isomorphic, the associated Morse graphs of the switching and extended systems are not in general isomorphic. That is, given a parameter node in CPG_Z and the corresponding node in CPG_H under isomorphism, the coarse dynamics of the systems can differ at this parameter node. This means that choosing to use the extended system over the switching system may result in nontrivial changes in the long term dynamics. See for example the difference between Figures 3c, 3d and Figures 3g, 3h.

It remains to show that if ψ(h) = ϕ, then we can recover the wall labeling associated to the parameter h ∈ H using only ϕ ∈ CPG_H in the same way that we recovered this information from ϕ ∈ CPG_Z in Theorem 2.27. This implies that the combinatorial parameters obtained from ψ are sufficient to recover all information necessary to construct a domain graph for the extended system.

We begin by defining an indicator function for the extension, as in (14).

Definition 2.32

Let C_j,i ⊂ E_X be a chain from β_i to β_j, and let χ_j = (χ_j,1, χ_j,2, …, χ_j,N ) be the extended indicator function, which we define here. If X_j,i = ∅, then

$${\chi }_{j,i}:=\stackrel{\sim }{\chi }(y_j,y_i;{\theta }_{j,i}),$$

referring back to (14). If X_j,i is non-empty, denote the last intermediary by xⁿ with artificial threshold ϑⁿ. Then

$${\chi }_{j,i}:=\stackrel{\sim }{\chi }(y_j,x^n;{\vartheta }^n).$$

If there is no edge (β_i, β_j) ∈ E, then χ_j,i is undefined.

As in (15), we note that χ_i is constant over any κ ∈ 𝒦(h), and

$$L_i({\chi }_i(\kappa ),j)=sgn({\mathrm{\Lambda }}_i(\kappa )-{\gamma }_i{\theta }_{j,i}).$$ (17)

Using this fact, we define a new wall labeling function similar to that in Definition 2.26.

Definition 2.33

Let (L,O) ∈ Φ be realizable by h ∈ H such that O(h) = O. Let (τ, κ) ∈ 𝒲(h) be such that τ is a face of κ on which μ ∈ V′ ∪ X′ is constant.

$$\mathcal{L}(\tau ,\kappa ):sgn(\tau ,\kappa ).\{\begin{array}{ll}{L}_i({\chi }_i(\kappa ),j)\hfill & \text{if}\mu =y_i\text{and}\tau \subset \{y_i={\theta }_{j,i}\}\hfill \\ sgn{(y_i-{\theta }_{j,i})\mid }_{\tau }\hfill & \text{if}\mu =x_{j,i}^1\text{and}\tau \subset \{x_{j,i}^1={\vartheta }_{j,i}^1\}\hfill \\ sgn{(x_{j,i}^{k-1}-{\vartheta }_{j,i}^{k-1})\mid }_{\tau }\hfill & \text{if}\mu =x_{j,i}^k\text{and}k>1\text{and}\tau \subset \{x_{j,i}^k={\vartheta }_{j,i}^k\}\hfill \end{array}$$

Then by (17), the following is immediate.

Theorem 2.34

Let h ∈ H and let ϕ = ψ(h). Then if (τ, κ) ∈ 𝒲(h), we have ℓ(τ, κ) = ℒ(τ, κ).

2.8 Conclusion

Using the wall-labeling function ℓ, we constructed a domain graph (𝔛, ℰ_h) as in Definition 2.20, substituting a parameter h ∈ H, and extended walls and domains for switching walls and domains (see Definition 2.21). From this domain graph we can extract Morse graphs as in Definition 2.22. Each node in the isomorphic combinatorial parameter graphs is associated to a Morse graph. Therefore we can compare Morse graphs between isomorphic nodes in CPG_Z and CPG_H. In Section 3, we will explore the relationship between the Morse graphs of the original and extended system in detail.

3 Morse Graph Theorems

Throughout the section, we will fix a regular parameter z ∈ Z for a switching system and h = (z, a, b) ∈ H for the associated canonical extension. We will explore the relationship between the Morse decompositions of (𝒱, ℰ_z) and (𝔛, ℰ_h). Our main result is the existence of an order preserving map of (MD((𝒱, ℰ_z)),≤) into (MD((𝔛, ℰ_h)),≤). In Section 4, we will provide several counterexamples to potential stronger relationships between the Morse decompositions.

Definition 3.1

For each node in the domain graph of the switching system, ξ ∈ 𝒱, we define the fiber over ξ to be the set

$$\{(\xi ,D)\mid D\in {\{-1,1\}}^{\mid X\mid }\}\subset \mathfrak{X}.$$

For the two self-loops (Figures 1a and 1c) there are two domains, (0, θ_1,1) and (θ_1,1,∞) in phase space, as can be seen in Figures 2a and 2c. Therefore two nodes, ξ₁ and ξ₂, in the respective domain graphs (Figures 3a and 3c. Hence in Figures 3e and 3g the fibers over ξ₁ and ξ₂ are {(ξ₁, 1), (ξ₁,−1)} and {(ξ₂, 1), (ξ₂,−1)}, respectively.

Definition 3.2

For each ξ ∈ 𝒱, we define the *-element (ξ,D^*) of the fiber over ξ in the following way. Pick D^* ∈ {−1, 1}^|X| such that for each $x_{j,i}^k\in X^{\prime }$,

$$\begin{gathered} \text{if}{y}_i<{\theta }_{j,i}\text{on}{f}_z^{-1}(\xi ),\text{then}{x}_{j,i}^k<{\vartheta }_{j,i}^k\text{on}{f}_h^{-1}((\xi ,D^{\ast })) \\ \text{if}{y}_i>{\theta }_{j,i}\text{on}{f}_z^{-1}(\xi ),\text{then}{x}_{j,i}^k>{\vartheta }_{j,i}^k\text{on}{f}_h^{-1}((\xi ,D^{\ast })) \end{gathered}$$

Note that this is equivalent to the following by Definition 2.21.

$$\begin{gathered} \text{if}{y}_i<{\theta }_{j,i}\text{on}{f}_z^{-1}(\xi ),\text{then}{D}^{\ast }(i,j,k)=-1 \\ \text{if}{y}_i>{\theta }_{j,i}\text{on}{f}_z^{-1}(\xi ),\text{then}{D}^{\ast }(i,j,k)=+1 \end{gathered}$$

In our canonical examples in Figures 3e and 3g, the *-elements over ξ₁ and ξ₂ are respectively (ξ₁,−1) and (ξ₂, 1).

We now prove that the wall-labeling of $f_h^{-1}((\xi ,D^{\ast }))$ is preserved from $f_z^{-1}(\xi )$ in the switching system.

Lemma 3.3

Let ξ ∈ 𝒱 with $\stackrel{\sim }{\kappa }=f_z^{-1}(\xi )$ and let $\kappa ={\int }_h^{-1}((\xi ,D^{\ast }))=\stackrel{\sim }{\kappa }\times \widehat{\mathrm{\Xi }}$ for some Ξ̂. Let τ = τ̃ × Ξ̂ where τ̃ is a face of κ̃. Then

$$\stackrel{\sim }{\ell }(\stackrel{\sim }{\tau },\stackrel{\sim }{\kappa })=\ell (\tau ,\kappa ).$$

Proof

By Definitions 2.5 and 2.8, there exist y_i ∈ V′ and y_j ∈ T(y_i) such that y_i = θ_j,i on τ̃ and τ. By Definitions 2.16 and 2.17, it suffices to show that sgn(τ̃, κ̃) = sgn(τ, κ) and Λ̃_i(κ̃) = Λ_i(κ).

It is clear from Definition 2.8 that τ̃ is a left face of κ̃ if and only if τ is a left y-face of κ, and τ̃ is a right face of κ̃ if and only if τ is a right y-face of κ. Thus sgn(τ̃, κ̃) = sgn(τ, κ).

For each y_s ∈ S(y_i), if X_i,s = ∅, recall that Λ̃_i(κ̃) = Λ_i(κ). If X_i,s is nonempty denote the final intermediary in the chain C_i,s by x^n_s and the associated threshold by ϑ^ns. By Definition 3.2, if y_s < θ_i,s on κ̃ then x^n_s < ϑ^n_s on κ and if y_s > θ_i,s on κ̃ then x^n_s > ϑ^n_s on κ. Recalling the definitions of Λ̃_i and Λ_i, it is now clear that Λ̃_i(κ̃) = Λ_i(κ).

Although in the above proof we only use the fact that the terminal signs match (sgn(y_s − θ_i,s) = sgn(x^n_s − ϑ^n_s)), the proof of Lemma 3.6 requires that all signs match in the *-element.

Lemma 3.3 implies that the labelings of the set of y-walls of $\stackrel{\sim }{\kappa }\times \widehat{\mathrm{\Xi }}=f_h^{-1}((\xi ,D^{\ast }))$ are fully determined by the labelings of the set of walls of $\stackrel{\sim }{\kappa }=f_z^{-1}(\xi )$. Lemma 3.4 relies on similar reasoning.

Recall the multi-valued map ℱ_h: 𝔛 ⇉𝔛 where the edge u ∈ 𝔛 to v ∈ 𝔛 exists if and only if v ∈ ℱ_h(u). In what follows, we will use the notation (u → v) ∈ ℰ_h when we want to emphasize the graph theoretic point of view of the dynamics.

Lemma 3.4

If (ξ → ξ′) ∈ ℰ_z and (ξ,D^*) is the *-element of the fiber over ξ, then ℰ_h contains the edge

$$(\xi ,D^{\ast })\to ({\xi }^{\prime },D^{\ast }).$$

Proof

Let $\stackrel{\sim }{\kappa }:=f_z^{-1}(\xi )$ and ${\stackrel{\sim }{\kappa }}^{\prime }:=f_z^{-1}({\xi }^{\prime })$. Because (ξ → ξ′) ∈ ℰ_z, κ̃ and κ̃′ share a face τ̃ such that ℓ̃(τ̃, κ̃) = −1. If $\kappa :=f_h^{-1}((\xi ,D^{\ast }))$ and ${\kappa }^{\prime }:=f_h^{-1}(({\xi }^{\prime },D^{\ast }))$, then κ and κ′ share a y-face τ = τ̃ × Ξ̂, and by Lemma 3.3, ℓ(τ, κ) = −1. Now, by Corollary 2.19, ℓ(τ, κ′) = 1, so the result follows.

The assumption of Lemma 3.4 is not satisfied in our ongoing switching system examples from Figures 1a and 1c, since the single face {θ_1,1} in the phase space does not admit a transverse flow, as can be seen by the inward and outward pointing arrows in the phase lines in Figures 2a and 2c. This results in a domain graph with no edges, as can be seen in Figure 3c.

Having established properties of the y-walls of the *-element, we now address the x-walls.

Definition 3.5

We say (ξ,D) ∈ 𝔛 is attracting in the fiber if every x-wall (τ_x, κ) is an incoming wall for $\kappa :=f_h^{-1}((\xi ,D))$.

Lemma 3.6

The *-element of the fiber is attracting in the fiber.

Proof

It is sufficient to show the following: let ξ ∈ 𝒱 and D ∈ {−1, 1}^|X| be such that ${\kappa }^{\prime }:=f_h^{-1}((\xi ,D))$ shares an x-face τ_x with $\kappa :=f_h^{-1}((\xi ,D^{\ast }))$. Then (ξ,D^*) ∈ ℱ_h((ξ,D)). Our hypotheses imply there exist i, j, k such that $x^k\in X_{j,i}^{\prime }$ with associated threshold ϑ^k satisfying either x^k < ϑ^k on κ and x^k > ϑ^k on κ′ or vice versa. Assume the first case for now. Then τ_x is a right face of κ and a left face of κ′, so sgn(τ_x, κ) = −1 and sgn(τ_x, κ′) = 1.

Now, by Definition 3.2, since x^k < ϑ^k on κ, we also have y_i < θ_j,i on κ. If k > 1, then x^k−1 < ϑ^k−1 on κ as well. Observe that because κ and κ′ share an x-face, all variables in (V ′∪X′)\{x^k} are fixed between the same respective pair of consecutive thresholds on κ′ as on κ. Thus on both κ and κ′, sgn(y_i − θ_j,i) = −1 and if x^k−1 exists, then sgn(x^k−1 − ϑ^k−1) = −1. By Definition 2.17, this means ℓ(τ_x, κ) = 1 and ℓ (τ_x, κ′) = −1. The result now follows from Definition 2.21.

If instead x^k > ϑ^k on κ and x^k < ϑ^k on κ′, the argument is analogous.

Recall that in Figures 3e and 3g the *-elements of the domain graphs are given by (ξ₁,−1) and (ξ₂, 1), respectively. As predicted by Lemma 3.6, we see the edges (ξ₁, 1) → (ξ₁,−1) and (ξ₂,−1) → (ξ₂, 1), showing attractiveness in the fiber.

We will now state another property of the *-element in the fiber over a particular ξ ∈ 𝒱, namely that this element is reachable from every other element of the same fiber via a path contained in that fiber. The proof of Lemma 3.7 is given in Appendix B.

Lemma 3.7

Let ξ ∈ 𝒱. For each element (ξ,D) in the fiber over ξ, there exists a path from (ξ,D) to (ξ,D^*) such that for each (ξ′,D′) in the path, we have ξ = ξ′.

Lemma 3.7 investigates how the domains in the fiber over a single domain ξ are connected. Clearly, in addition to connections within the fiber, there are additional connections between these and domains in neighboring fibers that differ in a y-coordinate.

Lemmas 3.3, 3.4, 3.6, and 3.7 establish key properties of the *-element of each fiber. It will become important that the *-element is the unique element of the fiber with the latter two properties (see Theorem 3.12 below). The next two results show that this is indeed the case.

Corollary 3.8

The *-element is the unique element in the fiber satisfying Lemma 3.7

Proof

By Lemma 3.6, the *-element is attracting in the fiber. Therefore there is no path restricted to the fiber from (ξ,D^*) to any other element (ξ,D).

Corollary 3.9

The *-element is the unique element in the fiber that is attracting in the fiber.

Proof

Because every element (ξ,D) ≠ (ξ,D^*) has a path to (ξ,D^*) by Lemma 3.7, each such (ξ,D) must have an outgoing x-wall. Hence it is not attracting in the fiber.

Definition 3.10

A recurrent component 𝒞 in (MD(G),≤), where G is either (𝒱, ℰ_z) or (𝔛, ℰ_h), is called a fixed point if it contains a single node ξ. A recurrent component is an attractor if there is no 𝒞′ ∈ MD(G) such that 𝒞′ is reachable from 𝒞.

Lemma 3.11

Every fixed point in (MD(G),≤), where G is either (𝒱, ℰ_z) or (𝔛, ℰ_h), is an attractor.

Proof

This is immediate from Definitions 2.20 and 2.21, because {u} a recurrent component in MD(G) is equivalent to u ∈ ℱ(u), where ℱ is either ℱ_z or ℱ_h. This in turn is equivalent to f⁻¹(u) attracting, where f is either f_z or f_h.

Theorem 3.12

There exists a fixed point 𝒞 = {ξ} ∈ MD((𝒱, ℰ_z)) if and only if 𝒞̂ = {(ξ,D^*)} ∈ MD((𝔛, ℰ_h)) is a fixed point. If there exists a fixed point 𝒞 = {(ξ,D)} in any fiber, it is the unique fixed point in that fiber.

Proof

Let ξ be the sole element of 𝒞 ∈ MD((𝒱, ℰ_z)) and let $\stackrel{\sim }{\kappa }:=f_z^{-1}(\xi )$ and $\kappa :=f_h^{-1}(\xi ,D^{\ast })$. Then ξ ∈ ℱ_z(ξ), and therefore κ̃ is an attracting domain. Therefore, for any face τ̃ of κ̃, ℓ̃(τ̃, κ̃) = 1. Then by Lemma 3.3, for each y-face τ of κ, ℓ(τ, κ) = 1. Furthermore, Lemma 3.6 implies that for each x-face τ_x of κ, ℓ(τ_x, κ) = 1. Thus κ is an attracting extended domain, so (ξ,D^*) ∈ ℱ_h((ξ,D^*)).

Now conversely let 𝒞̂ ∈ MD((𝔛, ℰ_h)) have a single element (ξ,D). By Lemma 3.9, the *-element is the only element in the fiber that is attracting in the fiber. Therefore since 𝒞̂ ∈ MD((𝔛, ℰ_h)) has a single element (ξ,D), we have D = D^*, giving uniqueness. Let $\kappa :=f_h^{-1}(\xi ,D^{\ast })$ and $\stackrel{\sim }{\kappa }=f_z^{-1}(\xi )$. We have that κ is an attracting extended domain by Definition 2.21 and so ℓ(τ, κ) = 1 for every face τ of κ. In particular, this holds for each y-face of κ. Then by Lemma 3.3, for each face τ̃ of κ̃, ℓ̃(τ̃, κ̃) = 1, so κ̃ is an attracting domain. Thus ξ ∈ ℱ_z(ξ), so the result follows.

Definition 3.13

Consider domain graphs (𝒱, ℰ_z) and (𝔛, ℰ_h). Recall that 𝔛 = 𝒱 × {−1, 1}^|X|. Let

$${\mathrm{\Pi }}^{\prime }:\mathfrak{X}\to \mathcal{V}$$

be a projection on the first component. Let 𝒯 be collection of all directed edges on vertex set 𝒱. Π′ induces a projection between edges

$${\mathrm{\Pi }}^{″}:{\mathcal{E}}_h\to \mathcal{T}$$

via

$${\mathrm{\Pi }}^{″}(({\xi }_1,D_1),({\xi }_2,D_2)):=\{\begin{array}{cc}({\mathrm{\Pi }}^{\prime }({\xi }_1,D_1),{\mathrm{\Pi }}^{\prime }({\xi }_2,D_2))& \text{if}{\xi }_1\ne {\xi }_2\text{or}({\xi }_1,D_1)=({\xi }_2,D_2)\\ \varnothing & \text{otherwise}\end{array}$$

Let 𝒮 (G) denote the collection of subgraphs of G. Then Π′ and Π″ induce a projection

$$\mathrm{\Pi }:\mathcal{S}((\mathfrak{X},{\mathcal{E}}_h))\to \mathcal{S}((\mathcal{V},\mathcal{T}))$$

via

$$\mathrm{\Pi }((X,E))=({\mathrm{\Pi }}^{\prime }(X),{\mathrm{\Pi }}^{″}(E))$$

for G = (X,E) a subgraph of (𝔛, ℰ_h).

Consider 𝒞 ∈ MD((𝒱, ℰ_z)), a recurrent component of (𝒱, ℰ_z). By Lemma 3.4, for each edge ξ → ξ′ in 𝒞, (𝔛, ℰ_h) contains the edge (ξ,D^*) → (ξ′,D^*). Furthermore, by Lemma 3.7, there exists a path from (ξ′,D^*) to (ξ′,D′^*) in (𝔛, ℰ_h), contained in the fiber over ξ′. Denote the set of such paths from (ξ′,D^*) to (ξ′,D′^*) by 𝒬(ξ, ξ′), where an element of 𝒬(ξ, ξ′) is given by:

$$({\xi }^{\prime },D^{\ast })=({\xi }^{\prime },D_1)\to ({\xi }^{\prime },D_2)\to \cdots \to ({\xi }^{\prime },D_m)=({\xi }^{\prime },{D^{\prime }}^{\ast })$$

Definition 3.14

If 𝒞 = (𝒱_𝒞, ℰ_𝒞) ∈ MD((𝒱, ℰ_z)) is a recurrent component of (𝒱, ℰ_z), then the *-subgraph over 𝒞 is the subgraph ${\mathcal{C}}^{\ast }:=({\mathfrak{X}}_{\mathcal{C}}^{\ast },{\mathcal{E}}_{\mathcal{C}}^{\ast })$ of (𝔛, ℰ_h) defined by

$$\begin{gathered} {\mathcal{E}}_{\mathcal{C}}^{\ast }:=\underset{(\xi ,{\xi }^{\prime })\in {\mathcal{E}}_{\mathcal{C}}}{\cup }\{((\xi ,D^{\ast }),({\xi }^{\prime },D^{\ast }))\}\cup \mathcal{Q}(\xi ,{\xi }^{\prime }) \\ {\mathfrak{X}}_{\mathcal{C}}^{\ast }:=\{(\xi ,D)\mid ((\xi ,D),({\xi }^{\prime },D^{\prime }))\in {\mathcal{E}}_{\mathcal{C}}^{\ast }\text{or}(({\xi }^{\prime },D^{\prime }),(\xi ,D))\in {\mathcal{E}}_{\mathcal{C}}^{\ast }\text{for}\text{some}{\xi }^{\prime }\text{and}{D}^{\prime }\}. \end{gathered}$$

We now prove our first main result. We will show that for the *-subgraphs 𝒞^* ⊂ (𝔛, ℰ_h), the projection Π(𝒞^*) is contained in 𝒮((𝒱, ℰ_z)) and not just 𝒮((𝒱, 𝒯)). That is, the projection of each edge in 𝒞^* is an edge in the set ℰ_z. Moreover, 𝒞^* is a strongly connected subgraph that projects onto a Morse set of the switching domain graph.

Theorem 3.15

Let 𝒞 = (𝒱_𝒞, ℰ_𝒞) ∈ MD((𝒱, ℰ_z)). Then the *-subgraph ${\mathcal{C}}^{\ast }=({\mathfrak{X}}_{\mathcal{C}}^{\ast },{\mathcal{E}}_{\mathcal{C}}^{\ast })$ over 𝒞 is a strongly connected subgraph of (𝔛, ℰ_h) such that

$$\mathrm{\Pi }({\mathcal{C}}^{\ast })=\mathcal{C}.$$

Proof

By Definitions 3.13 and 3.14

$$\begin{gathered} {\mathrm{\Pi }}^{″}({\mathcal{E}}_{\mathcal{C}}^{\ast })=\underset{{\mathcal{E}}_{\mathcal{C}}}{\cup }\{(\xi ,{\xi }^{\prime })\} \\ {\mathrm{\Pi }}^{\prime }({\mathfrak{X}}_{\mathcal{C}}^{\ast })=\underset{{\mathcal{V}}_{\mathcal{C}}}{\cup }\{\xi \} \end{gathered}$$

so that 𝒞^* projects onto 𝒞, Π(𝒞^*) = 𝒞.

It remains to be shown that 𝒞^* is strongly connected. Let u, v ∈ 𝒞^*. Because 𝒞 is a recurrent component, there exists a path in 𝒞 from Π′(u) to Π′(v). Let ξ₁ := Π′(u) and ξ_m := Π′(v) and denote this path by ξ₁ → ξ₂ → ⋯ → ξ_m. Because this path is contained in 𝒞, 𝒞^* contains the edge $({\xi }_p,D_p^{\ast })\to ({\xi }_{p+1},D_p^{\ast })$ for p = 1, 2, …, m − 1 by Lemma 3.4 and Definition 3.14. By Lemma 3.7, there exists a path in the fiber over ξ_p+1 (and therefore in 𝒞^*) from (ξ_p+1, $D_p^{\ast }$) to (ξ_p+1, $D_{p+1}^{\ast }$). By our assumptions, u is in the fiber over ξ₁, so 𝒞^* also contains a path from u to (ξ₁, $D_1^{\ast }$), and likewise there exists a path from (ξ_m, $D_{m-1}^{\ast }$) to v. Concatenating these paths together, we see that 𝒞^* contains a path

$$u\to \cdots \to ({\xi }_1,D_1^{\ast })\to ({\xi }_2,D_1^{\ast })\to \cdots \to ({\xi }_2,D_2^{\ast })\to \cdots \to ({\xi }_m,D_{m-1}^{\ast })\to \cdots \to v$$

Remark 3.16

Note that Theorem 3.15 does not imply the stronger result that if there exists a recurrent component 𝒞 ∈ MD((𝒱, ℰ_z)), then there exists a recurrent component 𝒞̂ ∈ MD((𝔛, ℰ_h)) that projects onto 𝒞. The subgraph 𝒞^* in Theorem 3.15 may not be a maximal strongly connected component, as Definition 2.22 of recurrent component requires. We present in Example 4.4 a case where disjoint components 𝒞₁, 𝒞₂ ∈ MD((𝒱, ℰ_z)) have *-subgraphs ${\mathcal{C}}_1^{\ast },{\mathcal{C}}_2^{\ast }$ that are subgraphs of a single strongly connected component.

Theorem 3.17

Let 𝒞_p, 𝒞_q ∈ MD((𝒱, ℰ_z)) be two recurrent components of (𝒱, ℰ_z) and let ${\mathcal{C}}_p^{\ast }$ and ${\mathcal{C}}_q^{\ast }$ be the *-subgraphs over 𝒞_p and 𝒞_q, respectively. If there exists a path in (𝒱, ℰ_z) from an element of 𝒞_p to an element of 𝒞_q, then there exists a path in (𝔛, ℰ_h) from an element of ${\mathcal{C}}_p^{\ast }$ to an element of ${\mathcal{C}}_q^{\ast }$.

Proof

Let ξ₁ ∈ 𝒞_p and ξ_m ∈ 𝒞_q and assume that (𝒱, ℰ_z) contains a path ξ₁ → ξ₂ → ⋯ → ξ_m. By Definition 3.14, ${\mathcal{C}}_p^{\ast }$ and ${\mathcal{C}}_q^{\ast }$ contain (ξ₁, $D_1^{\ast }$) and (ξ_m, $D_m^{\ast }$) as vertices, respectively. By Lemmas 3.4 and 3.7, (𝔛, ℰ_h) contains a path

$$({\xi }_1,D_1^{\ast })\to ({\xi }_2,D_1^{\ast })\to \cdots \to ({\xi }_2,D_2^{\ast })\to \cdots \to ({\xi }_m,D_{m-1}^{\ast })\to \cdots \to ({\xi }_m,D_m^{\ast })$$

using a similar concatenation technique to that used in the proof of Theorem 3.15.

Definition 3.18

We define the component map φ : MD((𝒱, ℰ_z)) → MD((𝔛, ℰ_h)) such that for each 𝒞 ∈ MD((𝒱, ℰ_z)), φ(𝒞) is the Morse node of (𝔛, ℰ_h) containing the *-subgraph 𝒞^* over 𝒞.

Theorem 3.19

φ : MD((𝒱, ℰ_z)) → MD((𝔛, ℰ_h)) is an order-preserving map.

Proof

First we show that φ is well-defined. Let 𝒞 ∈ MD((𝒱, ℰ_z)). Then 𝒞^* is a strongly connected component of (𝔛, ℰ_h). Therefore, 𝒞^* is contained in a unique recurrent component of (𝔛, ℰ_h).

Now let 𝒞_p, 𝒞_q ∈ (MD((𝒱, ℰ_z)),≤) be such that q ≤ p. Then there exist elements ξ ∈ 𝒞_p and ξ′ ∈ 𝒞_q and a path in (𝒱, ℰ_z) from ξ to ξ′ by Definition 2.22. If ${\mathcal{C}}_p^{\ast }$ and ${\mathcal{C}}_q^{\ast }$ are the *-subgraphs over these two components, then by Theorem 3.17, there exists a path from an element of ${\mathcal{C}}_p^{\ast }$ to an element of ${\mathcal{C}}_q^{\ast }$. Let 𝒞̂_p and 𝒞̂_q be the Morse nodes of (𝔛, ℰ_h) containing these *-subgraphs. Then this same path is from an element of 𝒞̂_p to one of 𝒞̂_q. Thus q ≤ p in (MD((𝔛, ℰ_h)),≤).

Theorem 3.19 shows the existence of an order-preserving map φ : MD((𝒱, ℰ_z)) → MD((𝔛, ℰ_h)). A natural question is whether there is a stronger relationship between MD((𝒱, ℰ_z)) and MD((𝔛, ℰ_h)). We show in the following section that φ is not in general either injective or surjective. In particular, we give an example where MD((𝒱, ℰ_z)) consists of a single element and MD((𝔛, ℰ_h)) contains more than one element; and we give another example where two elements of MD((𝒱, ℰ_z)) map to a single element of MD((𝔛, ℰ_h)).

4 Examples

In this section we provide three examples that demonstrate that, in general, a few natural candidates for a stronger Theorem 3.19 are not valid.

1. In general, there does not exist a surjection, order preserving or otherwise, from MD((𝒱, ℰ_z)) onto MD((𝔛, ℰ_h)). As a consequence MG((𝒱, ℰ_z)) and MG((𝔛, ℰ_h)) are not isomorphic. We provide two examples. In the first example, there are two Morse sets 𝒞₁, 𝒞₂ ∈ MD((𝔛, ℰ_h)), but only one Morse set 𝒞 ∈ MD((𝒱, ℰ_z)). Clearly, since the cardinality of MD((𝒱, ℰ_z)) is less than the cardinality of MD((𝔛, ℰ_h)), there can be no surjection from the first to the second. However, we also show that Π(𝒞₁) = 𝒞 and Π(𝒞₂) ∈ 𝒮(𝒞, 𝒯 \ℰ_z)). In other words, the vertices of 𝒞₂ project onto vertices of 𝒞, but none of the edges in Π(𝒞₂) appear in the domain graph (𝒱, ℰ_z).

   In the second example, we likewise show the lack of a surjection in which there is a Morse set 𝒞₁ ∈ MD((𝔛, ℰ_h)) that does not project onto any Morse set of MD((𝒱, ℰ_z)). In this case, there are vertices in 𝒞₁ that do not project onto vertices of any Morse set in MD((𝒱, ℰ_z))

2. The map φ is not, in general, injective. In the third example, we show that two Morse sets in MD((𝒱, ℰ_z)) have *-subgraphs that embed into the same recurrent component of (𝔛, ℰ_h).

We will make the following annotations to the Morse sets when displaying the Morse graphs for the parameterized ODE systems of a regulatory network RN and its canonical extension EX.

Definition 4.1

Let 𝒞 be a recurrent component of either (𝒱, ℰ_z) or (𝔛, ℰ_h). Recall from Definition 3.10 that 𝒞 is a fixed point if and only if 𝒞 contains a single node. In this case we annotate 𝒞 by FP. Otherwise we say 𝒞 is a cycle and annotate it by C.

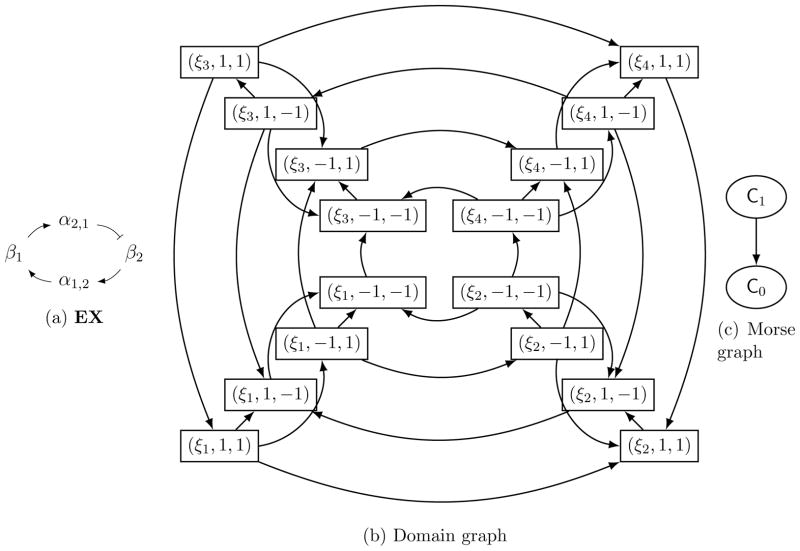
Example 4.2

The first example will show that in general there is no surjection from MD((𝒱, ℰ_z)) onto MD((𝔛, ℰ_h)) and therefore no isomorphism between MD((𝒱, ℰ_z)) and MD((𝔛, ℰ_h)).

Let RN = (V,E) where V = {β₁, β₂} and E = {β₁ ⊣ β₂, β₂ → β₁}, as shown in Figure 5a. The associated switching system is on the left below (on the right is the extended system associated to a canonical extension defined below).

Figure 5.

Example 4.2: (a) RN, (b) phase space of the switching system, (c) domain graph of the switching system with the parameter in the text, and (d) Morse graph of the domain graph.

$$\begin{array}{ll}{\stackrel{.}{y}}_1=-{\gamma }_1{y}_1+{\stackrel{\sim }{\mathrm{\Lambda }}}_1(y)\hfill & \hfill {\stackrel{.}{y}}_1=-{\gamma }_1{y}_1+{\mathrm{\Lambda }}_1(y,x)\\ \hfill & \hfill {\stackrel{.}{x}}_{2,1}=-a_{2,1}{x}_{2,1}+b_{2,1}{y}_1\\ {\stackrel{.}{y}}_2=-{\gamma }_2{y}_2+{\stackrel{\sim }{\mathrm{\Lambda }}}_2(y)\hfill & \hfill {\stackrel{.}{y}}_2=-{\gamma }_2{y}_2+{\mathrm{\Lambda }}_2(y,x)\\ \hfill & \hfill {\stackrel{.}{x}}_{1,2}=-a_{1,2}{x}_{1,2}+b_{1,2}{y}_2\end{array}$$

Note that there exist four domains in the phase space of the switching system, as seen in Figure 5b.

We must make a choice of combinatorial parameter in order to construct the domain graph (𝒱, ℰ_z). By Defintion 2.24, a combinatorial parameter choice in this example is equivalent to a choice of order between each γ₁θ_2,1 and the values of Λ̃₁, a choice of order between γ₂θ_1,2 and the values of Λ̃₂, and a choice of order on the set of thresholds associated to each y_i ∈ V. We will pick the combinatorial parameter (L,O) such that l_1,2 < γ₁θ_2,1 < u_1,2 and l_2,1 < γ₂θ_1,2 < u_2,1. This results in the domain graph (𝒱, ℰ_z) in Figure 5c. Clearly the entire domain graph comprises a recurrent component. The result is the Morse graph MG((𝒱, ℰ_z)) with a single component C, as shown in Figure 5d.

Let EX = (V ∪ X, E_X) where X = {α_2,1, α_1,2} and E_X is the union of two chains C_2,1 := {β₁ → α_2,1, α_2,1 ⊣ β₂} and C_1,2 := {{β₂ → α_1,2, α_1,2 → β₁} as shown in Figure 6a. The canonical extension of the regulatory network, maintaining the combinatorial parameter for RN above, produces the domain graph seen in Figure 6b. It is relatively easy to see that the subgraphs induced by the two vertex sets

Figure 6.

Example 4.2: (a) EX, (b) domain graph of the extended system with the parameter in the text, and (c) Morse graph of the domain graph.

$$\begin{gathered} \mathfrak{X}({\mathrm{C}}_0):=\{({\xi }_1,-1,-1),({\xi }_3,-1,-1),({\xi }_3,-1,1),({\xi }_4,-1,1),({\xi }_4,1,1),({\xi }_2,1,1),({\xi }_2,1,-1),({\xi }_1,1,-1)\} \\ \mathfrak{X}({\mathrm{C}}_1):=\{({\xi }_1,1,1),({\xi }_1,-1,1),({\xi }_2,-1,1),({\xi }_2,-1,-1),({\xi }_4,-1,-1),({\xi }_4,1,-1),({\xi }_3,1,-1),({\xi }_3,1,1)\} \end{gathered}$$

are recurrent components, C₀ and C₁ respectively, and that these are the only recurrent components of the system. Moreover, there is a path from C₁ to C₀ in the domain graph, leading to the Morse graph shown in Figure 6c. We leave the reader to check that C₀ is the *-subgraph over the single recurrent component C of (𝒱, ℰ_z). Since C₁ cycles in the opposite direction through the same projected nodes, Π′(𝔛(C₀)) = Π′(𝔛(C₁)), we have that C₁ ∈ 𝒮((𝒱, ℰ_z)^T), where (𝒱, ℰ_z)^T is the transpose graph of (𝒱, ℰ_z) where all directed edges are reversed. Thus Π(C₁) shares no edges with (𝒱, ℰ_z).

Note that the dynamics observed in this example are consistent with results about cyclic feedback systems [34, 22, 19]. RN is a negative cyclic feedback system with two variables and EX is a negative cyclic feedback system with four variables.

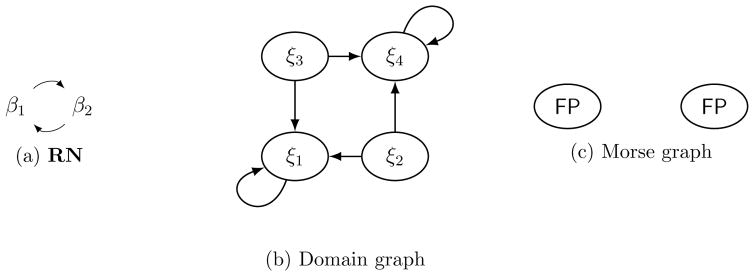
Example 4.3

Note that by Example 4.2, not every element of MD((𝔛, ℰ_h)) projects onto an element of MD((𝒱, ℰ_z)) via our projection map Π, as the edges in the non-attracting cycle in MD((𝔛, ℰ_h)) do not project onto the edges of the unique Morse node of MD((𝒱, ℰ_z)). However, the vertex set of the former does project onto that of the latter. The following example shows that there may be Morse sets of MD((𝔛, ℰ_h)) that do not even share nodes with a Morse set of MD((𝒱, ℰ_z)).

Let RN = (V, E) where V = {β₁, β₂} and E = {β₁ → β₂, β₂ → β₁} as shown in Figure 7a. Since the only difference between this example and Example 4.2 is the sign of the feedback from β₁ to β₂, the domain structure of the phase space for RN is the same between these two examples. The direction of arrows in the domain graphs will be different between these examples. We pick the same combinatorial parameter (L, O) as in Example 4.2: l_1,2 < γ₁θ_2,1 < u_1,2 and l_2,1 < γ₂θ_1,2 < u_2,1. The results are the domain graph and Morse graph in Figures 7b and 7c.

Figure 7.

RN and the domain and Morse graphs of the switching system for Example 4.3. The phase space of the associated switching system is the same as in Example 4.2 (see Figure 5b).

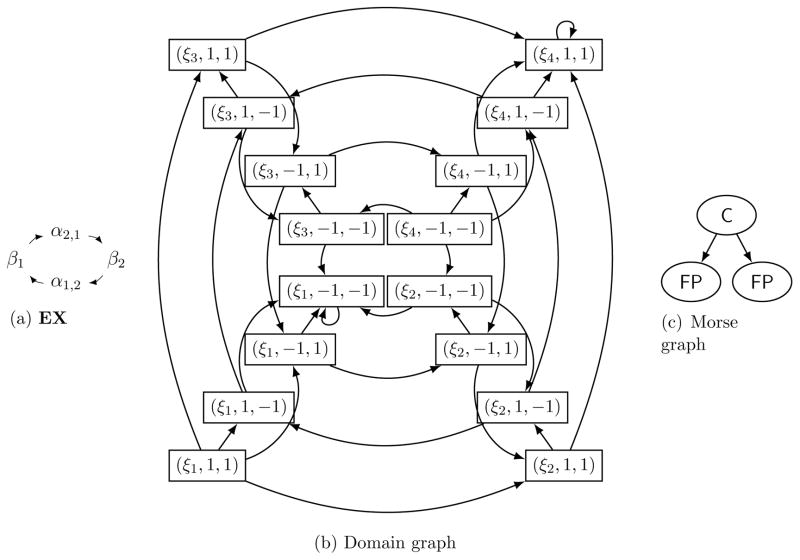
Let EX = (V ∪ X, E_X) where X = {α_2,1, α_1,2} and E_X is the union of two chains C_2,1 := {β₁ → α_2,1, α_2,1 → β₂} and C_1,2 := {β₂ → α_1,2, α_1,2 → β₁}, as shown in Figure 8a. Again, we maintain the combinatorial parameter for RN from above. The canonical extension gives rise to the domain graph in Figure 8b.

Figure 8.

Example 4.3: (a) EX, (b) domain graph of the extended system with the parameter in the text, and (c) Morse graph of the domain graph.

Note that as predicted by Theorem 3.12, there exist exactly two one-element recurrent components, namely the subgraphs induced by {(ξ₁, −1, −1)} and {(ξ₄, 1, 1)}. However, there exists an additional recurrent component: the subgraph induced by the set

$$\begin{gathered} \{({\xi }_1,-1,1),({\xi }_1,1,-1),({\xi }_2,-1,-1),({\xi }_2,-1,1),({\xi }_2,1,-1),({\xi }_2,1,1), \\ ({\xi }_3,-1,-1),({\xi }_3,-1,1),({\xi }_3,1,-1),({\xi }_3,1,1),({\xi }_4,-1,1),({\xi }_4,1,-1)\}. \end{gathered}$$

Note there also exist paths, for instance, from (ξ₁, −1, 1) to (ξ₁, −1, −1) and from (ξ₄, 1, −1) to (ξ₄, 1, 1). The result is the Morse graph in Figure 8c. Note also that even the vertex set of the cycle does not project onto that of any recurrent component of (𝒱, ℰ_z).

As in Example 4.2, the dynamics observed in this example are consistent with results about cyclic feedback systems [34, 22, 19]. RN is a positive cyclic feedback system with two variables and EX is a positive cyclic feedback system with four variables.

Example 4.4

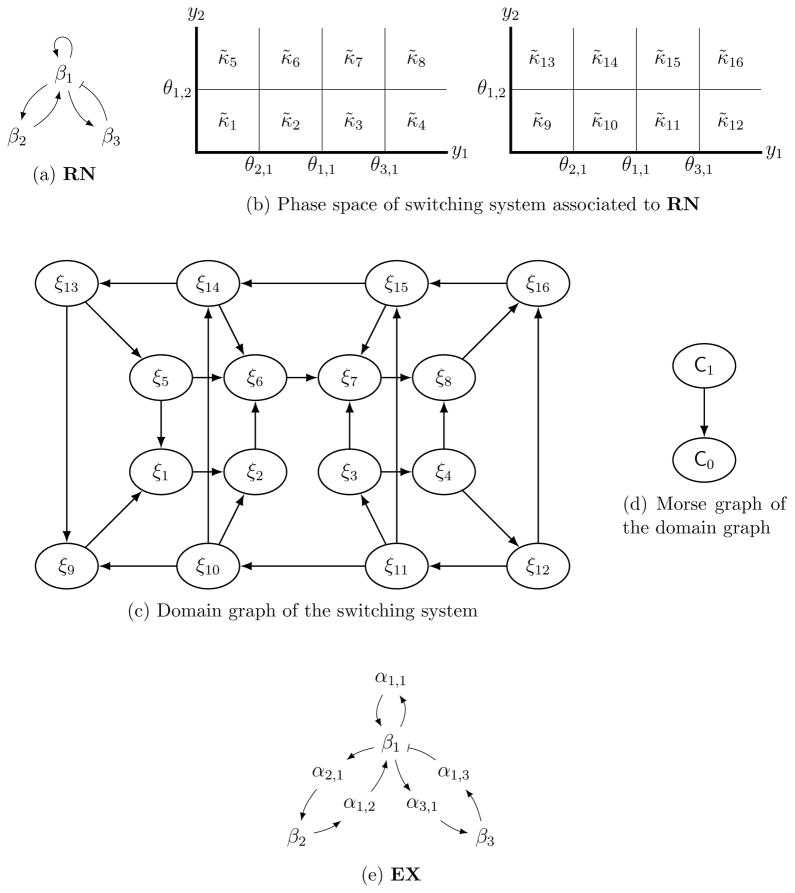
In this final example, we show that the map φ is not, in general, injective. Recall that φ maps a recurrent component 𝒞 of (𝒱, ℰ_z) to the recurrent component of (𝔛, ℰ_h) containing the *-subgraph 𝒞^* over 𝒞. In this example the *-subgraphs over the two distinct Morse nodes of (𝒱, ℰ_z) are contained in the same recurrent component of (𝔛, ℰ_h).

Let RN = (V, E) where V = {β₁, β₂, β₃} and

$$E=\{{\beta }_1\to {\beta }_1,{\beta }_1\to {\beta }_2,{\beta }_1\to {\beta }_3,{\beta }_2\to {\beta }_1,{\beta }_3⊣{\beta }_1\}$$

For any arbitrary regular parameter z ∈ Z, the switching system associated to RN is as follows

$$\begin{gathered} {\stackrel{.}{y}}_1=-{\gamma }_1{y}_1+{\stackrel{\sim }{\mathrm{\Lambda }}}_1(y) \\ {\stackrel{.}{y}}_2=-{\gamma }_2{y}_2+{\stackrel{\sim }{\mathrm{\Lambda }}}_2(y) \\ {\stackrel{.}{y}}_3=-{\gamma }_1{y}_3+{\stackrel{\sim }{\mathrm{\Lambda }}}_3(y) \end{gathered}$$

The phase space of the switching system is partitioned into sixteen domains, as shown in Figure 9b. For clarity, we divide the domains into two “layers.” On the left are the domains on which y₃ < θ_1,3, while on the right, y₃ > θ_1,3.

Figure 9.

RN, the phase space of the associated switching system, the domain and Morse graphs for the parameterized switching system, and EX in Example 4.4.

We will assume that the logic function M₁ associated to y₁ is additive; that is, Λ̃₁ = M₁ ∘ σ̃₁ = σ̃_1,1 + σ̃_1,2 + σ̃_1,3. Furthermore, we will pick the combinatorial parameter that stipulates the following.

$$\begin{array}{lll}{\theta }_{2,1}<{\theta }_{1,1}<{\theta }_{3,1}\hfill & \hfill & \hfill \\ l_{1,1}+l_{1,2}+l_{1,3}\hfill & <{\gamma }_1{\theta }_{2,1}\hfill & {\gamma }_1{\theta }_{2,1}<l_{1,1}+l_{1,2}+u_{1,3}<{\gamma }_1{\theta }_{1,1}\hfill \\ u_{1,1}+l_{1,2}+l_{1,3}\hfill & <{\gamma }_1{\theta }_{2,1}\hfill & {\gamma }_1{\theta }_{1,1}<l_{1,1}+u_{1,2}+u_{1,3}<{\gamma }_1{\theta }_{3,1}\hfill \\ l_{1,1}+u_{1,2}+l_{1,3}\hfill & <{\gamma }_1{\theta }_{2,1}\hfill & {\gamma }_1{\theta }_{3,1}<u_{1,1}+l_{1,2}+u_{1,3}\hfill \\ u_{1,1}+u_{1,2}+l_{1,3}\hfill & <{\gamma }_1{\theta }_{2,1}\hfill & {\gamma }_1{\theta }_{3,1}<u_{1,1}+u_{1,2}+u_{1,3}\hfill \\ l_{2,1}<{\gamma }_2{\theta }_{1,2}<u_{2,1}\hfill & \hfill & \hfill \\ l_{3,1}<{\gamma }_3{\theta }_{1,3}<u_{3,1}\hfill & \hfill & \hfill \end{array}$$

This parameter choice gives rise to the domain graph in Figure 9c.

It is relatively easy to find that the sets {ξ₁, ξ₂, ξ₅, ξ₆, ξ₇, ξ₈, ξ₉, ξ₁₃, ξ₁₄, ξ₁₅, ξ₁₆} and {ξ₃, ξ₄, ξ₁₁, ξ₁₂} both induce subgraphs that are recurrent components of (𝒱, ℰ_z), C₀ and C₁ respectively. Furthermore, there exists a path from ξ₃ to ξ₇, resulting in the Morse graph in Figure 9d.

Now let EX = (V ∪ X, E_X) where X = {α_1,1, α_2,1, α_3,1, α_1,2, α_1,3} and E_X is the union of the five chains shown in Figure 9e. The extended system for h ∈ H is

$$\begin{gathered} {\stackrel{.}{y}}_1=-{\gamma }_1{y}_1+{\mathrm{\Lambda }}_1(x) \\ {\stackrel{.}{x}}_{2,1}=-a_{2,1}{x}_{2,1}+b_{2,1}{y}_1 \\ {\stackrel{.}{x}}_{3,1}=-a_{3,1}{x}_{3,1}+b_{3,1}{y}_1 \\ {\stackrel{.}{y}}_2=-{\gamma }_2{y}_2+{\mathrm{\Lambda }}_2(x) \\ {\stackrel{.}{x}}_{1,2}=-a_{1,2}{x}_{1,2}+b_{1,2}{y}_2 \\ {\stackrel{.}{y}}_3=-{\gamma }_3{y}_3+{\mathrm{\Lambda }}_3(x) \\ {\stackrel{.}{x}}_{1,3}=-a_{1,3}{x}_{1,3}+b_{1,3}{y}_3 \end{gathered}$$

Consider now the *-subgraphs ${\mathrm{C}}_1^{\ast }$ and ${\mathrm{C}}_0^{\ast }$ in (𝔛, ℰ_h) over the two Morse nodes C₁ and C₀ in MD((𝒱, ℰ_z)), respectively, while maintaining our combinatorial parameter and assuming that all elements of the parameter sets a and b are strictly positive. Because both ${\mathrm{C}}_1^{\ast }$ and ${\mathrm{C}}_0^{\ast }$ project onto a recurrent component of (𝒱, ℰ_z), each is a strongly connected graph. However, as we now show, each fails to be a maximal strongly connected component of (𝔛, ℰ_h). We first note that Theorem 3.17 implies that there exists a path in (𝔛, ℰ_h) from ${\mathrm{C}}_1^{\ast }$ to ${\mathrm{C}}_0^{\ast }$. As we will show now, there is also a path from ${\mathrm{C}}_0^{\ast }$ to ${\mathrm{C}}_1^{\ast }$ which shows that both of them are parts of a single strongly connected component of (𝔛, ℰ_h).

First note that (ξ₅, $D_5^{\ast }$) is a node in ${\mathrm{C}}_0^{\ast }$ and that (ξ₃, $D_3^{\ast }$) is a node in ${\mathrm{C}}_1^{\ast }$. We will show that there is a path

$$({\xi }_5,D_5^{\ast })\to ({\xi }_1,D_5^{\ast })\to ({\xi }_2,D_5^{\ast })\to ({\xi }_3,D_5^{\ast })\to \cdots \to ({\xi }_3,D_3^{\ast })$$

in (𝔛, ℰ_h). The first edge follows from Lemma 3.4 and the final path from (ξ₃, $D_5^{\ast }$) to (ξ₃, $D_3^{\ast }$) follows from Lemma 3.7. We have no result in general for the second and third edges, but we justify these edges as follows.

Let $\kappa :=f_h^{-1}(({\xi }_1,D_5^{\ast })),{\kappa }^{\prime }:=f_h^{-1}(({\xi }_2,D_5^{\ast }))$, and notice that these two domains are adjacent in phase space separated by a y-face τ where y₁ = θ_2,1 (see Figure 9b). Also from Figure 9b, we see that y₁ < θ_2,1 on κ and y₁ > θ_2,1 on κ′, so

$$sgn(\tau ,\kappa )=-1\text{and}sgn(\tau ,{\kappa }^{\prime })=1$$

by the definition of left and right faces. Moreover, from the definition of the *-element $D_5^{\ast }$ and the location of κ̃₅ we see that on κ and κ′, x_1,1 < ϑ_1,1, x_1,2 > ϑ_1,2, and x_1,3 < ϑ_1,3. Then Λ₁(κ) = Λ₁(κ′) = l_1,1 + u_1,2 + u_1,3 > γ₁θ_2,1. Hence

$$sgn(-{\gamma }_1{\theta }_{2,1}+{\mathrm{\Lambda }}_1(\kappa ))=sgn(-{\gamma }_1{\theta }_{2,1}+{\mathrm{\Lambda }}_1({\kappa }^{\prime }))=1,$$

and so

$$\ell (\tau ,\kappa )=-1\text{and}\ell (\tau ,{\kappa }^{\prime })=1,$$

This satisfies the condition for an edge from f_h(κ) to f_h(κ′) in (𝔛, ℰ_h).

We similarly show the existence of the edge $({\xi }_2,D_5^{\ast })\to ({\xi }_3,D_5^{\ast })$ by first letting ${\kappa }^{\prime }=f_h^{-1}(({\xi }_2,D_5^{\ast }))$ as before, and ${\kappa }^{″}:=f_h^{-1}(({\xi }_3,D_5^{\ast }))$. These two domains are adjacent in phase space separated by a face τ′ where y₁ = θ_1,1, and

$$sgn({\tau }^{\prime },{\kappa }^{\prime })=-1\text{and}sgn({\tau }^{\prime },{\kappa }^{″})=1.$$

Because no intermediaries cross their associated thresholds at τ′, we have

$${\mathrm{\Lambda }}_1({\kappa }^{\prime })={\mathrm{\Lambda }}_1({\kappa }^{″})=l_{1,1}+u_{1,2}+u_{1,3}>{\gamma }_1{\theta }_{1,1},$$

implying

$$\ell ({\tau }^{\prime },{\kappa }^{\prime })=-1\text{and}\ell ({\tau }^{\prime },{\kappa }^{″})=1$$

which gives the edge f_h(κ′) to f_h(κ″) in (𝔛, ℰ_h), and completes the path.

Let C^* be the recurrent component of (𝔛, ℰ_h) which contains ${\mathrm{C}}_0^{\ast }\cup {\mathrm{C}}_1^{\ast }$. Then

$$\phi ({\mathrm{C}}_0)=\phi ({\mathrm{C}}_1)={\mathrm{C}}^{\ast },$$

so that φ is not injective.

5 Discussion

We have explored the dynamical behavior of the extension of a nonlinear switching system into a mixed nonlinear-linear model that allows differential modeling of protein and mRNA in gene regulatory networks. Mathematically, the switching system permits a partition of phase space into distinct domains with the property that neighboring domains have a well defined direction of flow between them. This gives rise to a state transition graph, which is a discrete representation of the flow. The strongly connected components of the state transition diagram are the nodes of a graph called a Morse graph with edges determined by reachability conditions in the state transition diagram. This is a coarse representation of the long-term dynamics of the system, in which nodes represent recurrent dynamics and edges represent gradient-like dynamics. The lower sets of the Morse graph correspond to attracting regions in phase space. Furthermore, the coarse description of the dynamics leads to an explicit decomposition of the parameter space into regions that admit the same state transition graph, and hence the same Morse graph. This decomposition is characterized by a parameter graph, whose nodes represent the parameter regions and whose edges represent co-dimension 1 boundaries between the regions [11].

We show that the extended system also permits the construction of a similar partition, state transition diagram, Morse graph, and parameter graph. A surprising result is that the parameter graph of a switching system and any of its extensions is the same. This result shows that even though there are a different number of parameters in each system, the partition of the parameter space into regions with the same essential dynamics is the same. We then compare the Morse graphs of the switching system and any canonical extension for the parameters that correspond to the same parameter node in the common parameter graph. We show that there is an order-preserving map between the Morse graph of the switching system and its extension, but that stronger relationships do not hold. In particular, there are neither injections nor surjections in general from the switching Morse graph to the extended Morse graph. We conclude that there are nontrivial changes in the long-term dynamics between systems, and we give several examples demonstrating this fact.

There are two main barriers to proving a stronger result than Theorem 3.19. The more technical reason is the fact that while the direction of the edge $({\xi }_1,D_1^{\ast })\to ({\xi }_2,D_1^{\ast })$ in (𝔛, ℰ_h) is the same as the direction of the edge ξ₁ → ξ₂ in (𝒱, ℰ_z), we do not have control over edges between (ξ₁,D) and (ξ₂,D) in (𝔛, ℰ_h) for $D\ne D_1^{\ast }$. Since in principle these edges can go in the opposite direction (ξ₂,D) → (ξ₁,D), there are limits on the relationship between MD((𝒱, ℰ_z)) and MD((𝔛, ℰ_h)).

Another more intriguing reason may be the fact that the Morse decomposition MD((𝒱, ℰ_z)) is incomplete in the sense that a perturbation of a switching system to a smooth approximation can increase the number of Morse sets. While we are not considering such perturbations in this paper, we will illustrate this idea on Example 4.3, where the Morse decomposition MD((𝒱, ℰ_z)) consists of two attracting fixed points A₁, A₂. It is easy to see by a topological argument that any small perturbation to a smooth system will contain not only these attracting fixed points, but also contain a saddle point whose stable manifold separates the basins of attraction of the two attracting fixed points. If we now consider the extension (𝔛, ℰ_h) of the system (𝒱, ℰ_z), its Morse decomposition MD((𝔛, ℰ_h)) contains two attracting fixed points (as required by Theorem 3.12) that project to A₁ and A₂ respectively. However, it also contains a saddle-like set C that separates their basins of attraction and which has no corresponding Morse set in MD((𝒱, ℰ_z)). This suggests an intriguing conjecture that there is a stronger relationship between an appropriately defined “completion” of the Morse decomposition MD((𝒱, ℰ_z)) and the Morse decomposition MD((𝔛, ℰ_h)). Such a completion would include Morse sets of all sufficiently near smooth perturbations of the switching system associated to RN. A closely related conjecture is that the solutions of a Filippov extension of a switching system [7], viewed as a multivalued flow, admit a Morse decomposition with a stronger relationship to MD((𝔛, ℰ_h)) than that described in Theorem 3.19 between MD((𝒱, ℰ_z)) of the switching system and MD((𝔛, ℰ_h)).

Our results indicate that explicitly modeling the translation process from mRNA to protein may fundamentally change the prediction of the model, and that the choice of model between switching system and extension is a nontrivial decision. Therefore experimentalists can directly compare the outcome of a switching model versus an extension and decide on the best model given observed data.

Highlights.

• We study switching systems (SS), where nonlinearities are piece-wise constant

• We characterize global structure of dynamics in parameter space by parameter graphs

• Extensions of SS replace some of direct interactions by chains of linear equations

• We show that parameter graphs of SS and their extensions are identical

• We discuss relationship between Morse graphs of SS and their extensions.

Appendix A Nullclines

In this appendix we provide some geometric motivation for our choice of thresholds in Definition 2.6 for the intermediaries $x_{j,i}^k$. This motivation revolves around the nullclines of the extended system (5).

Definition A.1

Let EX be a canonical extension of a regulatory network RN, and let h be a regular parameter for EX. By Definition 2.4 there exists an extended system associated to EX at h. Let y_i ∈ V′. We define the y_i-nullcline under h to be the set

$${\mathcal{Y}}_i(h):=\{p\in {(0,\infty )}^{\mid V\cup X\mid }{\mid {\stackrel{.}{y}}_i\mid }_p=0\}$$

Let β_j ∈ T(β_i) and let X_j,i = {α¹, α², …, αⁿ} with associated variables {x^k}. For k = 1, 2, …, n, the x^k-nullcline under h is the set

$${\mathcal{X}}^k(h):=\{p\in {(0,\infty )}^{\mid V\cup X\mid }{\mid {\stackrel{.}{x}}^k\mid }_p=0\}$$

Remark A.2

Observe that by Definition 2.4, for each y_i ∈ V′ the y_i-nullcline under h can be characterized as

$${\mathcal{Y}}_i(h)=\left\{p\in {(0,\infty )}^{\mid V\cup X\mid }{|y_i\mid }_p=\frac{{\mathrm{\Lambda }}_i(p)}{{\gamma }_i}\right\}.$$

Also observe that by Definition 2.6, the x^k-nullcline under h can be characterized in a similar way for k = 1, 2, …, n:

$$\begin{gathered} {\mathcal{X}}^1(h)=\left\{p\in {(0,\infty )}^{\mid V\cup X\mid }{|x^1\mid }_p=\frac{b^1}{a_1}{y_i\mid }_p\right\} \\ {\mathcal{X}}^k(h)=\left\{p\in {(0,\infty )}^{\mid V\cup X\mid }{|x^k\mid }_p=\frac{b^k}{a^k}{x^{k-1}\mid }_p\right\},k=2,3,\dots ,n. \end{gathered}$$

From Remark A.2 it can be seen that the choice of thresholds ϑ¹, …, ϑⁿ for the intermediaries x¹, …, xⁿ, respectively, is due directly to the locations of these nullclines in phase space. In particular, we choose ϑ¹ such that the intersection of the two hyperplanes {y_i = θ_j,i} and {x¹ = ϑ¹} is contained in the x₁-nullcline. Similarly, for k = 2, …, n, the intersection of the hyperplanes {x^k−1 = ϑ^k−1} and {x^k = ϑ^k} is contained in the x^k-nullcline. We give a key consequence of these observations in Lemma A.3. This leads to an alternative derivation of Theorem 2.15 and consequently Corollary 2.19, which we provide here.

Lemma A.3

Fix a regular parameter h ∈ H for EX and let y_i ∈ V′ and y_j ∈ T(y_i). Consider the chain C_j,i = {(β_i, α¹), (α¹, α²), …, (αⁿ, β_j)}. Let τ_y be a y-face on which y_i = θ_j,i. Let τ_x be an x-face on which x^k = ϑ^k. Then

$${\tau }_y\cap {\mathcal{Y}}_i(h)={\tau }_x\cap {\mathcal{X}}^k(h)=\varnothing$$

Proof

By Lemma 2.14, we note that for each p ∈ τ_y,

$${\mathrm{\Lambda }}_i(\kappa )={\mathrm{\Lambda }}_i({\kappa }^{\prime })={\mathrm{\Lambda }}_i(p)$$

Because h is a regular parameter,

$${\theta }_{j,i}\ne \frac{{\mathrm{\Lambda }}_i(\kappa )}{{\gamma }_i}$$

and therefore at each p ∈ τ_y,

$${y_i\mid }_p\ne \frac{{\mathrm{\Lambda }}_i(p)}{{\gamma }_i}$$

so we conclude that p ∉ 𝒴_i(h) for any p ∈ τ_y.

Now let p ∈ τ_x. If k = 1, then by Definitions 2.6 and 2.8 $x^1={\vartheta }^1=\frac{b^1}{a^1}{\theta }_{j,i}$ at p. Because p ∈ τ_x, y_i ∈ (θ_vi,i, θ_wi,i) at p, for some pair of consecutive thresholds θ_vi,i and θ_wi,i, and hence y_i|_p ≠ θ_j,i. Therefore $x^1\ne \frac{b^1}{a^1}{y}_i$. We conclude p ∉ 𝒳¹(h) for any p ∈ τ_x.

In a very similar fashion, we observe that if p ∈ τ_x and k > 1, then at p, $x^k=\frac{b^k}{a^k}{\vartheta }^{k-1}$ and x^k−1 ≠ ϑ^k−1. This implies $x^k\ne \frac{b^k}{a^k}{x}^{k-1}$ at any p ∈ τ_x, and so p ∉ 𝒳^k(h).

Using Lemma A.3, we can now prove Theorem 2.15 geometrically, with the theorem restated here for reference.

Theorem

Let EX be a canonical extension where the associated extended system has a regular parameter h = (z, a, b) ∈ H. Let τ be a face on which μ ∈ V′ ∪ X′ is constant. Then sgn(μ̇ ) is constant and nonzero on τ.

Proof

The first part of the proof of Lemma A.3 establishes that ẏ_i is constant and nonzero on any face where y_i is constant, implying that sgn(ẏ_i) is constant and nonzero as well.

Consider now x^k = ϑ^k on a wall τ_x with nullcline 𝒳^k(h). By Lemma A.3, τ_x∩𝒳^k(h) = ∅. Therefore ẋ^k and therefore sgn(ẋ^k) are nonzero everywhere on τ^x. Suppose for a contradiction that sgn(ẋ^k) is nonconstant. By the continuity of ẋ^k and the Intermediate Value Theorem, there then exists a point r ∈ τ_x such that ẋ^k|_r = 0, a contradiction.

Appendix B Proof of Lemma 3.7

For reference, we repeat the lemma here:

Lemma

Let ξ ∈ 𝒱. For each element (ξ, D) in the fiber over ξ, there exists a path from (ξ, D) to (ξ, D^*) such that for each (ξ′,D′) in the path, we have ξ = ξ′.

The proof of this lemma is equivalent to a proof of correctness of Algorithm 1:

Algorithm 1.

Path-Finding Problem

procedure PathFinder((ξ,D1))	procedure OppositeSigns(𝒯, κ, yi, yj)
℘ ← list((ξ,D1))	𝒯′ ← list()
for yi ∈ V′ do	for τ ∈ 𝒯 do
for yj ∈ T(yi) do	Identify k such that $x_{j,i}^k={\vartheta }_{j,i}^k$ on τ
$\kappa \leftarrow f_h^{-1}(\mathcal{P}(\text{last}))$	$S\leftarrow sgn(y_i-{\theta }_{j,i})\text{sgn}{(x_{j,i}^k-{\vartheta }_{j,i}^k)|}_{\kappa }$
𝒯 ←{τ | τ is an x-face of κ}	if S is −1 then
𝒯′ ← OppositeSigns(𝒯, κ, yi, yj)	Append τ to 𝒯′
for τ ∈ 𝒯′ do	end if
κ′ ← Neighbor(τ, κ)	end for
Append fh(κ′) to ℘	𝒯′ ← 𝒯′ sorted by increasing k
end for	return 𝒯′
end for	end procedure
end for	procedure Neighbor(τ, κ)
return ℘	where (τ, κ′) is a wall and κ′ ≠ κ
end procedure	return κ′
	end procedure

Lemma B.1

Given ξ ∈ 𝒱 and any (ξ, D₁) in the fiber over ξ, Algorithm 1 constructs a path

$$(\xi ,D_1)\to (\xi ,D_2)\to \cdots \to (\xi ,D^{\ast }).$$

The procedure PathFinder takes an initial starting point (ξ, D₁) and builds an ordered list of nodes. The key to the proof of correctness of Algorithm 1 is to show first that this list is a path in the domain graph restricted to the fiber over ξ, and secondly to show that the terminal element of this list is (ξ, D^*). We note that the algorithm must terminate with a list of some nonzero length, since it iterates over finite sets and consists at least of the initial node (ξ, D₁).

The procedure PathFinder in Algorithm 1 builds a list ℘ starting with (ξ,D₁) by iterating over every variable y_i and all of the targets T(y_i) of y_i in RN (that is, the iteration occurs over all of the y_j such that (β_i, β_j) ∈ E). For each y_i, y_j pair, we take the last node (ξ_m, D_m) in ℘ and find the corresponding domain κ_m. Then we collect all of the x-faces of κ_m, each of which is a subset of a hyperplane { $x_{j,i}^k={\vartheta }_{j,i}^k$} for some k. Notice that there will be exactly |X| x-faces of κ_m for every m, because $x_{j,i}^k$ has exactly one threshold and therefore the hyperplane { $x_{j,i}^k={\vartheta }_{j,i}^k$} borders every κ ∈ 𝒦(h).

Subsequently, the procedure OppositeSigns finds the subset of the x-faces where $sgn(x_{j,i}^k-{\vartheta }_{j,i}^k)$ disagrees with sgn(y_i − θ_j,i) on κ_m. This is returned as a list sorted in order of increasing k. For each x-face τ_k with a disagreeing sign on κ_m, the procedure Neighbor finds the unique neighboring domain κ_m+1 that shares face τ_k with κ_m. The node (ξ_m+1,D_m+1) = f_h(κ_m+1) then appended to the output list of PathFinder. We prove that every node in the output list of PathFinder is necessarily in the fiber over ξ, that the list is a path in the domain graph, and that the list terminates at (ξ, D^*). We now proceed to the proof of Lemma B.1.

Proof

Consider the output list ℘ = PathFinder((ξ, D₁)). We need to show that

1. every element (ξ_m, D_m) ∈ ℘ is well-defined;

2. every element (ξ_m, D_m) ∈ ℘ satisfies ξ_m = ξ;

3. every consecutive pair of elements (ξ_m, D_m), (ξ_m+1, D_m+1) ∈ ℘ satisfies

   $$(({\xi }_m,D_m),({\xi }_{m+1},D_{m+1}))\in {\mathcal{E}}_h;$$

4. ℘ is finite and terminates in (ξ, D^*).

Statement 1

Let (ξ_m, D_m) ∈ ℘. We will show via induction that if D_m ≠ D^*, then the subsequent element (ξ_m+1, D_m+1) exists. Base case: (ξ, D₁) ∈ ℘, and by definition, $\kappa :=f_h^{-1}((\xi ,D_1))$ exists. Since X is nonempty, κ has a collection of x-faces 𝒯. Since D₁ ≠ D^*, there exists at least one triple i, j, k such that τ_x is an x-face of κ where $x_{j,i}^k={\vartheta }_{j,i}^k$ and

$$sgn(y_i-{\theta }_{j,i})\text{sgn}{(x_{j,i}^k-{\vartheta }_{j,i}^k)\mid }_{\kappa }=-1,$$ (18)

by the definition of the *-element. This is equivalent to τ_x ∈ OppositeSigns(𝒯, κ, y_i, y_j). By the definition of faces, there exists exactly one κ′ that shares the face τ_x with κ; that is, κ′ = Neighbor(τ_x, κ) is uniquely defined. Thus f_h(κ′) is uniquely defined and becomes (ξ₂,D₂) ∈ ℘. If we now assume (ξ_m,D_m) ∈ ℘ is well-defined with D_m ≠ D^*, then the induction follows an identical argument.

Statement 2

Let (ξ_m,D_m) = f_h(κ_m) and (ξ_m+1,D_m+1) = f_h(κ_m+1) be consecutive elements in ℘. Then κ_m+1 = Neighbor(τ_x, κ_m) is a neighbor of κ across an x-face. In other words, if

$${\kappa }_m=\stackrel{\sim }{\kappa }\times \prod _{s=1,s\ne k}^N\mathrm{\Xi }(s)\times \mathrm{\Xi }(k)$$

then

$${\kappa }_{m+1}=\stackrel{\sim }{\kappa }\times \prod _{s=1,s\ne k}^N\mathrm{\Xi }(s)\times {\mathrm{\Xi }}^{\prime }(k)$$

where Ξ(k) ≠ Ξ′(k), but all other terms are identical. Then,

$$f_h({\kappa }_m)=(f_z(\stackrel{\sim }{\kappa }),D_m)=({\xi }_m,D_m);f_h({\kappa }_{m+1})=(f_z(\stackrel{\sim }{\kappa }),D_{m+1})=({\xi }_{m+1},D_{m+1})$$

so that ξ_m = ξ_m+1, which must be ξ by induction.

Statement 3

Let (ξ,D_m) = f_h(κ_m) and (ξ,D_m+1) = f_h(κ_m+1) be consecutive elements in ℘ such that κ_m and κ_m+1 are separated by a face τ_k where $x_{j,i}^k={\vartheta }_{j,i}^k$. Recalling the definitions of left and right faces, we note that

$$sgn({\tau }_k,{\kappa }_m)\text{sgn}({\tau }_k,{\kappa }_{m+1})=-1.$$

Then we recall the wall labeling function

$$\begin{gathered} \ell ({\tau }_k,{\kappa }_m)=sgn({\tau }_{\kappa },{\kappa }_m)\text{sgn}{(\mu -\theta )\mid }_{{\tau }_k} \\ \ell ({\tau }_k,{\kappa }_{m+1})=-sgn({\tau }_k,{\kappa }_m)\text{sgn}{(\mu -\theta )\mid }_{{\tau }_k,} \end{gathered}$$

where

$$\mu -\theta =\{\begin{array}{cc}{y}_i-{\theta }_{j,i}& \text{if}k=1\\ x_{j,i}^{k-1}-{\vartheta }_{j,i}^{k-1}& \text{if}k>1\end{array}$$

So ℓ(τ_x, κ_m)ℓ(τ_x, κ_m+1) = −1 and there is an edge going from one domain to the other. We still require the direction of the arrow.

By necessity, τ_k ∈ OppositeSigns(𝒯, κ_m, y_i, y_j), which implies that

$$\begin{gathered} sgn(y_i-{\theta }_{j,i})\text{sgn}{(x_{j,i}^k-{\vartheta }_{j,i}^k)|}_{{\kappa }_m}=-1 \\ sgn(y_i-{\theta }_{j,i})\text{sgn}{(x_{j,i}^k-{\vartheta }_{j,i}^k)|}_{{\kappa }_{m+1}}=1. \end{gathered}$$

These expressions summarize the fact that if τ_k ∈ OppositeSigns(𝒯, κ_m, i, j), then by construction τ_k ∉ OppositeSigns(𝒯, κ_m+1, y_i, y_j). Since we cross an x-wall, it must be true that sgn(y_i − θ_j,i) is constant on κ_m ∪ κ_m+1, and so the change in sign occurs in $sgn(x_{j,i}^k-{\vartheta }_{j,i}^k)$ across the two domains.

First suppose y_i > θ_j,i; then $x_{j,i}^k<{\vartheta }_{j,i}^k$ on κ_m, so that τ_k is a right face of κ_m. By definition of a right face,

$$sgn({\tau }_k,{\kappa }_m)=-1.$$

If k = 1, then

$$sgn{(\mu -\theta )\mid }_{{\tau }_k}=sgn{(y_i-{\theta }_{j,i})|}_{{\kappa }_m\cup {\kappa }_{m+1}}=1$$

and

$$\ell ({\tau }_k,{\kappa }_m)=-1;\ell ({\tau }_k,{\kappa }_{m+1})=1$$

as desired for an edge (ξ,D_m) → (ξ,D_m+1) in the domain graph.

On the other hand, if k > 1, then we know that

$$sgn(y_i-{\theta }_{j,i})\text{sgn}{(x_{j,i}^{k-1}-{\vartheta }_{j,i}^{k-1})|}_{{\kappa }_m}=1,$$

either because τ_k−1 ∉ OppositeSigns(𝒯, κ_m, y_i, y_j), or because the procedure OppositeSigns returns a sorted list in increasing k. In other words, if τ_k−1 ∈ OppositeSigns(𝒯, κ_m, y_i, y_j), then it is resolved before τ_k. Thus, for y_i > θ_j,i, τ_k−1 is a left face of κ_m. Then $x_{j,i}^{k-1}>{\vartheta }_{j,i}^{k-1}$ on κ_m ∪ κ_m+1. Using that sgn(τ_k, κ_m) = −1, we have as before

$$\ell ({\tau }_k,{\kappa }_m)=-1;\ell ({\tau }_k,{\kappa }_{m+1})=1.$$

The argument for y_i < θ_j,i is similar and returns the same result. So we have shown that each consecutive pair of elements has an edge between them, and thus the list ℘ is a path in the domain graph.

Statement 4

℘ is necessarily finite because it is the result of iterations over finite sets. After the last element (ξ,D_n) is added, it is true that OppositeSigns(𝒯, κ_n, y_i, y_j) is empty for all i, j. If not, then the algorithm has not yet terminated, since if τ_k ∈ OppositeSigns(𝒯, κ_n, y_i, y_j), then by construction there exists κ_n+1 where τ_k ∉ OppositeSigns(𝒯, κ_n+1, y_i, y_j). So by Definition 3.2, D_n = D^*.