Enhanced Spectral Density Mapping through Combined Multiple-Field Deuterium ¹³CH₂D Methyl Spin Relaxation NMR Spectroscopy

Abstract

Quadrupolar relaxation of ²H (D) nuclear spins is a powerful probe of conformational dynamics in biological macromolecules. Deuterium relaxation rate constants are determined by the spectral density function for reorientation of the C-D bond vector at zero, single-quantum, and doublequantum ²H frequencies. In the present work, ²H relaxation rate constants were measured for an E. coli ribonuclease H [U-²H, ¹⁵N] ILV-[¹³CH₂D] sample using 400, 500, 800, and 900 MHz NMR spectrometers and analyzed by three approaches to determine spectral density values. First, data recorded at each static magnetic field were analyzed independently. Second, data recorded at 400 and 800 MHz were analyzed jointly and data recorded at other fields were analyzed independently. Third, data recorded at 400 and 500 MHz were interpolated to 450 MHz, and the resulting two pairs of data, corresponding to 400 MHz/800 MHz and 450 MHz/900 MHz, were analyzed jointly. The second and third approaches rely on the identity between the double quantum frequency at the lower field and the single quantum frequency at the higher field. Spectral density values for 32 of the 48 resolvable ILV methyl resonances were fit by the Lipari-Szabo model-free formalism and used to validate the three methods. The three spectral density mapping methods performed equally well in cross validation with data recorded at 700 MHz. However, the third method yielded approximately 10–15% more precise estimates of model-free parameters and consequently provides a general strategy for analysis of ²H spin relaxation data in biological macromolecules.

Graphical abstract

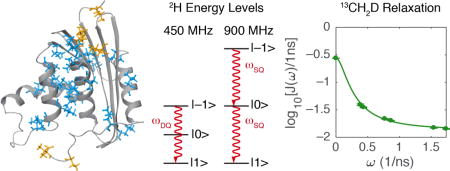
1. Introduction

Intramolecular dynamics of proteins and other biological macromolecules increasingly are recognized as playing important roles in function, including allostery, catalysis, molecular recognition, regulation, and signaling [1–3]. Spin relaxation in NMR spectroscopy is a powerful probe of dynamics and kinetics of biological macromolecules with atomic resolution and over a broad range of time scales [4, 5]. Methods and applications have been reported for ¹H, ²H, ¹³C, and ¹⁵N nuclei in proteins and nucleic acids [5, 6]. Deuterium (²H or D) relaxation offers advantages when compared with other nuclei in characterizing the dynamic properties of molecules in solution. First, ²H relaxation is dominated by the quadrupolar mechanism, and contributions from other mechanisms such as chemical shift anisotropy (CSA) and chemical exchange are negligible in comparison. Second, the quadrupolar Hamiltonian is axially symmetric and the principal axis is oriented along the carbon-deuterium bond, which simplifies interpretation of relaxation measurements. In contrast, CSA tensors may be rhombic and have principal axes systems that are rotated relative to convenient reference directions.

Kay and coworkers established methods for measuring relaxation of ²H spins in CH₂D methyl group isotopomers in proteins in solution [7, 8]. These methods subsequently were extended to CD, CHD, and CHD₂ moieties in proteins [9, 10] and CD and CHD moieties in RNA [11, 12]. The rate constants R₁, R_1ρ, R_Q, R_AP, and R_DQ describe ²H quadrupolar relaxation of longitudinal magnetization (D_z), transverse magnetization (D⁺), quadrupolar order (3D_z² − 2), antiphase coherence (D⁺D_z + D_zD⁺), and double-quantum coherence (D⁺²), respectively. At a given static magnetic field strength, the relaxation of the density operator is dependent on the values of the spectral density function, J(ω), at three frequencies: 0, ω_D, and 2ω_D, in which ω_D is the ²H Larmor frequency. Because the five relaxation rate constants measured for the deuterium spin are defined by the spectral density functions of three deuterium frequencies, the spectral density values can be determined if three or more relaxation rate constants are measured. Inversion of the relaxation equations to obtain the values of the spectral density function is called spectral density mapping [13, 14]

The present work examines three approaches for spectral density mapping when relaxation data have been acquired at more than one static magnetic field strength. In the simplest approach, termed the independent method, each static magnetic field is treated independently [7, 8, 15]. If data sets are obtained using two NMR spectrometers whose static magnetic field differ by a factor of two, then the double-quantum frequency, 2ω_D, at the lower field is equal to the single quantum frequency at the higher field [8, 16]. In this case, the relaxation data recorded at the two static magnetic fields can be analyzed simultaneously to obtain J(ω) at frequencies of 0, ω_D, 2ω_D, 4ω_D, in which ω_D is the Larmor frequency at the lower static magnetic field. This approach is termed the joint method [8]. To overcome the limited possible pairs of static magnetic fields available with existing NMR spectrometers, we developed a strategy that interpolates the data sets for any two static fields to obtain a third data set that can be paired with a fourth experimental data set. In this paper, we demonstrate this combined field-pairing and interpolated analysis, termed the joint-interpolated method, by obtaining relaxation rate data sets using a 400 MHz/800 MHz spectrometer pair and a 450 MHz/ 900 MHz spectrometer pair and analyzing them globally. In this scenario, the 450 MHz data set was interpolated from data sets originating from the 400 MHz and 500 MHz spectrometer pair. In total, this analysis yields spectral density values at seven frequencies, ω/2π: 0, 61.4, 69.1, 122.8, 138.2, 245.6, and 276.4 MHz with increased statistical degrees of freedom for subsequent model evaluation.

The different approaches for spectral density mapping were tested using relaxation data acquired for the E. coli ribonuclease H (RNase H) U-[²H, ¹⁵N] ILV (Ile δ, Ile γ2, Leu δ1, Leu δ2, Val γ1, Val γ2) [¹³CH₂D] sample. RNase H (EC 3.1.26.4) is a conserved endonuclease responsible for cleaving the RNA strand of DNA/RNA hybrids in various biological processes, including reverse transcription of the viral genome in retroviral reverse transcriptases and Okazaki fragment processing during the DNA replication of the lagging strand [17]. RNase H also belongs to a broader superfamily of nucleotidyl-transferases with conserved structure and mechanism, including retroviral integrases, Holliday junction resolvases, and transposases [18, 19]. RNase H has also been the subject of many investigations in folding, structure, and dynamics [20–22].

2. Methods

2.1. Sample Preparation

Isotopically labeled RNase H was produced by transformation of BL21(DE3) with a pAED4 plasmid encoding the E. coli ribonuclease HI gene. Bacterial cultures were grown in M9 minimal media containing 99% ²H₂O, ¹⁵N-ammonium chloride, and ²H₇-glucose to OD₆₀₀ = 0.7 before induction with 0.5 mM IPTG. Selective ¹³CH₂D group labeling was achieved by supplementing the minimal growth media with 50 mg/mL of 2-ketobutyric acid-4-¹³C,4-d₁(99% ¹³C, 97% ²H, Isotec, Sigma Aldrich) and 80 mg/mL of 2-keto-3-(methyl-¹³C,d₁)-butyric acid-3,4,4,4-d₄ (99% ¹³C, 98% ²H, Isotec, Sigma Aldrich) an hour before induction [23, 24]. Protein expression was allowed to proceed for 4 hours at 37° C. RNase H was purified as described previously [25–27].

2.2 NMR Spectroscopy

NMR samples contained 500 µM RNase H, 100 mM ²H₃-sodium acetate, pH = 5.5, and 99% ²H₂O in a 5 mm Shigemi NMR tube. Relaxation experiments were acquired at 9.4 T (400 MHz for ¹H spins) on a Varian Inova spectrometer with a room temperature probe and at 11.75 T (500 MHz), 16.45 T (700 MHz), 18.8 T (800 MHz), and 21.1 T (900 MHz) on Bruker AVANCE spectrometers with triple-resonance z-axis gradient CryoProbes. The static magnetic field strengths correspond to ²H Larmor frequencies of ω_D/2π = 61.4, 76.8, 107.4, 122.8, and 138.2 MHz. Calibration of sample temperature to 298 K was accomplished using 98% ²H₄-methanol [28] and small variations between spectrometers adjusted by matching chemical shifts. Relaxation rate constants R₁, R_1ρ, R_Q, R_AP were measured at five static B₀ fields using a modified pulse sequence with non-constant time ¹³C chemical shift evolution in the indirect dimension [7]. The double-quantum relaxation rate constant requires correction for interactions with remote spins and was not utilized in the present work. For all four ²H relaxation experiments, spectra were recorded with 32 scans per t₁ increment and 1024 × 200 complex points for t₂ × t₁. Spectral width for all relaxation experiments was 12 ppm × 20 ppm (t₂ × t₁). The carriers for ¹H and ¹³C were set to 4.70 ppm and 15.0 ppm, respectively. Relaxation delays were set to {1 ms, 10 ms, 20 ms, 30 ms, 40 ms, 50 ms} for measurement of ²H R₁ and R_Q, {1 ms, 4 ms, 8 ms, 12 ms, 16 ms, 20 ms} for measurement of ²H R_AP, and {0.5 ms, 3 ms, 5 ms, 10 ms, 15 ms, 20 ms} for measurement of ²H R_1ρ. Two or three duplicate measurements within each relaxation delay series were recorded for purposes of error estimation.

2.3 Data Processing, Assignment, and Determination of Relaxation Parameters

NMR spectra were processed using NMRPipe [29]. Identification of ¹H-¹³C methyl correlations from a ¹H-¹³C HSQC experiment utilized previously published E. coli ribonuclease HI chemical shift assignments [21, 30]. In all, 48 methyl peaks were observed: 7 Ile, 20 Leu, and 21 Val. An equivalent number of peaks was also observed for the shortest relaxation delay in each of the four ²H relaxation experiments. Spectra were visualized in Sparky [31] and peak heights determined at assigned peak positions. The unweighted peak intensities were fit to mono-exponential decay functions using the trust-region non-linear least-squares algorithm implemented in the MATLAB (version R2016b) exponential library model ‘exp1’. Uncertainties in fitted relaxation rate constants were determined by Monte Carlo simulations, using estimates of Gaussian noise obtained from variation in duplicate measurements, and by jackknife simulations. The larger of the two error estimates was used as the experimental uncertainty for subsequent spectral density mapping.

2.4 Deuterium Spectral Density Mapping

The ²H spin relaxation rate constants are given by [32]:

$$R_1=3{\xi }^2[J({\omega }_D)+4J(2{\omega }_D)]$$ (1)

$$R_{1\rho }=(\frac{3{\xi }^2}{2})[3J(0)+5J({\omega }_D)+2J(2{\omega }_D)]$$ (2)

$$R_Q=9{\xi }^2[J({\omega }_D)]$$ (3)

$$R_{\mathit{\text{AP}}}=(\frac{3{\xi }^2}{2})[3J(0)+J({\omega }_D)+2J(2{\omega }_D)]$$ (4)

in which:

$$\xi =\frac{\pi e^2\mathit{\text{qQ}}}{2h}$$ (5)

e is the charge on the electron, eq is the principal value of the electric field gradient tensor, Q is the nuclear quadrupole moment, h is Planck’s constant, and e²Qq/h is taken to be 167 kHz. J(ω) is the spectral density function at frequency ω, and ω_D is the ²H Larmor frequency. The following sections describe three methods of calculating the spectral density values from relaxation rate constants measured at more than one static magnetic field.

2.4.1 Independent Spectral Density Mapping

The relaxation rate constants, Eqs. 1–4, are written in matrix form as:

$$\left[\begin{array}{c}\hfill R_1\hfill \\ \hfill R_{1\rho }\hfill \\ \hfill R_Q\hfill \\ \hfill R_{\mathit{\text{AP}}}\hfill \end{array}\right]=3{\xi }^2\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 4\hfill \\ \hfill 3/2\hfill & \hfill 5/2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 3\hfill & \hfill 0\hfill \\ \hfill 3/2\hfill & \hfill 1/2\hfill & \hfill 1\hfill \end{array}\right]\left[\begin{array}{c}\hfill J(0)\hfill \\ \hfill J({\omega }_D)\hfill \\ \hfill J(2{\omega }_D)\hfill \end{array}\right]$$ (6)

and constitute an overdetermined system of linear equations. In the independent method, Eq. 6 is solved by least-squares methods (vide infra) to obtain values of J(0), J(ω_D), and J(2ω_D) at each static magnetic field [8, 15]. Thus, relaxation rates collected at ²H frequencies of 61.4, 76.8, 122.8, and 138.2 MHz were independently analyzed using Eq. 6 to generate the spectral densities for this method. At each of the four static magnetic fields, three spectral density values are derived from four relaxation rate constants, giving one degree of freedom per field or a total of four degrees of freedom. The four values of J(0) obtained for each methyl group were averaged, as were the values of J(2ω_D) = J(122.8) obtained from data acquired at 9.4 T (400 MHz for ¹H spins) and J(ω_D) = J(122.8) obtained from data acquired at 18.8 T (800 MHz). Thus, this analysis yields values for J(ω) at eight frequencies: J(0), J(61.4), J(76.8), J(122.8), J(138.2), J(153.6), J(245.6), and J(276.4), in which the frequencies are given as ω/(2π) in units of MHz.

2.4.2 Joint Spectral Density Mapping

In the second approach [8], relaxation data acquired at multiple static magnetic fields are analyzed jointly to take into account any spectral density values that contribute to the relaxation rate constants at more than one static field. In the present case, all data sets share a common value of J(0) and in addition, J(2ω_D), for data acquired at 9.4 T is identical to J(ω_D) for data acquired at 18.8 T. The resulting matrix equation is:

$$\left[\begin{array}{c}\hfill {\hat{\mathit{R}}}_{\mathbf{61.4}}\hfill \\ \hfill {\hat{\mathit{R}}}_{\mathbf{76.8}}\hfill \\ \hfill {\hat{\mathit{R}}}_{\mathbf{122.8}}\hfill \\ \hfill {\hat{\mathit{R}}}_{\mathbf{138.2}}\hfill \end{array}\right]=3{\xi }^2\left[\begin{array}{cccccccc}\hfill \mathit{V}\hfill & \hfill \mathit{W}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{X}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathit{V}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{W}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{X}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathit{V}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{W}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{X}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathit{V}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{W}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{X}\hfill \end{array}\right]\left[\begin{array}{c}\hfill J(0)\hfill \\ \hfill J(61.4)\hfill \\ \hfill J(76.8)\hfill \\ \hfill J(122.8)\hfill \\ \hfill J(138.2)\hfill \\ \hfill J(153.6)\hfill \\ \hfill J(245.6)\hfill \\ \hfill J(276.4)\hfill \end{array}\right]$$ (7)

in which R̂_i = [R_1,i, R_1ρ,i, R_Q,i, R_AP,i]^T, V = [0,3/2,0,3/2]^T, W = [1,5/2,3,1/2]^T, X = [4,1,0,1]^T, and 0 is a 4 × 1 zero-matrix. The least-squares solution of Eq. 7 yields values for J(ω) at eight frequencies and no post-analysis averaging of common values is needed. Eight spectral density values are derived from 16 relaxation rate constants, consequently with eight degrees of freedom.

2.4.3 Joint-Interpolated Spectral Density Mapping

The joint method shown in Eq. 7 links relaxation data acquired at 9.4 T (400 MHz) and 18.8 T (800 MHz), fields that differ by a factor of two. The joint-interpolated method uses the data acquired at 9.4 T (400 MHz) and 11.7 T (500 MHz) to interpolate values of the relaxation rate constants at 10.55 T (450 MHz). The interpolated relaxation rate constants are then paired with the relaxation data acquired at 21.1 T (900 MHz) for joint analysis.

The normalized correlation function for reorientation of the C-D bond vector is described as [33, 34]:

$$C(t)=\frac{1}{5}{e}^{-\frac{t}{{\tau }_m}}(S^2+{\sum }_i{a}_i{e}^{-\frac{t}{{\tau }_{e,i}}})$$ (8)

in which τ_m is the overall rotational correlation time, S² is the generalized order parameter, and a_i and τ_e,i are the amplitude and time constant for the ith term in the internal correlation function. Taking the real part of the Fourier transform of C(t) yields the spectral density function:

$$J(\omega )=\frac{2}{5}\{\frac{S^2{\tau }_m}{1+{\omega }^2{\tau }_m^2}+\sum \frac{a_i{\stackrel{\sim }{\tau }}_i}{1+{\omega }^2{{\stackrel{\sim }{\tau }}_i}^2}\}$$ (9)

in which:

$${\stackrel{\sim }{\tau }}_i={(\frac{1}{{\tau }_m}+\frac{1}{{\tau }_{e,i}})}^{-1}$$ (10)

If ${\omega }^2{\tau }_m^2\gg 1$ and τ_e,i ≪ τ_m, the spectral density function reduces to:

$$J(\omega )\approx \frac{2}{5}\{\frac{S^2}{{\omega }^2{\tau }_m}+{\sum }_i{a}_i{\stackrel{\sim }{\tau }}_i\}$$ (11)

which is a linear function of ω⁻². With this insight, a first-order Taylor series approximation of a given relaxation rate constant with respect to ω⁻² yields:

$$R_{m,{\omega }_{D2}}\approx R_{m,{\omega }_{D1}}+(R_{m,{\omega }_{D2}}-R_{m,{\omega }_{D1}})(\frac{1}{{\omega }_{D2}^2}-\frac{1}{{\omega }_{D1}^2})$$ (12)

$$R_{m,{\omega }_{D2}}\approx R_{m,{\omega }_{D3}}+(R_{m,{\omega }_{D2}}-R_{m,{\omega }_{D3}})(\frac{1}{{\omega }_{D2}^2}-\frac{1}{{\omega }_{D3}^2})$$ (13)

in which R_m,ωDj is a relaxation rate constant m = {R₁, R_1ρ, R_Q, R_AP} at a static magnetic field with ²H Larmor frequency ω_Dj. Averaging Eqs. 12 and 13 yields an interpolation formula for relaxation rate constants at a field for which experimental values are unavailable:

$$R_{m,{\omega }_{D2}}\approx \frac{R_{m,{\omega }_{D1}}+R_{m,{\omega }_{D3}}}{2}+(R_{m,{\omega }_{D1}}-R_{m,{\omega }_{D3}})\frac{2{\omega }_{D2}^{-2}-{\omega }_{D1}^{-2}-{\omega }_{D3}^{-2}}{2({\omega }_{D1}^{-2}-{\omega }_{D3}^{-2})}$$ (14)

Based on this derivation, relaxation rate constants at 10.55 T (ω_D/(2π) = 69.1 MHz) are estimated from data recorded at 9.4 T (61.4 MHz) and 11.74 T (76.8 MHz) using:

$$R_{m,69.1}=\frac{R_{m,61.4}+R_{m,76.8}}{2}+(R_{m,61.4}-R_{m,76.8})\frac{2\times {69.1}^{-2}-{61.4}^{-2}-{76.8}^{-2}}{2\times ({61.4}^{-2}-{76.8}^{-2})}$$ (15)

which can be expressed as:

$$R_{m,69.1}=R_{m,61.4}(\frac{1}{2}+\kappa )+R_{m,76.8}(\frac{1}{2}-\kappa )$$ (16)

in which:

$$\kappa =\frac{2\times {69.1}^{-2}-{61.4}^{-2}-{76.8}^{-2}}{2\times ({61.4}^{-2}-{76.8}^{-2})}$$ (17)

In matrix form, the relationship between the relaxation rate constants at the three static magnetic fields becomes:

$$\left[\begin{array}{c}\hfill R_{m,61.4}\hfill \\ \hfill R_{m,76.8}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill -\frac{1+2\kappa }{1-2\kappa }\hfill & \hfill \frac{2}{1-2\kappa }\hfill \end{array}\right]\left[\begin{array}{c}\hfill R_{m,61.4}\hfill \\ \hfill R_{m,69.1}\hfill \end{array}\right]$$ (18)

Consequently, for relaxation rates collected at deuterium frequencies of 61.4, 76.8, 122.8, and 138.2 Hz:

$$\left[\begin{array}{c}\hfill {\hat{\mathit{R}}}_{\mathbf{61.4}}\hfill \\ \hfill {\hat{\mathit{R}}}_{\mathbf{76.8}}\hfill \\ \hfill {\hat{\mathit{R}}}_{\mathbf{122.8}}\hfill \\ \hfill {\hat{\mathit{R}}}_{\mathbf{138.2}}\hfill \end{array}\right]=3{\xi }^2\left[\begin{array}{cccc}\hfill \mathit{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathit{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill -\frac{1+2\kappa }{1-2\kappa }\mathit{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{2}{1-2\kappa }\mathit{I}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{I}\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill \mathit{Y}\hfill & \hfill \mathit{Z}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathit{Y}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{Z}\hfill \end{array}\right]\left[\begin{array}{c}\hfill J(0)\hfill \\ \hfill J(61.4)\hfill \\ \hfill J(122.8)\hfill \\ \hfill J(245.6)\hfill \\ \hfill J(69.1)\hfill \\ \hfill J(138.2)\hfill \\ \hfill J(276.4)\hfill \end{array}\right]$$ (19)

in which:

$$\mathit{Y}=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 3/2\hfill \\ \hfill 0\hfill \\ \hfill 3/2\hfill \\ \hfill 0\hfill \\ \hfill 3/2\hfill \\ \hfill 0\hfill \\ \hfill 3/2\hfill \end{array}\right]\mathit{Z}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 4\hfill & \hfill 0\hfill \\ \hfill 5/2\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1/2\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 4\hfill \\ \hfill 0\hfill & \hfill 5/2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1/2\hfill & \hfill 1\hfill \end{array}\right]$$ (20)

and 0 and I are 4-dimensional zero and identity matrices, respectively. Equation 19 is the main theoretical result of the present work. The solution of Eq. 19 yields values of the spectral density function at seven frequencies, consequently with nine degrees of freedom.

For each of the three spectral density mapping methods, spectral density values were obtained from the relaxation rates R₁, R_1ρ, R_Q, and R_AP measured at deuterium frequencies 61.4, 76.8, 122.8, and 138.2 MHz by solving Eqs. 6, 7, or 19 by singular value decomposition. Uncertainties in the spectral density values were obtained from the covariance matrix.

2.5. Model-Free Analysis

Spectral density values obtained by the independent, joint, and joint-interpolated methods were fit with the Lipari-Szabo model-free spectral density function [8, 33]:

$$J(\omega )=\frac{2}{5}(\frac{\frac{1}{9}{S}_{\mathit{\text{axis}}}^2{\tau }_m}{1+{\omega }^2{\tau }_m^2}+\frac{(1-\frac{1}{9}{S}_{\mathit{\text{axis}}}^2)\tau }{1+{\omega }^2{\tau }^2})$$ (21)

in which S²_axis is the generalized order parameter for a unit vector oriented along the symmetry axis of the methyl group, the factor of 1/9 accounts for (assumed rapid) rotation of the methyl group, and τ = (1/τ_m + 1/τ_e)⁻¹. Fitting was performed by minimizing

$${\chi }^2={\sum }_{k=1}^K{\left[\frac{J({\omega }_k)-\hat{J}({\omega }_k)}{{\sigma }_k}\right]}^2$$ (22)

in which K is the number of spectral density values being fit, σ_k are the uncertainties in spectral density values determined as described above, and Ĵ(ω_k) is the fitted value of the spectral density function. Minimization was performed using weighted non-linear least-squares in MATLAB. Uncertainties in fitted model-free parameters were obtained from Monte Carlo simulations. Values of S², τ_m, and τ_e were restricted to the ranges [0, 1], [0 ns, 20 ns], and [0 ns, 20 ns], respectively. Goodness-of-fit to Eq. 21 was tested by comparing the χ² residual from the curve-fitting procedure for each methyl group to critical values obtained for a Bonferroni-corrected confidence level p = α/N, where α = 0.05 and N = 48 is the number of methyl groups analyzed. The critical χ² values for the independent, joint, and joint-interpolated methods are 27.8, 20.4, and 18.4, respectively.

3. Results

3.1 Simulation of 69.1 MHz Deuterium Frequency Relaxation Rate Interpolation

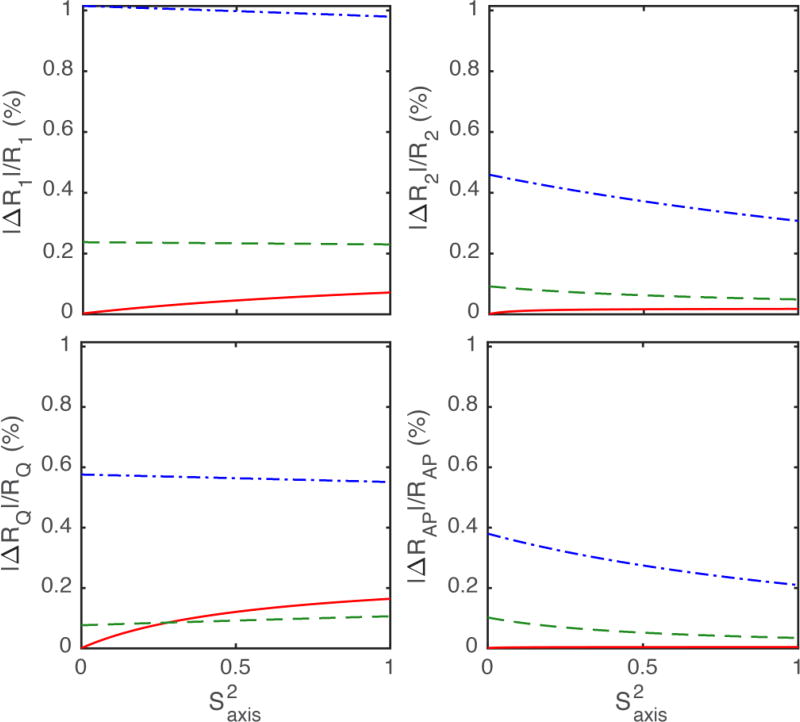
The accuracy of the proposed method for interpolation of relaxation rate constants necessary for the joint-interpolated approach was evaluated by theoretical calculations. Relaxation rates at 9.4 T, 10.55 T, and 11.7 T were calculated using Eqs. 1–4 and the Lipari-Szabo model-free formalism, Eq. 21. The percentage differences between the interpolated and exact values of the relaxation rate constants at 10.55 T are shown in Figure 1. The predicted rates show errors of ≤ 1% up to a τ_e of 1 ns, consistent with the experimental uncertainties in measured ²H relaxation rates (~1–2%).

Figure 1.

Predicted errors for Eq. 16 over a range of methyl axis order parameters $S_{\mathit{\text{axis}}}^2$ from 0 to 1, given an overall tumbling time τ_m of 10 nanoseconds (ns), and effective correlation times τ_e of (solid, red) 0.03 ns, (dashed, green) 0.3 ns, and (dot-dashed, blue) 1 ns.

3.2 Model Selection

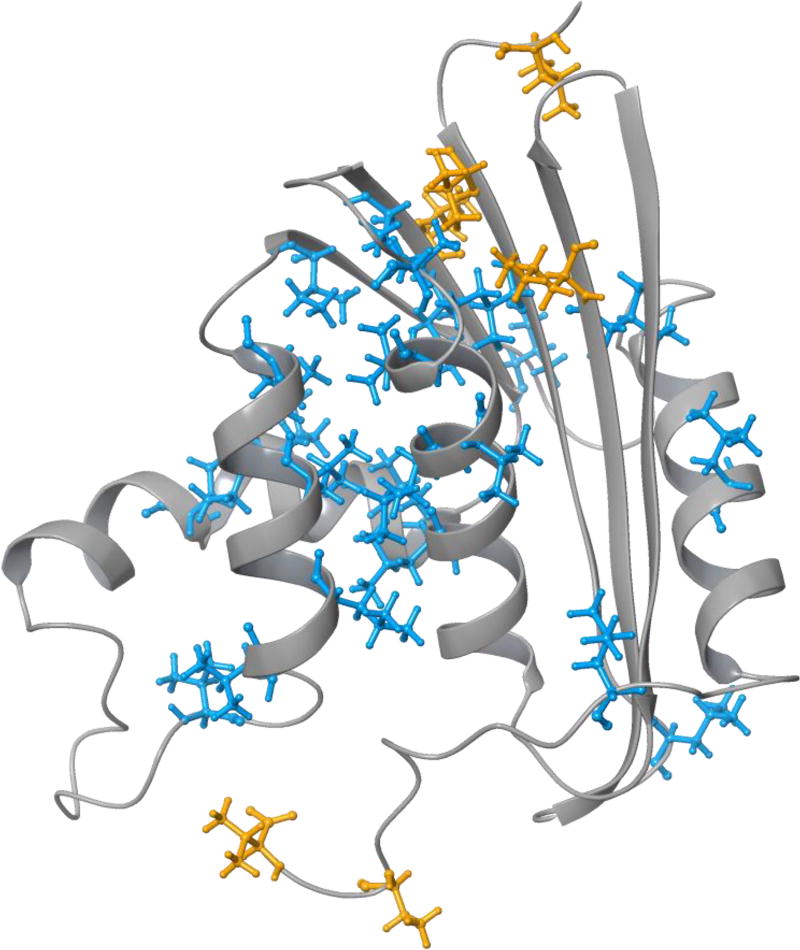
Spectral density values for each methyl resonance determined by each spectral density mapping method were fit with Eq. 21. If any of the three fits for a particular methyl group yielded a χ² value that was less than or equal to the respective critical χ² value, then that methyl group was included in subsequent comparisons between the three spectral density mapping methods. Methyl groups that did not meet this criterion were not considered further; these methyl groups require fitting with more complex motional models than Eq. 21 [8]. Overall, 33 of the 48 ILV methyl resonances satisfied this criterion. Fits to data for Leu 103 δ1 converged poorly and yielded large errors for τ_m; consequently, this methyl group was also not considered further. Figure 2 shows the locations of ILV amino acids in RNase H. Most of the methyl groups chosen for analysis are in residues located either in α-helices or β-sheets, while the other methyl groups are typically located in dynamic loops or termini.

Figure 2.

Ribbon diagram of RNase H with the observable ILV residues in stick representations. The ILV residues containing methyl relaxation data fit with the Lipari-Szabo model-free formalism, Eq. 21, are colored blue; excluded ILV residues are colored orange.

3.3 Representative Spectral Density Functions

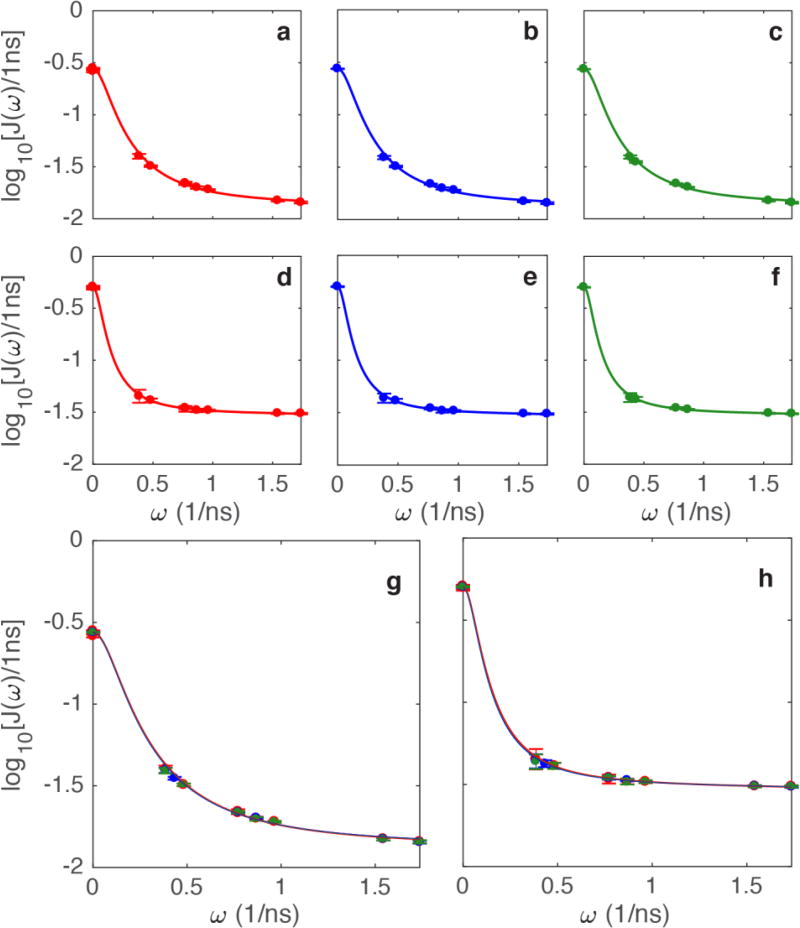
Examples of the Lipari-Szabo model-free fits to the spectral density values obtained from the three spectral density mapping methods are shown in Figure 3. Values of τ_m were optimized independently for each methyl group and consequently τ_m represents an effective local correlation time and could be smaller than the global rotational correlation time of RNase H, as determined from ¹⁵N spin relaxation [27]. Results are shown for Val 121 γ2, with a local correlation time of ~7 ns and Leucine 56 δ1 with a local correlation time of ~14 ns.

Figure 3.

(a–f) represent the individual fits for (red) independent, (blue) joint, and (green) joint-interpolated). The first row (a–c) shows plots for Val 121 γ2, with each method, plotted individually. The second row (d–f) shows plots for Leu 56 δ1, with each method also plotted individually. Superposition of data and fits for the three methods are shown for (g) Val 121 γ2 and (h) Leu 56 δ1.

3.4 Accuracy and Precision of Model Free Parameters

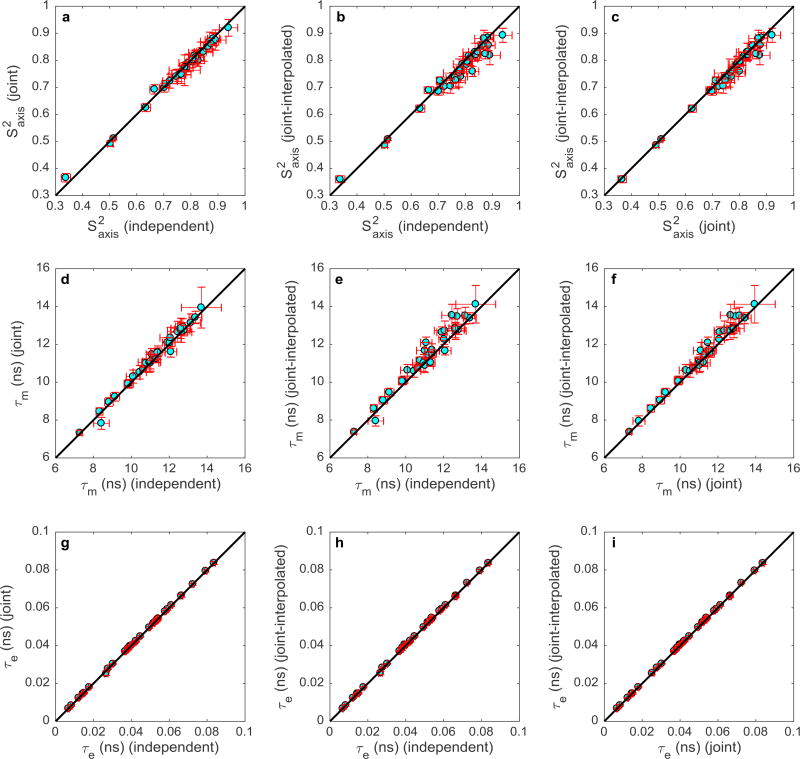
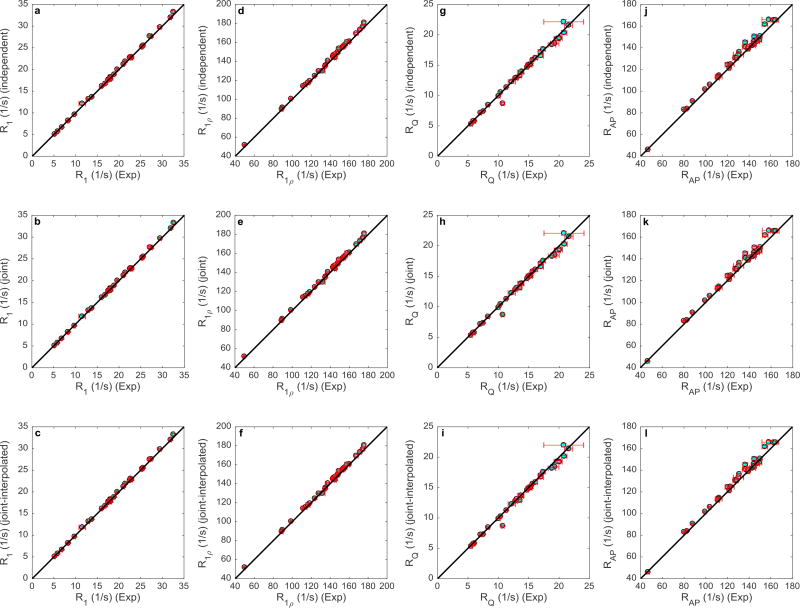
Figure 4 summarizes the results of fitting the spectral densities to the Lipari-Szabo model-free formalism to obtain $S_{\mathit{\text{axis}}}^2$, τ_m, and τ_e for 32 methyl groups. Each graph in the figure shows a one-on-one comparison between model-free parameters determined by two of the three spectral density mapping procedures. Coefficients of determination, R², were calculated for each of the plots based on the y = x line in Figure 4. The R² values were 0.99, 0.94, and 0.97, respectively, for $S_{\mathit{\text{axis}}}^2$ comparisons, Figures 4a–c; 0.98, 0.93, and 0.97, respectively, for τ_m comparisons, Figures 4d–f; and 1.00 for all three τ_e comparisons, Figures 4g–i. Slopes of least-squares fitted lines were 0.99, 0.97, and 0.98, respectively, for $S_{\mathit{\text{axis}}}^2$ comparisons, Figures 4a–c; 1.01, 1.02, and 1.02, respectively, for τ_m comparisons, Figures 4d–f; and 1.00 for all three τ_e comparisons, Figures 4g–i. The average uncertainties in the fitted Lipari-Szabo parameters, S²_axis, τ_m, and τ_e, differed between the three methods of spectral density mapping. The joint-interpolated method yielded the smallest parameter uncertainties and Table 1 presents the percentage improvement in average uncertainties for this method compared with the independent and joint approaches.

Figure 4.

Correlation plots for $S_{\mathit{\text{axis}}}^2$ (top row a–c), τ_m (middle row d–f), and τ_e (bottom row g–i). Each row compares the model free parameters generated from the independent, joint, and joint-interpolated methods. The parameters of the 32 residues are shown in cyan, while the error bars are depicted in red. The black line represents y=x.

Table 1.

Improvement in precision of fitted model-free parameters

% More Precise	Joint-Interpolated vs. Independent	Joint-Interpolated vs. Joint
S2	14.6%	10.8%
τm	10.5%	7.8%
τe	12.8%	10.1%

3.5 Cross Validation with 700 MHz Spectrometer-Generated Data

The fitted model-free parameters were cross-validated by back-calculating relaxation rate constants expected for data acquired at 16.4 T (700 MHz, ω_D/(2π) = 107.5 MHz) using Eqs. 1–4 and Eq. 21 and then compared to experimental data acquired at 16.4 T. Uncertainties in back-calculated relaxation rate constants were generated by Monte Carlo simulations. The cross-validated results are shown in Figure 5. The three methods of spectral density mapping gave equally accurate back-predictions of the relaxation rate constants compared with experimental values. R₁ comparisons had R² values of 1.00, R_1ρ comparisons had R² values of 0.99, R_Q comparisons had R² values of 0.99, and R_AP comparisons had R² values of 0.98. R₁ and R_1ρ comparisons had slopes of 1.01, R_Q comparisons for independent and joint methods had slopes of 0.99, R_Q comparison for the joint-interpolated method had a slope of 0.98, and R_AP comparisons had slopes of 1.02.

Figure 5.

Back-calculated 700 MHz relaxation rate constants (y-axis) are compared to the experimental results (x-axis). Each row represents a method of spectral density mapping, while each column represents a relaxation rate constant. The relaxation rates of the 32 residues are shown in cyan, while the error bars are depicted in red. The black line represents y=x.

3.6 Local Diffusion Times

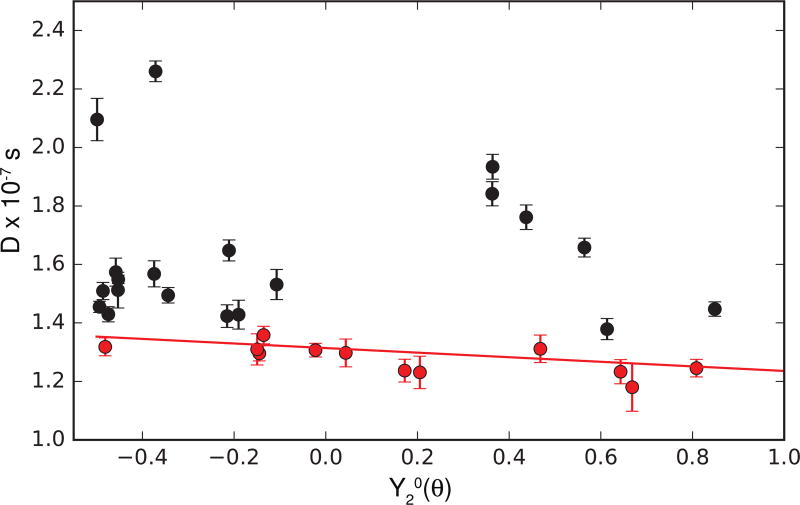
The values of τ_m obtained for the most rigid methyl-bearing side chains in RNase H are expected to report on the overall rotational diffusion tensor, which has been determined previously by ¹⁵N spin relaxation [27]. As shown in Figure 6, the values of the local diffusion constants, D = 1/(6τ_m), for the 12 methyl groups with the largest values of τ_m (smallest values of D; shown in red) agree well with the predictions derived from the diffusion tensor obtained from ¹⁵N spin relaxation. This agreement provides additional evidence for the accuracy of the proposed analysis for determination of rotational diffusion tensors of proteins, particularly in cases for which orientations of N-H amide bond vectors are not uniformly distributed [35].

Figure 6.

Local diffusion times (D = 1/(6τ_m)) plotted versus Y₂⁰(θ), in which θ is the orientation of the methyl symmetry axis in the structure of RNase H oriented in the principal axis system of the diffusion tensor determined from ¹⁵N spin relaxation. The values of D for the 12 slowest tumbling residues (for which internal motions are well-separated from overall rotation) are shown in red and agree quantitatively with predictions from the overall rotational diffusion tensor determined from ¹⁵N relaxation data (red line), when adjusted for the sample temperature and D₂O viscosity.

3.7 Extent of Interpolation and Extrapolation

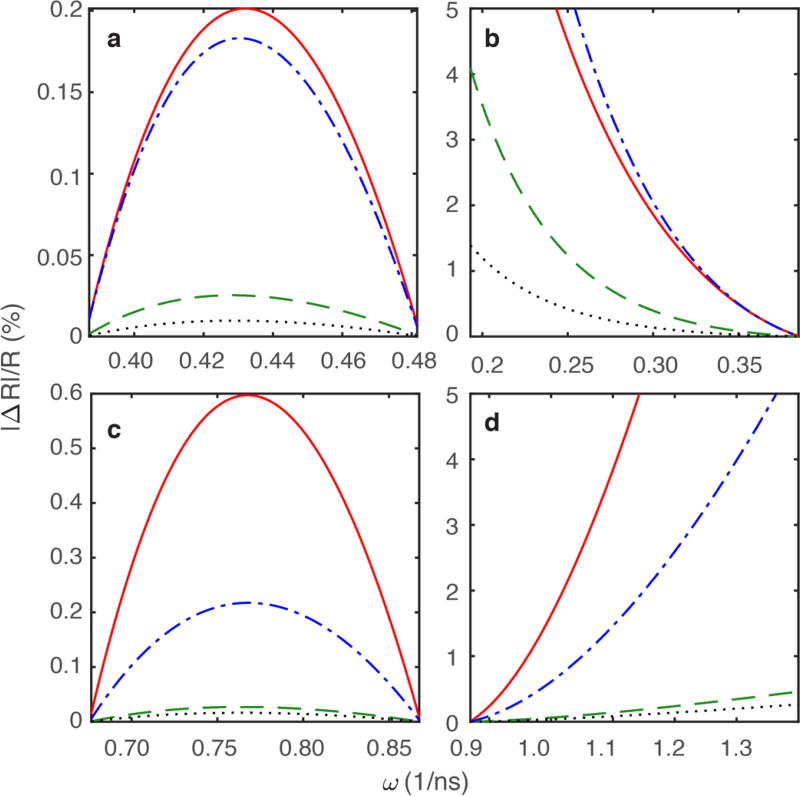
Given the success of the above method for the interpolation of relaxation rate constants necessary for the joint-interpolated approach, the accuracy of either interpolation or extrapolation was evaluated further by theoretical calculations and simulations that tested the bounds of Eq. 14. Relaxation rates at 9.4 T, 11.7 T, 18.8 T, and 21.1 T (corresponding to the two lowest and two highest experimentally-collected fields) were calculated using Eqs. 1–4 and the Lipari-Szabo model-free formalism, Eq. 21, with set values for the input variables. Four separate simulations were conducted as shown in Figure 7. Relaxation rate constants were interpolated for methyl frequencies between ω_D/(2π) = 61.4 MHz – 76.8 MHz (Fig. 7a) and extrapolated for relaxation rate constants for methyl frequencies below ω_D/(2π) = 61.4 MHz using the ω_D/(2π) = 61.4 and 76.8 MHz pair of relaxation rate constants (Fig. 7b). Relaxation rate constants were interpolated for methyl frequencies between ω_D/(2π) = 107.4 MHz – 138.2 MHz (Fig. 7c) and extrapolated for methyl frequencies above ω_D/(2π) = 138.2 MHz (Fig. 7d) for the ω_D/(2π) = 107.4 MHz and 138.2 MHz pair of relaxation rate constants.

Figure 7.

Predicted errors for Eq. 14 over a range of methyl frequencies ω(1/ns), given set values of methyl axis order parameters $S_{\mathit{\text{axis}}}^2$ of 0.5, overall tumbling time τ_m of 10 nanoseconds, and effective correlation times τ_e of 0.3 nanoseconds. The red solid line represents R₁, the green dashed line represents R_1ρ, the blue dot-dashed line represents R_Q, and the black dotted line represents R_AP. (a) Interpolated for methyl frequencies between ω_D/(2π) = 61.4 MHz – 76.8 MHz. (b) Extrapolated for methyl frequencies below ω_D/(2π) = 61.4 MHz using the ω_D/(2π) = 61.4 and 76.8 MHz pair of relaxation rate constants. (c) Interpolation for methyl frequencies between ω_D/(2π) = 107.4 MHz – 138.2 MHz. (d) Extrapolation above ω_D/(2π) = 138.2 MHz for the ω_D/(2π) = 107.4 MHz and 138.2 MHz pair of relaxation rate constants.

Percentage differences between the interpolated/extrapolated and exact values of the relaxation rate constants are shown in Figure 7. The R_1ρ and R_AP relaxation rate constants generally have smaller percentage errors compared to R₁ and R_Q, likely because the J(0) contributions to Eqs. 2 and 4 remain constant regardless of method of calculation. Given that the experimental uncertainties in measured ²H relaxation rates range from ~1–2%, extrapolation or interpolation of relaxation rate constants is generally accurate for methyl frequencies that are within ~15 MHz of one of the given pair of available measurements.

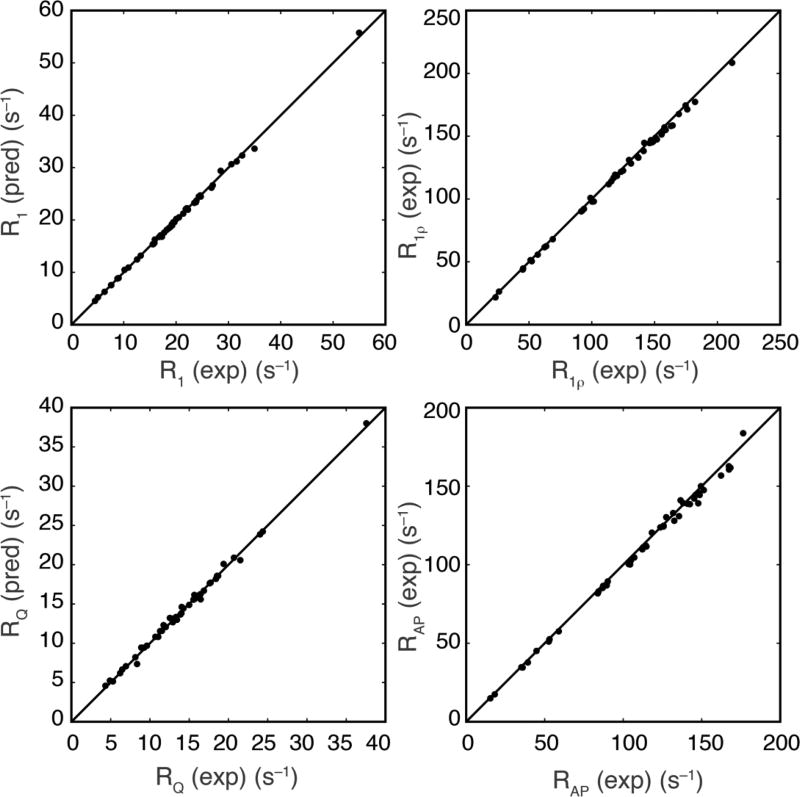
The interpolation results shown in Fig. 7d were tested experimentally by using the experimental data recorded for values of ω_D/(2π) = 107.4 MHz and 138.2 MHz to interpolate values of relaxation rate constants for ω_D/(2π) = 122.8 MHz. Figure 8 compares the interpolated and measured values of the relaxation rate constants at 122.8 MHz. The root-mean-square percentage deviations between the predicted and measured relaxation rate constants are very similar to the measured experimental uncertainties in the measured rate constants, consistent with the predictions of Fig. 7d and further confirming the accuracy of the proposed method of interpolation.

Figure 8.

Comparison of ²H relaxation rate constants (pred) interpolated and (exp) measured at ω_D/(2π) = 122.8 MHz. Interpolation was performed using measured values of the relaxation rate constants with ω_D/(2π) = 107.4 MHz and 138.2 MHz. For R₁, the slope of a line fitted through the origin was 0.997, the root-mean-square (rms) relative variation was 1.0%. The rms relative uncertainty in the measured values was 1.8%. For R_1ρ, the slope of a line fitted through the origin was 0.984, the rms relative variation was 1.5%. The rms relative uncertainty in the measured values was 1.6%. For R_Q, the slope of a line fitted through the origin was 0.983, the rms relative variation was 2.2%. The rms relative uncertainty in the measured values was 2.7%. For R_AP, the slope of a line fitted through the origin was 0.997, the root-mean-square percent variation was 1.9%. The rms relative uncertainty in the measured values was 2.2%. The rms relative variations between predicted and experimental values shown above were divided by 2^1/2 to allow direct comparison to relative variation in experimental values.

4. Discussion and Conclusion

NMR spin relaxation methods are powerful approaches for characterizing conformational dynamics of biological macromolecules. Weaknesses of these methods are that the target spectral density function can only be sampled at the discrete eigenfrequencies of the spin system being studied and that model spectral density functions can have many optimizable parameters. Both of these weaknesses are alleviated by acquiring additional relaxation data at multiple static magnetic fields [36].

The present work examined three methods of performing spectral density mapping of ²H relaxation in ¹³CH₂D methyl group isotopomers, which have been termed independent, joint, and joint-interpolated. The latter two approaches make use of a unique feature of ²H quadrupolar relaxation: the number of spectral density values entering into the relaxation equations is reduced if data are acquired at pairs of static magnetic fields that differ by a factor of two. As relatively few such paired fields are available at present (in the current work, only 400 MHz/800 MHz), the joint-interpolation method approximates such pairings, in the current work by interpolating between 400 MHz and 500 MHz to generate relaxation data at 450 MHz for pairing with 900 MHz data. The major advantages of the joint and joint-interpolation methods are the consequent additional increases in the statistical degrees of freedom compared with the independent method.

Comparisons among the three spectral density mapping methods and cross validation with an independent data set indicated that the three approaches were equally accurate; however, the joint-interpolation method yielded an improvement in precision for the final fitted model-free parameters of between 10–15% compared to the independent method and of between 7–11% compared with the joint analysis. These results would make the joint-interpolation method preferable over the other two methods. Notably, no additional data need to be acquired to implement the joint-interpolated method and as more commercial NMR spectrometers with frequencies of 1000 MHz and 1200 MHz become available, additional pairs of fields become accessible, further increasing the power of this method.

Highlights.

1. ²H relaxation rates for E. coli ribonuclease H at four static magnetic fields

2. Evaluation of three approaches for spectral density mapping of multiple field data

3. Cross validation with a fifth magnetic field establishes accuracy of all methods

4. Novel interpolation strategy improves precision of fitted model-free parameters