Ultrafast nonthermal heating of water initiated by an X-ray Free-Electron Laser

Significance

X-ray Free-Electron Lasers have opened the door to a new era in structural biology, enabling imaging of biomolecules and dynamics that were impossible to access with conventional methods. A vast majority of imaging experiments, including Serial Femtosecond Crystallography, use a liquid jet to deliver the sample into the interaction region. We have observed structural changes in the carrying water during X-ray exposure, showing how it transforms from the liquid phase to a plasma. This ultrafast phase transition observed in water provides evidence that any biological structure exposed to these X-ray pulses is destroyed during the X-ray exposure.

Abstract

The bright ultrafast pulses of X-ray Free-Electron Lasers allow investigation into the structure of matter under extreme conditions. We have used single pulses to ionize and probe water as it undergoes a phase transition from liquid to plasma. We report changes in the structure of liquid water on a femtosecond time scale when irradiated by single 6.86 keV X-ray pulses of more than 10⁶ J/cm². These observations are supported by simulations based on molecular dynamics and plasma dynamics of a water system that is rapidly ionized and driven out of equilibrium. This exotic ionic and disordered state with the density of a liquid is suggested to be structurally different from a neutral thermally disordered state.

Heating, as when boiling water, traditionally involves adding kinetic energy to molecules vibrationally by convection or excitation by thermal radiation. We consider a different pathway, where energy is deposited through ionization caused by femtosecond (fs) X-ray pulses. Tightly focused pulses from an X-ray Free-Electron Laser (XFEL) cause severe ionization, leading to an exotic plasma state (1–3), known as warm dense matter. We used X-ray fluences above 10⁶ J/cm² to photoionize a micrometer-size jet of water and bring it to temperatures above 100,000 K and pressures above 1 Mbar. These extreme conditions while the sample is still at liquid density are unique on Earth and lead to a phase transition from liquid into warm dense matter within femtoseconds. To elucidate the intermolecular information encoded in the X-ray diffraction pattern, we modeled the nonequilibrium dynamics of the ions and electrons excited during the pulse by molecular dynamics (MD) and plasma simulations.

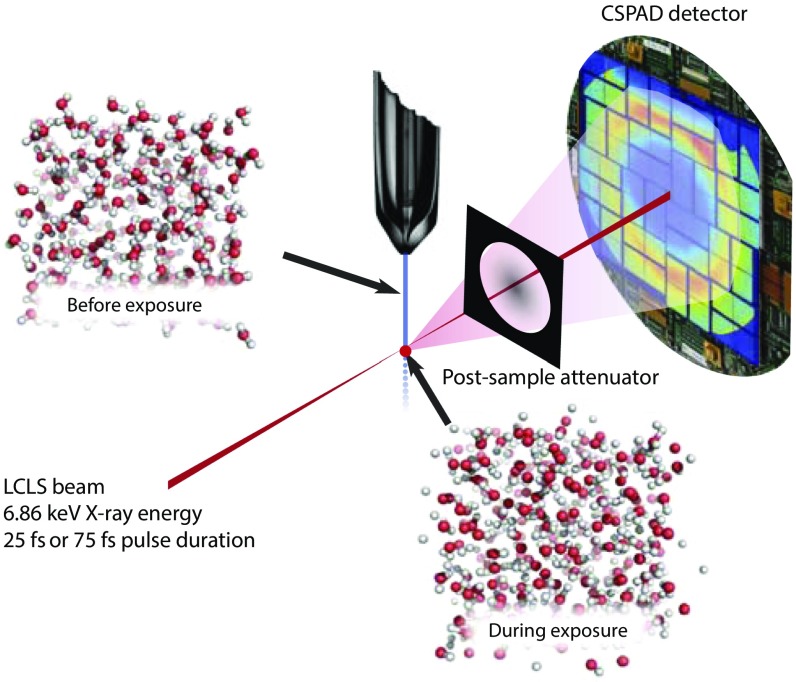
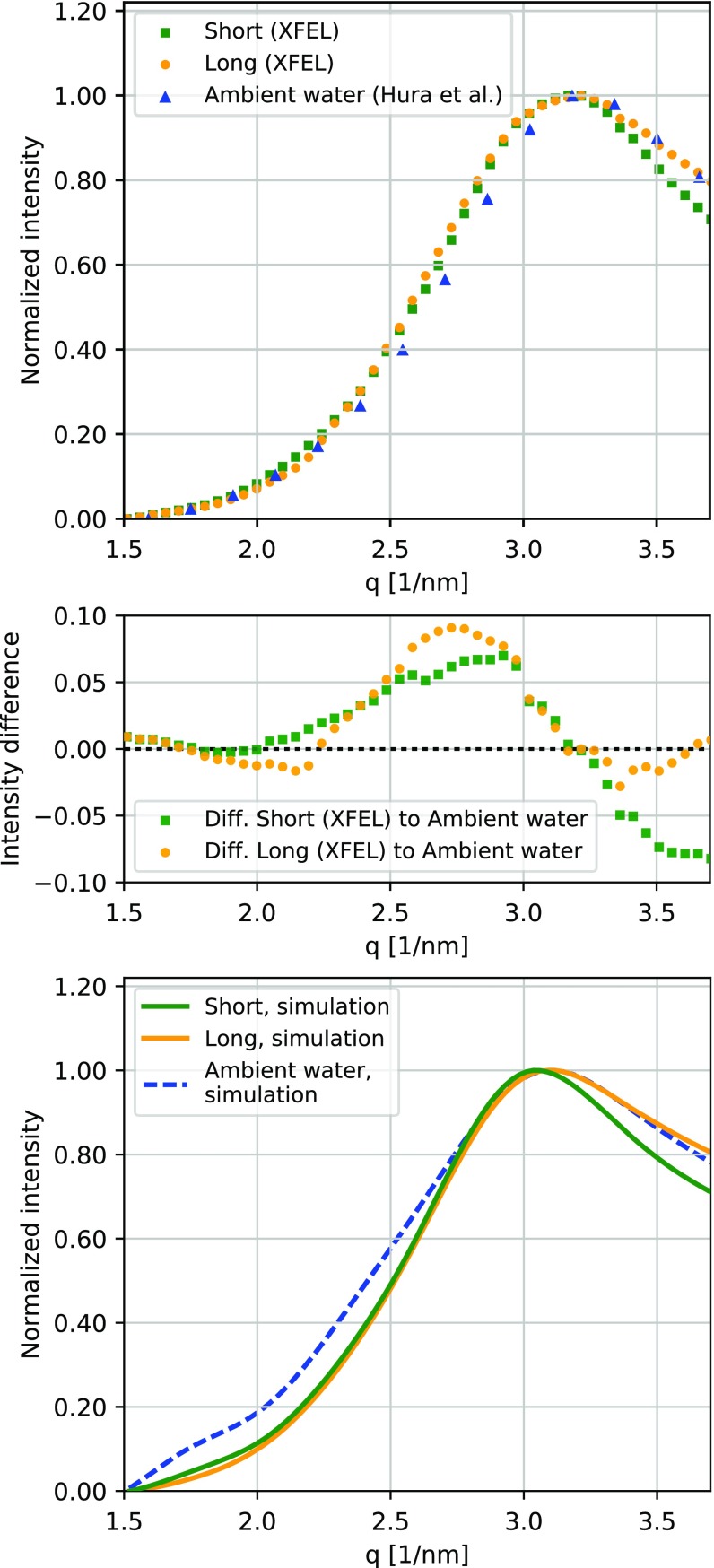
The experimental setup (Fig. 1) consisted of a water jet produced by a gas dynamic virtual nozzle (GDVN) (4, 5), which was intersected by a submicrometer focused X-ray beam of the Coherent X-Ray Imaging (CXI) instrument of the Linac Coherent Light Source (LCLS) (6). Single 6.86 keV X-ray pulses with 25 (short) and 75 (long) fs duration and an average fluence of 1.35 $\cdot$ 10⁶ J/cm² were used. The main experimental results are the plots of scattering intensity as a function of the magnitude of the scattering vector, $q=2\sin \left(\theta \right)/\lambda$ (where $2\theta$ is the scattering angle and $\lambda$ is the wavelength), shown in Fig. 2, obtained after binning, masking and radial averaging the diffracted signal collected on a Cornell-SLAC hybrid Pixel Array Detector (CS-PAD) detector (7) (see Materials and Methods). The scattering intensity as a function of $q$ for ambient water using a synchrotron beamline (8) is also shown for comparison and is used to calculate differences (Fig. 2). Each measurement condition is found to result in a slightly different scattering curve. The peak in the XFEL measurements is shifted to lower scattering vector $q$ and is narrower than the ambient water peak. The largest shift is seen in the short pulse measurement and the largest broadening in the long pulse measurement. At a first glance, the shift in the scattering intensity curves compared with the ambient case seem to contradict what one would expect. The curve for the long (75 fs) exposure shows a behavior similar to that of ambient water, whereas the short pulse (25 fs) exposure shows a narrower peak. To explain these observations and unravel the electronic and structural evolution of the system, we have used atomistic simulations linking ionization and MD.

Fig. 1.

A narrow jet of room temperature water was injected using a GDVN into the 200 nm X-ray focus of the CXI end station of the LCLS. Diffraction patterns from single pulses were recorded on a CS-PAD detector with a postsample attenuator made of a Tungsten alloy film positioned downstream of the sample. The scattered signals from pulses of short (25 fs) and long (75 fs) duration were processed and analyzed. A combination of NLTE modeling and MD simulations was used to follow the dynamics of the atoms during the exposure to intense X-ray radiation. Upper Left and Lower Right depict the broken bonds found in the simulations. The water transitions into a warm dense matter state during the pulse and leads ultimately to a local explosion of the water jet (12).

Fig. 2.

Scattered X-ray intensity from water. (Upper) Measured scattering intensity as a function of scattering vector $q=2\sin \left(\theta \right)/\lambda$, for experiments using an XFEL pulse of 25 fs and 75 fs duration (both with a fluence of 1.35$\cdot$10⁶ J/cm²) and data from water at ambient conditions taken from Hura et al. (8). The SE on normalized intensity for all measurements is smaller than 0.2%. All curves are normalized to the maximum of the peak with the minimum subtracted. (Middle) Difference between measured scattering intensity using XFEL pulses and a linear interpolation of the scattering intensity from water at ambient conditions (8). (Lower) Simulated scattered intensities as a function of scattering vector $q$, based on MD and NLTE simulations, calculated from the O–O radial distribution function (RDF) and the electronic states of the system. The X-ray parameters are chosen to match the experimental. All curves are normalized to 1. Direct comparisons of simulations to experiments are available in SI Appendix, Fig. S1. Tabulated data $q$ vs. intensity are available in SI Appendix.

We conducted a combination of Non-Local Thermodynamic Equilibrium (NLTE) and MD simulations that allows us to computationally investigate the effects of ionization and heating separately. We started by simulating the light–matter interaction using an NLTE code (9), which predicts ionization states, temperature, and collision rates. The average ionization of the oxygen atoms at the end of both XFEL exposures was similar, reaching states as high as +6 (SI Appendix, Fig. S2). This type of extreme ionization led to molecular bond breaking that pushed the system into a plasma state. The main difference found between the two XFEL exposures was the temperature. At the end of the 25 fs pulse, it was estimated to be 4 eV (46,000 K), while at the end of the 75 fs pulse, it was 13 eV (160,000 K) (SI Appendix, Fig. S2). A higher temperature is synonymous with a higher degree of disorder in the system and is reflected in a broader distribution of oxygen–oxygen distances, as we find by MD simulations (see Materials and Methods). This already gives an indication as to why the water peak measured with a 75 fs XFEL pulse shown in Fig. 2 is broader than that of the 25 fs pulse.

Based on the calculated temperatures and collision frequencies, we estimated the average displacements of the atoms or ions in the sample (10). The average displacement of the oxygens was calculated to be 0.06 nm within the short pulse and increased to 0.47 nm for the long pulse—corresponding to average velocities of 2,544 m/s and 6,266 m/s, respectively. For comparison, the speed of sound in water is around 1,500 m/s. The high velocities predicted for our systems are due to an increase of ion collisions driven by Coulomb forces and are characteristic for plasmas. The difference in displacements for the two pulses indicates that the energy deposited from ionization still needs time to affect the water structure, in line with earlier studies (10). The water in the X-ray–exposed region of the jet cannot expand significantly during the pulse (11), the volume of the system is constant, and the increased ion–ion collision rate leads to a pressure increase up to a few megabars. Analysis of the plasma coupling parameter shows that the system begins a structural change to a warm dense matter state within the first 5 fs of the pulse (see Materials and Methods).

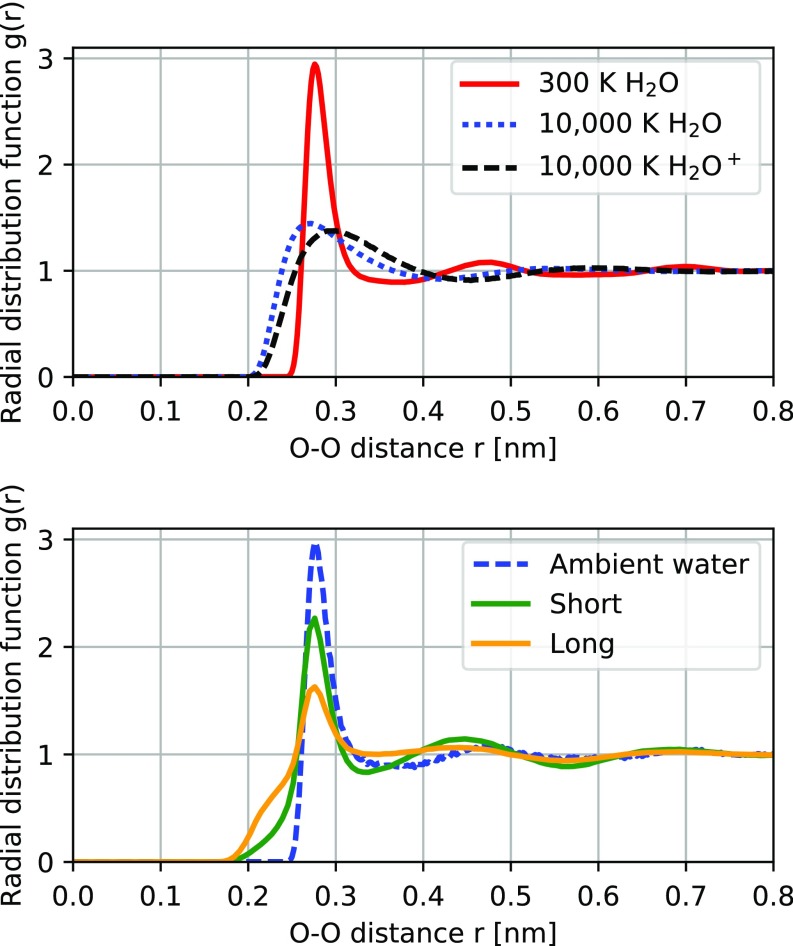
To understand qualitatively the effect of ionization on the structure of water and the intermolecular distances at these high temperatures, we carried out idealized test MD simulations on water at 300 K, 10,000 K without ionization, and 10,000 K with ionization, where each molecule was given an average charge of +1. The structural differences between these three states are found in the oxygen–oxygen radial distribution functions (RDFs) shown in Fig. 3. The first peak in the RDF for the neutral high temperature state is shifted toward shorter distances and broadened compared with that of the room temperature state. Meanwhile, the second and the third peaks of the high temperature state are almost washed out. Therefore, at a higher temperature but constant volume, the minimum distance between oxygen atoms decreased (13) from the increased pressure, and the internal structure beyond the first coordination shell disappeared. When the high temperature water molecules were given an average ionization of +1, the first peak in the RDF shifted to longer distances compared with the nonionized high temperature case. This suggests that the intermolecular structure of this ionized state is different from that of a purely high temperature state and that the oxygen ions are pushed further apart. Our NLTE simulations suggest that the experimental system could reach ionization states up to +6, which could lead to even longer average oxygen distances. However, this ionization state is predicted to only exist at the end of the pulse and in the center of the X-ray focus where the intensity is at its maximum.

Fig. 3.

Radial distribution functions of oxygen–oxygen distance in water calculated from MD simulations. (Upper) Test simulations for 300 K and 10,000 K neutral systems and an 10,000 K ionized system (charge +1). Heated systems will have a lower degree of coordination in higher number solvation shells. (Lower) MD simulations using the experimental parameters for the X-ray pulse.

To simulate the experimental conditions and follow the femtosecond structural evolution of the system, we coupled the ionization evolution from NLTE simulations into MD simulations at each time step (see Materials and Methods). Based on the RDF and atomic form factor for each time point, we calculated the radially averaged diffraction patterns from the simulations. The scattering intensities retrieved from the simulations are shown in Fig. 2, Lower. The simulations reproduce the experimental trends in relative peak broadening. Notably the peak for the short pulse case is narrower compared with the ambient water in both simulation and experiment. The absolute peak position is, however, not reproduced by the simulations (see direct comparison in SI Appendix). This is likely due to the water model used in the MD simulations, extended single point charge model (SPC/E) (14), which is known to have a slightly shifted peak position compared with experiments (15).

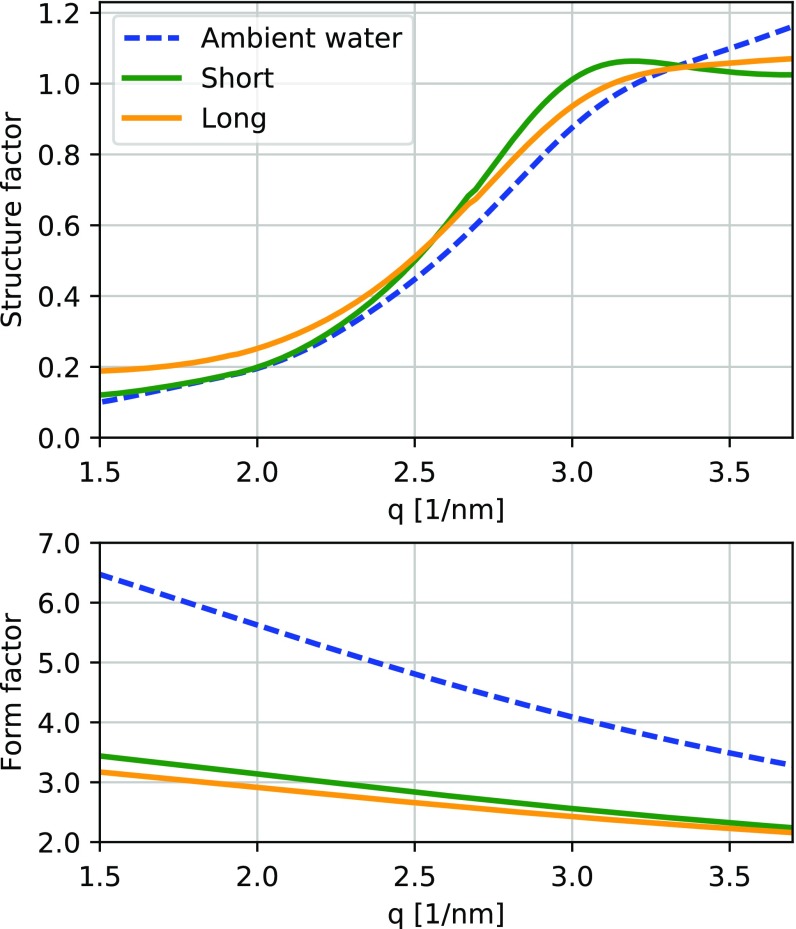
The diffracted X-ray signal can be expressed in terms of the structure factor $S\left(q\right)$, which encodes the atomic position, and the atomic form factor $f\left(q\right)$, which depends on the ionization states. Both the ionization states and the atomic positions are changing dynamically during the exposure. The time integrated form and structure factors were calculated separately in the simulations and are shown in Fig. 4. The atomic form factors in the XFEL cases are very similar to each other, and they are nearly linear in the measured q range due to similar ionization dynamics (SI Appendix, Fig. S3). Larger differences are seen in the structure factors, suggesting that the observed differences in the diffraction patterns are in fact due to structural rearrangement. Increased disorder in the long pulse case leads to a broadening of the structure factor peak.

Fig. 4.

Simulated structure factors and form factors. (Upper) Time integrated simulated structure factor as a function of scattering vector $q$ for the 75 fs (long) and 25 fs (short) XFEL pulses as well as for the ambient case. The structural changes that happen in the last part of the long pulse create distinct differences, especially in the slope at high $q$, which is of the opposite sign. (Lower) Time integrated simulated form factor as a function of scattering vector for the same cases. The form factors for the intense XFEL pulses are at all $q$ values very close in magnitude and slope. The time integrated product of the squared form factor and the structure factor gives the scattered intensity, which can be directly compared with the experiment. Given the limited range in $q$ and that both factors change during the pulse, these cannot be extracted unambiguously from the experimental data.

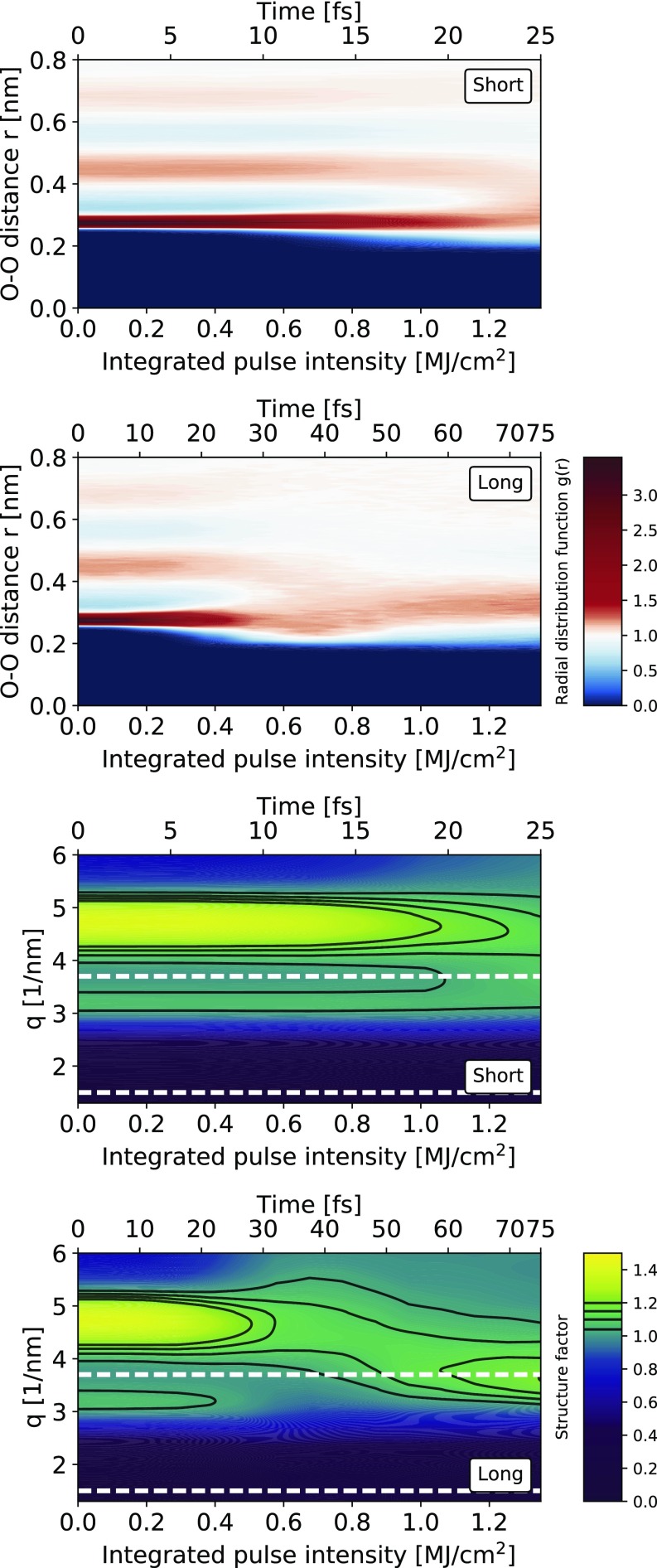
The full-time evolutions of the structural changes during the short- and long-pulse simulations are shown in Fig. 5. For the short pulse, the RDF shows that the oxygen–oxygen coordination stayed intact for more than half the pulse duration. Electronically and energetically, the sample was considered a plasma after a couple of femtoseconds, but the RDF shows that the sample kept its water structure 15–20 fs longer, until the end of the exposure when it was washed out.

Fig. 5.

Simulation of the time evolution of the RDF and structure factors. (Top and Upper Middle) Time evolution of the RDF during the X-ray pulse, shown as a function of integrated intensity for the two pulses. The short (25 fs) and long (75 fs) pulses have the same total intensity. In both cases, the structure of water does not appear to change until roughly 20 fs. (Lower Middle and Bottom) Time evolution of the structure factor, calculated from the RDF above. The experimental measurements displayed in Fig. 2 were made from $1.5$ to $3.7$ nm⁻¹, marked here with dashed white lines.

In the long-pulse case, we observe a similar behavior, with the water signature visible during the first 25 fs. After that point, the first and the second peak of the RDF, corresponding to the first and the second solvation shell, were washed out, and a new broad peak emerged at a distance of 3.5 Å. Note that the experimental data consisted of the time-averaged signal, which was found to be in good agreement with the simulations (Fig. 2).

In conclusion, our experiments and simulations suggest the intense femtosecond X-ray pulses cause a rapid rise of temperature and ionization in water during the pulse. The heating arises from the heavy X-ray bombardment and the subsequent ionization, leading to a nonthermal heating process originating from the sudden increase of positive ions and free electrons in the system. This implies structural changes involving displacements of a few Ångström within femtosecond time scales. For fluences of 10⁶ J/cm², the system is found to be in a warm dense matter state within 5 fs, both energetically and electronically. A structural transformation requires more time as the nuclei carry more inertia. Within a 25 fs pulse, the sample shows similar structural features to water and begins to exhibit some disordering toward the end of the pulse. Similar structural changes are present during the first half of a 75 fs pulse, after which the disorder in the system increases such that the second and third coordination shell are no longer visible. The first coordination shell also shifts to longer distances, in response to the high ionization states of oxygen. Most of what is recorded on the detector comes from a sample that is no longer structurally liquid water but rather a dense plasma state.

Our findings suggest that it is important to consider the induced disorder in water during an intense X-ray pulse, in particular for experiments dedicated to single particle imaging or scattering in solution. Water is present in biological samples and is the main solvent used in structural determination experiments (where it is used to deliver biological samples in the interaction region). With comparable density and ionization pathways, water also serves as a good model for studying radiation damage in biological matter. The transition into a warm dense matter state, a unique ionically disorder state that we suggest is structurally different from the neutral thermal disorder states, could have an impact on structural determination. Crystallography using XFEL sources is immune, to some degree, to the loss of structural coherence caused by the ionization, due to the self-gating of Bragg diffraction (10, 16). On the other hand, for scattering measurements of noncrystalline samples, such as liquids, using intense XFEL pulses, these effects must be considered. At the same time, this warm dense matter gives insight into a regime relevant for other fields of science, such as physics of inertial confinement fusion, planetary cores, and shockwaves in dense material.

Materials and Methods

Experiment and Data Analysis.

The XFEL experimental data were collected using the 0.1 μm focus sample chamber of the CXI instrument at the LCLS (17). Data were collected during the water washes between sample runs in experiment L764 (2013), and the experimental setup has been described in detail previously (18). A schematic view of the experimental geometry is shown in Fig. 1. Room temperature, Milli-Q purified water was injected into the vacuum using a GDVN (4, 5) at a flow rate of 25–30 μL/min, corresponding to a jet diameter of about 5 μm. The 6.86 keV X-ray beam was focused on the continuous region of the jet with an approximate 200 nm focal spot size. The LCLS was tuned to collect sets of diffraction data with different X-ray pulse durations at a repetition rate of 120 Hz. The average durations and standard deviations of pulses as measured by the X-band transverse deflecting cavity (XTCAV) diagnostic tool of LCLS were 26.3 $\pm$ 1.8 fs and 74.0 $\pm$ 1.9 fs for the respective short and long pulse datasets. In both cases, only pulses with energies of 1.35 $\pm$ 0.05 mJ measured by the front end enclosure (FEE) gas detector of LCLS were averaged together. The beamline transmission downstream of this detector is estimated to be 40%, resulting in approximately 0.54 $\pm$ 0.02 mJ pulse energies at the sample position. This pulse energy and focus correspond to average fluence on the water jet of 1.35$\cdot$10⁶ J/cm². While collecting these data, a detector distance of 100 mm was used and a postsample attenuator (18) was placed at a distance 23 mm downstream of the sample.

The raw CS-PAD detector (7) data were filtered and corrected before calculating the radially averaged pattern. The data from each event in the dataset were first corrected for dark current and panel common mode response. A pixel mask was applied to exclude pixels that have fluctuations greater than 5 SDs during the dark measurement, regions of the detector shadowed by the postsample attenuator mount, and bright regions on the detector due to small cracks in the postsample attenuator. Events were binned in terms of the pulse energy, measured by the FEE gas detector, and the average unmasked pixel intensity on the detector. This allows for the data to be filtered by these quantities, and their correlation separates the stability of the jet and response of the detector. Average diffraction patterns were calculated from events with FEE measured pulse energies in the range of 1.3–1.4 mJ data. In all cases, only events with an average unmasked pixel intensity in the range of 10.0–11.3 ADU were considered. These parameters were selected to form a more controlled dataset from the collected data, while averaging enough events to obtain a reliable signal. After this filtering, 133 and 2,247 events contributed to the average pattern of the short pulse and long pulse datasets, respectively. The detector panel position and relative orientations were refined by optimizing the indexing success rate of diffraction patterns from protein crystals, which were measured at a different time during the experiment (18). The average pattern was then corrected for the effects of X-ray polarization, pixel solid angle (13), and the postsample attenuator transmission (18) when it was in place. The one-dimensional solution scattering curves were then calculated by binning the intensity in each pixel by its corresponding scattering vector magnitude and normalizing by the number of pixels contributing to each bin. The resulting average scattering curves are shown in Fig. 2. Uncertainty in the obtained average was calculated from the pixel-wise variance of each diffraction pattern from the mean and averaged into the 1-D bins in terms of the scattering vector magnitude, q. The SE as a function of q was then calculated from the corresponding SD scaled by the square root of the product of the number of patterns contributing to the average and the number of pixels in a bin. Given that the size of the pixel detector is 1516 $\times$ 1516 pixels and the number of pixels contributing to each bin is increasing with increasing scattering angle, this gives a very low error.

The described strategy of only considering events with the same average intensity on the detector was adopted to avoid differences in the detector response. This approach has the consequence of only using between 0.1% and 2% of the recorded data, resulting in total data collection times on the order of 20 min for each presented average pattern. A larger acceptance window of these parameters was not possible as the detector behavior appeared to be nonlinear in terms of the incident intensity and the long pulse data seemed to be sensitive to the pulse energy. Instead of filtering, a nonlinear correction based on a pixel-wise parameterization using the signal on the detector from the water pattern was also attempted (19), however it was not found to correct for the observed detector response. This might be due to the fact that this parameterization was devised for signal levels that are much higher than those observed in this experiment.

It should be noted that the spatial profile of the X-ray focus contains a high-intensity central spot with a diameter on the order of 200 nm, which is smaller than the water jet. The spatial profile of the focus around this central spot is not well known and may contain a large fraction of the total photons. A recent diffraction study on aerosolized nanoparticles (20) found a large uncertainty in determining the spatial intensity profile of the X-ray pulse. This profile can be fitted with a Lorentzian, however the full-width-half-maximum depends strongly on the assumed beamline transmission. The temporal profile of the X-ray pulse is not known from shot to shot, and how this is modeled has been shown to influence the scattering (21). Therefore, we have chosen to show simulations only for the peak pulse intensity and a flat temporal profile (details below), to capture the main mechanisms that lead to changes in scattering. We note that the experimental measurements reflect a volume weighted average diffraction pattern, where volumes of water irradiated by lower X-ray intensities outside the central focus also contribute to the measured intensity, and this could influence the contribution from the peak fluence in the final experimental results.

Simulations.

To model the effects of ionization and the subsequent heating on the atomic structure of the system, we have used a two-step approach.

First, we simulated the interaction between the XFEL beam and water with a NLTE code, Cretin (9), using the experimental parameters. More explicitly, we have used photons of 6.86 keV energy, pulses of 25–75 fs duration, and intensities from 10⁴ to 10⁶ J/cm². These simulations follow the atomic kinetics and radiation transport and provide ionization, ion temperature, ion collision frequency, and pressure in the water during the X-ray exposure. The physical processes modeled in the NLTE approach and the calculation of the atomic displacement are described and compared with experiments in earlier studies (10, 16, 21); we have made available the simulations for water and other materials in an open web-tool database for XFEL damage (22).

We used the plasma coupling parameter $\mathrm{\Gamma }$, defined as the ratio between the average potential and average kinetic energy of a system, to characterize the plasma state of the sample (SI Appendix, Fig. S4). As long as $\mathrm{\Gamma }<<1$, a system is considered to be in a weakly bound regime associated with room-temperature conditions. Our simulations show that the sample left this regime after 1–2 fs, signifying its energetic and electronic transition to a warm dense matter state. Within 5 fs, the system reached high ion temperatures ($T>1000$ K) and pressures ($P>1$ Mbar), signaling the beginning of the structural change to a warm dense matter state.

In the second step, we use MD to simulate the structural changes. The MD simulations (presented in Figs. 2 and 3) were done using the software package Gromacs version 3.3 (23), similar to what has been done in earlier studies (11, 24), however the ionization and heating dynamics were modified in such a way that they follow the ones calculated using the NLTE code. We used a modified version of the SPC/E water model (14), where we have given the hydrogen atoms a radius, similar to that used in the CHARMM TIP3P water model (25). This is necessary to keep the particle nature of the hydrogen atoms even after bond breaking. For the nonequilibrium simulations (Figs. 2 and 3), the oxygen–hydrogen bonds were treated as a Morse potential (26), allowing bonds to break. The simulations were performed using periodic boundary conditions, with a constant box size and 1,728 water molecules, and a starting temperature of 300 K. The ejected electrons are treated as a uniform background charge to keep the neutrality of the system.

Both Cretin and Gromacs are classical methods that do not treat all quantum processes relevant to high-density degenerate plasmas. In our simulations, the degeneracy parameter was $\mathrm{\Theta }>1$ (SI Appendix, Fig. S5), indicating that the classic approach is a valid approximation. Alternatively, one can use quantum-based particle dynamics codes, like ddcMD (27), at a higher computational cost.

The scattering intensity shown in Fig. 2 was calculated from the structure factors $S\left(q\right)$ using the Fourier transform of the oxygen–oxygen RDF and the form factor $f\left(q\right)$ for the electronic states of the system, for all of the experimental parameters that were simulated. The expected scattered intensity is a sum over all time steps:

$$I\left(q\right)=\frac{1}{T}\sum _{t=0}^T{f}_{\mathrm{t}\mathrm{o}\mathrm{t}}{\left(q,t\right)}^2\cdot S\left(q,t\right),$$ [1]

where $T$ is the pulse duration, $t$ is the simulation time step, and $q$ is the momentum transfer. The total form factor $f_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(q,t\right)$ is calculated as a weighted sum over the time-dependent form factors $f_i\left(q,t\right)$ and will change with the fraction of the ion population present as

$$f_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(q,t\right)=\frac{\sum _i{f}_i\left(q,t\right)\cdot c_i\left(t\right)}{\sum _i{c}_i\left(t\right)},$$ [2]

where $\sum _i$ is the sum over all ionized states including core holes (21) for oxygen. The fraction of ions $c_i\left(t\right)$ in state $i$ is obtained from plasma simulations for each time $t$ during the pulse. The atomic form factors have been calculated earlier (16) and have been validated with similar calculations (28). In our simulations, the quasi-free electrons were uniformly distributed in the sample and assumed not to contribute to the diffraction signal. The calculated systems shown here are only for intensities of $1.35\cdot 10^6$ J/cm² and do not take into account the spatial distribution of the X-rays in the focus. The experimental distribution of intensities in the focus is not exactly known, and it is expected to play some role, however here we aim to identify the largest effects and study the mechanisms corresponding to the highest intensities in the focus.

To visualize the effect of heating and ionization separately, we also made test simulations of a water box, containing 1,000 molecules in thermal equilibrium (Fig. 3, Top). The simulations were done using the Berendsen temperature coupling (29) at two temperatures, 300 K and 10,000 K. The higher temperature corresponds to around 1 eV and was chosen to match the temperature where warm dense matter properties start to emerge. Simulations were 200 ps long and with a 100 ps presimulation to ensure for an equilibrated system. These simulations were done using the water model described above as well as with a model where the oxygen charge was modified to +1. Snapshots of the molecules in the simulations for the cases of 300 K and ionized 10,000 K water are shown in Fig. 1.