Pacing of Paleozoic macroevolutionary rates by Milankovitch grand cycles

Significance

There has been long-standing debate about the relative roles of intrinsic biotic interactions vs. extrinsic environmental factors as drivers of biodiversity change. Here, we show that, relatively early in the history of complex life, Milankovitch “grand cycles” associated with astronomical rhythms explain between 9 and 16% of variation in species turnover probability (extinction probability plus speciation probability) in a major Early Paleozoic zooplankton group, the graptoloids. These grand cycles would have modulated climate variability, alternating times of relative stability in the environment with times of maximum volatility, which influenced oceanic circulation and structure and thus, phytoplankton populations at the base of the marine food web.

Abstract

Periodic fluctuations in past biodiversity, speciation, and extinction have been proposed, with extremely long periods ranging from 26 to 62 million years, although forcing mechanisms remain speculative. In contrast, well-understood periodic Milankovitch climate forcing represents a viable driver for macroevolutionary fluctuations, although little evidence for such fluctuation exists except during the Late Cenozoic. The reality, magnitude, and drivers of periodic fluctuations in macroevolutionary rates are of interest given long-standing debate surrounding the relative roles of intrinsic biotic interactions vs. extrinsic environmental factors as drivers of biodiversity change. Here, we show that, over a time span of 60 million years, between 9 and 16% of the variance in biological turnover (i.e., speciation probability plus species extinction probability) in a major Early Paleozoic zooplankton group, the graptoloids, can be explained by long-period astronomical cycles (Milankovitch “grand cycles”) associated with Earth’s orbital eccentricity (2.6 million years) and obliquity (1.3 million years). These grand cycles modulate climate variability, alternating times of relative stability in the environment with times of maximum volatility. We infer that these cycles influenced graptolite speciation and extinction through climate-driven changes to oceanic circulation and structure. Our results confirm the existence of Milankovitch grand cycles in the Early Paleozoic Era and show that known processes related to the mechanics of the Solar System were shaping marine macroevolutionary rates comparatively early in the history of complex life. We present an application of hidden Markov models to macroevolutionary time series and protocols for the evaluation of statistical significance in spectral analysis.

The relative roles of intrinsic biotic interactions vs. extrinsic environmental factors as drivers of biodiversity change have been much debated and are still uncertain (1, 2). One facet of this debate concerns the reality and causes of putative periodic fluctuations in diversity, speciation rate, and extinction rate. In particular, quasiregular fluctuations with extremely long periods ranging from 26 (3) to 62 (4) My have been proposed, although the forcing mechanisms have remained speculative (5). With the exception of the Late Cenozoic (6), no studies have shown the role of well-understood astronomical cycles on rates of evolution or extinction or quantified the proportion of variance in macroevolutionary time series that can be explained by these cycles. Here, we show that long-period astronomical cycles, Milankovitch “grand cycles,” played a significant role in pacing species turnover in a major Early Paleozoic zooplankton group, the graptoloids.

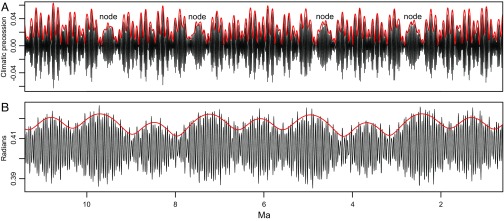
Milankovitch grand cycles (7) are astronomical rhythms associated with the amplitude modulation of Earth’s climatic precession cycle and axial obliquity cycle. During the Late Cenozoic, the amplitude modulation of precession by eccentricity results in a 2.4-My cycle in addition to the well-known cycles of 405,000 and ∼100,000 y; the long-period obliquity amplitude modulation is ∼1.2 My (Fig. 1) (8, 9). These relate to g₄-g₃, the orbital perihelion precession rates of Mars and Earth, and s₄-s₃, the orbital inclination rates of Mars and Earth, respectively. These grand cycles have been implicated as controls on Late Cenozoic ice sheet history (10) and sea-level variability into the Mesozoic (11). The environmental impact of the grand cycles is to produce long-term “nodes” of stability (e.g., little difference in climate between maximum and minimum of obliquity) that alternate with times of maximum volatility (e.g., strong climatic differences between maximum and minimum of obliquity). Whereas this multimillion year control on environmental stability has obvious implications for biological evolution, its presence has not been clearly detected in evolutionary rate data, except in the case of the Neogene mammalian record (6). A major obstacle in this regard has been the availability of records of appropriate duration and sampling frequency to permit a robust evaluation.

Fig. 1.

Illustrations of Milankovitch grand cycles over the past 1–11 My generated from the astronomical solution in ref. 9. (A) Amplitude modulation of precession by eccentricity. The black line is the climatic precession [= eccentricity × sin(precession angle)]; the red line is the amplitude modulation and reveals cycles at ∼100,000 and ∼405,000 y and grand cycle nodes at ∼2.4 My. (B) Amplitude modulation of obliquity. The black line is the obliquity solution; the red line is the amplitude modulation of the dominant 41,000-y obliquity cycle, with a conspicuous ∼1.2-My grand cycle.

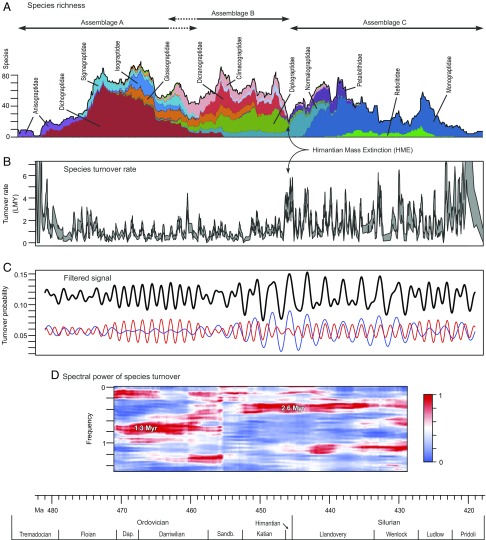
Graptoloids (order Graptoloidea) are an extinct group of colonial, filter-feeding hemichordates that constituted the main component of the Paleozoic macrozooplankton as preserved in the fossil record (12, 13) from the beginning of the Ordovician Period (486 Ma) to the Early Devonian (411 Ma) (14, 15). They have a very short median species life span—1.27 and 0.69 My in the Ordovician and Silurian, respectively (16)—meaning that they provide a rich dataset for analysis of speciation and extinction rates (Fig. 2). For this reason and due to their abundance and the resultant highly resolved record, they provide a model clade to investigate million year-scale astronomical influence on macroevolution during the Paleozoic.

Fig. 2.

Graptoloid diversity, turnover, and spectral analysis of turnover. (A) Standing species richness with main families shown (17). (B) Smoothed species turnover rate per lineage million years (LMY) (18) shown as bootstrapped ±1 SE region. This was constructed as the sum of LMY rates for speciation and extinction calculated using a 0.25-My moving window centered at each speciation and extinction event level in the CONOP composite; bootstrapping was based on resampling species across the entire composite (1,000 iterations). (C) The 2.6-My (blue), 1.3-My (red), and summed (black; centered at two times mean value for clarity) bandpass-filtered signals (19) from the time series of species turnover probability based on summed predicted-state probabilities for HMMs of speciation (four state) and extinction (three state). Note that the time series used for spectral analysis is much more highly resolved than the smoothed turnover history shown in B and too finely resolved to be shown in its entirety here (Materials and Methods). The bandpass filters are 3.1–2.1 and 1.47–1.18 My, respectively. (D) EPSA of turnover probability time series. Strong spectral power at periods of ∼1.3 and ∼2.6 My is indicated. EPSA utilizes three 2π prolate tapers, with a 20-My moving window; the maximum power in each window is normalized to unity.

Graptoloid colony size generally ranged from a few millimeters up to ∼200 mm in maximum dimension, although the individual zooids measured less than 2 mm in length (20). The colonies lived suspended in the ocean waters at a range of depth zones and are inferred to have filtered out microphytoplankton, bacterioplankton, and other particulate organic matter as their principal food source (21–23). The graptoloids are, therefore, inferred to have been primary consumers in the food chain and consequently, would have been sensitive to environmental parameters that controlled their main trophic resource, namely nutrient flux, ocean stratification and chemistry, redox profile, local and global ocean circulation systems, and therefore, global marine climate (16, 21, 24, 25). In support of this environmental sensitivity, positive excursions in the global δ¹³C_carb isotope curve—interpreted as reflecting carbon burial and associated global cooling (26–28)—coincide with falling or minimal values in the graptoloid raw species richness curve, although the causal linkage was complex and is not fully understood (16). Furthermore, the transition in global climate from greenhouse to icehouse in the Late Ordovician is marked by a step change in the graptoloid species extinction rate (16, 17), a change from background to episodic extinction, and a change in the dependence of extinction risk on species age (17).

To evaluate periodic environmental pacing in the graptoloid macroevolutionary record, it is necessary to have a long time series of speciation and extinction observations and to minimize aliasing of frequencies. These data should, therefore, be as highly resolved as possible. Here, we use the high-resolution time series of graptoloid speciation and extinction probabilities derived from the global composite that was developed using constrained optimization (CONOP) (29) from 518 stratigraphic sections. The complete composite spans the entire history of the clade from 491 to 411 Ma, contains 2,041 species, has been calibrated directly by 23 integrated radioisotopic dates, and is the basis of the Ordovician and Silurian global geological timescales (14, 15). To reduce stochastic noise in the signal while retaining maximum resolution, we fit discrete time hidden Markov models (HMMs) (30) to the raw time series of speciation and extinction probabilities at a temporal resolution of 0.05 My (Materials and Methods).

Results

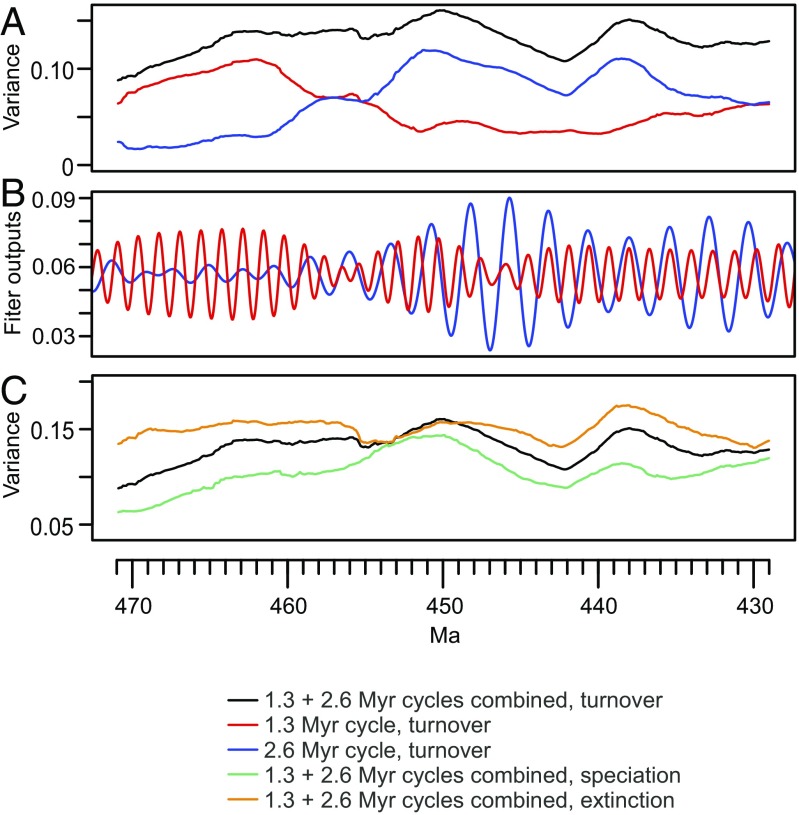
The time series of graptolite HMM species turnover (speciation plus extinction HMM probabilities) reveals a strong 2.6-My rhythm expressed in both the time frequency result (Figs. 2 C and D and 3 and Figs. S3 and S5) and power spectrum for the entire study interval (Fig. S2); this rhythm is close to that of the modern day orbital eccentricity grand cycle. In contrast, a ∼1.3-My rhythm that is weak in the total spectrum is dominant in the early portion of the record, with a transition between the two in the interval from 460 to 453 Ma (Figs. 2 C and D and 3 and Fig. S4). This signal is close to that of the modern day obliquity grand cycle. Together, these two cycles explain between 9 and 16% of the total variance in the turnover signal (Fig. 3A). Both rhythms are statistically significant. The testing of statistical significance in time series analysis is a complex issue that is addressed in detail in Materials and Methods and Supporting Information.

Fig. 3.

Temporal evolution of the observed ∼1.3- and ∼2.6-My cycles in graptoloid HMM species turnover, speciation, and extinction. (A) Proportion of variance associated with the ∼1.3- and ∼2.6-My cycles individually and combined for the default species turnover probability time series used in Fig. 2 C and D. Proportion determined by integration of the EPSA results (Fig. 2D) from 0.21 to 0.52 cycles per 1 My (∼1.3-My cycle) and from 0.53 to 0.90 cycles per 1 My (∼2.6-My cycle). (B) The ∼1.3-My (red) and ∼2.6-My (blue) filtered signals for species turnover determined using the Taner method (19) (compare with Fig. 2C). (C) Proportion of variance associated with the combined ∼1.3- and ∼2.6-My cycles for turnover as in A compared with the same proportions for the component HMM speciation and extinction time series (i.e., those illustrated in Fig. 4 C and F; corresponding EPSA results are shown in Fig. S5 D and E).

Although the grand cycles are expected to have influenced Paleozoic climate, the tempo of the Milankovitch cycles for this distant time interval cannot be predicted reliably from theory (9). This study suggests the existence of a 2:1 resonance of the grand cycles as is observed in the Late Cenozoic. These 2.6- and 1.3-My cycles emerge from time series derived from a single HMM (our key result) (Figs. 2 C and D and 3 A and B and Fig. S5A) and from averaging of many HMMs (Supporting Information and Fig. S5B). They are evident in time series based on raw probabilities (Supporting Information and Fig. S5C), and our conclusions are, therefore, not dependent on the fitting of HMMs, although the signal is weakened somewhat by noise in comparison with the HMM time series. Furthermore, these cycles are also observed in the time series of HMM speciation and extinction analyzed separately (Fig. S5 D and E), although the 1.3-My cycle is weak in the result for speciation. Finally, our conclusions are not affected if we allow for phyletic gradualism in the graptoloid clade, even when modeled with unrealistically high levels of pseudospeciation and pseudoextinction (Supporting Information and Fig. S5F).

Discussion

The inferred transition from obliquity-dominated to eccentricity-dominated grand cycles (Figs. 2 C and D and 3) in the Late Darriwilian coincided with the peak of the Great Ordovician Biodiversification Event—the greatest expansion of global biodiversity in the history of life—and the onset of the first cooling event in the transition from greenhouse to icehouse climate (31). It also coincided with a major reorganization of the graptoloid clade. Before this time, the families Dichograptidae, Sigmagraptidae, and Isograptidae dominated (assemblage A in Fig. 2A); during the Darriwilian, the families Dicranograptidae, Diplograptidae, and Normalograptidae originated and along with the Climacograptidae and Glossograptidae, came to dominate during the later Ordovician (assemblage B in Fig. 2A). The faunal transition resulted in a change in general colony design from dominantly multibranched, uniserial, and spreading colonies, giving a low density of zooids per unit volume of water, to dominantly compact colonies composed of two branches growing back to back, giving a high density of zooids per unit volume of water. The ecological and functional significance of this transition in gross colony form is uncertain, although it would have affected feeding efficiency and probably, life mode of the colony (22). The faunal transition coincides with the widespread change in the marine pelagic environment resulting from global cooling and development of strong latitudinal temperature gradients in the Late Ordovician (32, 33).

An even more dramatic reorganization of the graptoloid clade accompanied the mass depletion in the Late Ordovician, during which there was a 77% drop in graptolite species richness driven largely by a drop in speciation rate in the Late Katian and a spike in extinction rate in the Hirnantian [Hirnantian mass extinction (HME)] (16, 17). At this time, just one group of three families comprising the Neograptina survived to give rise to the Silurian diversity, which expanded rapidly to reach species richness levels comparable with those in the Ordovician (assemblage C in Fig. 2A). Although the HME was selective for depth facies and taxonomic groups (34) and species age (17), it was not selective with respect to morphology (35). The range of colony designs in the Silurian includes several that mimic the Ordovician designs, but interpretation of the largest group, the monograptids, is uncertain, as there are no convincing ecological models for their feeding efficiency.

It seems, therefore, that Darriwilian reorganization of the graptoloids might well have been adaptive and related directly or indirectly to progressively changing global climatic conditions that were themselves related in some way to the transition from obliquity- to eccentricity-dominated grand cycles. In contrast, graptoloid reorganization that accompanied the HME resulted from a mass extinction associated with rapid environmental change, although the role of Milankovitch cycles in forcing this rapid change remains unclear. In addition to these major transitions, this analysis shows that, throughout the entire lifespan of the graptoloid clade, species turnover was driven in part by fluctuations in climatic volatility related to the Milankovitch grand cycles.

During the Late Cenozoic, long-period mammalian turnover pulses coincided with 1.2-My obliquity and 2.4-My eccentricity nodes in the theoretical astronomical solution (6, 9) during times of minimum variability in insolation that were associated with global cooling and ice sheet expansion. We cannot determine the phase relationship between the Paleozoic grand cycles in graptolite turnover and astronomical forcing, since accurate astronomical solutions are not available for the Ordovician and Silurian. Integration of the graptolite species turnover results with climate proxy time series, however, would allow phase relationships between climate volatility at the scale of the grand cycles and graptoloid turnover to be determined.

We cannot say with certainty whether the observed cyclicity in graptoloid species turnover is driven more by speciation or extinction. Correlations between both processes and turnover are about the same, suggesting that they are equally important in driving turnover, and speciation and extinction are themselves significantly cross-correlated (Pearson correlation coefficients: HMM speciation vs. turnover 0.854, P < 0.001; HMM extinction vs. turnover 0.873, P < 0.001; HMM speciation vs. extinction 0.492, P < 0.001). That said, however, separate spectral analyses of HMM speciation and extinction time series show that the grand cycles consistently explain a higher proportion of the spectral variance for extinction than origination (Fig. 3C and Fig. S5 D and E). This may suggest that extinction in the graptoloids was influenced more strongly by these astronomical cycles than speciation, although further testing is required.

Materials and Methods

Because graptoloid diversity is low at each end of the CONOP composite and stochastic errors are, therefore, large, we restrict our analyses to the interval 481–419 Ma and ignore the intervals between 491–481 and 419–411 Ma. We also remove 247 species that have been assigned a zero range in the composite—those that have first appearance age equal to the last appearance age. These species are removed because we assume that they are most likely to be rare and undersampled taxa; indeed, of the 247 zero-range species, 210 are known from a single section only, and nearly all of the rest are known from just two sections, where a section is an outcrop or core from which species have been identified from one or more rock layers. In contrast, the remaining species are found in an average of 5.5 sections each. Our final composite contains 1,794 species with range ends that are resolved to 1,902 distinct levels (time horizons). The average spacing of CONOP levels in time is 0.033 My, and the median is 0.012 My. Because uneven spacing of levels hampers interpretation of extinction and speciation probabilities used here, we move speciation and extinction events at each of the CONOP-derived levels onto a series of 0.05-My-spaced “pseudolevels.”

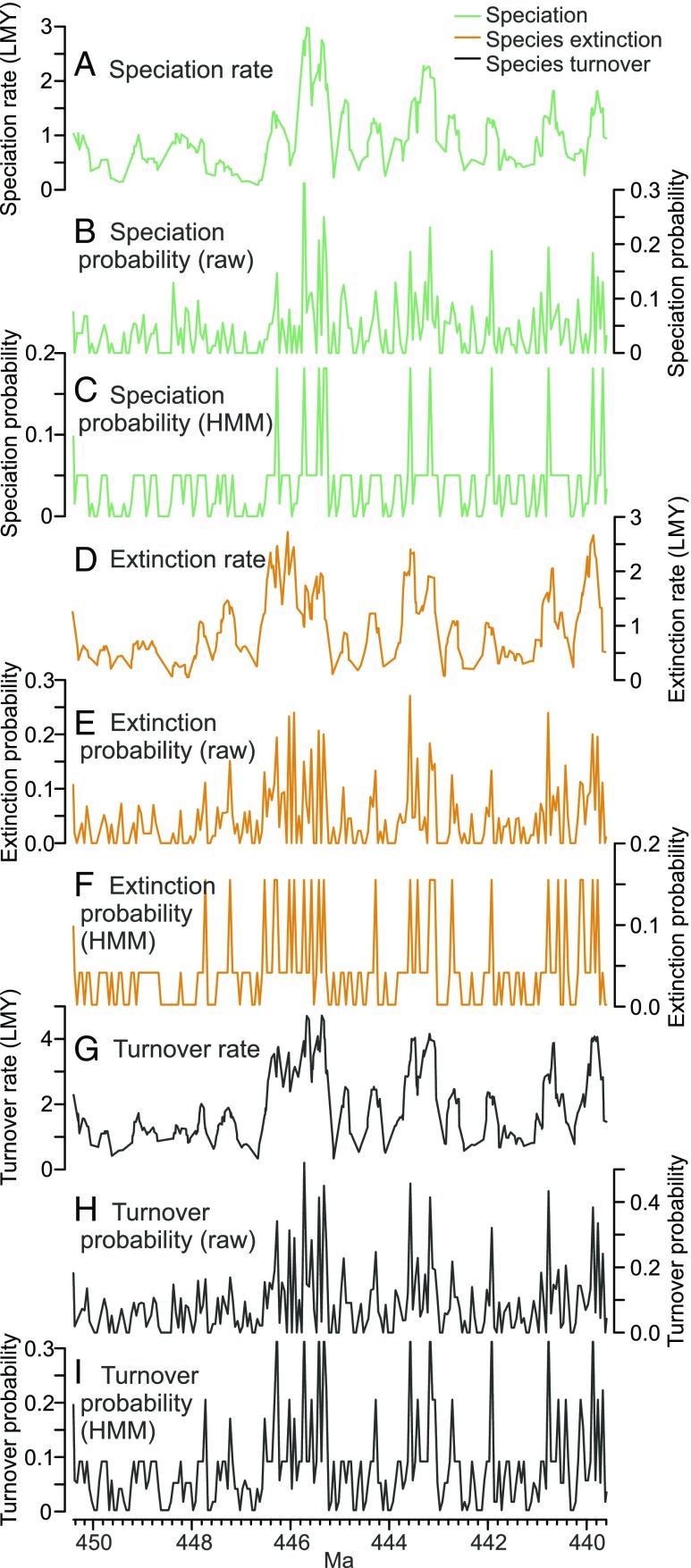
To extract high-resolution macroevolutionary time series, we have used discrete time HMMs (30) to identify a parsimonious set of discrete speciation and extinction probability states in the data and to predict time series of those states given the observations. “Raw” speciation and extinction probabilities are calculated as the number of speciations or species extinctions at each pseudolevel, respectively, divided by the number of species extant at each level (Supporting Information). The use of HMMs reduces stochastic noise in the signal and avoids loss of resolution that would result from use of coarser time bins as required by standard macroevolutionary rate metrics or use of moving window metrics and the resultant imposed autocorrelation. In particular, because of the limited numbers of speciations and/or extinctions at each pseudolevel, the raw probabilities are expected to be noisy; HMMs are an effective tool for change point analysis and can be used to determine whether abrupt changes in the time series exceed the noise and should be considered meaningful or not. As implemented here, the HMMs assume that the observed process obeys a binomial distribution, where the number of “successes” at each pseudolevel is the number of speciations or extinctions and the number of Bernoulli trials is the total number of species crossing that level. For the results presented here, we have calculated species turnover as the sum of HMM speciation-state probability and extinction-state probability at each pseudolevel. Relationships between different rate and probability metrics, for a short segment of our time series, are illustrated in Fig. 4, which shows the smoothed per lineage million years rates (18), the raw speciation and extinction probabilities at each pseudolevel, the HMM speciation and extinction probability states at each pseudolevel, and the resulting turnover time series.

Fig. 4.

Segment of time series of graptoloid speciation, extinction, and turnover rates and probabilities calculated in different ways to illustrate the methods adopted here and relationships between the time series. Because of the high resolution of our data, we do not illustrate the complete time series, which can instead be retrieved with the Supporting Information. (A and D) Speciation and species extinction rates per lineage million years (LMY) (18) calculated using a 0.25-My moving window centered at each level in the CONOP composite. (B and E) Raw speciation and species extinction probabilities calculated at each pseudolevel as the number of speciations or extinctions divided by the number of species extant. (C and F) Speciation and species extinction probabilities derived from four-state and three-state HMMs of speciation and extinction, respectively, and based on the time series shown in B and E. (G) Species turnover rate per LMY calculated as the sum of speciation and extinction rates shown in A and D. (H) Raw species turnover probability calculated as the sum of time series shown in B and E. (I) Species turnover probability calculated as the sum of the HMM probabilities shown in C and F. This is part of the default HMM turnover probability series used for the analyses in Fig. 2 C and D and other key results discussed throughout this study.

We test for candidate grand cycles in the resultant graptoloid HMM turnover record using multitaper method (36) spectral techniques, which permit a robust assessment of the variance in turnover that is associated with the grand cycles. In addition, temporal evolution of potential grand cycles is evaluated using Evolutive Power Spectral Analysis (EPSA) (37), Evolutive Harmonic Analysis (EHA) (38), and Taner bandpass filtering (19). EPSA and EHA utilize three 2π prolate tapers with a 20-My moving window, and a linear trend is removed from each window before analysis. During spectral analysis, we use Monte Carlo simulation of stochastic surrogates, which have the same sampling characteristics and noise model parameters as observed in the data, to assess the suitability of particular background noise models (autoregressive lag-1 and power law models) in the estimation of statistical significance. These tests use a range of standard spectral methods and identify particular background estimation approaches that are optimal for our data. At the same time, we apply several multiple statistical test corrections to protect against inflated false-positive rates that result from the simultaneous testing of many null hypotheses at different spectral frequencies. Again, given dependence of false-positive rates on the noise model used, the multiple test corrections are evaluated using surrogate simulations. During estimation of statistical significance, we investigate specific frequency bands of interest that are relevant to the grand cycles but also present “global” confidence limits. Results of these tests will be specific to any given dataset: for example, we use the age-scaled CONOP time series; in contrast, the use of more normal depth-scaled data may require the investigator to prospect across a wider range of frequencies than tested here. To facilitate broader application of these approaches, we provide a series of functions in the open source software used here for time series analysis (see below).

Significance levels of correlation coefficients between different time series are evaluated using the phase randomized surrogate approach (39) for serially correlated data.

All of these analyses were undertaken in the R language for statistical computing (40). Details of data manipulation, HMM-fitting procedures, time series analyses, and sensitivity analyses are presented in Supporting Information along with the data and R code used to generate the analyses.