Cochlear amplification and tuning depend on the cellular arrangement within the organ of Corti

Significance

While the near-crystalline structure of the organ-of-Corti cytoarchitecture in the mammalian cochlea has been known for some time, its functional consequences on hearing remain to be established. The present computational-modeling studies show that individual outer hair cells (OHCs) can work together to produce high hearing sensitivity and frequency selectivity because of the overlapping asymmetrical Y-shaped structures that they form with the Deiters’ cells (DCs) and phalangeal processes (PhPs). Altering the geometry and material properties of these structures reveals that all three components have a profound effect on basilar-membrane and reticular-lamina amplification and tuning. One implication is that the DCs and PhPs are not just supporting structures, but that they must also be properly restored in emerging therapies to regenerate OHCs.

Abstract

The field of cochlear mechanics has been undergoing a revolution due to recent findings made possible by advancements in measurement techniques. While it has long been assumed that basilar-membrane (BM) motion is the most important determinant of sound transduction by the inner hair cells (IHCs), it turns out that other parts of the sensory epithelium closer to the IHCs, such as the reticular lamina (RL), move with significantly greater amplitude for weaker sounds. It has not been established how these findings are related to the complex cytoarchitecture of the organ of Corti between the BM and RL, which is composed of a lattice of asymmetric Y-shaped elements, each consisting of a basally slanted outer hair cell (OHC), an apically slanted phalangeal process (PhP), and a supporting Deiters’ cell (DC). Here, a computational model of the mouse cochlea supports the hypothesis that the OHC micromotors require this Y-shaped geometry for their contribution to the exquisite sensitivity and frequency selectivity of the mammalian cochlea. By varying only the OHC gain parameter, the model can reproduce measurements of BM and RL gain and tuning for a variety of input sound levels. Malformations such as reversing the orientations of the OHCs and PhPs or removing the PhPs altogether greatly reduce the effectiveness of the OHC motors. These results imply that the DCs and PhPs must be properly accounted for in emerging OHC regeneration therapies.

Classical models of the cochlea have focused on basilar membrane (BM) mechanics, because the BM is subjected to the hydrodynamic pressure gradient between the cochlear scalae. According to the more than 100-y-old ter Kuile model (1), the excitations of the outer and inner hair cells (OHCs and IHCs) occur by a simple geometrical transformation of BM motion. Recent measurements show, however, that vibrations of the reticular lamina (RL) and the tectorial membrane (TM) are significantly different from those of the BM (2, 3). These results are transforming our conception of the relative motions within the organ of Corti (OoC). Because the RL is closer to the stereocilia bundles of the hair cells, these results demonstrate that just knowing the BM motion is insufficient both for understanding what drives the IHCs and for understanding the hearing process (4, 5).

Scanning electron microscopy and other imaging methods have shown that the complex and highly organized cytoarchitecture of the OoC features a repeating pattern of asymmetrical Y-shaped elements between the RL and BM along the cochlear length from base to apex (Fig. 1). Each Y-shaped element consists of a Deiters’ cell (DC) that rises up from the BM and splits into an apically oriented phalangeal process (PhP) and an attached basally oriented OHC, both of which extend toward the RL and attach to it at different locations. The OHCs, the biological micromotors of the inner ear, exhibit a well-characterized piezoelectric-like property that enables each OHC to produce a force in response to the stimulation of its stereocilia hair bundle (HB) (6, 7). However, the contribution of the mechanically passive cells (i.e., the DCs and their corresponding PhPs) in BM and RL amplification is not fully understood. We hypothesize that the Y-shaped elements of the OoC cytoarchitecture are a basic building block for BM and RL amplification and play a key role in the relative motion between the BM and RL.

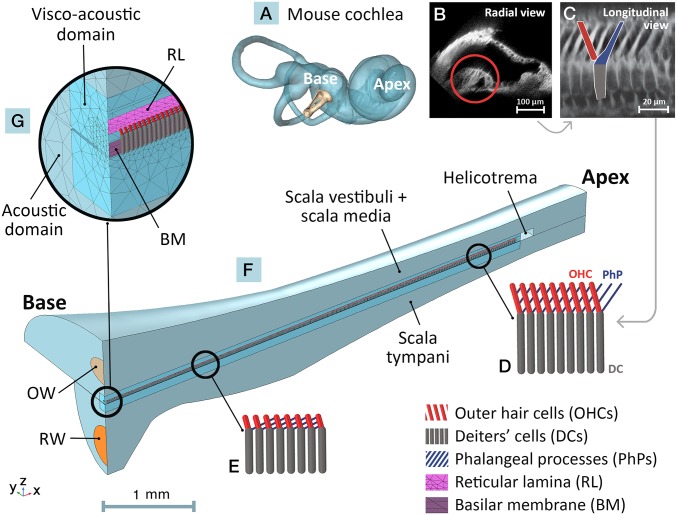
Fig. 1.

Depictions of mouse cochlear anatomy (A–C) and corresponding structures in the FE model (D–G). (A) Reconstructed mouse inner ear from µCT imaging. The base and apex of the coiled cochlea are indicated along with the stapes at the oval window (OW). (B) A two-photon image of a radial cross section of the mouse scala media, with the OoC circled. (C) A longitudinal OoC cross-section showing the overlapping Y-shaped cytoarchitectural elements. A single element composed of a DC (gray), a basally oriented OHC (red), and an apically oriented PhP (blue) is outlined. The dimensions and longitudinal orientations of the Y-shaped elements vary along the BM length (10), as indicated by beam representations for sample apical (D) and basal (E) regions. (F) The FE model of the uncoiled mouse cochlea, spanning from base to apex, consisting of the scala vestibuli (including the scala-media) and scala tympani fluid chambers joined at the apical end by the helicotrema opening. Input sound passes through the OW and the round window (RW) is represented by a flexible membrane. The longitudinal, radial, and transverse directions correspond to the x, y, and z axes, respectively. (G) The fluid chambers are divided into near-field viscoacoustic domains (close to the RL and BM, taking viscosity of the fluid into account) and far-field acoustic domains (neglecting fluid viscosity). A single row of overlapping Y-shaped elements is sandwiched between the RL and BM in the model.

In a number of animals, including moles of genus Talpa (8), mole rats (9), mice (10), horseshoe bats (11), gerbils (12), and humans (13), it has been shown that the PhPs are always tilted toward the apex and the OHCs are always tilted toward the base. The frame of the Y-shaped elements, with two connections at the RL and one at the BM, adds both transverse and longitudinal coupling between the BM and RL [cf. braced frames in construction (14)]. Across different animals, the number of OHCs that one PhP spans across varies from 3 (rows 1 and 2) to 1 (row 3) in the mouse (10), 4 to 5 in the mole rat (9), and even up to 12 in moles of genus Talpa (8). The role that the PhPs play in the sensitivity and frequency selectivity of hearing in animals with different frequency ranges of hearing is not known.

Finite-element (FE) modeling, when rooted in realistic anatomy, material properties, and mechanics, can facilitate the analysis and interpretation of experimental measurements and offer predictions and insights regarding the function of the OoC. In the present work, we aim to understand the mechanisms that support the high sensitivity, high frequency resolution, and wide bandwidth (BW) of normal hearing. We hypothesize that such sophisticated function critically depends not only on the OHCs themselves but also on their specific arrangement within the structures of the OoC. To test this, we developed a full-length FE model of the mouse cochlea that explicitly incorporates the cytoarchitectural geometries of the OHCs, DCs, and PhPs, which were recently quantified using a two-photon imaging approach (10). This “baseline” model has been tested against two sets of recent experimental measurements of BM and RL vibrations from the 10-kHz apical region (2) and 48-kHz basal region (3). In addition, the model is able to generate stimulus-frequency otoacoustic emissions that are comparable with experimental measurements (15). In contrast to earlier work that used an asymptotic method (16, 17), in which algebraic expressions were formulated for the “feed-forward” and “feed-backward” mechanisms of the Y-shaped structures, in the present model the geometry is incorporated directly.

As there are no known mutations that change the orientation and geometry of the Y-shaped elements, we used the baseline model as a “numerical genetics laboratory” by making a series of changes to the geometry and material properties of the Y-shaped structures, so as to evaluate the extent to which normal BM and RL tuning and amplification depend upon the natural arrangement of the Y-shaped elements. The geometric alterations to the repeating and overlapping Y-shaped structures include (i) flipping the orientation of the OHCs and PhPs so that the OHCs are oriented apically and the PhPs are oriented basally, (ii) deleting the PhPs altogether, and (iii) altering the PhP length and angle, which changes the number of OHCs that each PhP spans across. We also performed sensitivity analyses of the material properties by increasing and decreasing the Young’s moduli (stiffnesses) of the OHCs, DCs, PhPs, and RL. This modeling study provides a first step toward understanding the implications of the OoC cytoarchitecture on cochlear amplification and tuning and has far-reaching implications for emerging regeneration methods that aim to restore in vivo OHC function but not necessarily the normal cytoarchitecture of the OoC.

Results

Testing the Baseline Model Against Physiological Measurements.

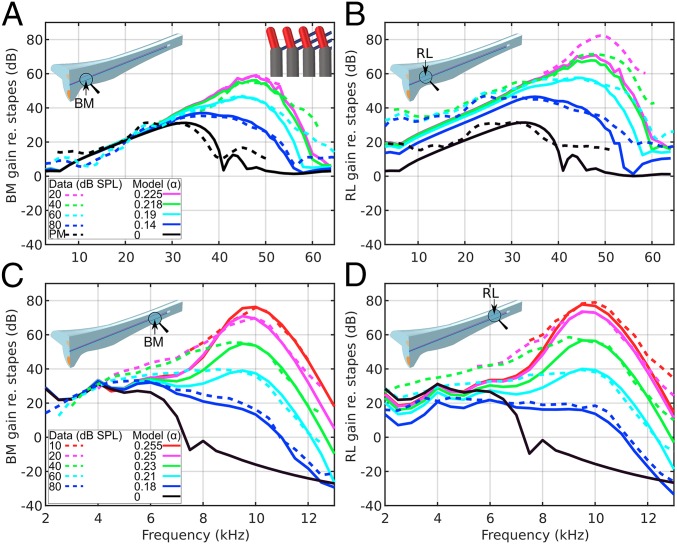
By varying only the OHC gain-factor value α, the FE model of the uncoiled mouse cochlea (Fig. 1 and Methods) produces RL and BM velocities (normalized by the oval-window input velocity) that are generally consistent with the magnitude of measured motions from the basal (Fig. 2 A and B) and apical (Fig. 2 C and D) regions (normalized by the middle-ear motion). In the basal region, the postmortem BM motion has a broad peak of ∼30 dB near 35 kHz (Fig. 2A, black lines). For the 20-dB sound pressure level (SPL) input (α = 0.225), the peak increases by 30 dB and approaches the best frequency (BF) of 48 kHz, and the BW of the response becomes narrower (Fig. 2A, magenta lines). The experimental data for input levels of 40, 60, and 80 dB SPL are reproduced by the model with lower α values. For input frequencies below 30 kHz, the gains are similar for all input levels.

Fig. 2.

BM (A and C) and RL (B and D) vibration data from the cochlear base (A and B, 48 kHz; ref. 3) and apex (C and D, 10 kHz; ref. 2), measured in response to different input intensities (dashed lines), are compared against model results with different OHC gain-factor values α (solid lines). The model results were obtained on the BM and RL at the locations indicated by arrows. The model with α = 0 is compared with postmortem (PM) data. In the baseline model, each PhP spans across three OHCs, indicated by an inset in the top right of A.

A new set of α gain factors reproduces the experimental BM data at the apex (Fig. 2C). For an input level of 80 dB SPL (model α = 0.18), the BM has a broad peak of ∼30 dB near 4–6 kHz (Fig. 2C, blue lines). For the 10-dB SPL input level (α = 0.255), the peak increases by 45 dB and approaches the BF of 10 kHz with a narrower BW (Fig. 2C, red lines). The experimental data for input levels of 20, 40, and 60 dB SPL are reproduced by the model with lower α values. For input frequencies below about 4 kHz, the gains for all input levels are similar.

Similar to the BM, lower stimulus levels cause the RL gain to increase and the BF peaks to shift to higher frequencies, in both the basal and apical regions. However, unlike the BM, which exhibits linear regions below 30 kHz at the base and 5 kHz at the apex (Fig. 2 A and C, respectively), where all curves merge regardless of input level, the RL exhibits level-dependent gain in these regions. This model demonstrates RL gain below BF consistent with measurements (Fig. 2 B and D). In addition, whereas the basal results show that RL motion is higher (for active cases) than the corresponding BM motion (by more than 10 dB at the 48-kHz BF for a 20-dB SPL input), in the apical region the RL/BM motion ratio decreases from 2 dB to −10 dB when the input changes from 10-dB SPL (Fig. 2 C and D, red lines at 10 kHz) to 80-dB SPL (Fig. 2 C and D, blue lines at 6 kHz).

At 10-kHz and 10-dB SPL (the lowest reported level), the BM and RL Q_{3 dB} values in Lee et al. (2) were 11.7 and 9.0, respectively, versus 9.1 and 9.6 in the present model. At 48-kHz and 20-dB SPL (the lowest reported level), the BM and RL Q_{3 dB} values in Ren et al. (3) were 6.7 and 9.1, respectively, versus 8.8 and 8.0 in the present model.

The model shows a sharper phase roll-off than the experimental data, and the phase decay increases as the gain factor α increases (Fig. S1). The measured BM and RL motions are nearly in phase at low frequencies (Fig. S1 C and D, dashed lines), whereas at high frequencies there are significant phase differences (Fig. S1 A and B, dashed lines). However, the active models show that the BM and RL differ by approximately one-half cycle up to BF for high (Fig. 1 A and B, solid lines) and low frequencies (Fig. 1 C and D, solid lines). These phase relationships can be observed in the traveling wave near BF on the BM and RL, at the base (Movie S1) and apex (Movie S2), consistent with measurements made at the mouse apex (movie S1 in ref. 18).

Flipping the Orientation of the OHCs and PhPs.

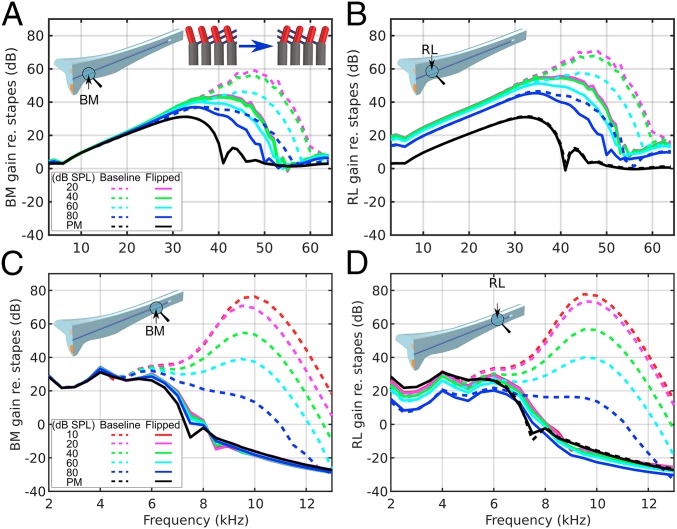
To evaluate the significance of the natural orientations of the OHCs and PhPs, we “flipped” the OHCs and PhPs about the y–z plane of the DCs (Fig. 1F) and compare (Fig. 3) the resultant tuning characteristics (solid lines) with the baseline results (dashed lines). Both the BM and RL gains are significantly reduced, but more dramatically at the apex (Fig. 3 C and D) than at the base (Fig. 3 A and B). The basal results still show amplification, although with broader peaks, lower gain, and a smaller BF shift from the passive to active cases (approximately one-third octave compared with one-half octave in the baseline model). The basal RL motion is still higher than the BM for all nonzero α values, however, and it keeps the level-dependent gain below 30 kHz (Fig. 3B). At the apex, there is almost no BM amplification, and all active cases (α > 0) resemble the passive response (α = 0), with most deviations around the 7.5-kHz notch (Fig. 3C). Similar to the baseline results, the apical RL gain shows level-dependent compression below 5 kHz (Fig. 3D).

Fig. 3.

Comparison of model vibration results between the baseline (dashed lines) and a version with flipped OHCs and PhPs (solid lines) for the BM (A and C) and RL (B and D) at the cochlear base (A and B) and apex (C and D). The BM and RL gains are reduced most dramatically at the apex. An inset in the top right of A shows the alteration of the Y-shaped elements by flipping the OHCs and PhPs. The Fig. 2 legend lists the corresponding α values.

The spatial response of the BM in the long-wave region (i.e., when the phase is between 0 and −0.5 cycles in Fig. S2B) at different frequencies, with fixed α = 0.23 (corresponding to 20- and 40-dB SPL at the basal and apical locations, respectively), is largely unaffected by flipping the OHCs and PhPs (Fig. S2A, solid and dashed lines). However, in the BF short-wave region (i.e., where the phase decreases rapidly in Fig. S2B, in the vicinity of the star symbols), lower gains are produced in the altered model (solid lines), which can also be observed in the traveling wave at the base (Movie S3) and apex (Movie S4). All of the phase responses plateau with fewer cycles than the baseline response (Fig. S2B).

Deleting the PhPs.

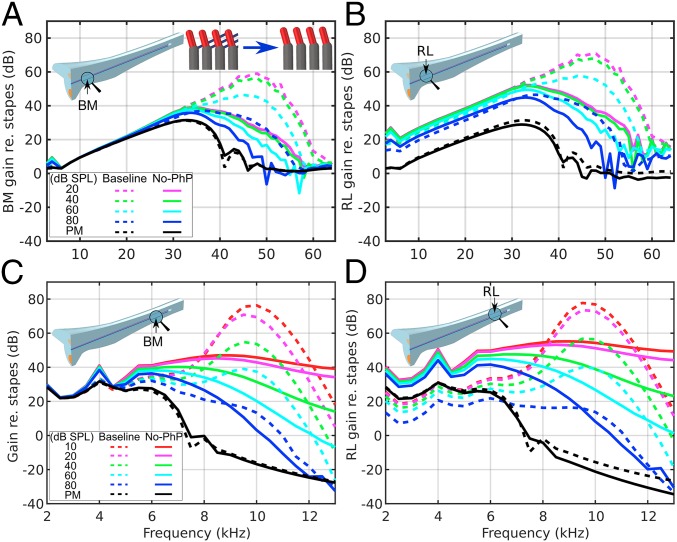
For a second alteration (Fig. 4), we deleted the PhPs (solid lines) and compare the results to the baseline model (dashed lines) to evaluate their role in the tuning characteristics. Deleting the PhPs, similar to flipping the OHCs and PhPs, significantly reduces both the BM and RL gains (Fig. 4). The basal responses still have amplification, although with broader peaks, lower gains, and almost no BF shift (Fig. 4 A and B). The RL motion is still generally higher than the BM motion for all nonzero α values, and it keeps the level-dependent gain compression below 30 kHz (Fig. 4B). At the apex (Fig. 4 C and D), unlike when swapping the orientations of the OHCs and PhPs, the gain responses still increase when α is increased, with broad peaks. The RL motion is always higher than the BM motion, with a difference of about 10 dB at frequencies below 6 kHz.

Fig. 4.

Comparison of model vibration results between the baseline (dashed lines) and a version with deleted PhPs (solid lines) for the BM (A and C) and RL (B and D) at the cochlear base (A and B) and apex (C and D). In this case the BM and RL gains are reduced more significantly at the base. At the base the peaks do not shift to higher frequencies, whereas at the apex the peaks are very broad. An inset in A shows the alteration of the Y-shaped elements by deleting the PhPs. The Fig. 2 legend lists the corresponding α values.

Similar to the spatial responses after flipping the OHCs and PhPs (Fig. S2), deleting the PhPs does not affect the long-wave region but does affect the short-wave region (Fig. S3A), causing lower gains and broader tuning, which can also be observed in the traveling wave at the base (Movie S5) and apex (Movie S6). The spatial responses often show noisy behavior above BF on the apical side. The phase rolls off similarly to the baseline around the BF locations (Fig. S3B).

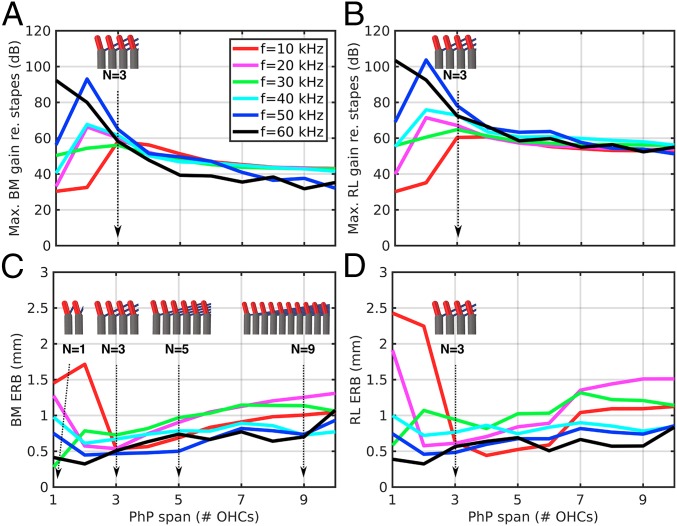
Changing the PhP Span.

For the third alteration (Fig. 5), we varied from 1 to 10 the number of OHCs that the PhPs extend across, which we refer to as the “span number” (N). Instead of plotting frequency–response tuning curves, we summarize these results by comparing the maximum gain and equivalent rectangular bandwidth (ERB), which is similar to the critical BW as a measure of the sharpness of the peak, as a function of N, for a constant OHC gain factor of α = 0.23.

Fig. 5.

The effects of the PhP span on the maximum gain (A and B) and ERB (C and D) of the BM (A and C) and RL (B and D) model vibrations. The lengths and angles of the PhPs are varied such that the number of OHCs that one PhP spans across varies from 1 to 10. The inset figures show the configuration of the Y-shaped elements for different Ns.

The gain maxima and ERBs for both the BM and RL are dependent on frequency and N. At low spans of 1 and 2, higher frequencies have higher gain maxima and narrower ERBs (Fig. 5, black and blue lines). Lower frequencies conversely exhibit lower gain maxima and wider ERBs (red, magenta, green, and cyan lines). The BM gain maxima generally converge at n = 3 for the baseline model, to about 60 dB, and reach a minimum ERB of 0.5–0.7 mm (Fig. 5 A and C). Above this N, the gain maxima decrease and the ERBs generally increase. The RL gain maxima show similar converging behavior at n = 3 (60–78 dB) and a general decrease for n > 3 (Fig. 5B). The ERBs are generally higher (i.e., with broader peaks) for the RL.

Changing OoC Material Properties.

We performed sensitivity analyses on the stiffness of individual OoC components by separately varying the Young’s moduli of the OHCs (E_OHC), DCs (E_DC), PhPs (E_PhP), and RL (E_RL) by several orders of magnitude (Fig. S4). These parameters contribute to the stiffness of the individual model components, as well as to the overall longitudinal stiffness of the OoC due to the mechanical coupling of the Y-shaped structures across multiple OHCs.

The BM and RL gain maxima are functions of E_OHC up to ∼10 MPa (Fig. S4 A and B), but above that the gain decreases and converges toward the passive case (dashed gray lines) for all input frequencies (i.e., amplification goes away). This indicates that the OHC motility force is not strong enough to expand stiffer OHCs to produce amplification. For uniform gain across frequencies, E_OHC should decrease monotonically from base to apex. This variation, accompanied by the changes of the length and diameter of the OHCs along the cochlear length, produces a decreasing stiffness gradient from base to apex, similar to the stiffness gradient of the BM.

The BM and RL gain maxima are also affected by E_PhP and E_DC (Fig. S4 C–F), but less dramatically than by E_OHC. The BM and RL gain maxima are not very sensitive to E_PhP and E_DC from 4 to 100 MPa, over which they converge into a narrow band of 55–60 and 60–70 dB, respectively. DCs softer than 1 MPa result in significant loss of gain (Fig. S4 E and F). However, PhPs or DCs stiffer than 100 MPa result in gains that depend on frequency.

A more complicated relationship is observed for E_RL (Fig. S4 G and H). At 10 kHz, the BM gain has a peak around 0.1 MPa then decreases toward the passive response (Fig. S4G, red line). The other frequencies maintain more gain until E_RL reaches 100 MPa, at which point the BM and RL gain maxima reduce dramatically. This is because the Y-shaped elements are sandwiched between two stiff membranes in that case, both the BM and the RL, such that the OHCs cannot push them apart to generate amplification.

Sensitivity analyses were also performed for the altered models (i.e., the cases with flipped OHCs and PhPs, and deleted PhPs). Through the course of these analyses we were not able to find parameters that resulted in BM and RL gains and BWs similar to measured data (see Supporting Information for a summary). This further strengthens the argument for the importance of the natural arrangement of the Y-shaped elements.

Discussion

Model Development and Testing.

The FE model of the mouse cochlea was developed as a numerical laboratory to test the hypothesis that the asymmetrical Y-shaped elements are necessary for amplification and sharp tuning. With a single anatomical configuration (Fig. 1) and corresponding material properties (Table S1), the adjustment of a single parameter representing the OHC gain factor (α) allows the model to reproduce RL and BM motion measurements (Fig. 2) from the apical (10 kHz) and basal (48 kHz) BF locations in response to input levels ranging from 10- to 80-dB SPL (2, 3). This agreement with measurements is achieved through the asymmetrical arrangement of the OoC cytoarchitecture in the baseline model (Fig. 1).

A striking feature of the model results and measurements is that the RL motion is typically greater than the BM motion (Fig. 2). The main exception to this is for input levels higher than 40-dB SPL in the apical region (Fig. 2 C and D). As has been shown previously in several species (19–21), the BM gain becomes level-independent, without compression, about one octave below BF (Fig. 2 A and C). However, the RL gain continues to be a function of input level even below BF, indicating some degree of compression (Fig. 2 B and D). These results are consistent with the enhancement of auditory-nerve responses by active processes several octaves below BF, as shown by their inhibition from medial-efferent activity (22) and suppression by high-level, low-frequency “bias” tones (23). Since the excitation of the OHCs (and also the IHCs) is a function of the deflection of their HBs, which are in close proximity to the RL, these results suggest the possibility of yet-to-be-discovered excitation mechanisms that depend on input level and frequency.

Alterations to the Y-Shaped Structures.

Flipping the OHCs and PhPs or deleting the PhPs demonstrates that cochlear amplification in the baseline model depends on basally oriented OHCs with axial motor forces and apically oriented PhPs. These results suggest that the DCs and PhPs are not just supporting structures but are essential for cochlear function.

When the OHCs and PhPs are flipped, the OHC forces become apically oriented and thus cannot efficiently boost the traveling wave. The situation is worse at the apex because there is no gain. At the base, there is some gain, but still less than the baseline response (Fig. S2, blue and black solid lines).

With no PhPs, the gain is reduced from the baseline (Fig. S3). However, compared with the passive case there is some gain with broad peaks (Fig. 4, PM) due to the basally oriented OHC axial forces. The lack of anchoring by the PhPs leads to more motion at the OHC–DC junctions and less coupling of the OHC forces to the RL and BM (Movies S5 and S6, Bottom), which thus produces less amplification. Similar, but smaller, motions at the OHC–DC junctions are seen in the baseline model as well (Movies S4 and S6, Top), which may be related to phenomena reported as “hot spots” in the gerbil OoC hook region (24).

Increasing N beyond the normal baseline case of three OHCs (N = 3) has a deleterious effect on the maximum gain (Fig. 5 A and B) and sharpness of tuning (ERB; Fig. 5 C and D) of the BM and RL. However, the behavior is very different for the N = 1 and 2 cases, with the effect on the gain and sharpness of tuning being frequency-dependent. This indicates that for the mouse the trade-off between gain and sharpness is relatively uniform for all frequencies when the PhPs span across 3 OHCs, which is consistent with anatomical measurements of the PhP span from the first two rows of Y-shaped structures (10).

Longitudinal Coupling.

An implication of the present analyses is that the longitudinal coupling of forces in the forward and backward directions in the OoC, due to the cross-bracing arrangement of the Y-shaped structures, appears to play a critical role in OoC amplification and the sharpness of auditory-nerve tuning, and could have possible consequences for speech and music processing by the OoC. Since the intercellular distance between the Y-shaped elements in the model is 8 µm from base to apex and one PhP spans across three OHCs, the longitudinal-coupling distance for a Y-shaped element in the forward direction is ∼24 µm. Because the overlapping Y-shaped elements are coupled through the RL and BM stiffness in both the forward and reverse directions, however, the overall longitudinal reach is estimated to be 48 µm. The wavelength of the BM and RL traveling wave near BF (in the short-wave region) is presently calculated to be 80–100 µm for all frequencies tested for the active case, which is close to twice the longitudinal-coupling distance of the Y-shaped structures. The relationship between these lengths is critical for amplification because it leads to phase differences in the basally oriented OHC forces relative to the apically oriented PhP forces.

It has been shown that the TM exhibits wave motion and longitudinal coupling (25, 26). The TM wavelength was estimated to be 415 and 560 µm at 3.5 and 18 kHz, respectively, within an isolated passive mouse TM. In the present passive model, the RL and BM wavelengths are calculated to be in the 800- to 2,000-µm range, for input frequencies from 60 to 10 kHz, which is nearly two to four times longer. Sandwiched between the TM and RL are the stiff HBs of the OHCs that deflect due to radial shearing motion arising from transverse motion of the TM and RL. The present formulation does not take into account possible sharpening effects of the TM on RL and BM motions.

RL–BM Phase Difference.

Active force production by in situ OHCs should generally result in the RL’s and BM’s being one-half cycle out of phase. The model calculations show that this phase difference is one-half cycle at low frequencies but that it decreases to about 0.35 cycles at 48 kHz near BF for an orthogonal measurement beam (Fig. S5, black line). The measured RL–BM phase difference has been reported to be about one-half cycle at low frequencies, but it decreases to 0 at the 48-kHz BF (3). However, the angle of the measurement beam between the RL and BM was not reported.

We test the hypothesis that this discrepancy between the model and measurements could be due to a nonorthogonal measurement-beam angle of the optical probe (Fig. S5). For the largest angle tested (+39°, corresponding to a 40 µm or 5-OHC longitudinal deviation of the beam in the apical direction), the phase difference decreases to about 0 cycles near BF (magenta line) and approaches the measured phase data (3). Still, below BF the model RL–BM phase difference remains higher than the measured phase. It has been proposed that the measured decrease with frequency of the RL–BM phase difference is due to in part to an intrinsic OHC delay of ∼20 µs (27). In the present model the OHC gain α has no phase, but incorporating such a delay in future models could produce better agreement.

Comparison with Modeling Studies in the Literature.

Some of the earliest models of BM transverse motion incorporated forces from basally oriented OHCs coupled to DCs (28, 29). In later studies, full Y-shaped elements were formulated to add forces from apically oriented PhPs (16, 17). In both cases forward- and backward-directed forces were algebraically summed with fluid pressure, without any inertial frame of reference to push against. While those asymptotic models helped to establish the importance of these forces, motions of the RL were not considered.

FE models, in contrast, can explicitly incorporate the microanatomy of the Y-shaped elements. However, most initial attempts, as well as recent studies, have neglected the specific geometry of the OoC and often do not consider the PhPs (30, 31). A prime motivator for many of these simplifications and assumptions is to reduce computational cost. For example, many models treat the cochlear fluid as inviscid (32), which is not appropriate because a primary reason for OHC amplification is to overcome the dissipation of mechanical power due to viscous losses (17). Nam and Fettiplace (32) were the first to develop FE models incorporating the Y-shaped elements, but again with an inviscid 2D fluid formulation. In their later models, viscosity effects were replaced with additional damping in the BM (33), which is still a simplification for computational efficiency.

Limitations.

For any modeling study, judicious simplifications are a necessity. Presently, the OoC cytoarchitecture is represented by Y-shaped structures between the BM and RL in a single row, rather the typical three rows, and without a tunnel of Corti. The model does not explicitly include the TM, and thus its mechanics and subtectorial viscous losses are not incorporated. The OHC HB deflection, proportional to the shear displacement of the HBs, is assumed to be proportional to the pressure gradient across the BM according to a simplified model of OoC equilibrium (34). A constant value of α through the whole cochlear length is assumed for each input level. This invokes de Boer’s EQ-NL theorem that an equivalent linear model corresponding to each OHC gain factor can represent the nonlinear function of the cochlea (35). The theorem as originally formulated is valid for a white-noise input that effectively linearizes an otherwise nonlinear system, although in the present case it is assumed to remain valid for sinusoidal inputs. The microanatomy of the Y-shaped structures is represented as beam elements without fluid interaction, which underestimates viscous losses. The alternative is to use 3D elements, but this ends up causing a large increase in computational cost that would have made running the simulations impractical. While the anatomical parameters of the Y-shaped elements were recently measured (10), not all of the material properties are well characterized, and thus some parameters, especially the Young’s moduli, have been chosen based on a priori estimates (36) followed by sensitivity analyses (Fig. S4).

When active amplification occurs in the model, the wavelength of the traveling wave becomes short near BF, which results in a sharper phase roll-off compared with measurements (Figs. S2 and S3, dashed lines). This phase discrepancy has been seen in other modeling studies as well (16, 17, 33, 34) and continues to be an active area of investigation toward further improving cochlear models. Possible areas for improvement include accounting for the arch-shaped cross-section of the pectinate zone of the mouse BM (37), the phase delay of OHC activity (27), and TM viscoelastic behavior (25, 26, 38), none of which have been implemented in this model. It has been shown that power generation from OHC motility has an approximately linear dependence on the wavenumber (17), so the steeper phase in the model indicates greater power generation by approximately a factor of four according to a previous estimate (17).

Suggestions for Future Work.

For the third row of Y-shaped structures, the longitudinal span of the PhPs is on average about 10 µm, which corresponds to a PhP span across just one OHC (N = 1). This indicates that the third row of Y-shaped structures may be capable of generating more amplification than the neighboring rows, particularly for higher frequencies (Fig. 5 A and B, black and blue lines). A full model incorporating all three rows of OHCs is needed to test the effects of PhP span when integrated across the three rows. The model can be further improved by taking into account the arched BM of the pectinate zone (37), adding an overlying viscoelastic TM, and incorporating OHC HB transduction, which should result in a more robust baseline model, from which the altered cases can also be further tested.

Implications for Regenerative Therapy.

Because mammalian OHCs do not regenerate, irreversible loss of hearing can occur due to aging, noise exposure, and other forms of cochlear insult. To remedy this, significant efforts are underway to develop therapies for regenerating OHCs. For example, McLean et al. (39) have shown that OoC supporting cells, when combined with appropriate drugs and growth factors, can differentiate into OHCs in a 3D cell-culture environment. Even if the OHCs could be regenerated in situ, however, that does not guarantee that cochlear function will return to normal. The present model suggests that the functional efficacy of the OHCs depends critically on their arrangement with respect to the connected DCs and PhPs. As such, if a strategy for restoring the OHCs fails to reconstruct the normal in situ cellular arrangement, it may prove disappointing when it comes to restoring cochlear function. For this reason, it may behoove researchers to not only verify the genetic characteristics, morphology, and physiology of restored OHCs but to also ensure that the DCs and PhPs are maintained or regenerated in close to their natural arrangement with respect to the OHCs, to fully restore cochlear function.

Methods

An FE-model representation of the uncoiled mouse cochlea was developed (Fig. 1), in which the cross-sectional areas of the scala vestibuli (including scala media) and scala tympani chambers were obtained from microcomputed tomography (μCT) measurements (40). Symmetry of the half-cochlea with respect to the x–z plane is assumed for computational efficiency for all but the cytoarchitecture (Fig. 1F). The OoC is represented by a single row of overlapping asymmetrical Y-shaped elements arranged along the longitudinal (x) direction (Fig. 1 D–F), sandwiched between the acellular BM and RL (Fig. 1G), whose varying dimensions and angles are based on measurements in mouse (Fig. 1 C–E) (10).

The cochlear fluid is divided into two domains: the viscous fluid in the vicinity of and within the OoC that interacts with the BM and RL and the inviscid fluid elsewhere that only solves for the acoustic pressure. Linear elastic shell elements are used to model the BM (orthotropic) and the RL and RW (isotropic), which interact with the fluid. For computational efficiency, the Y-shaped elements of the OoC are modeled as linear elastic beams. The material properties of the model components were defined either from data available in the literature or were adjusted by a priori estimates (36) followed by sensitivity analyses (Fig. S4).

The biological micromotor function of the OHCs is well-established (41). Prestin proteins in the OHC plasma membrane provide a piezoelectric effect, such that depolarization causes axial contraction and hyperpolarization causes axial expansion (7). In this model, the resulting compression and tension are represented by equal and opposite axial forces acting on the OHC ends. The OHC gain factor, α, is defined as the ratio of the OHC axial-output force to the HB-input shear force (Fig. S1). We adjust α from 0.255 to 0.14 to replicate experimentally measured BM responses corresponding to different stimulus levels ranging from 10- to 80-dB SPL (2). As stimulus intensity increases further, α decreases to 0 in the model, which also corresponds to the postmortem condition. Further model details are found in Supporting Information and Table S1.