The glycolipid GM1 reshapes asymmetric biomembranes and giant vesicles by curvature generation

Significance

The multifaceted involvement of GM1 as a ligand in many cellular functions has been well recognized. We find that GM1 readily desorbs from the membrane of cell-sized model biomimetic systems (giant unilamellar vesicles). The desorption is unbalanced, creating an asymmetry between the bilayer leaflets. This results in reshaping weakly curved membranes into nanotubular invaginations stabilized by the membrane spontaneous curvature, which we quantify experimentally. Computer simulations confirm the experimental results. Uncovering the role of GM1 as a fine regulator of membrane curvature broadens our perspective on its important function in reshaping neuronal membranes and emphasizes that GM1 desorption can strongly affect the cell membrane morphology.

Abstract

The ganglioside GM1 is present in neuronal membranes at elevated concentrations with an asymmetric spatial distribution. It is known to generate curvature and can be expected to strongly influence the neuron morphology. To elucidate these effects, we prepared giant vesicles with GM1 predominantly present in one leaflet of the membrane, mimicking the asymmetric GM1 distribution in neuronal membranes. Based on pulling inward and outward tubes, we developed a technique that allowed the direct measurement of the membrane spontaneous curvature. Using vesicle electroporation and fluorescence intensity analysis, we were able to quantify the GM1 asymmetry across the membrane and to subsequently estimate the local curvature generated by the molecule in the bilayer. Molecular-dynamics simulations confirm the experimentally determined dependence of the membrane spontaneous curvature as a function of GM1 asymmetry. GM1 plays a crucial role in connection with receptor proteins. Our results on curvature generation of GM1 point to an additional important role of this ganglioside, namely in shaping neuronal membranes.

Gangliosides (1, 2), glycosphingolipids that contain sialic acid residues, are important components of all animal cell membranes and are more abundantly expressed in the nervous system. These complex lipids consist of a large saccharidic head group and a two-tail hydrophobic moiety (ceramide). The vast diversity in their structure stems from the heterogeneity in the oligosaccharide chain. Even though gangliosides were discovered already in 1939 (3), their role in the regulation of many biomembrane functions is not yet understood. It is now known that despite being present as the smallest fraction among the lipids of different cell plasma membranes, gangliosides modulate a number of cell surface receptor activities and play a crucial role in neuronal differentiation and development processes. Importantly, gangliosides accumulate at high levels in brain tissue and are believed to be related in major neurological disorders such as the Guillain–Barré syndrome, Alzheimer’s disease, and parkinsonism (4, 5). The monosialoganglioside GM1, widely considered as the ganglioside paradigm displaying the characteristic features identifying gangliosides, has been shown to affect membrane curvature (1, 2) and can be expected to strongly influence the neuron morphology. The curvature effect of GM1 is not only expected to be important in specific tubular morphologies of neuron cells but also, as recently pointed out, in the formation of long connecting nanotubes between cancer cells (6) promoting direct intercellular transfer of cytoplasmic components, which may even include chemotherapy-resistive genes (7). However, so far, the effect of GM1 on membrane curvature is only poorly understood. Although the artificial model membrane systems like small unilamellar vesicles of very high curvature or thin membrane nanotubes pulled out of giant unilamellar vesicles (GUVs) are being often used to perform quantitative investigations on the curvature-related properties of membrane lipids (8, 9), there are some major challenges in characterizing gangliosides such as GM1 using these techniques. First, GM1 molecules have a prominent asymmetrical localization in the outer cell membrane (10), and the asymmetric distribution is crucial for their effect on membrane curvature. However, mimicking such an asymmetry in model membrane systems such as GUVs poses a major challenge. Second, the above-mentioned techniques require associating the GM1 molecules with suitable fluorophores. A very widely employed method for staining GM1 in cell membranes is to use a fluorophore moiety conjugated with cholera toxin that subsequently binds to GM1 (11–15). However, the curvature generated by these aggregates is significantly different from that of individual GM1 molecules both in sign and value (6, 14). Alternative approaches of using labeled GM1, as for example the boron-dipyrromethene (BODIPY)–GM1 complex, suffer from the drawback that the labeling alters the molecule partitioning in domains (16) and increases the volume of the hydrophobic part of GM1, thereby changing its molecular shape from the natural inverted conical shape (17). Furthermore, in biological systems, compositional differences between various membrane compartments are well known and are believed to be primarily driven by sorting of lipids coupled to membrane curvatures (18–21). The enrichment of GM1 at the tips of the echinocyte spiculae and curved exovesicles, attributed to the intrinsic spontaneous curvature of the molecule, is well known (17). In addition, GM1 plays very important roles in axonal growth in neuron cells and has been shown to be highly enriched in the tubular morphology of axons (22). Although these observations provide qualitative evidence for the curvature effect of GM1, no quantitative estimates for the GM1-generated curvature have been obtained so far.

Here, we report the results of our investigations on GM1-doped membranes in which GM1 distributes asymmetrically between the two membrane leaflets of giant vesicles. This asymmetry generates spontaneous tubulation in GUVs, with tubes being stabilized by negative spontaneous curvature. We developed an assay to assess the asymmetric distribution of GM1 across the membrane. To measure the spontaneous curvature associated with this asymmetry, we used an experimental approach for which a membrane nanotube could be pulled from a giant vesicle using an optically trapped latex bead as a handle. In addition, the force transducer property of the optical trap allowed for measuring tube pulling forces with high precision (23, 24). We demonstrate that via pulling inward and outward tubes on the same vesicle, it is possible to assess mechanical properties such as the membrane bending rigidity and spontaneous curvature without considering the membrane tension. The results for the spontaneous curvature are compared with coarse-grained molecular-dynamics simulations.

Results and Discussion

Inward Tubulation Resulting from Asymmetric GM1 Desorption.

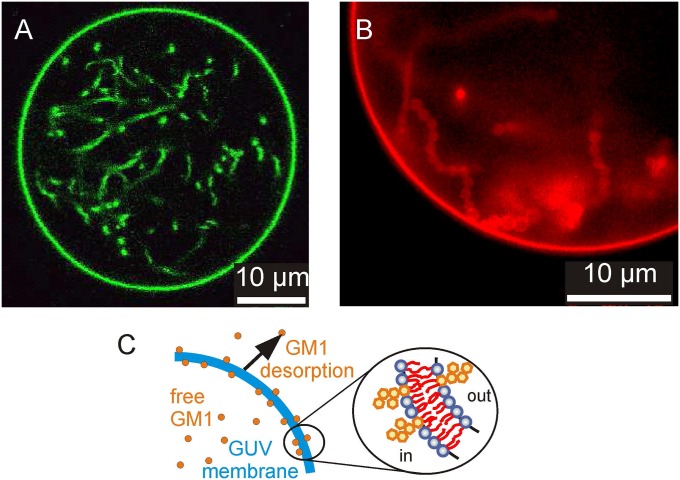
GUVs were prepared from palmitoyloleoylphosphatidylcholine (POPC) and various mole fractions of GM1 in 1 mM Hepes buffer (Materials and Methods and SI Appendix, section S1). Note that, at room temperature, membranes containing GM1 above around 5 mol% exhibit gel-like domains (25). Thus, observations on vesicles with higher content of GM1 were performed at 40 °C; for a partial phase diagram of the system, see ref. 25. After preparation, the vesicles appeared clean, without internal structures. Upon 10-fold (isotonic) dilution in vesicle-free 1 mM Hepes solution, the GUVs exhibited a large number of internal tubes (Fig. 1 and SI Appendix, section S2) (similar observations were made in aqueous solutions without Hepes). This observation is consistent with protrusions detected on asymmetric supported bilayers (26). The tubes we observe can adopt cylindrical or necklace-like morphologies depending on their length and growth kinetics (27).

Fig. 1.

Vesicles prepared from POPC with 10 mol% GM1 in 1 mM Hepes exhibit internal tubes upon 10-fold dilution; observed at 40 °C. (A) Confocal cross-section of a GUV labeled with 0.1 mol% BODIPY-GM1. (B) Epifluorescence image of a part of a GUV labeled with 0.1 mol% TR-DHPE. The necklace-like structure of the membrane tubes is visible. (C) Schematic illustration of the asymmetric distribution of GM1 across the membrane resulting from GM1 desorption upon dilution of the GUV external medium. The Inset illustrates the decreased density of GM1 on the outer leaflet and the associated generation of negative spontaneous curvature in the membrane, which stabilizes inward tubes.

The formation of internal nanotubes in the GM1-doped vesicles upon dilution of the external medium suggests that an asymmetric distribution of GM1 between the leaflets arises by the desorption of GM1 from the outer leaflet (Fig. 1C). As a consequence, the density of GM1 in the inner leaflet exceeds the density in the outer leaflet, which gives rise to a negative spontaneous curvature. To confirm this conclusion, we carried out experiments in which GM1 was externally added to the tubulated vesicles (SI Appendix, section S3). For small amounts of added GM1, the in-tubes were retracted, suggesting a symmetric distribution of the ganglioside resulting in zero spontaneous curvature. Upon further addition of GM1, the formation of external tubes was observed, indicating the generation of positive spontaneous curvature as more GM1 was inserted into the outer leaflet of the vesicle membrane.

Assessing the Concentration of GM1 in Each Leaflet.

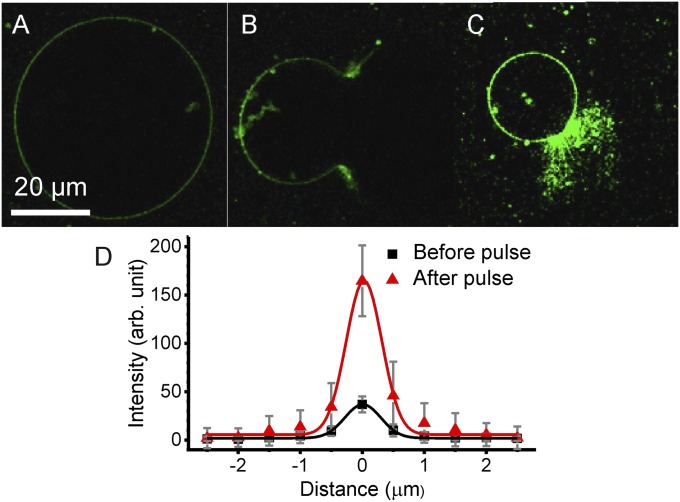
To assess the amount of GM1 in the individual leaflets of 10-fold diluted vesicles with internal tubes, we developed the following experimental assay based on electroporation (SI Appendix, section S4). First, Alexa Fluor-conjugated cholera toxin B (CTB-Alexa) was added to the vesicle solution. Since the vesicles were intact, each CTB predominantly binds to five GM1 molecules present over the outer leaflet of the vesicle membrane. The fluorescence signal appeared uniform, suggesting no microscopic phase separation as observed in other membrane compositions (12). The vesicles were imaged after 10-min incubation time under a confocal microscope. After recording the fluorescence from CTB-Alexa bound to the GM1 molecules only in the outer leaflet (Fig. 2A), a short electric DC pulse (50-ms duration, amplitude between 7 and 10 kV/m) was applied. The electric field induces the formation of micrometer-sized pores in the membrane (28–31). Consistent with the negative spontaneous curvature, the membrane in the vicinity of the pore was observed to curl outward (SI Appendix, Fig. S4). The large pores allowed exposing the inner membrane leaflet to the external solution containing CTB-Alexa and maybe also interleaflet exchange along the pore rim. This led to a visible increase in the membrane fluorescence resulting from additional binding of CTB to GM1 in the inner leaflet (Fig. 2 B and C). The duration of the pore opening (∼10 min) should be sufficient for CTB to access the entire vesicle interior (as explained below), while at the same time desorption of GM1 from the membrane should be negligible as it is slow (32). To a good approximation, the diffusion coefficient, D, of CTB is on the order of 60 µm²/s or higher [taking ∼4 nm for the hydrodynamic radius of CTB (33)], suggesting that within a couple of seconds CTB will explore a distance, L, comparable to the vesicle size: $L=\sqrt{2dDt}>20$ µm, where d = 3 is dimensionality and t is time. Indeed, time-lap observations suggest that the fluorescence signal from CTB-Alexa saturates already in the first couple of seconds after the pore opens (SI Appendix, Fig. S3B).

Fig. 2.

Electroporation assay for assessing the asymmetric distribution of GM1 between the membrane leaflets. (A) Confocal image of a vesicle prepared with 4 mol% GM1 and incubated with CTB-Alexa (green), which binds to GM1 located only in the outer leaflet of the membrane. (B) Electroporation of the vesicle using a DC pulse (10 kV/m, 50 ms). The large pore allows binding of CTB to GM1 present also in the inner leaflet of the membrane. (C) The fluorescence intensity quickly attains a steady value, and after about 10 min, the vesicle membrane closes to form a smaller vesicle. All images in A–C were recorded for the same setting of the microscope and processed in the same way. (D) Intensity profiles across the membrane averaged over the circular part of the membrane contour before (A) and after poration (C) (SI Appendix, section S4). The solid curves are Gaussian fits. Errors have been estimated as SD of values along the vesicle contour.

To estimate the ratio of GM1 coverage in the membrane leaflets, we plotted the mean intensity across the membrane before and after poration (the signal was averaged over many line scans across the vesicle membrane from different confocal sections following an approach in ref. 34) (Fig. 2D and SI Appendix, section S4). A twofold signal increase signifies symmetric distribution of GM1 between the inner and outer leaflets, as demonstrated on the symmetric membranes (SI Appendix, section S4). Higher signal indicates a higher concentration of GM1 in the inner leaflet, while lower signal would suggest the opposite. The intensity profiles measured across the membrane have a ratio of the integrated peak areas equal to ∼4.73. This indicates predominant localization of GM1 in the inner leaflet.

Because the partitioning coefficient of GM1 between the membrane and the bulk (inside and outside the vesicles) is the same before and after dilution, one can roughly estimate the molar concentrations of the ganglioside present in the inner and outer leaflets taking into account the total lipid concentration in the samples (SI Appendix, section S5). Table 1 shows results for the fractions of GM1 with respect to the total number of lipids in the inner and outer leaflets, ${\varphi }_{\text{in}}$ and ${\varphi }_{\text{out}}$, respectively. The SE from measurements on different vesicles is of the order of 14% (six vesicles with 4 mol% GM1 and five vesicles with 2 mol% GM1 were examined). The measurements were performed at room temperature; therefore, high GM1 fractions, at which the membrane undergoes phase separation (25), were not explored.

Table 1.

Molar fractions of GM1 in the inner and outer leaflets, ${\varphi }_{\text{in}}$ and ${\varphi }_{\text{out}}$, and membrane spontaneous curvature

Total mol% GM1	Intensity ratio $I_{\text{after}}/I_{\text{before}}$	GM1 fraction mol%		Asymmetry, $\mathrm{\Delta }\varphi ={\varphi }_{\text{in}}-{\varphi }_{\text{out}}$, mol%	Spontaneous curvature $m^{-1}$, nm
		${\varphi }_{\text{in}}$	${\varphi }_{\text{out}}$		Out-tubes	In-tubes
2	5.19	1.98	0.47	1.51	−510 ± 142	−411 ± 110
4	4.73	3.97	1.07	2.90	−235 ± 45	−213 ± 29

A Method to Measure the Membrane Spontaneous Curvature.

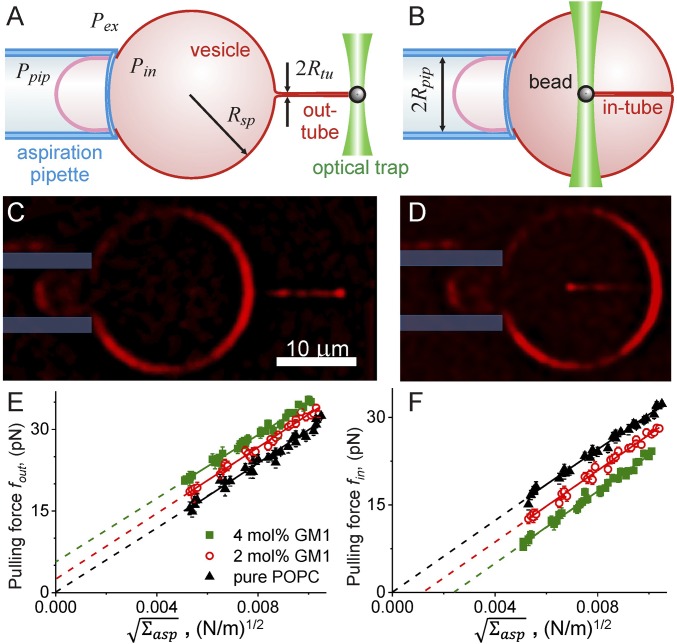
To measure the spontaneous curvature of these asymmetric membranes, we developed a technique based on pulling inward and outward tubes. The experimental assay combines a micropipette for aspirating GUVs and optical tweezers to extrude a membrane tube as shown in Fig. 3. The setup can simultaneously measure the force acting on the tube, perform epifluorescence imaging, and control membrane tension via micropipette aspiration (SI Appendix, sections S6 and S7; Materials and Methods). By varying the aspiration pressure in the micropipette, one changes the membrane tension of the GUV. A latex sphere attached to the GUV membrane is trapped using the optical tweezers and manipulated to the GUV and away from the membrane to form membrane tubes both inwardly as well as outwardly (SI Appendix, section S8). Outward tubes with similar setups have been pulled by several groups (see, e.g., refs. 23 and 35–37). Pulling inward tubes has been established only recently (38) whereby hydrodynamic forces were employed. Here, we combine the two approaches to assess membrane material properties such as the spontaneous curvature and bending rigidity. We also demonstrate that to assess the spontaneous curvature, no prior knowledge of the membrane tension is needed as long as outward and inward tubes are pulled on the same vesicle.

Fig. 3.

Experimental assay for measuring spontaneous curvature and bending rigidity. The vesicle membrane tension ${\mathrm{\Sigma }}_{\mathrm{asp}}$ is set by the suction pressure of the micropipette. A membrane-bound bead is trapped with optical tweezers to pull membrane tubes from the aspirated vesicle either (A and C) outwardly or (B and D) inwardly. The tubes can be observed with epifluorescence (C and D): for these examples, the aspirated vesicle (labeled with 0.1 mol% TR-DHPE) is held at aspiration pressure corresponding to ∼0.01 mN/m. Fourier filtering has been used for improved visibility of pulled nanotubes. The plots of force versus $\sqrt{{\text{Σ}}_{\mathrm{asp}}}$ for vesicles prepared with varying GM1 concentrations are given for outward (E) and inward (F) tubes. The same vesicles were used for pulling in-tubes and out-tubes. The data are collected from five vesicles for each membrane composition. The solid lines are fits following Eqs. 6 and 7. The intercepts with the y axis can be used to deduce the membrane spontaneous curvature following Eq. 9.

To analyze the shape of the GUVs in Fig. 3 A and B, we distinguish three membrane segments: the small spherical segment within the pipette, which has the radius $R_{\mathrm{pip}}$; the large spherical segment outside of the pipette, which has the radius $R_{\mathrm{sp}}$; and the pulled nanotube, which we take to be cylindrical with radius $R_{\mathrm{tu}}$. We now assume that the vesicle membrane is uniform in the sense that all of these membrane segments have the same spontaneous curvature $m$ and the same bending rigidity $\kappa$. The small spherical segment, which is exposed to the pressure difference $P_{\text{in}}-P_{\mathrm{pip}}$, is then governed by the shape equation

$$P_{\text{in}}-P_{\mathrm{pip}}=2\left(\text{Σ}+2\kappa m^2\right)\frac{1}{R_{\mathrm{pip}}}-4\kappa m\frac{1}{R_{\mathrm{pip}}^2},$$ [1]

which also depends on the mechanical tension $\text{Σ}$ and on the spontaneous tension $2\kappa m^2$. The large spherical segment is exposed to the pressure difference $P_{\text{in}}-P_{\mathrm{ex}}$, and its radius $R_{\mathrm{sp}}$ satisfies the shape equation

$$P_{\text{in}}-P_{\mathrm{ex}}=2\left(\text{Σ}+2\kappa m^2\right)\frac{1}{R_{\mathrm{sp}}}-4\kappa m\frac{1}{R_{\mathrm{sp}}^2}.$$ [2]

Combining these two equations, we obtain the suction pressure

$$\mathrm{\Delta }P=P_{\mathrm{ex}}-P_{\mathrm{pip}}\approx 2\left(\text{Σ}+2\kappa m^2\right)\left(\frac{1}{R_{\mathrm{pip}}}-\frac{1}{R_{\mathrm{sp}}}\right),$$ [3]

where correction terms of order $m/R_{\mathrm{pip}}^2$ and $m/R_{\mathrm{sp}}^2$ have been ignored. When we rearrange the terms in the latter equation, we obtain the relation

$$\text{Σ}+2\kappa m^2\approx \mathrm{\Delta }P\frac{R_{\mathrm{sp}}{R}_{\mathrm{pip}}}{2\left(R_{\mathrm{sp}}-R_{\mathrm{pip}}\right)}\equiv {\text{Σ}}_{\mathrm{asp}},$$ [4]

which defines the aspiration tension ${\text{Σ}}_{\mathrm{asp}}$. Thus, up to this order, the total membrane tension,

$$\widehat{\text{Σ}}\equiv \text{Σ}+2\kappa m^2,$$ [5]

is equal to the aspiration tension ${\text{Σ}}_{\mathrm{asp}}$, which can be controlled via the suction pressure $\mathrm{\Delta }P$.

The out-tube with positive mean curvature is exposed both to the pressure difference $P_{\text{in}}-P_{\mathrm{ex}}$ and to the local pulling force $f_{\text{out}}$. Likewise, the in-tube with negative mean curvature is exposed both to $P_{\text{in}}-P_{\mathrm{ex}}$ and $f_{\text{in}}$. Using the results of ref. 39, we obtain the equations

$$f_{\text{in}}=2\pi \sqrt{2\kappa \left(\text{Σ}+2\kappa m^2\right)}+4\pi \kappa m\approx 2\pi \sqrt{2\kappa {\text{Σ}}_{\mathrm{asp}}}+4\pi \kappa m$$ [6]

for in-tubes, and

$$f_{\text{out}}=2\pi \sqrt{2\kappa \left(\text{Σ}+2\kappa m^2\right)}-4\pi \kappa m\approx 2\pi \sqrt{2\kappa {\text{Σ}}_{\mathrm{asp}}}-4\pi \kappa m$$ [7]

for out-tubes. Therefore, for m < 0, the force $f_{\text{in}}$ vanishes at

$${\mathrm{\Sigma }}_{\mathrm{asp}}^0=2\kappa m^2\hspace{1em}\mathrm{for}\text{in}-\text{tubes},$$ [8]

which represents the spontaneous tension generated by the spontaneous curvature. For out-tubes and in-tubes, the pulling forces at vanishing tension are given by

$$f_{\text{out}}^0=-4\pi \kappa m\hspace{1em}\text{and}\hspace{1em}{f}_{\mathrm{in}}^0=4\pi \kappa m.$$ [9]

From Eqs. 6 and 7, one also sees that pulling an in-tube and an out-tube and measuring the respective forces at a fixed membrane tension allows us to directly estimate the spontaneous curvature from the force difference, $f_{\text{out}}-f_{\text{in}}=-8\pi \kappa m$, which does not depend on the membrane tension (SI Appendix, Fig. S5) as we confirm experimentally below on vesicles aspirated in micropipettes. Thus, no prior knowledge of the membrane tension is needed. Therefore, as long as the vesicle is immobilized (for example by adhesion to a substrate), such measurements can be performed on nonaspirated vesicles, avoiding the need of having a complex micropipette aspiration setup. The only condition is that the unbound part of the vesicle retains its spherical cap morphology and the pulling of in- and out-tubes does not perturb it.

The tube pulling force was studied in vesicles prepared with varying concentrations of GM1. Both an in-tube and an out-tube were pulled from the same vesicle and the forces were measured under changing membrane tension. Fig. 3 E and F shows the tube pulling force with increasing tension. The slope of linear fits following Eqs. 6 and 7 provides an estimate for the bending modulus, whereby the value obtained from inward tubes (κ = 1.20 ± 0.07 × 10⁻¹⁹ J) is consistent with that from outward tubes (κ = 1.10 ± 0.11 × 10⁻¹⁹ J); every vesicle was analyzed independently, and then the results were averaged; the error represents the maximal error from individual vesicle fits. This value is also consistent with literature data for POPC membranes (40). It is relatively constant over samples with and without GM1 and varies within 10%, which is comparable to the measurement errors for the present experiments as well as that of the electroporation experiments for assessing the GM1 distribution. One may expect a decrease in the bending stiffness of the vesicle membrane with the addition of GM1 as reported in ref. 25; however, in the latter study, the GM1 concentration on the membrane was higher as no dilution of the vesicles was done (i.e., no significant desorption of GM1 occurred).

The linear fits to the data for pure POPC vesicles in Fig. 3 E and F go through the origin. This is understandable as these membranes exhibit no asymmetry and thus have zero spontaneous curvature (Eq. 9). For vesicles prepared with GM1, the intercept of the fits is positive for outward tubes and negative for inward tubes consistent with a negative value for the membrane spontaneous curvature resulting from the asymmetric distribution of GM1. The membrane curvatures $m^{-1}$ estimated from the intercepts (Eq. 9) for in-tubes are consistent with values obtained from pulling out-tubes (Table 1). With increasing GM1 concentration, higher forces are required to pull outward membrane tubes at a given tension (Fig. 3E). Simultaneously, the inward tube pulling force vanishes at higher values of ${\text{Σ}}_{\mathrm{asp}}^0$ (Fig. 3F and Eq. 8). This implies that at higher concentrations of GM1 in the membrane, spontaneously formed tubes will be stable even at higher aspiration tension applied on the vesicle. Indeed, this result was found consistent with another set of experiments for higher GM1 fractions, where we explored the threshold membrane tension below which tubes spontaneously reform (for details, see SI Appendix, section S9). A similar approach was previously applied to another system (see ref. 41). Here, the membrane tension was modulated either via micropipette aspiration or vesicle electrodeformation (25, 42). The threshold membrane tension was observed to increase up to around 0.025 mN/m for membranes prepared with 10 mol% GM1 (SI Appendix, Fig. S6).

Comparison with Simulations: Independence of Membrane Mechanical Properties on Local Clustering of GM1.

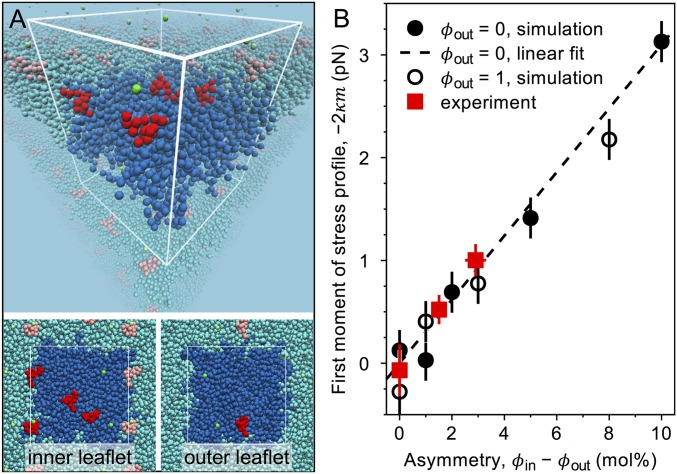
We performed simulations using the MARTINI coarse-grained molecular-dynamics simulation model with a GM1 parameterization that combines the bonded parameters by López et al. (43) with the nonbonded parameters by Gu et al. (44) (Fig. 4A, Materials and Methods, and SI Appendix, section S10). The effect of GM1 on the bilayer spontaneous curvature as assessed from the first moment of the stress profile, which is equal to $-2\kappa m$, is shown in Fig. 4B as a function of the bilayer asymmetry ${\varphi }_{\text{in}}-{\varphi }_{\text{out}}$, where ${\varphi }_{\text{in}}$ and ${\varphi }_{\text{out}}$ are the mole fractions of GM1 in the inner and the outer leaflet. For comparison, experimental data as deduced from the measured pulling force for vanishing tension (Eq. 9 and Table 1) are also plotted in Fig. 4B. The simulations showed an overall negative spontaneous curvature for the range of studied asymmetry values, consistent with the experimental data. Interestingly, the simulation data are well fitted by a straight line in agreement with theoretical predictions (39). Note that the fit shown in Fig. 4B (dashed line) was obtained for the simulation data with ${\varphi }_{\text{out}}=0$, that is, when the outer leaflet contained pure POPC, but simulation data with ${\varphi }_{\text{out}}=1$, that is, when the outer leaflet contained a single GM1 followed the same dependence on bilayer asymmetry. Furthermore, this linear relation captured also the dependence of our experimental data quantitatively. The original model by López et al. (43) also captured the experimental data quantitatively (SI Appendix, Fig. S8), despite the fact that this model suffers from unphysically strong GM1 clustering [see Gu et al. (44) and SI Appendix, Figs. S7A and S8A]. As our model reproduces all of the other properties [including the GM1 shape (SI Appendix, Fig. S7B)] of the López model except for the clustering, our simulation results demonstrate that the effect GM1 has on the membrane mechanical properties (Fig. 4B and SI Appendix, Fig. S8B) is, interestingly, independent of the local clustering of GM1.

Fig. 4.

Simulation results and comparison with experiment. (A) A simulation snapshot of the inner bilayer leaflet (upper monolayer within the white wireframe) and the outer leaflet (lower monolayer) for GM1 molar fractions ${\varphi }_{\text{in}}=4$ mol% and ${\varphi }_{\text{out}}=1$ mol% using the MARTINI coarse-grained molecular-dynamics simulation model with GM1 parameters developed in this work by combining the bonded parameters by López et al. (43) with the nonbonded parameters by Gu et al. (44). Leaflet-wise mole fractions directly indicate the numbers of lipids: ${\varphi }_{\text{in}}=4$ corresponds to 4 GM1 and 96 POPC molecules in the inner leaflet. The white wire frame with the strongly colored species (GM1, red; POPC, blue; sodium, green; water, not shown) shows the simulation box, and the lightly colored molecules indicate its periodic images. (B) Comparison of simulation results to experiments. The first moment of the lateral stress profile ($-2\kappa m$) is plotted as a function of the bilayer asymmetry ${\varphi }_{\text{in}}-{\varphi }_{\text{out}}$ for bilayers when the outer leaflet is pure POPC (${\varphi }_{\text{out}}=0$, solid circles), and when it contains one GM1 (${\varphi }_{\text{out}}=1$, open circles). Error bars indicate SEM. The dashed line represents the linear fit $-2\kappa m=0.31\left({\varphi }_{\text{in}}-{\varphi }_{\text{out}}\right)$ to the data for ${\varphi }_{\text{out}}=0$. The dependence is quantitatively consistent with the experimental results (red squares) obtained from the pulling force for vanishing tension (Eq. 9).

Estimate for Local Curvature Generated by GM1.

The spontaneous tension generated by the tubes, ${\text{Σ}}_{\mathrm{asp}}^0$, and the pulling forces at vanishing tension, $f_{\text{out}}^0$ and $f_{\text{in}}^0$, can be used to obtain an estimate for the local curvature generated by a single GM1, $\stackrel{\sim }{m}$, via the relation $m=\mathrm{\Delta }\varphi \alpha \stackrel{\sim }{m}$, where $\mathrm{\Delta }\varphi ={\varphi }_{\text{in}}-{\varphi }_{\text{out}}$ represents the membrane asymmetry deduced from the electroporation assay (Table 1), and $\alpha$ is a correction factor accounting for the molecular surface areas of GM1 and POPC, $\alpha =a_{\mathrm{GM}1}/a_{\mathrm{POPC}}$. The average bilayer area occupied by the GM1 molecule is reported to be between 70 and 85 Ų (45), that is, $a_{\mathrm{GM}1}\cong 77$ Ų, while that of POPC is $a_{\mathrm{POPC}}$ $\cong$ 63 Ų (46), yielding $\alpha \cong 1.2$. Second-order curves for the dependence of ${\text{Σ}}_{\mathrm{asp}}^0$ on $\mathrm{\Delta }\varphi$ for vesicles prepared from pure POPC ($\mathrm{\Delta }\varphi =0$) and with 2 and 4 mol% GM1 give ${\stackrel{\sim }{m}}^{-1}=7.38\pm 1.49$ nm for data from pulled in-tubes. Linear fits of the out-tube and in-tube pulling forces at vanishing tension as a function of $\mathrm{\Delta }\varphi$ yield ${\stackrel{\sim }{m}}^{-1}=8.07\pm 1.74$ nm. These results are in excellent agreement. The combined results for the local curvature generated by GM1 in POPC membranes lead to ${\stackrel{\sim }{m}}^{-1}=7.73\pm 1.62$ nm. Alternatively, the projected membrane surface area under a GM1 head group can be assessed from simulation data yielding ${\alpha }_{\mathrm{sim}}\cong 2$ and, correspondingly, ${\stackrel{\sim }{m}}_{\mathrm{sim}}^{-1}=12.56\pm 0.50$ nm. It is pertinent to note here that $\stackrel{\sim }{m}$ is the local curvature generated by GM1 molecules in bilayer membranes and represents a molecular characteristic. For comparison, in lipid-free systems, as examined extensively in the past, it can be estimated from the radius of GM1 micelles. Sonnino et al. (47) have reported a hydrodynamic radius of ∼5.87 nm for GM1 micelles. Note, however, that in micelles, the molecular environment of the molecule is very different compared with that in the lipid bilayer.

Conclusions

The involvement of gangliosides in important cellular processes like neuronal functioning is now well known, and the curvature properties of these glycosphingolipids play a crucial role in axonal sprouting and important neuron repair processes. We have used an optical-tweezers–based approach to pull thin tubes from giant vesicles made with GM1 lipids and studied the tube pulling force to obtain a fairly accurate estimate of the spontaneous curvature generated by GM1 molecules. Since an important aspect of curvature-inducing characteristic of GM1 is its localization primarily on one leaflet of cell membranes, we prepared vesicles with asymmetric GM1 distribution across the bilayer. This was achieved based on our finding that GM1 desorbs from the membrane. One important practical aspect to emphasize here is that the large number of studies based on using model and cell membranes containing GM1 should consider the desorption aspects ensuing from sample dilution to allow for data comparison across laboratories and for appropriate interpretation of results (especially when membrane morphology is studied). The dilution steps will presumably alter the affinity of GM1-doped membranes to various receptors. Here, we quantified GM1 desorption and the resulting leaflet asymmetry by an approach involving generation of transient pores in giant vesicles by electroporation. We also determined the dependence of the membrane spontaneous curvature on GM1 asymmetry. Coarse-grained molecular-dynamics simulations captured the experimentally obtained data quantitatively correctly and showed that the effect of GM1 on bilayer mechanical properties does not depend on the local clustering of GM1. We expect our GM1 model to have the predictive power for assessing the membrane curvature at higher asymmetries, characteristic for neuronal membranes. However, we expect that this predictive ability is sensitive to the details of the parameterization and that future studies will allow us to bring light to the importance of head group orientation on the ability of GM1 (and glycolipids in general) to modify membrane mechanical properties. The multitasking role of GM1 and its involvement in a large number of essential functions in the membrane has been well recognized, in particular, its involvement in neuronal development and differentiation (48, 49) and neurite sprouting (50). Our results on curvature generation of GM1 point to an additional important role of this ganglioside, namely, shaping neuronal membranes.

Materials and Methods

Vesicle Preparation.

GUVs were grown in 1 mM Hepes using the electroformation technique from a mixture of ∼3 mM POPC and GM1 with varying concentration of up to 10 mol% of the total lipid content (25) (SI Appendix, section S1). For fluorescence imaging of the vesicles, 0.1 mol% Texas Red dihexadecanoyl-glycerophosphoethanolamine (TR–DHPE) or 0.1 mol% BODIPY FL C5–ganglioside GM1 (BODIPY–GM1) was added. Occasionally, CTB labeled with Alexa 488 (CTB-Alexa) (purchased from Invitrogen) was added, and the vesicles were imaged with a confocal microscope (SP5 DMI 6000; Leica Microsystems).

Optical Tweezers and Force Measurements.

The optical tweezers were built around a motorized inverted microscope (Axiovert 200M; Zeiss) by focusing a 1,064-nm, continuous-wave beam from a Nd:YAG laser through a 100×, 1.25 N.A. objective lens (51). The bead position was determined using centroid tracking algorithm (52). The trap stiffness of the tweezers was found to be typically ∼110 pN/µm/W (SI Appendix, section S6). All force-measurement experiments were performed at room temperature, 23 ± 1 °C.

Micropipette Manipulation and Aspiration of GUVs.

Micropipettes were fashioned from glass capillaries at desired inner diameters of ∼6 μm. The aspiration pressure was controlled through movement of a water reservoir. More details on the vesicle micromanipulation procedure are given in SI Appendix, sections S7 and S8.

Coarse-Grained Molecular-Dynamics Simulations.

We used the fast, flexible, and free GROMACS (53) engine, version 5.1.1, to run MARTINI (54) coarse-grained molecular-dynamics simulations (SI Appendix, section S10). The GM1-containing POPC bilayers at full hydration (at least 15 water beads, equivalent of 60 water molecules, per lipid), were simulated using a GM1 parameterization that combined the bonded parameters in ref. 43, with the nonbonded parameters in ref. 44, see SI Appendix, section S10. The lateral stress profiles of the bilayers were calculated with GROMACS-LS (55). The simulation lengths were 100 μs (except for the ${\varphi }_{\text{in}}\left|{\varphi }_{\text{out}}=1\right|1$ system, 20 μs) with sampling rate of 100 ps.

Note Added in Proof.

Bhatia et al. (56) have recently determined the spontaneous curvature of GUVs doped with GM1 by an alternative method.