Harnessing bistability for directional propulsion of soft, untethered robots

Significance

A major challenge in soft robotics is the integration of sensing, actuation, control, and propulsion. Here, we propose a material-based approach for designing soft robots. We show an untethered, soft swimming robot, which can complete preprogrammed tasks without the need for electronics, controllers, or power sources on board. To achieve propulsion, we use bistable shape memory polymer muscles connected to paddles that amplify actuation forces. As a proof of principle, we show that these robots can be preprogrammed to follow specific routes or deliver a cargo and navigate back to their deployment point. The proposed design principle can have a broad impact in soft robotics based on programed materials.

Abstract

In most macroscale robotic systems, propulsion and controls are enabled through a physical tether or complex onboard electronics and batteries. A tether simplifies the design process but limits the range of motion of the robot, while onboard controls and power supplies are heavy and complicate the design process. Here, we present a simple design principle for an untethered, soft swimming robot with preprogrammed, directional propulsion without a battery or onboard electronics. Locomotion is achieved by using actuators that harness the large displacements of bistable elements triggered by surrounding temperature changes. Powered by shape memory polymer (SMP) muscles, the bistable elements in turn actuate the robot’s fins. Our robots are fabricated using a commercially available 3D printer in a single print. As a proof of concept, we show the ability to program a vessel, which can autonomously deliver a cargo and navigate back to the deployment point.

Soft robotics (1–5) and robotic materials (also known as programmable matter) (6–8) are blurring the boundary between materials and machines while promising a better, simpler, safer, and more adaptive interface with humans (9, 10). Propulsion and navigation are core to both soft and rigid robotic systems. Autonomous (or preprogrammed) propulsion is a central element in the road map for future autonomous systems, enabling, for example, unguided traversal of open waters [e.g., studying marine biology (11) or ocean dynamics (12)]. Power supply to enable propulsion remains one of the major obstacles in all forms of locomotion. One of the easiest solutions for supplying power to soft robots is the use of a tether (2). Tethered pneumatics, for example, enabled active agonistic and antagonistic motion (13) and an undulating serpentine (14). Dielectric elastomers were used to create tethered soft crawlers (15) and to simulate the up and down motion of a jellyfish (16). Electromagnetics were used to create a tethered earthworm-like robot (17) and untethered microswimmers under a rotating magnetic field (18). A pressure deforming elastomer was used to design an artificial fish tail that can perform maneuvers (19). Untethered robots, on the contrary, sacrifice simplicity in design for moving freedom without restriction. An untethered robot needs to encapsulate programing, sensing, actuation, and more importantly, an onboard power source.

The demonstration of an entirely soft (composed of materials with elasticity moduli on the order of $10^4-10^9$ Pa) untethered robot, “the Octobot” (4), opened the door for a new generation of robots (5). The Octobot is powered through regulated pressure generating a chemical reaction. Fabrication of the Octobot requires a combination of lithography, molding, and 3D printing. However, it does not exhibit locomotion. A common feature of all current demonstrations of soft robots is the presence of a complex internal architecture as a result of a multistep fabrication and assembly process. Here, we present a methodology for designing an untethered, soft robot, which can propel itself and can be preprogrammed to follow selected trajectories. Furthermore, the robot can be preprogrammed to reach a destination, deliver a cargo, and then reverse its propulsion direction to return back to its initial deployment point. The robot can be fabricated using a commercially available 3D printer in a single print. However, the presented prototypes are partitioned to highlight the different components and speed up the printing process.

We focus on the actuation, design, and fabrication of a robot that exploits bistable actuation for propulsion and responds to temperature changes in the environment to control its directional locomotion. We use shape memory polymers (SMPs) to create bistable “muscles” that respond to temperature changes in the environment. Bistable actuation is often found in biological systems, like the Venus fly trap (20) and the Mantis shrimp (21). When working near instabilities, bistability can amplify displacements with the application of a small incremental force (22). Engineers started to integrate instabilities in design (10) [for example, in space structures (23), energy absorption mechanisms (24, 25), and fly-trapping robots (26)]. By amplifying the response of soft SMP muscles, snap-through instabilities can instantaneously exert high force and trigger large geometrical changes (27). Bistability has also been used to sustain a propagating solitary wave in a soft medium (22). More recently, bistability enabled the realization of the first purely acoustic transistor and mechanical calculator (28). A typical bistability is found in the Von Mises truss design, which allows a simple 1D system to have two stable states (29). Combining this principle with multimaterial 3D printing, it is possible to realize bistable actuators with a tunable activation force through material and geometry changes (30). These actuators can be used to create load-bearing, multistate reconfigurable 3D-printed structures, where large shape changes are possible due to the long stroke length of the bistable actuator design. To activate them, they can be combined with 3D-printed shape memory strips, which respond to different temperatures, to create time-sequenced linear actuators and 4D deployable structures (31). Here, we build on these works to create untethered robots.

Robot Design Principle

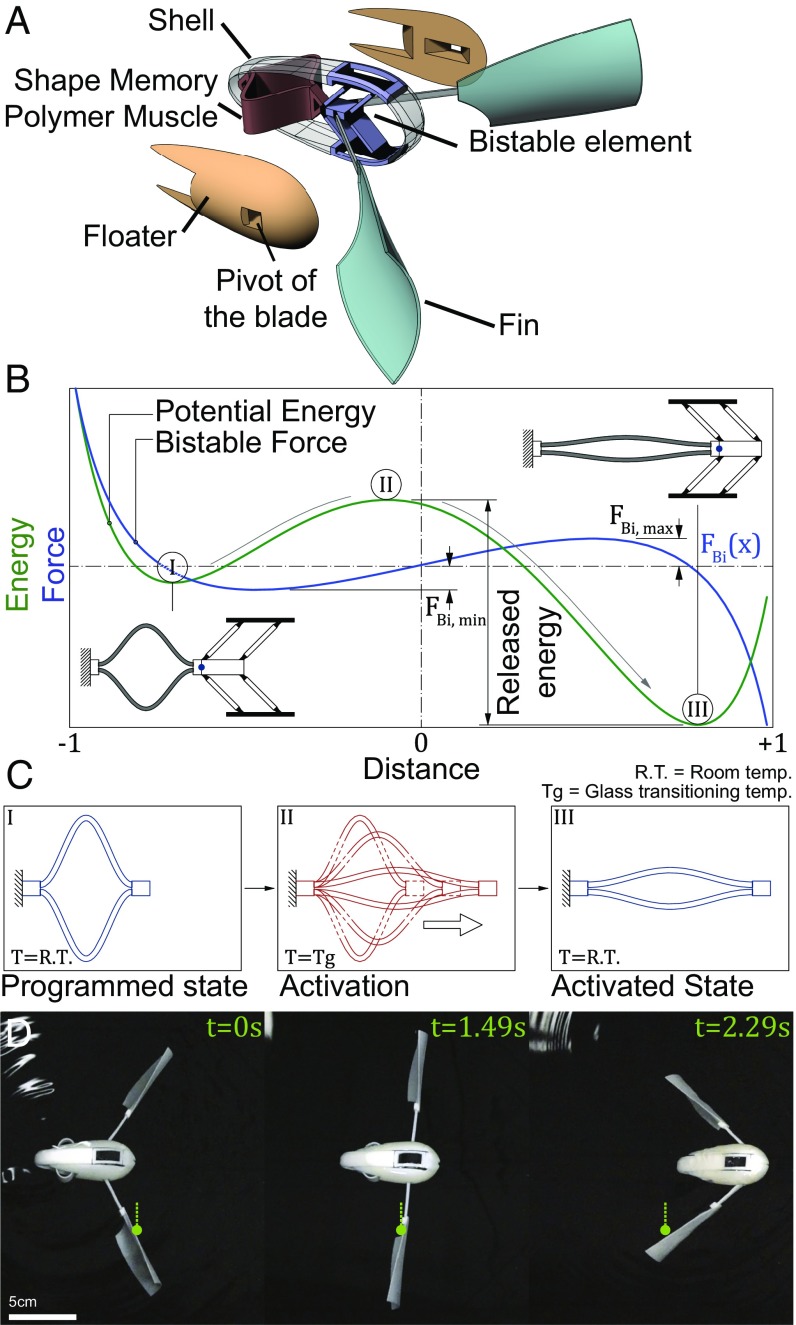
To show the underlying principle of our design concept, we first study a robot propelled by a single actuator (Fig. 1 and SI Appendix, Fig. S1). The actuator consists of two strips of SMP material acting like a muscle connected to a bistable element. To reduce design complexity and ease prototyping, the robot is decomposed into five parts [outer shell, floaters, fins, bistable element, and shape memory muscle (Fig. 1A)]. The shell supports the bistable element to ensure linear actuation and provide stability for the robot. The floaters ensure that, in the vertical direction, the SMP strips are fully submerged in water. The groove in the floaters provides the pivot point for the fins. The fins are attached to the bistable element with elastomeric joints, ensuring flexibility.

Fig. 1.

Propulsion through bistability. (A) Schematic of a 3D-printed soft robot (parts are false colored for visualization). (B) Energy potential of the bistable element with two stable states: I and III. The asymmetry in the curve indicates the need for a larger amount of energy to move backward than forward. The SMP muscle shown in Insets is rotated 90° with respect to the bistable element for visualization. (C) The SMP muscle in the deployed (I), transitioning (II), and activated phases (III). (D) Screen captures of the deployed robot in temperature ($T\ge T_{\mathrm{g}}$) at the different phases of activation.

The propulsion mechanism follows the forward motion of many organisms with fins submerged in water (32). The fins, which perform a paddling motion, are driven primarily by destabilizing buckling trusses. The SMP muscle used to trigger the bistable element is a pair of 3D-printed curved beams that exhibit shape memory behavior (33). One limitation of shape memory materials is their slow activation speed. To overcome this, we attach the muscle to a bistable element (Fig. 1B) with the fins mounted on it. In addition to amplifying the output force (31), the bistability transforms the slow, small motion of the SMP beams into a rapid, amplified one, propelling the robot forward. It is often recognized that, in a physical implementation of a bistable element using compliant joints, the two equilibrium states are not equally energetic (i.e., $\left|F_{\mathrm{B}\mathrm{i},\mathrm{m}\mathrm{i}\mathrm{n}}\right|<\left|F_{\mathrm{B}\mathrm{i},\mathrm{m}\mathrm{a}\mathrm{x}}\right|$). Due to the rotational stiffness of the flexible joints, the fabricated state is more stable than the activated state (30). While this is a disadvantage when constructing multistable systems, it can be exploited when directional transformation is desirable (22).

Before deploying the robot, we heat the printed SMP muscle past its glass transition temperature ($T_{\mathrm{g}}$) and mechanically deform it to the programed shape. After deploying the robot in water (state I) with temperature equal to or larger than $T_{\mathrm{g}}$, the muscle relaxes, transforming back into its original/printed shape (state II). Since this is a constrained relaxation, the muscle must overcome the activation force of the bistable element at all points between states I and II [i.e., $F_{\mathrm{S}\mathrm{M}\mathrm{P}}\left(x\right)>F_{\mathrm{B}\mathrm{i}}\left(x\right)\hspace{0.17em}\hspace{0.17em}\forall x=-1,\dots ,0$]. After actuation, the system transitions into state III. Recent advances in straining the material during printing may eliminate this programing step (34). This would allow the presented robots to function immediately after fabrication.

The vertical equilibrium of the robot is achieved by balancing buoyancy and weight forces; in-plane acceleration occurs when propulsion overcomes drag. The forward motion of the robot occurs in the transition between states I and III, consisting of pre- and postsnapping (Fig. 1B). Before the onset of the instability (Fig. 1D), the shape memory muscle moves the bistable element and drives the fins backward until they are perpendicular to the direction of motion (state II). This is a relatively slow motion with low energy output. Immediately after, the bistable element snaps to its second equilibrium position. This drives the fins rapidly and increases the velocity of the robot (Movie S1).

Bistable Element–Muscle Pair

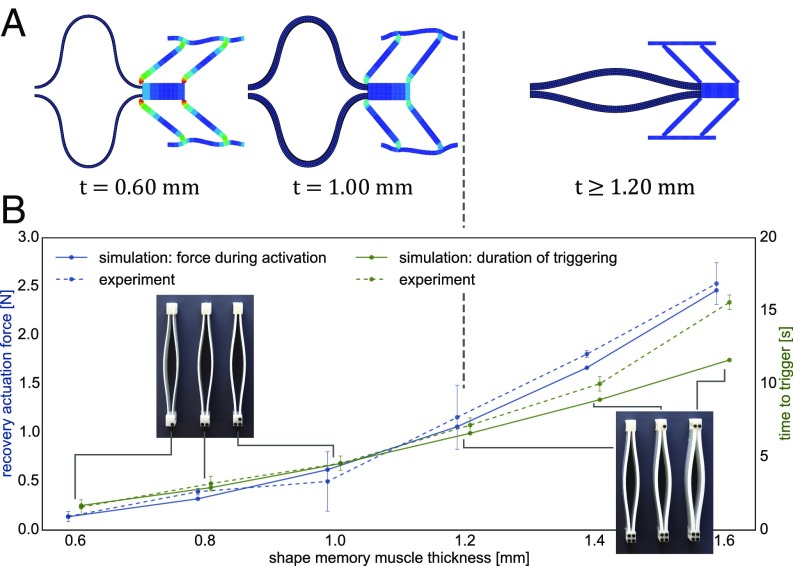
To trigger the instability, the actuation force must overcome the energy barrier of the bistable element (Fig. 1B). To determine the range of operational actuation forces, we use the finite element method to simulate the constrained recovery of the actuation pair (i.e., the bistable element and the SMP muscle) (SI Appendix, Fig. S2). We vary the thickness of the SMP beams between 0.6 and 1.6 mm. Full recovery (i.e., snapping of the bistable element) does not occur for beams with thicknesses lower than 1.2 mm (Fig. 2A). Thinner beams induce localized stresses in the bistable element, although not enough to cause it to snap. The recovery forces of the muscle range from 0.2 to 2.1 N in simulation (Fig. 2B). However, we experimentally observe slightly larger forces at higher thickness values due to the fusion of the two SMP beam strips at both ends of the muscle during polymerization. To determine the activation time needed, we simulate the actuation process using an invariant boundary temperature, while calculating the time for the muscles to reach thermal equilibrium through conductive heating. To characterize the activation time experimentally, six SMP muscles were first programed and then submerged in hot water simultaneously. The time of activation is extracted from the recorded video (Movie S2). At equal length, the force supplied by the muscles as well as the actuation time increase with thickness (Fig. 2B).

Fig. 2.

Actuator design. (A) Finite element (FE) simulations of the constrained recovery of the bistable–muscle pair. The vertical dashed black line separates thicknesses unable to activate the bistable element (Left) from functional thicknesses (Right). (B) Experimental and numerical correlation between the thickness of the SMP muscle and its recovery forces as well as the time that it takes to heat to its original shape. Insets show the different muscles tested. The error bars in the force readings represent the SD. The error bars for the activation times represent the errors in reading the times from video recordings of the experiments.

It is worth noting, however, that the distance traveled by the robot depends mainly on the bistable element rather than the muscle. This is shown by fabricating and testing the same robot with different muscle thicknesses (SI Appendix, Fig. S3). Regardless of the force output of the muscle, the robot travels the same distance (115% of its length). Such demonstration shows the significance of the bistability and long stroke length for the propulsion of soft robots, regardless of the initial actuation force. Since inducing a stroke depends on overcoming the bistable energy barrier rather than the actuator force, the bistable element can be designed with a very small energy barrier (28) and high asymmetry (22). This is also promising for the miniaturization of the actuators and the increase of the number of actuators in a given robot.

Sequential and Directional Propulsion

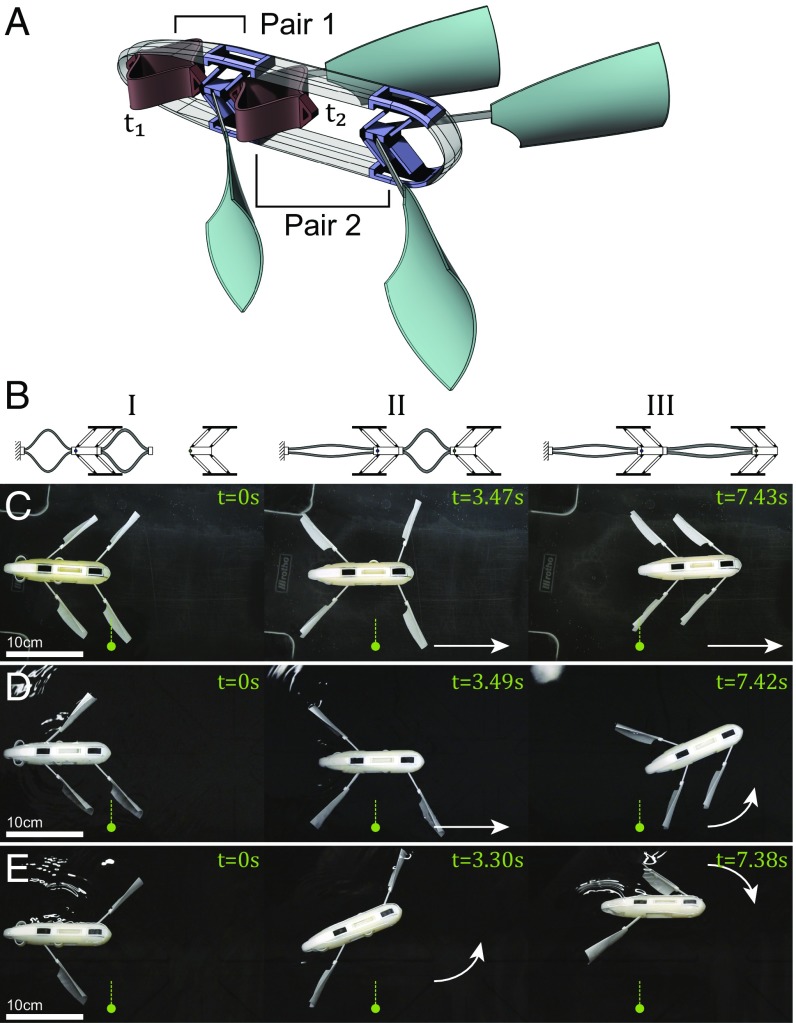
The use of bistability for propulsion can be expanded from a single-stroke to a multistroke robot (Fig. 3A). Multiple bistable element–muscle pairs can be compacted into the same robot in either a connected or separate fashion. If $N$ pairs are completely disconnected, they can induce $N$ independent strokes that are either simultaneous (using identical pairs) or sequenced (using different ones). If the pairs are connected in series (e.g., the muscle of pair 2 is attached to the bistable element of pair 1), they can create synchronized strokes based on the propagation of a soliton-like actuation (35) (Fig. 3B). This guarantees that a stroke $n$ will always be executed before the $n+1$ stroke.

Fig. 3.

Sequential and directional propulsion. (A) A schematic of a robot with two bistable element–muscle pairs. A thinner muscle with faster actuation time is placed at the rear (i.e., $t_1<t_2$). (B) Three distinct phases of the actuation. Activation sequence. (I) Initial state with both muscles programed. (II) The thinner muscle activates, triggering the first bistable element and pushing the second muscle to touch the second bistable element. (III) The second (thicker) muscle triggers the second bistable element. (C–E) Snapshots from deploying three configurations of the multistroke swimmer that show three different directional motions at each of three phases.

Postactivation of actuation pair 1, muscle 2 is moved into position to activate the bistable element of pair 2 (Fig. 3B, II). As the combined force of the already activated bistable element and the muscle from pair 1 is greater than the actuation force of muscle 2 (i.e., $F_{\mathrm{A}\mathrm{c}\mathrm{t},1}+F_{\mathrm{B}\mathrm{i},\mathrm{m}\mathrm{a}\mathrm{x}}>F_{\mathrm{A}\mathrm{c}\mathrm{t},2}>F_{\mathrm{B}\mathrm{i},\mathrm{m}\mathrm{i}\mathrm{n}}$), muscle 2 displaces more in the forward direction and activates the second bistable element. This creates a forward chain action.

In addition to the increased net forward motion, due to the added actuation pairs, propulsion in various directions can be achieved by adjusting the placement of the fins. Having two fins (one on each side) induces a symmetric moment that moves the robot forward. When one of the fins is removed, an asymmetric moment arises, giving the robot a push toward the direction of the missing fin. By strategically placing the fins, navigation can be preprogrammed in advance, setting the robot on a predefined path. The sequential nature of actuation allows for predictable directional change at each stage.

To show the sequential forward motion of the robot, four fins are placed symmetrically on the sides of two actuation pairs. The force needed to trigger the bistable element is identical to that of the single-stroke robot. The thickness of the rear muscle is 1.2 mm, while the front one is 1.6 mm, which gives a sufficient time gap between the two activations. After deployed, two consecutive forward motions are executed, increasing the overall distance traveled to 190% of a single-stroke robot length (Fig. 3C and Movie S3). Next, we remove the front left fin and deploy the robot again (Fig. 3D). The rear (symmetric) actuation induces a forward motion followed by a left turn with $\approx$23.85° (Movie S4). Afterward, we deploy the robot with only two fins placed asymmetrically in the front left and rear right positions (Fig. 3D). The robot takes a left turn of $\approx$21.64° followed by a right one of $\approx$−21.45° (Movie S5). By designing different sizes of fins, one can control the turn angle of the robot.

Cargo Deployment and Reverse Navigation

In many scenarios, such as cargo deployment or retrieval, a robot is required to navigate back to the starting point of its journey after the required operation is completed. The sequential and directional motions of the robot presented so far are based on identical muscles (i.e., same material) with varying thickness. This thickness variation translates into different activation times at the same temperature.

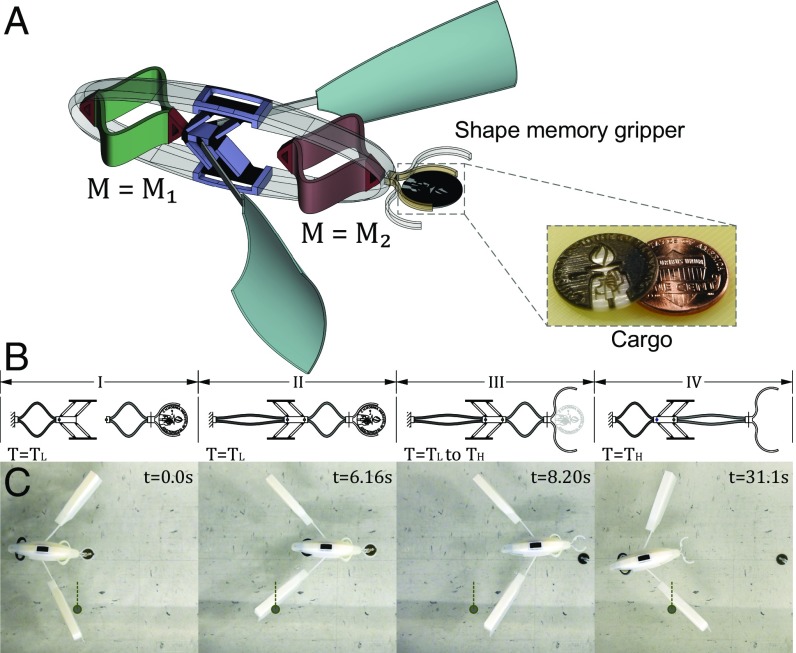
To design our robot to reverse its navigation path, we incorporate an extra muscle on the other side of the bistable element (Fig. 4 A and B). For the second set of muscles (i.e., for reverse navigation), we add an extra dimension to the design (that is, the activation temperatures). It has been shown that, by varying the constituting inkjet materials, one can achieve different glass transition temperatures (36). Using this property, we fabricate two identical muscles with two different materials and therefore, activation temperatures $T_{\mathrm{L}}$ and $T_{\mathrm{H}}$ (Movie S6). The second muscle induces enough force to overcome both the bistable potential and the first muscle. Such force can trigger the instability, producing a force in the opposite direction to the initial actuation and causing the robot to reverse its navigation direction.

Fig. 4.

Reverse navigation. (A) Schematic of a robot with two muscles and a single bistable element. The first muscle, $M_1$, is fabricated with a material that activates at $T_{\mathrm{L}}$. The second muscle, $M_2$, activates at $T_{\mathrm{H}}$, which is higher than $T_{\mathrm{L}}$. (B) Sequence of activation. (I) At room temperature, $T_{\mathrm{R}.\mathrm{T}.}$, both muscles are programed. (II) As water temperature increases to $T_{\mathrm{L}}$, the first muscle triggers the bistable element and propels the swimmer forward. (III) As water heats to $T_{\mathrm{H}}$, the grippers relax and release the cargo. (IV) When the water temperature reaches $T_{\mathrm{H}}$, the second muscle reverses both the bistable element and reprograms the first muscle. (C) Snapshots from the deployment of the robot showing the four different phases.

To show cargo delivery and robot return, we add a shape memory gripper at the front of the robot to hold a 3D-printed penny (Fig. 4 A and B). After the robot is deployed in water with temperature $T_{\mathrm{L}}$, the first muscle activates and triggers the bistable element, thus propelling the swimmer forward to the delivery point (Fig. 4C). After the water temperature reaches the glass transition temperature of the gripper, it relaxes to its original shape and releases the penny. When the temperature reaches $T_{\mathrm{H}}$, the second muscle triggers the bistable element in the reverse direction, causing the robot to move backward to its original deployment point (Movie S7). The principle of reverse propulsion can be easily extended to more complex trajectories and multiple cargoes. Future improvements of this technology could include the use of prestrained materials (34), reversible SMPs (37), or liquid crystal elastomers (LCEs) (38, 39) in the muscles. LCEs activated by light (38) or temperature variations (39), for example, could achieve cyclic actuation in response to diurnal/nocturnal cycles.

Outlook

This work presents a 3D-printable swimming robot that requires neither complex onboard components nor a tether to achieve directional propulsion. Instead, programed SMP muscles are used as the power supply, a bistable element is used as the “engine,” and a set of fins is used as the propellers. By reacting to varying external temperatures, the robot can move forward, turn, reverse, and/or deliver a cargo. At constant temperature, the robot response time can be controlled by varying the geometry and material properties of both the bistable elements and the shape memory strips. This shows a first step in the realization of soft locomotive robots that are potentially applicable in a variety of applications, such as navigation and delivery.

Materials and Methods

All components are fabricated with a multimaterial Stratasys Connex printer. The SMP muscles are fabricated with VeroWhitePlus plastic ($T_{\mathrm{g}}\simeq {60}^{○}$), with the exception of $M_1$ in Fig. 4, which is fabricated with FLX9895 ($T_{\mathrm{g}}\simeq {35}^{○}$). The compliant components within the bistable element are fabricated with Agilus30 with $T_{\mathrm{g}}<{-5}^{○}$ and therefore, remain in the rubbery state throughout the experiments. All remaining components are fabricated with a high temperature-resistant material, RGD525 ($T_{\mathrm{g}}>{80}^{○}$), which retains its stiffness throughout the activation process (33). The stiffness values of the materials used in the actuator are 1 GPa (VeroWhitePlus) and 1 MPa (Agilus30), which fall within the range of soft materials ($10^4-10^9$ Pa) as defined in ref. 4. The dimensions for the water container used to show the single and sequential motion are 967 mm (length) × 555 mm (width) × 393 mm (height). The water is heated by an Atwood heating element, which keeps the water temperature consistently above the glass transition temperature of the used materials. Finite element simulations are implemented using Abaqus 14.1 (geometrical nonlinear solver with thermal–viscoelastic material model).