Optocapacitive Generation of Action Potentials by Microsecond Laser Pulses of Nanojoule Energy

Abstract

Millisecond pulses of laser light delivered to gold nanoparticles residing in close proximity to the surface membrane of neurons can induce membrane depolarization and initiate an action potential. An optocapacitance mechanism proposed as the basis of this effect posits that the membrane-interfaced particle photothermally induces a cell-depolarizing capacitive current, and predicts that delivering a given laser pulse energy within a shorter period should increase the pulse’s action-potential-generating effectiveness by increasing the magnitude of this capacitive current. Experiments on dorsal root ganglion cells show that, for each of a group of interfaced gold nanoparticles and microscale carbon particles, reducing pulse duration from milliseconds to microseconds markedly decreases the minimal pulse energy required for AP generation, providing strong support for the optocapacitance mechanism hypothesis.

Main Text

The artificial stimulation of neuronal activity with light is a topic of major interest in neuroscience research. Recently, we presented a technique that enables light-induced depolarization and resulting action potential (AP) generation by excitable cells. Unlike optogenetics or optopharmacology (1, 2, 3, 4, 5, 6, 7, 8, 9, 10), it does not require either genetic modification of the neuron or the development/preparation of a chemical photoswitch. The mechanism whereby the technique works was unveiled by Shapiro et al. (11), who demonstrated that IR radiation is able to increase the cell membrane temperature and increase its electric capacitance. The current needed to satisfy the equation Q = C × V depolarizes the membrane, reaching its excitation voltage threshold and eliciting an action potential. The amount of change in temperature is small, but it occurs quickly, a property that led Shapiro et al. (11) to hypothesize and show a capacitance change during IR pulses. However, IR radiation is absorbed by water in the bulk medium, yielding slow and spatially imprecise photostimulation and requiring more light energy to boost the generated capacitive current. As a means of increasing the spatial localization and, potentially, the physiological effectiveness of the photostimulus, we have investigated the ability of 20 nm spherical gold nanoparticles (AuNPs) to serve as light-to-heat transducers when positioned close to neuronal membranes by specific binders (12). These experiments, which involved 532 nm laser pulses (a wavelength that penetrates water well and is near the peak of the plasmon absorbance band of these AuNPs), indicated robust light-induced AP generation with millisecond flashes, and provided further evidence for the dependence of this photoresponsiveness on a thermally induced change in membrane capacitance. Based on the evident role of membrane capacitance change in transducing light energy into cell depolarization and AP generation, we have adopted the term “optocapacitance” to refer to the technique and the hypothesized operative mechanism.

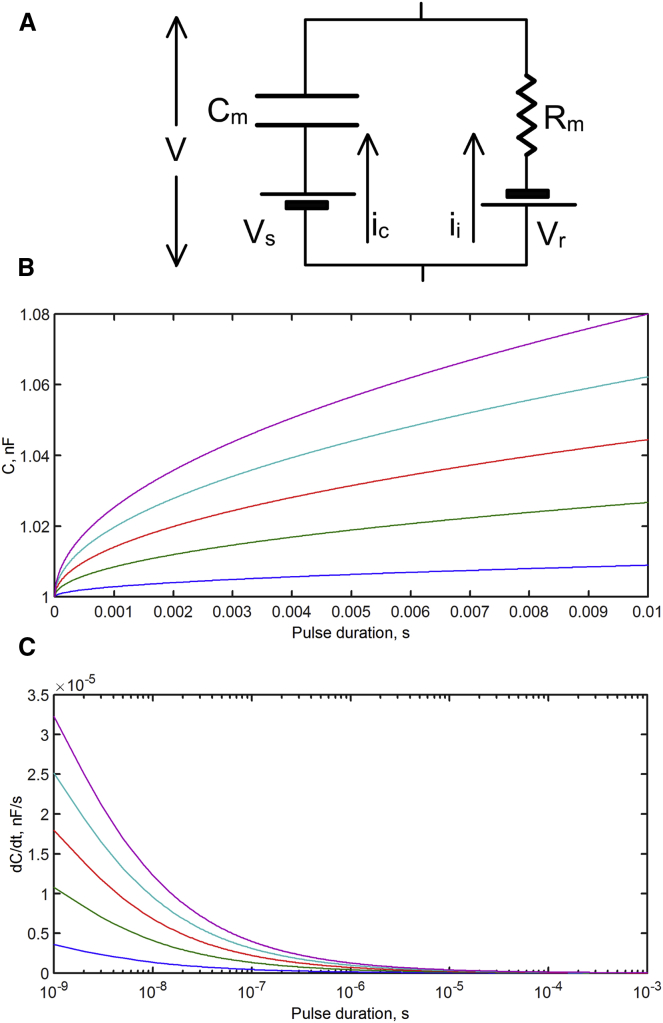
The optocapacitance mechanism posits that a temperature-induced change in capacitance (C_m) establishes a charge debt that is met by depolarization of the membrane. It is then reasonable to suspect that if the capacitance changes more quickly, the necessary charge debt can be achieved within a shorter time (t) period of stimulation (the duration of the light pulse). Conceptually, the greater the value of dC_m/dt, the larger is the current which, in turn, will produce more membrane depolarization, thus making it easier to reach excitation threshold. Most importantly, at the moment of initiation of a virtually square pulse of laser energy to the preparation, the system exhibits a maximum rate of temperature change and thus of capacitance change. Over the duration of the pulse, the rate of change in temperature, and thus the rate of capacitance change, decreases continuously, making necessary the delivery of more energy to the system. To formulate this quantitatively, we represent the equivalent circuit of the membrane with its capacitance, membrane resistance, and batteries as shown in Fig. 1 A. We make the cell membrane capacitance C_m a function of the time-dependent (t-dependent) change in temperature T (i.e., C_m = C_m(T(t))), and the current needed to charge or discharge the capacitance (capacitive current, i_C) is given by the time derivative of the equation that relates C_m and voltage across the capacitor V−V_s with the transmembrane charge difference Q. That is,

$$Q=C_m\left(V-V_s\right),$$ (1a)

$$i_C=\frac{dQ}{dt}=C_m\frac{d\left(V-V_s\right)}{dt}+\left(V-V_s\right)\frac{d{C}_m}{dt}=C_m\frac{dV}{dt}+\left(V-V_s\right)\frac{d{C}_m}{dt},$$ (1b)

where V is the membrane potential and V_s is the net surface potential of the membrane. The current through the ionic conductances, i_i, depends on the conductances and their reversal potentials and can be represented by a Thevenin equivalent as

$$i_i=\frac{V-V_r}{R_m},$$ (2)

where R_m is the membrane resistance and V_r is the Thevenin potential that corresponds to the membrane potential in a resting cell. In the absence of any stimulation of the cell, the total membrane current (i_C + i_i) is zero, therefore we can write

$$\frac{dV}{dt}=-\left(\frac{\left(V-V_s\right)}{C_m\left(t\right)}\frac{d{C}_m}{dt}+\frac{V-V_r}{C_m\left(t\right)R_m}\right),$$ (3)

a differential equation that can be solved for V, knowing the time course of C_m. Central to this formulation is the notion that the instantaneous magnitude of C_m is a function of the prevailing temperature. Therefore, a fast change in temperature produces a large dC_m/dt, consequently changing the membrane voltage V. In 1965, Taylor determined that membrane capacitance increases ∼1% per degree K increase (13). A simple relation for the C_m dependence on temperature T is thus

$$C_m\left(T\right)=C_0+C_0\gamma \left(T\left(t\right)-T_0\right),$$ (4)

where γ is ∼0.01 and T₀ is a reference temperature. The value of T(t) – T₀ is proportional to the power P of the incident laser pulse, and P = E/Δt, where E is the total energy and Δt is the pulse duration. The time dependence of the temperature change (T(t) – T₀) produced by a given pulse power at the surface of the nanoparticle of radius b can be obtained from the solution of the heat equation published by Carvalho-de-Souza et al. (12):

$$T\left(b,t\right)-T_0=\frac{A_0\alpha }{k}\left[\sqrt{\frac{t}{\alpha \pi }}\left(b\text{exp}\left[\frac{-b^2}{4\alpha t}\right]\right)+t-\left(t+\frac{b^2}{2\alpha }\right)\text{erfc}\left[\frac{b}{2\sqrt{\alpha t}}\right]\right].$$ (5)

Here, α and k are the thermal diffusivity and conductivity of water, respectively, and A₀ is the heat generated by the particles during the laser pulse which is proportional to the power P. Thus,

$$T\left(b,t\right)-T_0=cP\left[\sqrt{\frac{t}{\alpha \pi }}\left(b\text{exp}\left[\frac{-b^2}{4\alpha t}\right]\right)+t-\left(t+\frac{b^2}{2\alpha }\right)\text{erfc}\left[\frac{b}{2\sqrt{\alpha t}}\right]\right]=PF\left(t\right),$$ (6)

where c is a constant that includes α, k, the fractional occupancy of the particles and the plasmon resonance properties of the gold particle (12), and where Eq. 6. defines the function F(t). We can thereby write the time course of capacitance for a pulse of energy E and Δt:

$$C_m\left(t\right)=C_0+C_0\gamma E\frac{F\left(t\right)}{\Delta t}.$$ (7)

Fig. 1 B shows examples of the capacitance change during pulses of different power, and Fig. 1 C shows rates of change in capacitance for different pulse powers, with time shown in log scale. Because at shorter times the rate of change in temperature is maximal, the highest dC_m/dt occurs at the beginning of the pulse, and the occurrence of maximum dC_m/dt at pulse initiation is the main reason why shorter pulses are expected to be more efficient, because they require lower total energy in generating APs. We can obtain an estimate of the energy required to initiate an AP by solving Eq. 3 for V and determining how the threshold voltage V_Th (for simplicity, assumed constant) for AP initiation depends on parameters of the stimulating pulse. If the membrane resistance is very high, Eq. 3 can be solved analytically and, when combined with the temperature dependence of the capacitance Eq. 4, yields E_Th, the energy required for threshold:

$$E_{\text{Th}}=\Delta t\frac{V_r-V_{\text{Th}}}{\gamma F\left(t\right)\left(V_{\text{Th}}-V_s\right)}.$$ (8)

Because b² is much larger than α, for values of t ranging from 1 μs to 10 ms, Eq. 6 reduces to

$$T\left(t\right)-T_0=cP\sqrt{t}=PF\left(t\right),$$ (9)

and thus F(t) is proportional to $\sqrt{t}$. Replacing this time-dependence of F(t) in Eq. 8, we see that the energy required to reach threshold will increase with pulse duration as a power function with exponent of 1/2. The model thus predicts that, with decreasing pulse duration, more power but less total energy is required to reach AP threshold.

Figure 1.

Theoretical prediction of increased efficiency of optocapacitance as photostimulating pulse duration is decreased. (A) Equivalent circuit of the membrane shows V as the transmembrane voltage, C_m as the membrane capacitance, V_S as the net surface potential of the membrane, I_C as the capacitive current, R_m as the membrane resistance, V_r as the reversal potential of the ionic current, and I_i as the ionic current. Arrows indicate the outward current direction. (B) Plots of Eq. 7 predict the fractional increase in C_m during laser pulses of different powers with the highest as the top trace and the lowest as the bottom trace. (C) Time derivative of C_m that was plotted in (B), predicting that I_C is highest at the time of pulse initiation and then decays with time. To see this figure in color, go online.

When stimulating with current pulses of amplitude (I) and different durations (Δt), the classical excitability curve to reach threshold is a hyperbolic relationship described by the Lapicque equation

$$I=b_r\left(1+\frac{c_r}{\Delta t}\right),$$ (10)

where b_r is the rheobase, and c_r is chronaxie (14). The current amplitude I is inversely proportional to Δt and the energy required to reach threshold shows a minimum at a duration equal to the chronaxie (14). In contrast, when stimulating with light pulses, the pulse amplitude (power) is inversely proportional to $\sqrt{\Delta t}$ and the energy required to reach threshold increases monotonically with $\sqrt{\Delta t}$ (see Eqs. 8 and 9).

To test the generality of the optocapacitance mechanism, and specifically to test the prediction that reducing Δt decreases E_Th, we investigated the ability of a group of plasmonic and nonplasmonic particles to enable light-induced AP generation by isolated, single-cell preparations of rat dorsal root ganglion (DRG) neurons under varying conditions of laser pulse energy and Δt. For each of the particle types, the investigation of AP generation involved the recording of pulse-by-pulse voltage responses to laser pulses of differing power/duration. For a given setting of pulse power/duration, the response of the cell was examined in a series of trials. These trials were conducted within consecutive 3-s intervals, and each trial consisted of a pair of stimuli. The first stimulus of each pair was a suprathreshold 1-ms depolarizing current injection pulse, intended to verify the neuron’s excitability. The second stimulus, delivered 240 ms later, was a sweep-by-sweep time- and power-varying laser pulse. With laser pulses of fixed power and duration, we typically observed variability among trials in the time course of the membrane potential’s approach to AP generation threshold, as well as the absence of AP generation in some trials. This variability can be attributed to normal intertrial fluctuations of the resting potential that affect AP generation threshold (15).

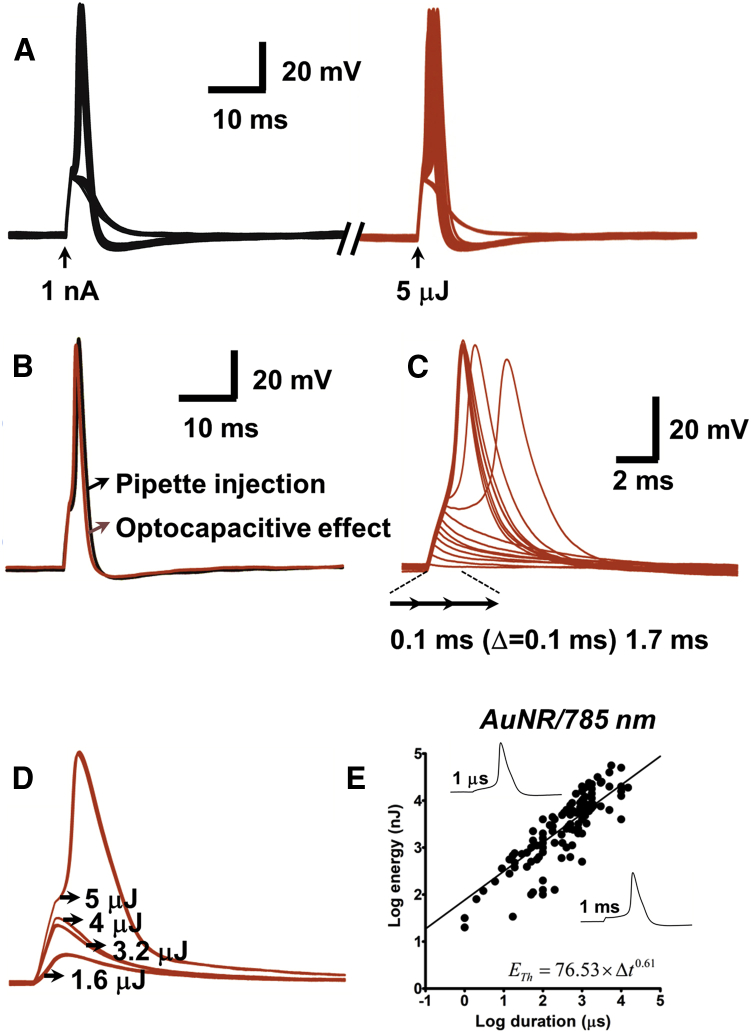
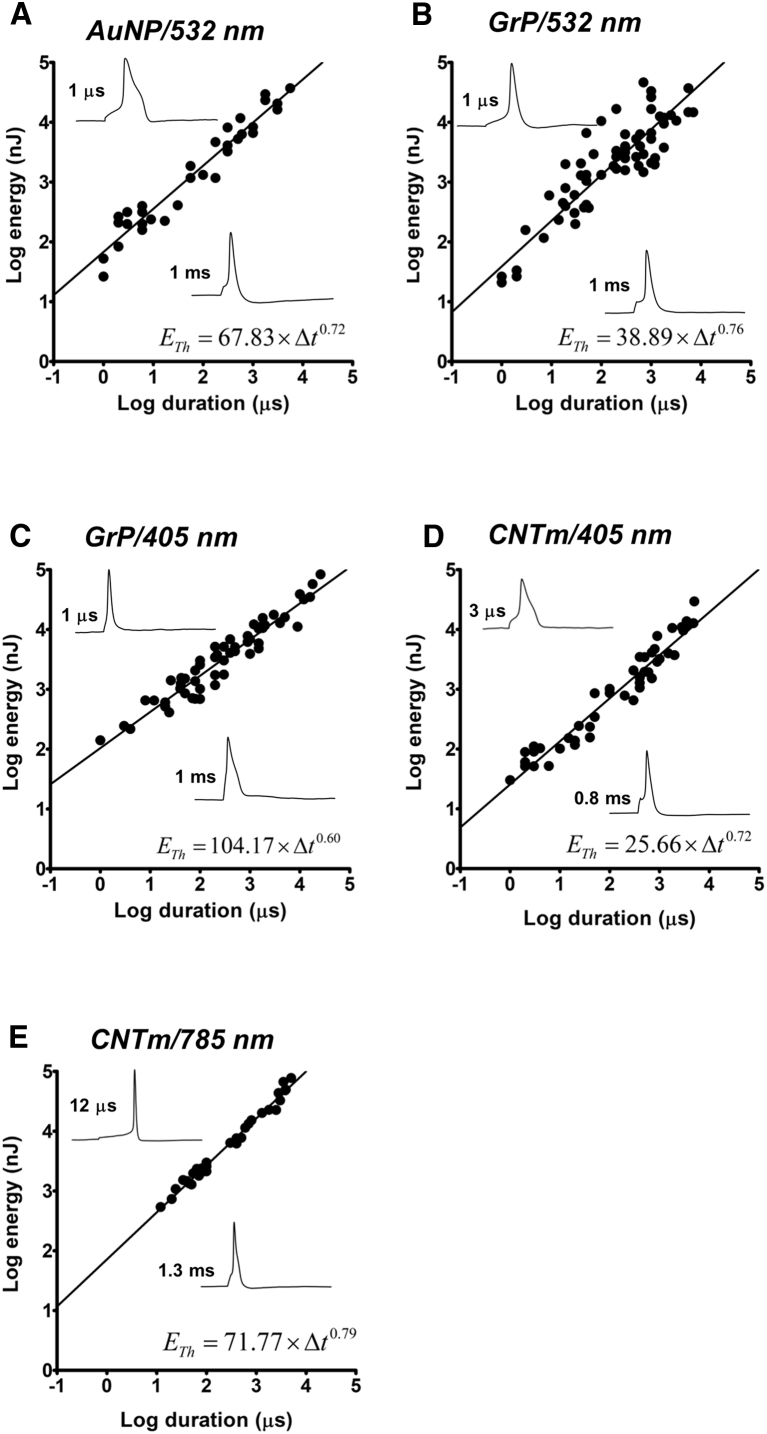
Near-infrared-absorbing gold nanorods (AuNRs), which offer advantages of importance to multiple areas of neuroscience research (16, 17, 18, 19), were of particular interest for study. Fig. 2, A and B show membrane voltage responses of a DRG neuron that was treated with 25 × 94 nm AuNRs. The illustrated AP responses and (in some trials) subthreshold responses were elicited by depolarizing current injection (black traces) and 785 nm laser pulses (red traces); in Fig. 2 B, representative single responses of each type are superimposed. The fact that nearly identical AP waveshapes were elicited by these differing ways of depolarizing the neuron to its AP threshold suggests that they injected nearly identical amounts of current in time. Fig. 2, C and D, shows responses of a different DRG neuron to laser pulses of varying duration (Fig. 2 C) and varying power (Fig. 2 D). Using the protocol described in Fig. 2 A, we varied the power and duration of laser pulses presented to AuNR-treated DRG neurons to determine the relationship between pulse duration Δt and E_Th, the minimal pulse energy at AP generation threshold. For these threshold determinations in the AuNR experiments, as in the other experiments described below, a pulse of given duration and power was taken as representing the minimal threshold energy E_Th when an AP was elicited by 50% of the presented pulses. Fig. 2 E shows, in log-log coordinates, the results of threshold energy determinations for cells treated with AuNRs. The function fitted to the E_Th−Δt data shows that the dependence of E_Th on Δt is well described by a power law function of exponent 0.61. That is, a 10-fold decrease in Δt was associated with a fourfold decrease in E_Th. Building on our earlier finding that treatment of DRG neurons with 20 nm AuNPs enables AP generation by 50 μJ laser pulses at 532 nm (12), we similarly investigated the relationship between E_Th and Δt in DRG neurons treated with this type of AuNP. Fig. 3 A shows that the E_Th−Δt plot for these cells exhibited a power law dependence of exponent 0.72, a value similar to that obtained with the 25 × 94 nm AuNRs.

Figure 2.

Photosensitivity of DRG neurons mediated by 25 × 94 nm AuNRs. All laser pulses were at 785 nm. (A) Given here are membrane voltage responses of a single cell to depolarizing current (1 nA, 1 ms) (left traces) and a 5 μJ laser pulse (5 mW, 1 ms) (right traces) delivered over a series of 37 trials. In recording sweeps where current injection failed to produce an AP, the laser pulse similarly failed to generate an AP. At the moment of laser pulse delivery, the membrane was clamped at I_m = 0 A by the patch amplifier; all of the observed depolarizing current was thus due to the optocapacitive effect. Occurrences of subthreshold current-injection-induced and laser-pulse-induced responses are attributable to intertrial fluctuations. (B) Given here are pipette current injection-induced (black trace) and laser pulse-induced (red trace) APs recorded within the same 3-s trial. (C) Shown here are responses to 5.5-mW laser pulses of durations ranging from 0.1 to 1.7 ms in 0.1-ms increments. AP threshold was reached at a duration of 0.9 ms. (D) Given here are responses to 1-ms pulses of differing power (1.6–5 μJ). (E) Given here is a log-log plot of E_Th (minimal pulse energy required for AP generation) versus pulse duration (Δt). Data were obtained from a total of 17 DRG neurons. (Fitted line) Given here is the power law relation E_Th = aΔt^b, with values of coefficient a and exponent b shown in the figure. (Insets) Given here are representative APs elicited by pulses of 1 μs (76.5 mW, 76 nJ) and 1 ms (5.2 mW, 5.2 μJ). To see this figure in color, go online.

Figure 3.

Photosensitivity mediated by 20 nm AuNPs and carbon-based microparticles. Shown here are log-log plots of laser pulse energy E_Th versus pulse duration. DRG neurons treated with 20 nm spherical AuNPs (A), ∼2 μm GrPs (B and C), or ∼2 μm CNTms (D and E) received laser pulses of 532 nm (A and B), 405 nm (C and D), or 785 nm (E). Results in (A–E) were obtained, respectively, from a total of 6, 10, 11, 9, and 5 cells. Fitted lines plot the illustrated power law relations. (Insets) Representative responses obtained with pulses are as follows: in (A), 67.8 mW, 67.8 nJ is for the 1 μs pulse and 9.8 mW, 9.8 μJ is for the 1 ms pulse; in (B), 38.89 mW and 38.9 nJ is for the 1 μs pulse, and 7.41 mW and 7.41 μJ is for the 1 ms pulse; in (C), 104.17 mW and 104.17 nJ is for the 1 μs pulse, and 6.57 mW and 6.57 μJ is for the 1 ms pulse; in (D), 18.8 mW and 56.6 nJ is for the 3 μs pulse, and 3.95 mW and 3.158 μJ is for the 0.8 ms pulse; and in (E), 42.5 mW and 510 nJ is for the 12 μs pulse, and 15.92 mW and 20.7 μJ is for the 1.3 ms pulse.

We conducted similar experiments on two types of carbon-based particles of dimensions ∼2 μm: graphite particles (GrP), and meshes of 5 × 5000 nm single-walled OH-functionalized carbon nanotubes (CNTm). We found that these two carbon-based materials can serve as light absorbers and subsequent heat emitters, similar to Si-based amorphous micrometer-size particles (20). With the use of 1-ms laser pulses of relatively high energy (3.7–7.6 μJ), we first confirmed that both of these carbon-based materials enable AP generation by DRG neurons. The presence of a single particle in evident contact with the neuron’s surface membrane was sufficient to provide photosensitivity to the cell, enabling AP generation by laser pulses. Importantly, with the use of 405-nm laser pulses with CNTm-treated cells, irreversible depolarizations were produced, suggesting cell damage. This damage was prevented by the addition of a reducing agent (10 mM dithiothreitol) to the recording chamber. This finding is in line with previously reported deleterious effects of light-induced reactive oxygen species generated by the nanotubes (21) and by voltage-sensitive dye phototoxicity (22). No irreversible depolarization of CNTm-treated neurons was observed with 785-nm laser pulses, indicating that the damaging effect seen with 405-nm pulses was a consequence of reactive oxygen species generation by the higher-energy 405-nm photons. Using these carbon-based materials as light absorbers, we obtained E_Th−Δt plots for each material/laser-wavelength pair. As shown in Fig. 3, B–E, results obtained with GrP/532 nm (Fig. 3 B ), GrP/405 nm (Fig. 3 C ), CNTm/405 nm (Fig. 3 D), and CNTm/785 nm (Fig. 3 E) exhibited power law dependences of exponents 0.76, 0.60, 0.72, and 0.79, respectively.

These results show that, despite differences in the structure, composition and plasmonic versus nonplasmonic light absorption properties among the investigated materials, photoexcitation of these materials in close proximity to the surface membrane of DRG neurons enables AP generation. The APs induced upon light absorption by these differing materials exhibit similar waveforms. Furthermore, energy thresholds for AP generation mediated by these materials exhibit remarkably similar power law dependences on laser pulse duration, and the nearly common value (∼0.7) of the exponent for these power law relationships is robust, representing an approximately fivefold decrease in energy E_Th for a 10-fold decrease in pulse duration. We interpret these findings as strong indication that light-induced AP generation with these materials has its basis in an optocapacitance mechanism in which cell membrane heating by the gold nanoparticles, GrPs, or CNTms is transduced into cell depolarization by a capacitive current resulting from a change in membrane capacitance. Additional support for this conclusion comes from the similar power law dependence of the model and the experimentally determined exponent. The discrepancy between Eqs. 8 and 9 that gives an exponent of 0.5 and the experimental value of ∼0.7 can be explained by two factors. First, Eq. 8 is the solution of Eq. 3, assuming infinite membrane resistance. When the membrane resistance is considered in solving Eq. 3, the exponent increases. Second, the model assumes a constant threshold for AP generation regardless of pulse duration. This constancy is a simplification because, as the depolarization is prolonged, the threshold increases due to sodium channel inactivation, thus necessitating even more energy for pulses of long duration.

Beyond providing, to our knowledge, new information relevant to the optocapacitance hypothesis, the results show that interfacing a variety of light-absorbing materials ranging from nanometers to micrometers in size with the surface membrane enables AP generation by excitable cells with laser pulses in the nanojoule energy range. The AP-inducing capacity of pulse energies as low as several nanojoules, which indicates a photosensitivity of the optocapacitance technique considerably greater than that previously demonstrated (12), is a finding of importance to maximizing the biocompatibility of the technique, i.e., to minimizing the delivered light energy required for neural stimulation. Overall, these data encourage further development of the optocapacitance technique as a possible alternative to optogenetic or optopharmacological approaches to achieve photocontrol of AP generation, by a single light pulse, with the capability to control cell excitability with microseconds of radiation pulses. Of particular interest also is our demonstration that the 25 × 94 nm AuNRs are able to induce photosensitivity in neurons with the use of near-infrared (785 nm) radiation. This wavelength is preferable to 532 nm, used with 20 nm AuNPs, because it avoids the absorption by hemoglobin, and it is in the optical window of choice for living tissue penetration by avoiding absorption by water at wavelengths longer than 900 nm. This finding is important because it introduces a rapid and efficient way to stimulate neurons with deep penetrating radiation, a property highly desirable for in vivo research investigations and possibly for clinical applications.

Author Contributions

F.B., D.R.P., and J.L.C.-d.-S. designed research, analyzed data, and wrote the manuscript. J.L.C.-d.-S. and B.I.P. performed research. F.B. contributed analytic tools.

Editor: Brian Salzberg.