How to Connect Cardiac Excitation to the Atomic Interactions of Ion Channels

Abstract

Many have worked to create cardiac action potential models that explicitly represent atomic-level details of ion channel structure. Such models have the potential to define new therapeutic directions and to show how nanoscale perturbations to channel function predispose patients to deadly cardiac arrhythmia. However, there have been significant experimental and theoretical barriers that have limited model usefulness. Recently, many of these barriers have come down, suggesting that considerable progress toward creating these long-sought models may be possible in the near term.

Main Text

Nanoscale atomic interactions within cardiac ion channels propagate across time- and space scales to affect the whole-heart electrophysiology. These molecular-level interactions include channel binding by therapeutic anti-arrhythmic molecules, pro-arrhythmic off-target interactions by drugs targeting other organs, and altered channel function by genetic mutations that subtly change channel structure. The pro- or anti-arrhythmic consequences of these molecular-level interactions are extraordinarily difficult to predict, because channels are closely connected to each other via the membrane potential. Consequently, current through each channel affects not only its own gating but that of all the other channels in the membrane, leading to emergent properties at the cell and tissue levels that are not readily intuited.

Computational models that meticulously represent each of the major channels and transporters with sets of differential equations offer the promise of new insight to overcome this complexity, inspire new therapeutic approaches, and provide insight into why certain mutations predispose patients to sudden cardiac death (1). There are many fronts currently being explored to improve the predictive ability of these models, including understanding patient-to-patient variability (2, 3), connecting channel dynamics to the three-dimensional heart (4, 5), using nonlinear dynamics and systems biology approaches to determine how channels interact to cause arrhythmia (6, 7, 8), and understanding the role of small-molecule pharmacodynamics in determining drug efficacy (9). One front that remains particularly challenging is the inclusion of molecular-level detail to explicitly represent a druggable target or the molecular consequences of a genetic mutation. The reasons for this lack of detail are multi-fold and include many theoretical and experimental limitations. However, recent developments on both fronts suggest that molecularly detailed models may be feasible in the near term.

By connecting the conformations of ion channels to the tissue-level dynamics, molecularly detailed models offer the potential to rapidly screen channel-drug interactions at the molecular level to assess their ability to stabilize the heart rhythm or, in the case of off-target interactions, provide an indication of cardiotoxicity. These models could also be used to identify combination therapies with multiple targets that would not necessarily be discovered intuitively. From the opposite direction, the inclusion of atomic interactions would provide a theoretical basis for predicting whether ion-channel genetic variants of unknown significance will predispose patients to cardiac arrhythmias. This approach could also suggest the best small-molecule options to treat patients with specific mutations, offering a route to personalized medicine.

Although these are only a few of the potential benefits of creating such models, the route to building them has been historically daunting.

Previous work

The idea that computational models of ion channel currents can be connected to the structure of ion channels is particularly tantalizing because of the correlation between the Hodgkin-Huxley (HH) models of the Na⁺ and K⁺ currents (10) and the structures of the channels that were discovered many years later. The HH model of the K⁺ current includes four independent “gates” (n⁴), and all four must reside in an activated conformation for the channel to open and conduct current. For the heart, the primary voltage-gated K⁺ channels that carry the delayed rectifier K⁺ currents, K_V11.1 and K_V7.1, form functional channels comprising four identical subunits, each with a voltage-sensing domain (VSD) that must be in the activated conformation for the channel to open. The HH Na⁺ current was modeled as three gates (m³) that remain closed at negative and open at depolarized potentials, and a fourth gate that is open at negative potential and closes, or inactivates, at higher potentials (h). Consistently, recent work has shown that the first three domains of the Na⁺ channel (DI–DIII) regulate channel activation, whereas the fourth domain (DIV) is more closely connected to channel inactivation (11, 12). Thus, even the very first models of the action potential represented the structures of channels to some degree.

Nevertheless, careful investigation of channel gating and single-channel recordings revealed that the assumption that each of the “gates” moves independently does not reflect the behavior of the primary currents that generate the cardiac action potential, including the Na⁺ current, delayed rectifier K⁺ currents, and the L-type Ca²⁺ current. To include the state dependence of channel gating, the field began using discrete-state Markov (DSM) models, which are a superset of the HH-type models (13). DSM models use states to represent the probability that channels reside in a conformation or set of conformations. Voltage-dependent transition rates between these states allow these probabilities to evolve over time and respond to changes in transmembrane potential. Clancy and Rudy used a DSM model to accurately simulate the single-channel kinetics of the cardiac Na⁺ channel and a mutant form that is found in patients with the long-QT syndrome. These models recapitulated single-channel behavior of the wild-type and mutant channels, and they were used to connect single-channel dynamics to the cellular-level phenotype (14). However, even though models based on this work are widely used, the model states are not meaningfully connected to the channel structure.

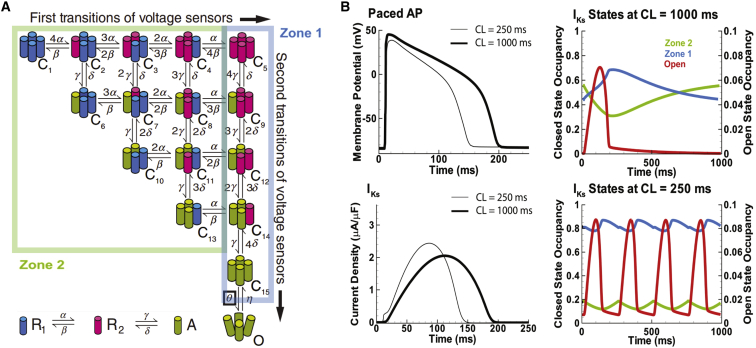
As with the HH-type models, more detailed Markov models do have the ability to reflect channel structure. For example, each state of the model could represent a permutation of activated or deactivated VSDs. We used this approach, following previous work from the Aldrich group (15), to model the slow component of the delayed-rectifier K⁺ current, I_Ks (16). Each of the four channel VSDs could occupy a resting, intermediate, or activated conformation, and channels could only transition to a permissive state once all four VSDs reached the activated conformation (Fig. 1 A). This model explicitly connected the conformations of the VSDs to ionic current kinetics and showed a role for the VSDs in determining how I_Ks participates in rate-dependent shortening of the action potential (Fig. 1 B). However, it was not clear at the molecular level what each state represented. For example, in each VSD state, we could not specify how far across the electric field the positive charges that cause channel gating were and which negative charges they were interacting with.

Figure 1.

Connecting the VSD state to the cardiac action potential. A model of slow delayed rectifier K⁺ current (I_Ks) was built to explicitly represent the VSDs and to understand how their state affects action potential dynamics. This figure was adapted from (16). (A) Following previous work (15), a 16-state model was built on the assumption that each VSD can occupy three potential states, resting (R1), intermediate (R2), and active (A). When all four VSDs enter the active state, the channel is permitted to make a cooperative transition into the open state. The model is divided into two zones. Zone 1 contains channels where all four VSDs have already accomplished the R1 to R2 transition. Zone 2 contains channels that have yet to make the transition. (B) Inserting the model into the action potential demonstrates that the I_Ks current increases at rapid pacing rates, which causes shortening of the action-potential duration. This rate-dependent shortening of the action potential allows for ventricular filling during diastole. Examining VSD occupancy shows that at fast rates, channels reside in Zone 1, where they are ready to open, increasing I_Ks for the next action potential.

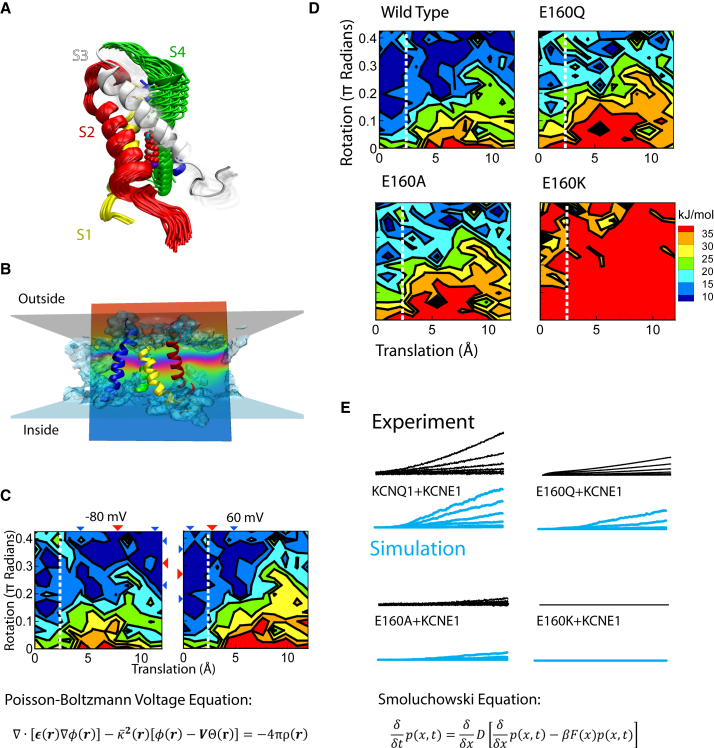
The contemporary release of the first mammalian K⁺ channel structure (17), K_V1.2, offered the opportunity to answer questions regarding the connection between the atomic-level details of channel structure and the states of the model. Work by others (18, 19) had shown that energy landscapes produced by electrostatic models could recapitulate channel dynamics with reasonable accuracy. Our goal was to create an I_Ks current model that included the interactions of charged amino acids indicated by the K_V1.2 structure (20). To begin, we created a K_V7.1 homology model of the VSD based on the K_V1.2 structure, which included the first four transmembrane segments (S1–S4) of one subunit. S4 carries most of the charge that moves in response to changes in membrane potential, so we created a series of structures where this segment was sequentially positioned at different translations and rotations along a plausible pathway toward activation (Fig. 2 A). The free energy for each of these poses was calculated using the Poisson-Boltzmann equation, which was modified by Roux to include the contribution from the transmembrane potential ((21); Fig. 2 B), to create an energy landscape that determines the VSD dynamics (Fig. 2 C). The Poisson-Boltzmann voltage equation has terms that account for charge screening, the dielectric constant in an implicit membrane, coulombic interaction between charges in the protein, and the membrane potential (Fig. 2 C, equation). The last step was to devise a means to move along the landscape, and we used the approach of Sigg and Bezanilla (18), employing the Smoluchowski equation to determine how a particle moves from point to point. The Smoluchowski equation contains two terms, one that accounts for particle diffusion and a second that reflects the force on the particle from the hills and valleys of the energy landscape (Fig. 2 E, equation).

Figure 2.

Probing the molecular underpinnings of VSD transitions and their role in the action potential. Electrostatic calculations were performed on a series of poses to create an energy landscape of VSD activation. This landscape was inserted into an action-potential model to predict ionic currents. By calculating the electrostatic impact on the energy landscape of mutating a negatively charged residue, the consequences for the current and the action potential could be predicted. This figure is modified from (20). (A) As a first pass at simulating VSD activation, several rotations and translations of the S4 helix were investigated. (B) The free energy for each pose was calculated with the Poisson-Boltzmann Voltage equation (21), which is accomplished by inserting the channel model into an implicit solvent. This solvent included a low-dielectric lipid, a transition region, and water. (C) Top: Points on the energy landscape represent a Boltzmann-weighted average of many poses, and after scaling, application of the membrane potential causes the VSDs to transition to the active state at positive potentials and the resting state at negative potentials. Bottom: The Poisson-Boltzmann voltage equation, where φ is the reduced electrostatic potential, r is the position, ϵ is the inhomogeneous dielectric constant, ρ is the density of charge within the protein, $\overline{\kappa }$² represents ionic screening, V is the transmembrane potential, and $\text{Θ}$ is a Heaviside step function. See reference supplement for details (20). (D) Mutating a negative charge on the S2 segment that is positioned to interact with positive charges on the S4 segment caused dramatic changes to the energy landscapes of the VSDs. (E) Top: Using the Smoluchowski equation (18) to allow the four VSDs to travel along these landscapes predicted currents that strongly resembled experimental recordings. Bottom: The Smoluchowski equation, where p(x,t) is the probability of finding a particle at a position x at time t, D is the diffusion constant, F(x) is the force on the particle, and β is 1 over the thermal energy. See reference supplement for details (20).

The model was successful at predicting how a series of mutations to a negative charge in the S2 segment would affect ionic-current kinetics (20) (Fig. 2, D and E). Moreover, it provided a potential route for investigating how molecular-level changes by mutations or drug interactions affect the cell and tissue-level phenotypes. However, there were several key limitations, which significantly limited the usefulness of this approach (22). First was reliance on a homology model, which brought in a questionable assumption that the charged interactions observed in the K_V1.2 structure were the same as those in K_V7.1. More importantly, there were very little experimental data available to test the model. We were missing data that measured the dynamics of the S4 movement and how mutations altered its trajectory.

Thus, although the model was successful in demonstrating a route for connecting the molecular, cellular, and tissue levels, it was of limited utility, particularly because experimental verification of many of the key assumptions was unavailable. In fact, channel models that are commonly used for action potential simulations today do not typically have states that are representative of the protein structure. Recently, there have been several key advances with the potential to address these difficulties and facilitate the creation and adoption of molecularly based models.

Experimental developments and limitations

One key limitation for many years has been the lack of structures for the key channels that create the cardiac action potential. However, cryo-electron microscopes have recently achieved the resolution needed to obtain structures of voltage-gated cardiac channels at atomic or near-atomic resolution. This year, the K_V11.1 (23) and K_V7.1 (24) structures were released. The importance of having a structure is highlighted by K_V11.1, whose VSDs are not domain-swapped as was observed in K_V1.2, a major structural feature that would be essential for creating a useful VSD model. Also of note are the first structures of four-domain Ca_V and Na_V channels (25, 26). The increasing pace at which these structures are being released suggests that the barriers presented by using homology models will not be as significant.

However, it is important to note that these structures typically represent channels that are in the open or inactivated states. This is unsurprising, because cell membranes reside at negative potentials at rest and channels are closed. In the depolarized conditions that channel structures are derived from, it is most likely that the VSDs will be in the activated or inactivated positions. As a result, homology models that are built on closed-state conformations from other channels are still often used to simulate the closed states of voltage-gated channels. Future work that shows these channels in many different states would greatly facilitate molecular-level simulations.

Structures are also inherently static and do not provide the dynamic data that is required for action-potential simulations. From the perspective of representing VSD dynamics in the action potential, key data come from an experimental protocol known as voltage-clamp fluorometry (VCF). During these experiments, a cysteine is introduced into the charge-carrying S4 segment of the VSD (27) that moves in response to changes in membrane potential. Once channels are expressed, a sulfhydryl-reactive fluorophore is conjugated to the introduced cysteine. As the VSD conformation changes, it alters the environment around the fluorophore to produce a measurable change in fluorescence magnitude. Simultaneously, ionic current through the channel pore can be observed via two-electrode or cut-open voltage clamp (28, 29). By providing a measure of VSD conformational changes while ionic currents are observed, VCF data provide an essential connection between VSD conformational dynamics and channel gating.

Recently, protocols to perform VCF experiments have been developed for each of the major cardiac voltage-gated channels (30), including K_V11.1 (31), K_V7.1 (32), and more recently for Ca_V1.2 (33) and Na_V1.5 (34). For the K⁺ channels, this work has shown how the VSDs couple to channel opening. Different states of the K_V7.1 VSD cause channel opening, depending on whether an accessory subunit, KCNE1, is present. VCF has also shown that Ca_V and Na_V channels are similar in that the domain IV VSD activates more slowly than the others with kinetics that are consistent with channel inactivation (12, 33). Recently we also showed that the domain III VSD of Na_V1.5 determines recovery from inactivation after action-potential length pulses, suggesting that it significantly contributes to the refractory period that follows excitation (35). These results demonstrate the potential for these methods to connect localized conformational dynamics to channel gating, and these are precisely the data that are required to test models that explicitly represent the VSDs.

A primary limitation of current VCF protocols is that, for the most part, they are limited to the Xenopus oocyte expression system. Although these cells provide the benefit of a relatively clean membrane where channels can be examined precisely and reproducibly, they also lack the accessory subunits and connections to intracellular proteins that native channels possess. However, because oocytes are quite large, 1 mm across, and produce currents in microampere range, they are ideal for detecting small changes in fluorescence magnitude. Conversely, the fluorescence signal from a mammalian cell will be smaller and the background relative to the change in fluorescence will be higher. Although the ability to perform VCF in these cells has been demonstrated (36), the protocols have not evolved to the point where they are regularly applied.

Although much has been gained from cryo-electron microscopy and VCF experiments, additional information could be gleaned from observing single-channel conformational dynamics. Such experiments could eventually provide probabilistic data that allow us to precisely understand how the movements of different channel domains participate in channel gating and its regulation. Recently, Wang et al. (37) applied single-molecule FRET to investigate the gating dynamics of the inward rectifier K⁺ (K_IR) channel, showing that the extracellular region remains rigid, whereas intracellular C- and N-terminal domains undergo significant conformational changes when the channel moves from closed to open. Such data could be used to test whether model dynamics are reflecting channel behavior and to simplify simulations by focusing them on the parts of the channel that are known to move and participate in channel gating.

The fluorescence methods described so far are compelling, because they provide data on the milliseconds to seconds time domains, which are of interest for understanding the dynamics of action potentials whose durations are typically in the hundreds of milliseconds. However, molecular dynamics simulations typically take femtosecond steps, and data reflecting fluctuations that take place at the micro- and nanoscales would certainly be of use. Recently developed NMR pulse sequences can reveal dynamics in the microsecond to millisecond range (38). As a proof of concept, we applied this approach to study the bacterial nonselective cation channel, NaK, and showed a dynamic connection between the selectivity filter and an intracellular constriction point within the channel pore (39). Although larger voltage-gated channels are much more difficult to study, such difficulty is outweighed by the potential of applying this and similar methods to aid in simulating time domains that are not as easily resolved with fluorescence-based methods.

Theoretical developments and limitations

Computational power presents a significant limitation to the size of the molecule that can be simulated and the duration of the simulation. Although processor speeds have been steadily increasing, they still do not approach the power that is necessary to run many trajectories that last for hundreds of milliseconds on a channel with thousands of residues that is situated inside of an explicit membrane and surrounded by water molecules. Nevertheless, a large step forward was made with the development of Anton by the D. E. Shaw Research laboratory. Their approach was to develop a new supercomputer that was specifically engineered for molecular dynamics simulations. This computer uses application-specific integrated circuits that are connected by a specialized network and custom software to greatly accelerate the molecular dynamics calculations (40).

The first VSD trajectory, using the K_V1.2 structure, was accomplished using Anton, and the results of the simulation recapitulated many different historic observations. Still, to accomplish this feat, many different simulations had to be stitched together and membrane potentials of 375–500 mV were required to cause significant movement of the VSD (41). Another limitation is that only a single trajectory was accomplished, so other paths traversed by the VSD, which may even be more likely, could not be explored. An installation of Anton at the Pittsburg Supercomputer Center has been recently used to simulate permeation through different channels including the bacterial voltage-gated Na⁺ channel (42, 43), although progress in completing additional VSD simulations has been limited.

More recently, Delemotte et al. (44) simulated the VSD trajectory of K_V1.2 by applying a modified version of well-tempered metadynamics, an approach where a repulsive potential is applied along certain reaction coordinates to prevent the simulation from repeatedly visiting the same conformations and allowing it to explore a much larger configuration space. With this approach, they were able to identify multiple pathways between different metastable states, demonstrating that the energy landscape that describes the VSD is rough and that there are likely to be many paths from one stable state to another. This year, the same group has extended this approach to create a DSM model to calculate K_V1.2 gating currents (45), connecting all-atom molecular dynamics simulations to channel electrophysiology.

Another promising approach, which has been used to create Markov state models for smaller proteins, is to use many (hundreds) of short simulations of varying duration (nanoseconds to microseconds) to identify a large number of states (∼10,000). A sophisticated algorithm is then used to cluster conformations together to define a state and to identify the transition probabilities between each of these states (46). Although this method has not yet been applied to ion-channel dynamics, due to their size, it offers a promising future way forward to directly create Markov state models from molecular dynamics simulation data.

The development of clever simulation strategies and the inevitable increase in computational power that is on the horizon suggest that it will eventually be possible to simulate atomic interactions within large voltage-gated channels. However, a key challenge remains in that these models are likely to be incredibly complex, to the point where they may not be useful. For example, the cardiac Na⁺ channel contains many subdomains with distinct functionality that has been defined experimentally. Each of the four domains (DI–DIV) contains a VSD, and each one is allosterically coupled to a pore domain for a total of eight components. In addition, the DIII-DIV linker causes inactivation, and its action can be stabilized by the C-terminal domain. Thus, without adding the effects of many accessory subunits (47), and assuming that each of these components can only occupy two states, we require 2¹⁰ states to account for every permutation that could be occupied by this model. Moreover, based on the simulation results from Delemotte (44) and experimental data probing VSD conformations, a two-state assumption for each component does not appear wise.

One approach to solving this dilemma is to reduce the size of the manifold by assuming that some of these states are similar (48). For example, when simulating a K⁺ channel, a state where one of the VSDs is in the deactivated state represents four different possible channel conformations, because each channel has four subunits. However, since all of the subunits are identical, it can be assumed that these states can be lumped into a single state, as in Fig. 1 A. Similarly, for the Na⁺ channel activation gates to be represented by m³, one must assume that the DI–DIII VSDs are similar enough to be represented as an identical entity. Unfortunately, a multitude of experimental evidence strongly suggests that this is not the case. Thus, there are limits to how many states can be removed using this approach.

Still, the highly complex gating of Na_V and Ca_V channels can be well represented by models with <10 states. Between models that comprise 10 states and those that require 2¹⁰ states, there is a middle ground. Such a middle ground may be found by focusing on a region of interest, for example, representing the molecular dynamics of one or two VSDs in detail while representing the rest of the channel more coarsely. However, a remaining challenge is how to construct the rest of the model. One promising approach has been put forward by Menon et al. (49), who developed a state-mutating algorithm that optimizes not only Markov model rates but also the number of states and the connections between them. Although the original publication used a genetic algorithm for this optimization, we found that using multi-chain simulated annealing allowed the algorithm to identify suitable models much more reliably (50). Still, we have noted that adding states to the model causes a large jump across the minimization landscape before the neighborhood is adequately explored. Thus, as model complexity increases and more protocols are added, the optimization is less likely to converge. Additional improvements to the optimization algorithm could eventually make this approach more reliable.

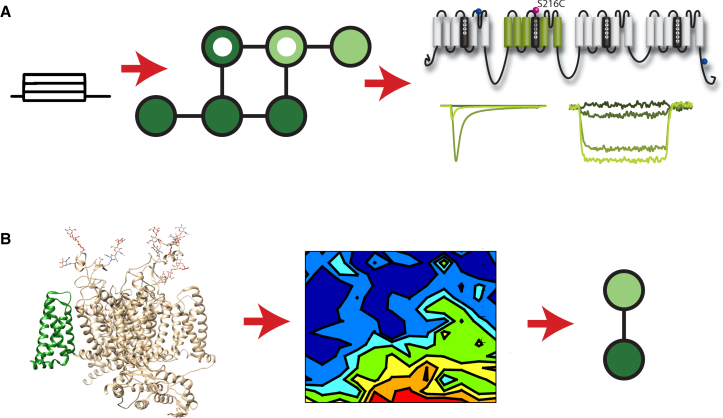
Currently, the state-mutating approach, even if it need be accomplished via brute force, offers tremendous promise. For example, to create a model that explicitly represents VSD kinetics, the state-mutating algorithm would be used to reproduce voltage-dependent VSD dynamics as tracked by fluorescence output and ionic-current kinetics (Fig. 3 A). Fluorescence collected from channels with mutations (34, 51) that simultaneously perturb gating and VSD activation could be used to iteratively improve the models. Once the connection between VSD and the rest of the coarsely modeled channel is understood, the energy landscape from a molecular dynamics simulation could be substituted in to understand the role of atomic interactions in shaping the ionic current and the action potential (Fig. 3 B).

Figure 3.

A path to molecularly detailed kinetic models of complex channels. The complexity of four-domain channels complicates the approach used for K⁺ channels in Figs. 1 and 2. An alternative approach is to use VCF experiments in combination with state-mutating algorithms to create models that represent only a single VSD. VCF data in the figure are adapted from (34). (A) Kinetic models of ion channels are typically parameterized to recapitulate ionic-current dynamics that result from a series of pulse protocols. One or more states in the model graph are identified as open (inner white circles). By also identifying states as having a resting (darker circles) or active (lighter circles) VSD, fluorescence dynamics can also be simulated, allowing a single VSD in a complex channel to be explicitly represented. Shown are the fluorescence-reporting conformation of domain II of the cardiac Na⁺ channel and the ionic current that was recorded simultaneously. (B) Once the relationship between the VSD transition and the rest of the channel is modeled, an energy landscape derived from MD simulations can be used to simulate the VSD transition. The structure shown was rendered from PDB: 5X0M (26) of the eukaryotic cockroach Na⁺ channel with the domain II VSD shown in green. This approach reduces the need to derive models from simulations of the whole channel, which are not currently tenable.

Concluding remarks

In the last several years, many significant barriers that have historically stood in the way of molecularly based models have come down. Yet significant hurdles still need to be addressed before atomically detailed models of full channels can be incorporated into action-potential models. Until then, recent work has made detailed models that focus on one or two VSDs possible. Although not the end goal, these models have the potential to greatly improve our understanding of how molecular-level defects and drug interactions shape channel gating, the action potential, and the ability of the heart to initiate and sustain arrhythmia.

Editor: Brian Salzberg.