Mechanisms of Plastic Deformation in Collagen Networks Induced by Cellular Forces

Abstract

Contractile cells can reorganize fibrous extracellular matrices and form dense tracts of fibers between neighboring cells. These tracts guide the development of tubular tissue structures and provide paths for the invasion of cancer cells. Here, we studied the mechanisms of the mechanical plasticity of collagen tracts formed by contractile premalignant acinar cells and fibroblasts. Using fluorescence microscopy and second harmonic generation, we quantified the collagen densification, fiber alignment, and strains that remain within the tracts after cellular forces are abolished. We explained these observations using a theoretical fiber network model that accounts for the stretch-dependent formation of weak cross-links between nearby fibers. We tested the predictions of our model using shear rheology experiments. Both our model and rheological experiments demonstrated that increasing collagen concentration leads to substantial increases in plasticity. We also considered the effect of permanent elongation of fibers on network plasticity and derived a phase diagram that classifies the dominant mechanisms of plasticity based on the rate and magnitude of deformation and the mechanical properties of individual fibers. Plasticity is caused by the formation of new cross-links if moderate strains are applied at small rates or due to permanent fiber elongation if large strains are applied over short periods. Finally, we developed a coarse-grained model for plastic deformation of collagen networks that can be employed to simulate multicellular interactions in processes such as morphogenesis, cancer invasion, and fibrosis.

Introduction

The behavior of living cells is affected by both elastic (1, 2) and inelastic (3, 4) mechanical properties of the microenvironment. Inelastic mechanics of the extracellular matrix (ECM) may be viscoelastic or plastic (5, 6), the latter leading to long-term irreversible deformations. Given that the architecture and stiffness of the ECM influence cell spreading, motility, and differentiation (1, 2), the degree of matrix plasticity after mechanical reorganization is likely to be a major determinant of cell behavior. For example, the persistence of fiber alignment in the ECM results in the continued presence of mechanical cues that guide the orientation and migration of normal (7) and cancer cells (8, 9). Several previous cell-ECM studies reported residual mechanical effects in fibrous matrices after removing external physical forces. For instance, previous studies have shown that fibroblasts can generate substantial pulling forces (10), and contract the matrix (11), which leads to the formation of patterns (12) including ligament-like straps of fibers (13), all of which persist after cellular forces are eliminated (10, 11, 12, 13, 14). These experiments implicate plasticity as a relevant mechanism in cell-ECM interactions.

Type I collagen is the most abundant protein in the ECM, and collagen fiber networks are the primary determinants of the mechanics of connective tissues (15). Therefore, reconstituted collagen hydrogels are commonly used as models for studying the mechanics of fibrous ECMs (15). Collagen type I networks are linearly elastic before reaching a critical strain, after which they transition to an exponential stress-strain regime (16). Previous shear rheology studies have demonstrated that the viscoelastic behavior of collagen (17, 18, 19) is nonlinear at large strains (20, 21), exhibiting faster stress relaxation with growing strain (21), and may lead to residual strains that remain after the networks are unloaded (14). Similarly, plastic effects have been reported when subjecting collagen networks to compression (22, 23, 24, 25) and tension (26). Previous studies have shown that collagenous tissues show strain-stiffening and nonlinearly viscoelastic properties as well (27, 28, 29). The peculiar elastic and viscoelastic behaviors are explained using model networks that allow the connection of fibers by weak cross-links modeled as slip bonds (21). The plasticity of collagen networks, however, remains poorly understood in comparison with elasticity and viscoelasticity. Furthermore, the existing models for ECM mechanics (5, 6, 14), used in modeling processes such as cancer metastasis (30, 31), fail to capture fiber densification and plastic effects, which are involved in mechanical remodeling of ECMs.

In this work, we studied the mechanisms of plastic deformation of fibrous ECMs using contractile clusters of mammary acini and fibroblast spheroids placed atop collagen type I gels. We combined experimentation with theoretical modeling to quantify the plastic effects in collagen fiber networks and identified the mechanisms of plasticity depending on the rate and amplitude of strain and the mechanical properties of fibers. Based on our observations of large transverse contraction and densification in the tracts, we developed a fiber network model that explains plasticity by the stretch-dependent formation of weak cross-links. We validated predictions from this model using shear rheology experiments. Our tests indicated that plastic effects are substantially enhanced with increased collagen concentration. We also assessed the possibility of network plasticity by the permanent elongation of individual fibers. We used the network models to quantify and classify network plasticity depending on the amplitude and rate of the applied strain and fiber properties. Finally, we developed a coarse-grained continuum model that reproduces both network densification and plasticity by accounting for the formation and dissociation of transient cross-links.

Materials and Methods

Acini cell-ECM experiments

Rat tail collagen (Corning, Corning, NY) was gelled at 2.0 mg/mL on prechilled glass-bottom imaging dishes (MatTek, Ashland, MA) according to the manufacturer’s protocol. Briefly, solubilized collagen was diluted to 2.0 mg/mL using 10× Tris-buffered saline and 5 mM NaOH; 300 μL was plated on the 20-mm glass-bottom portion of a 35-mm dish (MatTek). For measuring substrate displacement, 1 μm Nile Red (535/575) fluorescent beads (Life Technologies, Carlsbad, CA) were added at 2000× dilution from a 2% (wt/vol) stock. Dishes were incubated at 37°C for 30 min. MCF10AT acini were cultured and extracted as described previously (32, 33). Collagen gels were rinsed with MCF10A media and acini were seeded on the gel portion of the dish. The dishes were incubated at 37°C for 2 h to allow acini to settle before adding more media, collagen staining, and live imaging. Collagen was stained with purified CNA35-SNAP. Contractility inhibitor drugs (2 μg/mL Latrunculin B, 2 μg/mL Cytochalasin D, and 25 μM FAK inhibitor 14) were added 10 h post-acini seeding on collagen. In the experiments, which tested the effect of lysyl oxidase (LOX) on plasticity, β-aminopropionitrile (BAPN; Sigma-Aldrich, Saint Louis, MO) was used to inhibit the formation of new cross-links by LOX. In these experiments, BAPN was added when acini were seeded. Local collagen concentration was estimated by scaling the CNA35-SNAP647 intensity far from the acini to a mean value of 2 mg/mL, which corresponds to the initially undeformed concentration of collagen in gels. Estimations are performed for each time point to account for photobleaching or variation in imaging throughout the time-lapse acquisition. Local enhancement of CNA35-SNAP647 intensity was used to estimate collagen concentration (Fig. S1).

Fibroblast spheroid experiments

NIH 3T3 fibroblasts were cultured in growth media (high glucose DMEM, 10% fetal bovine serum, 1% penicillin/streptomycin, and 0.5% fungizone). Approximately 500 cells were suspended in a 20 μL hanging droplet in a hydrated Petri dish. Cells were cultured inverted for five days during which spheroids formed. Collagen gels were prepared at a concentration 1.5 mg/mL (see the Supporting Material for more details). Note the slight difference in the collagen concentration in comparison with the acini experiments.

The gels were rinsed with media, and single spheroids were manually transferred to the gel with pairs placed ∼500 μm apart. Spheroids were allowed to adhere to the gel for 3 h, and then 2 mL of appropriate media was added to the dish. Inhibitors (1 μM blebbistatin (Sigma-Aldrich) or 0.05% trypsin (Sigma-Aldrich)) were added to the media 24 h after seeding. Next, the plates were fixed for 10 min in 10% neutral buffered formalin (Fisher, Hampton, NH), washed twice with PBS, sealed with Parafilm (Bemis NA, Neenah, WI), and stored at 4°C. Fibrillar collagen was visualized by second harmonic generation (SHG) imaging (see the Supporting Material for more details).

Shear rheology experiments

To assess the plasticity of collagen networks, creep and recovery tests were performed using an AR-G2 stress-controlled rheometer (TA Instruments, Newcastle, DE) with 25-mm-diameter geometry for the top and bottom plates. Poly-L-lysine-coated coverslips (25 mm; Neuvitro, El Monte, CA) were glued to the surface of the plates to enhance attachments of collagen gels. Collagen solutions of varying concentrations were deposited onto the bottom plate; the top plate was immediately brought down to form a ∼50 μm gap between the two plates. The exposed surfaces of the collagen gels between the two plates were sealed with mineral oil (Sigma-Aldrich) to avoid dehydration. Continuous oscillations at a strain amplitude and frequency of 0.01 and 1 rad/s were applied to monitor the storage modulus of collagen solution during gelation. When the storage modulus reached an equilibrium value, creep tests were performed. In creep tests, the adjusted stress was applied to reach a similar magnitude of strain at the end of the creep test. Then, the stress was removed in recovery tests, and the relaxation of strain was monitored for an hour and 15 min. The degree of plasticity was calculated as the ratio of the residual strain after recovery to the maximum strain at the creep tests (14).

Statistical analysis

One-way analysis of variance (ANOVA) followed by Holm-Sidak multiple comparisons tests was used to evaluate the significance of the plastic effects observed using the mean intensity of alignment obtained from SHG microscopy. To determine the statistical significance of the increase in the degree of plasticity caused by the increase of collagen concentration, we performed Spearman’s correlation test and ANOVA followed by Tukey’s multiple comparisons test.

Discrete fiber network models

To theoretically investigate the microstructural deformation of the fibrous matrices, we used discrete fiber network models. A random network of fibers deposited on a planar domain was used to model the possibility of plastic deformation by the formation of new cross-links between fibers. Three-dimensional diluted lattice and Voronoi network models were also used to study the possibility of plastic network deformation by the permanent elongation of fibers. The fiber network simulation methods are further explained in the Supporting Material.

Continuum coarse-grained constitutive model

We implemented our constitutive model as a user material in the finite element package, Abaqus (34). In all tests, the domain boundaries were located at least 500 μm away from the contractile cells. The boundaries were fixed in place except in tests with a single pair of acini, where symmetric boundary conditions were employed. Calculations were performed using a geometrically nonlinear, implicit finite element method. The time integrals were numerically implemented by using 40 discretization time points in the creep and recovery tests and three time points in the acini tests. At each time point, t, new cross-links were formed at the rate ${\overline{k}}_{\text{on}}-{\overline{k}}_{\text{off}}$ρ(t), where ρ(t) is the density of cross-links at time t and ${\overline{k}}_{\text{on}}$ and ${\overline{k}}_{\text{off}}$ are evaluated using the deformation gradient at t, F(t). At time t, the cross-links formed at previous time points, τ, were dissociated at the rate ${\overline{k}}_{\text{off}}\rho \left(\tau \right)$, where ${\overline{k}}_{\text{off}}$ was evaluated using the relative deformation gradient from τ to t, F_c(τ, t). Two types of weak cross-links were considered to model the viscoplastic strain response of the matrix. The kinetics of the second type of cross-links is governed in the same fashion as the first type, while using a different set of parameters, ${\overline{k}}_{\text{off}}^{\prime 0}$, ${\overline{k}}_{\text{on}}^{\prime 0}$, ${\overline{\epsilon }}_0^{\prime }$, ${\overline{\lambda }}_0^{\prime }$, and ${\overline{\lambda }}_{\text{eq}}^{\prime }$. Because the variation of the matrix volume is proportional to the determinant of the deformation gradient, |F(t)|, the change in matrix concentration was calculated by evaluating | F(t)|⁻¹. The strain energy of the cross-links, W_c, was evaluated as αW_b. The value W_b denotes the energy of the isotropic fibers, previously used in our fibrous constitutive model (6), and α is the ratio of the energy of one cross-links to the unit volume of isotropic fibers at the same state of deformation. Model parameters are given in Table S1.

Results

Collagen densification and matrix strains persist in the tracts induced by contractile acini after abolishing cellular forces

We first examined the mechanical plasticity of collagen tracts that bridge groups of mammary acini. Fluorescent beads embedded in type I collagen gels (2.0 mg/mL) were used to calculate the displacement fields (an example measurement is shown in Fig. S1 a) and stretches at the top layer of the gels. Gels were also stained with a dye-labeled collagen binding protein (CNA35-SNAP-Alexa647) to provide estimations of the local variations in collagen concentration. Control experiments using gels of different concentrations showed that the changes in the maximum fluorescence intensity through the depth of the gels are approximately proportional to the changes in the concentration of collagen (Fig. S1 b). We, therefore, used this relation to quantify collagen densification by measuring fluorescence intensity.

Mammary acini were formed by embedding MCF10AT premalignant mammary gland epithelial cells within a reconstituted basement membrane matrix. After 8 d, the acini were extracted, washed, and seeded atop collagen gels (Fig. 1 a). We examined acini in two settings: first, groups of acini interacting with each other, where a single acinus was involved in multiple pairwise interactions (Fig. 1, a–d; Fig. S2); and second, isolated pairs of acini interacting only with each other (Fig. S3). As previously reported (33, 35), the acini are contractile and begin pulling the matrix toward themselves after adhering to the fibrous matrix. Within a few hours, the accumulated strains lead to large-scale fiber alignment and matrix densification, and high-concentration collagen tracts form along the axes connecting adjacent acini (Fig. 1 b). The corresponding fluorescence image and stretch maps are plotted in Fig. S2. Ten hours after seeding, we observed increased collagen concentration around the acini and along the tracts, connecting pairs of acini (Fig. 1 b). Larger densification effects were observed along the tracts formed by isolated pairs. The fluorescence image and local concentration plots obtained 4 and 17 h after seeding an isolated pair of acini are shown in Fig. S3.

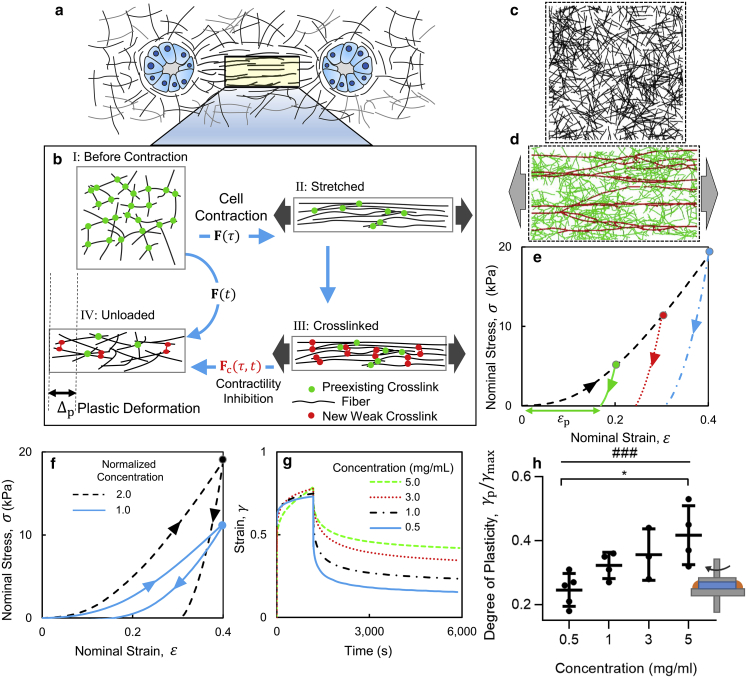
Figure 1.

Mechanical plasticity leads to the persistence of collagen densification and alignment within the tracts induced by cell forces after abolishing cell contractility. (a–d) Collagen densification remained in the tracts formed between adjacent contractile mammary acini after we eliminated cellular forces. (e–h) Fiber alignment persisted in the fibrous tracts formed between adjacent contractile spheroids of fibroblasts. (a) Collagen concentration is given in a system of four interacting acini 4 h after they were seeded, (b) at the onset of inhibiting contractility (10 h after seeding), and (c) 24 h after inhibiting contractility. (d) Estimated collagen concentration in (circles) regions 1, (triangles) 2, (diamonds) 3, and (crosses, background) 4 (marked in (b)) plotted against time after seeding. The acini experiments were repeated four times using distinct collagen gels, and plasticity was observed in all samples. (e) The intensity of collagen fiber alignment was calculated using the intensity of SHG (in blue) between pairs of fibroblast spheroids and cellular autofluorescence (in green) after incubation for 12 h atop a collagen type I gel. The tracts of aligned fibers persisted 24 h after (f) inhibiting cellular contractility using blebbistatin and (g) dissociating the spheroids from the matrix using trypsin. The small white spot in (f) and the blue streak in (g) near the bottom spheroid are imaging artifacts. (h) The SHG intensity of fiber alignment is given, along the region enclosed by the dashed lines versus distance from the axis connecting the midpoints of two cell clusters; SDs are used to plot the pale curves (averaging was performed over 8–12 samples). The fibroblast SHG experiments were repeated using three distinct collagen gels, and plasticity was observed in all samples. To see this figure in color, go online.

We quantified the persistence of strains and collagen densification within the tracts by inhibiting cell contractility in the gels with established tracts (10 h after seeding). We treated the culture with a drug cocktail (latrunculin, cytochalasin D, and focal adhesion kinase inhibitor 14) to inhibit cellular traction forces. After adding the cocktail, matrix reorganization stopped, strains began to relax, and collagen concentration at the tracts slightly decreased. We observed that significant residual strains and densification effects remained in the tracts even 24 h after drug treatment (Fig. 1 c). A similar result was observed in experiments using an isolated pair of acini (Fig. S3 d, 2.5 h after treatment with drugs). Measurements of collagen concentration in regions of interest along the tracts quantify the densification and its persistence during our experiments (Fig. 1 d; Fig. S3 e). Our preliminary experiments also demonstrated that the plastic effects persisted when BAPN was added to inhibit the formation of new cross-links by LOX after the acini where seeded (Fig. S4). We, therefore, conclude that the formation of new cross-links by the activity of LOX is unlikely to cause the plastic effects observed in our experiments.

Our strain analysis revealed large Poisson effects and plastic strains in the matrix. To calculate displacement fields, we tracked fluorescent beads using particle velocimetry. The maximum and minimum principal stretch fields, λ_max and λ_min, and their ratio, λ_max/λ_min, were calculated for the multiple-acini experiments (Fig. S2, b–d). We found large stretch ratios (λ_max > 1) along the tracts and significant contractions (λ_min < 1) in the in-plane transverse direction (Fig. S5). We found large Poisson effects (i.e., large contractions transverse to the stretch direction in the collagen tracts) with apparent Poisson’s ratios higher than 1.0. The stretch plots show that the cell-induced strains were not relaxed after we eliminated cellular forces. Approximately 40% strain (stretch ratio of ∼1.4) developed along the tracts at the onset of eliminating contractility (Fig. S5 a). Only ∼10% of the strain was relaxed after we eliminated cellular forces, resulting in ∼30% plastic strain (Fig. S5 d).

Persistence of fiber alignment in the tracts formed by contractile fibroblast spheroids

Fibroblast cell spheroids seeded atop collagen type I gels were used to study mechanical plasticity in the collagen-rich tracts that form between the contracting spheroids. In these experiments, we used SHG imaging to quantify fiber alignment while avoiding the possible mechanical artifacts caused by fluorescent labeling (36). Pairs of NIH 3T3 fibroblast spheroids, formed by the hanging droplet method (37), were seeded ∼500 μm apart on 1.5 mg/mL collagen gels. Similar to the mammary acini, pairs of contractile spheroids formed tracts of aligned collagen fibers (Fig. 1 e). The SHG signal was significantly more intense along the axis connecting the spheroids in comparison with regions away from it (Fig. 1 e), and substantial fiber alignment was found along the axis.

We next eliminated contractility of the fibroblasts using blebbistatin and trypsin, which inhibit myosin activity and detach cells from the matrix, respectively. We observed that fiber alignment persisted in the matrix 24 h after eliminating contractility. The intensity and the anisotropy of the SHG signal slightly decreased after eliminating contractility, whereas the intensity of alignment at the tract remained substantially larger (p < 0.005, one-way ANOVA followed by Holm-Sidak multiple comparisons test) than that in the background (Fig. 1, f–h; Fig. S6). Together with the mammary acini experiments, these results demonstrate the persistence of fiber alignment and the plasticity of matrix deformation induced by the cells.

Plastic deformation of collagen networks by the formation of weak cross-links

Our cell-ECM experiments showed that cell contractility induces significant strains in the matrix (Fig. S5 a). When the collagen network is deformed, fibers reorient and align along the direction of stretch. Network stretching is accompanied by a significant contraction in the in-plane transverse direction (38) and a large Poisson’s ratio (39). These effects bring the aligned fibers close to each other and create highly dense tracts. Previous studies suggest that when a fibrous matrix is reorganized, the adjacent fibers fuse (10, 11) or adhere by weak physical forces (10). Other studies indicate that new cross-links may form between fibers that preserve residual stresses in fibrous ECMs, reorganized by cellular forces (40, 41). We hypothesized that as the network is stretched, new cross-links form in a stretch-dependent manner when aligned fibers come close. As the external forces are removed, these cross-links prevent the elastic recovery of network deformation (Fig. 2, a and b). We tested this hypothesis using a micromechanical fiber network model. The network model produces plastic strains consistent with our experimental results and predicts a correlation between collagen concentration and the plastic effects.

Figure 2.

Plastic deformation of collagen networks by the formation of weak cross-links. (a) Schematic representation illustrates two contractile cell clusters in a fibrous collagen gel. (b) Schematic illustration shows the origin of the plasticity of networks by the formation of weak cross-links within the aligned tract of fibers. The high Poisson’s ratio of fibrous networks in tension and the formation of cross-links between stretched fibers leads to plastic deformation, Δ_p, when the network is unloaded. Snapshots are given of the interpenetrating fiber network model that accounts for the formation of new cross-links (c) at the initial state and (d) after 20% stretch. The highly stretched fibers are highlighted in red. The other fibers are shown in green. (e) Stress-strain curves of networks are unloaded at different amplitudes of strain. (f) The network model predicts an increase in plastic strain with increasing collagen concentration. (g) Strain against time is given in shear rheology creep and recovery tests performed at different concentrations of collagen. (h) The plot of the degree of plasticity against collagen concentration from shear rheology experiments confirms that plasticity increases with increasing collagen concentration (###p < 0.0005, Spearman’s rank correlation and ^∗p < 0.05, one-way ANOVA test with Tukey’s multiple comparisons test). Three to five distinct samples were tested at each concentration. The mean ± SD is plotted at each concentration. The inset shows a schematic of the shear rheology experiments. To see this figure in color, go online.

Our model is based on a random network of interpenetrating fibers that we previously used to study the elastic deformation of biopolymer networks (42). Briefly, we generated a network by randomly placing fiber segments in a rectangular domain and forming cross-links at the intersection of fibers (Fig. 2 c). We stretched the network by horizontally displacing the nodes of fibers located on the left and right network boundaries in opposite directions (Fig. 2 d). The network exhibited a strain-stiffening stress-strain response (38) accompanied by alignment of fibers in the loading direction (Fig. 2, e and d). We modeled stretch-dependent formation of weak cross-links by attaching the fibers that come in contact; the rate constant for the formation of new cross-links is denoted by k₀. The new cross-links are stress-free when they first form, and undergo deformation when the network is further loaded. When the network is unloaded, in the absence of new cross-links, the network expands perpendicular to the stretch direction, and the aligned fibers return to their original (isotropic) orientations. In the presence of new cross-links, however, the aligned fibers are held together, and the cross-links resist the complete recovery of the network. Therefore, a plastic axial strain, ε_p, emerges when the applied forces are removed (Fig. 2 e). Using a rate constant of 0.01 h⁻¹ for the formation of new cross-links, we obtained 30% plastic strain after unloading the network, which was initially deformed to 40% nominal strain (Fig. 2 e). This result is consistent with the plastic strains observed along the collagen tracts in our experiments.

The network model predicts that plasticity due to the formation of new cross-links depends on the density of fibers in the network. In a denser network, more cross-links form because more fibers come in contact when the network is stretched. This effect leads to larger plastic strains. The predicted stress-strain curves from the network model at two different fiber densities are plotted in Fig. 2 f. We tested this prediction using shear rheology experiments described in the next section.

Increasing collagen concentration enhances plastic deformation

We used shear rheology experiments to test our model’s prediction that there is a correlation between plastic strain and collagen concentration. Collagen type I gels were formed between the two plates of a stress-controlled rheometer. The tests comprised two steps: creep and recovery (14). In the creep step, we applied a constant stress to the sample for 20 min, deforming it up to a maximum shear strain, γ_max. Next, we removed the applied stress and allowed the sample to relax. The sheared sample did not completely undeform to its original shape and significant residual shear strains, γ_p, remained in the network (Fig. 2 g). We quantified the degree of plasticity as plastic shear strain normalized by the maximum strain. By testing gels with collagen concentrations of 0.5, 1.0, 3.0, and 5.0 mg/mL, we found that the degree of plasticity increases with increasing collagen concentration (Fig. 2 h, Spearman’s rank correlation, p < 0.0005, and one way ANOVA test with Tukey’s multiple comparisons test, p < 0.05). These experiments verified the prediction of our network model.

A coarse-grained constitutive model for collagen plasticity through the formation and dissociation of weak cross-links

Fiber network models provide insights into the microstructural mechanisms of deformation in fibrous matrices. However, they are computationally expensive for simulating multicellular interactions in a tissue, given the large numbers of fibers and cells that must be considered. Coarse-grained continuum models were therefore used to model fibrous matrices to study biological processes such as cancer invasion (30, 31). We used insights from our experiments and network models to develop a coarse-grained constitutive model that enabled us to model inelastic matrix deformation at the tissue scale. Our model can be used in the quantitative analysis of biological processes such as morphogenesis, cancer metastasis, and fibrosis by providing an accurate description of matrix densification and plasticity.

This model builds on the elastic fibrous constitutive law we previously developed for modeling long-range force transmission in fibrous matrices (6, 43, 44). The previous constitutive law models the mechanical behavior of fibrous matrices by accounting for network contraction in the transverse directions and strain-stiffening along the direction of the largest tensile principal stretches. In this model, the deformation of the material at time t is quantified by the deformation gradient tensor, F(t), and the strain energy density required to deform the matrix by F(t) is denoted by W(F(t)). The present model extends the previous model to account for plastic effects. We account for both the preexisting cross-links and the cross-links formed during deformation. At time τ, cross-links form and dissociate at rates ${\overline{k}}_{\text{on}}$ and ${\overline{k}}_{\text{off}}$ρ(t), where ρ(t) is the density of cross-links at time τ. We modeled the stretch-dependent formation of new cross-links (45, 46) using a rate constant ${\overline{k}}_{\text{on}}={\overline{k}}_{\text{on}}^0\text{exp}\left(-\left({\lambda }_{\text{min}}^2-{\overline{\lambda }}_{\text{eq}}^2\right)/{\overline{\lambda }}_0^2\right)$, where λ_min is the smallest principal stretch ratio (Fig. S7 a), ${\overline{k}}_{\text{on}}^0$ is the association rate constant before deformation, and ${\overline{\lambda }}_{\text{eq}}$ and ${\overline{\lambda }}_0$ control the sensitivity of the association rate to matrix stretch. The formation of weak cross-links is enhanced by increasing the stretch ratio because the aligned, stretched fibers in regions of large tensile strains have more new neighbors and are therefore more likely to form new cross-links. We also adopted a stretch-dependent relation for the dissociation rate of cross-links: ${\overline{k}}_{\text{off}}={\overline{k}}_{\text{off}}^0\text{exp}\left(\left({\lambda }_{\text{max}}-1\right)/{\overline{\epsilon }}_0\right)$, where ${\overline{k}}_{\text{off}}^0$ is the cross-link dissociation rate constant before deformation; λ_max is the largest principal stretch ratio (Fig. S7 a); and ${\overline{\epsilon }}_0$ is a parameter similar to${\overline{\lambda }}_0$. Stretch-dependent disassociation was modeled based on previous experimental results (21).

Strain energy of the cross-links is zero when they first form, but it increases with further deformation of the matrix. The cross-link strain energy density, W_c, is therefore evaluated as a function of the relative deformation with respect to the mechanical state where the cross-links were formed. At time t we quantify the deformation of a cross-link formed at time τ by a relative deformation gradient F_c(τ, t) (Fig. 2 b; Fig. S7 b). The deformation gradient at t can be decomposed as the deformation gradient at τ left-multiplied by the relative deformation gradient from t to τ. Therefore, the relative deformation gradient from time τ to time t can be evaluated as

$${\mathbf{F}}_{\text{c}}\left(\tau ,t\right)=\mathbf{F}\left(t\right)\mathbf{F}{\left(\tau \right)}^{-1}.$$ (1)

At time t, the strain energy of a cross-link formed at time τ can be expressed as W_c(F_c(τ, t)). We calculate the total strain energy density of the network by integrating the energy density of cross-links over time and adding the deformation energy stored in the fibers as

$$W^{\ast }\left(t\right)=\underset{0}{\overset{t}{\int }}{W}_{\text{c}}\left({\mathbf{F}}_{\text{c}}\left(\tau ,t\right)\right)\dot{\rho }\left(\tau \right)d\tau +W\left(\mathbf{F}\left(t\right)\right).$$ (2)

Here $\dot{\rho }$(t) denotes the rate of change of the density of cross-links. Further details about the evaluation of ρ(t) are described in the Materials and Methods. We determined the parameters of the model using viscoplastic shear rheology experiments and tested the model by reproducing the densification and plasticity observed in our cell-ECM experiments.

The chemo-mechanical parameters for the formation and dissociation of cross-links were chosen to reproduce our creep and recovery experiments using collagen (14). At the creep stage, a constant shear stress of 80 Pa was applied (Fig. 3 a, inset) for 300 s, and the resulting time-dependent strain was measured. At the recovery stage, the applied shear stress was removed, and we allowed the gel to relax. Two types of cross-links were used to model the behavior of collagen gels. The gradual dissociation of the first type of cross-links causes the creep response under constant stress. Weak cross-links of the second type form when new fibers come in contact as the gel is deformed and remain after external loading is removed. Within the updated reference framework used in the coarse-grained model, this behavior led to residual strains, after the sample was unloaded.

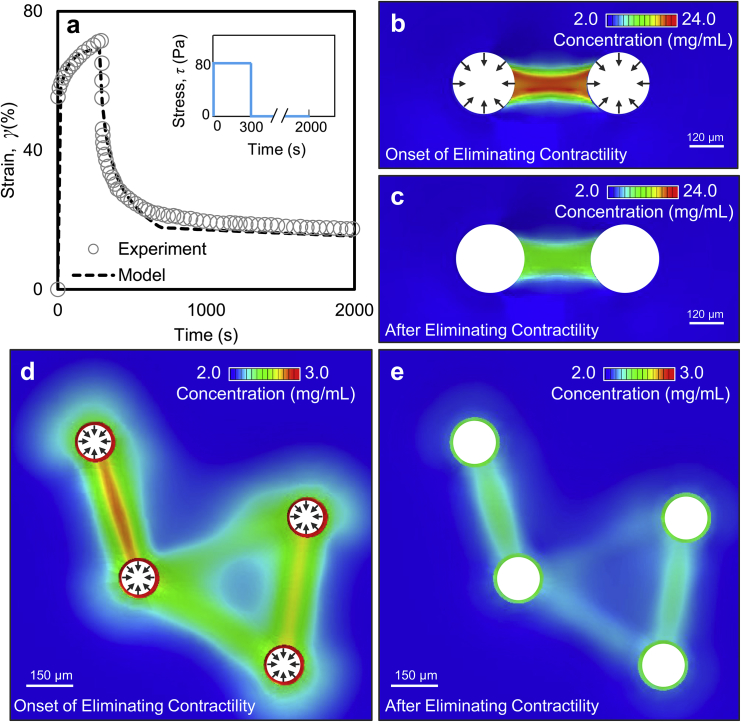
Figure 3.

A coarse-grained constitutive model for collagen plasticity. (a) Shown here is shear strain in creep and recovery tests from rheology experiments (14) and the constitutive model. The inset shows the applied stress as a function of time. Local collagen concentration is given in the presence of two contractile cell clusters (b) before and (c) after eliminating cell contractility (at steady state). Collagen concentration is given in a system of four contractile cell clusters (d) before and (e) after elimination of contractility (at steady state). To see this figure in color, go online.

Using parameters given in Table S1, we obtained excellent agreement between the strain response from the constitutive model and the experimental results (Fig. 3 a). The cross-link kinetic parameters determined from the creep and recovery tests were then used to model the formation of collagen tracts and plasticity that ensues after eliminating cellular forces. We began by modeling the formation of a fibrous tract between a pair of interacting cell clusters (Fig. S3). The initial model geometry was generated by replicating the dimensions and spacing of cell clusters in our experiments using mammary acini. The experimentally measured displacements at the periphery of the acini were then applied to the matrix. As the acini began to deform the matrix, significant stretches emerged along the axis connecting the two acini accompanied by contractions in the transverse direction. In agreement with our experimental observations (Fig. S3), ECM deformation by a pair of contractile acini was accompanied by a substantial increase (approximately sixfold on average) in matrix concentration along the tract axis (Fig. 3 b).

To model plastic deformation at the tracts, we next eliminated cellular forces by reducing the contraction applied to the matrix gradually until the forces at the periphery of the acini vanished. The resulting deformations indicated that on average approximately half of the matrix concentration persists at the tracts after cellular forces are eliminated, which agreed with our experimental results (Fig. 3 c). Similarly, we modeled tract formation and plasticity in the experiments with four interacting acini. In agreement with our experiments, we observed matrix densification at the tracts bridging the adjacent pairs of acini (Fig. 3 d). The constitutive model showed that when a third cell cluster is added to a contractile pair, it pulls the matrix away from the tract connecting the original pair, decreasing matrix concentration at the first tract. As observed in our acini experiments, this effect leads to a reduction in matrix densification in the presence of larger numbers of interacting acini (Fig. 1 d in comparison to Fig. S3 e). Finally, we removed the applied cellular forces and observed the permanence of densification at the tracts. As in the case of two interacting acini, approximately half of the initial matrix concentration remained at the tracts after removing the externally applied contractile forces (Fig. 3 e). These observations indicate that, in addition to explaining the viscoplastic shear rheology tests, our model provides an accurate description of the spatially inhomogeneous plastic deformation of collagen matrices in the presence of cellular forces.

Influence of permanent fiber elongation on network plasticity

We also investigated whether the plasticity of the tracts can be explained by plastic elongation of individual fibers. Our investigation was motivated by a recent study indicating that the permanent elongation of individual fibers leads to changes in the mechanical response of collagen and fibrin gels to large-strain cyclic loading. The permanent elongation of fibers has been attributed to dissipative processes such as sliding of protofibrils within individual fibers (47). We incorporated the single-fiber plastic behavior in a randomly diluted 3D lattice fiber network that we recently developed to model the effect of pore size on network elasticity (44) (Fig. 4, a–c; Fig. S8, a–c). We modeled the permanent elongation of fibers by employing a piecewise linear plastic hardening material model. This model describes the experimentally measured behavior of thin fibers (48, 49) as a linear elastic material of modulus E₁ up to a yield strain, ε_y, followed by a plastic regime with postyield modulus E₂ (Fig. 4 d). The individual fibers become permanently elongated at strains larger than ε_y. To assess the sensitivity of network mechanics to fiber properties, we conducted a parametric study over a broad range of values previously reported for ε_y and E₂ of collagen fibers (48, 49).

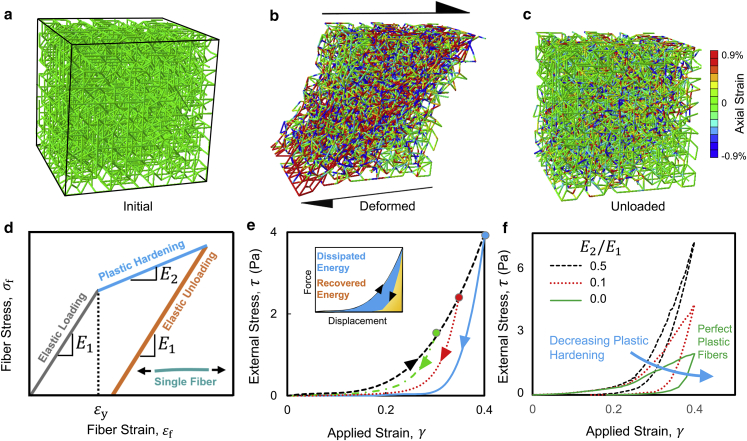
Figure 4.

Effect of permanent elongation of fibers on the mechanics of fiber networks. Snapshots of the diluted lattice fiber network model are given in the (a) initial, (b) deformed, and (c) unloaded states. (d) A plastic material model is used for the permanent elongation of individual fibers. Stress-strain curve of an individual fiber with an elastic response is given at small strains followed by plastic yielding and elastic unloading. (e) Network stress-strain curves in loading-unloading tests are given at various amplitudes of network strain. The inset shows partitioning of the total expended energy into the dissipated and the recovered energies. (f) Stress-strain curves for networks are given at different values of fiber post-yield modulus, E₂ (defined in (d)). To see this figure in color, go online.

To mimic the previous shear rheology experiments on fibrin and collagen gels (47), we tested networks in simple shear loading. A shear strain, γ, was applied to the network by horizontally displacing the nodes of the fibers at the top and the bottom boundaries in opposite directions (Fig. 4 b). To study the plastic effects, the network was subsequently unloaded by moving the boundary nodes back to their initial positions (Fig. 4 c). We applied strains of 30, 35, and 40% to test the networks using the matrix deformations observed in our acini experiments and calculated the network stress-strain response. We observed no significant macroscopic plastic strains in the stress-strain curves (Fig. 4 e). We then tested fibers with smaller yield strains and postyield moduli. These tests showed that the dissipation of energy (Fig. 4 e, inset) increases with decreasing fiber yield strain and postyield modulus (Fig. 4 f; Fig. S8 d). However, under the strain amplitudes in our cell-ECM experiments, the networks exhibited no macroscale plastic strains for all tested fiber properties (Fig. 4 f). We further verified our results by examining a Voronoi network (50) in stretch tests (Fig. S9). These tests verified the absence of macroscale plastic strains under deformations similar to those in our cell-ECM experiments, indicating that this result is independent of the network type and connectivity.

We studied the network microstructure to explain the absence of macroscale plastic strains (Fig. S8). When we loaded the network, fibers that were initially oriented along the elongated diagonal of the network became highly stretched. Some of these fibers were strained beyond the elastic limit and became permanently elongated (Fig. S8, a and b). Distribution of fiber-level strain in the network demonstrates that these fibers only make up a small portion of the network (Fig. S8 e). In agreement with the previous experimental observations (47), when the network is unloaded, the plastically elongated fibers buckle (Fig. S8 c). When we unload the network, the elastically deformed fibers try to restore the network to the initial state, whereas the plastically elongated fibers are compressed and resist the recovery of network deformation (Fig. S8 f). The elastic fibers, however, overcome this resistance because they are greater in number and because the fibers are substantially softer in compression than in tension. Therefore, the elastic fibers that have not permanently deformed pull the network back to its original state, when external forces are removed. The fiber network model demonstrates that at the strain amplitudes observed in our cell-ECM experiments, permanent elongation of fibers does not lead to the macroscale plastic strains observed in the tracts. However, fiber-level plasticity leads to important plastic effects such as residual strains in individual fibers (Fig. 4 c) and dissipation of the energy expended to deform the network (Fig. 4 e).

A map of the possible mechanisms of plasticity in collagen networks

We used the fiber network models to elucidate the mechanisms of plastic deformation as a function of the rate and amplitude of the applied strain and the threshold for plastic yielding of individual fibers. Our network model, which accounts for the stretch-dependent formation of weak cross-links, indicates that plasticity is enhanced by decreasing the rate of strain and increasing its amplitude (Fig. 5 a). If the network is deformed at a slower rate, more cross-links form, which in turn prevents the elastic recovery of the network deformation. Similarly, larger amplitudes of strain enhance transverse network contractions and bring fibers closer to each other, thereby enhancing the formation of cross-links between adjacent fibers. These results are consistent with our shear rheology experiments, which exhibit an increase in the degree of plasticity with increasing duration of creep and applied stress (Fig. 5 b).

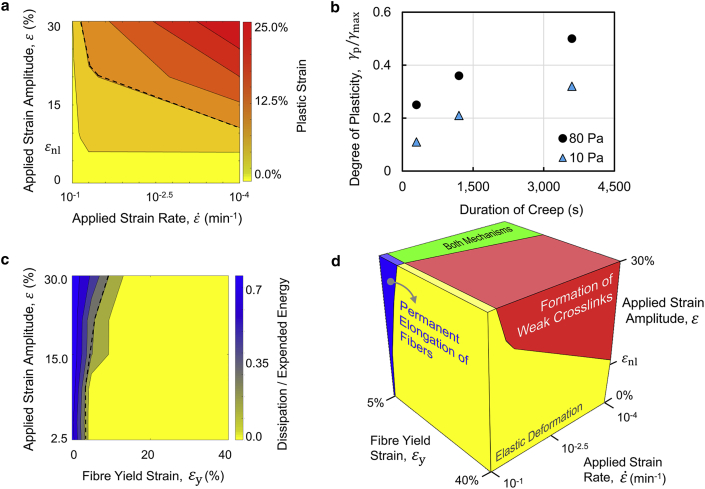
Figure 5.

Mechanism of plasticity depends on strain rate and amplitude and the mechanical properties of fibers. (a) Macroscopic plastic strain is given as a function of strain rate and amplitude. The dashed curve marks the boundary chosen for the plastic deformation regime. The horizontal axis is displayed in the reverse order. (b) The plot of the degree of plasticity versus the duration of creep in creep and recovery tests indicates that the degree of plasticity increases with increasing duration of creep and applied stress. The shear rheology tests are performed using 5-mg/mL collagen gels. (c) Normalized energy dissipation is given as a function of applied strain amplitude and fiber yield strain. (d) Schematic map shows the possible mechanism of plasticity at various levels of applied strain rate and amplitude and fiber yield strain. ε_nl marks the strain at which the network starts to stiffen. The applied strain rate is displayed in logarithmic scale and reverse order. To see this figure in color, go online.

We then used the network model, which accounts for the permanent elongation of fibers, to explore the extent of network plasticity at various levels of fiber yield strain (49) and amplitude of applied strain. The model indicates that the amount of plastic deformation increases with increasing strain amplitude and decreasing fiber yield strain (Fig. 5 c). Predictions from the network models are summarized in a schematic map of possible mechanisms of plasticity (Fig. 5 d). This map classifies the deformation of collagen networks into four categories: elastic, plastic dominantly by the formation of cross-links, plastic dominantly by the permanent elongation of fibers, and plastic by significant contributions from both mechanisms. We find that collagen networks deform elastically in small-strain tests and tests performed during a few minutes or less. However, they become plastic if tests are conducted over hour-long timescales or when high strains are applied, and if fibers yield more easily (as in the case of fibrin (51)).

Discussion

Here, we reported the existence of mechanical plasticity in the concentration and alignment in fibrous tracts formed by cell contractility and demonstrated that increasing collagen concentration enhances the plastic effects. Previous studies have shown that the invasion of cancer cells is enhanced by the presence of the fibrous tracts (33). Therefore, the existence of plasticity in the tracts suggests that by forming a persistent fibrous tract, a group of contractile cells paves the way for further invasion by other cells, possibly in a collective manner. Our network model consistently explains the plasticity of the tracts and its dependence on collagen concentration by accounting for the stretch-dependent formation of weak cross-links. We used insights from our network model to develop a coarse-grained model that describes matrix densification and plasticity at the scale of the interacting cells. The coarse-grained model can be integrated into the existing models of cell-ECM interaction to study biological processes such as the invasion of cancer cells (30, 31). These results can be used in future studies to assess the effectiveness of strategies to perturb collagen cross-linking to slow the rate of cancer cell invasion (52).

Our network model, which accounts for the permanent elongation of individual collagen fibers, predicts several behaviors that are also consistent with experimental observations of inelastic deformation of fibrin networks (20, 47). First, most of the fibers that become permanently elongated are initially oriented in the direction of the largest principal stretch (Fig. S8 b). Second, the permanently elongated fibers buckle when the network is unloaded (Fig. S8 c). Finally, the macroscale stress is close to zero when strain is returned to zero (47) (Fig. 4, e and f). Additionally, recent experiments have demonstrated that under moderate strains, fibrin networks are mechanically remodeled by the formation of new bonds, whereas at high strains, plasticity is caused by the permanent deformation of individual fibers (51). This result is consistent with observations from our fiber network models, which exhibit no macroscopic plastic strains at the moderate strains observed at the tracts, suggesting that our network model may be generalized to fibrin networks.

Recent force spectroscopy experiments into the nature of the adhesions between collagen fibers indicated the presence of weak interfiber cross-links between compacted fibers that exhibit a Bell-like behavior under tension (21). These bonds, however, have not been chemically isolated, and their nature remains elusive. Our tests demonstrated that preventing the formation of cross-links by LOX does not prevent the plastic effects, indicating that the formation of cross-links by LOX is not likely to be important in our experiments. This result is consistent with the previous experiments, which have demonstrated that although cross-links formed by LOX influence the mechanical behavior of matrices at timescales of days and longer (53), they are not important at times shorter than a day (54). Electrostatic and hydrophobic interactions (55), chemical cross-linking, the fusion of the nearby fibers (11), and the synthesis of collagen by the cells might be involved in the adhesion of the compacted fibers and the plasticity of collagen at the tracts. Future research into the nature of these cross-links may elucidate new methods for tuning tissue mechanics by perturbing the cross-linking of collagen.

Our coarse-grained model was partly motivated by the fact that the existing continuum-scale constitutive laws fail to model the plasticity and densification of the ECMs at the same time: models of cellular force transmission in fibrous matrices focus on elastic deformation (6, 43, 56) and lack the capability to model plastic effects. The models previously used for ECM plasticity (e.g., the Bingham plastic model) (57) reproduce the viscoplastic response of collagen matrices in shear (14) but fail to reproduce matrix densification and the formation of tracts between the mechanically communicating cells. To address these shortcomings, we incorporated the stretch-dependent formation and dissociation of weak cross-links into elastic models of long-range force transmission in fibrous ECMs (6). Our tests demonstrated that the present model accurately describes both fiber densification and plasticity in our cell-ECM experiments (Fig. 3, b–e) and the viscoplastic behaviors observed in shear rheology experiments (33) (Fig. 3 a). Our coarse-grained constitutive law can be utilized to enhance the accuracy of modeling the matrix in physical models of cancer metastasis (30, 31), which currently do not account for the mechanical plasticity of fibrous ECMs.

The predictive capabilities of this model can be improved by including strain-dependent degradation of collagen (58, 59, 60) and the role of proteoglycans in modulating the mechanics, swelling, and plasticity of collagen networks. More accurate understanding and modeling of the rich mechanics of ECMs will facilitate the study of biological processes such as fibrosis, morphogenesis, and cancer cell invasion. Theoretical modeling of disease states can potentially be used to explore the space of possible treatments, predict the progression of diseases, and narrow down treatment options in a patient-specific manner.

Author Contributions

V.B.S. conceived the project. E.B., H.W., and V.B.S. designed and implemented the theoretical models and carried out the computations. J.M.F., S.N., L.R.S., R.G.W., O.C., and J.T.L. designed the experiments. J.M.F., S.N., and L.R.S. conducted the experiments. E.B., J.M.F., S.N., L.R.S., R.G.W., O.C., J.T.L., and V.B.S. analyzed and interpreted the data and wrote the article.

Editor: Alissa Weaver.

Supporting Citations

References (61, 62, 63, 64, 65, 66) appear in the Supporting Material.