Impact of Tissue Factor Localization on Blood Clot Structure and Resistance under Venous Shear

Abstract

The structure and growth of a blood clot depend on the localization of tissue factor (TF), which can trigger clotting during the hemostatic process or promote thrombosis when exposed to blood under pathological conditions. We sought to understand how the growth, structure, and mechanical properties of clots under flow are shaped by the simultaneously varying TF surface density and its exposure area. We used an eight-channel microfluidic device equipped with a 20- or 100-μm-long collagen surface patterned with lipidated TF of surface densities ∼0.1 and ∼2 molecules/μm². Human whole blood was perfused at venous shear, and clot growth was continually measured. Using our recently developed computational model of clot formation, we performed simulations to gain insights into the clot’s structure and its resistance to blood flow. An increase in TF exposure area resulted not only in accelerated bulk platelet, thrombin, and fibrin accumulation, but also in increased height of the platelet mass and increased clot resistance to flow. Moreover, increasing the TF surface density or exposure area enhanced platelet deposition by approximately twofold, and thrombin and fibrin generation by greater than threefold, thereby increasing both clot size and its viscous resistance. Finally, TF effects on blood flow occlusion were more pronounced for the longer thrombogenic surface than for the shorter one. Our results suggest that TF surface density and its exposure area can independently enhance both the clot’s occlusivity and its resistance to blood flow. These findings provide, to our knowledge, new insights into how TF affects thrombus growth in time and space under flow.

Introduction

Blood clot formation is normally triggered when tissue factor (TF) and collagen in the subendothelium are exposed to blood components, such as coagulation proteins and platelets, after a vascular injury (1, 2, 3). The resulting blood clot forms a barrier preventing blood loss from a penetrating injury and thereby effecting hemostasis (3, 4, 5, 6, 7). At the same time, pathological phenomena, such as TF exposure on the surfaces of immune and endothelial cells, can cause clot formation inside intact vessels, leading to blood-flow occlusion (i.e., thrombosis) (8, 9, 10, 11). Clot-triggering regions can vary in size (e.g., large or small groups of TF-exposing cells, or vessel injuries of different sizes). This variation, which affects the extent of TF and collagen exposure to blood, may thereby elicit distinct spatiotemporal dynamics of clot formation. Moreover, TF distribution varies between (and possibly within) organs or tissues, resulting in hemostatic potential variations (12). For example, high TF levels in the brain, lungs, placenta, and heart ensure that additional, potentially life-saving, hemostatic protection is provided to these vital organs during injury (13). Mechanistic insights into the effects of TF localization—i.e., TF levels and spatial distribution—on clot formation kinetics, structure, and mechanical properties may improve our understanding of how clots behave and how they can be managed therapeutically under pathological conditions.

TF and its role in the extrinsic pathway of blood coagulation have been extensively investigated, with recent studies of TF effects under flow focusing primarily on threshold regulation (10, 14, 15, 16, 17). Indeed, computational and experimental studies demonstrated the possibility of a threshold in the dependence of fibrin generation under flow on the level of TF exposed on a thrombogenic surface (15, 17). The threshold dependence is not only limited to TF concentration, but has also been reported for TF exposure area and flow shear rate (17, 18, 19). Such threshold responses may regulate the degree of vessel occlusion (20). Yet, under certain venous blood-flow conditions, TF can initiate clot formation and generate platelet-localized thrombin and fibrin on a single collagen fiber, suggesting that threshold behavior may not always occur (21).

Taken together, the existing evidence suggests that blood flow directly modulates the effects of TF on clot growth. However, it remains unclear what are the relative contributions of the TF surface density and the TF exposure area, which can vary simultaneously, to clot formation kinetics under flow. Particularly, it is not known how these two factors compare with respect to their effects on the distinct outputs of the clot formation process: platelet deposition, thrombin generation, and fibrin accumulation. Furthermore, it is not apparent how variations in TF localization affect the mechanical properties of the clot, such as its permeability, viscous resistance, and intrathrombus flow velocity, which ultimately define the clot’s ability to divert or stop the flow of blood in both hemostasis and thrombosis. The main purpose of this study is to investigate these questions in the context of blood-flow microfluidics.

In vitro experiments, in vivo experiments, and computational models have been used to study blood coagulation under flow (1, 3, 6, 15, 16, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34). Although established experimental methods exist to investigate clot structure, computational modeling can complement laboratory studies by providing insights into the mechanical aspects of clot formation (such as spatiotemporal changes in clot permeability) that may be impossible to measure directly and simultaneously with the clot structure measurements. Here, we performed computational fluid dynamics modeling and microfluidic experiments to investigate TF localization and its effects on blood clot structure and mechanical properties. We hypothesized that both increased TF surface density and increased TF area of exposure to blood flow typically result in clots that are larger, more occlusive, and more resistant to shear forces. To investigate this hypothesis, we used our recently developed computational model (24), tailored to study human whole-blood clotting, to simulate clot formation under venous flow conditions (i.e., venous shear). Using this model, we simulated spatiotemporal distribution of platelet deposition, thrombin generation, and fibrin accumulation. We then used a microfluidic device to perfuse whole blood at a shear rate typical for veins (100 s⁻¹) (35). Unique features of this microfluidic device include thrombogenic surfaces patterned with both collagen and TF to study whole blood clotting, and a pressure-relief mode of operation that allows for physiological clot growth in the microfluidic channels (1). We investigated the effects of TF localization on blood clotting and blood flow at two TF surface densities on two thrombogenic surfaces varying in length (and having a fixed width, so that varying length translated to varying surface area). Using fluorescence microscopy, we visualized and monitored platelet deposition, thrombin generation, and fibrin accumulation. Subsequently, we used model simulations to correlate the spatiotemporal clot-structure patterns with clot viscous resistance and blood flow velocity.

Our computational model captured the general dynamics of experimentally measured spatiotemporal clot growth. We found that a longer thrombogenic surface, compared to a shorter one, was characterized by accelerated clot formation kinetics associated with increased growth in both clot length and height. Moreover, increasing the TF surface density differentially enhanced platelet deposition, thrombin generation, and fibrin accumulation, thereby increasing both clot size and resistance. Finally, our model simulations demonstrated that the degree of blood-flow occlusion may depend more strongly on the TF surface density for the longer thrombogenic surface than for the shorter one.

Materials and Methods

Sample collection and preparation

Blood samples were collected from five healthy donors (three men and two women) via venipuncture into corn trypsin inhibitor (CTI, FXIIa inhibitor, 40 μg/mL), which ensured that coagulation initiation by the contact pathway was inhibited during the entire course of the experiments (36). All flow experiments were initiated within 5 min after phlebotomy. The donors reported themselves to be free of alcohol use and medication for at least 72 h before blood collection. All donors provided written informed consent, and samples were collected with the approval of the University of Pennsylvania Institutional Review Board (Philadelphia, PA) and of the Human Research Protection Office, Office of Research Protections, US Army Medical Research and Materiel Command (Fort Detrick, MD). Platelets were labeled with anti-human CD41a antibody (BD Biosciences, San Jose, CA). To enable simultaneous detection of platelet-associated thrombin during experiments, a thrombin-sensitive platelet-binding sensor, synthesized as previously described, was added to blood (1:10 v/v %) before perfusion (37). Finally, fluorescent fibrinogen was added (1 mg/mL stock solution, 1:80 (volume/volume) in whole blood) to measure fibrin accumulation (38).

Microfluidic device fabrication

Silicon masters with designed features were fabricated using standard photolithography and secured to polystyrene Petri dishes. Mixed (poly)dimethylsiloxane (PDMS) prepolymer and curing reagent (Dow Corning, Midland, MI) were degassed under vacuum and cured over the master wafers at 65°C for 3 h. After cooling, the molded PDMS were peeled off and cut into individual devices. Fluidic and vacuum ports were added using Harris Uni-Core (Ted Pells, Redding, CA). Before use, PDMS devices were cleaned in 1 N hydrochloric acid followed by immersion in acetone and subsequently ethanol for 15 min each in an ultrasonic cleaning bath.

Thrombogenic surface patterning

Glass slides were coated with Sigmacote (Sigma-Aldrich, St. Louis, MO) and then dried with filtered air. A volume of 5 μL collagen (1 mg/mL; Chrono-log, Havertown, PA) was perfused through two different patterned channels (20 and 100 μm in length) of a microfluidic device to create fibrillar collagen strips as previously described (39). Lipidated TF was then sorbed to the collagen surface by introducing 5 μL of Dade Innovin PT reagent (20 nM stock concentration; Siemens, Munich, Germany) (40) diluted 300- and fivefold with HEPES-buffered saline to obtain TF surfaces with estimated densities of ∼0.1 and ∼2 TF molecules/μm², respectively, by imaging the sorbed fluorescein-annexin V-stained (FITC) vesicles (Fig. S1) (38). Some heterogeneity in the TF distribution can be observed because the TF liposomes tend to bind with the linear strands of the collagen, which is consistent with our previous studies (Fig. S1) (38). In all experiments, the PT reagent was incubated with the collagen for 30 min without flow. This was followed by rinsing and blocking with 20 μL bovine serum albumin buffer (0.1%).

Microfluidic device experiments

The microfluidic device used to generate thrombi under flow consisted of eight parallel polydimethylsiloxane channels (250 μm width × 60 μm height) with separate inlets and a common outlet (Fig. 1) (1, 21, 25, 26). The experiments were performed under the pressure relief mode (constant pressure drop (ΔP) condition), in which the inlets were held at a constant pressure and a constant outflow was maintained at the outlet by withdrawing blood through a syringe pump (Harvard Apparatus PHD 2000, Holliston, MA) (Fig. 1) (1). The pressure relief mode is considered physiologically more relevant in that thrombus growth is promoted under this condition (1). Blood was perfused in the microfluidic device with an initial shear rate of 100 s⁻¹ over two thrombogenic surfaces varying in length (i.e., 20 and 100 μm) at two different TF surface densities (i.e., ∼0.1 and ∼2 TF molecules/μm²) (Fig. S1). Blood from the channel outlets was withdrawn through a syringe pump (Harvard Apparatus PHD 2000, Holliston, MA), which was maintained at a constant pressure (1). The resulting sets of four experimental conditions were each repeated four times for each donor sample (five donors in total).

Figure 1.

2D geometric representation of the microfluidic device. The arrows show the blood flow direction. (A) Photograph of the overall setup of the microfluidic device. Image reproduced with permission (1). Operating under the pressure relief mode requires a set of two channels, one with and one without a thrombogenic surface. Thus, the eight channels were divided into four pairs, and each pair was utilized to study one clotting event. In a given pair, under the pressure relief mode, one of the channels was coated with a thrombogenic (collagen + TF) surface to promote thrombus growth, while blood could flow freely through the other. To abolish platelet adhesion in the second channel and allow free flow of blood, EDTA-treated blood was delivered through its dedicated inlet. CTI-treated blood was delivered in the channels with the thrombogenic surface (1). Thrombus formation is initiated when blood flows over the thrombogenic surfaces in the microfluidic device channels. When CTI-treated blood formed a clot over the thrombogenic surface, it started occluding the channel. As a consequence, blood flow automatically increased in the corresponding EDTA channel to maintain a constant outflow (withdrawn from a syringe at the outlet) (1, 21, 24, 25). Thus, the eight-channel microfluidic device allowed us to induce and monitor four separate clotting events simultaneously. (B) 3D geometry of the microfluidic device section that consists of two separate inlets and a single outlet. The dimensions of the channels are as indicated in the figure. (C) 2D vertical representation of the microfluidic device (following (1)). This 2D geometry was constructed so that it maintained a channel height of 60 μm. The channel without a thrombogenic surface is stacked above the channel with one. This geometry allowed us to perform simulations in the pressure-relief mode in a 2D setting. Also indicated are the flow boundary conditions used in our simulations. Finally, no-slip and no-penetration conditions were imposed on the walls.

Epifluorescence microscopy (IX81; Olympus America, Center Valley, PA) was employed to continually visualize and monitor clot growth (i.e., platelet, thrombin, and fibrin accumulation) in real time during the experiment. Thrombin and fibrin formation were measured as previously described (38). Real-time images were captured with a CCD camera (Hamamatsu, Bridgewater, NJ) at 60-s or 50-s intervals and were subsequently analyzed (ImageJ software; NIH, Bethesda, MD) to obtain the mean fluorescence intensity of platelets, thrombin, and fibrin (1, 21). Representative images of platelet, thrombin, and fibrin fluorescence are given in Figs. S2–S5. Platelet fluorescence data were used to determine the real-time thrombus height (1). The height at each location was assumed to be proportional to the maximal fluorescence intensity observed in the endpoint platelet fluorescence images, which corresponds to the final clot height. The final height of each clot was determined by endpoint confocal imaging (2 μm increments) with a disk spinning unit (IX2; Olympus America) (1). As described previously, clot profiles were generated by a custom MATLAB R2015b (The MathWorks, Natick, MA) script, in which the average of 20 line scans (in the flow direction) was considered for each individual thrombus (1). The fluorescence intensity of platelets, thrombin, and fibrin, as well as the platelet profiles, were averaged across donors to calculate the overall clotting kinetics and profiles. Before averaging, the individual platelet deposition profiles (showing clot height as a function of location over the thrombogenic surface) for a given experimental condition were aligned using custom MATLAB scripts. The fluorescence intensity values for each of the five donors were the average values calculated from the four individual clotting events (i.e., repeated measurements) analyzed per donor sample for each considered experimental condition.

Statistical analysis

A two-tailed Student’s t-test was used to determine statistical significance after testing the data for normality. The Jarque-Bera test was used for normality testing (41). A p-value of <0.05 was considered statistically significant.

Computational modeling of thrombus formation under flow

Our computational model, which had been previously validated using microfluidic data on platelet and fibrin deposition (24), was used to simulate clot formation in an average subject under the experimental conditions described above. The model was implemented using the computational fluid dynamics package FLUENT (v. 17.1; ANSYS, Canonsburg, PA). Our model accounts for the essential biochemical reactions, as well as for platelet activation and deposition, during clot formation under flow, while taking into consideration the presence of red blood cells (RBCs) in whole blood (Fig. S6) (24). In our model, the spatiotemporal kinetics of the platelet transport and those of the biochemical species were governed by the convection-diffusion-reaction equation, whose general form is as follows:

$$\frac{\partial C_i}{\partial t}=-\nabla \cdot \left(\overrightarrow{u}{C}_i\right)+\nabla \cdot \left(D_i\nabla C_i\right)+R_i,$$ (1)

where C_i denotes the concentration of species i, $\overrightarrow{u}$ denotes the blood flow velocity vector (each biochemical species passively moves with its surrounding fluid), D_i denotes the individual species diffusivity, and R_i represents the source term that governs the interactions, such as platelet and protein activation and protein depletion.

To capture the effective diffusivity of platelets and plasma proteins due to the presence of RBC motion, our computational model is implemented with an enhanced diffusivity model originally proposed by Zydney and Colton (42):

$$D_i^e=D_i^b+k{d}_{\text{rbc}}^2\phi {\left(1-\phi \right)}^{\eta }\dot{\gamma },$$ (2)

where D^e_i and D^b_i represent the enhanced diffusivity and Brownian diffusivity, respectively, of species i, k, and η denote empirical constants, d_rbc represents the RBC diameter, φ denotes the local hematocrit (which varies along the height of the microfluidic channel), and $\dot{\gamma }$ denotes the local shear rate. To define the inlet hematocrit profile, we used the blunt profile, which had been previously shown to produce an improved agreement with experimental data (24, 43). Furthermore, the RBC motion causes the platelets to marginate toward the walls, resulting in an increased near-wall platelet concentration (44, 45, 46). We modeled this by implementing a platelet margination model proposed by Bark and Ku (44).

Blood is assumed to be Newtonian, and its flow is governed by the incompressible Navier-Stokes equation. The effect of clot growth on the blood flow was represented by an increase in viscous resistance, thus resulting in a reduction of blood-flow velocity in the region occupied by the growing clot. To this end, the growing clot was modeled as a porous medium, whose permeability depends on the increasing fractions of deposited platelets and the concentration of fibrin protomers (24). The standard incompressible Navier-Stokes equations were modified by incorporating additional source terms to the momentum equation and are given as follows:

$$\nabla \cdot \left(\overrightarrow{u}\right)=0,$$ (3)

$$\rho \left(\frac{\partial \overrightarrow{u}}{\partial t}+\left(\overrightarrow{u}\cdot \nabla \right)\overrightarrow{u}\right)=-\nabla p+\mu \Delta \overrightarrow{u}-\frac{\mu }{K_t\left(x\right)}\overrightarrow{u},$$ (4)

where ρ, $\overrightarrow{u}$, p, and μ represent the blood density, fluid velocity vector, fluid pressure, and the dynamic viscosity of blood, respectively. The source term μ/K_t(x) in Eq. 4 is known as the Brinkman term, where K_t(x) (which depends on the space point x) represents the permeability of a porous medium, and 1/K_t(x) represents its viscous resistance. The viscous resistance is imparted by the deposited platelets and fibrin, and their individual contributions are added to define the term 1/K_t in Eq. 4 as follows (47, 48):

$$\frac{1}{K_t}=\frac{1}{K_p}+\frac{1}{K_f},$$ (5)

where K_p and K_f denote the permeabilities of the deposited platelet mass and the fibrin mass, respectively. The contribution of the platelets to the total clot viscous resistance is given by the following formula (16, 24):

$$\frac{1}{K_p}={\alpha }_{\max }\left(\frac{{\left({\phi }^b\right)}^2}{{\left({\phi }_o^b\right)}^2+{\left({\phi }^b\right)}^2}\right),$$ (6)

where φ^b represents the fraction of bound platelets, which is the ratio of bound platelets to the maximal possible platelet density, and φ^b₀ is a constant. The contribution of fibrin to the clot’s viscous resistance is computed using the Davis equation (49), which has been used to estimate the permeability of fibrin gels in blood clots (24, 48, 50, 51):

$$\frac{1}{K_f}=\frac{16{\phi }_f^{1.5}\left(1+56{\phi }_f^3\right)}{a_f^2},$$ (7)

where a_f denotes the fiber radius and φ_f represents the ratio of the fibrin concentration to that of fibrinogen. Additional details on the computational procedure used to solve the above equations, as well as further details, such as model parameter values, variable definitions, and a full set of model equations, are provided in the Supporting Material.

Simulation conditions and additional flow simulations

The 2D computational domain in our simulations represented a set of two separate channels and a common outlet to model a single clotting event (Fig. 1 C) (24). As in the experimental setup, thrombus formation was initiated in one of the channels (i.e., the one containing a thrombogenic surface), whereas blood flowed freely in the other. No-slip and no-penetration conditions were imposed at the device walls, and the inlet was defined to have atmospheric pressure to represent the pressure relief mode. The simulations were carried out for 420 s with a 0.01-s time step. A constant flow rate of 2 μL/min, which corresponds to initial shear rate of 100 s⁻¹, was specified at the outlet with a parabolic velocity profile.

Additional flow simulations (solving Eqs. 3, 4, and 5) were performed after incorporating the 2D profiles of the clot (i.e., platelet deposition) region (see Microfluidic Device Experiments) into the microfluidic device geometry. The clot region was assumed to consist of two homogeneous porous bodies: a core composed of deposited fibrin and platelets, and an outer shell made of deposited platelets. This simplified representation was based on the results of this study (see the Results), which are consistent with several previous studies (24, 52, 53, 54). The characteristics of the fibrin accumulation profiles used in these simulations, such as the shapes of the fibrin accumulation domains and the ratios between the heights of the fibrin accumulation and the corresponding platelet deposition domains, were also obtained from the predictions generated by our fully coupled computational model (Eqs. 1, 2, 3, 4, 5, 6, and 7; and see the Supporting Material). The profiles of the core and shell regions, thus obtained, were defined as two distinct zones during the meshing process and as two corresponding porous zones during flow computation in FLUENT. To determine the appropriate viscous resistance values for the core and shell regions, we used the viscous resistance values predicted by our fully coupled model (see Eqs. 6 and 7). [In our simulations using the fully coupled model, a fibrin concentration threshold of 1 nM was used to define the core region boundary. The shell region was defined as the low-velocity area based on visual inspection of the corresponding axial velocity plots (blue areas in the plots); see fourth subsection of the Results.] For the core region (assumed to be composed of deposited fibrin and platelets), we calculated the average value of viscous resistance imparted by fibrin accumulation (Eq. 7) and added it to the calculated value of average viscous resistance imparted by the deposited platelets (Eq. 6). For the shell region (assumed to be made of deposited platelets), we used the average viscous resistance imparted by the deposited platelets alone. All simulation conditions were as specified in the preceding paragraph. These porous body simulations allowed us to compute the shear rate over the experimentally measured clot region and the intrathrombus blood flow velocity.

Results

Clotting kinetics is accelerated on the longer thrombogenic surface

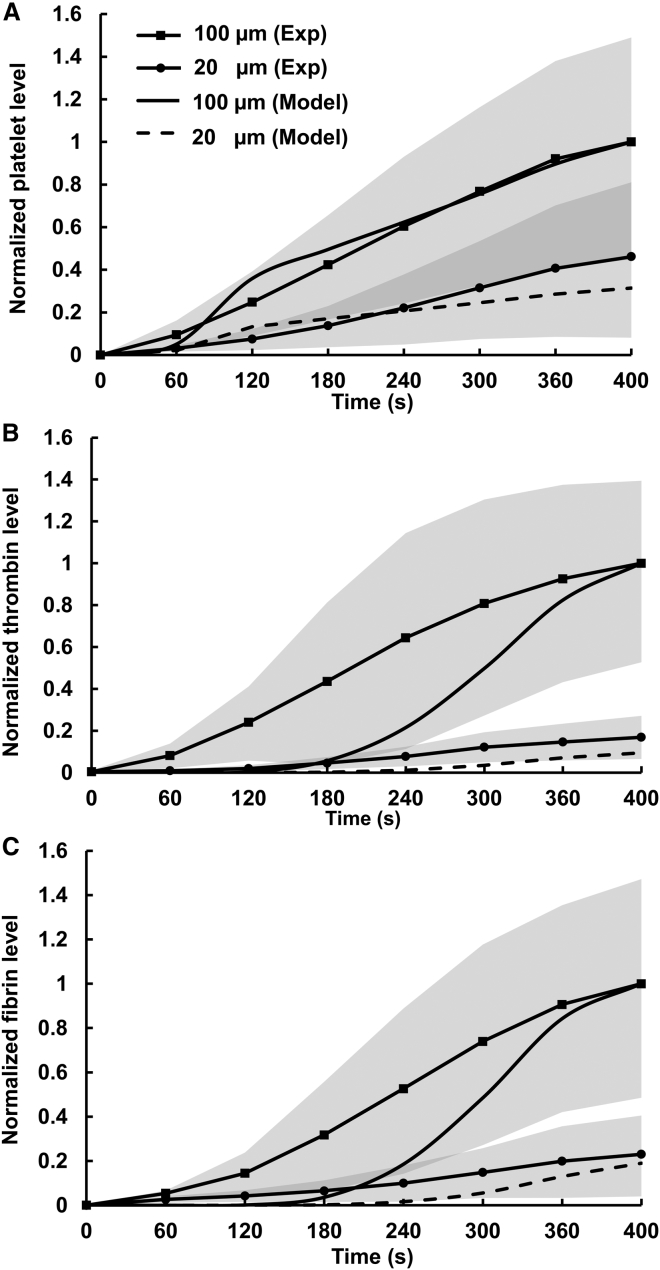
Our computational model predicted that, for the high TF surface density (i.e., ∼2 TF molecules/μm²), the processes of platelet deposition, thrombin generation, and fibrin accumulation on the long thrombogenic surface (i.e., 100 μm) should occur at faster rates than on the short one (i.e., 20 μm) (Fig. 2). Subsequent experimental measurements confirmed this prediction (Fig. 2). Indeed, bulk platelet deposition on the long thrombogenic surface exceeded that on the short one at all times (Fig. 2 A). At 400 s, the average amount of measured platelets deposited on the long thrombogenic surface was approximately twofold larger than that for the short surface, which was in reasonable agreement with our model simulations (Fig. 2 A). Whereas our model predicted platelet deposition kinetics that compared reasonably well with experimental measurements, it over-predicted the initial delay in the bulk thrombin (Fig. 2 B) and bulk fibrin (Fig. 2 C) production. Nevertheless, it captured the general delayed-growth trend demonstrated in the experiments. The faster accumulation of thrombin in our experiment (compared to our simulations) may be attributed to the initial presence of thrombin in plasma, which may have resulted from coagulation activation during sample collection, as suggested previously (24). Because fibrin generation is catalyzed by thrombin, this may also explain the faster fibrin generation in our experiment than in the simulations (Fig. 2 C). Interestingly, both model simulations and experimental data showed that the differences in thrombin and fibrin generation kinetics between the two thrombogenic surfaces were larger than the corresponding difference in platelet deposition (Fig. 2, B and C).

Figure 2.

Clotting kinetics measured in the microfluidic channels and those predicted by our computational model for the high TF surface density (∼2 TF molecules/μm²). For proper comparisons between model predictions and experimental data, normalization was necessary because of differences in reporting units between experimental data and model predictions. (A) Model-predicted and experimentally measured platelet accumulation. The solid line (no markers) and the dashed line show the normalized model-predicted values of the mean concentrations of bound platelets calculated over the entire flow domain with the 100- and 20-μm thrombogenic surfaces, respectively. The solid lines with square and circular markers show the normalized values of the mean platelet fluorescence intensity, which represent the levels of platelet accumulation measured in the microfluidic channels with the 100- and 20-μm thrombogenic surfaces, respectively. For each donor blood sample, experiments were repeated four times (i.e., four independent clotting events were measured) to obtain the average time course for that sample. Finally, the overall mean of the average time courses obtained for each donor was calculated to represent the average behavior across all donors (N = 5). Shaded regions represent one standard deviation corresponding to the overall mean and characterizing interdonor variability. Clotting events were measured at 60-s time intervals, and the data points (represented by the markers) were connected with solid lines to enhance the visual representation of the displayed trends. The experimental data were normalized by dividing by the maximal average value; the model-generated time courses were normalized by dividing by the maximal simulated value. (B) Thrombin generation simulated by our computational model and those obtained from experimental measurements, as explained above. Time-course normalization was performed similarly to the platelet data. (C) Fibrin accumulation simulated by our computational model and that obtained from experimental measurements. Time-course normalization was performed similarly to the platelet data. The differences in the experimentally measured platelet deposition, thrombin generation, and fibrin accumulation between the 100- and 20-μm surfaces at 400 s were statistically significant (in the respective pairwise comparisons).

Thrombin generation on the long thrombogenic surface proceeded much faster than that on the short surface throughout the duration of the experiment (Fig. 2 B). Indeed, at 400 s, the average level of thrombin generated on the long thrombogenic surface was approximately sixfold higher than that for the short surface (Fig. 2 B). Both model simulations and experimental data showed that fibrin formation, catalyzed by thrombin, followed a trend similar to that of thrombin kinetics. Consistent with thrombin generation, fibrin formation at 400 s was approximately fivefold higher on the long thrombogenic surface than on the short one (Fig. 2 C). Taken together, these results suggest that the increase in thrombogenic surface length from 20 to 100 μm had a greater influence on thrombin and fibrin generation than on platelet deposition.

Interestingly, the effect of the thrombogenic surface length on clotting kinetics was largely independent of the TF surface density. Consistent with our model predictions, the experimentally measured levels of platelets, thrombin, and fibrin generated for the low TF surface density were lower than the corresponding levels generated for the high TF surface density on the thrombogenic surfaces having the same length (Figs. 2 and S7). At the same time, the differences in clotting kinetics between the 20- and 100-μm thrombogenic surfaces with the low TF density (i.e., ∼0.1 TF molecules/μm²) were quantitatively similar to those with the high TF density (Figs. 2 and S7). Specifically, at 400 s, the amounts of platelets deposited, thrombin generated, and fibrin accumulated on the 100-μm surface with the low TF density were, respectively, approximately three-, four-, and fourfold larger than that for the 20-μm surface with the same TF density (Fig. S7), which was comparable to the fold increase detected for the high TF density (Fig. 2).

Increase in thrombogenic surface length results in increased length and height of the platelet deposition domain

Intuitively, the bulk kinetics acceleration in the previous subsection could be attributed merely to a longer platelet deposition region for the long thrombogenic surface (Fig. 2). However, surprisingly, for the high TF surface density, the long surface resulted in a platelet deposition region that was both longer and higher than that for the short thrombogenic surface (Fig. 3). Importantly, this suggests that the long surface can cause a higher degree of microfluidic channel occlusion. The average platelet deposition over the 20-μm surface attained a height of ∼12 μm at 400 s, with the bulk of the platelets depositing on the thrombogenic surface in a roughly triangular-ridge shape (Fig. 3 A). In contrast, platelet growth on the 100-μm surface had a taller and broader profile than that on the 20-μm surface (Fig. 3 B). At 400 s, the average platelet deposition attained a total height of ∼26 μm, which was approximately twofold higher than that on the 20-μm surface. This correlated with faster platelet bulk accumulation on the long thrombogenic surface (Fig. 2 A). Previous studies suggested that clot size is determined predominantly by the size of the platelet deposition region, whereas clot resistance to shear may be enhanced by fibrin accumulation (1, 24). Therefore, our results suggest that increasing the thrombogenic surface length may enhance both the size (Fig. 3) and viscous resistance (Fig. 2 C) of the clot. Our platelet deposition data for the low TF surface density corroborated this conclusion, although the effect was less pronounced (Fig. S8).

Figure 3.

Profiles of the average platelet deposition region at 400 s over thrombogenic surfaces with the high TF surface density (∼2 TF molecules/μm²). The profiles (black lines) are shown for the 20-μm (A) and 100-μm (B) thrombogenic surfaces; shaded regions represent one standard deviation. The x axis represents the horizontal coordinate along the microfluidic channel (and thrombogenic surface) length. The profiles shown were obtained by averaging platelet deposition profiles across all donors (N = 5). Before averaging, individual clot profiles were aligned with respect to the middle of the thrombogenic surface (shown by thick horizontal black lines). The alignment was performed under the assumption that the clot’s upstream and downstream sides are roughly symmetrical with respect to the thrombogenic patch location. The upstream and downstream edges of the platelet deposition domains were defined as the first positions where the clot height increased above and decreased below, respectively, 5% of the maximal height.

Increase in TF surface density differentially accelerates platelet deposition, thrombin generation, and fibrin accumulation

Both our model predictions and experimental measurements showed that, for the 100-μm thrombogenic surface, an increase in TF surface density leads to an increase not only in thrombin generation, but also in platelet deposition and fibrin accumulation (Fig. 4). Consistent with the trend predicted by our computational model, the average platelet deposition for the low TF density was at all times diminished, compared to that for the high TF density (Fig. 4 A). The average platelet deposition on the high TF density thrombogenic surface at 420 s was approximately twofold higher than that on the low TF density surface (Fig. 4 A).

Figure 4.

Clotting kinetics measured in the microfluidic channels and those predicted by our computational model for the 100-μm thrombogenic surface. (Left and right panels) Clotting kinetics detected for the low and high TF density surfaces, respectively. For proper comparisons between model predictions and experimental data, normalization was necessary because of differences in reporting units between experimental data and model predictions. Lines with square markers show normalized mean fluorescence intensities (N = 5), which represent the clotting kinetics of individual donor blood samples. The color-shaded areas correspond to one standard deviation. Lines with circular markers represent the clotting kinetics averaged across all donors. Clotting events were measured at 60-s time intervals, and the data points (represented by the markers) were connected with solid lines to enhance visual presentation. Thick black lines (no markers) show the normalized model-predicted values of the mean concentrations of bound platelets calculated over the entire flow domain. (A) Platelet accumulation. The experimental data were normalized by dividing by the maximal average value; the model-generated time courses were normalized by dividing by the maximal simulated value. The differences in the experimentally measured platelet deposition between the high and low TF surface density cases at 420 s were statistically nonsignificant (in the pairwise comparisons). (B) Thrombin generation. (C) Fibrin accumulation. Time-course normalization for thrombin and fibrin was performed similarly to the platelet data. The differences in the experimentally measured thrombin generation and fibrin accumulation between the high and low TF surface density cases at 420 s were statistically significant (in the respective pairwise comparisons). To see this figure in color, go online.

The differences in thrombin and fibrin kinetics between the thrombogenic surfaces with the two distinct TF densities were even larger than those for the platelets. Thrombin generation and fibrin production on the low TF density surface were modest for the entire 420 s of measured clot formation in comparison with the high TF density surface, which was qualitatively captured by our computational model (Fig. 4, B and C). Although our model overpredicted the duration of the initial period of very small increases in the thrombin level, it captured the general trend demonstrated in the experiments. At 420 s, the average levels of thrombin and fibrin generated for the high TF density were ∼3.7- and ∼5.8-fold higher, respectively, than the corresponding levels for the low TF density (Fig. 4, B and C). These results indicate that an increase in TF surface density can result in an increase in platelet deposition, a larger increase in thrombin generation, and an even larger increase in fibrin accumulation. Our findings for the shorter thrombogenic surface corroborated this trend.

Fig. 4 demonstrates the presence of significant interdonor variability in our data. This variability exceeds the intradonor variability, which is possibly due to the stochasticity of clot growth initiation events in different channels perfused with blood from the same donor. Because the microfluidic device and flow conditions for the distinct donors were the same, the interdonor variations are likely attributable to the donor-specific concentrations of the coagulation proteins in the blood samples, as well as to donor-specific rates of the biochemical reactions driving clot formation. This is consistent with the substantial intersubject variability in thrombin generation present in static in vitro systems (55, 56). Moreover, the possibility of donor-specific reaction rate variations affecting clot formation kinetics is in accord with a recent study demonstrating that model parameter estimation should be subject-specific to achieve quantitative modeling accuracy (55).

Our model simulations predicted that, at 400 s, the 100-μm thrombogenic surface with high TF density should be characterized by larger spatial regions (and, correspondingly, higher local levels) of platelet, thrombin, and fibrin accumulation than the surface with low TF density (Fig. 5). Our experimental data on platelet deposition confirmed this prediction (Fig. 5 A). Moreover, the model-predicted thrombus height was in a quantitative agreement with the experimental data on platelet deposition for both the long (Fig. 5 A) and short (Fig. S9) thrombogenic surfaces. Interestingly, TF surface density increase on the 100-μm thrombogenic surface made the area of high platelet deposition (shown in red) more symmetrical (Fig. 5 A). By contrast, this increase shifted the areas of high thrombin and fibrin deposition from the downstream to the upstream regions of the thrombogenic surface (Fig. 5, B and C), showing that the spatial distributions of these clot components are also differentially regulated by TF surface density.

Figure 5.

Model-predicted spatial distribution of the clot at 400 s. (Left and right panels) Model-predicted spatial distributions of clots on low and high TF density surfaces, respectively, where the thrombogenic surface (100 μm) was centered at 300 μm from the origin. The blood flow direction is from left to right. (A) Our computational model captured the spatial distribution of the platelet deposition domain in the microfluidic device. The experimentally measured platelet deposition is indicated by the white line superimposed over the density plot of model-predicted platelet deposition. (The white lines in the left and right panels correspond to the data also shown as the black lines in Figs. 3B and S8B, respectively.) (B) Model-predicted thrombin generation. (C) Model-predicted fibrin accumulation. To see this figure in color, go online.

The effect of TF on the channel occlusion is reduced for the shorter thrombogenic surface

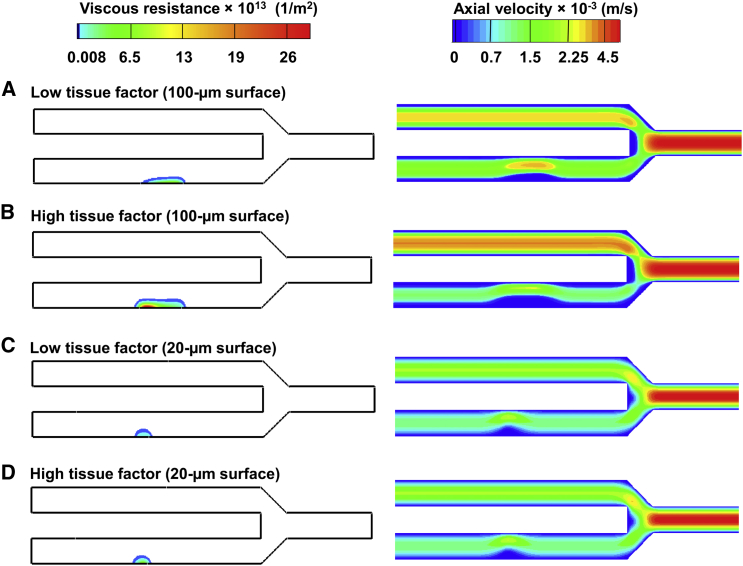
Our computational model predicted that, at 400 s, the increased platelet deposition and fibrin accumulation on the long thrombogenic surface should lead to an increase in clot viscous resistance compared to the short thrombogenic surface (Fig. 6) For example, for the high TF surface density, the maximal viscous resistance is approximately fivefold higher for the long surface than for the short one (Fig. 6, B and D, left panels; the area of high resistance is shown in red). Moreover, our model simulations showed that an increase in the TF surface density should result in a larger increase in the degree of occlusion in a channel with a 100-μm thrombogenic surface than that in a channel with a 20-μm thrombogenic surface (Fig. 6). Indeed, the simulations indicated that both maximal clot resistance and occlusion degree in the channel with the 100-μm thrombogenic surface should be greater by ∼5.3- and ∼1.5-fold, respectively, for the high TF density than for the low TF density (Fig. 6, A and B). In contrast, the occlusion of the channels with the 20-μm thrombogenic surfaces did not show any significant TF density dependence. The model-predicted maximal clot viscous resistance in the channel with the 20-μm thrombogenic surface was ∼3.7-fold greater for the high, than for the low, TF surface density. However, the clot boundaries in both cases were nearly the same (Fig. 6, C and D). Consistent with this model prediction, experimental data showed only a modest difference in platelet height between low and high TF densities for the 20-μm thrombogenic surface (Figs. 3 A and S8 A). This suggests that platelets may be unable to grow beyond a certain height on the 20-μm surface. Taken together, these results imply that the clots formed over the 20- and 100-μm surfaces with the two considered TF levels could all resist blood flow and partially occlude the channels under the given flow conditions. Nevertheless, the effect of TF on blood-flow occlusion was greater for the long thrombogenic surface than for the short one.

Figure 6.

Model-predicted clot viscous resistance and axial velocity at 400 s. The lower channel of the microfluidic device was occluded, owing to the resistance imparted by platelet and fibrin deposition at the thrombogenic surface. The blood flow direction is from left to right. (A–D) (Left panels) Density plots of viscous resistance, whose magnitude depends on the deposited platelets and fibrin. (Right panels) Density plots of the resultant axial velocity, which is reduced owing to an increased viscous resistance leading to blood flow occlusion over the thrombogenic surface. As the channel with the thrombogenic surface becomes occluded, blood flow is diverted to the upper channel, which has no thrombogenic surfaces. To see this figure in color, go online.

To gain further insights into the fluid-dynamical differences between the high and low TF surface density clots, we simulated blood flow (without clot formation) over experimentally derived platelet deposition profiles for the 100-μm thrombogenic surface. Interestingly, our simulations showed that the shear rate distribution over the porous clot surface was significantly different between the two considered TF surface densities, the shear being higher for the high TF surface density (Figs. 7 A, S10 A, S10 C, S11 A, and S11 C). This is due to a higher viscous resistance that characterized the clots formed on the thrombogenic surface with the high TF density (Fig. 6, A and B). Indeed, the higher viscous resistance made such clots less permeable to blood flow and, consequently, increased the bulk flow over the clot, thereby increasing the shear rate at the clot boundaries. The increased bulk flow for the high TF surface density also resulted in a higher intrathrombus blood-flow velocity (shown in red in the figures; right panels), but that was limited only to the upper (i.e., flow-exposed) layers of the clots due to an increased viscous resistance (Figs. 7 B, S10 B, S10 D, S11 B, and S11 D). By contrast, for the low TF surface density, the fast-flow region penetrated much more deeply inside the clot due an increased permeability (i.e., decreased viscous resistance) (Figs. 7 B, S10 B, S10 D, S11 B, and S11 D). These results suggest that, while the outer layers of the clots for the high TF surface density are more labile, their inner regions provide an environment with a high residence time for coagulation factors. This could result in enhanced thrombin generation and fibrin production compared to the low TF surface density case.

Figure 7.

Computational fluid dynamics predictions of shear rate and intrathrombus velocity patterns for a representative platelet deposition profile (donor #5) over the 100-μm thrombogenic surface at 420 s. The platelet deposition profiles were assumed to be porous. (A) Shear rate distribution on the clot boundaries for the high and low TF density. (B) The colors represent blood flow velocity inside the porous clot region (i.e., the intrathrombus blood flow velocity). (Top and bottom panels) Intrathrombus blood flow velocity for the high and low TF surface density, respectively. The thrombogenic surface was centered at 300 μm. The blood flow direction is from left to right. Note that the shear rate magnitudes at the upstream and downstream points of the clot are small but nonzero values (due to the small velocity gradients in these regions). To see this figure in color, go online.

In our simulations, the high TF density clots produced large shear oscillations on the upper clot boundaries (Figs. 7 A, S10 A, S10 C, S11 A, and S11 C). We hypothesized that these large oscillations could result from the increased viscous resistance of the high TF surface density clots, which is due to an increase in platelet deposition and fibrin accumulation. Indeed, the increased viscous resistance (i.e., a low-permeability clot) can potentially divert more blood from the clot domain, thereby increasing the bulk flow velocity over the clot. This, in turn, can produce larger velocity gradients and thereby increase the shear. The increased velocity will then amplify the shear oscillations, which are a reflection of the surface irregularities on the surface of the platelet deposition profile defining the clot boundary.

To test this hypothesis, we performed an additional flow simulation on the high TF surface density clot for donor #5, in which we decreased the average viscous resistance values in the clot core (i.e., the platelet and fibrin deposition region) and the clot shell (i.e., the platelet deposition region). These decreased average values corresponded to the low TF surface density clot and were taken from our simulations performed using the fully coupled computational model (Fig. 6 A). Similarly, we performed another simulation for the low TF surface density clot for donor #5 with increased viscous resistance values, which were obtained from the high TF surface density clot simulation shown in Fig. 6 B. All other conditions were kept the same, as explained in the Materials and Methods. The results showed that the shear oscillations decreased when we decreased the viscous resistance values in the high-TF (larger) clot, and that they increased when we increased the viscous resistance values in the low-TF (smaller) clot, thus confirming our hypothesis (Fig. S12). These additional results imply that clots with low permeability (i.e., high viscous resistance) can introduce large shear oscillations on the upper clot surfaces, which can potentially influence platelet behavior.

Discussion

When TF is exposed on a thrombogenic surface, the total abundance of TF can be characterized quantitatively by its surface density (or surface concentration) and the area of the thrombogenic surface. Here, we explored how these two characteristics affect clot structure, the mechanical properties (primarily, viscous resistance) of the clot, and the resulting axial velocity of the blood flow inside, and in the vicinity, of the growing clot. The physiological function of a blood thrombus is to stop the bleeding when the blood vessel wall is breached. Although we did not explicitly investigate hemorrhage, the fundamental hydrodynamic features of clot resistance and the resulting blood flow velocity reduction, investigated here, should naturally be expected to determine the ability of a clot to perform its function.

Our results demonstrated that the platelet deposition region was larger on the long surface (Figs. 3 and S7), and the thrombogenic surface length effect was even more pronounced for thrombin and fibrin generation (Figs. 2, B and C, and S7, B and C). These findings suggested that the long thrombogenic surface promoted the formation of a larger (and more occlusive) clot, which may additionally be more resistant to shear forces owing to increased fibrin production (24). Moreover, our analysis revealed that an increase in the TF surface density led to an increase not only in thrombin (and, therefore, in fibrin) generation, but also in platelet deposition (which was, however, affected to a lesser degree) (Fig. 4). Furthermore, our computational model simulations yielded larger spatial regions of platelet, thrombin, and fibrin accumulation over the high TF density surface than over the surface with the low TF density (Fig. 5). Finally, our simulations suggested that the TF effects on blood-flow occlusion should be more pronounced for larger thrombogenic lesions than for smaller ones (Fig. 6).

Both our model simulations and experimental data showed that, under the considered conditions, the spatial distribution domain of deposited platelets exceeded that of fibrin (and thrombin) accumulation (Fig. 5). Importantly, however, this clot structure is not inconsistent with the thrombin- and fibrin-driven thrombus formation that may occur in venous thrombosis (10, 57). Indeed, by model construction, thrombin generation is a strong contributor to platelet activation (see the model description and equations in the Supporting Material), and fibrin is a major determinant of clot permeability (Eqs. 6 and 7). Although platelet deposition shapes the outer boundary of the clot, it is fibrin that ultimately defines its viscous resistance and, therefore, its ability to affect blood flow (Figs. 5 and 6). This is in accord with our previous study, which suggested that supplementing a few essential procoagulant proteins and fibrinogen can restore nearly normal clot mechanical properties in diluted blood under flow (24).

The model-predicted heterogeneous clot structure is in accord with the core-shell architecture observed in both microfluidic experiments and in vivo experiments on mouse models (27, 52, 53, 54). The core-shell architecture appears to be closely linked to the hemodynamics and intrathrombus agonist transport. Indeed, it has been shown that the size of the shell region decreases with increased shear rate (27). Our computational model predicted a higher intrathrombus blood flow velocity at the upper layers of the clot (where shear rates are high) than in its interior (Figs. 7, S10, and S11). This suggests that, whereas convective transport dominates at the clot boundaries, diffusive transport can dominate over convection in the clot interior. Thus, the clot interior allows thrombin to effectively diffuse within it (27), thereby promoting fibrin generation and leading to a tightly packed clot core. Our results (Figs. 5, B and C, and 6, B and C) suggest that increased TF surface density will enhance this phenomenon.

In our model simulations and experiments, an increase in the TF surface density led to a faster platelet, thrombin, and fibrin accumulation, thereby contributing to the formation of both the clot’s core and its shell (Figs. 4 and 5). This is consistent with in vivo observations that thrombus size is reduced in mice expressing low TF levels (8). At the same time, our results showed that both platelet deposition height and fibrin accumulation increased with the thrombogenic surface length, suggesting that thrombogenic surface size may also play a role in enhancing both the clot’s core and shell formation (Figs. 2 and 3). However, the additional experiments that we performed with a 1000-μm thrombogenic surface (for both low and high TF levels) showed that the rates of platelet deposition, thrombin generation, and fibrin accumulation could decrease in comparison with the 100-μm thrombogenic surface. This is in accord with a recent report suggesting that 1000-μm surfaces are less efficient than 250-μm surfaces in producing thrombin (58). Thus, surface length may have a nonmonotonic influence on clot growth. This observation warrants further investigation of the possibility that an optimal thrombogenic surface length exists for clotting.

The height of the platelet deposition domain is a key indicator of clot growth with direct (patho)physiological consequences. Indeed, if the clot boundary is determined by the platelet deposition domain (as follows from our analysis), then the height of this domain defines the degree of vessel occlusion due to clot growth. The increased platelet domain height occurring on a longer (and, therefore, larger) thrombogenic surface may be due to three plausible mechanisms. First, the probability of initial platelet adhesion to the collagen surface is, evidently, higher for a larger surface, leading to a larger number of collagen-adhered platelets. This sets the stage for a second plausible mechanism, because the probability of a mobile platelet adhering to a collagen- (or platelet-) bound platelet is higher if the number of bound platelets is higher. Third, the clot formation occurring on the (larger) thrombogenic surface sides can result in increased generation of thrombin that, due to diffusion, contributes to increased platelet activation and adhesion near the center of the thrombogenic surface, thereby magnifying the effect of the thrombin generated at the center. Although plausible, however, these mechanisms do not explain the reduced platelet deposition on the 1000-μm surface, which has been attributed to the platelet boundary layer depletion (58). A detailed investigation of the relative contribution of these mechanisms would be necessary to understand how platelet growth varies across a wide range of thrombogenic surface sizes.

This work investigates clot formation under flow with venous shear. Yet, it is conceivable that our approach and main results also apply to arterial flows and have implications for thrombosis resulting from atherosclerotic plaque rupture. The likelihood of plaque rupture and subsequent thrombosis, which is a leading cause of morbidity and mortality in the developed world, is determined by plaque composition (59, 60). High TF content in plaque lesions provides a powerful trigger for the coagulation cascade initiation (61). Our results suggest that fibrin-rich clots over thrombogenic surfaces with a high TF density are not only larger, but also are more occlusive and can resist greater hemodynamic forces than clots formed over surfaces with low TF density (Figs. 4, 5, and 6, A and B; see also (24)). This implies that clots forming after high-TF plaque rupture may have a pathologically greater ability to withstand shear forces than those formed during a normal hemostatic process. This notion is supported by an immunohistochemical and morphometric study of thrombi from ruptured plaques of human coronary arteries, which reported high abundance of fibrin in thrombi (62). The same study also detected high TF levels in ruptured plaques (62). These fibrin-rich, highly resistant thrombi can occlude the blood vessel at the site of clot formation or break away without disintegrating during their transport, leading to thromboembolism.

Our computational model is based on the continuum approach first introduced by Leiderman and Fogelson (16, 63). In this approach, platelets are modeled as point tracer particles, and RBCs are represented implicitly. Application of this simulation strategy to our microfluidic device of given dimensions (Fig. 1) is consistent with the original work of Leiderman and Fogelson (16, 63), who applied their continuum model to flows in a 60-μm-high 2D channel. Moreover, this approach is in accord with previous applications of continuum models to blood coagulation in a microfluidic device analyzed by our group (24) and by others (22). The use of continuum models is justified when the flow domain is much larger than the typical diameters of RBCs (6–8 μm) and platelets (2 μm) (64). Thus, the 60-μm height of our microfluidic device exceeds the dimensions of those cell types by ∼10-fold or more, suggesting that the accuracy of the continuum approximation, and of the spatial averaging involved, can be sufficient for our modeling purposes. Indeed, a recent study showed that a continuum model of RBC-dependent platelet transport serves as an excellent approximation to both explicit particle-based simulations and experimental data over a wide range of channel heights (65). The grid size in our study was approximately equal to the platelet size. This choice was a tradeoff between expected spatial resolution and computational expediency, and was consistent with the work of Leiderman and Fogelson (16) and with our own modeling efforts (24).

It is known that whole blood is a non-Newtonian fluid for smaller channels (<100 μm in diameter) at shear rates <100 s⁻¹ (64, 66). This is manifested via nonconstant blood viscosity, which can depend on the shear (shear-thinning) and hematocrit (67, 68, 69). A well-studied special case of the hematocrit dependence is the Fahraeus-Lindqvist effect, in which the apparent viscosity of blood flowing through thin tubes decreases with decreasing tube diameter (64). Thus, the assumption of constant blood viscosity in this study (Eq. 4) and in the work of Leiderman and Fogelson (16, 63) is an approximation. Yet, in this study, the microfluidic channel dimensions and the inlet shear rate were fixed, and blood from the same subject group was used in all experiments. Therefore, the computationally and experimentally detected trends in this study can be attributed to the factors of interest (i.e., TF localization), rather than to possible deviations from the Newtonian blood rheology assumption. Furthermore, the agreement between computational predictions and experimental data (Figs. 2, 4, 5, S7, and S9) supports the notion that the Newtonian rheology approximation is meaningful under the considered conditions.

Our study has limitations. The microfluidic channels used in our experiments cannot capture the hemodynamics introduced by the tortuosity or flexibility of blood vessels. Nevertheless, besides allowing us to study clot formation in human whole blood, microfluidic experiments offer flexibility and control. The limitations of our computational model include the 2D representation of 3D microfluidic channels, as well as the continuum approach and the constant viscosity assumption (i.e., Newtonian behavior of blood) discussed above. Because the channels’ width exceeded their height, we could assume that wall effects on clot formation and flow would be minimized, which provided the basis for our 2D representation. Furthermore, in our simulations, we assumed a continuous, uniform distribution of TF on the thrombogenic surface, whereas the thrombogenic surface patterned for the experiments had a measure of heterogeneity (Fig. S1). This assumption, which is consistent with our overall continuum modeling approach, was made to allow modeling flexibility and to simplify the definition of boundary conditions for the simulations. The continuum-based approach allows for future model extensions, such as the modeling of large blood vessel geometries in 3D and the reflection the non-Newtonian behavior by incorporating an explicit dependency of blood viscosity on the shear and hematocrit (67, 68, 69). As another limitation, we did not study the balance of major pro- and anticoagulant factors (such as antithrombin), which, together with the role of fibrinogen, was shown to be critical for normal clotting in a static system (55, 70). Finally, the influence of TF localization may depend on the flow conditions and may differ between venous- and arterial-shear flows, as well as between blood vessels of different sizes. We intend to address the influence of these factors in follow-on publications.

In summary, our results demonstrate that TF localization has diverse effects on platelet deposition, thrombin generation, and fibrin accumulation under venous flow conditions. Thus, it has the capacity to strongly affect the formation, structure, and mechanical properties of blood clots. Our results may contribute to an improved understanding of how high TF levels in tissues of vital organs, such as brain, heart, and kidneys, shape their increased hemostatic potential. Moreover, our findings may provide insights into how high TF content on the surfaces of endothelial and immune cells, as well as the total amount of such TF-expressing cells localized inside a blood vessel, could affect clot formation and its effects on blood flow during thrombosis.

Author Contributions

V.G., S.L.D., J.R., and A.Y.M. designed research. V.G., S.Z., R.L., Y.L., and A.Y.M. performed research. V.G., J.R., and A.Y.M. analyzed data and wrote the paper.

Editor: Fazoil Ataullakhanov.

Supporting Citations

References (71, 72, 73, 74, 75, 76, 77, 78) appear in the Supporting Material.