Theory of Epithelial Cell Shape Transitions Induced by Mechanoactive Chemical Gradients

Abstract

Cell shape is determined by a balance of intrinsic properties of the cell as well as its mechanochemical environment. Inhomogeneous shape changes underlie many morphogenetic events and involve spatial gradients in active cellular forces induced by complex chemical signaling. Here, we introduce a mechanochemical model based on the notion that cell shape changes may be induced by external diffusible biomolecules that influence cellular contractility (or equivalently, adhesions) in a concentration-dependent manner—and whose spatial profile in turn is affected by cell shape. We map out theoretically the possible interplay between chemical concentration and cellular structure. Besides providing a direct route to spatial gradients in cell shape profiles in tissues, we show that the dependence on cell shape helps create robust mechanochemical gradients.

Introduction

The shape of a cell is governed by its intrinsic material properties and active stresses as well as by external regulation through chemical and mechanical cues (1, 2). Adhesive and cytoskeletal forces, mediated by the Rho family of GTPases, are found to play a particularly important role in determining cell shape (1, 3). Cell shape transitions occur during division, growth, and morphogenetic events such as tissue and organ development (4, 5, 6). For example, the folding of sheets of epithelial cells during organogenesis proceeds through the constriction of individual cells, driven by contractile forces generated in the actomyosin network at the cell surface (1, 6). The simplest mechanisms controlling this process rely on the spatial patterning of apical cell contractility (7) by complex chemical signaling pathways. Attempts are being made to relate the measurable spatial distribution of signaling molecules to shape changes during tissue development (8). The chemical signaling can in turn be induced by mechanical cues such as forces (9) and deformations (10, 11), thus underscoring the inherently mechanochemical nature of development.

Here, motivated by the notion of morphogens (12), diffusible biomolecules that induce cell fate changes in a concentration-dependent manner during embryogenesis, we explore the notion of “mechanogens” (13). These specifically influence mechanical properties, such as cell-cell adhesion and cellular contractility (and therefore, cell shape), and create spatial gradients in cell structure in a tissue. Such a model could describe cell shape transitions as seen in developing embryos such as during Drosophila oogenesis or wing disk morphogenesis, where an initially cuboidal collection of epithelial cells becomes part squamous, part columnar (14), at least partly in response to diffusible biochemical signals (15, 16). Similarly, Barrett’s esophagus, a risk factor for esophageal adenocarcinoma, is characterized by a phase transition from squamous to columnar epithelia in localized regions (17). To theoretically map out the various mechanical effects of a biochemical gradient, we consider both possible scenarios, that the biochemical gradient enhances and represses cellular contractility: processes that we term “mechanoinductive” and “mechanoreductive” respectively. Whereas a purely mechanical theory of cell shape does allow for coexistence of two different cell types within a tissue under confinement (5), the biochemical gradient provides a more direct route to realize such transitions in shape that are independent of specific mechanical boundary conditions of the tissue.

In addition to this direct effect of mechanogens on cell shape, the concentration profile of mechanogens can, in principle, be affected by the mechanical state of the cells. This is because the uptake rate of mechanogens from solution and subsequent degradation may be affected by the shape and contractility of the cell. This results in a mechanochemical cell shape-mechanogen feedback that could be both positive or negative, depending on the specific mechanism through which uptake rate depends on cell shape. We term these distinct scenarios as “self-enhanced” or “self-repressed” degradation. Self-enhanced feedback has been explored earlier in the context of reaction-diffusion of multiple morphogen species and has implications for the range and robustness of the biochemical gradient to noisy molecular fluctuations (18, 19).

Methods

Theoretical model and approach

Mechanicochemical model for cell shape. Cell shape is determined by a balance of contractile forces actively generated by the cell using the actomyosin machinery in its cytoskeleton (20) and those exerted on it by its environment—adhesive interactions with neighboring cells in the case of closely packed epithelial cells. The minimal description for epithelial cell shape, for instance in vertex models (21, 22, 23, 24, 25, 26), then involves a balance between the contractility of the actin belt, which acts as a corset to constrict the cell’s apical surface and the adhesions, which favor increased area of contact with the underlying substrate or with neighboring cells.

We consider here a minimal mechanical description of force balance that determines epithelial cell aspect ratio (5). Because the specific geometry of the tissue does not concern us here, we model each cell as a cylinder of radius, r, and height, h, as shown in Fig. 1 A. The effective mechanical energy of the cell has the following contributions: ∼−γ_b·r² from adhesions of cells to the substrate at their basal surface, ∼−α_l·r·h from lateral adhesions to neighboring cells, and ∼A_a·r from the apical belt tension due to actomyosin contractility that tends to reduce the apical circumference. Here, the adhesive molecules at both basal and lateral surface are considered to generate an effectively negative surface tension (27, 28, 29). In general, the surface energy has contributions of opposite sign from adhesions, which favor increased area of contact, and contractile tension, which tends to constrict the surface (27). We focus here on lateral and basal adhesions (α_l, γ_b > 0) for clarity of discussion, although the theory can be easily modified to account for lateral contractility (5). Finally, an energetic cost of crowding or confinement A, keeps the cell from becoming infinitely thin or flat.

Figure 1.

Mechanochemical model for cell shape gradients. (A) Phase diagram in the adhesion(α_l)-apical contractility (Λ_a) parameter space illustrating the regions where both squamous-and-columnar (1), only columnar (2), only squamous (3), or cuboidal (4) cell shapes are stable. This is calculated based on the mechanical free energy in Eq. 1 introduced in (5). The illustration on the right side depicts our minimal model of an epithelial cell as a cylinder whose shape is determined by a balance of apical contractility, Λ_a, and adhesions with the substrate, γ_b, and with neighboring cells, α_l. (B) Illustration of possible feedback between biochemical mechanogen gradient and epithelial shape through an effect on cell contractility. As apical cellular contractility is modulated by a mechanogen gradient, the cell shape changes, which in turn affects mechanogen degradation that happens through uptake at the cell surface. A few possible feedback scenarios are discussed in the text. (C) Scheme of the model showing a collection of cells (tissue) subject to a gradient of diffusible biomolecules (mechanogens) that induce shape change by binding to the apical (upper) cell surface and triggering changes in cellular contractility. The rate of uptake of the mechanogens by the cells can depend on the local mechanogen concentration through its dependence on local cell shape, like in the feedback described in (B). (D). Illustration of mechanogen concentration profiles for three distinct cases with plots based on the approximate analytic expression in Eq. 4: mechanoreduction leading to self-enhanced degradation (negative feedback) (Red); mechanoinduction leading to self-repressed degradation (positive feedback) (Blue); and the case where degradation does not depend on cell area, i.e., no feedback (Green). Inset shows a semilog plot, indicating that the no-feedback profile, where the degradation rate does not depend on cell surface area, is a simple exponential. To see this figure in color, go online.

This confinement energy (estimated from the crowding of cytoskeletal components), A ∼ 10⁻²⁴ Jm² (5) and the fixed volume of nearly incompressible cells (30, 31), V₀ ∼ 10⁻¹⁵ m⁻³ (14), set the energy and length scales in the mechanical model. With only three rescaled parameters which we rename as ${\gamma }_b{V}_0^{4/3}/A\to {\gamma }_b$, ${\alpha }_l/\left(A{V}_0^{2/3}\right)\to {\alpha }_l$, ${\text{Λ}}_a{V}_0^{2/3}/A\to {\text{Λ}}_a$, we obtain a force balance expression for cell shape by minimizing the effective free energy (5) as

$$f\left(r\right)=-{\gamma }_b{r}^2-\frac{{\alpha }_l}{r}+{\text{Λ}}_{a}r+r^4+\frac{2}{r^2},$$ (1)

where the cell radius is rescaled as r/V₀^1/3 → r, the height is fixed by the incompressibility constraint h ∼ V₀/r², and the last two terms represent the confinement energy of cytoskeletal elements within a fixed, finite cell volume. Using the experimentally measured values for cell adhesion energy and contractility given in Table 1, the nondimensional mechanical parameters in Eq. 1 can be estimated as γ_b, α_l, Λ_a ∼ 10.

Table 1.

Parameters Used in this Model along with Corresponding Sources Where They Have Been Measured or Estimated

Parameter	Symbol	Estimate	References
Adhesions	γb, αl	10−3 N/m	(28, 29)
Contractility	Λa	10−8 N	(46)
Confinement	A	10−24 J⋅m2	(5)
Cell volume	V0	10−15 m3	(14)
Diffusion	D	10−12 m2/s	(33, 47)
Uptake rate	β	0.01 /s	(32, 33)

The first three are related to cell structure and mechanics, whereas the last two are for a biochemical morphogen gradient (Dpp) that potentially acts as a mechanogen.

The model energy in Eq. 1 is bistable for certain ranges of the parameter values as shown in the phase diagram in Fig. 1 A, with both squamous (flat, wide) and columnar (tall, thin) cell shapes possible (5). We note that this model is a minimal description of epithelial cell shape in that it essentially balances contractility and adhesions, and the remaining terms are required for stability so that the free energy minimum does not occur at vanishingly small cell radius or height. Finally, the assumptions of cylindrical shape and incompressibility are made only to simplify the discussion and relaxing these assumptions does not qualitatively alter our results (5).

Here, we consider the interplay of this mechanical force balance with a biochemical gradient for inhomogeneous tissue during differentiation and growth. Indeed, biological inhomogeneities are typically induced by gradients (12) of diffusible biomolecules that encode specific biochemical information (32). Interestingly, the morphogen Dpp, which influences myosin II contractility (16), is involved both in actively promoting a cuboidal to columnar transition in the wing disk (16) by increasing apical contractility, and in a cuboidal to squamous transition in the oocyte (15), by biophysical mechanisms that remain unclear. The properties of the biochemical gradient of the morphogen Dpp are, however, experimentally well characterized in terms of its diffusion and uptake rates as tabulated above (33).

From Eq. 1, two possible candidates for the latter would be an upregulation of lateral contractility, and a downregulation of lateral adhesion (both correspond to decreasing α_l), as overexpressing the lateral adhesion molecule FasII prevents this cell shape transition (34). Although our mechanochemical theory could be easily generalized to consider the possibility of mechanogens affecting lateral adhesion, we focus here on the more generic scenario where diffusing biomolecules (mechanogens) reduce or increase cellular area. To linear order, this is equivalent to a dependence of the local apical cellular contractility, Λ_a(x) (Fig. 1 B), on the local mechanogen concentration, c(x), as

$${\text{Λ}}_a\left(x\right)\simeq {\text{Λ}}_0\pm \frac{\partial \text{Λ}}{\partial c}|,$$ (2)

where the total apical contractility, Λ_a, is a sum of Λ₀, an intrinsic cellular contractility, and χc(x), the change in contractility induced by the mechanogen through a susceptibility, $\chi \equiv \frac{\partial \text{Λ}}{\partial c}|$. We rescale the concentration as χc → c, so that the magnitude of mechanogen is quantified only in terms of the contractility it induces. The sign of the coupling of contractility to mechanogen concentration represents the tendency of mechanogens to enhance (+, i.e., mechanoinduction) or reduce (−, i.e., mechanoreduction) apical contractility, and therefore to correspondingly decrease or increase apical surface area. Although this mechanochemical coupling, χ, has not been directly quantitatively measured, we estimate that the effect of c is comparable to Λ₀ based on (16), which shows a transition from columnar to cuboidal cell shape when Dpp is inhibited.

For simplicity, we consider spatial gradients in one dimension (x direction; Fig. 1 C) induced by a planar source in the y,z plane at x = 0 (representing a strip of special mechanogen-producing cells, for example). We consider a confluent cellular monolayer where we treat the local cell radius, r(x), as a continuous variable that depends on the local balance of forces acting on the cell at position x. This is valid when the cell shape changes gradually in space over a length scale that is significantly larger than the cell size.

Cell shape-dependent chemical uptake. The mechanogen concentration gradient reaches a steady state, c(x), when its production at the local source is balanced by degradation by the cells. In the simplest scenario, this happens through binding of the mechanogen ligands to receptors on the cell’s surface and subsequent receptor-mediated endocytosis (Fig. 1 C) (18, 32). The local rate of degradation can in principle depend on the cell shape, here described by the cell radius, r(x), because of differences in effective area available for uptake. The diffusion-degradation relation for mechanogens at the steady state, for a cellular monolayer, can then be written as

$$\begin{array}{c}D{\nabla }^{2}c\left(x\right)-\beta \left(r\left[{\text{Λ}}_a\left(x\right)\right]\right)c\left(x\right)=0\\ \Rightarrow {\nabla }^{2}c\left(x\right)-{\lambda }_d^{-2}\left(x\right)c\left(x\right)=0,\end{array}$$ (3)

where D is the diffusion constant, and β(r(x)), the local uptake rate of mechanogens. This depends on the local cell radius, r(x), which in turn depends on cellular contractility in accordance with the mechanical model of Eq. 1. We write the cell radius, r[Λ_a(x)], as a function of the corresponding local apical contractility, Λ_a(x), to indicate that cell shape is determined by a local force balance. We note here that the bulk mechanical free energy density in Eq. 1 should in principle be modified for an inhomogeneous collection of cells by including an interfacial energy, which to lowest order in gradients is B(dr/dx)², where B is an interfacial energy parameter that corresponds to adhesive interactions between neighboring cells that disfavor changes in cell shape. In the Supporting Material, we introduce this term and justify when it can be ignored for small spatial gradients in cell shape. In this simplified case, the local balance of diffusion and degradation in Eq. 3 results in an effective slowly varying decay length, λ_d(x).

One must thus write a dependency between the mechanogen uptake rate and the cell shape, for which there is a variety of conceivable biological mechanisms, to close this set of equations. In the simplest case of subconfluent monolayers, it is easy to see that uptake rate scales with the available apical area for receptors: β ∼ r². In the special case of confluent monolayers with receptors localized at the apical area, with density independent of cell shape, the uptake rate would be independent of r. However, a number of recent studies indicate that β would depend on r in many biological systems. For instance, it was recently shown that human embryonic stem cells localize their Tgf-β receptors on their lateral surface (35), which should result in higher uptake rate for confluent columnar cells. This implies a qualitatively different scaling of uptake rate with cell radius: β ∼ r⁻³, because the lateral area of an individual incompressible cell scales as r⁻¹, and the number of cells per unit area as r⁻². Similarly, receptors restricted to a local region of the apical area, for instance the perimeter, would result in a β ∼ r¹ dependency. Biochemical regulations of the receptor density with cell shape would result in more complex dependencies. Finally, the rate of endocytotic uptake can also be affected by membrane tension (36, 37), which depends on contractility that also determines cell shape, thus hinting at an indirect relationship of cell shape and uptake rate. Crucially, however, we emphasize that all of these feedback effects (38) are accounted for in a generic manner at first order, i.e., as long as such effects are small, and there is no sharp change in cell shape. Indeed, in the limit of low mechanogen concentration (or weak mechanochemical coupling), the cell radius changes slowly across the tissue: r(x) $\simeq$ r₀ ± r′ (Λ_a)c(x), and the diffusion-degradation equation in Eq. 3 simplifies to

$${\nabla }^{2}c-{\lambda }_d^{-2}c\left(x\right)\pm {\beta }_1{c}^2\left(x\right)=0.$$ (4)

Thus, we get a diffusion equation with a linear degradation given by decay length, λ_d, that depends on the average cell radius r₀, and a quadratic degradation term whose coefficient, β₁, depends on the parameters in the theory (derived in the Supporting Material). The sign of the quadratic term depends both on the biochemical effect of the mechanogen on mechanical parameters and on the sign of the coupling between cell shape and degradation rate.

The perturbative description for mechanogen gradient in Eq. 4 is valid when the cell radius changes slowly across the domain. A complementary simple limit is where there is a sharp transition in uptake rate at some position, x_c, in which the decay length of mechanogen concentration is nearly uniform on either side of this crossover point. This is presented subsequently in Eq. 5.

Results and Discussion

An analysis of mechanochemical gradients

The resulting steady states of the chemical and cell shape gradients depend crucially on the statistical ensemble considered, or the boundary conditions of tissue. In particular, for nondividing tissues (fixed number of cells), there are the two limiting cases of a tissue constrained to a fixed area, or a tissue freely choosing its overall area, so that the shape profile of the cells is strictly fixed by the biochemical gradient. This is especially important in the bistable region of the phase diagram, because in the absence of gradients, phase coexistence can only occur at a fixed area, based on energy minimization. In this case, the fraction of squamous and columnar cells depends only on the average cell density and the coefficients Λ_a and γ_l (5), so that the position of an interface between squamous and columnar epithelia, here labeled x_c, scales with the system size, L (at given average density). In analogy to liquid-gas phase transitions (where fixing volume or pressure has different consequences for phase coexistence), at fixed area, cells cannot minimize their energy by globally changing radius, and must thus rely on phase separation to do so. Conversely, at free total area, without chemical gradients, cells simply minimize energy by all adopting the same minimum energy shape. In the Drosophila oocyte, a change in overall area of the surrounding epithelium occurs via growth of the underlying germline cells, which has been proposed to play a role in the phase separation into squamous and columnar cells (14), consistent with our theoretical framework. Nevertheless, as squamous cells are always positioned at the anterior poles, gradients would need to exist to provide positional cues for the phase separation. Interestingly, however, in the presence of biochemical gradients, phase separation can occur in a tissue with freely adjustable area, which is more physiological because cells can adjust their density via division or extrusion in response to mechanical cues (39). Therefore, in the next paragraphs, we explore the coupling between chemical gradients and cell mechanics for the shape profile of epithelial sheets.

The approximate diffusion-degradation equation, Eq. 4, has an exact solution for large tissue size, L. These solutions (given in Eq. S7 in the Supporting Material) are plotted in Fig. 1 D for different signs of the nonlinear degradation term. Such a nonlinear diffusion equation has implications for the range (13) and robustness (19, 40) of morphogen profiles. The mechanoinductive profile undergoes slower rate of decay near the source whereas the mechanoreductive profile decays rapidly near the source. These are in contrast with the uniformly decaying mechanogen profiles that would occur in the absence of shape-dependent degradation. Note that although we focus on fixed c(0) gradients in most of this article for clarity, the representative plots in Fig. 1 D have different source concentrations. This is possible because various mechanogen source boundary conditions may occur, such as fixed source concentration or fixed source flux, a point detailed in the Supporting Material.

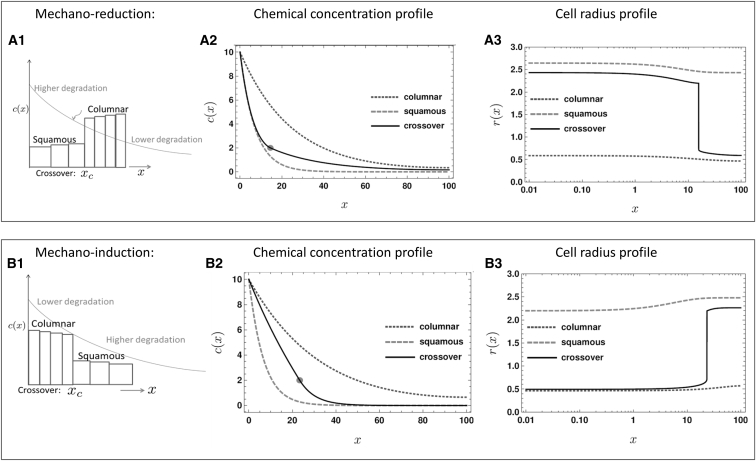
We now address the possibility that the mechanogen concentration induces an abrupt change in cell shape by tuning the contractility through its transition value in the mechanical phase diagram of Fig. 1 A. As the schematics in Fig. 2, A1 and B1 suggest, we consider a gradual spatial variation of the cell radius r(x) and the corresponding height, except at the crossover point x_c where there is a discontinuous jump from columnar to squamous cells. Minimizing the mechanical energy in Eq. 1 gives the stable cell radius as a function of the local apical contractility for fixed lateral and basal adhesion: r(x) = r(Λ_a(x), α_l, γ_b). Representative values of the cell shape parameters used here are chosen to allow squamous-columnar coexistence (5): lateral adhesion, α_l = 4, and basal adhesion, γ_b = 15. These are consistent with the estimates listed in Table 1. The crossover in cell shape occurs for these parameters at a critical contractility, Λ_c $\simeq$ 23 (Fig. 1 A), which defines the crossover position through Eq. 2 as: c(x_c) = (Λ_c − Λ₀).

Figure 2.

Comparison of spatial gradients of chemical concentration and cell shape for. mechanoreduction (A) and mechanoinduction (B), i.e. the cases where the diffusing biomolecule promotes/suppresses cellular contractility, and when their uptake rate scales with cell apical area. (A1 and B1) are schematics showing coexistence of two structural cell types. The cell radius varies slowly in space in response to the mechanogen concentration, except when there is a sharp transition in cell shape (at the crossover position, x_c). The crossover position is indicated in (A2 and B2) by a dot. (A) Mechanoreduction: Mechanogen concentration and cell radius profiles are shown for three different cases decided by the intrinsic cell contractility, Λ₀. Dotted line: Λ₀ = 35 (all columnar); solid, black line: Λ₀ = 25 (part squamous and part columnar); dashed line is for Λ₀ = 15 (all squamous). (B) Mechanoinduction: Mechanogen concentration and cell radius profiles are shown for three different cases decided by the intrinsic cell contractility, Λ₀. Dotted line: Λ₀ = 25 (all columnar); solid, black line: Λ₀ = 21 (part squamous and part columnar); dashed line is for Λ₀ = 13 (all squamous). The results displayed here are numeric solutions of the diffusion-degradation equation in Eq. 3, in conjunction with Eq. 2 and the mechanical model for stable cell radius in Eq. 1. In all cases, the contractility at squamous-columnar crossover is Λ_c = 23, and the mechanogen source concentration is fixed at c₀ = 10. See text for units and other parameter values used.

The exact steady-state mechanogen concentration profile for the given choice of parameters is obtained by numerically solving the diffusion equation in Eq. 3 with boundary conditions similar to the source-sink models of morphogen gradient formation (12). Here, we suppose c(0) = c₀ (fixed concentration maintained at the source in the inner region) and c′(L) = 0, zero flux at the outer boundary, where L is the size of the tissue. The numerical method is described in the Supporting Material.

We calculate the representative mechanochemical gradients shown in Fig. 2 for a simple, illustrative choice of the dependence of degradation on local cell radius: β = β₀r²(x). Such an increase of uptake rate with apical area is justifiable if a large proportion of the surface of columnar cells is given to forming junctions with neighboring cells, thereby reducing the effective area available for mechanogen uptake (Fig. S1). The rate constant, β₀, may be expressed in the form of a length scale, λ₀ ≡ D/β₀. In Fig. 2, we show typical mechanogen concentration, c(x), and corresponding cell radius profiles, r(x), for both mechanoinduction and mechanoreduction for three possible cases: where the cells remain either wholly squamous, or wholly columnar, or are part squamous-part columnar with a sharp crossover. The last case corresponds to the oogenesis scenario (15), but the other cases are also potentially realized in biology. The crossover happens in the narrow coexistence region of columnar and squamous cell types (between the spinodal lines shown in Fig. 1 A) and its exact location depends on the history of the system such as initial contractility, Λ₀, and the source mechanogen concentration, c₀, in addition to the mechanical parameters discussed before. An alternative scenario where ligand uptake occurs primarily through the lateral cell surface (35) and therefore, scales as r⁻³, is presented in Fig. S2. Here, unlike in Fig. 2, columnar cells result in higher degradation than squamous ones. The essential conclusions of our model are unchanged.

Note that the general theory for cell shape (5) predicts intermediate cell shapes (cuboidal) allowing a more gradual change in shape in other regions of the parameter space in Fig. 1 A such as below the critical point (where the spinodal lines meet). Such gradients can be described by the general diffusion equations for slowly varying cell shape in Eq. 4. Here, we focus on the sharp squamous-columnar transition, which occurs, for example, in Drosophila oogenesis. Thus, we consider here the scenario where adhesion outweighs contractility in the lateral cell surface (α_l > 0). The presence of a finite basal adhesion, γ_b > 0, allows the possibility of cell shape coexistence in this case. Fig. S3 shows the part of the phase diagram where lateral contractility is important.

We now discuss the location of the position of the interface between squamous and columnar epithelia, x_c, of cell shape in relation to tissue size, L, for the free area ensemble described before. The exact value of λ between the spinodal lines shown in the phase diagram in Fig. 1 A, depends on the initial conditions and history of the cells. This is because a collection of developing cells is out of equilibrium, and may not necessarily relax to the free energy minima of the mechanical model in Eq. 1. x_c also depends on the intrinsic contractility without mechanogens, Λ₀.

The numerically solved cell radius profiles in Fig. 2, A3 and B3 demonstrate that for the parameters considered here, the cell radius changes very slowly in the squamous and columnar regions (that is, except near the sharp squamous-columnar transition) and can therefore be approximated as nearly uniform. For a given set of parameter values, we denote these nearly uniform cell radius values for squamous and columnar cell types by r_sq and r_col, respectively. The nonlinear diffusion equation of Eq. 3 can then be approximated piecewise as

$$\begin{array}{l}{\nabla }^{2}c\left(x\right)-{\lambda }_i^{-2}c\left(x\right)\simeq 0,c\left(x\right)<c_c,\\ {\nabla }^{2}c\left(x\right)-{\lambda }_o^{-2}c\left(x\right)\simeq 0,c\left(x\right)>c_c,\end{array}$$ (5)

where λ_i and λ_o are the decay lengths in the inner and outer region of the profile, and, c_c = c(x_c), the crossover mechanogen concentration at which the cell shape changes abruptly. In Fig. S4, we show that solutions of Eq. 5 approximate well the corresponding numerically solved exact concentration profiles. For given size, L, and boundary conditions, we require that the profile is well behaved at the crossover point, x_c. This fixes the crossover point (details in the Supporting Material) to be a solution of

$$\frac{1}{{\lambda }_i}\left[c_0\text{csch}\left(\frac{x_c}{{\lambda }_i}\right)-c_c\text{coth}\left(\frac{x_c}{{\lambda }_i}\right)\right]=\frac{c_c}{{\lambda }_o}\text{tanh}\left(\frac{L-x_c}{{\lambda }_o}\right).$$ (6)

In Fig. 3, we show the values of x_c for a range of values of tissue size, L, for both possible types of feedback: self-enhanced degradation where λ_i < λ_o, i.e., when more mechanogen implies higher rate of decay, and self-repressed degradation, λ_i > λ_o. In our simple illustrative example for the dependence of mechanogen uptake on cell area, β ∼ r², these correspond to the mechanoreductive and inductive cases, respectively. The shorter and longer decay lengths are then determined by the columnar and squamous cell radius, respectively. We illustrate the x_c versus L dependence for the other, β ∼ r⁻³ scenario in Fig. S5. Also, Fig. S6 illustrates the slow variation of x_c versus L for the self-enhanced degradation case in Fig. 3 but for a larger range of values of L, in tissue sizes.

Figure 3.

Dependence of cell shape crossover position, x_c on tissue size, L for self-repressed mechanogen degradation (blue), self-enhanced mechanogen degradation (red), and uniform degradation without feedback (green). These correspond simply to whether the degradation rate is lower, higher, or unchanged for high mechanogen concentration near the source. In each case, the plot terminates at the minimum L for which a crossover can occur. The physically meaningful lower bound of x_c = L (dashed gray line) is realized for the self-enhanced degradation and no feedback cases but there is a minimum L_m required for crossover for self-repressed degradation (indicated by the red dot). The inset illustrates the possible solutions for x_c as a function of L in Eq. 6 for self-repressed degradation. The dashed black line is the left side, and the colored lines are the right side of Eq. 6 for different values of L (increasing from left to right). This shows two branches of solution of x_c, with the closed circles showing solutions that vary slowly with L and exhibit a minimum, L_m = 33.2, below which no solution exists; and the open circles indicate possible x_c values that depend strongly on L. We plot the former more realistic solutions in the main figure as the blue points. To see this figure in color, go online.

Although there exists a solution for x_c as L is lowered for the self-enhanced degradation profiles, there is a minimum value (L_m) in the self-repressed degradation case below which a crossover does not occur. This is an outcome of the nonlinearity inherent in Eq. 5 that leads to two possible branches of solutions for x_c from Eq. 6, for given L within a certain range of values. These are depicted as solid and open black circles in the inset to Fig. 3, which is a graphical solution of x_c for the self-repressed case. The broken line represents the L-independent left side of Eq. 6, whereas the family of colored lines is the right side of Eq. 6 as L is increased. In Fig. 3, we use parameter values: λ_i = λ₀/r_col and λ_o = λ₀/r_sq (reverse for the self-enhanced case), and λ₀ = 16, c₀ = 10, c_c = 2. This choice results in a minimum size, L_m = 33.2, for crossover in the self-repressed case. The solutions for x_c indicated by solid circles are more physical and consistent with tissue growth because they change slowly with tissue size, whereas the branch of solutions shown as open circles lead to exponential sensitivity of crossover position to tissue size.

Even for the gradients with sharp transitions, such as those we consider in Figs. 2 and 3, the cell radius changes slowly across the tissue when the two domains, x < x_c or x > x_c, are considered separately. The weakly nonlinear Eq. 4 then corrects the results of the linear piecewise approximate description of the gradients presented in Fig. 3. Equations 4 and 5 are thus two mutually consistent and complementary limiting descriptions that approximately describe the entire gradient, except for the narrow region near the sharp transition between the two domains. This, together with the nonequilibrium effects mentioned earlier, implies that the exact crossover position is difficult to determine, and needs to be approximately described as done in obtaining the results of Fig. 3.

Phase behavior of cell shape

The diffusing mechanogens in this theory induce a spatial gradient in the actomyosin contractility, Λ_x(x), for fixed adhesion energies, and thus correspond to a horizontal section taken through the contractility lateral adhesion phase diagram as shown in Fig. 1 A. A transition from one cell type to another within the same tissue can be mechanochemically induced if the mechanogens change the value of apical contractility from the squamous-only to the columnar-only part of the phase diagram as indicated in Fig. 1 A, while not affecting lateral adhesion. The apical contractility at which a columnar-to-squamous transition occurs is denoted Λ_c.

The part of the contractility adhesion phase diagram sampled along a gradient depends on the mechanogen source strength, c₀, the diffusion and degradation constants, and the intrinsic cell contractility without mechanogen, Λ₀. Based on these considerations, we calculate two possible phase diagrams of cell shapes in terms of the biochemical parameters (Fig. 4) again for β = β₀r². Fig. 4, A1 and B1, corresponding to mechanoreduction and induction, respectively, relate properties of the extracellular mechanogen gradient: the mechanogen source concentration (c₀) and an uptake rate, $\sqrt{{\beta }_0/D}={\lambda }_0^{-1}$. Fig. 4, A2 and B2, on the other hand, describes the effect of the intrinsic cell contractility, Λ₀, which is set by the cell independently of mechanogens. The two phase boundaries in each case are determined by the limiting conditions at the source and end points of the mechanogen profile,

$$\begin{array}{l}{\text{Λ}}_0\pm c_0={\text{Λ}}_c,\\ {\text{Λ}}_0\pm c_i\left(L\right)={\text{Λ}}_c,\end{array}$$ (7)

where “±” signs are for mechanoinductive and reductive cases, respectively; and c_i(x) is the concentration at a position in the inner region, x < x_c. These correspond to the maximum and minimum mechanogen concentration, at the source and far end of the profile, respectively, being higher and lower than the critical value, c_c = Λ₀ − Λ_c, for phase coexistence.

Figure 4.

Phase diagrams in biochemical parameters for mechanoreduction (upper panel) and mechanoinduction (lower panel) for a fixed value of lateral adhesion, α_l = 4 and an intrinsic cell contractility, Λ_c = 25, in (A) and Λ_c = 21 in (B). (A1 and B1) are phase diagrams for the mechanogen source concentration, c₀, and biochemical degradation rate, λ₀⁻¹. If the source concentration is lower than a certain threshold value, related to the crossover contractility, Λ_c = 23, all cells are columnar (squamous). The upper phase boundary between squamous (columnar)-only and coexistence regions is calculated numerically (solid dots) and approximated analytically (dashed line) in Eq. 8. (A2 and B2) are alternative phase diagrams in terms of the intrinsic biochemically set cell contractility, Λ₀, for a constant mechanogen concentration at the source, c₀ = 3. The system size is fixed to L = 10 in the cases considered here.

In these phase diagrams, the wholly squamous (columnar)-coexistence phase boundary in the mechanoreduction (induction) corresponds to a limiting profile where the critical contractility, Λ_c, required for columnar-squamous transition, is just attained at the far end of the profile, corresponding to the second condition in Eq. 7. This is captured by the approximate expression

$$c_{0,c}\simeq \left({\text{Λ}}_0-{\text{Λ}}_c\right)\text{cosh}\left[\frac{L{r}_i}{{\lambda }_0}\right],$$ (8)

where r_i = r_sq for mechanoreduction (r_i = r_col for mechanoinduction). This shows that the critical source concentration needed for coexistence, c_0,c, increases exponentially with the degradation rate, which is proportional to λ₀⁻¹. This result implies that as the degradation rate increases, a stronger source is required to keep the cells columnar at the far end of the tissue in the mechanoreduction case. This analytic approximation (details in the Supporting Material) is confirmed by a numeric solution of the phase boundary as shown in Fig. 4, A1 and A2.

Conclusions

Biological processes are inherently mechanochemical (32), and tissue development, in particular, occurs via spatial gradients of biochemical signaling (12). Although the exact mechanisms governing the spatial and temporal cell shape transitions in the course of tissue development in vivo have not been conclusively established, it is natural to ask if gradients in cell shape across tissues, as observed in various biological contexts, are connected to such biochemical gradients.

We emphasize that we describe two independent effects here: 1) that diffusive chemical signals (mechanogens) affect cell contractility (Eq. 2) and this potentially drives a spatial transition in cell shape; and 2) there may also be a feedback from cell shape on the chemical gradient through modified, shape-dependent degradation (Eq. 4). So irrespective of the size of the second effect, the notion of mechanogens provides a mechanism that biology could, in principle, employ to attain spatial profiles in cell shape. Both smooth or sharp cell shape gradients may result within the same tissue, depending on the part of the parameter space in Fig. 1 A probed by the mechanogen gradient. Mechanogens can also be considered to act on other mechanical properties of the cell apart from apical contractility. In Fig. S7, for example, we show mechanochemical gradients analogous to Fig. 2 for the scenario when mechanogens affect lateral adhesions. Thus, mechanogens provide additional flexibility to tune cell shapes through the different phases predicted by the mechanical model without relying upon specific mechanical boundary conditions or confinement (5). This mechanism may explain the cellular shape transition along the epithelium lining the egg chamber of Drosophila, including the anterior positioning of squamous cells in that context (41). The latter may result from the presence of a localized source of mechanogens that explicitly breaks symmetry during pattern formation (32). The cellular phase separation in tissue could thus be guided and accentuated by biochemical gradients.

We note also that although the mechanical model we present describes epithelial cell shape, the effect of soluble mechanoactive factors on cellular contractility is not limited to epithelial cells. Other cell types undergo morphological changes including change in their spread area in response to soluble factors such as thrombin for endothelial cells in blood vessels (42), or pharmacological inhibitors of contractility in fibroblasts in culture (43). Such cells in culture may provide a controlled setting for experimentally studying the effect of soluble factors on cell contractility, and further, the effect of cell area on the uptake of these soluble factors that we theoretically explore. In addition to the local interactions considered here, cells cultured on soft substrates are also known to interact through long-range elastic deformations of the substrate (44) or of the cell monolayer itself, which can, in principle, affect cell shape and mechanogen gradients (13). However, for a collection of cells with nearly uniform contractility as considered here, and also due to the frequent junctional remodeling in developing tissue (1), these long-range stresses relax over timescales of minutes and are expected to be weak in relation to the direct adhesive interactions between neighboring cells that we focus on. The steady state of mechanogen gradients that we focus on is attained within reasonable timescales of less than an hour, unless diffusion is extremely slow (a simple example of a dynamic nonlinear diffusion profile is shown in Fig. S8). The dynamics of evolution of mechanogen gradients raises interesting questions of cell and cytoskeletal remodeling dynamics in relation to diffusion and degradation timescales that we do not consider here.

The theory also provides a mechanism for the control of the concentration gradient of biomolecules in solution. Nonlinear reaction-diffusion equations such as Eq. 4 have been used to model pattern formation in developing tissue following the original proposal by Turing (45). A key desirable feature of the biochemical gradients responsible for such patterning is their robustness to noise (18, 40). For a morphogen profile with a uniform decay rate, i.e., with an exponential concentration profile, a change in the source concentration, say from c₁ to c₂, will result in a shift in the position of a cell fate boundary, δx ∼ λ_dlog(c₁/c₂). This suggests that smaller decay length, λ_d, improves robustness but for the morphogens to pattern tissue effectively, their gradient must be long-ranged and scale with tissue size (18). The negative feedback or self-enhanced degradation profile we consider, in particular, undergoes sharper decay near the source (short λ_i), which buffers fluctuations in mechanogen concentration at the source. This feedback helps create longer-range profiles with slow decay far from the source (long λ_o), which is consistent with robust long-ranged gradients required in development (19). Prior theoretical analysis of stability of gradients when subject to stochastic noise confirms that such qualitatively similar nonlinear decay (stronger decay near source and less far from it) is important for robustness (40). In particular, if the perturbatively derived nonlinear diffusion-degradation relation in Eq. 4 were generally valid, then close to the source (where c(x) is higher), we obtain a quadratic degradation relation considered before in (19) and (40) to theoretically demonstrate robustness. The crossover position, x_c, also is less sensitive to changes in tissue size, L, for the self-enhanced degradation case as shown in Fig. 3. Taken together, these results suggest that mechanochemical gradients resulting from self-enhanced degradation have desirable biological features over gradients without any feedback from cell state.

Such robustness and extension of the gradient of morphogens is usually explained in terms of the coupled reaction and diffusion of two or more chemical species (19), whereas, here we show that coupling of one chemical species to cell shape and mechanics can have an equivalent effect. Further experimental studies will be required to confirm and identify these various factors that can drive robust cell shape changes during tissue development.

Author Contributions

K.D., E.H., and N.S.G. designed the research, performed the research, and wrote the manuscript. K.D. performed numeric calculations with inputs from E.H. and N.S.G.

Editor: Vivek Shenoy.