Motor Reattachment Kinetics Play a Dominant Role in Multimotor-Driven Cargo Transport

Abstract

Kinesin-based cargo transport in cells frequently involves the coordinated activity of multiple motors, including kinesins from different families that move at different speeds. However, compared to the progress at the single-molecule level, mechanisms by which multiple kinesins coordinate their activity during cargo transport are poorly understood. To understand these multimotor coordination mechanisms, defined pairs of kinesin-1 and kinesin-2 motors were assembled on DNA scaffolds and their motility examined in vitro. Although less processive than kinesin-1 at the single-molecule level, addition of kinesin-2 motors more effectively amplified cargo run lengths. By applying the law of total expectation to cargo binding durations in ADP, the kinesin-2 microtubule reattachment rate was shown to be fourfold faster than that of kinesin-1. This difference in microtubule binding rates was also observed in solution by stopped-flow. High-resolution tracking of a gold-nanoparticle-labeled motor with 1 ms and 2 nm precision revealed that kinesin-2 motors detach and rebind to the microtubule much more frequently than does kinesin-1. Finally, compared to cargo transported by two kinesin-1, cargo transported by two kinesin-2 motors more effectively navigated roadblocks on the microtubule track. These results highlight the importance of motor reattachment kinetics during multimotor transport and suggest a coordinated transport model in which kinesin-1 motors step effectively against loads whereas kinesin-2 motors rapidly unbind and rebind to the microtubule. This dynamic tethering by kinesin-2 maintains the cargo near the microtubule and enables effective navigation along crowded microtubules.

Introduction

Kinesin motor proteins transport a diverse array of cargos to specific destinations in cells. One feature that helps to specify particular cargo to specific cellular locations is the spatial diversity of tubulin posttranslational modifications and microtubule associated proteins (MAPs), with different kinesins walking preferentially on particular subsets of microtubules (1). Importantly, transport in axons and dendrites is generally bidirectional; hence cargo have both plus-ended kinesin motors and minus-ended dynein motors attached (2). Adding to this complexity, specific cargo can have two classes of kinesins simultaneously bound; for instance, synaptotagmin-rich axonal vesicles were shown to be transported simultaneously by kinesin-1 and kinesin-2 motors (3). Thus, to understand how specific cargo are targeted to specific locations in axons and dendrites, it is important to understand how motors coordinate their activities during multimotor transport.

Because kinesin-1 and kinesin-2 motors move with twofold different speeds in the absence of load (4), they do not appear to be an optimal pair for cotransport of intracellular cargos. They differ in other ways as well—compared to kinesin-1, heterotrimeric kinesin-2 motors are less processive and they detach much more readily under load (4, 5, 6, 7, 8, 9). In contrast, kinesin-2 stepping is less affected than kinesin-1 by roadblocks such as MAPs (10). A comprehensive understanding of bidirectional transport in neurons, and the transport defects that underlie neurodegenerative disease, requires understanding how uniform population motors coordinate their transport activities and how diverse motors attached to a single cargo compete and coordinate to target cargo to their proper intracellular locations.

Although single kinesin-1 motors are robust transporters, previous experimental and theoretical work has suggested that they do not coordinate their activities well (11, 12, 13). This property contrasts with dyneins—the finding that cargo stall forces are integer multiples of the single-dynein stall force has been used to argue that dyneins efficiently couple their activities during multimotor transport (14, 15). The ability of different motors to coordinate their activities depends on their inherent unloaded velocity and directionality, as well as their ability to generate force and remain bound under load—properties that have been investigated extensively in single-motor experiments (2, 4, 6). In contrast, the rate that detached motors reattach to the microtubule during multimotor transport is an equally important but understudied parameter. The importance of reattachment kinetics can be appreciated by taking the limits: if motor reattachment is instantaneous, then all motors will be contributing to the transport at all times; however, if motor reattachment is very slow then cargo movements are carried out by only one motor at any given time. Because experiments to date generally follow cargo position, rather than the dynamics of individual motors in a population, this reattachment rate is very difficult to determine experimentally, and in any case, it is expected to vary with the geometry of the cargo and motor-cargo linkages. Experiments with kinesin-driven membrane tethers estimated a reattachment rate of 4.7 s⁻¹ in that particular geometry (16), and in modeling work, a reattachment rate of 5 s⁻¹ has been used extensively for all kinesin and dynein isoforms (16, 17, 18, 19). However, how this parameter varies for different motors and in different geometries is not clear.

The goal of this work is to compare the degrees to which kinesin-1 and kinesin-2 coordinate their activities during multimotor transport. In particular, we focus on the motor reattachment rate, and we find that kinesin-2 has a fourfold faster reattachment rate than kinesin-1. This finding suggests a multimotor coordination scheme in which kinesin-1 provides sustained loads during long-distance transport and reattaches slowly once it dissociates from the microtubule, whereas kinesin-2 frequently detaches and rapidly reattaches to the microtubule. This fast reattachment enables kinesin-2 to more efficiently explore the local microtubule landscape in cells and overcome roadblocks on microtubules such as MAPs and other cargos that may impede transport.

Materials and Methods

Protein purification

Kinesin-1 assemblies consisted of Drosophila KHC truncated at 559 and fused to a C-terminus eGFP and His6 tag (4). Kinesin-2 consisted of the head and 17-amino-acid neck-linker domain of Mus musculus KIF3A fused to the coiled-coil of Drosophila KHC followed by eGFP and His6 tag, as previously described (4). Motors were bacterially expressed, purified by Ni column, and stored at −80°C, following previously published protocols (4). For high-resolution tracking experiments, N-term biotinylated kinesin-1 and kinesin-2 motors were generated and attached to streptavidin-coated 30 nm gold nanoparticles (BBI Solutions, Cardiff, UK) as previously described (20). Tubulin was purified from bovine brain as described (4). SNAP-tagged, His6-tagged GFP nano-body (GBP) (a gift from the Grischuck lab, University of Pennsylvania) was bacterially expressed and purified following protocols developed for motors (4).

Generating oligo-functionalized GBP

Benzylguanine (BG) functionalized oligonucleotides were generated by reacting Benzylguanine-GLA N-hydroxysuccinimide (New England BioLabs, Ipswich, MA) with C6-amine modified oligonucleotides (BG-oligo 1 and BG-oligo 2; Fig. S1 A) in a 50 mM HEPES pH 8.5 buffer (21) for 30 min, followed by purification through a Sephadex G-25 Superfine desalting column (GE Healthcare, Little Chalfont, UK). BG oligos were then mixed with SNAP-tagged GBP for 1 h at 4°C, followed by purification through the Ni column to remove unreacted BG-oligos. GBP1 and GBP2 concentrations were quantified by mixing with varying known concentrations of complementary strands and running on SDS-PAGE gels to determine the concentration needed to completely shift the band to the higher molecular weight (Fig. S1 B).

Single molecule experiments

DNA scaffolds were labeled with Qdots (Thermo Fisher Scientific, Waltham, MA). Motility solutions containing DNA scaffolds, oligo-functionalized GBP, motors, ATP or ADP were diluted in BRB80 (80 mM PIPES, 1 mM EGTA, 1 mM MgCl₂, pH 6.8) to single molecule range (5 nM to 100 pM) with taxol, casein, BSA, and antifade components, as described previously (4, 22). Taxol-stabilized microtubules were adsorbed onto coverslips by full-length rigor kinesin, as previously described (20). Motility solution was then introduced, and DNA scaffolds imaged by total internal reflection fluorescence microscopy (TIRFM) using a TE2000 microscope (60×, 1.45 NA PlanApo; Nikon, Melville, NY). Experiments were carried out at 21–23°C. Images were captured using a Cascade 512b EMCCD camera (Roper Scientific, Tucson, AZ) controlled by MetaVue software (Molecular Devices, Downingtown, PA). Run lengths and durations were analyzed by ImageJ (Image J, National Institutes of Health, Bethesda, MD; MtrackJ plugin; https://imagescience.org/meijering/software/mtrackj/) using a pixel size of 71.0 nm. Kymographs were generated using the Kymo-analyzer package (23). To ensure that run lengths were reliably captured, only run lengths >200 nm were analyzed, and to estimate the average run length, this minimum distance was subtracted from all runs (Fig S1 E). Motors that ran off the ends of microtubules were not counted in the distributions (see correction below).

High-resolution tracking of gold nanoparticles was carried out by dark-field total internal reflection microscopy. Details of the microscopy and associated image processing are described fully in earlier publications (20, 24).

Data analysis

Mean and 95% confidence interval for run lengths and microtubule binding durations were estimated by bootstrapping using MATLAB (The MathWorks, Natick, MA). Every data set was resampled with replacement 100 times, and generated data were fit to the exponential CDF, $1-\text{exp}\left(-(x-a)/b\right)$. Reported mean and 95% confidence intervals were then calculated from the 100 resampled data sets (25).

SE for kinesin-1 and kinesin-2 reattachment rates were calculated using the Error Propagation method (26). From Eq. 2,

$$k_{\text{reattach}}=\frac{2\ast T_2}{T_1\ast T_1}-\frac{2}{T_1},$$

the SE was calculated as

$$SE=\sqrt{e_2^2+3\ast e_1^2},$$

where e₁ and e₂ are the percent error of T₁ and T₂, respectively.

Run lengths reported in the text were not corrected for finite microtubule lengths, which can lead to an underestimate of run lengths (27, 28). To determine the effect of microtubule length, we first measured microtubule lengths and found a mean 12.6 μm and SD of 3 μm. To estimate the correction factor when motors that run off the plus-end are not counted, we carried out the following simulation. First, draw a run length value “RL(i)” from exponential distribution with mean value, RL_actual, corresponding to the actual run length. Next, draw an initial motor position value “InitPos(i)” from a uniform distribution corresponding to the mean microtubule length of 12.6 μm. If RL(i) > InitPos(i), meaning the motor runs off the end of the microtubule, then the event is not counted. The process is repeated 1000 times, and the mean of all values where RL(i) < InitPos(i) is computed to give the observed mean run length, RL_obs. The predicted RL_obs is calculated across a range of RL_actual to find the proper correction. We found that for the run lengths measured, this correction was between 0 and 30%. The corrected values are presented in Table S1.

Stopped-flow experiments

Stopped-flow experiments were carried out in BRB80 buffer in 23°C as previously described (29).

Roadblock experiments

Microtubules with varying densities of roadblocks were made by polymerizing microtubules using varying ratios of biotinylated and unlabeled tubulin, incubating with saturating concentrations (16 μM) of neutravidin, and pelleting and resuspending to remove excess neutravidin. Based on previous work by Korten and Diez (30), this protocol should result in every biotinylated tubulin having a bound neutravidin. Total tubulin concentration was measured by A_{280 nm}, and biotin concentration was measured using the HABA assay (Thermo Fisher Scientific).

Results

Two-motor kinesin-2 assemblies have longer run lengths than two-motor kinesin-1 assemblies

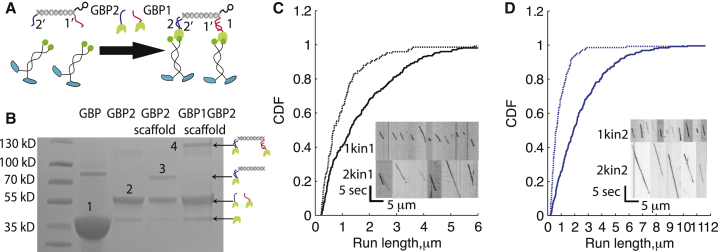
To investigate defined teams of kinesin-1 and kinesin-2 motors, a SNAP-tagged anti-GFP nanobody (GBP; 1 nM K_D for GFP (31)) was used to link GFP-labeled motors to a quantum dot-functionalized DNA scaffold (Fig. 1 A). Scaffolds containing either one or two motors were created by incubating scaffolds and free motors with either one or both GBP adapters (shown by gel in Fig. 1 B). The kinesin-1 and -2 motors, which were fully characterized in previous work (4, 6, 32), share an identical coiled-coil domain and only differ by their motor domains, thus avoiding uncertainties regarding the effect of tether length or tail structure on motor behavior. One- and two-motor run lengths measured by TIRFM were 0.77 ± 0.16 and 1.62 ± 0.23 μm, respectively, for kinesin-1 (Fig. 1 C; Table S1). The corresponding kinesin-2 run lengths were 0.65 ± 0.13 and 2.38 ± 0.26 μm (Fig. 1 D; Table S1). Thus, adding a second motor increased the kinesin-1 run length by 2.1-fold and the kinesin-2 run length by 3.7-fold. Because a scaffold carried by two motors will continue to move as long as at least one motor is bound to the microtubule, the observed run lengths arise from two factors: the load-dependent detachment kinetics of each motor, and the rebinding rates of cargo-bound motors that have dissociated from the microtubule. A previous optical trapping study showed that the detachment rate of kinesin-2 is considerably more force dependent than that of kinesin-1 (6). Thus, the enhanced two-motor kinesin-2 run length suggests that the kinesin-2 reattachment kinetics are considerably faster than those of kinesin-1.

Figure 1.

Assembly of defined multimotor assemblies using the DNA scaffold. (A) Schematic of DNA-motor assemblies. GFP binding proteins GBP1 and GBP2 were generated by covalently linking oligos 1 and 2 to the GBP through a C-terminal SNAP tag. GFP-labeled motors were then linked to the DNA scaffolds via overhanging single-stranded 1′ and 2′ appendages on the scaffold. Scaffolds were tracked by linking quantum dots to a third overhanging ssDNA on the scaffold (Fig S1A). (B) SDS-PAGE gel of DNA-protein assemblies. Electrophoresis was performed on a 4–20% polyacrylamide gel. Labeled bands are 1) unreacted GBP, 2) oligo-labeled GBP, 3) scaffold with one GBP bound, and 4) scaffold with two GBP bound. The ∼80-kDa band in the GBP lane is a minor impurity from Ni-column purification. (C) Run lengths for assemblies containing one (dashed line) or two (solid line) kinesin-1 motors in 3 mM ATP, presented as cumulative distributions. Biotin-labeled scaffolds were mixed with GBP1 and excess motors to generate one-motor assemblies, and with both GBP1 and GBP2 to generate two-motor assemblies (Fig. S1, C and D). (Inset) Kymographs of one-motor (upper) and two-motor (lower) runs for kinesin-1. Mean run lengths were 0.77 ± 0.16 and 1.62 ± 0.23 μm (mean ± 95% confidence interval, N = 150 and N = 283) for scaffolds containing one or two kinesin-1 motors, respectively. (D) Distributions and kymographs (inset) of kinesin-2 run lengths for one- (dashed line) and two- (solid line) kinesin-2 assemblies in 3 mM ATP. Mean run lengths were 0.65 ± 0.13 μm (N = 145) and 2.38 ± 0.26 μm (N = 257) for scaffolds containing one or two kinesin-2 motors, respectively. To see this figure in color, go online.

Kinesin-2 has a faster reattachment rate than kinesin-1

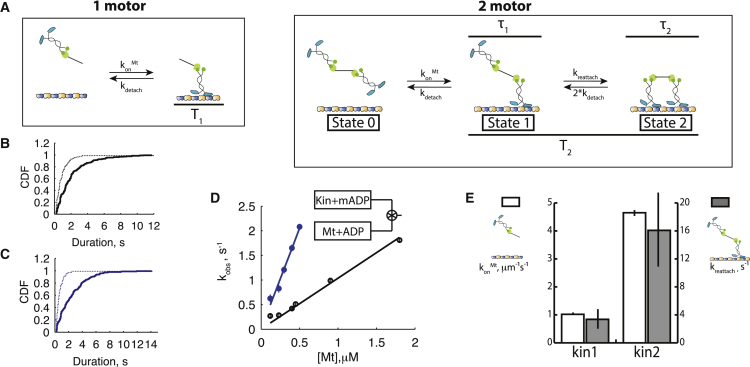
A parameter that, to our knowledge, has never been directly measured in a multimotor complex is the rate that a dissociated motor bound to a cargo reattaches to the microtubule. To test our hypothesis that kinesin-2 has a faster reattachment rate than kinesin-1, we measured the binding duration of one- and two-motor assemblies in saturating ADP. In ADP, motors only bind to the microtubule and do not generate force, enabling us to make the important assumption that the detachment rate of each individual motor in a two-motor construct is the same as the detachment rate of one motor in ADP. Furthermore, because ADP release is the rate-limiting step in solution (33), motors are initially in the ADP state upon microtubule binding independent of the nucleotide in solution, thus k_reattach measured in ADP should be the same as that in ATP. Using this approach, measured binding durations were interpreted using the model shown in Fig. 2 A. Using TIRFM similar to the run length experiments, the mean one- and two-motor microtubule binding durations in ADP were T₁ = 0.72 ± 0.15 and T₂ = 1.86 ± 0.31 s for kinesin-1, and T₁ = 0.50 ± 0.11 and T₂ = 2.51 ± 0.39 s for kinesin-2 (Fig. 2, B and C; Table S1).

Figure 2.

Calculating kinesin-1 and kinesin-2 reattachment rates from microtubule binding durations of one and two-motor assemblies in ADP. (A) Models used to analyze microtubule-binding durations. For one-motor assemblies (left), the microtubule binding duration in ADP (T₁) is governed solely by the unbinding rate constant, k_detach. For two-motor assemblies (right), a second parameter, the reattachment rate constant (k_reattach), is introduced and an expression is derived for the expected two-motor binding duration in ADP (T₂). See text for derivation. (B) Distribution of one- (dashed line) and two- (solid line) motor binding durations for kinesin-1 in 3 mM ADP. Mean binding durations were 0.72 ± 0.15 s (N = 90) and 1.86 ± 0.31 s (N = 223) for scaffolds containing one and two kinesin-1, respectively. See Fig. S2A for example kymographs. (C) Distribution of one- (dashed line) and two- (solid line) motor binding durations for kinesin-2 in in 3 mM ADP. Mean binding durations were 0.50 ± 0.11 s (N = 128) and 2.51 ± 0.39 s (N = 213) for scaffolds containing one and two-motor kinesin-2, respectively. See Fig. S2B for example kymographs. (D) Bimolecular on-rates for microtubule binding measured by stopped-flow. Observed motor binding rates were measured by fitting exponentials to the mantADP signal decay at varying microtubule concentrations (Fig. S2, E and F). Fitting a line to the measured rates at limiting [Mt] gives the bimolecular on-rate for microtubule binding k_on^Mt. Calculated k_on^Mt were 1.1 ± 0.05 μM⁻¹ s⁻¹ (regression ± RMS error) for kinesin-1 (open symbols) and 4.6 ± 0.10 μM⁻¹ s⁻¹ for kinesin-2 (filled symbols) (Fig. S2, E and F). (E) Comparison of bimolecular on-rates in solution to microtubule reattachment rates on scaffolds. Second-order k_on^Mt (left axis, open bars from Fig. 2D) is 4.2-fold higher for kinesin-2 than kinesin-1. Similarly, the calculated first-order k_reattach (right axis, gray bars) is 3.6-fold faster for kinesin-2 than kinesin-1. To see this figure in color, go online.

For one motor, the measured mean binding duration, T₁, is simply the inverse of the first-order detachment rate, k_detach. Thus, in saturating ADP, k_detach = 1.39 ± 0.29 s⁻¹ for kinesin-1, and k_detach = 2.00 ± 0.44 s⁻¹ for kinesin-2. For a two-motor complex, the observed binding duration, T₂, includes states having either one or both motors attached. The importance of the k_reattach parameter is clear from inspection—a fast reattachment rate minimizes the probability that the complex is attached to the microtubule by only one motor, and hence minimizes the rate of detachment of the complex from the microtubule.

Based on the law of total expectation (34), we can calculate the reattachment rate for each motor from the measured T₁ and T₂, as follows. Starting from the initial state with one motor bound to the microtubule, there are two possibilities—either that motor will detach, terminating the event, or the second motor will attach to the microtubule. If the second motor attaches, then the complex will reside in a two-motor-bound state (state 2 in Fig. 2 A) until either motor detaches, returning to the initial one-motor-bound state (state 1 in Fig. 2 A). Because the system is memoryless, the duration starting from this revisited one-motor-bound state (state 1) is T₂, just as before. Hence, if τ₁ is the duration spent in state 1, τ₂ is the duration spent in state 2, and P₁₂ is the probability of the second motor binding (rather than the first motor dissociating), then the total binding duration can be calculated as

$$T_2={\tau }_1+P_{12}\ast \left({\tau }_2+T_2\right).$$

In this equation, the duration spent in state 1 is controlled by two transitions:

$${\tau }_1=\frac{1}{k_{\text{detach}}+k_{\text{reattach}}}.$$

The duration spent in state 2 is

$${\tau }_2=\frac{1}{2\ast k_{\text{detach}}},$$

where the factor 2 is due to the fact that either motor can unbind, each with a rate k_detach. Finally, the probability of the second motor binding (rather than the first motor detaching) is

$$P_{12}=\frac{k_{\text{reattach}}}{k_{\text{reattach}}+k_{\text{detach}}}.$$

Solving for T₂ (Fig. 2 A), we get

$$T_2=\frac{1}{k_{\text{detach}}}\ast \left(1+\frac{k_{\text{reattach}}}{2\ast k_{\text{detach}}}\right).$$ (1)

Solving for k_reattach in terms of the measured T₁ and T₂, we get

$$k_{\text{reattach}}=\frac{2}{T_1}\ast \frac{\left(T_2-T_1\right)}{T_1}.$$ (2)

Plugging in the measured binding durations from Fig. 2, B and C, k_reattach = 4.41 ± 1.75 s⁻¹ for kinesin-1 and k_reattach = 16.1 ± 6.6 s⁻¹ for kinesin-2, indicating that the reattachment rate of kinesin-2 is 3.6-fold faster than kinesin-1. To validate our result, we varied k_detach by lowering the level of ADP to 10 μM, which causes the motor to reside in the tight-binding apo state for a larger fraction of time, and repeated the analysis (Fig. S2, C and D; Table S1). This independent experiment, which generated different T₁ and T₂ durations, resulted in similar k_reattach values of 4.6 ± 3.2 s⁻¹ for kinesin-1 and 18.7 ± 8.0 s⁻¹ for kinesin-2. This agreement supports the validity of the measurement and additionally confirms that the reattachment rate is independent of nucleotide conditions.

Solution microtubule on-rates are also faster for kinesin-2 than kinesin-1

Because microtubule binding by a motor is inherently a bimolecular process, the first-order k_reattach parameter can be thought of as the product of a second-order microtubule on-rate multiplied by the effective local concentration of tubulin binding sites. Importantly, the scaffold, attachment, and coiled-coil domains are identical for the kinesin-1 and kinesin-2 assemblies used; hence the effective local [tubulin] should be identical for the two motors. In contrast, due to sequence differences in the microtubule binding domains and kinetic differences in their hydrolysis cycles, k_on^Mt is expected to differ between kinesin-1 and kinesin-2. To test whether the different reattachment rates result from differences in the motor domains, we carried out stopped-flow experiments using the ADP analog 2′(3′)-O-(N-methylanthraniloyl)adenosine 5′-diphosphate (mantADP) to measure the bimolecular binding rate (k_on^Mt) for kinesin-1 and kinesin-2 (Fig. 2 D). When motors incubated in mantADP are flushed against microtubules, microtubule binding triggers release of mantADP by the motor, which generates a decrease in mant fluorescence (Fig. S2, E and F). The process involves sequential steps of microtubule binding followed by mantADP release; hence, at saturating [Mt] the observed rate represents the mantADP off-rate of the microtubule-bound motor, whereas at limiting [Mt] the observed rate represents the on-rate for microtubule binding, k_on^Mt (29). At each [Mt], fluorescence traces were fit by first-order exponentials (Fig. S2, E and F). The observed rate constants were then plotted as a function of [Mt] and fit with a line to obtain k_on^Mt of 1.1 ± 0.05 μM⁻¹ s⁻¹ for kinesin-1 and 4.6 ± 0.10 μM⁻¹ s⁻¹ for kinesin-2 (Fig. 2, D and E). Thus, the 3.6-fold higher k_reattach measured for kinesin-2 in the scaffold experiment matches the 4.2-fold higher k_on^Mt for kinesin-2 in solution.

High-resolution tracking reveals fast detachment/reattachment kinetics of kinesin-2

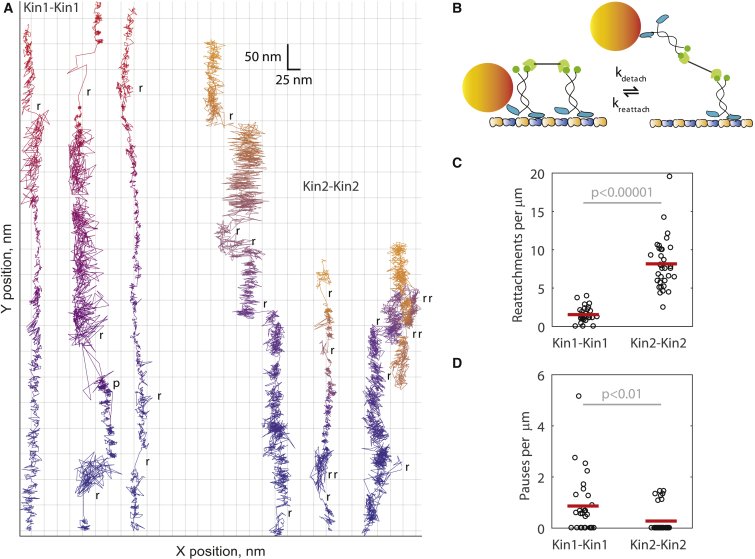
To measure detachment and reattachment events directly, we used high-resolution single-molecule tracking to measure the time-dependent position of one kinesin in a two-motor pair attached to a DNA scaffold (Fig. 3, A and B). A kinesin-1 or -2 with a single motor domain biotinylated and tagged with a 30-nm gold nanoparticle (20, 24) was attached to one end in the scaffold, and an unlabeled motor was attached to the other (Fig. 3 B). The particle position was then tracked at 1 ms temporal resolution using dark-field total internal reflection microscopy, as previously described (24). Example traces of Kin1-Kin1 and Kin2-Kin2 pairs are shown in Fig. 3 A. Given that only one motor domain of one kinesin is labeled and the motors walk in a hand-over-hand manner, we expected to see low-variance ∼16 nm steps when the labeled kinesin was engaged with microtubule, higher-variance ∼8 nm steps when the labeled kinesin was not engaged with the microtubule, and large, abrupt positional changes when switching between these two configurations (Fig. 3 B). We indeed observed these phenomena (Fig. 3 A) among other features of note: 1) kinesin-1 spent longer durations with higher variance than kinein-2, as expected for their different reattachment rates; 2) newly reattaching kinesins landed both in front of and behind the currently engaged kinesin; and 3) kinesins commonly reattached to different protofilaments of the microtubule (as seen by positional changes perpendicular to the direction of motion).

Figure 3.

High resolution single-molecule tracking reveals that kinesin-2 reattaches more often and pauses less often than kinesin-1. (A) Example 1000 frames per second traces of Kin1-Kin1 (blue-red) and Kin2-Kin2 (blue-yellow) pairs. A single motor domain of one motor was tagged with a 30-nm gold nanoparticle (shown in diagram in B), and the particle position imaged by dark-field total internal reflection microscopy (see Materials and Methods). Time information is encoded in color (see Fig. S4 for the same data displayed as position versus time). Of note are abrupt positional changes that intersperse normal stepping, indicating reattachment events, and areas of high versus low variance, indicating whether labeled motors are engaged with the microtubule. Scored rebinding events (r) and pauses (p) are highlighted on each trace. (C) Kin2-Kin2 pairs reattach more often than Kin1-Kin1 pairs. Reattachments were scored as jumps >40 nm in the Y position (parallel to the microtubule) or >15 nm in the X position (sidesteps). Kin1-Kin1 pairs reattached 1.54 ± 0.19 times, whereas Kin2-Kin2 pairs reattached 8.16 ± 0.58 times per micron traveled (mean ± SE; N = 29 and N = 33 traces, respectively, with plot showing one point per trace and mean values as red bars). A 2-sample t-test indicated that the difference in reattachment frequency was significant (p < 0.00001). (D) Kin1-Kin1 pairs pause more often than Kin2-Kin2 pairs. Pauses were scored as instances of no positional change lasting longer than 10 step durations (137 ms for kinesin-1 and 410 ms for kinesin-2). Kin1-Kin1 pairs paused 0.86 ± 0.21 times per micron traveled (mean ± SE, N = 29 traces), whereas Kin2-Kin2 paused 0.28 ± 0.09 times per micron traveled (mean ± SE, N = 33 traces). A Mann-Whitney U-test indicated that the difference in pausing frequency was significant (p < 0.01).

To quantify the data, we scored detachment-reattachment events as positional jumps >40 nm (five tubulin lengths) parallel to the microtubule or >15 nm perpendicular to the microtubule. We observed that Kin2-Kin2 pairs reattached fivefold more frequently per micron traveled than Kin1-Kin1 pairs (8.16 vs. 1.54 reattachments/micron, respectively; Fig. 3 C), in agreement with the reattachment rates in ADP (Fig. 2). We also scored the pausing frequency, defined as the frequency the scaffold became stuck in a single position for more than 10 step-time durations. Kin1-Kin1 pairs paused threefold more frequently per micron traveled than Kin2-Kin2 pairs (0.86 vs. 0.28 pauses/μm, respectively; Fig. 3 D). These measurements are consistent with previous work that found kinesin-1 detachment is less sensitive to force than kinesin-2 (6, 7) and, together with the reattachment data, paint a picture of kinesin-1 being a fast, stable, but stubborn partner and kinesin-2 being a slow, vacillating, but adaptable partner in multimotor transport.

Kinesin-2 motors undergo fast detach/reattach cycles during multimotor transport

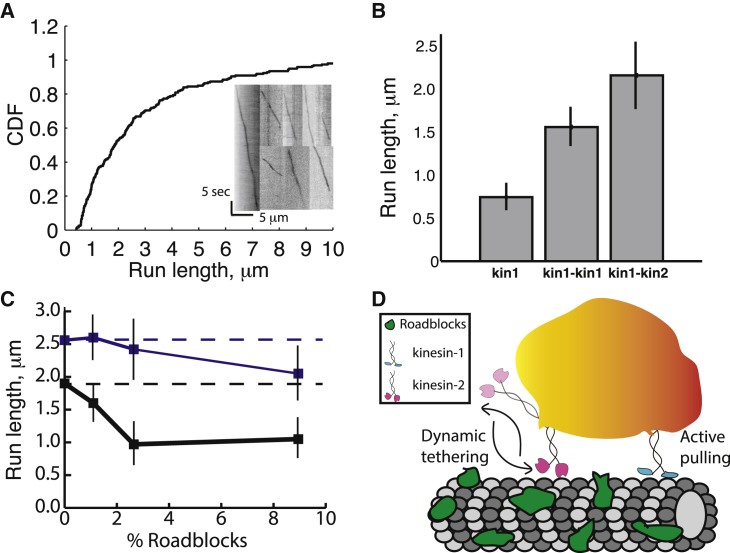
To understand coordination between kinesin-1 and kinesin-2 motors during multimotor transport, we measured the run length of Kin1-Kin2 pairs. Interestingly, despite the fact that kinesin-2 has a shorter single-motor run length and a twofold slower unloaded velocity than kinesin-1, the run length of Kin1-Kin2 pairs, 2.1$8\pm 0.39$μm (Fig. 4 A), was longer than for two kinesin-1 motors 1.62 ± 0.23 μm (Fig. 4 B). Thus, the faster reattachment rate of kinesin-2 appears to be the key feature that enhances the multimotor run length in motor pairs.

Figure 4.

Cargo-bound kinesin-2 motors undergo fast detachment/reattachment to facilitate longer run lengths and avoid roadblocks. (A) Run length distributions and kymographs (inset) for Kin1-Kin2 pairs in 3 mM ATP. Mean Kin1-Kin2 run length was 2.18 ± 0.39 μm (mean ± 95% confidence interval, N = 199). See Fig. S5A for details of assembly. (B) Run lengths of single kinesin-1, Kin1-Kin1 pairs and Kin1-Kin2 pairs. Single kinesin-1 and Kin1-Kin1 run lengths are from Fig. 1C. (C) Run lengths of Kin1-Kin1 (black) and Kin2-Kin2 (blue) pairs on crowded microtubules. Dashed lines are run lengths without roadblocks for comparison. Roadblock concentrations are defined as the fraction of biotinylated tubulin in the microtubules with bound neutravidin (see Materials and Methods for details). Run lengths are presented as mean ± 95% confidence intervals for between 25 and 117 measurements at each condition. See Fig. S5, B–D, for raw data. (D) Dynamic tethering model of kinesin-2 motors during intracellular cargo transport. In multimotor assemblies, kinesin-2 motors (pink, back) will rapidly detach and reattach to the microtubule, whereas kinesin-1 motors (blue, front) will tend to remain bound to the microtubule and act as primary force generators. This dynamic tethering of cargo to microtubules by kinesin-2 facilitates long distance transport and helps cargos navigate crowded microtubules. To see this figure in color, go online.

To test the ability of multimotor assemblies to avoid roadblocks such as MAPs, we bound neutravidin to microtubules containing varying fractions of biotinylated tubulin and compared run lengths. Consistent with their fast detachment/reattachment kinetics, Kin2-Kin2 pairs were less affected by roadblocks than Kin1-Kin1 pairs (Figs. 4 C and S5, C and D). Thus kinesin-2 motors, despite moving slower and having both a shorter unloaded run length and greater sensitivity of detachment to load, are able to coordinate their activities to achieve long multimotor run lengths and navigate crowded microtubules.

Discussion

In cells, kinesin-1 and kinesin-2 each transport specific cargo, but they also colocalize on a subset of vesicles, suggesting that they also carry out coordinated transport (2, 3). In this work, we show that kinesin-2 motors, despite being less processive than kinesin-1, enhance multimotor run lengths to a greater degree and enable navigation of crowded microtubules. This behavior emphasizes the importance of motor reattachment rates on multimotor transport.

Fast reattachment is an inherent property of kinesin-2

Despite the observed functional differences between kinesin-1 and kinesin-2, the specific amino acid sequences in the kinesin-2 motor domain that confer faster microtubule rebinding kinetics are not clear. For kinesin-3, the high initial microtubule binding rate is a result of its loop 12 domain, which has six positively charged residues compared to only one for kinesin-1 (35). However, the kinesin-2 (KIF3A) loop 12 is nearly identical to kinesin-1, with the exception of having one less negatively charged residue (29). Similarly, the ADP off-rate upon microtubule binding is fast for both kinesin-1 and kinesin-2 (20, 29), suggesting that the probability of tight binding after collision with a microtubule is similar for the two motors. One possibility is that the fast microtubule on-rate of kinesin-2 is related to the motor’s propensity to remain associated with the microtubule in its weakly bound state (29).

An important finding from comparing the measured bimolecular on-rates to the first-order reattachment rates is that the effective local tubulin concentration is ∼30-fold lower than predicted from simple geometry considerations. This can be seen by considering that the reattachment rate is equal to the bimolecular on-rate multiplied by the effective local tubulin concentration, k_reattach = k_on^{Mt ∗} [tubulin]. The predicted local tubulin concentration based on the motor-scaffold geometry can be calculated as follows. If the tethered motor searches a hemispherical volume with a radius of ∼100 nm that contains six protofilaments (the top-half of the microtubule), the tubulin concentration in this hemisphere is 125 μM (see Fig. S3 B). Multiplying this concentration by the measured k_on^Mt = 4.6 μM⁻¹ s⁻¹ for kinesin-2 (Fig. 3 D) results in a predicted k_reattach of >500 s⁻¹, compared to the 16 s⁻¹ measured value. The source of this discrepancy is not clear. It should be noted that including elasticity of the motor-scaffold complex, which leads to a smaller search volume, predicts an even higher reattachment rate (see Fig. S3 B). Also, the tubulin occupied by the bound motor represents a small fraction of the possible binding sites in the microtubule lattice that the tethered motor can interact with, discounting steric blocking by the bound motor as an important contribution to the slow reattachment rate.

One intriguing finding from comparing this work to previous studies of defined pairs of kinesin-1 motors linked through DNA (36, 37) or protein scaffolds (38, 39) is that the run length enhancement from adding a second motor is consistently quite small, ranging from 1.3-fold to 2.5-fold (36, 37, 38). Furthermore, previous work showed that when the length and rigidity of a DNA linker connecting the motors was systematically varied over a large range, there was very little effect on run length (36), consistent with the motor reattachment rate being relatively insensitive to the specific properties of the linker that connects the two motors or the length of the motor coiled-coil domain. The reattachment rate of kinesin-1 motors attached to membranes was previously estimated at 4.7 s⁻¹, matching our estimate, despite the very different geometries (16). The enhancement of run length by kinesin-2 observed here suggests that the microtubule binding properties of the motor domains play the dominant role in motor reattachment kinetics rather than the specific geometry of the scaffold. Understanding the tethered diffusion that leads to these observed motor reattachment rates is an important area for future investigations.

Kinesin-1 and -2 motors are tuned for different cellular roles in multimotor transport

The fast kinesin-2 reattachment rate measured here provides resolution for earlier work that showed detachment of heterotrimeric kinesin-2 depends strongly on load (6, 7, 8, 9). This work establishes that the propensity of kinesin-2 to detach under load is balanced by rapid reattachment, which results in the motor actually spending most of its time bound to the microtubule in a multimotor system. This work also provides an explanation for the earlier finding that purified neuronal vesicles have both kinesin-1 and kinesin-2 motors bound, despite the fact that the motors move at twofold different speeds (3). We propose a model in which kinesin-1 is an active puller that generates the force needed for transport whereas kinesin-2 serves as a dynamic tether (Fig. 4 D). This dynamic tethering serves first to maintain association of the cargo with the microtubule when kinesin-1 motors detach, and second to enable cargos to navigate along microtubules crowded with MAPs and other impediments without becoming stalled. A similar model was proposed for the enhancement of kinesin-1 run length by myosin-Va attached to the same vesicle, but in that case the run length enhancement results from nonspecific electrostatic interactions between myosin-Va and microtubules rather than the motor stepping activity (40).

Previous work showed that at roadblocks, kinesins can either pause, detach, or sidestep around the impediments (41). Compared to kinesin-1, kinesin-2 motors were shown to sidestep more frequently and their run length to be relatively less affected by roadblocks (10, 42). However, in that work, kinesin-1 run lengths in the presence of roadblocks were still greater than or equal to kinesin-2 run lengths under similar conditions. Therefore, the single-motor stepping properties of kinesin-2 are not in themselves sufficient to explain the longer run lengths of Kin2-Kin2 pairs in the presence of roadblocks, and the finding that kinesin-2 pairs have a greater run length than kinesin-1 pairs in the presence of roadblocks is best explained by the fast kinesin-2 microtubule reattachment rate.

This tethering activity of kinesin-2 may explain a body of previous work on bidirectional transport that found that inhibiting either kinesin or dynein alone diminishes transport in both directions (2). If tethering also helps to maintain cargo association with the microtubule while dynein is pulling the cargo, then inhibiting kinesin may diminish this tethering activity and thus diminish dynein-driven transport. Because kinesin-3 is able to diffuse on microtubules and has fast initial microtubule attachment kinetics (1, 38), this behavior is predicted to extend to kinesin-3 as well.

In conclusion, this work presents a method for quantifying the motor reattachment rate in multimotor assemblies and demonstrates that k_reattach is fourfold faster for kinesin-2 than kinesin-1. The prediction of fast binding/unbinding kinetics for kinesin-2 is directly demonstrated using high-resolution tracking of one motor in a multimotor population, a technique that can be extended to more complex multimotor geometries. Finally, we show that kinesin-2 motor pairs more effectively navigate crowded microtubules. This work provides important foundational pillars for quantitatively understanding the complex motor dynamics underlying bidirectional transport of vesicles in cells.

Author Contributions

Q.F. constructed the one and two-motor assemblies, carried out motility experiments, and wrote the manuscript. K.J.M. carried out high frequency experiments and analysis. G.-Y.C. contributed to stopped-flow experiments and derived the reattachment calculation. W.O.H. designed the experiments and wrote the manuscript.

Editor: Stefan Diez.