FRET Image Correlation Spectroscopy Reveals RNAPII-Independent P-TEFb Recruitment on Chromatin

Abstract

Biochemical studies have revealed that the RNA Polymerase II (RNAPII) pause release is triggered by phosphorylation of the transcription machinery by the positive transcription elongation factor b (P-TEFb). However, there are no direct report that P-TEFb and RNA polymerase II interact in single living cells and the biophysical mechanisms mediating this association are still unclear. Förster resonance energy transfer (FRET) detects molecular interactions at the subcellular level. Time domain fluorescence lifetime imaging provides an accurate quantification of FRET efficiency, E_FRET, because it is fluorochrome concentration-independent and insensitive to fluorescence bleed-through. However, the way FRET signal is usually analyzed does not provide information about the areas where protein-protein interactions take place. In this work, we developed a method, dubbed FRET image correlation spectroscopy (FICS), which relied on FRET fluorescence lifetime imaging image acquisition and image correlation spectroscopy of E_FRET clusters to quantify the spatial distribution of interaction clusters in the nucleus. The combination of high content FRET microscopy with batch image analysis allowed a robust statistical analysis. By applying FICS, we characterized the area and density of interaction clusters between P-TEFb and RNAPII or histone H2A in single living cells. The FICS method applied to cells expressing genetically engineered mutated proteins confirmed that the histidine-rich domain of P-TEFb is required for its interaction with RNAPII. Furthermore, it demonstrated that P-TEFb was also located in close vicinity to histone H2A, independently of its interactions with RNAPII. These results support the hypothesis that P-TEFb dynamics on chromatin regulate its recruitment on RNAPII.

Introduction

During the whole transcription process, paused RNAPII release, mRNA polymerization, and neosynthesized mRNA 3′ cleavage are controlled via phosphorylation of the transcription machinery by the positive transcription elongation factor b (P-TEFb; reviewed in (1)). Functional P-TEFb is a dimer of cyclin T1 (CT1) and cyclin-dependent kinase 9 (Cdk9), which has been found free (active) or bound (inactive) to a molecular complex composed of the noncoding 7SK RNA (2, 3), Hexim1/2 (4), Larp7 (5), and 7SK snRNA methylphosphate capping enzyme, MePCE (6). Both Cdk9 (7) and CT1 (8) have been reported to mediate the interaction between P-TEFb and the RNAPII subunit RPB1. Indeed, a specific RNAPII-interacting domain has been identified in CT1 from residue 480 to 551 by a two-hybrid screening and confirmed by GST pull-down (8). This region enriched in histidine residues is therefore called the histidine-rich domain (HR). Although dynamics of the spatial distribution of RNAPII, of Cdk9, and of nascent mRNAs have been studied by optical microscopy (9, 10, 11), to our knowledge the interaction between RNAPII and CT1 has not been documented in living cells. FRAP experiments revealed no stable interaction between P-TEFb and RNAPII at the HSP locus in individual Drosophila gland salivary nuclei (12). The interaction between P-TEFb and the C-terminal domain of RNAPII has been detected by bimolecular fluorescence complementation (13). However, the drastic modification of the partners’ dissociation constant resulting from the assembly of the two half parts of GFP disqualifies bimolecular fluorescence complementation for quantifying the biophysical properties of such interactions (14). This prompted us to investigate whether P-TEFb spatial organization could be orchestrated by its interaction with RPB1. Fluorochrome concentration-independent determination of FRET efficiency, E_FRET (15), is advantageously achieved by fluorescence lifetime measurement (FLIM). To describe and quantify the topological organization of the interactions between wt CT1 or its mutants and RPB1, we have reexamined the Förster resonance energy transfer (FRET) method and developed a half-automated method based on image correlation spectroscopy of E_FRET clusters.

The sensitivity of the FRET-FLIM reporting system relies on four main parameters: 1) the biophysical properties of fluorescent proteins (brightness and quantum yield), 2) the steric effects associated with the size and structure of the macromolecular complex studied, 3) the signal/electronic and biological noise, and 4) the interaction lifetime. To optimize FRET efficiency, we took advantage of the recent development of a more efficient FRET pair of fluorescent proteins: monomeric Turquoise 2 fluorescent protein, mT2 (16), and the dark yellow fluorescent protein, Reach2 (17). Additionally, we developed a variable length linker (VLL) between these fluorescent proteins and the protein of interest to increase the flexibility of the chimera and consequently improve FRET occurrence in the crowded environment of a supramolecular complex such as RNAPII. With the aim to accurately detect P-TEFb/RPB1 interactions in living cells, we performed time-correlated single photon counting (TCSPC) FRET FLIM on a laser scanning microscope. To quantify the FRET efficiency patterns and to statistically discriminate the differences between them, we developed a half-automated method based on FRET image correlation spectroscopy (FICS). This method allowed us to characterize interaction clusters between P-TEFb and RNAPII in single living cells. Moreover, we confirmed that the histidine-rich domain of CT1 is required for its efficient interaction with RNAPII. Finally, we provide evidence that P-TEFb recruitment on chromatin is partly independent of its interaction with RNAPII, which supports a model of multipartner contribution for P-TEFb recruitment on chromatin.

Materials and Methods

Cell line culture

U2OS cell lines (from the American Type Culture Collection, Manassas, VA) have been cultured in DMEM medium (Gibco Laboratories, Gaithersburg, MD) supplemented with 10% FCS (vol/vol) and penicillin/streptomycin (100 μg/mL). A U2OS cell line overexpressing RPB1-Reach2 was selected with a 1-week α-amanitin treatment (2 μg/mL). In this cell model, α-amanitin-resistant RPB1-Reach2 was expressed at an endogenous level whereas native RPB1 was degraded. For live-cell imaging, cells were plated on 35-mm glass-bottom dishes (MatTek, Ashland, MA), filled with L-15 medium without Phenol Red (Life Technologies, Carlsbad, CA), and incubated at 37°C in a thermostatic chamber (Life Imaging Services, Basel, Switzerland).

Transfection

500 ng of plasmid were transfected in 100,000 cells with Fugene Transfection Reagent (Roche, Basel, Switzerland) following the manufacturer recommendations. For H2A-fused chimera, 100 ng of plasmid were sufficient for a proper transfection.

pVLL vector design. The VLL is a home-made cloning site substituted to the multicloning site of pEGFP-N1 vector. VLLs accept 5′-cloning of DNA with NheI + AgeI, and 3′-cloning with SacII + Not1 (scheme is depicted in Fig. S1 A). This vector was designed rationally to improve the FRET occurrence by permitting the selection of one linker among three different linker lengths (12, 22, and 42 amino acids) whose sequences have been enriched in glycine and valine residues to limit misfolding of the chimera and increase the flexibility. Labels given to these vectors are intuitive: X-VLL(size)-FP-N or X-VLL(size)-FP-C, where X is the protein of interest and FP is the fluorescent protein that lies at the N- or the C-terminus of the chimera, respectively. The amino acids sequences of the three linkers are: 5'-TGGVGAGGGGGLPVVGGVVGGGVVGGVVGVGLPGGAGGVGRG-3' (VLL42), 5'-TGGVGAGGGGGLPGGAGGVGRG-3' (VLL22) and 5'-TGGVGAGGVGRG-3' (VLL12).

Cloning

Cloning in pVLL vectors was achieved by PCR amplification of CT1wt, RPB1, and H2A with oligonucleotides incorporating the specific restriction sites for directional cloning (sequences are presented in Table S1). PCR were performed with High Fidelity Phusion DNA polymerase (Finnzymes; Thermo Fisher Scientific, Waltham, MA). After a 0.8% (w/vol) agarose-gel extraction of specific DNA bands (Wizard SV gel and PCR Clean-Up System; Promega, Madison, WI), PCR products and recipient vectors were digested with High Fidelity NheI + AgeI, or High Fidelity SacII + NotI (New England Biolabs, Ipswich, MA) at 37°C overnight. After a further PCR cleanup step, PCR products and recipient vectors were ligated with T4 ligase (New England Biolabs) at 16°C overnight and transformed in JM109 chemo-competent bacteria (New England Biolabs). Final plasmids were extracted and sequenced before transfection experiments.

Mutagenesis

Deletions were achieved with a Q5 Site-Directed Mutagenesis Kit (New England Biolabs) as recommended by the manufacturer. Oligonucleotides were designed with the online software NEBasChanger (http://nebasechanger.neb.com).

Immunoblotting

An ice-cold buffer (pH 7.5) containing 25 mM Tris-HCl buffer pH 7.5, 150 mM NaCl, 1% Triton X-100, 1% sodium deoxycholate, 0.1% SDS, 10 mM iodoacetamine, 100 μM PMSF, and a mixture of protease inhibitors (Roche), was added to phosphate-buffered saline (PBS)-washed cells in dishes. After 30 min incubation on ice, the protein extract was transferred to 1.5 mL tubes and sonicated. After a 15-min centrifugation at 16,000 × g, the supernatant was aspirated and placed in a tube before a determination of the protein concentration using a BCA Protein Assay (Thermo Fisher Scientific). Ten micrograms of total protein were loaded onto a 12% polyacrylamide gel and separated by SDS-PAGE. After electrophoresis, proteins were transferred to a polyvinylidene difluoride membrane using a Trans-Blot Turbo Transfer System (Bio-Rad, Hercules, CA). The membrane was blocked in a PBS-T mixture (137 mM NaCl, 2.7 mM KCl, 10 mM Na₂HPO₄, 1.76 mM KH₂PO₄, 0.05% TWEEN 20) +5% (w/v) nonfat dried milk for 1 h at room temperature, then soaked in primary antibody diluted in PBS-T + 5% milk overnight at +4°C. After three washes in PBS-T + 5% milk and one wash in PBS-T, the membrane was soaked in secondary antibody diluted in PBS-T for 1 h at room temperature. After three washes in PBS, the membrane was processed for chemiluminescence detection using Clarity Western ECL Substrate (Bio-Rad) according to the manufacturer’s instructions. Signal intensity was quantified with a MicroChemi system (DNR Bio Imaging Systems, Neve Yamin, Israel). The primary antibodies were 1/5000 of rabbit anti-GFP (Ab6556; Abcam, Cambridge, UK), 1/1000 of rabbit anti-RNA polymerase II carboxy terminal domain repeat YSPTSPS (phospho S5) (Ab5131; Abcam), and 1/1000 of rabbit anti-Cyclin T1(Ab2098; Abcam).

Immunoprecipitation

For each sample, cells at 80% confluence in a 10-cm dish were rinsed with cold PBS-T, scraped into 2 mL PBS. After centrifugation, the pellet was diluted in an ice-cold buffer containing 25 mM Tris-HCl buffer pH 7.5, 150 mM NaCl, 1% Triton X-100, 1% sodium deoxycholate, 0.1% SDS, 10 mM iodoacetamine, 100 μM PMSF, and a mixture of protease inhibitors (Roche) and set on ice for 30 min. Cell lysates were then spun at 16,000 RPM for 15 min at 4°C, and the supernatants incubated with GFP-Trap_A beads (ChromoTek, Planegg-Martinsried, Germany) at 4°C overnight. After three washes of the beads in buffer (10 mM Tris/HCl pH 7.5, 150 mM NaCl, 0.5 mM EDTA), protein complexes were dissociated by heating in Laemmli buffer (Bio-Rad) at 95°C for 20 min and SDS-PAGE was performed as described above. After protein quantification, the immunoprecipitation yield was calculated as the ratio between the coprecipitated protein amount and the precipitated protein amount.

Calculation of E_FRET as a function of the interfluorophore distance, r

The R₀ Förster radius of fluorophore pairs (18, 19, 20) was extracted from the literature except for the mT2/Reach2 pair, which has not been studied so far. To estimate mT2/Reach2 R₀, we used fusion proteins of mT2-pVLL22-SYFP2 and mT2-pVLL22-Reach2 in which fluorescent proteins were separated by a 22-amino-acid linker. These chimeras only differed by the two point mutations in the Reach2 protein that would unlikely modify the average inter fluorophore distance, r. We obtained average FRET efficiency, E, for each pair by TCSPC and calculated the mean r for mT2 to SYFP2 distance from the Förster equation

$$E=\frac{1}{1+{\left(\frac{r}{R_0}\right)}^6},$$ (1)

$$r=R_0.{\left(\frac{1}{E}-1\right)}^{\frac{1}{6}},$$ (2)

where R_0(mT2/SYFP2) = 5.90 nm (16).

As shown in the Fig. S1 C, we measured the FRET efficiency of mT2-SYFP2 dimer: E_(mT2/SYFP2) = 0.17 ± 0.03% (Fig. S1 C) and the distance between the two fluorescent proteins fused in cis was r_(mT2/SYFP2) = 7.75 ± 0.28 nm.

Because the structure of mT2-SYFP2 dimer was equivalent to that of the T2-SYFP2 dimer, we assumed that r_(mT2/Reach2) = r_(mT2/SYFP2) = 7.75 nm. The FRET efficiency of mT2-SYFP2 dimer was measured in our experiment as E_(mT2/Reach2) = 0.30 ± 0.04% (Fig. S1 C). After calculation, this gave R_{0 (mT2/Reach2)}: 6.71 ± 0.22 nm.

Time domain-fluorescence lifetime imaging microscopy

FLIM was performed with a TCS SP5 X confocal head (Leica Microsystems, Wetzlar, Germany) with the SMD upgrade, mounted on an inverted microscope (DMI6000; Leica Microsystems). A pulsed diode laser, PDL 800-B (PicoQuant, Berlin, Germany), delivered 20-MHz repetitive rate pulses at 405 nm. The confocal pinhole was set to 1 Airy, for a 0.921-μm optical slice. Single photons originating from the illuminated voxel were collected through a 63×/1.2 NA water-immersion objective and detected through a 483/32 single-bandpass filter (Semrock, Rochester, NY) on single photon avalanche photodiodes (PDM Series; PicoQuant). Arrival time of single photons was measured with a TCSPC counting card (HydraHarp 400; PicoQuant). The image size was set to 128 × 128 pixels. Data were acquired using the softwares SymPhoTime (PicoQuant) and LAS AF (Leica Microsystems). To obtain the best resolution of nuclei, an 18-fold zoom factor was applied, giving a pixel size of 0.108 μm and an image size of 13.67 × 13.67 μm. Because the statistical determination of the distribution of single photon arrival times requires a minimum of 100 photons per pixel that was reached in ∼120 frames, therefore 120 frames were acquired at 2 Hz for each TCSPC recording.

Frequency domain-fluorescence lifetime imaging microscopy

Frequency domain-FLIM was implemented for the initial FRET optimization steps. Cells were imaged through a 63×/1.2NA water-immersion objective using a CSU-X1 spinning disk confocal scanner (Yokogawa Electric, Tokyo, Japan) mounted on an inverted microscope (DMI6000; Leica Microsystems). FLIM images were acquired using a LIFA System (Lambert Instruments, Groningen, The Netherlands) with a 405-nm laser illumination. Resulting images sizes were 696 × 520 pixels. The software LI-FLIM (v. 1.2.0; Lambert Instruments) was used for image acquisition.

Image correlation spectroscopy

The image correlation spectroscopy (ICS) analysis of each image involved calculating an autocorrelation function r(ξ,γ) with ξ and γ as orthogonal parameters of correlation, following procedures outlined by Petersen et al. (21). A Gaussian function was fitted to each autocorrelation function, with a three-parameter nonlinear least-squares fitting procedure as previously described (22):

$$r\left(\xi ,\gamma \right)=g_{\left(\mathrm{0,0}\right)}{e}^{-\left(\frac{{\xi }^2+{\gamma }^2}{{\omega }^2}\right)}+g_o.$$ (3)

As described in (21), the fitting parameters are an autocorrelation function (ACF) at zero spatial lag g(0,0), which is an estimate of the true autocorrelation function amplitude above background); the best fit beam radius (ω); and a baseline offset fit parameter (g_o). As proposed by Wiseman and Petersen (23), correction of the g(0,0) value for the white noise component simply involves normalization of the mean square fluctuation terms by the white-noise corrected mean intensity. The mean square fluctuation terms may be isolated simply by multiplying the g(0,0) value by the normalizing factor, the square of mean intensity.

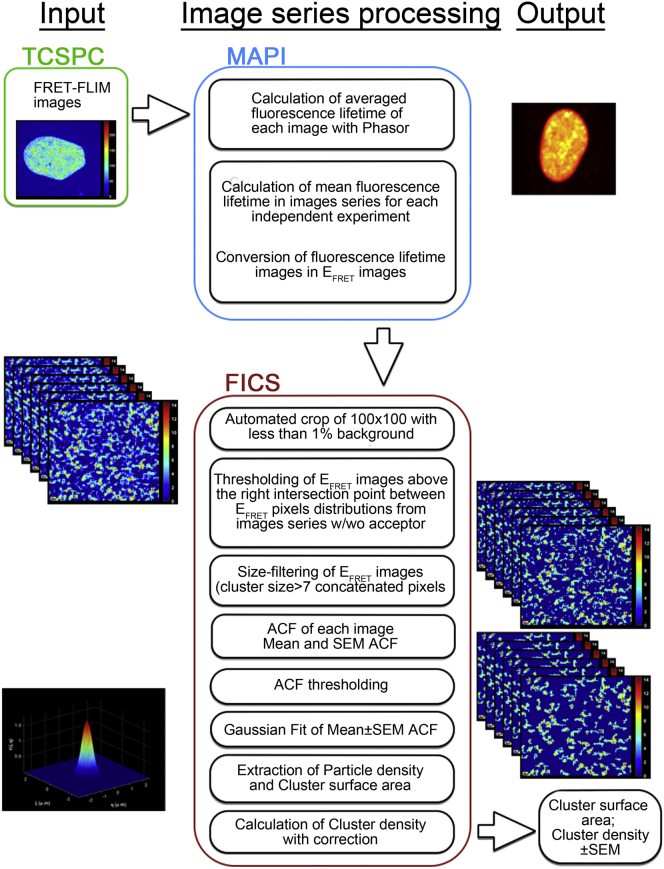
FICS analysis

Computer analyses were performed in the software MATLAB (The MathWorks, Natick, MA) on a personal computer (3.4 GHz, 8 GB RAM). The development was done on an existing custom-made software called MAPI (24) and on the adaptation and automation of the ICS technique. MAPI was developed to analyze TCSPC datasets using the polar approach. Briefly, this software calculates the phase and modulation lifetimes using the Fourier sine and cosine transforms of all of the experimental points of the image (24). Lifetime image series were transformed in E_FRET image series by calculating E_FRET in each pixel (E_FRET;pixel) as

$$E_{\left(\text{FRET},\text{pixel}\right)}=1-\frac{{\tau }_{\text{DA}}}{{\tau }_{D\text{mean}}}.$$ (4)

Mean fluorescence lifetime of the donor alone (τ_Dmean) corresponded to the average, for an image dataset, of the mean fluorescence lifetime of each image and it was calculated in each experiment on a minimum of 20 cells transfected with the fluorescence donor alone. Fluorescence lifetime of the donor-acceptor in each pixel (τ_DA;pixel) is measured in all images by TCSPC. Briefly, the E_FRET calculation method relied on dividing the lifetime value in each pixel by the average value of mean image lifetime distribution of the whole image dataset. This led to the generation of negative E_FRET values that were scaled to 0, as they were unphysical.

The image correlation is based on the MATLAB program of Wiseman’s team described in (23). Some adjustments have been operated to open and automate the whole analysis as a unique script with different packages: full analysis on a database of E_FRET images or analysis on a unique FRET couple repertory. First, each 128 × 128 image was automatically cropped to obtain a 100 × 100 image with a maximum background (low signal out of nucleus) of 1% of the image area. For each independent image dataset, the algorithm automatically determined and extracted the intersection point of the general distributions of E_FRET for donor alone versus donor and acceptor. This intersection value was used as a threshold applied on each E_FRET map from the donor and acceptor. These maps were then autocorrelated one by one by ICS. At the end of the computation, we calculated three different images: the mean ACF, the mean ACF plus the mean ± SE, and the mean ACF minus the mean ± SE. After applying an ACF thresholding, the algorithm fits the three ACFs with a Gaussian function and gets three sets of parameters, respectively, for the mean and upper and lower bounds of the data set. Calculated values by ICS were: 1) the cluster surface area (μm²), which was also known as beam area (21) and was equivalent to the particle surface area in simulated binary images when particles did not overlap; and 2) the mean count of particles within the cluster surface area, which was also known as “particle density” (21) (count.beam area⁻¹). Cluster density (count.μm⁻²) was given by the multiplication of mean number of particles by cluster surface area.

Error in the cluster density estimated by ICS in simulated images was

$$\text{Fold}\text{error}=\frac{\left(\text{ICS }\text{values}\right)}{\text{Implemented}\text{values}}=\frac{\left(\text{Cluster}\text{density}\text{×}\text{cluster}\text{surface}\text{area}\text{×}\text{image}\text{size}\right)}{\left(\text{Integrated}\text{surface}\text{of}\text{pixel}\text{with}\text{intensity>0}\right)}.$$ (5)

ACF thresholding

E_FRET clusters showed irregularly serrated borders that produced a large number of high spatial frequency computations (i.e., smallest spatial lags in the ACF). We have chosen to threshold these clusters smaller than the e⁻¹ radius parameter of the point spread function (PSF)-modeled by a Gaussian function (21). Equation 6 shows that the autocorrelation of a 1D Gaussian function was a Gaussian function with an e⁻¹ radius, β-parameter, multiplied by the square root of 2:

$$\text{ ACF}\left(e^{\frac{-x^2}{{\beta }^2}}\right)=\frac{\beta }{2}{e}^{\frac{-{\eta }^2}{{\left(\sqrt{2}\text{∗}\beta \right)}^2}},$$ (6)

where the value β was the e⁻¹ radius parameter of the PSF, and η was the spatial lag in the ACF.

With β = 227 nm, the misshaped e⁻¹ radius parameter of the PSF was equal to 320 nm. The surface area at the e⁻¹ radius parameter, equal to the exclusion surface, was 0.322 μm².

Fluorescence correlation spectroscopy

FCS measurements were performed on a TCS SP5 X (Leica Microsystems) confocal head with the SMD upgrade, mounted on an inverted microscope (DMI6000; Leica Microsystems). In all experiments, a 63×/1.2 water immersion objective and the 488-nm line of an Argon-Ion laser were used. Fluorescence was detected through a 525/50 single bandpass filter (Semrock) on a single photon avalanche photodiode (Micro Photon Devices, Bolzano, Italy). Single photon events were recorded by HydraHarp 400 (PicoQuant). Measurements were made with the softwares LAS AF (Leica Microsystems) and SymPhoTime32 (PicoQuant). Acquisition time for one FCS measurement was 30 s.

Time-resolved raw data were exported and autocorrelated data were generated with the software F2COR (25). Autocorrelated data was then imported in the software QuickFIT 3.0 (26) and fitted in batch with an anomalous 3D diffusion model. The observation volume was calibrated with a nanomolar concentration solution of ATTO 488 in water, whose diffusion coefficient is known (27).

Data analysis

Each experiment was repeated at least three times and the results were expressed as mean ± SE. The data were analyzed and graphs plotted using the software GraphPad Prism (GraphPad Software, San Diego, CA). For statistical analysis, mean values were compared using either unpaired t-test with Welch’s corrected test (two groups) or one-way ANOVA with Dunnett’s multiple comparison test. Statistical significance was reached for p < 0.05.

Results and Discussion

Live cell superresolution approaches revealed the existence of two types of short-lived RNAPII clusters: large nontranscribing clusters gathering ∼80 RNAPII molecules and smaller but actively transcribing RNAPII clusters with ∼12 molecules (10, 28). P-TEFb interaction with RPB1, the main subunit of RNAPII, is a dynamic process that results in the phosphorylation of the carboxy terminal domain of RPB1 on the serine residues of its hexapeptide repeats (29). Considering these dynamic features, we aimed to assess the spatial organization of P-TEFb/RPB1 interactions by mapping FRET efficiencies in living cells. We started by optimizing biological reporters and we subsequently calibrated TCSPC FRET-FLIM experiments to improve the overall sensitivity and specificity of our method.

Optimization of the FRET system and calibration of the FRET-FLIM setup

FRET efficiency (E_FRET) is dependent on quantum yield, orientation of the dipole, and the distance between the fluorescent protein pair. Although the former parameter is intrinsic to the fluorescent protein, the two latter modalities are very sensitive to steric hindrance (30) in supramolecular complexes such as the transcription machinery. Increasing the mobility of the fluorescent proteins within the chimera could thus help improve E_FRET in the supramolecular complexes. We thus optimized the linker length in the fused proteins and we carefully selected the couple of fluorochromes. To assess the effect of the linker size, we modified the multicloning site of pEGFP-N vector as described in the Materials and Methods, by adding a VLL with a basal length of 42 amino acids reducible to either 22 or 12 amino acids (Fig. S1 A). We also examined the effect of linker length on the FRET efficiency between N- and C-terminal fusion chimeras of CT1-mT2 and RPB1-SYFP2. By the mean of frequency domain FRET-FLIM achieved on transfected U2OS cells, we found that RPB1- SYFP2-C and CT1-mT2-N variants showed a significant FRET at the exclusion of the 12-amino-acid-VLL variants in (Fig. S1 B). Fusion of mT2 at the C-terminus of CT1 or fusion of SYFP22 at the N-terminus of RPB1 both prevented FRET detection. From this screening, we selected CT1-VLL42-mT2-N and RPB1-VLL22- SYFP2-C as the most efficient FRET pair.

With a 93% quantum yield, mT2 (16) was appropriate because photon counting (i.e., 100 photons/pixel) could be reached within <1 min at a low physiological level of expression (50–200 nM as measured by fluorescence correlation spectroscopy in our experiments), resulting in a minimal perturbation of the endogenous system. As an acceptor of FRET, we subsequently compared SYFP2 with its dark variant. Reach2 was found to generate the most efficient signal (Fig. S1 C). From the E_FRET values we measured (Eq. 4) and from the published mT2/SYFP2 Förster radius (R₀) (17), we estimated the theoretical mT2/Reach2 Förster radius (R₀) as described in the Materials and Methods (Eqs. 1 and 2). A simulation of E_FRET values as a function of the radius between mT2/Reach2 pair and other FRET pairs found this mT2/Reach2 pair to be one of the most efficient (Fig. S1 D).

After this reporter optimization step, we shifted to time domain FRET-FLIM by TCSPC to achieve the best resolved images. FRET images were analyzed by the Phasor method within the software MAPI (24) and the mean fluorescence lifetime was figured out. CT1-mT2 fluorescence lifetime was 3.81 ± 0.06 and 3.74 ± 0.11 ns, respectively, in the absence or presence of RPB1-Reach2 (p < 0.001; 40 cells in each group). In our P-TEFb RNAPII model, interactions are dynamic over the acquisition time by TCSPC and, in addition, complexes bound to chromatin are subjected to chromatin motion. This implies that the E_FRET values result from a spatiotemporal average of the FRET signal over the acquisition time. The dynamic feature of the interaction between CT1-mT2 + RPB1-Reach2 in U2OS nuclei is illustrated (Fig. 1, A and B) by changes in the E_FRET clusters while we accumulated more frames (equivalent to a longer acquisition time). To avoid inconsistencies related to the spatial drift of clusters, we restricted the duration of one FLIM image acquisition to 1 min. This was also fitting with the minimal time span to get ∼100 photons/pixel to reliably determine the fluorescence lifetime by the phasor method (24). CT1 imaging showed a singular pattern in the whole cell nucleus (Fig. 2 A) where clusters of pixels with higher CT1 fluorescence intensity were observed. Lifetime image series were transformed into an E_FRET image series as described in the Materials and Methods (Fig. 2, B and C), and revealed the existence of higher E_FRET clusters. The heterogeneity of cluster shapes, irregularity of cluster borders, orientation, and distribution of these clusters make any visual interpretations difficult. Besides, intranucleus and internucleus heterogeneities in FRET signal generated variability (Fig. S2). We have therefore chosen a statistical approach based on ICS to overcome these issues.

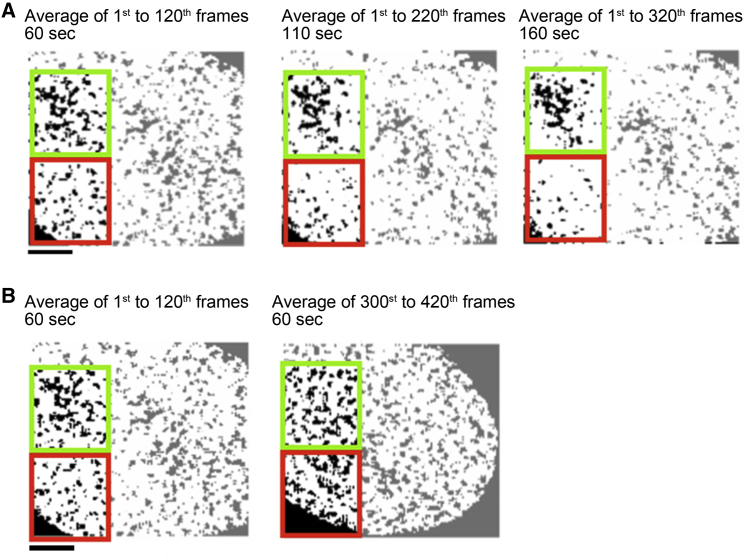
Figure 1.

Temporal drift of nuclear structures in lifetime image during acquisition. (A) Lifetime images of a U2OS single nucleus expressing Cyclin T1 fused in frame to mTurquoise2 fluorescent protein (CT1-mT2) and RPB1 subunit of RNAPII fused in frame to Reach2 fluorescent protein (RPB1-Reach2). Images were generated from 420 TCSPC frames and postprocessed to keep the first 120, 220, or 320 frames as indicated in the figure. Pixels in the images were arbitrarily segmented below 3.67 ns and a 1-pixel sliding binning was operated. Alternatively, images were generated from the first 120 frames or the last 120 frames. (B) Green and red squares highlight clusters with different dynamics over the acquisition time. Extranuclear pixels were excluded from analysis. Scale bars, 2 μm. To see this figure in color, go online.

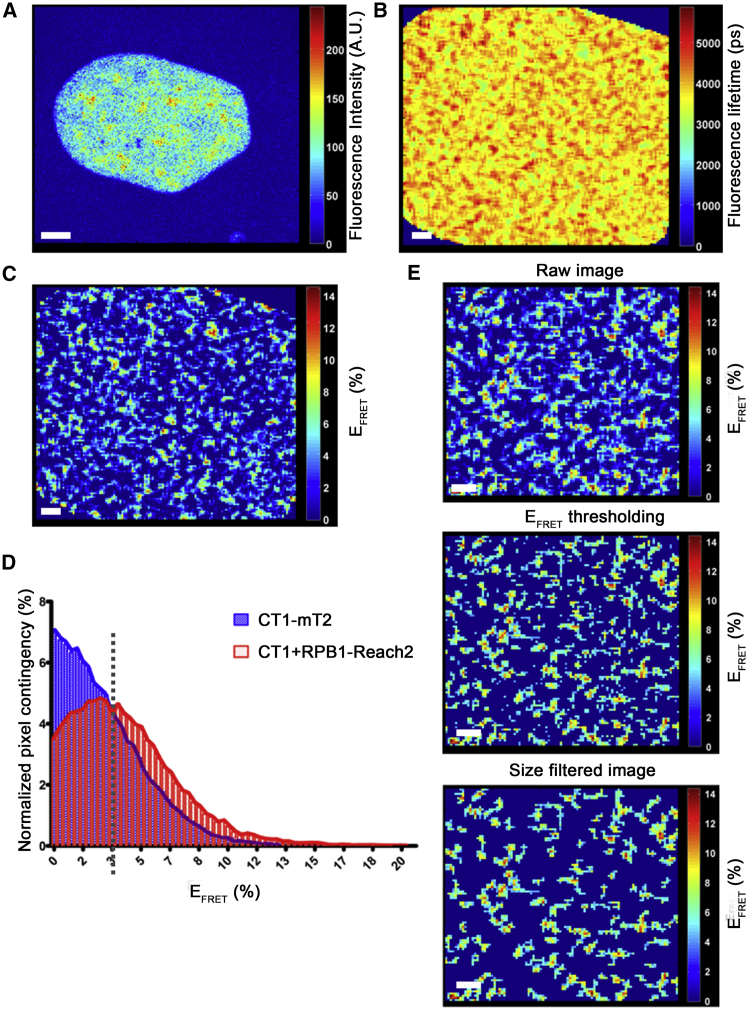
Figure 2.

CT1-RPB1 FRET signal is heterogeneously distributed in the cell nucleus and forms microdomains. (A) Fluorescence intensity image acquired with a confocal microscope (scale bar, 2 μm), (B) lifetime image of the nucleus, and (C) transformed E_FRET image of a U2OS nucleus expressing CT1-mT2 and RPB1-Reach2. (D) Cumulative histograms of the pixels of 60 images of U2OS nuclei as a function of E_FRET, after removal of negative E_FRET values. The intersection value between the two histograms is used as a threshold (represented by the dashed line) to increase the proportion of high E_FRET pixels in the whole pixel population in the image series. (E) A representative E_FRET image of CT1-mT2+RPB1-Reach2 expressing nucleus before (top) and after (middle) its thresholding above the intersection value. Segmented images were subsequently cleaned by the removal of pixel groups smaller than the PSF (bottom image). Color bar: FRET efficiency (%). Scale bars, 1 μm. To see this figure in color, go online.

Overcoming signal noise and heterogeneity in FRET-FLIM images

E_FRET consists of the normalization of the pixel lifetime by the average lifetime of the alone donor. E_FRET normalization smoothens lifetime variations between different kinds of donor chimera (mT2, CT1-mT2…) and between independent experiments (Fig. S2). E_FRET images were subjected to a median-filtering with the software MAPI to smoothen the instrumental noise (Fig. S3). Pixel values in each image were cut off to the positive E_FRET values, and the pixel distribution was plotted as a function of their E_FRET values. As shown in Fig. 2 D, positive E_FRET values could be detected in an image recorded on cells expressing the donor of FRET alone, which was related to the E_FRET calculation method as explained in the Materials and Methods. The presence of the FRET acceptor, RPB1-Reach2, resulted in a small rightward shift in the cumulative E_FRET distributions of pixels from image series of cells transfected with CT1-mT2. This rightward shift in the distribution of CT1-mT2+RPB1-Reach2 revealed a true donor-to-acceptor FRET signal (<10% of the pixel population in each image). Because we could not straightforwardly discriminate pixels with true FRET signal from those with FRET noise signal, we determined a threshold that allowed us to get rid of pixels with the least probable E_FRET content. The intersection point of the two curves fitting the distributions (given as the E_FRET value at which the percentage of pixels for the donor+acceptor overtakes that of the donor alone) was set automatically as the cutoff value for the image segmentation in our process (Fig. 2 E, E_FRET thresholding image). This reduced the risk of an overstatement of the cluster size. In addition, we removed isolated pixels and groups of pixels smaller than the PSF size in E_FRET images (Fig. 2 E, size-filtered image). These pretreatments of E_FRET images improved the accuracy in the characterization of E_FRET clusters by ICS.

FICS, a novel method for the analysis of E_FRET images

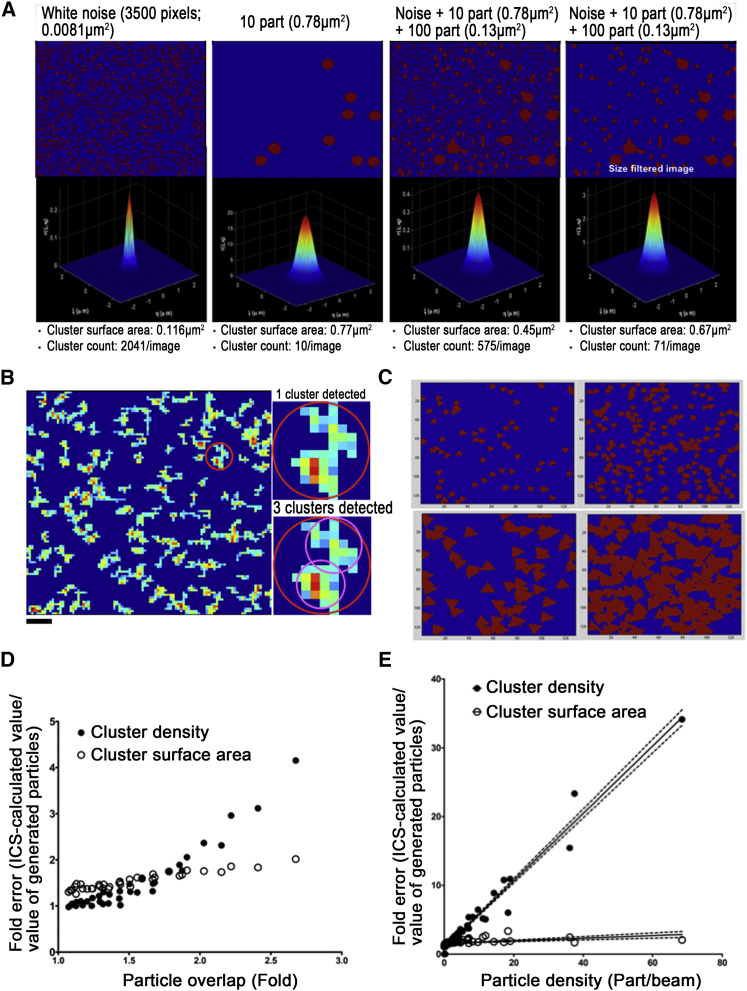
In biology, ICS has been originally adapted to fluorescence intensity images as a fast method for quantifying the average size and density of fluorescent spots (Eq. 3) reporting cell membrane microdomains (21, 22, 23, 31, 32). As described in the Materials and Methods, ICS enables the calculation of two parameters: cluster surface area (equal to the full area section at e⁻¹ radius parameter of the Gaussian function, β in Eq. 6) and the count of particles per cluster surface (23). In experimental images, this latter count may correspond to the count of subunits per cluster. From these two values, we could figure out the cluster density as explained in the Materials and Methods. Petersen et al. (21) have previously used ICS to study fluorescent clusters smaller than the excitation laser spot by confocal microscopy. To check if ICS was suited to analyze E_FRET images with clusters larger than β, we simulated image series implemented with different cluster surface areas and levels of noise with a homemade MATLAB-based script (Fig. 3 A). Our simulations showed that ICS correlated white noise (stochastically distributed individual pixels) and figured out a cluster surface area of 0.116 ± 0.002 μm². This was equivalent to a 3 × 3 pixel square that represented the minimal spatial resolution of ICS. The estimated cluster surface area and cluster density were accurately determined by ICS for homogenous single cluster population (10/10 clusters detected per image), but the cluster density was five times overestimated in a mixed cluster population (surface area: 0.13 and 0.78 μm²) in the presence of white noise. Removal of the white noise by filtering a small group of nine pixels improved the estimated cluster density (Fig. 3 A). Furthermore, the order of magnitude (0.67 μm²) of the surface area determined by ICS was related to surfaces of implemented clusters.

Figure 3.

Principles of image correlation spectroscopy on heterogeneous cluster shapes and heterogeneous image contents. (A) With a home-made MATLAB script, 20 random image series were generated containing either white noise (randomly scattered pixel; left panel), one size of round particles (0.78 μm² surface area on average in image series; second panel), a mix of noise (random pixels), or two sizes of round particles (10 particles of 0.78 μm² surface area on average in image series and 100 round particles of 0.13 μm² surface area in image series; third panel) or the latter set of images after filtering the noise (right panel) by removing a group of pixels with fewer than seven pixels. Gaussian fits (down row of figures) were figured out on the averaged ACF. Averaged cluster surface area and averaged cluster density were calculated by ICS. Pixel size: 100 nm. (B) Cropped size-filtered E_FRET image of CT1-mT2+RPB1-Reach2 is shown on the left. Red circle describes the average cluster surface area calculated by FICS and reported in Table 1. Right insets display the same-cropped area showing one noncompact E_FRET cluster and the different ways ICS could partition this E_FRET cluster in different subclusters (pink-line limited areas). Original image size: 128 × 128 pixels. Scale bars, 1 μm. (C) Examples of 128 × 128 pixels images generated with triangle particles of two different surfaces and at two different densities. These figures illustrate the formation of noncompact clusters with irregularly serrated borders from overlapping particles. (D) Graph plot showing ICS-mediated error in cluster surface area and cluster density as a function of the particle overlap occurring upon image generation. The particle overlap was calculated as the division of the product of implemented particle number and implemented particle surface area by the integrated surface area of the signal in images. ICS-mediated error in cluster density estimation was calculated as the ratio between ICS values and the values implemented in 108 image series. These series of 20 images were implemented with circles, squares, or triangles, with six possible object surface areas (3-, 5-, 7-, 9-, 11-, and 13-pixel) and six possible object densities (20, 70, 120, 170, 220, and 270 clusters per image). (E) Graph plot showing the linear relationship between ICS-mediated error in cluster surface area and cluster density as a function of the particle density. Values are extracted from the same dataset as in (D). Tendency curves (solid lines) and SD (dotted lines) are represented. To see this figure in color, go online.

We also observed that biological E_FRET images displayed a great variability in the shape of clusters (Fig. 2 E). ICS relies on a geometric-based analysis of object shapes. Therefore, clusters with heterogeneous shapes (several lobes, globular subdomains) and with irregular borders were correlated as a whole, but subpart and border irregularities also contributed to the correlation (Fig. 3 B). Indeed, subparts of clusters are highly correlated at the smallest spatial lags (i.e., high spatial frequencies) by the ACF that led to the overestimation of cluster density. To remove these high spatial frequencies, a threshold of 0.322 μm² (as described in the Materials and Methods; see Eq. 6) was applied to the ACF.

We next assessed to what extent the heterogeneity in cluster shape and border irregularity could make the ICS error-prone and whether the ACF thresholding was accurately correcting the overestimation in cluster density. We generated 108 series of 20 simulated images in which we modulated the size and the density of random particles characterized by smooth borders. The increasing density of particles induced their overlap, which led to the creation of particle aggregates, referenced here as clusters, with irregular borders and heterogeneous shapes of clusters (Figs. 3 C and S4). In these simulations, we assumed that the particle overlap mimicked both the heterogeneity of cluster shapes and the irregularity of cluster borders. Each series was implemented with one of three possible shapes of particles (circular, square, and triangular), six possible particle surface areas (3-, 5-, 7-, 9-, 11-, 13-pixel), and six possible particle densities (20, 70, 120, 170, 220, and 270 clusters per image). We found that the more the overlap rate increased, the more ICS overestimated cluster density (Fig. 3 D). This overestimation could be related to the fact that ICS is an unsupervised method and could not a priori define what is a cluster: generated particles or particle aggregates. Therefore, both implemented particles and clusters (i.e., particle aggregates) are accounting for the cluster density calculation by ICS. This implies that the more irregular the borders of E_FRET clusters were and the more heterogeneous the shapes of clusters in our experimental E_FRET images were, the more ICS could overestimate the E_FRET cluster density. We figured out the error in the estimation of cluster density as described in the Materials and Methods (Eq. 5). We noticed that this error is linearly related to the particle density calculated by ICS (see in Materials and Methods), but we found it was independent of particle surface area (Fig. 3 E). We therefore chose to correct values of cluster density with the linear fitting function (y = 0.49× + 0.87; y, fold error in cluster density and x, particle density) extracted from the cluster density error shown in the Fig. 3 E. We showed that this correction suppressed the error in the estimation of cluster density in simulations (Fig. S5 A)—as also reported by the decrease in the residuals (Fig. S5 B). We therefore used the same strategy to correct the calculation of the E_FRET cluster density values.

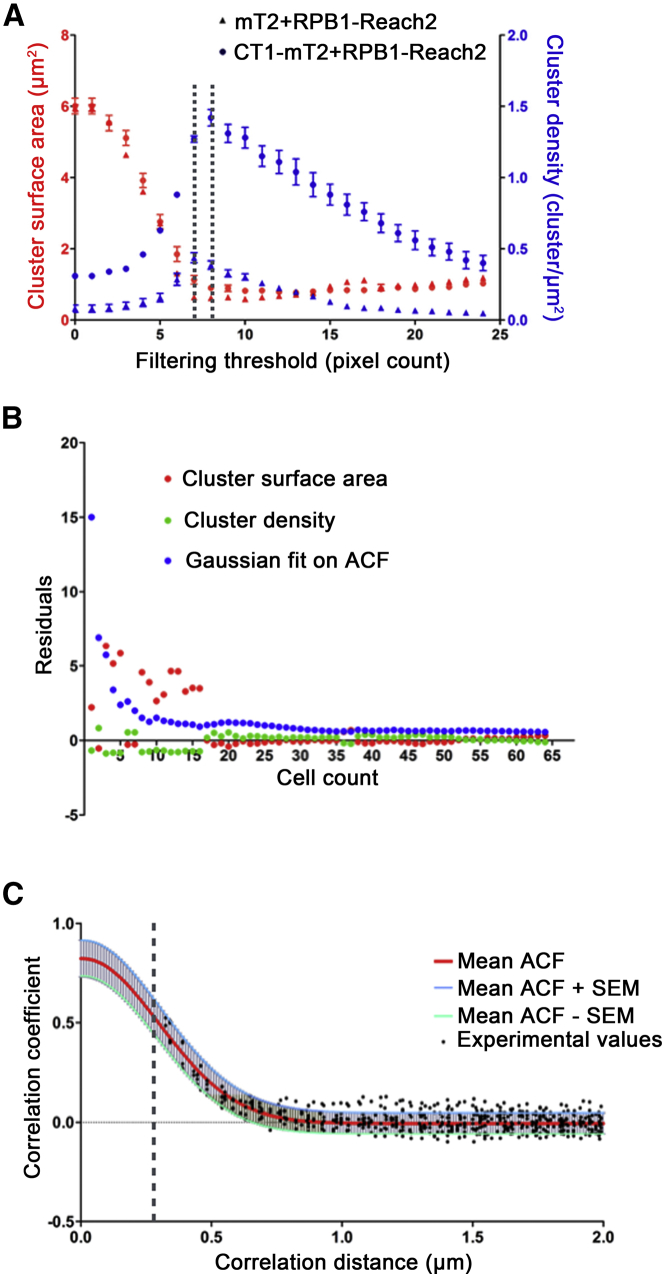
We finally checked how the whole FICS process modified both cluster surface area and cluster density calculated from E_FRET images. We first assessed the effect of filtering small groups of pixels. As shown in Fig. 4 A, cluster surface area and cluster density evolved, at first, in an antiparallel way, as we progressively increased the filtering threshold. This antiparallel evolution of both parameters was related to the effect of ACF thresholding whose size corresponds to a 5.25 × 5.25 pixels square area. Then from a filtering threshold value of 7–8 pixels, the cluster surface area value stabilized whereas the cluster density slowly declined—which was expected as more and more clusters were suppressed from the image. This result confirmed the requirement for filtering the small groups of pixels and the threshold was set to eight pixels.

Figure 4.

E_FRET image and ACF processing for an optimal estimation of size and density of E_FRET clusters. (A) Plots show cluster surface area (red curves) and cluster density (blue curves), calculated by FICS, as a function of the filtering threshold. ICS was performed on image series of U2OS cells expressing either mT2+RPB1-Reach2 (triangles) or CT1-mT2+RPB1-Reach2 (circles). Dotted black lines define the outer limits of the optimal size-filtering threshold. Values: mean ± SD. (B) Graph shows the accuracy of the Gaussian fitting of mean ACF (residuals) and the stability of the cluster surface area estimate (cluster surface area) as a function of the size of image series (one U2OS cell transfected by CT1-mT2+RPB1-Reach2 per image). (C) Given here is a 2D projection of Gaussian fits of minimum, mean, and maximum ACF and the measured ACF values as well. Dotted black line: ACF threshold. To see this figure in color, go online.

We then wondered how we could increase ICS accuracy by improving the Gaussian fit of the ACF. ICS is usually performed on a single image but the residuals of the ACF fit are rarely used to withdraw inaccurate fits. An original feature of our strategy is based on the idea of averaging ACFs from a batch of images to smoothen ACF error. We thus assessed to what extent the number of images in a series could improve the ACF fit accuracy. The residuals of 1) the ACF Gaussian fitting, 2) the cluster surface area estimation, and 3) the cluster density estimation significantly decreased when the number of cells counted increased, until this number reached 30. (Fig. 4 B). Our algorithm was thus implemented to figure out mean ± SE ACFs (Fig. 4 C).

In summary, as it is depicted in the workflow presented in Fig. 5, we set up the whole FICS procedure to estimate the average surface area and average density of protein-protein interaction clusters and we have provided simulations to demonstrate both its accuracy and specificity.

Figure 5.

Workflow of the whole FICS procedure. Three major steps can be distinguished in this procedure: 1) acquisition of one FRET-FLIM image per single nucleus at optimal spatial resolution (input, TCSPC); 2) image processing with MATLAB-based phasor analysis of FRET images (MAPI); and 3) quantification of biophysical characteristics of FRET clusters (output) with batched-ICS (FICS; MATLAB-based ICS script). To see this figure in color, go online.

FICS reveals the dual behavior of P-TEFb with RNAPII and chromatin

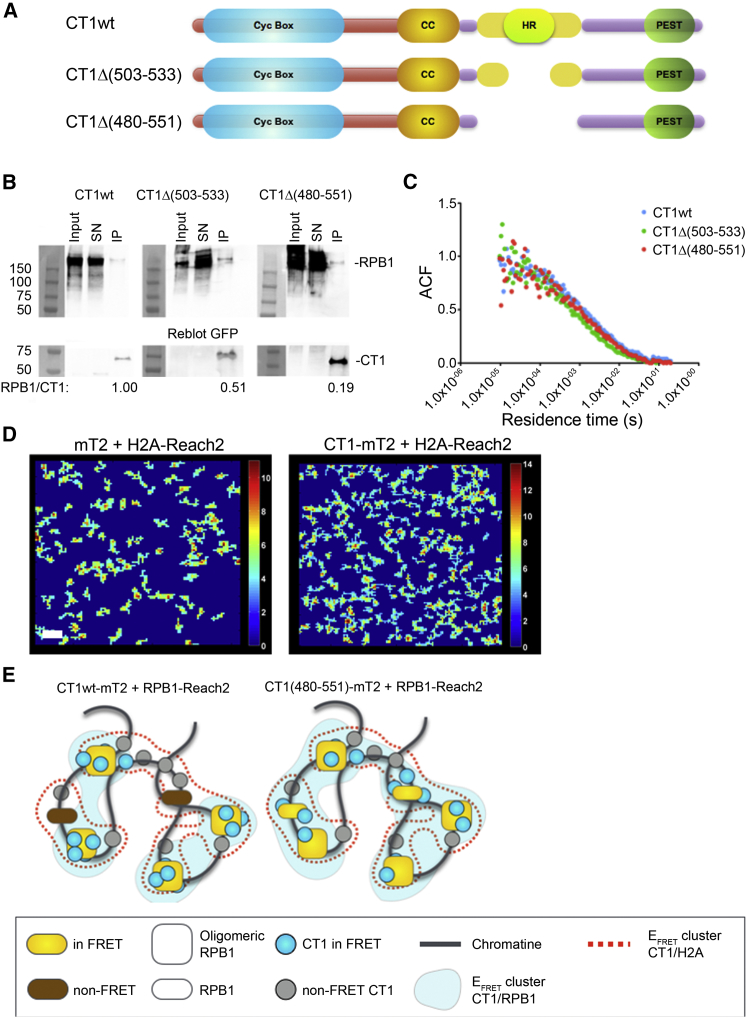
With FICS we finally investigated interactions within the RNAPII supramolecular complex. We first assessed interactions between CT1 and the RPB1 subunit of RNAPII. We used wild-type CT1 or CT1 mutants deleted of the HR domain (Fig. 6 A): CT1Δ(480–551) and Δ(503–533). CT1Δ(480–551) has been originally reported to fail to interact with RPB1 in an acellular pull-down assay (8), although P-TEFb (CT1+cdk9 dimer) conserved its cdk9-mediated interaction with RPB1. We engineered CT1Δ(503–533) to get a deletion restricted as much as possible to the HR domain. As shown in Fig. 6 B, the interaction between RPB1 and CT1Δ(503–533) or CT1Δ(480–551) was decreased two and five times, respectively, when compared to CT1wt, which allowed us to study the effects of a progressive loss of interaction between CT1 and RPB1.

Figure 6.

FICS analysis reveals a dual mechanism of CT1 recruitment on RNAPII and histones. (A) Given here is a schematic representation of CT1 structural domains: cyclin box (Cyc Box), coiled-coil domain (cc), HR domain (HR), and proline, glutamic acid, serine, and threonine (PEST) sequence. N-terminus of CT1 is shown in red whereas C-terminus is in violet. The yellow stretch indicates the binding domain for RPB1 subunit of RNAPII as reported in the literature (8). CT1 mutants investigated the result from the deletion of the HR domain: Δ(503–533) or Δ(480–551). (B) Immunoblots show the immunoprecipitation of mEGFP-fused CT1wt, CT1Δ(503–533), or CT1Δ(480–551) and the coprecipitation of RPB1. Total protein extract (Input), supernatant of immunoprecipitation (SN), and immunoprecipitated (IP) proteins were loaded. Averaged signal of detected protein was estimated by a numerical imager. Coimmunoprecipitated RPB1 was normalized by the CT1 amount effectively precipitated and is reported as a RPB1/CT1 ratio. (C) ACF of CT1-mEGFP fluorescence intensity fluctuations as measured by FCS. Wild-type and CT1 mutants were transfected in U2OS and cells expressing fluorescent chimera in their nuclei at <200 nM were recorded. (D) Given here are representative E_FRET images of mT2+H2A-Reach2 and CT1-mT2+H2A-Reach2 expressed in the nucleus of U2OS cells. Scale bars, 1 μm. (E) Model is shown for the involvement of CT1 in RPB1-dependent and RPB1-independent recruitment of P-TEFB on chromatin. Only CT1 proteins bound to chromatin are depicted. Scheme represents the FRET detected between CT1 and RPB1 at a given time. Two populations of RPB1 are depicted: oligomerized and transcriptionally active RPB1, as suggested in (10). CT1 mutants have a decreased propensity to be entrapped by oligomeric RPB1: they explore their environment more freely where they may briefly interact with nonoligomeric RPB1. As a consequence, the surface area of CT1-RPB1 FRET clusters increases with the mutants, whereas the surface area of CT1-H2A FRET clusters does not significantly vary. To see this figure in color, go online.

We next assessed by FICS whether these mutations modify the size or the number of the CT1 RPB1 E_FRET clusters in living cells. Free mT2 was used with RPB1-Reach2 to characterize the noise obtained for noninteracting proteins. As summarized in Table 1, a small cluster surface area (0.64 μm²) and a high cluster density (1.75 clusters/μm²) were obtained for this negative control. Conversely, CT1wt+RPB1 clusters were larger and less dense (1.48 μm² and 0.99 clusters/μm²). Besides, the cluster surface area significantly increased 2.03- and 2.43-fold, respectively, for both CT1Δ(503–533) and CT1Δ(480–551) mutants, respectively, compared to CT1wt whereas their cluster density decreased by approximately twofold. These experiments reveal that interactions between CT1 mutants and RPB1 occur in a more diffuse area than between CT1wt and RPB1. At first glance, this increased cluster surface area looks paradoxical but it could reflect the fact that the lower affinity of CT1 mutants for RPB1—as demonstrated by our immunoprecipitation assays—decreased their propensity to be entrapped by RPB1. This would increase the turnover of CT1 mutants on RPB1, when compared to wtCT1, and would enable CT1 mutants to explore larger domains to meet more frequently other RPB1 proteins. Altogether, our FRET-FLIM/ICS results confirm that the CT1 HR domain is required for its optimal interaction with RPB1.

Table 1.

Biophysical Characteristics of E_FRET Clusters in U2OS Cells Transfected with mTurquoise2-Fused Proteins

	Cluster Surface Area (μm2)	Mean ± SE	p Value	Cluster Density (Clusters/μm2)	Mean ± SE	p Value	Sample Count
+RPB1-Reach2
CT1 wt -mT2	1.48	0.12		0.99	0.058	—	50
CT1Δ(503–533)-mT2	3.01	0.14	0.001	0.41	0.001	0.001	48
CT1Δ(480–551)-mT2	3.60	0.01	0.001	0.46	0.004	0.001	65
mT2	0.64	0.006	0.001	1.75	0.024	0.001	50
+H2A-Reach2
CT1 wt -mT2	2.39	0.24		0.71	0.057		42
CT1Δ(503–533)-mT2	2.44	0.36	ns	0.69	0.075	ns	32
CT1Δ(480–551)-mT2	1.83	0.04	ns	0.83	0.001	ns	69
mT2	0.56	0.045	0.01	1.87	0.041	0.001	70

Cells were cotransfected with either a Reach2-fused RPB1 (RPB1-Reach2-fused histone H2A (H2A-Reach2)). Calculated biophysical characteristics of clusters are averaged cluster surface area, averaged cluster density, mean ± SE, statistical errors α (one-way ANOVA and Dunnett’s posttest), and number of cells. Significance was reached for p < 0.05. mT2, mTurquoise2-Fused protein.

TCSPC recordings integrate photon counting over the time, which implies that any change in CT1 diffusion properties could modify the physical features of the E_FRET clusters. We therefore conducted a diffusion analysis by fluorescence correlation spectroscopy with an anomalous model on CT1wt and the two CT1 mutants. We characterized CT1 averaged residence time in the voxel and their anomalous coefficient (corresponding to the slope of the autocorrelation function fit). An example of an autocorrelation function is shown in Fig. 6 C. Residence times of CT1wt, CT1Δ(480–551), and Δ(503–533) were 13.5 ± 0.43, 12.01 ± 2.34, and 11.82 ± 2.96 ms (mean ± SD), respectively, and their anomalous diffusion coefficients were 0.63 ± 0.02, 0.62 ± 0.02, and 0.65 ± 0.03. These results showed no changes in the diffusion properties of CT1wt and its two mutants and thus demonstrated that the HR domain did not constrain CT1 diffusion, although it is specifically involved in CT1-RPB1 interaction. Because diffusion of nuclear protein can be hindered by the fractal organization of chromatin (33) and by interactions with DNA-bound proteins, we next assessed whether the spatial distribution of CT1 could be constrained by chromatin and if this would be mediated by its interaction with RNAPII.

We postulated that diffusion of CT1 and its mutants could be spatially constrained by the chromatin fibers, which would keep CT1 in close proximity to RPB1 and enhance their interaction rate. Because we aimed to quantify CT1 spatial distribution with respect to the chromatin backbone, we chose to measure the proximity between CT1 and histones. Interestingly, we demonstrated that CT1 could generate a FRET signal with H2A (Fig. 6 D and Table 1). Even though P-TEFb has been shown to phosphorylate histone 1 (34), to the best of our knowledge, so far there has been no clear evidence of an interaction between CT1 and histones. Interestingly, CT1-H2A interaction clusters showed a bigger surface area than CT1-RBP1 clusters (2.39 ± 0.24 and 1.48 ± 0.12 μm², respectively), suggesting a more diffuse interaction area. Conversely to what happened between CT1 and RPB1, CT1 mutations did not significantly modify the CT1-H2A interaction clusters (Table 1). We thus concluded that the proximity between CT1 and H2A is partly independent from RPB1. CT1-H2A interaction clusters are likely constrained by the presence of CT1-anchoring partners on chromatin such as 1) genomic enhancers via Brd4 and JMJD6 proteins (35), 2) splicing factor SRSF2 (also known as SC35) (36), 3) RNA helicase DDX21 (37), 4) PPM1G/PP2Cγ (38), and androgen receptor enhancer RNAs (39).

Taken together, our results show that the deletion of CT1 HR domain decreases the affinity of P-TEFb for RPB1 while, strikingly, it increases the area in which CT1 interacts with RPB1. In their recent work, Cho et al. (10) reported that RPB1 is organized in three major populations: paused oligomeric RNAPII complexes, transcriptionally active RNAPII, and free diffusing RNAPII. We hypothesize that the paused oligomeric RNAPII entraps most P-TEFb molecules (Fig. 6 E, left panel). Deletion of CT1 HR domain decreases the avidity of oligomeric RNAPII for P-TEFb, and consequently this likely increases the number of CT1 molecules exploring the nucleoplasm and thus encountering more RNAPII over the time of acquisition (Fig. 6 E, right panel). This could explain why we detected an increase in the surface area of CT1Δ(HR)-RPB1 clusters. By comparison, the HR domain not being involved in the interaction of CT1 with H2A, deletion of this domain does not significantly modify the surface area of CT1-H2A interaction clusters.

In conclusion, we developed, to our knowledge, a new semiautomatic E_FRET-ICS procedure (FICS) for the quantification of protein-protein interaction maps that are available for high content screening. This method could theoretically be set for all molecular partners confined in clusters and might provide valuable information on the mechanisms driving the spatial distribution of these interaction clusters. As an example, we found that the P-TEFb recruitment on chromatin is unlikely to be driven by P-TEFb interaction with RNAPII in living cells.

Author Contributions

G.B. and L.H. designed research. G.B., C.L.N., M.G.P., M.H., and A.F. performed research. G.B., C.L.N., M.G.P., M.H., A.F., and L.H. analyzed data. G.B., C.L.N., M.G.P., A.F., O.B., B.V.B., and L.H. wrote the manuscript.

Editor: Jason Kahn.