Why Enveloped Viruses Need Cores—The Contribution of a Nucleocapsid Core to Viral Budding

Abstract

During the lifecycle of many enveloped viruses, a nucleocapsid core buds through the cell membrane to acquire an outer envelope of lipid membrane and viral glycoproteins. However, the presence of a nucleocapsid core is not required for assembly of infectious particles. To determine the role of the nucleocapsid core, we develop a coarse-grained computational model with which we investigate budding dynamics as a function of glycoprotein and nucleocapsid interactions, as well as budding in the absence of a nucleocapsid. We find that there is a transition between glycoprotein-directed budding and nucleocapsid-directed budding that occurs above a threshold strength of nucleocapsid interactions. The simulations predict that glycoprotein-directed budding leads to significantly increased size polydispersity and particle polymorphism. This polydispersity can be explained by a theoretical model accounting for the competition between bending energy of the membrane and the glycoprotein shell. The simulations also show that the geometry of a budding particle leads to a barrier to subunit diffusion, which can result in a stalled, partially budded state. We present a phase diagram for this and other morphologies of budded particles. Comparison of these structures against experiments could establish bounds on whether budding is directed by glycoprotein or nucleocapsid interactions. Although our model is motivated by alphaviruses, we discuss implications of our results for other enveloped viruses.

Introduction

Membrane remodeling is required for critical cellular processes including endocytosis, formation of multivesicular bodies, retrograde trafficking, and exosome formation. Viruses and other pathogens also reshape cellular membranes during different stages of their lifecycles including entry into the host cell, formation of replication complexes, construction of assembly factories, and exit (also called “egress” or “budding”). Understanding the mechanisms of viral budding and the forces that drive this process would advance our fundamental understanding of viral lifecycles, and shed light on analogous cellular processes in which membrane remodeling and vesicle formation are essential for function. In parallel, understanding fundamental determinants of budding and membrane dynamics would facilitate the design of viral nanoparticles. There is keen interest in reengineering enveloped viral nanoparticles to be used as targeted transport vehicles capable of crossing cell membranes through viral fusion (1, 2, 3, 4, 5).

All viruses contain a capsid protein, which primarily functions to protect the viral genome during viral transmission. In enveloped viruses, the internal capsid is surrounded by a host-derived lipid bilayer and viral glycoproteins (GPs) embedded in this membrane. Enveloped viruses can be subdivided into two groups based on their sequence of virion assembly and budding. For the first group (e.g., alphaviruses, hepatitis B, herpes), budding requires the assembly of a preformed nucleocapsid core (NC), which may be ordered or disordered depending on the virus. The core then binds to membrane-bound GPs and initiates budding (6, 7, 8, 9). For the second group (e.g. influenza, type C retroviruses (HIV)), capsid assembly occurs concomitant with budding (6, 8, 10). The advantage of one assembly mechanism over another is not obvious; particle infectivity, morphology, and stability may all influence the preferred budding process.

The importance of preformed capsids in alphavirus assembly is of particular interest because the presence of a capsid in the particle is not necessary for production of infectious particles. The traditional view is that alphaviruses follow the preassembled NC budding pathway (11, 12, 13, 14), based on the observation of high concentrations of NCs in the cytoplasm (15), and evidence that GP-GP and NC-GP interactions are required for virion formation (16, 17). However, several studies have challenged this conclusion. In particular, Forsell et al. (18) reported successful assembly and budding of alphavirus despite mutations that inhibited NC assembly by impairing interactions between NC proteins, whereas Ruiz-Guillen et al. (19) observed budding of infectious alphavirus particles from cells that did not express the capsid gene. In both cases, infectious particles were assembled and released or budded from the cell. These observations suggest that GP interactions may be sufficient for alphavirus budding. This begs the question: Why do enveloped viruses have internal nucleocapsid cores? Is there an advantage to having an NC during budding?

Molecular dynamics simulations can be a useful tool to bridge the gaps between the different steps of assembly that cannot be experimentally characterized. Computational studies have already provided insightful information about virus NC assembly (20), as well as the interactions between proteins and lipid membranes (21, 22, 23). Previous simulations on budding of nanoscale particles led to important insights but did not consider the effect of GPs (24, 25, 26, 27, 28, 29, 30, 31), although budding directed by GP adsorption or capsid assembly have been the subject of continuum theoretical modeling (32, 33, 34). The formation of clathrin cages during vesicle secretion, a process that bears similarities to viral budding, has also been the subject of modeling studies (35, 36, 37, 38). Most closely related to our work are previous simulations on the assembly and budding of 12-subunit capsids, which found that membrane adsorption can lower entropic barriers to assembly (39, 40) and that membrane microdomains can facilitate assembly and budding (41). In contrast to these earlier works, we consider the presence of a nucleocapsid, a larger shell (80 trimer subunits), and a different subunit geometry. We find that these modifications lead to qualitatively different assembly pathways and outcomes in some parameter ranges.

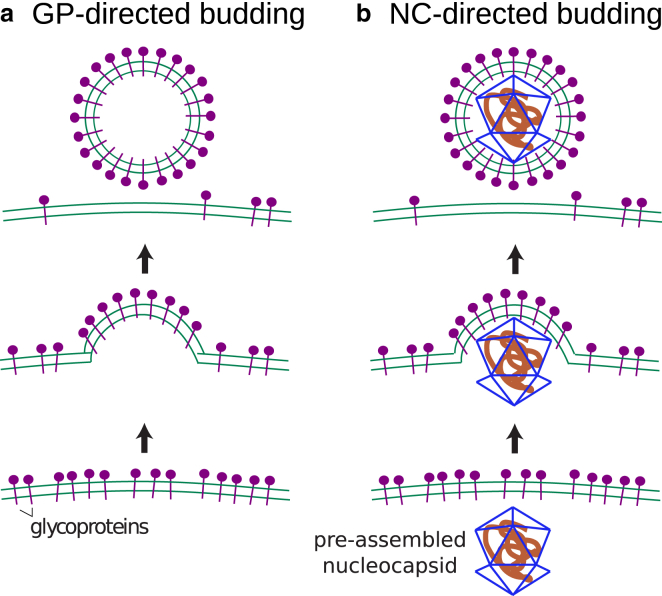
In this article, we perform molecular dynamics simulations on a coarse-grained model for GPs, the NC, and a lipid bilayer membrane to elucidate the forces driving enveloped virus budding. Our model is motivated by the alphavirus structure and experimental observations on alphavirus budding (12, 18, 19), but we consider our results in the broader context of enveloped viruses. To evaluate the relative roles of a preassembled NC compared to the assembly of transmembrane glycoproteins in driving budding, we perform two sets of simulations. The first focuses entirely on glycoprotein-directed budding (Fig. 1 a) by including only the membrane and model GPs, whose geometry and interactions drive formation of an icosahedral shell with the geometry of the alphavirus envelope. This model directly applies to experiments on budding from cells in which capsid assembly was eliminated (18, 19). The second set of simulations includes model GPs and a preassembled NC, thus allowing for NC-directed budding (Fig. 1 b).

Figure 1.

Mechanisms of enveloped virus budding on membranes: (a) GP-directed budding and (b) NC-directed budding.

We present phase diagrams describing how assembly morphologies depend on the strength of GP-GP and NC-GP interactions. The results demonstrate that the competition between the elastic energy of membrane deformations and deviations from preferred protein curvature can lead to polymorphic morphologies, and that templating by the NC can significantly decrease the resulting polydispersity. In the presence of a preassembled NC, there is a threshold strength of NC-GP interactions above which pathways transition from GP-directed to NC-directed budding. Our simulations enable visualization of the intermediates along each of these pathways. In both pathways, assembly proceeds rapidly until budding is ∼2/3 complete, after which negative Gaussian curvature of the membrane at the neck of the bud imposes a barrier to subunit diffusion that significantly slows subsequent assembly and budding. We discuss possible implications of this slowdown for enveloped viruses such as HIV that bud with incompletely formed capsids (42, 43).

Methods

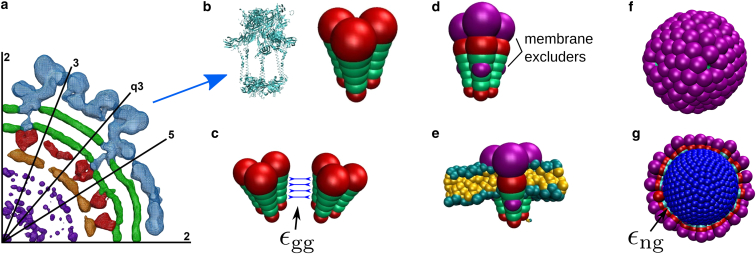
Although intact viruses can be simulated at atomistic or near-atomistic resolution (44, 45, 46, 47, 48), the timescales for alphavirus assembly (milliseconds to minutes) are prohibitive at such resolution. We thus consider a coarse-grained description for the viral GPs and the membrane, which enables tractable simulation of a large membrane over biologically relevant timescales while retaining the essential physical features of membranes and virus capsid and transmembrane proteins (see Fig. 2).

Figure 2.

Overview of the computational model. (a) Given here is the cryoEM density distribution of Sindbis virus (data from (53)). This central cross section shows the inner structure of α-viruses, with the RNA molecule (purple) enclosed by the NC (orange, red) and the lipid membrane (green) with the transmembrane GPs (blue). (b–g) Given here is the computational model of the α-virus GPs and NC. (b) Comparison between the GP trimer is as revealed by cryoEM (PDB: 3J0C (49)) and our coarse-grained model trimer. Trimers are modeled as rigid bodies comprising three cones, with each cone formed by six pseudoatoms of increasing diameter. (c) Each of the four inner pseudoatoms of a cone (green) interacts with its counterpart in a neighboring cone through a Morse potential with well-depth ε_gg. All pseudoatoms, including the excluders (red), interact through a repulsive Lennard-Jones potential. (d) Model glycoproteins are trapped in the membrane by membrane-excluders (purple), which interact with membrane pseudoatoms through a repulsive Lennard-Jones potential. (e) A complete trimer subunit embedded in the membrane. To aid visibility, in subsequent figures only the membrane excluders are shown. (f) Given here is a snapshot of a typical capsid assembled by model glycoproteins in the absence of a membrane, consisting of 80 trimer subunits. (g) Given here is a snapshot of typical capsid assembled by glycoproteins around the model nucleocapsid (NC, blue) in the absence of a membrane. The NC is modeled as a rigid spherical particle. NC pseudoatoms interact with the lowermost pseudoatom in each GP cone through a Morse potential with depth ε_ng. To see this figure in color, go online.

Here we give an overview of the computational model and the simulation implementation. Further details and the interaction potentials are provided in section S3 of the Supporting Material.

Glycoprotein model

Our model GPs are designed to roughly match the triangular shape, dimensions, and aspect ratio of Sindbis virus GP trimers (49, 50). Our GP trimer subunit comprises three cones, which are fused together and simulated as a rigid body. Each cone is represented by an array of six beads of increasing diameter, following the model described by Chen and Glotzer (51). However, our cones are truncated, so that they form a shell with an empty interior, as shown in Fig. 2. The cones experience lateral interactions, which in the absence of a membrane drive assembly into capsids containing 80 subunits, consistent with the 80 trimers in the alphavirus glycoprotein shell.

Each cone consists of a linear array of six beads of increasing diameter. Two nearby cones experience repulsive interactions, mediated by a repulsive Lennard-Jones potential between all pairs of beads, with size parameter σ equal to the bead diameter. In addition, each of the four inner beads experiences an attractive interaction with its counterpart (the bead with the same diameter) in the neighboring subunit, modeled by a Morse potential. The Morse potential depth ε_gg determines the subunit-subunit interaction strength, which is related to the GP-GP binding affinity. The equilibrium distance of the Morse potential r_e, and the Lennard-Jones diameter σ for each interacting pair, is chosen to drive binding toward a preferred trimer-trimer angle. We set the preferred angle so that in bulk simulations (in the absence of membrane) the subunits predominantly assemble into aggregates with the target size, 80 subunits. In our simulations the GPs are embedded within the membrane, where they freely tilt and diffuse but cannot escape on simulation timescales.

Membrane model

The membrane is represented by the solvent-free model presented by Cooke et al. (52), which can be tuned to match properties of biological membranes while allowing simulation of large systems. We study membrane sizes of 170 × 170 nm, and except where specified otherwise, the membrane bending modulus is set to κ_mem ≈ 14.5 k_BT.

Nucleocapsid model

Motivated by the recent observation that alphavirus nucleocapsids do not require icosahedral symmetry (53) to be infectious, we model the nucleocapsid as an isotropic sphere of radius similar to that estimated from cryoelectron microscopy (CryoEM) experiments, r_NC ≈ 18.0 nm. Because complete NCs have significantly higher rigidity than lipid membranes or GP-coated vesicles (54, 55), we model the NC as infinitely rigid. The NC experiences attractive interactions with the bottom part of the GP trimers, and excluded volume interactions with the membrane.

Subunit conformational changes

Experiments on several viral families suggest that viral proteins interconvert between “assembly active” and “assembly inactive” conformations, which are respectively compatible or incompatible with assembly into the virion (56, 57, 58). Computational models suggest that such conformational dynamics can suppress kinetic traps (59, 60). Conformational changes of the alphavirus GPs E1 and E2 are required for dimerization in the cytoplasm, and it has been proposed that the GPs interconvert between assembly inactive and assembly active conformations (58), possibly triggered by interaction with NC proteins (18). Based on these considerations, our GP model includes interconversion between assembly active and assembly inactive conformations, with an interconversion timescale τ_c. The two conformations have identical geometries, but only assembly active conformations experience attractive interactions to neighboring subunits.

To maintain a constant free subunit concentration during assembly, we couple the system to a bath of free subunits by allowing for insertion of new subunits into the membrane (far from assembling clusters). To allow for efficient insertion of transmembrane proteins, we included a third subunit type called “reservoir subunits”, which effectively acts as a reservoir of inactive subunits. Further details are in section S3 E of the Supporting Material.

Simulations

We performed simulations in the software HOOMD-blue, v. 1.3.1 (61), which makes use of GPUs to accelerate molecular simulations. Throughout the article we report dimensions of length, mass, and energy in units of σ, m₀, and the thermal energy k_BT. We fixed temperature at k_BT/ε₀ = 1.1. Physical sizes and timescales can be estimated as follows. We set the diameter of the lipid head as d_head = σ, so that considering a 5-nm-thick bilayer leads to σ ≈ 0.9 nm. The characteristic timescale of the simulation is determined by the subunit diffusion, which in our simulations is dominated by the interaction with the membrane lipids rather than with the bath. We define our unit of time τ₀ as the characteristic time of a subunit to diffuse a distance σ on the membrane. Comparing with a typical transmembrane protein diffusion constant ∼4 μm²/s (62, 63), we obtain τ₀ = 250 ns. We set the timescale for subunit conformational interconversion to τ_c = 3τ₀. The results are not sensitive to changing τ_c, provided it is short in comparison to assembly timescales.

Additional simulations

We have performed a number of sets of additional simulations to estimate parameter values and evaluate the effect of assumptions within the model, which are described in the Supporting Material. We estimated the membrane bending modulus κ_mem as a function of interaction parameters by analyzing the membrane height-height fluctuation spectrum (section S6 of the Supporting Material). We estimated the shell bending modulus κ_shell as a function of the interaction strength ε_gg by analytically approximating the energy cost associated with bending the shell away from its preferred curvature, based on the spatial organization of subunits that we observe in simulations (section S6 of the Supporting Material). We performed simulations with other subunit designs, to evaluate the relationship between the geometry of subunits and their ability to reshape the membrane (section S3 H of the Supporting Material). We compare assembly and budding efficiency with and without subunit conformational switching; see section S4 of the Supporting Material. We describe how the assembly yield and shell size distribution in bulk simulations (i.e., without the membrane) depends on ε_gg and the presence of the NC (section S5 of the Supporting Material). Finally, we performed simulations of dilute subunits in membranes to calculate the subunit and lipid diffusion constants (section S7 of the Supporting Material).

Results and Discussion

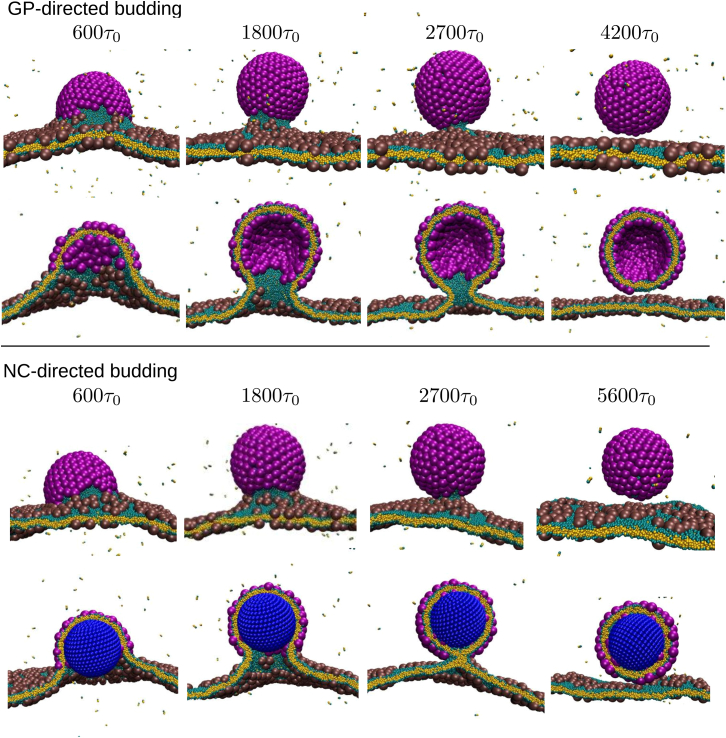
To elucidate the role of the NC in the assembly of enveloped viruses, we performed two sets of simulations. To model GP-directed budding, we embedded GP subunits in the membrane, including an initial preformed critical nucleus of active subunits and a high density of inactive subunits surrounding it. As shown in the top panel of Fig. 3, budding proceeds as an increasing number of subunits associate to the partial shell. To model NC-directed budding, we studied the same system, but initialized with an NC placed 7 nm below the membrane (Fig. 3, bottom). We chose this initialization because within the NC-directed hypothesis the NC assembles completely in the endoplasmic reticulum and is then transported by the secretory pathway to the budding site at the plasma membrane. To understand how these pathways depend on parameters that can be controlled in experiments or varied under evolutionary pressures, we simulated assembly as a function of parameters controlling the GP-GP interaction strength ε_gg, the NC-GP interaction strength ε_ng (when an NC is present), and the membrane bending modulus κ_mem. All energies are reported in units of the thermal energy, k_BT. For notational convenience, we refer to particles assembled from GPs only as GP-particles, and GPs assembled around the NC as GPNC-particles.

Figure 3.

Top: Shown here is a typical simulation trajectory of GP-directed budding, at simulation times 600, 1800, 2700, and 4200 τ₀, from left to right, with GP-GP interaction strength ε_gg = 2.3. Bottom: Given here is a simulation trajectory of NC-directed budding, at 600, 1800, 2700, and 5600 τ₀, with ε_gg = 2.5 and NC-GP interaction strength ε_ng = 3.5. The second time point in each row corresponds to an example of the intermediate with a constricted neck described in the text. Except where noted otherwise, the membrane bending modulus κ_mem ≈ 14.5 k_BT throughout the article. To see this figure in color, go online.

Budding includes an intermediate with a constricted neck

We show snapshots from typical trajectories for simulations in the presence and absence of an NC in Fig. 3. In both cases, assembly and membrane deformation proceed rapidly until the GP shell is ∼2/3 complete (the second time point in each row in Fig. 3), when the budding region is connected to the rest of the membrane by a narrow neck. Subunits within the neck experience restricted configurations due to the high negative Gaussian membrane curvature. Thus, the neck acts as a barrier that impedes subunit diffusion to the growing shell, causing the assembly rate to slow dramatically as the shell nears completion (Fig. 7). The neck continues to narrow as additional GPs assemble until it becomes a tether connecting the bud and membrane. In this article, we do not consider endosomal sorting complexes required for transport (ESCRT) or related scission-inducing proteins, and thus the bud separates from the membrane only when a large thermal fluctuation induces membrane fission leading to scission of the tether.

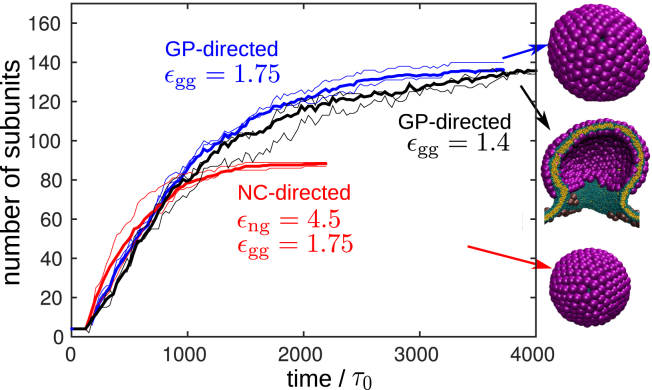
Figure 7.

Given here is the number of GP trimers in budding shells as a function of time for trajectories at different parameter values: GP-directed budding with ε_gg = 1.4 (black) or ε_gg = 1.75 (blue) and NC-directed budding with ε_ng = 4.5 and ε_gg = 1.75 (red). The snapshots to the right show the assembly products. For each parameter set, the thick line shows an average over three trajectories, and the two thin lines show two individual trajectories to give a sense of the size of fluctuations. The lines end when budding occurs, except for the GP-directed case with ε_gg = 1.4, which ended in the stalled partially budded state. To see this figure in color, go online.

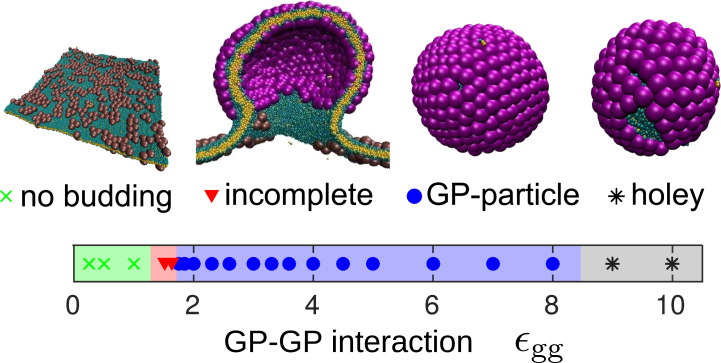
Glycoprotein-directed budding leads to complete but polydisperse particles

We first consider assembly in the absence of an NC, so that budding is necessarily GP-directed. Fig. 4 shows the most frequent end-product obtained as a function of the GP-GP interaction strength. For weak interactions (ε_gg < 1.4), assembly is unfavorable. In contrast, bulk simulations (model GPs in the absence of a membrane) exhibit shell assembly for ε_gg > 0.97 at trimer concentration ϕ_3D = 3.4 × 10⁻⁵ σ⁻³ (see Fig. S4 a, and see the Supporting Material), well below the effective concentration of trimers on the membrane ϕ_2D^eff = 0.001σ⁻³. (To compare the subunit concentration on the membrane with the concentration in bulk ϕ_3D = N_S/L³, where N_S is the number of subunits and L is the box size, we measure the standard deviation of height fluctuations of the subunits on the membrane, λ ≈ 4.5σ, and the effective concentration on the membrane is then given by ϕ_2D^eff = N_S/L³λ.) This result demonstrates that the membrane rigidity can introduce a substantial barrier to assembly (26).

Figure 4.

Predominant end-products for assembly without an NC as a function of GP-GP interaction strength, along with simulation snapshots that exemplify each class of end-product. The distributions of end-products for several representative values of ε_gg are shown in Fig. S9. To see this figure in color, go online.

Within a narrow range of interaction strengths 1.4 < ε_gg < 1.7, assembly and budding stalls at the constricted neck intermediate described above. For these parameters, the intermediate remains upon extending the simulation length to 10,500τ₀, suggesting that it corresponds to a true steady state or a very long-lived kinetic trap. This configuration resembles partially assembled states that were predicted theoretically (34, 64), but arises due to different physics. We find that the range of ε_gg over which the state arises depends on the subunit geometry, but the state exists for any geometry we considered (section S3 H of the Supporting Material). A similar configuration was observed during simulations of assembly and budding of a 12-subunit capsid on a membrane (41), suggesting it is a generic feature of assembly and budding. However, in that work, assembly never proceeded past the partially assembled state for any parameter set on a homogeneous membrane, possibly due to the to the small size of the simulated capsid.

For stronger interactions, we observe complete budding. However, the morphologies of the resulting GP-particles depend on the interaction strength in two ways. First, overly strong interactions (ε_gg > 9.0) drive rapid assembly that can proceed simultaneously along multiple fronts within a shell, leading to the formation of “holey” GP-particles (missing subunits; Fig. 4). This result is consistent with malformed capsids that assemble under strong interactions in bulk simulations (65, 66). Second, for moderate interactions (1.6 < ε_gg < 9.0), the shells are complete, with locally hexagonal packing and 12 fivefold disclinations. However, they are asymmetric, with sizes ranging over 95–140 subunits depending on the interaction strength. The origin of this polymorphism is discussed later in this section.

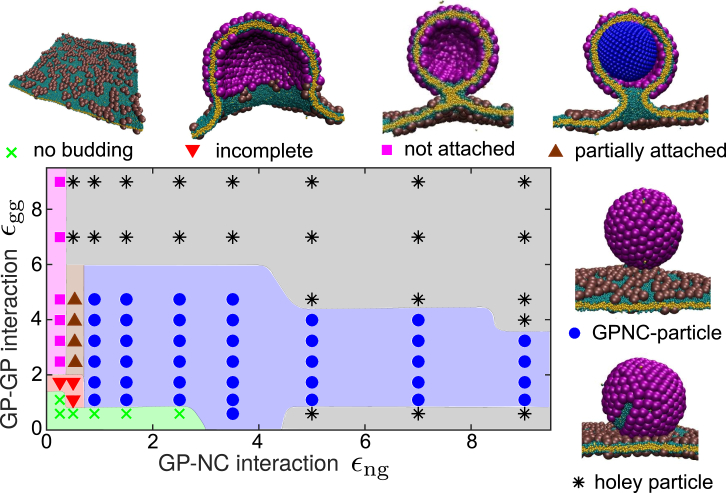
Nucleocapsid-directed budding leads to more monodisperse particles

The predominant end-products of assembly in the presence of an NC are shown in Fig. 5 as a function of the two interaction parameters: GP-GP (ε_gg) and NC-GP (ε_ng). We observe complete assembly and budding for ε_ng > 0.9 and 1 ≤ ε_gg ≤ 6 (Fig. 5, blue region), low to moderate GP-GP interactions. Compared to the GP-directed pathway, the presence of an NC allows assembly to occur at a lower ε_gg as evidenced by obtaining complete shells even for ε_gg as low as 0.9. These particles are usually not perfectly symmetric, containing 81–83 GP subunits. Outside of this range, several other end-products arise. For ε_ng < 0.4 (Fig. 5, pink region), the NC interactions are sufficiently weak that budding is entirely GP-directed (i.e., GP shells assemble and bud, but not around the NC). In the range 0.4 < ε_ng < 0.9 (Fig. 5, brown region), we observe an intermediate regime in which the NC promotes nucleation but fails to act as a perfect template. The GP shell initially starts assembling on the NC surface, but eventually separates from the surface to form a larger shell due to the effect of membrane rigidity (see next section). The result is an asymmetric shell that is partially attached to the NC; with a typical size of 95 subunits, it is smaller than a GP-particle but considerably larger than the intrinsic preferred shell size. These two assembly outcomes (GP shells partially attached or unattached to the NC) demonstrate that the presence of a NC does not necessarily imply NC-directed budding; there is a minimum NC-GP interaction strength required for the NC to direct the assembly and budding pathway.

Figure 5.

Predominant end-products of the NC-directed budding, as a function of the NC-subunit interaction ε_ng and the subunit-subunit interaction ε_gg, and snapshots showing representative examples of each outcome. To see this figure in color, go online.

Strong GP-GP interactions (ε_gg > 6; Fig. 5, upper gray region) lead to holey particles. This result can be explained as in the case of holey GP-particles described above; however, notice that the threshold value of ε_gg is smaller than in the absence of the NC (ε_gg = 9). Interestingly, we also observe holey GPNC-particles when strong NC-GP interactions are combined with weak GP-GP interactions (ε_gg < 1.0; Fig. 5, lower gray region). In this regime, NC uptake proceeds rapidly, but GP subunits do not associate quickly enough to form a complete shell as budding proceeds.

To further elucidate the interplay between the two interactions, Fig. S8 compares the total energetic contributions from GP-GP and NC-GP interactions for budded GPNC-particles. We see that GP-GP interactions account for the majority of the attractive energy stabilizing the shell, with the NC-GP providing as little as 10–20% of the total energy. These results highlight the delicate balance between GP-GP and NC-GP interactions required to obtain a well-formed GPNC-particle.

Membrane-induced polymorphism

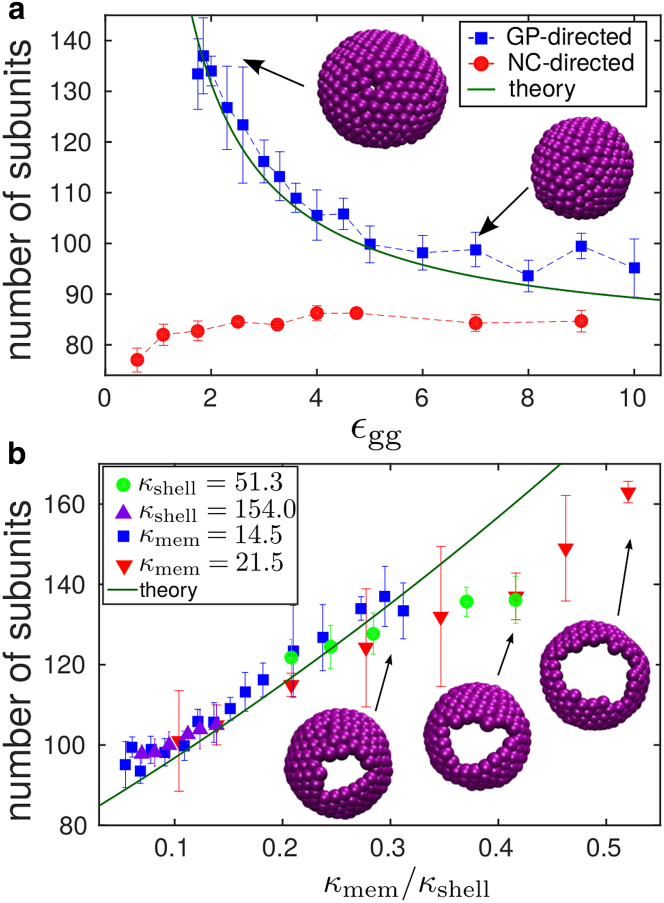
Although both GP-only budding and NC-directed budding lead to the formation of complete particles, the morphology of budded shells significantly differs between both mechanisms. Fig. 6 a shows the mean shell size as a function of interaction strength (averaged over all closed particles). For GP-directed budding, we see a strong dependence of particle size on subunit interactions: weak interactions lead to ovoid particles containing up to 140 trimers. For the weakest interaction strength ε_gg = 1.75, this corresponds to an increase in diameter of d/d_native ≈ 1.6, with d_native the diameter of particles assembled in bulk. As ε_gg increases, particles become smaller and more spherical, more closely resembling the shells that assemble in bulk simulations. We show snapshots of typical GP-shells assembled at weak and strong interactions. On the contrary, the size of GPNC-particles is nearly constant with ε_gg and only slightly larger (81–83 subunits) than the preferred size in bulk simulations.

Figure 6.

(a) Given here is the average number of subunits in budded particles as a function of GP-GP affinity, for GP-directed budding (▪) and NC-directed budding with ε_ng = 4.5 k_BT (●). The solid green line gives the theoretical prediction (Eq. 1) for the estimated capsid rigidity κ_shell = 25.66ε_gg (section S6 in the Supporting Material) and κ_mem 14.5 k_BT. (b) Given here is the average number of subunits in GP-shells as a function of the ratio between membrane and shell bending moduli, κ_mem/κ_shell. The data includes different sets of simulations in which either κ_mem or κ_shell is maintained constant, and we sweep over the other parameter: κ_mem = 14.5 (▪), κ_mem = 21.5 (▪), κ_shell = 51.3 (●), and κ_shell = 154.0 (▲). The theoretical prediction (Eq. 1) is shown as a solid green line. To see this figure in color, go online.

A theoretical model for membrane-induced polymorphism

Although shell assembly is necessarily out-of-equilibrium in finite-length simulations, we can understand the dependence of size on interaction strength from a simple equilibrium model that uses the Helfrich model (67) to account for the elastic energy associated with membrane deformation (which has no spontaneous curvature and thus favors flat configurations) and deviation of the GP shell from its preferred curvature. The calculation is detailed in section S2 of the Supporting Material. Minimizing the total free energy for a system with fixed number of GP subunits obtains that the most probable number of subunits in a shell n corresponds to the value that minimizes the elastic energy per subunit, given by

$$n=n_0{\left(1+\frac{{\kappa }_{\text{mem}}}{{\kappa }_{\text{shell}}}\right)}^2,$$ (1)

where n₀ is the number of subunits in the equilibrium configuration in the absence of a membrane (n₀ = 80 in our model), and κ_mem and κ_shell are the membrane and shell bending moduli. Thus, the preferred GP-particle size is determined by the ratio κ_mem/κ_shell, which quantifies the competition between the membrane and shell deformation energies. Only in the limit where the shell rigidity dominates, κ_mem/κ_shell → 0, will GP-particles exhibit the size observed in bulk simulations.

To compare the theoretical estimate to the shell sizes observed in simulations, we estimated the relationship between the GP interaction strength and the shell bending modulus as κ_shell ≈ 25.66ε_gg (we show the complete derivation in section S6 of the Supporting Material). This leads to a range of shell bending rigidities of ≈40–250 k_BT. This range coincides with bending rigidity values measured in AFM experiments on virus capsids (see the Discussion) (68, 69, 70). The prediction of Eq. 1 using this estimate and the estimated membrane rigidity κ_mem = 14.5 k_BT is shown in Fig. 6 a. The prediction is also compared against simulated particle sizes as a function of the parameter κ_mem/κ_shell for different membrane bending rigidities in Fig. 6 b. For moderate values of κ_mem/κ_shell we observe good agreement between the theory and simulation results, especially considering that there is no fit parameter. The agreement breaks down for κ_mem/κ_shell $\mathrm{\gtrsim }$ 0.3, likely for three reasons. First, our theory assumes a closed GP shell, whereas the size of the incomplete region of the GP shell increases in size with κ_mem/κ_shell, as illustrated by the snapshots in Fig. 6 b. Second, subunits within the largest GP particles are far from their preferred interaction angle, and thus their elastic response could be nonlinear. Third, finite-size effects could become nonnegligible for the largest buds.

In contrast to GP-directed assembly, Figs. 4 and 5 demonstrate that an NC can dramatically change the morphology of a GP shell by acting as a template over a broad range of interaction strengths. The observed monodispersity in GPNC-particles can be understood from Eq. 1 by noting that the NC is modeled as a perfectly rigid sphere in our simulations, and thus corresponds to the limit κ_shell → ∞ if it acts as a perfect template for the GP shell. The relevance of this approximation to enveloped viruses is considered in the Conclusions.

The nucleocapsid influences timescales for late-stage budding

Direct inference of assembly dynamics and timescales from our simulations is complicated by the fact that the coarse-grained models for the proteins and the membrane may have different coarse-grained timescales. However, comparing assembly dynamics in the presence and absence of the NC can still reveal qualitative information about its effect on assembly timescales. As noted above, assembly can be divided into two stages. In the initial stage, the shell grows rapidly until ∼2/3 completion; then in the second stage, neck curvature significantly slows subunit association (Fig. 7). The timescale for the second stage depends on the interaction parameters and whether an NC is present—for the small GPNC-particles assembly is completed quickly at ∼450τ₀, whereas in the large GP-particles with the broadest necks it may require up to 3000τ₀. In contrast, the timescale for the first stage is almost independent of interaction strengths and the NC, and depends only weakly on the membrane bending modulus. Furthermore, as shown in section S4 of the Supporting Material, conformational switching is not rate limiting—implying that assembly rates during the first stage are limited by subunit diffusion.

This observation parallels models for clathrin-independent receptor-mediated endocytosis, in which the endocytosis timescale is estimated from the time required for membrane receptors to diffuse to the enveloped particle (71, 72). Applying the same analysis to our simulations, the timescale for GPs to diffuse to the budding site is given by τ ∼ l²/D, with D_sub = σ²/τ₀ as the GP diffusion constant in our simulations, and l ≈ 45σ as the radius of the region around the budding site initially containing 80 trimers, enough to envelop the particle. This estimate yields ∼2400τ₀, which is reasonably close to the typical timescale for stage 1 observed in the simulations, ∼1000τ₀. Note that this model does not describe the timescale of the late stage of assembly, because the curved neck region imposes a barrier to subunit diffusion that increases as the particle nears completion.

GP conformational changes avoid kinetic traps

Finally, we note that when subunit conformation changes are not accounted for (i.e., all subunits are in the active state), we observe complete assembly and budding only under a narrow range of interaction strengths for NC-directed budding and not at all for GP-directed budding (see section S4 in the Supporting Material). For most interaction strengths, the simulated densities of GPs led to multiple small aggregates that failed to drive significant membrane deformation. This behavior is indicative of kinetic trapping, known to occur in assembly reactions at high concentrations or binding affinities (73, 74). The ability of an inactive conformation to avoid this trap is consistent with simulations of bulk assembly (59, 60), and the ability of budding to proceed in the presence of high subunit concentrations (when conformational changes are accounted for), which is consistent with the observation of high densities of GPs in the membranes of cells infected with Sindbis virus (75).

Conclusions

Advantages of NC-driven budding

We have described dynamical simulations of the assembly and budding of GPs in the presence and absence of a preassembled NC, and presented phase diagrams showing how assembly pathways and products depend on the relevant interaction parameters. The key difference between NC-directed and GP-directed budding identified by our results is variability of the budded particle size and morphology. The presence of the core directs the morphology of the particle, which may have direct consequences on particle stability during transmission and the conformational changes that occur during particle entry into a new host cell. The number of GPs in GP-particles (containing no NC) varies by >50% over the range of interaction parameters in which we observe successful budding, in comparison to a variation of <5% for GPNC-particles (containing an NC). A simple equilibrium model accounting for the competition between the energy costs associated with membrane deformation and deviation of the GP shell from its preferred curvature was qualitatively consistent with the simulation results. The membrane bending energy favors formation of larger particles, whereas a higher bending rigidity of the GP shell favors smaller particles. This prediction applies to any form of assembly on a fluid membrane, and thus is relevant to capsid-directed budding as well as the GP-directed budding studied here.

It is worth considering this observation in the context of recent experimental observations on budding in the absence of an NC, as well as experimental measurements on viral particle elastic properties. Several experimental studies have reported GP-directed budding from cells in which the NC proteins are impaired (18, 19). In particular, Ruiz-Guillen et al. (19) recently showed that cells expressing the genome and GPs, but not the capsid protein, for Sindbis and Semliki Forest virus generate infectious viral particles that can propagate in mammalian cells. For the wild-type virus, in which the GPs assemble around the NC, they estimated a virion diameter of 60–70 nm, whereas the GP-only particles were typically 100–150 nm. This size increase corresponds to the range d/d_native ∼ 1.5–2.15, consistent with our simulations and theoretical model, suggesting that the relatively low rigidity of the GP shell leads to the formation of large particles. However, there are two important caveats to this interpretation. First, the bending rigidity of the alphavirus GP shell has not been measured, so we cannot directly predict the increase in particle size. Second, our model assumes that the preferred curvature of the GP shell is commensurate with its size in a wild-type virion, for which there is no direct evidence. A recent study of herpes simplex virus nuclear egress complex (NEC), which consists of two viral envelope proteins, found that NEC particles budded in the absence of capsid are smaller than native viral particles (76). In our model, this observation would require that the intrinsic spontaneous curvature radius of the NEC complex is smaller than that of the capsid, as suggested by the authors (76).

In contrast to the ability of particles to bud in the absence of NC-GP interactions, Byrd and Kielian (77) recently showed that impairing the GP-GP interactions in Semliki Forest virus strongly suppressed budding. Comparison with our phase diagram (Fig. 5) suggests that this result places an upper bound on the strength of NC-GP interactions (ε_ng $\mathrm{\lesssim }$ 2.5 in our system, but this value would depend on the concentration of GPs and the membrane). In a simulation study (published after the initial version of this article appeared), Pak et al. (78) found that heterogeneous nucleation by the RNA can regulate HIV assembly and budding. We observe that the NC can have a similar affect in our system, particularly in the absence of subunit switching between active and inactive conformations (Fig. S3).

Requirement for scission machinery

A second commonality between the two scenarios investigated is that assembly slows down considerably after the GP shell reaches ∼2/3 completion, because the high negative Gaussian curvature of the neck region imposes a barrier to subunit diffusion. For weak interactions, this leads to a long-lived partially budded state. For stronger interactions budding eventually completes, but completion of the shell can be preempted by scission. Because spontaneous scission is a rare event, most viruses actively drive scission by either recruiting host cell machinery, such as the ESCRT protein complex in the case of HIV (79), or encoding their own machinery, such as the M2 protein in Influenza (80). In alphaviruses specifically, the scission machinery has not been identified, though it is known that alphavirus budding is independent of ESCRT proteins (81). Although in this article we do not consider the action of these scission-inducing mechanisms, our observation of a slowdown of assembly rates due to neck curvature could be relevant to HIV budding. If the association rate becomes sufficiently slow, ESCRT-directed scission will occur before assembly completes, leaving up to 40% of the shell incomplete, as is observed for immature HIV virions (42, 43). In support of this possibility, we note that although scission is a rare event in our simulations because there is no ESCRT, it usually occurs before the final 1–3 subunits assemble, causing the budded particle to have a small hole at the scission site.

Virus elasticity and GP spontaneous curvature affect budding morphology

Because Fig. 4 suggests that the elastic properties of the different viral components are key determinants of the assembly product, it is worth considering the validity of the model parameters. The mechanical properties of viruses have been extensively studied using AFM indentation (68, 69) and fluctuation spectrum analysis (70). Typical estimates lie within the range κ = 30–400 k_BT, with considerable variation depending on the specific virus and experimental technique. A recent work by Schaap et al. (54) explicitly compared the stiffness of the capsid protein coat of influenza virus with that of a lipid membrane, by AFM indentation of similarly sized particles, with the goal of identifying the contribution of the matrix proteins to the virus stiffness. They found that matrix coats are ∼10 times stiffer than bare membranes, κ_mem/κ_shell ∼ 0.1. This value lies within the range explored in our simulations. Similarly, Kol et al. (55) investigated the effect of HIV maturation on its mechanical properties. The immature HIV particle consists of a gag polyprotein capsid surrounded by a lipid bilayer containing viral envelope proteins. During maturation, the NC and capsid portions of gag are cleaved, leaving only a thin matrix layer and the envelope proteins in contact with the bilayer. Kol et al. (55) found that this cleavage softens the particles by an order of magnitude, suggesting that interprotein contacts of the underlying capsid layer are necessary for the high rigidity of immature virions.

Finally, we note that the membrane elasticity properties also play a role in determining particle morphology. Depending on the virus family and host cell type, enveloped viral particles bud through different cellular membranes (the plasma membrane, the ER, the ERGIC, or the nuclear membrane), all of which have different lipid compositions and thus different bending properties. Moreover, many viruses create and/or exploit membrane microdomains with different compositions (such as lipid rafts) as preferential locations for budding (8, 82, 83). The effect of inhomogeneous membrane elastic properties on particle morphology thus deserves further exploration. Although these ingredients can be incorporated into the model, the results described here demonstrate that the interplay among the elastic properties of membranes and viral proteins and the presence of an interior core can shape the morphology of a budding particle.

Author Contributions

All authors conceived and designed the project. G.R.L. designed the computational model, performed the simulations, and analyzed the simulation data. M.F.H. developed the theoretical model. All authors wrote the manuscript.

Editor: Ana-Suncana Smith.

Supporting Citations

References (84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94) appear in the Supporting Material.

Supporting Material

Movie S1. Animation of a Typical Simulation Showing GP-Directed Budding, for ε_gg = 2.5 and κ_mem = 14.5 k_BT

GPs, magenta; membrane headgroups, cyan; membrane tails, yellow. To show the membrane neck geometry more clearly, the inactive subunits are rendered invisible in this animation.

Movie S2. Same Simulation Trajectory as in Movie S1, But Rendered to Show a Central Cross Section of the Budding Shell and the Membrane

Inactive subunits are rendered brown in this animation.

Movie S3. Animation of a Typical Simulation Showing NC-Directed Budding, for ε_gg = 2.5, ε_ng = 3.5, and κ_mem = 14.5 k_BT

Colors are as in Movie S1, and the NC is colored blue. To show the membrane neck geometry more clearly, we do not show inactive subunits in this animation.

Movie S4. Same Simulation Trajectory as in Movie S3, But Rendered to Show a Central Cross Section of the NC-Directed Budding

Inactive subunits are shown in brown in this animation.