Orientations of Cells on Compliant Substrates under Biaxial Stretches: A Theoretical Study

Abstract

Mechanical cues from the microenvironments play a regulating role in many physiological and pathological processes, such as stem cell differentiation and cancer cell metastasis. Experiments showed that cells adhered on a compliant substrate may change orientation with an externally applied strain in the substrate. By accounting for actin polymerization, actin retrograde flow, and integrin binding dynamics, here we develop a mechanism-based tensegrity model to study the orientations of polarized cells on a compliant substrate under biaxial stretches. We show that the cell can actively regulate its mechanical state by generating different traction force levels along its polarized direction. Under static or ultralow-frequency cyclic stretches, stretching a softer substrate leads to a higher increase in the traction force and induces a narrower distribution of cell alignment. Compared to static loadings, high-frequency cyclic loadings have a more significant influence on cell reorientation on a stiff substrate. In addition, the width of the cellular angular distribution scales inversely with the stretch amplitude under both static and cyclic stretches. Our results are in agreement with a wide range of experimental observations, and provide fundamental insights into the functioning of cellular mechanosensing systems.

Introduction

The structures, functions, and fates of living cells are subtly regulated by both biochemical compositions and physical properties of the extracellular matrix (1, 2, 3, 4). There is increasing evidence that mechanical microenvironments play a crucial role in the biological processes of cells and their aggregates, e.g., angiogenesis, differentiation, tissue development, and wound healing (5, 6, 7, 8). Many experiments have demonstrated that cells form strong and stable focal adhesions (FAs) on stiff substrates, but weak and dynamic adhesions on soft ones (1), and that cell motion can be guided by the gradient of substrate stiffness (9).

Under physiological conditions (e.g., heart beating, pulsating blood vessels, and breathing), cells are exposed to various substrates under cyclic stretches. It has been shown that cells adhered on a substrate subjected to cyclic stretches can reorient from random orientations to a well-defined angle, depending on the stretch frequency and amplitude (10, 11, 12, 13, 14). Under uniaxial cyclic strains, cells align nearly perpendicular to the loading direction at high frequencies (∼1 Hz) (10, 11). Under biaxial cyclic strains, Livne et al. (14) showed that the most stable cellular orientation can be quantitatively determined by two parameters: the biaxial stretching ratio and the elastic anisotropy index of cells. It was then totally surprising to see that cells exposed to soft collagen gels align themselves parallel to the stretch direction even at high frequencies (15).

These experimental findings pose substantial challenges to theoretical efforts aimed to understand the fundamental mechanisms of cell reorientation under stretching (16, 17, 18, 19, 20, 21). Safran and co-workers (16, 17, 18) developed a force dipole model, in which the cell maintains its minimal stress or strain state under cyclic stretching. Livne et al.'s experimental data has been interpreted by a passively stored elastic energy model (14) or a 2D tensegrity model (21). Chen et al. (19) and Kong et al. (20) examined the binding dynamics of integrins under cyclic loadings and pointed out that the FAs may lose stability under high-frequency loadings. Interestingly, this molecular level model (19) can also reproduce the experimental phenomena of Livne et al.

In contrast to the above studies under cyclic stretches, the cellular responses to static or quasi-static stretches are less understood (22). It remains puzzling why cells exhibit distinct modes by aligning themselves randomly (12) or parallel to the stretching direction (23, 24, 25, 26) under different static strains. Interestingly, the distributions of cellular orientations under static stretches (23, 24, 25, 26) are generally broader than those under cyclic stretches (10, 11, 12, 13, 14). Goli-Malekabadi et al. (27) showed that static stretching is not as influential as dynamic stretching to direct cell reorientation. To date, however, it remains unclear how to integrate the biochemical and mechanical mechanisms that underlie the local dynamics of FAs into a theoretical model at the cellular level. In addition, the previous models for cell reorientation have not accounted for the effect of substrate stiffness on cellular alignment under different loading conditions.

In this article, we develop a mechanism-based tensegrity model, by incorporating the molecular mechanisms of FA dynamics, the actin polymerization and the actin retrograde flow, to investigate the orientations of polarized cells on compliant substrates under different loading conditions. Our analysis shows that stretching the substrate will align cells parallel to the tensile direction but has negligible effects for very stiff substrates under static or ultralow-frequency cyclic stretches. Furthermore, the width of cellular angular distribution scales inversely with the strain amplitude for both static and cyclic strains, whereas cyclic loading is more effective than static loading in directing cell reorientation on a stiff substrate. Compared to other existing models in the literature, our present model is more complete, integrates all known molecular mechanisms, and yields results in good agreement with a broad range of experimental observations.

Materials and Methods

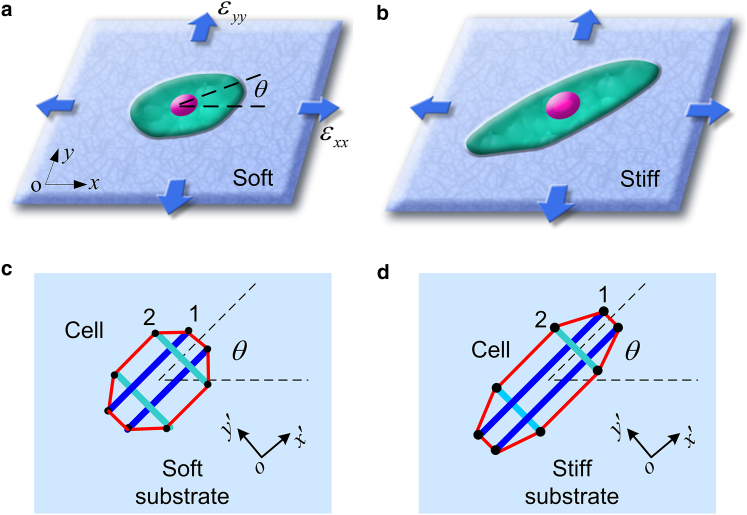
Consider a cell adhering on an elastic substrate subjected to biaxial, either static or cyclic, stretches. Fig. 1, a and b illustrate a polarized cell on a soft and a stiff substrate, respectively, recognizing the fact that substrate elasticity can remarkably affect cellular polarization (28, 29). Chen et al. (19) and Kong et al. (20) have used a simplified model, consisting of only two FAs and a single SF, to explain the experimental results of cell orientations under cyclic stretches. Ingber et al. (30) demonstrated that the cytoskeleton can be well described as a tensegrity. Here, we model the cell as a planar tensegrity structure consisting of four bars and eight strings; see Fig. 1, c and d. The direction of the cell’s long axis corresponds to the orientation of stress fibers (SFs) (13, 14) that are modeled as long bars in the tensegrity. In the lateral direction, the short bars, acting as the lateral support of the cytoskeleton, represent the contributions from microtubules and other biopolymer elements (31) perpendicular to the SF orientation. The strings represent actin microfilaments, which ensure the integrity of the entire cellular structure. At the ends of bars, FAs made of integrins at the cell-substrate interface provide the cellular traction force. As the substrate is stretched, the actins within the cell and the integrins at the cell-substrate interface would reorganize in response to the externally applied mechanical stimuli. In the following, we first investigate the rigidity-dependent dynamics of FAs, then describe the dynamical response of SFs, and finally present the free energy variation of the system under biaxial stretches.

Figure 1.

Schematic of a polarized cell adhered on (a) a soft or (b) a stiff substrate subjected to biaxial strains ε_xx and ε_yy. The cell is oriented at angle θ measured from the x direction. The tensegrity model, capturing the essential cell structure on (c) soft or (d) stiff substrates, consists of four bars, corresponding to the longitudinal SFs and lateral supports of the cytoskeleton, and eight strings, representing the microfilaments. To see this figure in color, go online.

Substrate stiffness-dependent traction forces of FAs

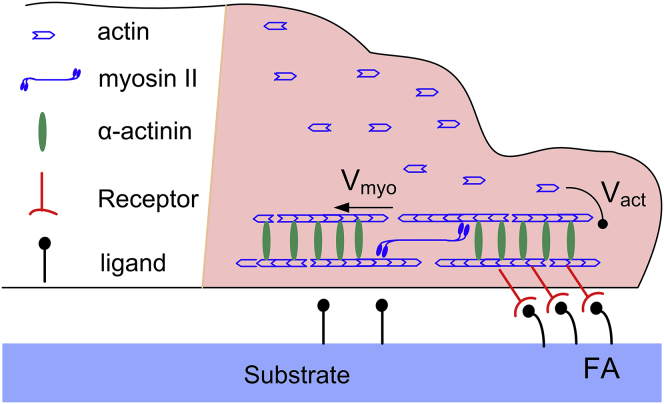
The extension and contraction of the polarized long bars are controlled by the collective dynamics of adhesion bonds (i.e., integrins), nonmuscle myosin II, and actins, as illustrated in Fig. 2. The mobility velocity V = V_act – V_myo of the cell front is dictated by two simultaneous and oppositely directed mechanisms: actin polymerization with a speed V_act, and actin retrograde flow with a speed V_myo caused by myosin motors. Experiments showed that at deceleration of cell spreading, the retrograde flow velocity V_myo increases, whereas the sum V_myo + V remains constant (32). Similar behaviors have been found in growth cone advancement (33, 34) and filopodia growth (35). Accordingly, V_act remains constant along the polarized direction in this study, as in a previous model for cell spreading (36).

Figure 2.

Schematic of major elements of the mechanosensing device at the front of a polarized cell. Actin polymerization occurs at the cell front. The sarcomeric unit of an SF includes actin filaments, myosin II motors, and cross-linker (α-actinin) proteins. The myosin II motors provide the contractive force with a retrograde flow velocity V_myo of actins. The relative movement of actin filaments and FAs generates a cell-substrate tangential force that can be determined by the binding dynamics of the receptors (i.e., integrins) and their complementary ligands. To see this figure in color, go online.

The retrograde flow of the actin network can induce local displacements of adhesion bonds in FAs at the cell-substrate interface. Based on the experimental observation of continuous actin retrograde flow (32, 37), the bonds in FAs can collectively give rise to a tangential force, also referred to as the traction force, at the cell-substrate interface. Let s denote the sum of the tangential stretching displacement of the bond and the displacement of the elastic substrate. The probability density function n(s,t) is related to the retrograde speed V_myo by (36, 38, 39)

$$\frac{\partial n}{\partial t}+V_{\text{myo}}\frac{\partial n}{\partial s}={\xi }_b\left(1-{\int }_0^{\infty }n\text{d}s\right)-{\xi }_{u}n,$$ (1)

where ξ_b and ξ_u are the integrin binding and unbind rate functions, respectively. The solution of Eq. 1 at steady state is

$$n\left(s\right)=\frac{\exp \left[-\frac{1}{V_{\text{myo}}}{\int }_0^s{\xi }_u\left(s^{\prime }\right)d{s}^{\prime }\right]}{\frac{V_{\text{myo}}}{{\xi }_b}+{\int }_0^{\infty }\exp \left[-\frac{1}{V_{\text{myo}}}{\int }_0^s{\xi }_u\left(s^{\prime }\right)d{s}^{\prime }\right]ds}.$$ (2)

For simplicity, we assume the unbinding rate ξ_u is constant. Let N₀ denote the total number of integrins associated within the focal adhesions. The number of bound integrins is $N_b=N_0{\int }_0^{\infty }n\left(s\right)ds=N_0{\xi }_b/\left({\xi }_b+{\xi }_u\right)$. The first and second moments of the tangential deformation s are written as

$$\langle s\rangle =\frac{{\int }_0^{\infty }{N}_{0}sn\left(s\right)ds}{N_b}=\frac{V_{\text{myo}}}{{\xi }_u},$$ (3)

$$\langle s^2\rangle =\frac{{\int }_0^{\infty }{N}_0{s}^{2}n\left(s\right)ds}{N_b}=\frac{2V_{\text{myo}}^2}{{\xi }_u^2}.$$ (4)

The tangential force between the FA and substrate is given by $f_{\text{fa}}=N_b{k}_{\text{int}}\langle s\rangle =k_{\text{fa}}\langle s\rangle ={\eta }_{\text{fa}}{V}_{\text{myo}}$, where k_fa = N_bk_int can be treated as the spring constant of FAs, k_int being the elasticity of each bond, and ${\eta }_{\text{fa}}=k_{\text{fa}}/{\xi }_u$ is the viscous coefficient resulting from the dynamics of FAs. The elastic energy of one FA is the sum of contributions from all bonds, that is, $u_{\text{fa}}=N_b{k}_{\text{int}}\langle s^2\rangle /2=f_{\text{fa}}\langle s\rangle$.

To account for the effect of the substrate stiffness, we define an effective elastic constant $1/{\overline{k}}_{\text{fa}}=1/k_{\text{fa}}+1/k_{\text{sub}}$ of FAs to describe the elasticity of the FA-substrate system, where k_sub ∝ E_sub with E_sub being the Young’s modulus of the substrate. At the steady state, V_myo = V_act, and the maximum tangential force, i.e., the traction force of FAs, is

$$f_{\text{fa}}^{\max }={\eta }_{\text{fa}}{V}_{\text{act}}=\frac{{\overline{k}}_{\text{fa}}}{{\xi }_u}{V}_{\text{act}}=\frac{k_{\text{fa}}{k}_{\text{sub}}}{k_{\text{fa}}+k_{\text{sub}}}{d}_0,$$ (5)

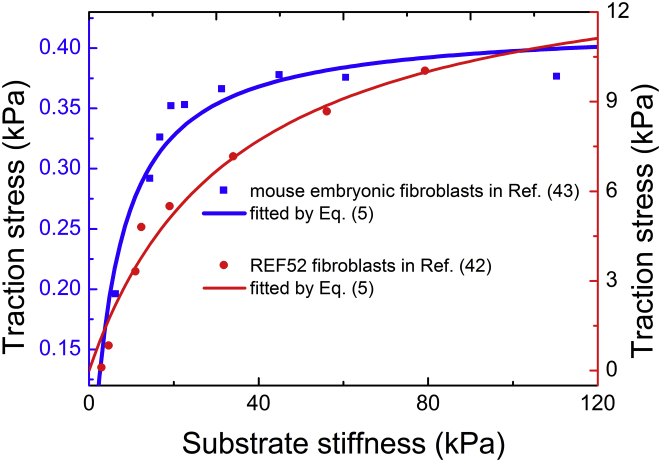
where d₀ = V_act/ξ_u represents an intrinsic length of the cell. Equation 5 shows that cell traction increases monotonously with the substrate stiffness. For softer substrates (k_fa ≫ k_sub), the traction force $f_{\text{fa}}^{\max }\approx k_{\text{sub}}{d}_0$ is proportional to the stiffness k_sub, suggesting that the cell sustains a constant substrate deformation. For stiffer substrates (k_sub ≫ k_fa), the traction force $f_{\text{fa}}^{\max }\approx k_{\text{fa}}{d}_0$ approaches a constant limited by the intrinsic length d₀, indicating that the cell exerts a constant stress on the substrate. This result sheds light on the debate whether the mechanosensing of cells is regulated by deformation or by force (40, 41). Indeed, recent experiments indicate that the cell generates identical deformation on soft substrates, but a constant traction stress on stiff substrates (42, 43). Our results are in perfect agreement with these experimental observations, and can be quantitatively fitted to the data of rigidity-dependent traction forces of FAs, as shown in Fig. 3.

Figure 3.

Traction stress with respect to the substrate stiffness. The theoretical predictions (Eq. 5) fit well with the experimental data reproduced from (43) and (42), respectively. To see this figure in color, go online.

In addition, the integrins within the focal adhesions may form catch bonds (19, 44), whose lifetime increases with the force when it is relatively small. In this case, the unbinding rate could be modeled as ${\xi }_u={\xi }_u^1+\left({\xi }_u^0-{\xi }_u^1\right)e^{-s/s_0}$, where ${\xi }_u^1$, ${\xi }_u^0$, and s₀ are constants. Using this unbinding rate function, Nisenholz et al. (36) showed that the number of bound integrins approaches a constant $N_b=N_0{\xi }_b/\left({\xi }_b+{\xi }_u^1\right)$ and the mean displacement 〈s〉 increases linearly with V_myo at relatively high retrograde speeds. This indicates that the tangential force f_ta = N_bk_int〈s〉 also increases linearly with V_myo, as in the case of a constant unbinding rate. Therefore, our results should hold also for catch bonds.

Dynamics of stress fibers

The dynamics of SFs is regulated by the passive movement of actin filaments and action of myosin II motors. As Kumar et al. (45) reported in their experiments, SFs can be described by a viscoelastic model consisting of a spring of stiffness k_sf, a dashpot of passive viscosity η_sf, and an active contractive force f_myo. These forces are balanced by the traction force f_fa from FAs. Thus, the force balance of SFs is expressed as

$$f_{\text{fa}}=k_{\text{sf}}\Delta L_{\text{sf}}+{\eta }_{\text{sf}}V+f_{\text{myo}},$$ (6)

where ΔL_sf is the length change of SFs and V is the velocity of SFs. The active contractive force f_myo originates from the action of myosin motors. According to Hill’s law (46),

$$f_{\text{myo}}=f_0\left(1-\frac{V_{\text{myo}}}{V_0}\right)=f_0-{\eta }_{\text{myo}}{V}_{\text{myo}},$$ (7)

where f₀ is the stall force of the motors, V₀ is the zero-load speed of the motors, and η_myo = f₀/V₀ represents the active viscosity of motor movements. Using V_myo = V_act − V, Eq. 6 becomes

$$\left({\eta }_{\text{fa}}+{\eta }_{\text{sf}}+{\eta }_{\text{myo}}\right)V+k_{\text{sf}}\Delta L_{\text{sf}}=\left({\eta }_{\text{fa}}+{\eta }_{\text{myo}}\right)V_{\text{act}}-f_0.$$ (8)

Substituting V = dΔL_sf/dt into the above equation leads to

$$L_{\text{sf}}\left(t\right)=L_{\text{ss}}-\left(L_{\text{ss}}-L_0\right)e^{-t/\tau },$$ (9)

where L₀ and $L_{\text{ss}}=\left({\eta }_{\text{fa}}+{\eta }_{\text{myo}}\right)V_{\text{act}}/k_{\text{sf}}-f_0/k_{\text{sf}}$ are the initial and steady lengths of SFs, respectively; and $\tau =\left({\eta }_{\text{fa}}+{\eta }_{\text{sf}}+{\eta }_{\text{myo}}\right)/k_{\text{sf}}$ is a characteristic time of SF depending on the dynamics of adhesion bonds, as well as the passive and active viscosities of SFs.

Free energy in the system under biaxial stretches

In the proposed tensegrity model of a cell, the total free energy $U$ includes the elastic energies of FAs (U_fa) and tensegrity elements (U_ten), as well as the energy of the pulling force (U_pull). The total elastic energy of FAs is written as $U_{\text{fa}}=4{\sum }_{i=1}^2{u}_i$, where u_i represents the elastic energy of each FA, subscripts 1 and 2 standing for the x′ and y′ directions, respectively. In the polarized direction, the cell undergoes active actin polymerization and myosin motor contraction. As described above, the elastic energy u₁ of one FA is the sum of all bonds: $u_1=N_b{k}_{\text{int}}\langle s^2\rangle /2=f_1\langle s\rangle =f_1\Delta l_1$, where f₁ is the traction force and Δl₁ = 〈s〉 is the mean displacement of the bonds. In the lateral direction, we assume the mechanical response of the adhesion connection is passive, i.e., $u_2=k_2\Delta l_2^2/2=f_2^2/2k_2$, where f₂ = k₂Δl₂ denotes the traction force, with k₂ and Δl₂ being the spring constant and length change of FAs, respectively. The work done by the traction force is $U_{\text{pull}}=-2f_1\Delta L_{x^{\prime }}-2f_2\Delta L_{y^{\prime }}$, where ΔL_x′ and ΔL_y′ are the responding length changes of cell structures. This form is also identified as an important constituent of the thermodynamic state of FAs (47). The elastic potential energy U_ten includes the contributions of all tensegrity elements. The elastic constant of microfilaments, modeled as strings, is much smaller than that of SFs, because both microfilaments and SFs are composed of actin filaments and the former has a much smaller cross-sectional area. Thus, we will neglect the contribution of strings to the free energy in this study. Noting that $\Delta L_{x^{\prime }}=\Delta L_1+2\Delta l_1$ and $\Delta L_{y^{\prime }}=\Delta L_2+2\Delta l_2$, the free energy variation ΔU in the system induced by the biaxial stretches is

$$\Delta U=\sum _{i=1}^2{K}_i\Delta L_i^2+2k_{\text{fa}}\Delta l_2^2-2\Delta f_1\Delta L_1-2\Delta f_2\Delta L_{y^{\prime }},$$ (10)

where K_i and ΔL_i are the spring constant and length change of bars, respectively; and Δf_i is the corresponding change in the traction force. Noticing ΔL_i = Δf_i/K_i, Eq. 10 can be rewritten as

$$\Delta U=-\sum _{i=1}^2\frac{\Delta f_i^2}{K_i}-2\frac{{\left(\Delta f_2\right)}^2}{k_2}\mathrm{or}\Delta U=-\sum _{i=1}^2{K}_i\Delta L_i^2-2k_2\Delta l_2^2.$$ (11)

For convenience, we assume that FAs have the same Young’s modulus E as the long and short bars in the tensegrity (21). Similar analysis can be made when their Young’s moduli are different without changing the main conclusions. Experiments showed that the characteristic size of FAs falls in the range of a few micrometers (14, 41), and the bars are approximately tens of micrometers in length (13, 14). It is known from the relation K = EA/L that k₁ ≫ K₁ and k₂ ≫ K₂. Therefore, Eq. 11 can be simplified as $\Delta U=-{\sum }_{i=1}^2\Delta f_i^2/K_i$ or $\Delta U=-{\sum }_{i=1}^2{K}_i\Delta L_i^2$.

Once the change in the traction force (Δf_i) or the bar length (ΔL_i) has been determined, the most stable cell orientation $\overline{\theta }$ can be determined from the condition ∂ΔU/∂θ = 0. Here, Δf₂ or ΔL₂ is easily calculated from the passive mechanical response of the lateral bars; and Δf₁ or ΔL₁ can be obtained through the active regulation of the cell to its optimal mechanical state in the polarized direction.

Results and Discussion

Orientations of cells under biaxial static stretches

First, consider the case where the substrate is subjected to a biaxial static stretch. As shown in Fig. 1 a, the strains in the x and y directions are denoted as ε_xx = ε₀ and ε_yy = −νε_xx, respectively, where ε₀ is the strain amplitude and ν is the biaxial ratio. The strains in the x′ and y′ directions are ${\epsilon }_{x^{\prime }{x}^{\prime }}={\epsilon }_0\left(co{s}^2\theta -\nu {\sin }^2\theta \right)$ and ${\epsilon }_{y^{\prime }{y}^{\prime }}={\epsilon }_0\left(si{n}^2\theta -\nu co{s}^2\theta \right)$, respectively.

The effective substrate stiffness ${\overline{E}}_{\text{sub}}$ will be increased due to the stretches because of the change of the reference configuration for strain measurement (23). For simplicity, the effective spring constant along the x′ direction is treated as ${\overline{k}}_{\text{sub}}=k_{\text{sub}}\left(1+{\epsilon }_{x^{\prime }{x}^{\prime }}\right)$. In this direction, the cell can actively adjust its traction force in response to the increased stiffness. Then, the change in the traction force due to the increased effective stiffness is

$$\Delta f_1=\left(\frac{k_{\text{fa}}{\overline{k}}_{\text{sub}}}{k_{\text{fa}}+{\overline{k}}_{\text{sub}}}-\frac{k_{\text{fa}}{k}_{\text{sub}}}{k_{\text{fa}}+k_{\text{sub}}}\right)d_0=\frac{k_{\text{fa}}{f}_1{\epsilon }_{x^{\prime }{x}^{\prime }}}{k_{\text{fa}}+k_{\text{sub}}\left(1+{\epsilon }_{x^{\prime }{x}^{\prime }}\right)},$$ (12)

and the length change is ΔL₁ = Δf₁/K₁. One can see that the traction force change Δf₁ depends on the substrate stiffness, the strain amplitude, and the cellular orientation. For softer substrates (k_fa ≫ k_sub), $\Delta f_1\approx f_1{\epsilon }_{x^{\prime }{x}^{\prime }}$ significantly increases with the stretch amplitude, whereas for stiffer substrates (k_sub ≫ k_fa), $\Delta f_1\approx k_{\text{fa}}{f}_1{\epsilon }_{x^{\prime }{x}^{\prime }}/\left[k_{\text{sub}}\left(1+{\epsilon }_{x^{\prime }{x}^{\prime }}\right)\right]$ is very small and could be neglected. In other words, stretching a softer substrate can provide a larger traction force in the tensile direction, whereas stretching a stiffer substrate has no significant effect on the traction force. In the lateral direction, one can calculate $\Delta l_2=K_2\Delta L_{y^{\prime }}/\left(2K_2+k_2\right)$ and $\Delta L_2=k_2\Delta L_{y^{\prime }}/\left(2K_2+k_2\right)$ by using the force balance and displacement constraint conditions. Using Eq. 11 and the initial length L₁ = f₁/K₁, the free energy difference ΔU at orientation θ is

$$\begin{array}{l}\Delta U\left(\theta \right)=-{\left[\frac{k_{\text{fa}}}{k_{\text{fa}}+k_{\text{sub}}\left(1+{\epsilon }_{x^{\prime }{x}^{\prime }}\right)}\right]}^2{K}_1{L}_1^2{\epsilon }_{x^{\prime }{x}^{\prime }}^2-K_2{L}_2^2{\epsilon }_{y^{\prime }{y}^{\prime }}^2\\ \approx -{\left(\frac{k_{\text{fa}}}{k_{\text{fa}}+k_{\text{sub}}}\right)}^2{K}_1{L}_1^2{\epsilon }_0^2{\left({\cos }^2\theta -\nu {\sin }^2\theta \right)}^2-K_2{L}_2^2{\epsilon }_0^2{\left({\sin }^2\theta -\nu {\cos }^2\theta \right)}^2.\end{array}$$ (13)

From ∂ΔU/∂θ = 0, we obtain three possible steady-state orientations: $\overline{\theta }=0$, π/2, and ${\cos }^{-1}\sqrt{({\xi }_{S2}+\nu {\xi }_{S1})/\left(1+\nu \right)\left({\xi }_{S1}+{\xi }_{S2}\right)}$, where ${\xi }_{S1}={K_1{L}_1^2{\epsilon }_0^2{k}_{\text{fa}}^2/\left(k_{\text{fa}}+k_{\text{sub}}\right)}^2$ and ${\xi }_{S2}=K_2{L}_2^2{\epsilon }_0^2$ are defined as the effective stiffnesses of the cell along the two directions under static stretches, respectively. Because the most stable state should have the minimal free energy among the three angles, the steady cellular orientation is determined to be $\overline{\theta }=0$ when ξ_S1 > ξ_S2, and $\overline{\theta }=\pi /2$ otherwise. Because the bar in the polarized direction is much longer than that in the lateral direction (14), we have ξ_S1 > ξ_S2, and the free energy change in the polarized direction plays a dominant role in the total free energy change. Therefore, the cell prefers aligning along the stretching direction (i.e., $\overline{\theta }=0$), as observed in experiments (23, 24, 25, 26). However, on very stiff substrates, the variation in ΔU for different orientations may become too small to induce a preferential alignment of cells. This can explain why cells align randomly on stiff substrates under nearly static stretches in experiments (12).

In addition to the stretching strain, the Young’s modulus of some collagen substrate materials can increase with stretching (48, 49), a phenomenon known as strain stiffening. For example, the Young’s modulus of actin gels is nearly a constant under small strains but increases with strain following a power law of exponent ∼3/2 once the strain level is above a threshold value (48). Therefore, for this type of substrate, the effective stiffness may significantly increase along the tensile direction, and drive the cell to align along this direction.

In biological environments, cells do not align perfectly in one direction due to stochastic variations. Based on statistical thermodynamics, we know that the frequency of a given cellular orientation in experiments should depend on its free energy difference via

$$P\left(\theta \right)=\frac{e^{-\Delta U\left(\theta \right)/k_{\text{B}}T}\Delta \theta }{{\int }_0^{\pi /2}{e}^{-\Delta U\left(\theta \right)/k_{\text{B}}T}\text{d}\theta },$$ (14)

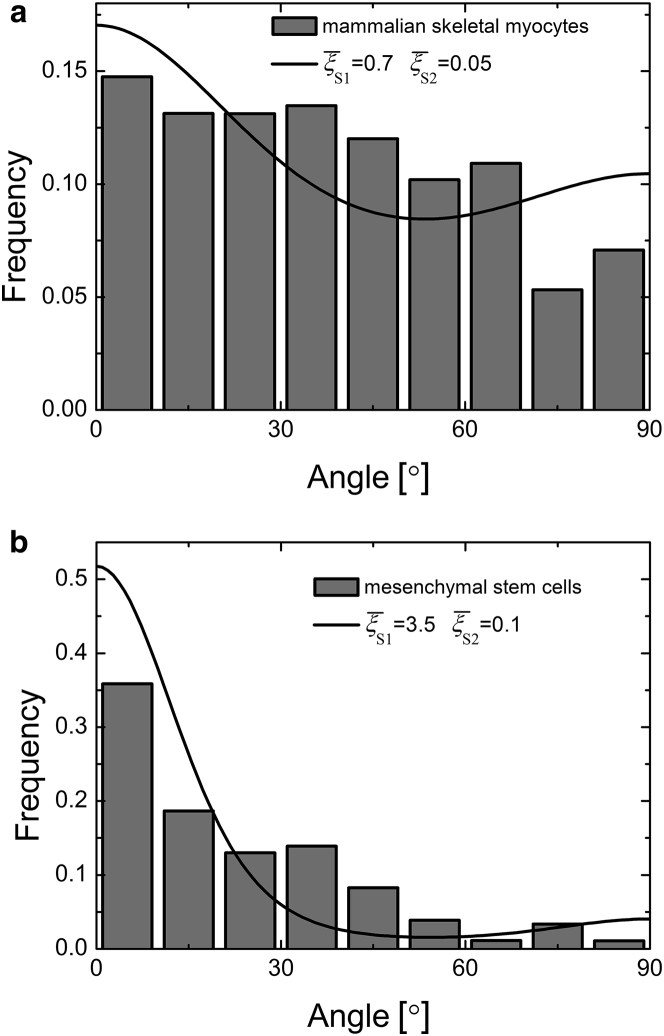
where k_B is the Boltzmann constant, T is the effective temperature, and Δθ is the angle interval used in experimental measurements. To verify this model, we compare our predictions with the experimental data of mammalian skeletal myocytes (26) and mesenchymal stem cells (23) under static stretches, and find a good agreement (Fig. 4). Comparing to Fig. 4 a, cells exhibit a narrower orientational distribution and prefer aligning along a well-defined angle (Fig. 4 b), because the scaled effective stiffness ${\overline{\xi }}_{S1}={\xi }_{S1}/k_{\text{B}}T$ is evidently larger than ${\overline{\xi }}_{S2}={\xi }_{S2}/k_{\text{B}}T$. On the right-hand side of Eq. 13, the two terms represent the energy changes in the polarized and lateral directions, respectively. The contributions from these two directions prefer the orientations θ_S1 = 0 and θ_S2 = π/2, respectively. When the scaled effective stiffness ${\overline{\xi }}_{\text{S}1}$ is much larger than ${\overline{\xi }}_{S2}$, the energy contribution in the polarized direction holds a great weight, and thereby cells are prone to aligning along the tensile direction (i.e., θ = 0) and exhibit a narrow orientational distribution.

Figure 4.

Angular distributions of cells under static stretches. The theoretical predictions (red lines) fit well with the experimental data of (a) mammalian skeletal myocytes (26) and (b) mesenchymal stem cells (23). Here, we have taken the strain amplitude ε₀ = 0.1 and the angle interval Δθ = 10⁰, as in the experiments (23, 26).

To quantitatively examine the scatter distribution of cell orientations, we use an order parameter S to denote the cell alignment:

$$S=\langle \cos 2\theta \rangle ={\int }_0^{\pi /2}P\left(\theta \right)\cos 2\theta \text{d}\theta ,$$ (15)

where θ is the cellular orientation and 〈···〉 denotes its average. Following this definition, S = 0 implies that the cells are randomly orientated; S = 1 and S = −1 correspond to cells aligning parallel and perpendicular to the stretching direction, respectively. Moreover, we describe the width of the angular distribution by its standard deviation

$${\sigma }^2=\langle {\theta }^2\rangle -{\langle \theta \rangle }^2={\int }_0^{\pi /2}P\left(\theta \right){\theta }^2\text{d}\theta -{\left({\int }_0^{\pi /2}P\left(\theta \right)\theta \text{d}\theta \right)}^2.$$ (16)

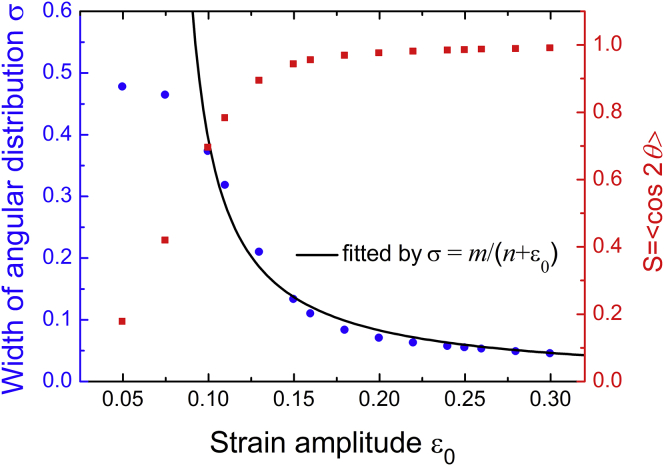
Using the parameters in Fig. 4 b, Fig. 5 plots the order parameter S and the width σ of the distribution as a function of the stretching amplitude ε₀. When ε₀ is small, the effective stiffness ${\overline{\xi }}_{S1}$ is also small. It then follows from Eq. 14 that the angular distribution will be roughly even, meaning that the cells tend to align randomly. With increasing ε₀, the value of S gradually increases and approaches 1, meaning that there are more cells aligning along the stretching direction. This is because the effective stiffness ${\overline{\xi }}_{S1}$ becomes larger and holds more weight in determining the cell alignment. Meanwhile, the width of the angular distribution decreases with ε₀, also indicating that the cells should align around a well-defined orientation under large-amplitude stretches. When ${\overline{\xi }}_{S1}$ is large (e.g., under large strains), the cellular orientations will approximately follow a Gaussian distribution, with the standard deviation σ inversely proportional to the strain amplitude. As shown in Fig. 5, the data for relatively large amplitude values can be fitted well by the function σ = m/(ε₀ + n). This finding suggests that the angular distribution width scales approximately with ${\epsilon }_0^{-1}$ under static stretches.

Figure 5.

Order parameter S = 〈cos2θ〉 (red square) and width σ of the cellular angular distribution (blue round) as a function of the strain amplitude ε₀ under static stretches. The width calculated by Eq. 16 can be fitted well by the function σ = m/(ε₀ + n), indicating that the width scales inversely with the strain amplitude at relatively large strain amplitude. Here, we used the parameters in Fig. 4b. To see this figure in color, go online.

Effects of prestretched substrates on cellular orientations

Most existing experiments focused on the effect of static stretches on cells seeded before stretching. The effect of a prestretch of the substrate has been rarely addressed previously. Recently, Liu et al. (23) observed that prestretched substrates are more effective than poststretched ones to direct cell reorientation. For prestretched substrates, we can calculate the free energy difference as $\Delta U_{\text{pre}}\approx -{\left(1+{\epsilon }_{x^{\prime }{x}^{\prime }}\right)}^2{K}_1{L}_1^2-{\left(1+{\epsilon }_{y^{\prime }{y}^{\prime }}\right)}^2{K}_2{L}_2^2$, where L₁ and L₂ are the longitudinal and lateral lengths, respectively, of cells seeded on the substrate without stretches. Comparing with ΔU_post in Eq. 13 for the poststretched case, ΔU_pre is evidently larger. This result can be understood as follows. For the prestretched case, the effective substrate stiffness is largest at the tensile direction. The cells can sense and respond to the largest substrate stiffness from the initial contact to the steady state. This is different from the poststretched case in which the cells respond to stretching from a random orientation to the steady state. In the former case, the cell will lose more energy, as described in the expression of ΔU_pre. Therefore, for the prestretched substrate, more cells align at the tensile direction, and the angular distribution is much narrower than those in the poststretched case. These predictions are in agreement with relevant experiments (23).

Orientations of cells under biaxial cyclic stretches

In this subsection, we investigate the orientational response of cells under a biaxial cyclic strain with ε_xx = 0.5 ε₀(1 – cos ωt) and ε_yy = −νε_xx, where ε₀ and ω are the strain amplitude and frequency, respectively. If the loading frequency is very low (e.g., ω = 0.0001 Hz), the cell has enough time to actively regulate its deformation and stays in its optimal mechanical state along the polarized direction. In this case, the mechanical response of polarized bars is determined by the traction force varying with the applied strain. Then, the dynamics of SFs can be described by

$${\eta }_1\frac{\text{d}\Delta L_1}{\text{d}t}+K_1\Delta L_1=\frac{k_{\text{fa}}{f}_1}{k_{\text{fa}}+k_{\text{sub}}}{\epsilon }_{x^{\prime }{x}^{\prime }}\left(1-\cos \omega t\right),$$ (17)

where η₁ = η_fa + η_sf + η_myo. The solution is

$$\Delta L_1=\left[\frac{1}{K_1}-\frac{\cos \omega t+\omega /{\omega }_1\sin \omega t+e^{-{\omega }_{1}t}{\omega }^2/{\omega }_1^2}{K_1\left(1+{\omega }^2/{\omega }_1^2\right)}\right]\frac{k_{\text{fa}}{f}_1}{k_{\text{fa}}+k_{\text{sub}}}{\epsilon }_{x^{\prime }{x}^{\prime }},$$ (18)

where ω₁ = K₁/η₁ is the characteristic frequency of the SFs. Note that ΔL₂ can be easily calculated by using the force balance and displacement constraint conditions in the lateral direction. When t → ∞, the free energy change ΔU per period is

$$\Delta U\left(\theta \right)=-{\xi }_{C1}^U{\left({\cos }^2\theta -\nu {\sin }^2\theta \right)}^2-{\xi }_{C2}^U{\left({\sin }^2\theta -\nu {\cos }^2\theta \right)}^2,$$ (19)

where ${\xi }_{C1}^U$ and ${\xi }_{C2}^U$ denote the effective stiffnesses along the two directions under ultralow-frequency cyclic stretches, respectively, as

$${\xi }_{C1}^U=\frac{K_1{L}_1^2{k}_{\text{fa}}^2{\epsilon }_0^2}{4{\left(k_{\text{fa}}+k_{\text{sub}}\right)}^2}\left[2+\frac{1}{1+{\left(\omega /{\omega }_1\right)}^2}\right]\text{and}{\xi }_{C2}^U=\frac{3}{8}{K}_2{L}_2^2{\epsilon }_0^2.$$ (20)

At very low frequencies, we have ${\xi }_{C1}^U=3K_1{L}_1^2{k}_{\text{fa}}^2{\epsilon }_0^2/\left[4{\left(k_{\text{fa}}+k_{\text{sub}}\right)}^2\right]=3{\xi }_{S1}/4$ and ${\xi }_{C2}^U=3{\xi }_{S2}/8$. Similar to the analysis of static stretches, the effective stiffness ${\xi }_{C1}^U$ is larger than ${\xi }_{C2}^U$, and the free energy change is dominated by the change in the polarized direction. Thus, the cell will have the minimal energy along the stretching direction (i.e., $\overline{\theta }=0$).

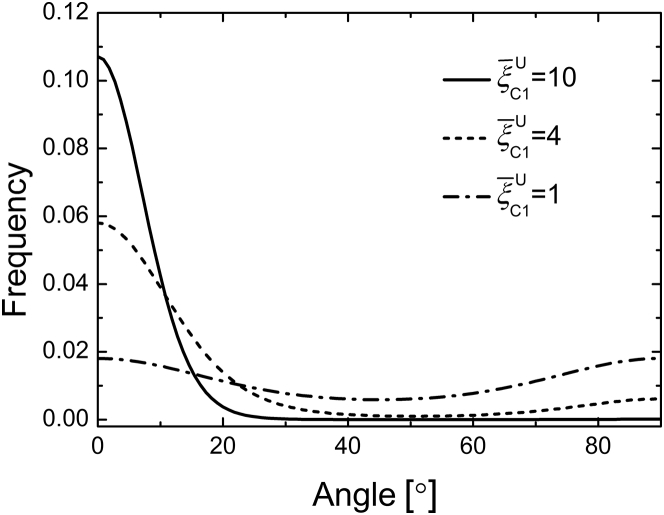
Next, we calculate the angular distributions of cells under different values of scaled effective stiffness ${\overline{\xi }}_{C1}^U={\xi }_{C1}^U/k_{\text{B}}T$ by using Eq. 14 (Fig. 6). Here, we fix ${\overline{\xi }}_{C2}^U={\xi }_{C2}^U/k_{\text{B}}T=1$. It can be seen that as the effective stiffness ${\xi }_{C1}^U$ increases, more cells concentrate along the tensile direction, and meanwhile, the angular distribution becomes narrower. This is because the effective stiffness ${\xi }_{C1}^U$ holds more weight in the orientational distribution and prefers θ = 0. If ${\xi }_{C1}^U$ is small (e.g., on stiff substrates or under small-amplitude stretches), the free energy difference ΔU is small, and thus the angular distribution is quite smooth over all orientations (see Fig. 6), meaning that cells tend to align randomly. This prediction is in agreement with the experiments that cells align randomly on stiff substrates under ultralow-frequency cyclic stretches (12).

Figure 6.

Angular distributions of cells for different scaled effective stiffnesses ${\overline{\xi }}_{C1}^U$ under ultralow-frequency cyclic stretches. The cells concentrate at the stretching direction for a large value of ${\overline{\xi }}_{C1}^U$, whereas they align randomly for a small value of ${\overline{\xi }}_{C1}^U$. Here, we have taken ${\overline{\xi }}_{C1}^U=1$.

At high loading frequencies, the cell does not have enough time to attain its optimal state in the polarized direction and, thus, it undergoes the same deformation extent as the applied displacement in the substrate. In this case, as demonstrated in the previous studies (16, 21), the cell only passively responds to the time average of varying stretches. The free energy difference at different orientations is (21)

$$\Delta U\left(\theta \right)={\xi }_{C1}^H{\left({\cos }^2\theta -\nu {\sin }^2\theta \right)}^2-{\xi }_{C2}^H{\left({\sin }^2\theta -\nu {\cos }^2\theta \right)}^2,$$ (21)

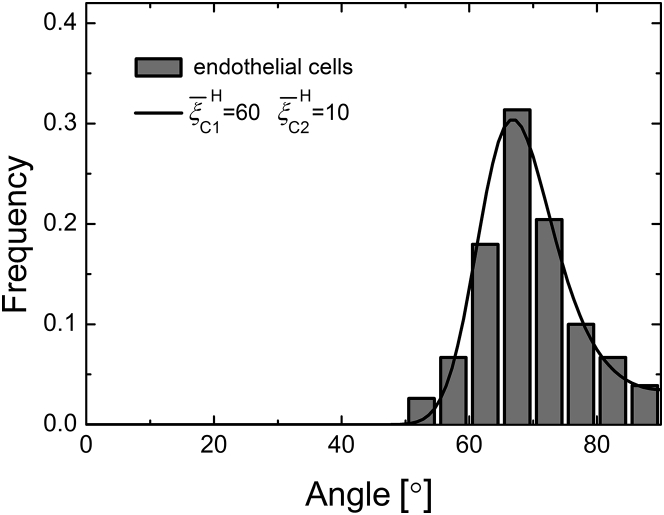
where ${\xi }_{C1}^H={\overline{k}}_{\text{fa}}{L}_1^2{\epsilon }_0^2\left({\overline{k}}_{\text{fa}}-6K_1\right)/\left[16\left({\overline{k}}_{\text{fa}}+2K_1\right)\right]$ and ${\xi }_{C2}^H=3K_2{L}_2^2{\epsilon }_0^2/8$. Using Eqs. 14 and 21, our prediction of the cellular angular distribution agrees well with the experimental results of endothelial cells under high-frequency cyclic stretches (11), as plotted in Fig. 7. It should be emphasized that if the FA-substrate system is stiffer than the SF (e.g., ${\overline{k}}_{\text{fa}}>6K_1$), the first term of ΔU in Eq. 21 is positive, stemming from the oscillating deformations of the polarized bars and the averaging of the external field over a period. The contributions from the longitudinal and lateral directions prefer the orientations ${\theta }_{C1}^H={\tan }^{-1}\left(1/\nu \right)$ and ${\theta }_{C2}^H=\pi /2$, respectively. At high frequencies (∼1 Hz), the most stable orientation is ${\overline{\theta }}_C^H={\cos }^{-1}\sqrt{(\nu {\xi }_{C1}^H-{\xi }_{C2}^H)/\left(1+\nu \right)\left({\xi }_{C1}^H-{\xi }_{C2}^H\right)}$. When ${\xi }_{C1}^H\approx 10{\xi }_{C2}^H$, we can reproduce all experimental data of Livne et al. (14) by this model. Under high-frequency cyclic stretches, the positive energy contribution in the longitudinal direction is different from the negative contributions under static and ultralow-frequency cyclic stretches, which can explain why the most stable orientations are different in these cases.

Figure 7.

Angular distribution of cells under high-frequency cyclic stretches. The theoretical prediction (red lines) fits well with the experimental data of endothelial cells (11). Here, we have taken ε₀ = 0.1 and Δθ = 5⁰, as in the experiments.

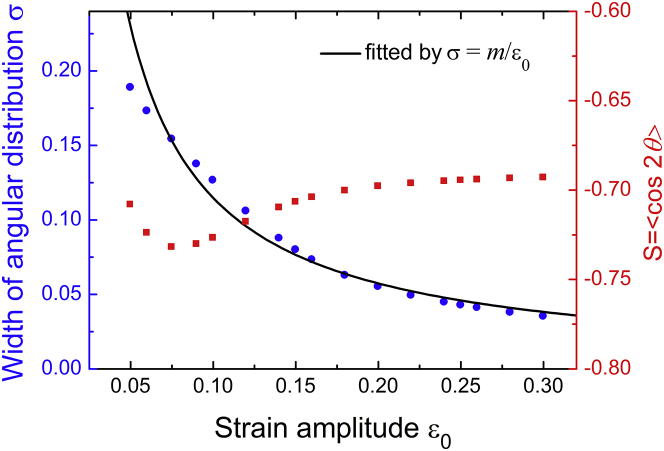
Using the parameters in Fig. 7, Fig. 8 plots the order parameter S and the width σ of the distribution with respect to the stretch amplitude ε₀. It can be seen that the order parameter S varies slightly with the amplitude in the range of 0.05–0.3. The steady orientation in this case is independent of the stretch amplitude (see the expression of ${\overline{\theta }}_C^H$), and the orientational distribution is approximately Gaussian, as shown in Fig. 7. Hence, the order parameter S changes slightly with ε₀. In addition, Fig. 8 shows that the angular distribution becomes narrower with increasing stretch amplitude, because the free energy difference around the most stable orientation ${\overline{\theta }}_C^H$ holds more weight in the orientational distribution. The data of the distribution width can be fitted very well by the function σ = m/ε₀. This finding suggests that the distribution width scales inversely with the loading amplitude ε₀ in the cyclic loading case, as well as in the static loading case.

Figure 8.

Order parameter S = 〈cos2θ 〉 (red square) and width σ of the cell angular distribution (blue round) as a function of the strain amplitude ε₀ under high-frequency cyclic stretches. The width obtained by Eq. 16 can be fitted well by the function σ = m/ε₀, indicating that the width scales inversely with the strain amplitude. Here, we used the parameters in Fig. 7. To see this figure in color, go online.

Comparison between static and cyclic stretches

We now compare the roles of static and cyclic stretches in cell alignment on compliant substrates. For a very soft substrate, the effective elasticity ${\overline{k}}_{\text{fa}}$ of FAs is dominated by the substrate elasticity, which may even be smaller than the elasticity K₁ of SFs. Under cyclic stretches, the contribution to ΔU in Eq. 21 from the longitudinal direction is negative, similar to the case of static stretches. Then, the effective stiffness in the longitudinal direction plays a dominant role in determining the free energy difference, and the cells prefer aligning along the tensile direction, as in the case of static stretch. This result is consistent with experiments of Tondon and Kaunas (15), who observed that cells on soft gels align along the stretching direction even under high-frequency cyclic stretches.

On stiff substrates (k_sub ≫ k_fa), ${\overline{k}}_{\text{fa}}$ is determined by the elasticity of FAs. As discussed in the previous subsection, the energy contributions from the longitudinal direction are positive and negative, respectively, for high-frequency cyclic and static stretches, resulting in different stable orientations in the two cases. Moreover, the longitudinal effective stiffness ${\xi }_{C1}^H=k_{\text{fa}}{L}_1^2{\epsilon }_0^2/16$ under high-frequency cyclic stretches is also much larger than the longitudinal effective stiffness ${\xi }_{S1}=K_1{L}_1^2{\epsilon }_0^2{k}_{\text{fa}}^2/k_{\text{sub}}^2$ under static stretches, although their effective stiffnesses in the lateral direction are comparable. In other words, the free energy change will be significantly larger under high-frequency cyclic stretches than under static stretches. Hence, on a stiff substrate, high-frequency cyclic loadings can more effectively affect cell reorientation than static loadings, and the orientational distribution of cells is much narrower under high-frequency cyclic stretches than under static stretches. These predictions are consistent with the experimental observation that static stretches are not as influential as cyclic stretches at frequency of 1.2 Hz to induce cell reorientation (27). In addition, because the free energy change is smaller under static stretches, our finding also suggests that cells need more time to respond to static loadings.

Conclusions

By incorporating the molecular mechanisms of integrin binding dynamics, actin polymerization, and actin retrograde flow into a cellular tensegrity model, we have investigated the orientational distribution of polarized cells on compliant substrates under biaxial static and cyclic stretches. We show that the cell can actively adjust its mechanical state and generate different traction forces along its polarized direction on substrates of varying rigidities. Under static and ultralow-frequency cyclic stretches, cells prefer aligning along the stretching direction, because the stretched substrates can provide larger traction forces in this direction. The free energy difference becomes smaller on stiffer substrates, whereby the stretching also plays a lesser role. Furthermore, we find that on stiff substrates, the free energy difference under high-frequency cyclic loading is significantly larger than that under static loading, and thus cells exhibit much narrower distributions under high-frequency cyclic stretches. Interestingly, for both static and cyclic loadings, the width of the angular distribution of cells scales inversely with the stretching amplitude. Our present model thus integrates all known molecular mechanisms to explain a wide range of experimental results and to capture the essential features of cellular mechanosensing.

In addition, it should be mentioned that the dynamics (e.g., deadhesion and reformation) of FAs constitutes fundamental molecular mechanisms of cell reorientation. Chen et al. (19, 44) showed that cyclic loadings induce oscillating forces on catch bonds in FAs and can destabilize FAs by reducing the bond lifetime. The resulting sliding and relocation of FAs further cause the SFs to gradually rotate to the most stable orientation with minimal force oscillations. The reorientation process involves complex molecular kinetics of many proteins, which deserves further study.

Author Contributions

G.-K.X., X.-Q.F., and H.G. designed the research. G.-K.X. and X.-Q.F. performed the research. G.-K.X., X.-Q.F., and H.G. analyzed the data and wrote the article.

Editor: Markus Buehler.