Data Programming: Creating Large Training Sets, Quickly

Abstract

Large labeled training sets are the critical building blocks of supervised learning methods and are key enablers of deep learning techniques. For some applications, creating labeled training sets is the most time-consuming and expensive part of applying machine learning. We therefore propose a paradigm for the programmatic creation of training sets called data programming in which users express weak supervision strategies or domain heuristics as labeling functions, which are programs that label subsets of the data, but that are noisy and may conflict. We show that by explicitly representing this training set labeling process as a generative model, we can “denoise” the generated training set, and establish theoretically that we can recover the parameters of these generative models in a handful of settings. We then show how to modify a discriminative loss function to make it noise-aware, and demonstrate our method over a range of discriminative models including logistic regression and LSTMs. Experimentally, on the 2014 TAC-KBP Slot Filling challenge, we show that data programming would have led to a new winning score, and also show that applying data programming to an LSTM model leads to a TAC-KBP score almost 6 F1 points over a state-of-the-art LSTM baseline (and into second place in the competition). Additionally, in initial user studies we observed that data programming may be an easier way for non-experts to create machine learning models when training data is limited or unavailable.

1 Introduction

Many of the major machine learning breakthroughs of the last decade have been catalyzed by the release of a new labeled training dataset.¹ Supervised learning approaches that use such datasets have increasingly become key building blocks of applications throughout science and industry. This trend has also been fueled by the recent empirical success of automated feature generation approaches, notably deep learning methods such as long short term memory (LSTM) networks [14], which ameliorate the burden of feature engineering given large enough labeled training sets. For many real-world applications, however, large hand-labeled training sets do not exist, and are prohibitively expensive to create due to requirements that labelers be experts in the application domain. Furthermore, applications’ needs often change, necessitating new or modified training sets.

To help reduce the cost of training set creation, we propose data programming, a paradigm for the programmatic creation and modeling of training datasets. Data programming provides a simple, unifying framework for weak supervision, in which training labels are noisy and may be from multiple, potentially overlapping sources. In data programming, users encode this weak supervision in the form of labeling functions, which are user-defined programs that each provide a label for some subset of the data, and collectively generate a large but potentially overlapping set of training labels. Many different weak supervision approaches can be expressed as labeling functions, such as strategies which utilize existing knowledge bases (as in distant supervision [22]), model many individual annotator’s labels (as in crowdsourcing), or leverage a combination of domain-specific patterns and dictionaries. Because of this, labeling functions may have widely varying error rates and may conflict on certain data points. To address this, we model the labeling functions as a generative process, which lets us automatically denoise the resulting training set by learning the accuracies of the labeling functions along with their correlation structure. In turn, we use this model of the training set to optimize a stochastic version of the loss function of the discriminative model that we desire to train. We show that, given certain conditions on the labeling functions, our method achieves the same asymptotic scaling as supervised learning methods, but that our scaling depends on the amount of unlabeled data, and uses only a fixed number of labeling functions.

Data programming is in part motivated by the challenges that users faced when applying prior programmatic supervision approaches, and is intended to be a new software engineering paradigm for the creation and management of training sets. For example, consider the scenario when two labeling functions of differing quality and scope overlap and possibly conflict on certain training examples; in prior approaches the user would have to decide which one to use, or how to somehow integrate the signal from both. In data programming, we accomplish this automatically by learning a model of the training set that includes both labeling functions. Additionally, users are often aware of, or able to induce, dependencies between their labeling functions. In data programming, users can provide a dependency graph to indicate, for example, that two labeling functions are similar, or that one “fixes” or “reinforces” another. We describe cases in which we can learn the strength of these dependencies, and for which our generalization is again asymptotically identical to the supervised case.

One further motivation for our method is driven by the observation that users often struggle with selecting features for their models, which is a traditional development bottleneck given fixed-size training sets. However, initial feedback from users suggests that writing labeling functions in the framework of data programming may be easier [12]. While the impact of a feature on end performance is dependent on the training set and on statistical characteristics of the model, a labeling function has a simple and intuitive optimality criterion: that it labels data correctly. Motivated by this, we explore whether we can flip the traditional machine learning development process on its head, having users instead focus on generating training sets large enough to support automatically-generated features.

Summary of Contributions and Outline

Our first contribution is the data programming framework, in which users can implicitly describe a rich generative model for a training set in a more flexible and general way than in previous approaches. In Section 3, we first explore a simple model in which labeling functions are conditionally independent. We show here that under certain conditions, the sample complexity is nearly the same as in the labeled case. In Section 4, we extend our results to more sophisticated data programming models, generalizing related results in crowdsourcing [17]. In Section 5, we validate our approach experimentally on large real-world text relation extraction tasks in genomics, pharmacogenomics and news domains, where we show an average 2.34 point F1 score improvement over a baseline distant supervision approach—including what would have been a new competition-winning score for the 2014 TAC-KBP Slot Filling competition. Using LSTM-generated features, we additionally would have placed second in this competition, achieving a 5.98 point F1 score gain over a state-of-the-art LSTM baseline [32]. Additionally, we describe promising feedback from a usability study with a group of bioinformatics users.

2 Related Work

Our work builds on many previous approaches in machine learning. Distant supervision is one approach for programmatically creating training sets. The canonical example is relation extraction from text, wherein a knowledge base of known relations is heuristically mapped to an input corpus [8,22]. Basic extensions group examples by surrounding textual patterns, and cast the problem as a multiple instance learning one [15,25]. Other extensions model the accuracy of these surrounding textual patterns using a discriminative feature-based model [26], or generative models such as hierarchical topic models [1,27,31]. Like our approach, these latter methods model a generative process of training set creation, however in a proscribed way that is not based on user input as in our approach. There is also a wealth of examples where additional heuristic patterns used to label training data are collected from unlabeled data [7] or directly from users [21,29], in a similar manner to our approach, but without any framework to deal with the fact that said labels are explicitly noisy.

Crowdsourcing is widely used for various machine learning tasks [13,18]. Of particular relevance to our problem setting is the theoretical question of how to model the accuracy of various experts without ground truth available, classically raised in the context of crowdsourcing [10]. More recent results provide formal guarantees even in the absence of labeled data using various approaches [4,9,16,17,24,33]. Our model can capture the basic model of the crowdsourcing setting, and can be considered equivalent in the independent case (Sec. 3). However, in addition to generalizing beyond getting inputs solely from human annotators, we also model user-supplied dependencies between the “labelers” in our model, which is not natural within the context of crowdsourcing. Additionally, while crowdsourcing results focus on the regime of a large number of labelers each labeling a small subset of the data, we consider a small set of labeling functions each labeling a large portion of the dataset.

Co-training is a classic procedure for effectively utilizing both a small amount of labeled data and a large amount of unlabeled data by selecting two conditionally independent views of the data [5]. In addition to not needing a set of labeled data, and allowing for more than two views (labeling functions in our case), our approach allows explicit modeling of dependencies between views, for example allowing observed issues with dependencies between views to be explicitly modeled [19].

Boosting is a well known procedure for combining the output of many “weak” classifiers to create a strong classifier in a supervised setting [28]. Recently, boosting-like methods have been proposed which leverage unlabeled data in addition to labeled data, which is also used to set constraints on the accuracies of the individual classifiers being ensembled [3]. This is similar in spirit to our approach, except that labeled data is not explicitly necessary in ours, and richer dependency structures between our “heuristic” classifiers (labeling functions) are supported.

The general case of learning with noisy labels is treated both in classical [20] and more recent contexts [23]. It has also been studied specifically in the context of label-noise robust logistic regression [6]. We consider the more general scenario where multiple noisy labeling functions can conflict and have dependencies.

3 The Data Programming Paradigm

In many applications, we would like to use machine learning, but we face the following challenges: (i) hand-labeled training data is not available, and is prohibitively expensive to obtain in sufficient quantities as it requires expensive domain expert labelers; (ii) related external knowledge bases are either unavailable or insufficiently specific, precluding a traditional distant supervision or co-training approach; (iii) application specifications are in flux, changing the model we ultimately wish to learn.

In such a setting, we would like a simple, scalable and adaptable approach for supervising a model applicable to our problem. More specifically, we would ideally like our approach to achieve ε expected loss with high probability, given O(1) inputs of some sort from a domain-expert user, rather than the traditional $\stackrel{\sim }{O}({\epsilon }^{-2})$ hand-labeled training examples required by most supervised methods (where $\stackrel{\sim }{O}$ notation hides logarithmic factors). To this end, we propose data programming, a paradigm for the programmatic creation of training sets, which enables domain-experts to more rapidly train machine learning systems and has the potential for this type of scaling of expected loss. In data programming, rather than manually labeling each example, users instead describe the processes by which these points could be labeled by providing a set of heuristic rules called labeling functions.

In the remainder of this paper, we focus on a binary classification task in which we have a distribution π over object and class pairs $(x,y)\in \mathcal{X}\times \{-1,1\}$, and we are concerned with minimizing the logistic loss under a linear model given some features,

$$l(w)={\mathbf{E}}_{(x,y)\sim \pi }\left[\log (1+\exp (-w^{T}f(x)y))\right],$$

where without loss of generality, we assume that ‖ f (x)‖ ≤ 1. Then, a labeling function ${\lambda }_i:\mathcal{X}\mapsto \{-1,0,1\}$ is a user-defined function that encodes some domain heuristic, which provides a (non-zero) label for some subset of the objects. As part of a data programming specification, a user provides some m labeling functions, which we denote in vectorized form as ${\lambda }_i:\mathcal{X}\mapsto {\{-1,0,1\}}^m$.

Example 3.1

To gain intuition about labeling functions, we describe a simple text relation extraction example. In Figure 1, we consider the task of classifying co-occurring gene and disease mentions as either expressing a causal relation or not. For example, given the sentence “Gene A causes disease B”, the object x = (A, B) has true class y = 1. To construct a training set, the user writes three labeling functions (Figure 1a). In λ₁, an external structured knowledge base is used to label a few objects with relatively high accuracy, and is equivalent to a traditional distant supervision rule (see Sec. 2). λ₂ uses a purely heuristic approach to label a much larger number of examples with lower accuracy. Finally, λ₃ is a “hybrid” labeling function, which leverages a knowledge base and a heuristic.

Figure 1.

An example of extracting mentions of gene-disease relations from the scientific literature.

A labeling function need not have perfect accuracy or recall; rather, it represents a pattern that the user wishes to impart to their model and that is easier to encode as a labeling function than as a set of hand-labeled examples. As illustrated in Ex. 3.1, labeling functions can be based on external knowledge bases, libraries or ontologies, can express heuristic patterns, or some hybrid of these types; we see evidence for the existence of such diversity in our experiments (Section 5). The use of labeling functions is also strictly more general than manual annotations, as a manual annotation can always be directly encoded by a labeling function. Importantly, labeling functions can overlap, conflict, and even have dependencies which users can provide as part of the data programming specification (see Section 4); our approach provides a simple framework for these inputs.

Independent Labeling Functions

We first describe a model in which the labeling functions label independently, given the true label class. Under this model, each labeling function λ_i has some probability β_i of labeling an object and then some probability α_i of labeling the object correctly; for simplicity we also assume here that each class has probability 0.5. This model has distribution

$${\mu }_{\alpha ,\beta }(\mathrm{\Lambda },Y)=\frac{1}{2}{\displaystyle \prod _{i=1}^m({\beta }_i{\alpha }_i{\mathbf{1}}_{\{{\mathrm{\Lambda }}_i=Y\}}+{\beta }_i(1-{\alpha }_i){\mathbf{1}}_{\{{\mathrm{\Lambda }}_i=-Y\}}+(1-{\beta }_i){\mathbf{1}}_{\{{\mathrm{\Lambda }}_i=0\}}),}$$ (1)

where Λ ∈ {−1, 0, 1}^m contains the labels output by the labeling functions, and Y ∈ {−1, 1}is the predicted class. If we allow the parameters α ∈ ℝ^m and β ∈ ℝ^m to vary, (1) specifies a family of generative models. In order to expose the scaling of the expected loss as the size of the unlabeled dataset changes, we will assume here that 0.3 ≤ β_i ≤ 0.5 and 0.8 ≤ α_i ≤ 0.9. We note that while these arbitrary constraints can be changed, they are roughly consistent with our applied experience, where users tend to write high-accuracy and high-coverage labeling functions.

Our first goal will be to learn which parameters (α, β) are most consistent with our observations—our unlabeled training set—using maximum likelihood estimation. To do this for a particular training set $S\subset \mathcal{X}$, we will solve the problem

$$(\widehat{\alpha },\widehat{\beta })=\arg \underset{\alpha ,\beta }{max}{\displaystyle \sum _{x\in S}\log }{\mathbf{P}}_{(\mathrm{\Lambda },Y)\sim {\mu }_{\alpha ,\beta }}(\mathrm{\Lambda }=\lambda (x))=\arg \underset{\alpha ,\beta }{max}{\displaystyle \sum _{x\in S}\log }\left({\displaystyle \sum _{y^{\prime }\in \{-1,1\}}{\mu }_{\alpha ,\beta }(\lambda (x),y^{\prime })}\right)$$ (2)

In other words, we are maximizing the probability that the observed labels produced on our training examples occur under the generative model in (1). In our experiments, we use stochastic gradient descent to solve this problem; since this is a standard technique, we defer its analysis to the appendix.

Noise-Aware Empirical Loss

Given that our parameter learning phase has successfully found some $\widehat{\alpha }$ and $\widehat{\beta }$ that accurately describe the training set, we can now proceed to estimate the parameter w which minimizes the expected risk of a linear model over our feature mapping f, given $\widehat{\alpha }$, $\widehat{\beta }$. To do so, we define the noise-aware empirical risk $L_{\widehat{\alpha },\widehat{\beta }}$ with regularization parameter ρ, and compute the noise-aware empirical risk minimizer

$$\widehat{w}=\arg \underset{w}{max}{L}_{\widehat{\alpha },\widehat{\beta }}(w;S)=\arg \underset{w}{max}\frac{1}{\left|S\right|}{\displaystyle \sum _{x\in S}{\mathbf{E}}_{(\mathrm{\Lambda },Y)\sim {\mu }_{\widehat{\alpha },\widehat{\beta }}}}\left[\log \left(1+e^{-w^{T}f(x)Y}\right)|\mathrm{\Lambda }=\lambda (x)\right]+\rho {\Vert w\Vert }^2$$ (3)

This is a logistic regression problem, so it can be solved using stochastic gradient descent as well.

We can in fact prove that stochastic gradient descent running on (2) and (3) is guaranteed to produce accurate estimates, under conditions which we describe now. First, the problem distribution π needs to be accurately modeled by some distribution μ in the family that we are trying to learn. That is, for some α* and β*,

$$\forall \mathrm{\Lambda }\in {\{-1,0,1\}}^m,Y\in \{-1,1\},{\mathbf{P}}_{(x,y)\sim \pi \ast }(\lambda (x)=\mathrm{\Lambda },y=Y)={\mu }_{\alpha \ast ,\beta \ast }(\mathrm{\Lambda },Y).$$ (4)

Second, given an example (x, y) ∼ π*, the class label y must be independent of the features f (x) given the labels λ(x). That is,

$$(x,y)\sim {\pi }^{\ast }\Rightarrow y\perp f(x)|\lambda (x).$$ (5)

This assumption encodes the idea that the labeling functions, while they may be arbitrarily dependent on the features, provide sufficient information to accurately identify the class. Third, we assume that the algorithm used to solve (3) has bounded generalization risk such that for some parameter χ,

$${\mathbf{E}}_{\widehat{w}}\left[{\mathbf{E}}_S\left[L_{\widehat{\alpha },\widehat{\beta }}(\widehat{w};S)\right]-\underset{w}{min}{\mathbf{E}}_S\left[L_{\widehat{\alpha },\widehat{\beta }}(\widehat{w};S)\right]\right]\le \chi .$$ (6)

Under these conditions, we make the following statement about the accuracy of our estimates, which is a simplified version of a theorem that is detailed in the appendix.

Theorem 1

Suppose that we run data programming, solving the problems in (2) and (3) using stochastic gradient descent to produce $(\widehat{\alpha },\widehat{\beta })$ and $\widehat{w}$. Suppose further that our setup satisfies the conditions (4), (5), and (6), and suppose that m ≥ 2000. Then for any ε > 0, if the number of labeling functions m and the size of the input dataset S are large enough that

$$\left|S\right|\ge \frac{356}{{\epsilon }^2}\log \left(\frac{m}{3\epsilon }\right)$$

then our expected parameter error and generalization risk can be bounded by

$$\mathbf{E}\left[{\Vert \widehat{\alpha }-{\alpha }^{\ast }\Vert }^2\right]\le m{\epsilon }^2\mathbf{E}\left[{\Vert \widehat{\beta }-{\beta }^{\ast }\Vert }^2\right]\le m{\epsilon }^2\mathbf{E}\left[l(\widehat{w})-\underset{w}{min}l(w)\right]\le \chi +\frac{\epsilon }{27\rho }.$$

We select m ≥ 2000 to simplify the statement of the theorem and give the reader a feel for how ε scales with respect to |S |. The full theorem with scaling in each parameter (and for arbitrary m) is presented in the appendix. This result establishes that to achieve both expected loss and parameter estimate error ε, it suffices to have only m = O(1) labeling functions and $\left|S\right|=\stackrel{\sim }{O}({\epsilon }^{-2})$ training examples, which is the same asymptotic scaling exhibited by methods that use labeled data. This means that data programming achieves the same learning rate as methods that use labeled data, while requiring asymptotically less work from its users, who need to specify O(1) labeling functions rather than manually label $\stackrel{\sim }{O}({\epsilon }^{-2})$ examples. In contrast, in the crowdsourcing setting [17], the number of workers m tends to infinity while here it is constant while the dataset grows. These results provide some explanation of why our experimental results suggest that a small number of rules with a large unlabeled training set can be effective at even complex natural language processing tasks.

4 Handling Dependencies

In our experience with data programming, we have found that users often write labeling functions that have clear dependencies among them. As more labeling functions are added as the system is developed, an implicit dependency structure arises naturally amongst the labeling functions: modeling these dependencies can in some cases improve accuracy. We describe a method by which the user can specify this dependency knowledge as a dependency graph, and show how the system can use it to produce better parameter estimates.

Label Function Dependency Graph

To support the injection of dependency information into the model, we augment the data programming specification with a label function dependency graph, $G\subset \mathcal{D}\times \{1,\dots m\}\times \{1,\dots m\}$, which is a directed graph over the labeling functions, each of the edges of which is associated with a dependency type from a class of dependencies $\mathcal{D}$ appropriate to the domain. From our experience with practitioners, we identified four commonly-occurring types of dependencies as illustrative examples: similar, fixing, reinforcing, and exclusive (see Figure 2).

Figure 2.

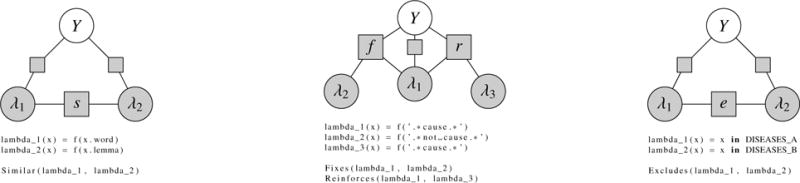
Examples of labeling function dependency predicates.

For example, suppose that we have two functions λ₁ and λ₂, and λ₂ typically labels only when (i) λ₁ also labels, (ii) λ₁ and λ₂ disagree in their labeling, and (iii) λ₂ is actually correct. We call this a fixing dependency, since λ₂ fixes mistakes made by λ₁. If λ₁ and λ₂ were to typically agree rather than disagree, this would be a reinforcing dependency, since λ₂ reinforces a subset of the labels of λ₁.

Modeling Dependencies

The presence of dependency information means that we can no longer model our labels using the simple Bayesian network in (1). Instead, we model our distribution as a factor graph. This standard technique lets us describe the family of generative distributions in terms of a known factor function h: {−1, 0, 1}^m × {−1, 1}↦ {−1, 0, 1}^M (in which each entry h_i represents a factor), and an unknown parameter θ ∈ ℝ^M as

$${\mu }_{\theta }(\mathrm{\Lambda },Y)=Z_{\theta }^{-1}\exp ({\theta }^{T}h(\mathrm{\Lambda },Y)),$$

where Z_θ is the partition function which ensures that μ is a distribution. Next, we will describe how we define h using information from the dependency graph.

To construct h, we will start with some base factors, which we inherit from (1), and then augment them with additional factors representing dependencies. For all i ∈ {1,…, m}, we let

$$h_0(\mathrm{\Lambda },Y)=Y,h_i(\mathrm{\Lambda },Y)={\mathrm{\Lambda }}_{i}Y,h_{m+i}(\mathrm{\Lambda },Y)={\mathrm{\Lambda }}_i,h_{2m+i}(\mathrm{\Lambda },Y)={\mathrm{\Lambda }}_i^{2}Y,h_{3m+i}(\mathrm{\Lambda },Y)={\mathrm{\Lambda }}_i^2.$$

These factors alone are sufficient to describe any distribution for which the labels are mutually independent, given the class: this includes the independent family in (1).

We now proceed by adding additional factors to h, which model the dependencies encoded in G. For each dependency edge (d, i, j), we add one or more factors to h as follows. For a near-duplicate dependency on (i, j), we add a single factor h_ι(Λ, Y) = 1{Λ_i = Λ_j}, which increases our prior probability that the labels will agree. For a fixing dependency, we add two factors, h_ι(Λ, Y) = −1{Λ_i = 0 ∧ Λ_j ≠ 0} and h_ι+1(Λ, Y) = 1 {Λ_i = −Y ˄ Λ_j = Y}, which encode the idea that λ_j labels only when λ_i does, and that λ_j fixes errors made by λ_i. The factors for a reinforcing dependency are the same, except that h_ι+1(Λ, Y) = 1{Λ_i = Y ∧ Λ_j = Y}. Finally, for an exclusive dependency, we have a single factor h_ι(Λ, Y) = −1{Λ_i ≠ 0 ∧ Λ_j ≠ 0}.

Learning with Dependencies

We can again solve a maximum likelihood problem like (2) to learn the parameter $\widehat{\theta }$. Using the results, we can continue on to find the noise-aware empirical loss minimizer by solving the problem in (3). In order to solve these problems in the dependent case, we typically invoke stochastic gradient descent, using Gibbs sampling to sample from the distributions used in the gradient update. Under conditions similar to those in Section 3, we can again provide a bound on the accuracy of these results. We define these conditions now. First, there must be some set Θ ⊂ ℝ^M that we know our parameter lies in. This is analogous to the assumptions on α_i and β_i we made in Section 3, and we can state the following analogue of (4):

$$\exists {\theta }^{\ast }\in \mathrm{\Theta }\mathrm{s}\text{.t}.\forall (\mathrm{\Lambda },Y)\in {\{-1,0,1\}}^m\times \{-1,1\},{\mathbf{P}}_{(x,y)\sim \pi \ast }(\lambda (x)=\mathrm{\Lambda },y=Y)={\mu }_{\theta \ast }(\mathrm{\Lambda },Y).$$ (7)

Second, for any θ ∈ Θ, it must be possible to accurately learn θ from full (i.e. labeled) samples of μ_θ. More specifically, there exists an unbiased estimator $\widehat{\theta }(T)$ that is a function of some dataset T of independent samples from μ_θ such that, for some c > 0 and for all θ ∈ Θ,

$$\mathbf{C}\mathbf{o}\mathbf{v}\left(\widehat{\theta }(T)\right)\le {(2c|T|)}^{-1}I.$$ (8)

Third, for any two feasible models θ₁ and θ₂ ∈ Θ,

$${\mathbf{E}}_{({\mathrm{\Lambda }}_1,Y_1)\sim {\mu }_{{\theta }_1}}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{({\mathrm{\Lambda }}_2,Y_2)\sim {\mu }_{{\theta }_2}}(Y_2|{\mathrm{\Lambda }}_1={\mathrm{\Lambda }}_2)\right]\le c{M}^{-1}.$$ (9)

That is, we’ll usually be reasonably sure in our guess for the value of Y, even if we guess using distribution ${\mu }_{{\theta }_2}$ while the the labeling functions were actually sampled from (the possibly totally different) ${\mu }_{{\theta }_1}$. We can now prove the following result about the accuracy of our estimates.

Theorem 2

Suppose that we run stochastic gradient descent to produce $\widehat{\theta }$ and $\widehat{w}$, and that our setup satisfies the conditions (5)-(9). Then for any ε > 0, if the input dataset S is large enough that

$$\left|S\right|\ge \frac{2}{c^2{\epsilon }^2}\log \left(\frac{2{\Vert {\theta }_0-{\theta }^{\ast }\Vert }^2}{\epsilon }\right),$$

then our expected parameter error and generalization risk can be bounded by

$$\mathbf{E}\left[{\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }^2\right]\le M{\epsilon }^2\mathbf{E}\left[l(\widehat{w})-\underset{w}{min}l(w)\right]\le \chi +\frac{c\epsilon }{2\rho }.$$

As in the independent case, this shows that we need only $\left|S\right|=\stackrel{\sim }{O}({\epsilon }^{-2})$ unlabeled training examples to achieve error O(ε), which is the same asymptotic scaling as supervised learning methods. This suggests that while we pay a computational penalty for richer dependency structures, we are no less statistically efficient. In the appendix, we provide more details, including an explicit description of the algorithm and the step size used to achieve this result.

5 Experiments

We seek to experimentally validate three claims about our approach. Our first claim is that data programming can be an effective paradigm for building high quality machine learning systems, which we test across three real-world relation extraction applications. Our second claim is that data programming can be used successfully in conjunction with automatic feature generation methods, such as LSTM models. Finally, our third claim is that data programming is an intuitive and productive framework for domain-expert users, and we report on our initial user studies.

Relation Mention Extraction

Tasks In the relation mention extraction task, our objects are relation mention candidates x = (e₁, e₂), which are pairs of entity mentions e₁, e₂ in unstructured text, and our goal is to learn a model that classifies each candidate as either a true textual assertion of the relation R(e₁, e₂) or not. We examine a news application from the 2014 TAC-KBP Slot Filling challenge², where we extract relations between real-world entities from articles [2]; a clinical genomics application, where we extract causal relations between genetic mutations and phenotypes from the scientific literature³; and a pharmacogenomics application where we extract interactions between genes, also from the scientific literature [21]; further details are included in the Appendix.

For each application, we or our collaborators originally built a system where a training set was programmatically generated by ordering the labeling functions as a sequence of if-then-return statements, and for each candidate, taking the first label emitted by this script as the training label. We refer to this as the if-then-return (ITR) approach, and note that it often required significant domain expert development time to tune (weeks or more). For this set of experiments, we then used the same labeling function sets within the framework of data programming. For all experiments, we evaluated on a blind hand-labeled evaluation set. In Table 1, we see that we achieve consistent improvements: on average by 2.34 points in F1 score, including what would have been a winning score on the 2014 TAC-KBP challenge [30].

Table 1.

Precision/Recall/F1 scores using data programming (DP), as compared to distant supervision ITR approach, with both hand-tuned and LSTM-generated features.

		KBP (News)			Genomics			Pharmacogenomics
Features	Method	Prec.	Rec.	F1	Prec.	Rec.	F1	Prec.	Rec.	F1
	ITR	51.15	26.72	35.10	83.76	41.67	55.65	68.16	49.32	57.23
Hand-tuned	DP	50.52	29.21	37.02	83.90	43.43	57.24	68.36	54.80	60.83
LSTM	ITR	37.68	28.81	32.66	69.07	50.76	58.52	32.35	43.84	37.23
	DP	47.47	27.88	35.78	75.48	48.48	58.99	37.63	47.95	42.17

We observed these performance gains across applications with very different labeling function sets. We describe the labeling function summary statistics—coverage is the percentage of objects that had at least one label, overlap is the percentage of objects with more than one label, and conflict is the percentage of objects with conflicting labels—and see in Table 2 that even in scenarios where m is small, and conflict and overlap is relatively less common, we still realize performance gains. Additionally, on a disease mention extraction task (see Usability Study), which was written from scratch within the data programming paradigm, allowing developers to supply dependencies of the basic types outlined in Sec. 4 led to a 2.3 point F1 score boost.

Table 2.

Labeling function (LF) summary statistics, sizes of generated training sets S_λ≠0 (only counting non-zero labels), and relative F1 score improvement over baseline IRT methods for hand-tuned (HT) and LSTM-generated (LSTM) feature sets.

Application	# of LFs	Coverage	|Sλ≠0|	Overlap	Conflict	F1 Score Improvement
						HT	LSTM
KBP (News)	40	29.39	2.03M	1.38	0.15	1.92	3.12
Genomics	146	53.61	256K	26.71	2.05	1.59	0.47
Pharmacogenomics	7	7.70	129K	0.35	0.32	3.60	4.94
Diseases	12	53.32	418K	31.81	0.98	N/A	N/A

Automatically-generated Features

We additionally compare both hand-tuned and automatically-generated features, where the latter are learned via an LSTM recurrent neural network (RNN) [14]. Conventional wisdom states that deep learning methods such as RNNs are prone to overfitting to the biases of the imperfect rules used for programmatic supervision. In our experiments, however, we find that using data programming to denoise the labels can mitigate this issue, and we report a 9.79 point boost to precision and a 3.12 point F1 score improvement on the benchmark 2014 TAC-KBP (News) task, over the baseline if-then-return approach. Additionally for comparison, our approach is a 5.98 point F1 score improvement over a state-of-the-art LSTM approach [32].

Usability Study

One of our hopes is that a user without expertise in ML will be more productive iterating on labeling functions than on features. To test this, we arranged a hackathon involving a handful of bioinformatics researchers, using our open-source information extraction framework Snorkel⁴ (formerly DDLite). Their goal was to build a disease tagging system which is a common and important challenge in the bioinformatics domain [11]. The hackathon participants did not have access to a labeled training set nor did they perform any feature engineering. The entire effort was restricted to iterative labeling function development and the setup of candidates to be classified. In under eight hours, they had created a training set that led to a model which scored within 10 points of F1 of the supervised baseline; the gap was mainly due to recall issue in the candidate extraction phase. This suggests data programming may be a promising way to build high quality extractors, quickly.

6 Conclusion and Future Work

We introduced data programming, a new approach to generating large labeled training sets. We demonstrated that our approach can be used with automatic feature generation techniques to achieve high quality results. We also provided anecdotal evidence that our methods may be easier for domain experts to use. We hope to explore the limits of our approach on other machine learning tasks that have been held back by the lack of high-quality supervised datasets, including those in other domains such imaging and structured prediction.

A General Theoretical Results

In this section, we will state the full form of the theoretical results we alluded to in the body of the paper. First, we restate, in long form, our setup and assumptions.

We assume that, for some function h: {−1, 0, 1}^m × {−1, 1} 7↦ {−1, 0, 1}^M of sufficient statistics, we are concerned with learning distributions, over the set Ω = {−1, 0, 1}^m × {−1, 1},of the form

$${\pi }_{\theta }(\mathrm{\Lambda },Y)=\frac{1}{Z_{\theta }}\exp ({\theta }^{T}h(\mathrm{\Lambda },Y)),$$ (10)

where θ ∈ ℝ^M is a parameter, and Z_θ is the partition function that makes this a distribution. We assume that we are given, i.e. can derive from the data programming specification, some set Θ of feasible parameters. This set must have the following two properties.

First, for any θ ∈ Θ, learning the parameter θ from (full) samples from π_θ is possible, at least in some sense. More specifically, there exists an unbiased estimator $\widehat{\theta }$ that is a function of some number D samples from π_θ (and is unbiased for all θ ∈ Θ) such that, for all θ ∈ Θ and for some c > 0,

$$\mathbf{C}\mathbf{o}\mathbf{v}\left(\widehat{\theta }\right)\le \frac{I}{2cD}.$$ (11)

Second, for any θ₁, θ₂ ∈ Θ,

$${\mathbf{E}}_{({\lambda }_2,y_2)\sim {\pi }_{{\theta }_2}}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{({\lambda }_1,y_1)\sim {\pi }_{{\theta }_1}}(y_1|{\lambda }_1={\lambda }_2)\right]\le \frac{c}{M}.$$ (12)

That is, we’ll always be reasonably certain in our guess for the value of y, even if we are totally wrong about the true parameter θ.

On the other hand, we are also concerned with a distribution π* which ranges over the set $\mathcal{X}\times \{-1,1\}$, and represents the distribution of training and test examples we are using to learn. These objects are associated with a labeling function $\lambda :\mathcal{X}\mapsto {\{-1,0,1\}}^m$ and a feature function $f:\mathcal{X}\mapsto {ℝ}^n$. We make three assumptions about this distribution. First, we assume that, given (x, y) ~ π*, the class label y is independent of the features f (x) given the labels λ(x). That is,

$$(x,y)\sim {\pi }^{\ast }\Rightarrow y\perp f(x)|\lambda (x).$$ (13)

Second, we assume that we can describe the relationship between λ(x) and y in terms of our family in (10) above. That is, for some parameter θ* ∈ Θ,

$${\mathbf{P}}_{(x,y)\sim \pi \ast }(\lambda (x)=\mathrm{\Lambda },y=Y)={\pi }_{\theta \ast }(\mathrm{\Lambda },Y).$$ (14)

Third, we assume that the features themselves are bounded; for all $x\in \mathcal{X}$,

$$\Vert f(x)\Vert \le 1.$$ (15)

Our goal is twofold. First, we want to recover some estimate $\widehat{\theta }$ of the true parameter θ*. Second, we want to produce a parameter $\widehat{w}$ that minimizes the regularized logistic loss

$$l(w)={\mathbf{E}}_{(x,y)\sim \pi \ast }\left[\log (1+\exp (-w^{T}f(x)y))\right]+\rho {\Vert w\Vert }^2.$$

We actually accomplish this by minimizing a noise-aware loss function, given our recovered parameter $\widehat{\theta }$,

$$l_{\widehat{\theta }}(w)={\mathbf{E}}_{(\overline{x},\overline{y})\sim \pi \ast }\left[{\mathbf{E}}_{(\mathrm{\Lambda },Y)\sim {\pi }_{\widehat{\theta }}}\left[\log (1+\exp (-w^{T}f(\overline{x})Y))|\mathrm{\Lambda }=\lambda (\overline{x})\right]\right]+\rho {\Vert w\Vert }^2.$$

In fact we can’t even minimize this; rather, we will be minimizing the empirical noise-aware loss function, which is only this in expectation. Since the analysis of logistic regression is not itself interesting, we assume that we are able to run some algorithm that produces an estimate $\widehat{w}$ which satisfies, for some χ > 0,

$$\mathbf{E}\left[l_{\widehat{\theta }}(\widehat{w})-\underset{w}{min}{l}_{\widehat{\theta }}(w)|\widehat{\theta }\right]\le \chi .$$ (16)

The algorithm chosen can be anything, but in practice, we use stochastic gradient descent.

We learn $\widehat{\theta }$ and $\widehat{w}$ by running the following algorithm.

Under these assumptions, we are able to prove the following theorem about the behavior of Algorithm 1.

Algorithm 1.

Data Programming

Require: Step size η, dataset $S\subset \mathcal{X}$, and initial parameter θ0 ∈ Θ.

θ → θ0

for all x ∈ S do

Independently sample (Λ, Y) from πθ, and $(\overline{\mathrm{\Lambda }},\overline{Y})$ from πθ conditionally given Λ = λ(x).

$\theta \leftarrow \theta +\eta (h(\mathrm{\Lambda },Y)-h(\overline{\mathrm{\Lambda }},\overline{Y})).$

θ = PΘ(θ) ⊳ Here, PΘ denotes orthogonal projection onto Θ.

end for

Compute $\widehat{w}$ using the algorithm described in (15)

return (θ, $\widehat{w}$).

Theorem A.1

Suppose that we run Algorithm 1 on a data programming specification that satisfies conditions (11), (12), (13), (14), (15), and (16). Suppose further that, for some parameter ε> 0, we use step size

$$\eta =\frac{c{\epsilon }^2}{4}$$

and our dataset is of a size that satisfies

$$\left|S\right|=\frac{2}{c^2{\epsilon }^2}\log \left(\frac{2{\Vert {\theta }_0-{\theta }^{\ast }\Vert }^2}{\epsilon }\right).$$

Then, we can bound the expected parameter error with

$$\mathbf{E}\left[{\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }^2\right]\le {\epsilon }^{2}M$$

and the expected risk with

$$\mathbf{E}\left[l(\widehat{w})-\underset{w}{min}l(w)\right]\le \chi +\frac{c\epsilon }{2\rho }.$$

This theorem’s conclusions and assumptions can readily be seen to be identical to those of Theorem 2 in the main body of the paper, except that they apply to the slightly more general case of arbitrary h, rather than h of the explicit form described in the body. Therefore, in order to prove Theorem 2, it suffices to prove Theorem A.1, which we will do in Section C.

B Theoretical Results for Independent Model

For the independent model, we can obtain a more specific version of Theorem A.1. In the independent model, the variables are, as before, Λ ∈ {−1, 0, 1}^m and Y ∈ {−1, 1}. The sufficient statistics are Λ_iY and ${\mathrm{\Lambda }}_i^2$.

To produce results that make intuitive sense, we also define the alternate parameterization

$${\mathbf{P}}_{\pi }\left({\mathrm{\Lambda }}_i|Y\right)=\{\begin{array}{ll}{\beta }_i\frac{1+{\gamma }_i}{2}\hfill & {\mathrm{\Lambda }}_i=Y\hfill \\ \left(1-{\beta }_i\right)\hfill & \mathrm{\Lambda }=0\hfill \\ {\beta }_i\frac{1-{\gamma }_i}{2}\hfill & {\mathrm{\Lambda }}_i=-Y\hfill \end{array}.$$

In comparison to the parameters used in the body of the paper, we have

$${\alpha }_i=\frac{1+{\gamma }_i}{2}.$$

Now, we are concerned with models that are feasible. For a model to be feasible (i.e. for θ ∈ Θ), we require that it satisfy, for some constants γ_min > 0, γ_max > 0, and β_min,

$${\gamma }_{min}\le {\gamma }_i\le {\gamma }_{max}{\beta }_{min}\le {\beta }_i\le \frac{1}{2}.$$

For 0 ≤ β ≤ 1 and − 1≤ γ ≤ 1.

For this model, we can prove the following corollary to Theorem A.1

Corollary B.1

Suppose that we run Algorithm 1 on an independent data programming specification that satisfies conditions (13), (14), (15), and (16). Furthermore, assume that the number of labeling functions we use satisfies

$$m\ge \frac{9.34\text{artanh}({\gamma }_{max})}{{(\gamma \beta )}_{min}{\gamma }_{min}^2}\log \left(\frac{24m}{{\beta }_{min}}\right).$$

Suppose further that, for some parameter ε > 0, we use step size

$$\eta =\frac{{\beta }_{min}{\epsilon }^2}{16}$$

and our dataset is of a size that satisfies

$$\left|S\right|=\frac{32}{{\beta }_{min}^2{\epsilon }^2}\log \left(\frac{2{\Vert {\theta }_0-{\theta }^{\ast }\Vert }^2}{\epsilon }\right).$$

Then, we can bound the expected parameter error with

$$\mathbf{E}\left[{\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }^2\right]\le {\epsilon }^{2}M$$

and the expected risk with

$$\mathbf{E}\left[l(\widehat{w})-\underset{w}{min}l(w)\right]\le \chi +\frac{{\beta }_{min}\epsilon }{8\rho }.$$

We can see that if, as stated in the body of the paper, β_i ≥ 0.3 and 0.8 ≤ α_i ≤ 0.9 (which is equivalent to 0.6 ≤ γ_i ≤ 0.8), then

$$2000\ge 1896.13=\frac{9.34\text{artanh}(0.8)}{0.3·{0.6}^3}\log \left(\frac{24·2000}{0.3}\right).$$

This means that, as stated in the paper, m = 2000 is sufficient for this corollary to hold with

$$\left|S\right|=\frac{32}{{0.3}^2·{\epsilon }^2}\log \left(\frac{2m{(\text{artanh}(0.8)-\text{artanh}(0.6))}^2}{\epsilon }\right)=\frac{356}{{\epsilon }^2}\log \left(\frac{m}{3\epsilon }\right).$$

Thus, proving Corollary B.1 is sufficient to prove Theorem 1 from the body of the paper. We will prove Corollary B.1 in Section E

C Proof of Theorem A.1

First, we state some lemmas that will be useful in the proof to come.

Lemma D.1

Given a family of maximum-entropy distributions

$${\pi }_{\theta }(x)=\frac{1}{Z_{\theta }}\exp ({\theta }^{T}h(x)),$$

for some function of sufficient statistics h: Ω ↦ ℝ^M, if we let J: ℝ^M ↦ ℝ be the maximum log-likelihood objective for some event A ⊆ Ω,

$$J(\theta )=\log {\mathbf{P}}_{x~{\pi }_{\theta }}(x\in A),$$

then its gradient is

$$\nabla J(\theta )={\mathbf{E}}_{x~{\pi }_{\theta }}[h(x)|x\in A]-{\mathbf{E}}_{x~{\pi }_{\theta }}[h(x)]$$

and its Hessian is

$${\nabla }^{2}J(\theta )=\mathbf{C}\mathbf{o}{\mathbf{v}}_{x~{\pi }_{\theta }}(h(x)|x\in A)-\mathbf{C}\mathbf{o}{\mathbf{v}}_{x~{\pi }_{\theta }}(h(x)).$$

Lemma D.2

Suppose that we are looking at a distribution from a data programming label model. That is, our maximum-entropy distribution can now be written in terms of two variables, the labeling function values λ ∈ {−1, 0, 1} and the class y ∈ {−1, 0, 1}, as

$${\pi }_{\theta }(\lambda ,y)=\frac{1}{Z_{\theta }}\exp ({\theta }^{T}h(\lambda ,y)),$$

where we assume without loss of generality that for some M, h(λ, y) ∈ ℝ^M and ‖h(λ, y)‖_∞ ≤ 1. If we let J: ℝ^M ↦ ℝ be the maximum expected log-likelihood objective, under another distribution π*, for the event associated with the observed labeling function values λ,

$$J(\theta )={\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\log {\mathbf{P}}_{(\lambda ,y)~{\pi }_{\theta }}(\lambda ={\lambda }^{\ast })\right],$$

then its Hessian can be bounded with

$${\nabla }^{2}J(\theta )\le MI{\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]-\mathcal{I}(\theta ),$$

where $\mathcal{I}(\theta )$ is the Fisher information.

Lemma D.3

Suppose that we are looking at a data programming distribution, as described in the text of Lemma D.2. Suppose further that we are concerned with some feasible set of parameters Θ ⊂ ℝ^M, such that the any model with parameters in this space satisfies the following two conditions.

First, for any θ ∈ Θ, learning the parameter θ from (full) samples from π_θ is possible, at least in some sense. More specifically, there exists an unbiased estimator $\widehat{\theta }$ that is a function of some number D samples from π_θ (and is unbiased for all θ ∈ Θ) such that, for all θ ∈ Θ and for some c > 0,

$$\mathbf{C}\mathbf{o}\mathbf{v}\left(\widehat{\theta }\right)\le \frac{1}{2cD}.$$

Second, for any θ, θ* ∈ Θ,

$${\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]\le \frac{c}{M}.$$

That is, we’ll always be reasonably certain in our guess for the value of y, even if we are totally wrong about the true parameter θ*.

Under these conditions, the function J is strongly concave on Θ with parameter of strong convexity c.

Lemma D.4

Suppose that we are looking at a data programming maximum likelihood estimation problem, as described in the text of Lemma D.2. Suppose further that the objective function J is strongly concave with parameter c > 0.

If we run stochastic gradient descent on objective J, using unbiased samples from a true distribution π_θ*, where θ* ∈ Θ, then if we use step size

$$\eta =\frac{c{\epsilon }^2}{4}$$

and run (using a fresh sample at each iteration) for T steps, where

$$T=\frac{2}{c^2{\epsilon }^2}\log \left(\frac{2{\Vert {\theta }_0-{\theta }^{\ast }\Vert }^2}{\epsilon }\right)$$

then we can bound the expected parameter estimation error with

$$\mathbf{E}\left[{\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }^2\right]\le {\epsilon }^{2}M.$$

Lemma D.5

Assume in our model that, without loss of generality, ‖f (x)‖ ≤ 1 for all x, and that in our true model π*, the class y is independent of the features f (x) given the labels λ(x).

Suppose that we now want to solve the expected loss minimization problem wherein we minimize the objective

$$l(w)={\mathbf{E}}_{(x,y)~{\pi }^{\ast }}\left[\log (1+\exp (-w^{T}f(x)y))\right]+\rho {\Vert w\Vert }^2.$$

We actually accomplish this by minimizing our noise-aware loss function, given our chosen parameter $\widehat{\theta }$,

$$l_{\widehat{\theta }}(w)={\mathbf{E}}_{(\overline{x},\overline{y})~{\pi }^{\ast }}\left[{\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\widehat{\theta }}}\left[\log (1+\exp (-w^{T}f(\overline{x})Y))|\mathrm{\Lambda }=\lambda (\overline{x})\right]\right]+\rho {\Vert w\Vert }^2.$$

In fact we can’t even minimize this; rather, we will be minimizing the empirical noise-aware loss function, which is only this in expectation. Suppose that doing so produces an estimate $\widehat{w}$ which satisfies, for some χ > 0,

$$\mathbf{E}\left[l_{\widehat{\theta }}(\widehat{w})-\underset{w}{min}{l}_{\widehat{\theta }}(w)|\widehat{\theta }\right]\le \chi .$$

(Here, the expectation is taken with respect to only the random variable $\widehat{w}$.) Then, we can bound the expected risk with

$$\mathbf{E}\left[l(\widehat{w})-\underset{w}{min}l(w)\right]\le \chi +\frac{c\epsilon }{2\rho }.$$

Now, we restate and prove our main theorem.

Theorem A.1

Suppose that we run Algorithm 1 on a data programming specification that satisfies conditions (11), (12), (13), (14), (15), and (16). Suppose further that, for some parameter ε > 0, we use step size

$$\eta =\frac{c{\epsilon }^2}{4}$$

and our dataset is of a size that satisfies

$$\left|S\right|=\frac{2}{c^2{\epsilon }^2}\log \left(\frac{2{\Vert {\theta }_0-{\theta }^{\ast }\Vert }^2}{\epsilon }\right).$$

Then, we can bound the expected parameter error with

$$\mathbf{E}\left[{\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }^2\right]\le {\epsilon }^{2}M$$

and the expected risk with

$$\mathbf{E}\left[l(\widehat{w})-\underset{w}{min}l(w)\right]\le \chi +\frac{c\epsilon }{2\rho }.$$

Proof

The bounds on the expected parameter estimation error follow directly from Lemma D.4, and the remainder of the theorem follows directly from Lemma D.5. □

D Proofs of Lemmas

Lemma D.1

Given a family of maximum-entropy distributions

$${\pi }_{\theta }(x)=\frac{1}{Z_{\theta }}\exp ({\theta }^{T}h(x)),$$

for some function of sufficient statistics h: Ω ↦ ℝ^M, if we let J: ℝ^M ↦ ℝ be the maximum log-likelihood objective for some event A ⊆ Ω,

$$J(\theta )=\log {\mathbf{P}}_{x~{\pi }_{\theta }}(x\in A),$$

then its gradient is

$$\nabla J(\theta )={\mathbf{E}}_{x~{\pi }_{\theta }}[h(x)|x\in A]-{\mathbf{E}}_{x~{\pi }_{\theta }}[h(x)]$$

and its Hessian is

$${\nabla }^{2}J(\theta )=\mathbf{C}\mathbf{o}{\mathbf{v}}_{x~{\pi }_{\theta }}(h(x)|x\in A)-\mathbf{C}\mathbf{o}{\mathbf{v}}_{x~{\pi }_{\theta }}(h(x)).$$

Proof

For the gradient,

$$\begin{gathered} \nabla J(\theta )=\nabla \log {\mathbf{P}}_{{\pi }_{\theta }}(A) \\ =\nabla \log \left(\frac{{\displaystyle {\sum }_{x\in A}\exp ({\theta }^{T}h(x))}}{{\displaystyle {\sum }_{x\in \Omega }\exp ({\theta }^{T}h(x))}}\right) \\ =\nabla \log \left({\displaystyle \sum _{x\in A}\exp ({\theta }^{T}h(x))}\right)-\nabla \log \left({\displaystyle \sum _{x\in \Omega }\exp ({\theta }^{T}h(x))}\right) \\ =\frac{{\displaystyle {\sum }_{x\in A}h(x)\exp ({\theta }^{T}h(x))}}{{\displaystyle {\sum }_{x\in A}\exp ({\theta }^{T}h(x))}}-\frac{{\displaystyle {\sum }_{x\in \Omega }h(x)\exp ({\theta }^{T}h(x))}}{{\displaystyle {\sum }_{x\in \Omega }\exp ({\theta }^{T}h(x))}} \\ ={\mathbf{E}}_{x~{\pi }_{\theta }}[h(x)|x\in A]-{\mathbf{E}}_{x~{\pi }_{\theta }}[h(x)]. \end{gathered}$$

And for the Hessian

$$\begin{gathered} {\nabla }^{2}J(\theta )=\nabla \frac{{\displaystyle {\sum }_{x\in A}h(x)\exp ({\theta }^{T}h(x))}}{{\displaystyle {\sum }_{x\in A}\exp ({\theta }^{T}h(x))}}-\nabla \frac{{\displaystyle {\sum }_{x\in \Omega }h(x)\exp ({\theta }^{T}h(x))}}{{\displaystyle {\sum }_{x\in \Omega }\exp ({\theta }^{T}h(x))}} \\ =\frac{{\displaystyle {\sum }_{x\in A}h(x)h{(x)}^T\exp ({\theta }^{T}h(x))}}{{\displaystyle {\sum }_{x\in A}\exp ({\theta }^{T}h(x))}}-\frac{‘{\displaystyle {\sum }_{x\in A}h(x)\exp ({\theta }^{T}h(x))}’{‘{\displaystyle {\sum }_{x\in A}h(x)\exp ({\theta }^{T}h(x))}’}^T}{{({\displaystyle {\sum }_{x\in A}\exp ({\theta }^{T}h(x))})}^2} \\ -‘\frac{{\displaystyle {\sum }_{x\in \Omega }h(x)\exp ({\theta }^{T}h(x))}}{{\displaystyle {\sum }_{x\in \Omega }\exp ({\theta }^{T}h(x))}}-\frac{‘{\displaystyle {\sum }_{x\in \Omega }h(x)\exp ({\theta }^{T}h(x))}’{‘{\displaystyle {\sum }_{x\in \Omega }h(x)\exp ({\theta }^{T}h(x))}’}^T}{{({\displaystyle {\sum }_{x\in \Omega }\exp ({\theta }^{T}h(x))})}^2}’ \\ ={\mathbf{E}}_{x~{\pi }_{\theta }}\left[h(x)h{(x)}^T|x\in A\right]-{\mathbf{E}}_{x~{\pi }_{\theta }}[h(x)|x\in A]{\mathbf{E}}_{x~{\pi }_{\theta }}{[h(x)|[h(x)]\in A]}^T \\ -‘{\mathbf{E}}_{x~x_{\theta }}[h(x)h{(x)}^T]-{\mathbf{E}}_{x~{\pi }_{\theta }}[h(x)]{[{\mathbf{E}}_{x~{\pi }_{\theta }}]}^T’ \\ =\mathbf{Co}{\mathbf{v}}_{x~{\pi }_{\theta }}(h(x)|x\in A)-\mathbf{Co}{\mathbf{v}}_{x~{\pi }_{\theta }}(h(x)). \end{gathered}$$

Lemma D.2

Suppose that we are looking at a distribution from a data programming label model. That is, our maximum-entropy distribution can now be written in terms of two variables, the labeling function values λ ∈ {−1, 0, 1} and the class y ∈ {−1, 1}, as

$${\pi }_{\theta }(\lambda ,y)=\frac{1}{Z_{\theta }}\exp ({\theta }^{T}h(\lambda ,y)),$$

where we assume without loss of generality that for some M, h(λ, y) ∈ ℝ^M and ‖h(λ, y)‖_∞ ≤ 1. If we let J: ℝ^M ↦ ℝ be the maximum expected log-likelihood objective, under another distribution π*, for the event associated with the observed labeling function values λ,

$$J(\theta )={\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\log {\mathbf{P}}_{(\lambda ,y)~{\pi }_{\theta }}(\lambda ={\lambda }^{\ast })\right],$$

then its Hessian can be bounded with

$${\nabla }^{2}J(\theta )\le MI{\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]-\mathcal{I}(\theta ),$$

where $\mathcal{I}(\theta )$ is the Fisher information.

Proof

From the result of Lemma D.1, we have that

$${\nabla }^{2}J(\theta )={\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\mathbf{C}\mathbf{o}{\mathbf{v}}_{(\lambda ,y)~{\pi }_{\theta }}(h(\lambda ,y)|\lambda ={\lambda }^{\ast })\right]-\mathbf{C}\mathbf{o}{\mathbf{v}}_{(\lambda ,y)~{\pi }_{\theta }}(h(\lambda ,y)).$$ (17)

We start byu defining h₀(λ) and h₁(λ) such that

$$h(\lambda ,y)=h(\lambda ,1)\frac{1+y}{2}+h(\lambda ,-1)\frac{1-y}{2}=\frac{h(\lambda ,1)+h(\lambda ,-1)}{2}+y\frac{h(\lambda ,1)-h(\lambda ,-1)}{2}=h_0(\lambda )+y{h}_1(\lambda ).$$

This allows us to reduce (17) to

$${\nabla }^{2}J(\theta )={\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[h_1({\lambda }^{\ast })h_1{({\lambda }^{\ast })}^T\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]-\mathbf{C}\mathbf{o}{\mathbf{v}}_{(\lambda ,y)~{\pi }_{\theta }}(h(\lambda ,y)).$$

On the other hand, the Fisher information of this model at θ is

$$\begin{gathered} \mathcal{I}(\theta )=\mathbf{E}\left[{({\nabla }_{\theta }\log {\pi }_{\theta }(x))}^2\right] \\ =\mathbf{E}\left[{\left({\nabla }_{\theta }\log \left(\frac{\exp ({\theta }^{T}h(x))}{{\displaystyle {\sum }_{z\in \Omega }\exp ({\theta }^{T}h(z))}}\right)\right)}^2\right] \\ =\mathbf{E}\left[{\left({\nabla }_{\theta }\log \left(\exp ({\theta }^{T}h(x))\right)-{\nabla }_{\theta }\log \left({\displaystyle \sum _{z\in \Omega }\exp ({\theta }^{T}h(z))}\right)\right)}^2\right] \\ =\mathbf{E}\left[{\left(h(x)-\frac{{\displaystyle {\sum }_{z\in \Omega }h(z)\exp ({\theta }^{T}h(z))}}{{\displaystyle {\sum }_{z\in \Omega }\exp ({\theta }^{T}h(z))}}\right)}^2\right] \\ =\mathbf{E}\left[{(h(x)-\mathbf{E}[h(z)])}^2\right] \\ =\mathbf{C}\mathbf{o}\mathbf{v}(h(x)). \end{gathered}$$

Therefore, we can write the second derivative of J as

$${\nabla }^{2}J(\theta )={\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[h_1({\lambda }^{\ast })h_1{({\lambda }^{\ast })}^T\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]-\mathcal{I}(\theta ).$$

If we apply the fact that

$$h_1({\lambda }^{\ast })h_1{({\lambda }^{\ast })}^T\le I{\Vert h_1({\lambda }^{\ast })\Vert }^2\le MI{\Vert h_1({\lambda }^{\ast })\Vert }_{\mathrm{\infty }}^2\le MI,$$

then we can reduce this to

$${\nabla }^{2}J(\theta )\le MI{\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]-\mathcal{I}(\theta ).$$

This is the desired result. □

Lemma D.3

Suppose that we are looking at a data programming distribution, as described in the text of Lemma D.2. Suppose further that we are concerned with some feasible set of parameters Θ ⊂ ℝ^M, such that the any model with parameters in this space satisfies the following two conditions.

First, for any θ ∈ Θ, learning the parameter θ from (full) samples from π_θ is possible, at least in some sense. More specifically, there exists an unbiased estimator $\widehat{\theta }$ that is a function of some number D samples from π_θ (and is unbiased for all θ ∈ Θ) such that, for all θ ∈ Θ and for some c > 0,

$$\mathbf{C}\mathbf{o}\mathbf{v}\left(\widehat{\theta }\right)\le \frac{I}{2cD}.$$

Second, for any θ, θ* ∈ Θ,

$${\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]\le \frac{c}{M}.$$

That is, we’ll always be reasonably certain in our guess for the value of y, even if we are totally wrong about the true parameter θ*.

Under these conditions, the function J is strongly concave on Θ with parameter of strong convexity c.

Proof

From the Cramér-Rao bound, we know in general that the variance of any unbiased estimator is bounded by the reciprocal of the Fisher information

$$\mathbf{C}\mathbf{o}\mathbf{v}\left(\widehat{\theta }\right)\ge {(\mathcal{I}(\theta ))}^{-1}.$$

Since for the estimator described in the lemma statement, we have D independent samples from the distribution, it follows that the Fisher information of this experiment is D times the Fisher information of a single sample. Combining this with the bound in the lemma statement on the covariance, we get

$$\frac{I}{2cD}\ge \mathbf{C}\mathbf{o}\mathbf{v}\left(\widehat{\theta }\right)\ge {(D\mathcal{I}(\theta ))}^{-1}.$$

It follows that

$$\mathcal{I}(\theta )\ge 2cI.$$

On the other hand, also from the lemma statement, we can conclude that

$$MI{\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]\le cI.$$

Therefore, for all θ ∈ Θ,

$${\nabla }^{2}J(\theta )\le MI{\mathbf{E}}_{({\lambda }^{\ast },y^{\ast })~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\lambda ,y)~{\pi }_{\theta }}(y|\lambda ={\lambda }^{\ast })\right]-\mathcal{I}(\theta )\le -cI.$$

This implies that J is strongly concave over Θ, with constant c, as desired. □

Lemma D.4

Suppose that we are looking at a data programming maximum likelihood estimation problem, as described in the text of Lemma D.2. Suppose further that the objective function J is strongly concave with parameter c > 0.

If we run stochastic gradient descent on objective J, using unbiased samples from a true distribution π_θ*, where θ* ∈ Θ, then if we use step size

$$\eta =\frac{c{\epsilon }^2}{4}$$

and run (using a fresh sample at each iteration) for T steps, where

$$T=\frac{2}{c^2{\epsilon }^2}\log \left(\frac{2{\Vert {\theta }_0-{\theta }^{\ast }\Vert }^2}{\epsilon }\right)$$

then we can bound the expected parameter estimation error with

$$\mathbf{E}\left[{\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }^2\right]\le {\epsilon }^{2}M.$$

Proof

First, we note that, in the proof to follow, we can ignore the projection onto the feasible set Θ, since this projection always takes us closer to the optimum θ*.

If we track the expected distance to the optimum θ*, then at the next timestep,

$${\Vert {\theta }_{t+1}-{\theta }^{\ast }\Vert }^2={\Vert {\theta }_t-{\theta }^{\ast }\Vert }^2+2\gamma ({\theta }_t-{\theta }^{\ast })\nabla \stackrel{\sim }{J}({\theta }_t)+{\gamma }^2{\Vert \nabla {\stackrel{\sim }{J}}_t({\theta }_t)\Vert }^2.$$

Since we can write our stochastic samples in the form

$$\nabla {\stackrel{\sim }{J}}_t({\theta }_t)=h({\lambda }_t,y_t)-h({\overline{\lambda }}_t,{\overline{y}}_t),$$

for some samples λ_t, y_t, ${\overline{\lambda }}_t$, and ${\overline{y}}_t$, we can conclude that

$${\Vert \nabla {\stackrel{\sim }{J}}_t({\theta }_t)\Vert }^2\le M{\Vert \nabla {\stackrel{\sim }{J}}_t({\theta }_t)\Vert }_{\mathrm{\infty }}^2\le 4M.$$

Therefore, taking the expected value conditioned on the filtration,

$$\mathbf{E}\left[{\Vert {\theta }_{t+1}-{\theta }^{\ast }\Vert }^2|{\mathcal{F}}_t\right]={\Vert {\theta }_t-{\theta }^{\ast }\Vert }^2+2\gamma ({\theta }_t-{\theta }^{\ast })\nabla J({\theta }_t)+4{\gamma }^{2}M.$$

Since J is strongly concave,

$$({\theta }_t-{\theta }^{\ast })\nabla J({\theta }_t)\le -c\Vert {\theta }_t-{\theta }^{\ast }{\Vert }^2;$$

and so,

$$\mathbf{E}\left[\Vert {\theta }_{t+1}-{\theta }^{\ast }{\Vert }^2|{\mathcal{F}}_t\right]\le (1-2\gamma c)\Vert {\theta }_t-{\theta }^{\ast }{\Vert }^2+4{\gamma }^{2}M.$$

If we take the full expectation and subtract the fixed point from both sides,

$$\mathbf{E}\left[\Vert {\theta }_{t+1}-{\theta }^{\ast }{\Vert }^2\right]-\frac{2\gamma M}{c}\le (1-2\gamma c)\mathbf{E}\left[\Vert {\theta }_t-{\theta }^{\ast }{\Vert }^2\right]+4{\gamma }^{2}M-\frac{2\gamma M}{c}=(1-2\gamma c)\left(\mathbf{E}\left[\Vert {\theta }_t-{\theta }^{\ast }{\Vert }^2\right]-\frac{2\gamma M}{c}\right).$$

Therefore,

$$\mathbf{E}\left[\Vert {\theta }_t-{\theta }^{\ast }{\Vert }^2\right]-\frac{2\gamma M}{c}\le {(1-2\gamma c)}^t\left(\Vert {\theta }_0-{\theta }^{\ast }{\Vert }^2-\frac{2\gamma M}{c}\right),$$

and so

$$\mathbf{E}\left[\Vert {\theta }_t-{\theta }^{\ast }{\Vert }^2\right]\le \exp (-2\gamma ct)\Vert {\theta }_0-{\theta }^{\ast }{\Vert }^2+\frac{2\gamma M}{c}.$$

In order to ensure that

$$\mathbf{E}\left[\Vert {\theta }_t-{\theta }^{\ast }{\Vert }^2\right]\le {\epsilon }^2,$$

it therefore suffices to pick

$$\gamma =\frac{c{\epsilon }^2}{4M}$$

and

$$t=\frac{2M}{c^2{\epsilon }^2}\log \left(\frac{2\Vert {\theta }_0-{\theta }^{\ast }{\Vert }^2}{\epsilon }\right).$$

Substituting ε² → ε²M produces the desired result. □

Lemma D.5

Assume in our model that, without loss of generality, ‖f(x)‖ ≤ 1 for all x, and that in our true model π*, the class y is independent of the features f (x) given the labels λ(x).

Suppose that we now want to solve the expected loss minimization problem wherein we minimize the objective

$$l(w)={\mathbf{E}}_{(x,y)~\pi \ast }\left[\log (1+\exp (-w^{T}f(x)y))\right]+\rho \Vert w{\Vert }^2.$$

We actually accomplish this by minimizing our noise-aware loss function, given our chosen parameter $\widehat{\theta }$,

$$l_{\widehat{\theta }}(w)={\mathbf{E}}_{(\overline{x},\overline{y})~\pi \ast }\left[{\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\widehat{\theta }}}\left[\log (1+\exp (-w^{T}f(\overline{x})Y))|\mathrm{\Lambda }=\lambda (\overline{x})\right]\right]+\rho \Vert w{\Vert }^2.$$

In fact we can’t even minimize this; rather, we will be minimizing the empirical noise-aware loss function, which is only this in expectation. Suppose that doing so produces an estimate $\widehat{w}$ which satisfies, for some χ > 0,

$$\mathbf{E}\left[l_{\widehat{\theta }}(\widehat{w})-\underset{w}{min}{l}_{\widehat{\theta }}(w)|\widehat{\theta }\right]\le \chi .$$

(Here, the expectation is taken with respect to only the random variable $\widehat{w}$.) Then, we can bound the expected risk with

$$\mathbf{E}\left[l(\widehat{w})-\underset{w}{min}l(w)\right]\le \chi +\frac{c\epsilon }{2\rho }.$$

Proof

(To simplify the symbols in this proof, we freely use θ when we mean $\widehat{\theta }$.)

The loss function we want to minimize is, in expectation,

$$l(w)={\mathbf{E}}_{(x,y)~\pi \ast }\left[\log (1+\exp (-w^{T}f(x)y))\right]+\rho \Vert w{\Vert }^2.$$

By the law of total expectation,

$$l(w)={\mathbf{E}}_{(\overline{x},\overline{y})~\pi \ast }\left[{\mathbf{E}}_{(x,y)~\pi \ast }\left[\log (1+\exp (-w^{T}f(\overline{x})y))|x=\overline{x}\right]\right]+\rho \Vert w{\Vert }^2,$$

and by our conditional independence assumption,

$$l(w)={\mathbf{E}}_{(\overline{x},\overline{y})~\pi \ast }\left[{\mathbf{E}}_{(x,y)~\pi \ast }\left[\log (1+\exp (-w^{T}f(\overline{x})y))|\lambda (x)=\lambda (\overline{x})\right]\right]+\rho \Vert w{\Vert }^2.$$

Since we know from our assumptions that, for the optimum parameter θ*,

$${\mathbf{P}}_{(x,y)~\pi \ast }(\lambda (x)=\mathrm{\Lambda },y=Y)={\mathbf{P}}_{(\lambda ,y)~{\pi }_{\theta \ast }}(\lambda =\mathrm{\Lambda },y=Y),$$

we can rewrite this as

$$l(w)={\mathbf{E}}_{(\overline{x},\overline{y})~\pi \ast }\left[{\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }\ast }\left[\log (1+\exp (-w^{T}f(\overline{x})Y))|\mathrm{\Lambda }=\lambda (\overline{x})\right]\right]+\rho \Vert w{\Vert }^2.$$

On the other hand, if we are minimizing the model we got from the previous step, we will be actually minimizing

$$l_{\theta }(w)={\mathbf{E}}_{(\overline{x},\overline{y})~\pi \ast }\left[{\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }}\left[\log (1+\exp (-w^{T}f(\overline{x})Y))|\mathrm{\Lambda }=\lambda (\overline{x})\right]\right]+\rho \Vert w{\Vert }^2.$$

We can reduce this further by noticing that

$$\begin{gathered} {\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }}\left[\log (1+\exp (-w^{T}f(\overline{x})Y))|\mathrm{\Lambda }=\lambda (\overline{x})\right] \\ ={\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }}\left[\log (1+\exp (-w^{T}f(\overline{x})))\frac{1+Y}{2}+\log (1+\exp (w^{T}f(\overline{x})))\frac{1-Y}{2}|\mathrm{\Lambda }=\lambda (\overline{x})\right] \\ =\frac{\log (1+\exp (-w^{T}f(\overline{x})))+\log (1+\exp (w^{T}f(\overline{x})))}{2} \\ +\frac{\log (1+\exp (-w^{T}f(\overline{x})))-\log (1+\exp (w^{T}f(\overline{x})))}{2}{\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }}[Y|\mathrm{\Lambda }=\lambda (\overline{x})] \\ =\frac{\log (1+\exp (-w^{T}f(\overline{x})))+\log (1+\exp (w^{T}f(\overline{x})))}{2} \\ -\frac{w^{T}f(\overline{x})}{2}{\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }}[Y|\mathrm{\Lambda }=\lambda (\overline{x})]. \end{gathered}$$

It follows that the difference between the loss functions will be

$$|l(w)-l_{\theta }(w)|=|{\mathbf{E}}_{(\stackrel{\sim }{x},\stackrel{\sim }{y})~{\pi }^{\ast }}\left[\frac{w^{T}f(\overline{x})}{2}({\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }}[Y|\mathrm{\Lambda }=\lambda (\overline{x})]-{\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta \ast }}[Y|\mathrm{\Lambda }=\lambda (\overline{x})])\right]|.$$

Now, we can compute that

$$\begin{gathered} {\nabla }_{\theta }{\mathbf{E}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }}[Y|\mathrm{\Lambda }=\lambda ]={\nabla }_{\theta }\frac{\exp ({\theta }^{T}h(\lambda ,1))-\exp ({\theta }^{T}h(\lambda ,-1))}{\exp ({\theta }^{T}h(\lambda ,1))+\exp ({\theta }^{T}h(\lambda ,-1))} \\ ={\nabla }_{\theta }\frac{\exp ({\theta }^T{h}_1(\lambda ))-\exp (-{\theta }^T{h}_1(\lambda ))}{\exp ({\theta }^T{h}_1(\lambda ))+\exp ({\theta }^T{h}_1(\lambda ))} \\ ={\nabla }_{\theta }\tanh ({\theta }^T{h}_1(\lambda )) \\ =h_1(\lambda )(1-{\tanh }^2({\theta }^T{h}_1(\lambda ))) \\ =h_1(\lambda )\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\mathrm{\Lambda },Y)~{\pi }_{\theta }}(Y|\Lambda =\lambda ). \end{gathered}$$

It follows by the mean value theorem that for some ψ, a linear combination of θ and θ*,

$$|l(w)-l_{\theta }(w)|=\left|{\mathbf{E}}_{(\overline{x},\overline{y})~{\pi }^{\ast }}\left[\frac{w^{T}f(\overline{x})}{2}{(\theta -{\theta }^{\ast })}^T{h}_1(\lambda )\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\mathrm{\Lambda },Y)~{\pi }_{\psi }}(Y|\mathrm{\Lambda }=\lambda )\right]\right|.$$

Since Θ is convex, clearly ψ ∈ Θ. From our assumption on the bound of the variance, we can conclude that

$${\mathbf{E}}_{(\overline{x},\overline{y})~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\mathrm{\Lambda },Y)~{\pi }_{\psi }}(Y|\mathrm{\Lambda }=\lambda )\right]\le \frac{c}{M}.$$

By the Cauchy-Schwarz inequality,

$$|l(w)-l_{\theta }(w)|\le \frac{1}{2}\left|E_{(\overline{x},\overline{y})~{\pi }^{\ast }}\left[\Vert w\Vert \Vert f(\overline{x})\Vert \Vert \theta -{\theta }^{\ast }\Vert \Vert h_1(\lambda )\Vert \mathbf{V}\mathbf{a}{\mathbf{r}}_{(\mathrm{\Lambda },Y)~{\pi }_{\psi }}(Y|\mathrm{\Lambda }=\lambda )\right]\right|.$$

Since (by assumption) ‖f(x)‖ ≤ 1 and $\Vert h_1(\lambda )\Vert \le \sqrt{M}$,

$$\begin{gathered} |l(w)-l_{\theta }(w)|\le \frac{\Vert w\Vert \Vert \theta -{\theta }^{\ast }\Vert \sqrt{M}}{2}\left|{\mathbf{E}}_{(\overline{x},\overline{y})~{\pi }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{(\mathrm{\Lambda },Y)~{\pi }_{\psi }}(Y|\mathrm{\Lambda }=\lambda )\right]\right| \\ \le \frac{\Vert w\Vert \Vert \theta -{\theta }^{\ast }\Vert \sqrt{M}}{2}\cdot \frac{c}{M} \\ =\frac{c\Vert w\Vert \Vert \theta -{\theta }^{\ast }\Vert }{2\sqrt{M}}. \end{gathered}$$

Now, for any w that could conceivably be a solution, it must be the case that

$$\Vert w\Vert \le \frac{1}{2\rho },$$

since otherwise the regularization term would be too large Therefore, for any possible solution w,

$$|l(w)-l_{\theta }(w)|\le \frac{c\Vert \theta -{\theta }^{\ast }\Vert }{4\rho \sqrt{M}}.$$

Now, we apply the assumption that we are able to solve the empirical problem, producing an estimate $\widehat{w}$ that satisfies

$$\mathbf{E}[l_{\theta }(\widehat{w})-l_{\theta }(w_{\theta }^{\ast })]\le \chi ,$$

where $w_{\theta }^{\ast }$ is the true solution to

$$w_{\theta }^{\ast }=\arg \underset{w}{min}{l}_{\theta }(w).$$

Therefore,

$$\begin{gathered} \mathbf{E}[l(\widehat{w})-l(w^{\ast })]=\mathbf{E}[l_{\theta }(\widehat{w})-l_{\theta }(w_{\theta }^{\ast })+l_{\theta }(w_{\theta }^{\ast })-l_{\theta }(\widehat{w})+l(\widehat{w})-l(w^{\ast })] \\ \le \chi +\mathbf{E}[l_{\theta }(w^{\ast })-l_{\theta }(\widehat{w})+l(\widehat{w})-l(w^{\ast })] \\ \le \chi +\mathbf{E}[|l_{\theta }(w^{\ast })-l(w^{\ast })|+|l_{\theta }(\widehat{w})-l(\widehat{w})|] \\ \le \chi +\mathbf{E}\left[\frac{c\Vert \theta -{\theta }^{\ast }\Vert }{2\rho \sqrt{M}}\right] \\ =\chi +\frac{c}{2\rho \sqrt{M}}\mathbf{E}[\Vert \theta -{\theta }^{\ast }\Vert ] \\ \le \chi +\frac{c}{2\rho \sqrt{M}}\sqrt{\mathbf{E}\left[\Vert \theta -{\theta }^{\ast }{\Vert }^2\right]}. \end{gathered}$$

We can now bound this using the result of Lemma D.4, which results in

$$\begin{gathered} \mathbf{E}[l(\widehat{w})-l(w^{\ast })]\le \chi +\frac{c}{2\rho \sqrt{M}}\sqrt{M{\epsilon }^2} \\ =\chi +\frac{c\epsilon }{2\rho }. \end{gathered}$$

This is the desired result. □

E Proofs of Results for the Independent Model

To restate, in the independent model, the variables are, as before, Λ ∈ {−1, 0, 1}^m and Y ∈ {−1, 1} The sufficient statistics are Λ_iY and ${\mathrm{\Lambda }}_i^2$. That is, for expanded parameter θ = (ψ, ϕ),

$${\pi }_{\theta }(\mathrm{\Lambda },Y)=\frac{1}{Z}\exp ({\Psi }^T\mathrm{\Lambda }Y+{\varphi }^T{\mathrm{\Lambda }}^2).$$

This can be combined with the simple assumption that $\mathbf{P}(Y)=\frac{1}{2}$ to complete a whole distribution. Using this, we can prove the following simple result about the moments of the sufficient statistics.

Lemma E.1

The expected values and covariances of the sufficient statistics are, for all i ≠ j,

$$\begin{gathered} \mathbf{E}[{\mathrm{\Lambda }}_{i}Y]={\beta }_i{\gamma }_i \\ \mathbf{E}[{\mathrm{\Lambda }}_i^2]={\beta }_i \\ \mathbf{V}\mathbf{a}\mathbf{r}[{\mathrm{\Lambda }}_{i}Y]={\beta }_i-{\beta }_i^2{\gamma }_i^2 \\ \mathbf{V}\mathbf{a}\mathbf{r}({\mathrm{\Lambda }}_i^2)={\beta }_i-{\beta }_i^2 \\ \mathbf{C}\mathbf{o}\mathbf{v}({\mathrm{\Lambda }}_{i}Y,{\mathrm{\Lambda }}_{j}Y)=0 \\ \mathbf{C}\mathbf{o}\mathbf{v}({\mathrm{\Lambda }}_i^2,{\mathrm{\Lambda }}_j^2)=0 \\ \mathbf{C}\mathbf{o}\mathbf{v}({\mathrm{\Lambda }}_{i}Y,{\mathrm{\Lambda }}_j^2)=0. \end{gathered}$$

We also prove the following basic lemma that relates ψ_i to γ_i.

Lemma E.2

It holds that

$${\gamma }_i=\text{tanh}({\psi }_i)$$

We also make the following claim about feasible models.

Lemma E.3

For any feasible model, it will be the case that, for any other feasible parameter vector $\widehat{\psi }$,

$$\mathbf{P}\left({\widehat{\psi }}^T\mathrm{\Lambda }Y\le \frac{m}{2}{\gamma }_{min}{(\gamma \beta )}_{min}\right)\le \left(-\frac{m{(\gamma \beta )}_{min}{\gamma }_{min}^2}{9.34\text{artanh}({\gamma }_{max})}\right).$$

We can also prove the following simple result about the conditional covariances

Lemma E.4

The covariances of the sufficient statistics, conditioned on Λ, are for all i ≠ j,

$$\begin{gathered} \mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_{i}Y,{\mathrm{\Lambda }}_{i}Y|\mathrm{\Lambda }\right)={\mathrm{\Lambda }}_i{\mathrm{\Lambda }}_j{\text{sech}}^2\left({\psi }^T\mathrm{\Lambda }\right) \\ \mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_i^2,{\mathrm{\Lambda }}_j^2|\mathrm{\Lambda }\right)=0. \end{gathered}$$

We can combine these two results to bound the expected variance of these conditional statistics.

Lemma E.5

If θ and θ* are two feasible models, then for any u,

$${\mathbf{E}}_{\theta \ast }\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{\theta }\left(Y|\mathrm{\Lambda }\right)\right]\le 3\exp \left(-\frac{m{\beta }_{min}^2{\gamma }_{min}^3}{8\text{artanh}\left({\gamma }_{max}\right)}\right).$$

We can now proceed to restate and prove the main corollary of Theorem A.1 that applies in the independent case.

Corollary B.1

Suppose that we run Algorithm 1 on an independent data programming specification that satisfies conditions (13), (14), (15), and (16). Furthermore, assume that the number of labeling functions we use satisfies

$$m\ge \frac{9.34\text{artanh}\left({\gamma }_{max}\right)}{{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2}\log \left(\frac{24m}{{\beta }_{min}}\right).$$

Suppose further that, for some parameter ε > 0, we use step size

$$\eta =\frac{{\beta }_{min}{\epsilon }^2}{16}$$

and our dataset is of a size that satisfies

$$\left|S\right|=\frac{32}{{\beta }_{min}^2{\epsilon }^2}\log \left(\frac{2{\Vert {\theta }_0-{\theta }^{\ast }\Vert }^2}{\epsilon }\right).$$

Then, we can bound the expected parameter error with

$$\mathbf{E}\left[{\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }^2\right]\le {\epsilon }^{2}M$$

and the expected risk with

$$\mathbf{E}\left[l\left(\widehat{w}\right)-\underset{w}{min}l\left(w\right)\right]\le \chi +\frac{{\beta }_{min}\epsilon }{8\rho }.$$

Proof

In order to apply Theorem A.1, we have to verify all its conditions hold in the independent case.

First, we notice that (11) is used only to bound the covariance of the sufficient statistics. From Lemma E.1, we know that these can be bounded by ${\beta }_i-{\beta }_i^2{\gamma }_i^2\ge \frac{{\beta }_{min}}{2}$. It follows that we can choose

$$c=\frac{{\beta }_{min}}{4},$$

and we can consider (11) satisfied, for the purposes of applying the theorem.

Second, to verify (12), we can use Lemma E.5. For this to work, we need

$$3\exp \left(-\frac{m{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2}{9.34\text{artanh}\left({\gamma }_{max}\right)}\right)\le \frac{c}{M}=\frac{{\beta }_{min}}{8m}.$$

This happens whenever the number of labeling functions satisfies

$$m\ge \frac{9.34\text{artanh}\left({\gamma }_{max}\right)}{{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2}\log \left(\frac{24m}{{\beta }_{min}}\right).$$

The remaining assumptions, (13), (14), (15), and (16), are satisfied directly by the assumptions of this corollary. So, we can apply Theorem A.1, which produces the desired result. □

F Proofs of Independent Model Lemmas

Lemma E.1

The expected values and covariances of the sufficient statistics are, for all i ≠ j,

$$\begin{gathered} \mathbf{E}\left[{\mathrm{\Lambda }}_{i}Y\right]={\beta }_i{\gamma }_i \\ \mathbf{E}\left[{\mathrm{\Lambda }}_i^2\right]={\beta }_i \\ \mathbf{V}\mathbf{a}\mathbf{r}\left({\mathrm{\Lambda }}_{i}Y\right)={\beta }_i-{\beta }_i^2{\gamma }_i^2 \\ \mathbf{V}\mathbf{a}\mathbf{r}\left({\mathrm{\Lambda }}_i^2\right)={\beta }_i-{\beta }_i^2 \\ \mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_{i}Y,{\mathrm{\Lambda }}_{j}Y\right)=0 \\ \mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_i^2,{\mathrm{\Lambda }}_j^2\right)=0 \\ \mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_{i}Y,{\mathrm{\Lambda }}_j^2\right)=0. \end{gathered}$$

Proof

We prove each of the statements in turn. For the first statement,

$$\begin{gathered} \mathbf{E}\left[{\mathrm{\Lambda }}_{i}Y\right]=\mathbf{P}\left({\mathrm{\Lambda }}_i=Y\right)-\mathbf{P}\left({\mathrm{\Lambda }}_i=-Y\right) \\ ={\beta }_i\frac{1+{\gamma }_i}{2}-{\beta }_i\frac{1-{\gamma }_i}{2} \\ ={\beta }_i{\gamma }_i. \end{gathered}$$

For the second statement,

$$\begin{gathered} \mathbf{E}\left[{\mathrm{\Lambda }}_i^2\right]=\mathbf{P}\left(\mathrm{\Lambda }=Y\right)+\mathbf{P}\left(\mathrm{\Lambda }=-Y\right) \\ ={\beta }_i\frac{1+{\gamma }_i}{2}+{\beta }_i\frac{1-{\gamma }_i}{2} \\ ={\beta }_i. \end{gathered}$$

For the remaining statements, we derive the second moments; converting these to an expression of the covariance is trivial. For the third statement,

$$\mathbf{E}\left[{\left({\mathrm{\Lambda }}_{i}Y\right)}^2\right]=\mathbf{E}\left[{\mathrm{\Lambda }}_i^2{Y}^2\right]=\mathbf{E}\left[{\mathrm{\Lambda }}_i^2\right]={\beta }_i.$$

For the fourth statement,

$$\mathbf{E}\left[{\left({\mathrm{\Lambda }}_i^2\right)}^2\right]=\mathbf{E}\left[{\mathrm{\Lambda }}_i^4\right]=\mathbf{E}\left[{\mathrm{\Lambda }}_i^2\right]={\beta }_i.$$

For subsequent statements, we first derive that

$$\mathbf{E}\left[{\mathrm{\Lambda }}_{i}Y|Y\right]={\beta }_i\frac{1+{\gamma }_i}{2}-{\beta }_i\frac{1-{\gamma }_i}{2}={\beta }_i{\gamma }_i$$

and

$$\mathbf{E}\left[{\mathrm{\Lambda }}_i^2|Y\right]={\beta }_i\frac{1+{\gamma }_i}{2}+{\beta }_i\frac{1-{\gamma }_i}{2}={\beta }_i.$$

Now, for the fifth statement,

$$\mathbf{E}\left[\left({\mathrm{\Lambda }}_{i}Y\right)\left({\mathrm{\Lambda }}_{j}Y\right)\right]=\mathbf{E}\left[\mathbf{E}\left[{\mathrm{\Lambda }}_{i}Y|Y\right]\mathbf{E}\left[{\mathrm{\Lambda }}_{j}Y|Y\right]\right]={\beta }_i{\gamma }_i{\beta }_j{\gamma }_j.$$

For the sixth statement,

$$\mathbf{E}\left[\left({\mathrm{\Lambda }}_i^2\right)\left({\mathrm{\Lambda }}_j^2\right)\right]=\mathbf{E}\left[\mathbf{E}\left[{\mathrm{\Lambda }}_i^2|Y\right]\mathbf{E}\left[{\mathrm{\Lambda }}_i^2|Y\right]\right]={\beta }_i{\beta }_j.$$

Finally, for the seventh statement,

$$\mathbf{E}\left[\left({\mathrm{\Lambda }}_{i}Y\right)\left({\mathrm{\Lambda }}_j^2\right)\right]=\mathbf{E}\left[\mathbf{E}\left[{\mathrm{\Lambda }}_{i}Y|Y\right]\mathbf{E}\left[{\mathrm{\Lambda }}_i^2|Y\right]\right]={\beta }_i{\gamma }_i{\beta }_j.$$

This completes the proof. □

Lemma E.2

It holds that

$${\gamma }_i=\text{tanh}({\psi }_i).$$

Proof

From the definitions,

$${\beta }_i=\frac{\exp \left({\psi }_i+{\varphi }_i\right)+\exp \left(-{\psi }_i+{\varphi }_i\right)}{\exp \left({\psi }_i+{\varphi }_i\right)+\exp \left(-{\psi }_i+{\varphi }_i\right)+1}$$

and

$${\beta }_i{\gamma }_i=\frac{\exp \left({\psi }_i+{\varphi }_i\right)-\exp \left(-{\psi }_i+{\varphi }_i\right)}{\exp \left({\psi }_i+{\varphi }_i\right)+\exp \left(-{\psi }_i+{\varphi }_i\right)+1}.$$

Therefore,

$${\gamma }_i=\frac{\exp \left({\psi }_i+{\varphi }_i\right)-\exp \left(-{\psi }_i+{\varphi }_i\right)}{\exp \left({\psi }_i+{\varphi }_i\right)+\exp \left(-{\psi }_i+{\varphi }_i\right)+1}=\tanh \left({\psi }_i\right),$$

which is the desired result. □

Lemma E.3

For any feasible model, it will be the case that, for any other feasible parameter vector $\widehat{\psi }$,

$$\mathbf{P}\left({\widehat{\psi }}^T\mathrm{\Lambda }Y\le \frac{m}{2}{\gamma }_{min}{\left(\gamma \beta \right)}_{min}\right)\le \exp \left(-\frac{m{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2}{9.34\text{artanh}\left({\gamma }_{max}\right)}\right).$$

Proof

We start by noticing that

$${\widehat{\psi }}^T\mathrm{\Lambda }Y={\displaystyle \sum _{i=1}^m{\widehat{\psi }}_i}{\mathrm{\Lambda }}_{i}Y.$$

Since in this model, all the Λ_iY are independent of each other, we can bound this sum using a concentration bound. First, we note that

$$\left|{\widehat{\psi }}_i{\mathrm{\Lambda }}_{i}Y\right|\le {\widehat{\psi }}_i$$

Second, we note that

$$\mathbf{E}\left|{\widehat{\psi }}_i{\mathrm{\Lambda }}_{i}Y\right|={\widehat{\psi }}_i{\beta }_i{\gamma }_i$$

and

$$\mathbf{V}\mathbf{a}\mathbf{r}\left({\widehat{\psi }}_i{\mathrm{\Lambda }}_{i}Y\right)={\widehat{\psi }}_i^2\left({\beta }_i-{\beta }_i^2{\gamma }_i^2\right)$$

but

$$\left|{\widehat{\psi }}_i{\mathrm{\Lambda }}_{i}Y\right|\le {\widehat{\psi }}_i\le \text{artanh}\left({\gamma }_{max}\right)\triangleq {\widehat{\psi }}_{max}$$

because, for feasible models, by definition

$${\gamma }_{min}\le \text{artanh}\left({\gamma }_{min}\right)\le {\widehat{\psi }}_i\le \text{artanh}\left({\gamma }_{max}\right).$$

Therefore, applying Bernstein’s inequality gives us, for any t,

$$\mathbf{P}\left({\displaystyle \sum _{i=1}^m{\widehat{\psi }}_i{\mathrm{\Lambda }}_{i}Y-{\displaystyle \sum _{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i\le -t}}\right)\le \exp \left(-\frac{3t^2}{6{\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i^2{\gamma }_i{\beta }_i{\gamma }_i+2{\widehat{\psi }}_{max}t}}\right).$$

It follows that, if we let

$$t=\frac{1}{2}{\displaystyle \sum _{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i},$$

then we get

$$\begin{gathered} \mathbf{P}\left({\displaystyle \sum _{i=1}^m{\widehat{\psi }}_i{\mathrm{\Lambda }}_{i}Y-{\displaystyle \sum _{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i\le -t}}\right)\le \exp \left(-\frac{3{\left(\frac{1}{2}{\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i}\right)}^2}{6{\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i^2{\gamma }_i{\beta }_i{\gamma }_i}+2{\widehat{\psi }}_{\max }\left(\frac{1}{2}{\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i}\right)}\right) \\ \le \exp \left(-\frac{3{\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i}}{24{\gamma }_{\max }{\widehat{\psi }}_{\max }+4{\widehat{\psi }}_{\max }}\right) \\ \le \exp \left(-\frac{3m\left(1-{\gamma }_{\max }\right)}{28{\widehat{\psi }}_{\max }}\right) \\ \le \exp \left(-\frac{3{\left({\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i}\right)}^2}{24{\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i^2{\beta }_i+4{\widehat{\psi }}_{\max }\left({\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i}\right)}}\right) \\ \le \exp \left(-\frac{3{\gamma }_{\min }\left({\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i}\right)\left({\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i}\right)}{24{\widehat{\psi }}_{\max }{\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i+4{\widehat{\psi }}_{\max }\left({\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i}\right)}}\right) \\ \le \exp \left(-\frac{3{\gamma }_{\min }\left({\displaystyle {\sum }_{i=1}^m{\widehat{\psi }}_i{\beta }_i{\gamma }_i}\right)}{28{\widehat{\psi }}_{\max }}\right) \\ \le \exp \left(-\frac{m{\gamma }_{\min }^2{\left(\gamma \beta \right)}_{\min }}{9.34{\widehat{\psi }}_{\max }}\right). \end{gathered}$$

This is the desired expression. □

Lemma E.4

The covariances of the sufficient statistics, conditioned on Λ, are for all i ≠ j,

$$\begin{gathered} \mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_{i}Y,{\mathrm{\Lambda }}_{j}Y|\mathrm{\Lambda }\right)={\mathrm{\Lambda }}_i{\mathrm{\Lambda }}_j{\mathrm{sech}}^2\left({\psi }^T\mathrm{\Lambda }\right) \\ \mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_i^2,{\mathrm{\Lambda }}_j^2|\mathrm{\Lambda }\right)=0. \end{gathered}$$

Proof

The second result is obvious, so it suffices to prove only the first result. Clearly,

$$\mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_{i}Y,{\mathrm{\Lambda }}_{j}Y|\mathrm{\Lambda }\right)={\mathrm{\Lambda }}_i{\mathrm{\Lambda }}_j\mathbf{V}\mathbf{a}\mathbf{r}\left(Y|\mathrm{\Lambda }\right)={\mathrm{\Lambda }}_i{\mathrm{\Lambda }}_j\left(1-\mathbf{E}{\left[Y|\mathrm{\Lambda }\right]}^2\right).$$

Plugging into the distribution formula lets us conclude that

$$\mathbf{E}\left[Y|\mathrm{\Lambda }\right]=\frac{\exp \left({\psi }^T\mathrm{\Lambda }+{\varphi }^T{\mathrm{\Lambda }}^2\right)-\exp \left(-{\psi }^T\mathrm{\Lambda }+{\varphi }^T{\mathrm{\Lambda }}^2\right)}{\exp \left({\psi }^T\mathrm{\Lambda }+{\varphi }^T{\mathrm{\Lambda }}^2\right)+\exp \left(-{\psi }^T\mathrm{\Lambda }+{\varphi }^T{\mathrm{\Lambda }}^2\right)}={\tanh }^2\left({\psi }^T\mathrm{\Lambda }\right),$$

and so

$$\mathbf{C}\mathbf{o}\mathbf{v}\left({\mathrm{\Lambda }}_{i}Y,{\mathrm{\Lambda }}_{j}Y|\mathrm{\Lambda }\right)={\mathrm{\Lambda }}_i{\mathrm{\Lambda }}_j\left(1-{\tanh }^2\left({\psi }^T\mathrm{\Lambda }\right)\right)={\mathrm{\Lambda }}_i{\mathrm{\Lambda }}_j{\mathrm{sech}}^2\left({\psi }^T\mathrm{\Lambda }\right),$$

which is the desired result. □

Lemma E.5

If θ and θ* are two feasible models, then for any u

$${\mathbf{E}}_{{\theta }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{\theta }\left(Y|\mathrm{\Lambda }\right)\right]\le 3\exp \left(-\frac{m{\beta }_{min}^2{\gamma }_{min}^3}{8\text{artanh}\left({\gamma }_{max}\right)}\right).$$

Proof

First, we note that, by the result of Lemma E.4,

$$\mathbf{V}\mathbf{a}{\mathbf{r}}_{\theta }\left(Y|\mathrm{\Lambda }\right)={\mathrm{sech}}^2\left({\psi }^T\mathrm{\Lambda }\right).$$

Therefore,

$${\mathbf{E}}_{{\theta }^{\ast }}\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{\theta }\left(Y|\mathrm{\Lambda }\right)\right]={\mathbf{E}}_{{\theta }^{\ast }}\left[{\mathrm{sech}}^2\left({\psi }^T\mathrm{\Lambda }\right)\right].$$

Applying Lemma E.3, we can bound this with

$$\begin{gathered} {\mathbf{E}}_{\theta \ast }\left[\mathbf{V}\mathbf{a}{\mathbf{r}}_{\theta }\left(u^T\mathrm{\Lambda }Y|\mathrm{\Lambda }\right)\right]\le \left({\text{sech}}^2\left(\frac{m}{2}{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2\right)+\exp \left(-\frac{m{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2}{9.34\text{artanh}\left({\gamma }_{max}\right)}\right)\right) \\ \le \left(2\exp \left(-\frac{m}{2}{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2\right)+\exp \left(-\frac{m{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2}{9.34\text{artanh}\left({\gamma }_{max}\right)}\right)\right) \\ \le 3\exp \left(-\frac{m{\left(\gamma \beta \right)}_{min}{\gamma }_{min}^2}{9.34\text{artanh}\left({\gamma }_{max}\right)}\right). \end{gathered}$$

This is the desired expression. □

G Additional Experimental Details

G.1 Relation Extraction Experiments

G.1.1 Systems

The original distantly-supervised experiments which we compare against as baselines–which we refer to as using the if-then-return (ITR) approach of distant or programmatic supervision–were implemented using DeepDive, an open-source system for building extraction systems.⁵ For our primary experiments, we adapted these programs to the framework and approach described in this paper, directly utilizing distant supervision rules as labeling functions.

In the disease tagging user experiments, we used an early version of our new lightweight extraction framework based around data programming, formerly called DDLite [12], now Snorkel.⁶ Snorkel is based around a Jupyter-notebook based interface, allowing users to iteratively develop labeling functions in Python for basic extraction tasks involving simple models. Details of the basic discriminative models used can be found in the Snorkel repository; in particular, Snorkel uses a simple logistic regression model with generic features defined in part over dependency paths⁷, and a basic LSTM model implemented using the Theano library.⁸ Snorkel is currently under continued development, and all versions are open-source.

G.1.2 Applications

We consider three primary applications which involve the extraction of binary relation mentions of some specific type from unstructured text input data. At a high level, all three system pipelines consist of an initial candidate extraction phase which leverages some upstream model or suite of models to extract mentions of involved entities, and then considers each pair of such mentions that occurs within the same local neighborhood in a document as a candidate relation mention to be potentially extracted. In each case, the discriminative model that we are aiming to train–and that we evaluate in this paper–is a binary classifier over these candidate relation mentions, which will decide which ones to output as final true extractions. In all tasks, we preprocessed raw input text with Stanford CoreNLP⁹, and then either used CoreNLP’s NER module or our own entity-extraction models to extract entity mentions. Further details of the basic information extraction pipeline utilized can be seen in the tutorials of the systems used, and in the referenced papers below.

In the 2014 TAC-KBP Slot Filling task, which we also refer to as the News application, we train a set of extraction models for a variety of relation types from news articles [30]. In reported results in this paper, we average over scores from each relation type. We utilized CoreNLP’s NER module for candidate extraction, and utilized CoreNLP outputs in developing the distant supervision rules/labeling functions for these tasks. We also considered a slightly simpler discriminative model than the one submitted in the 2014 competition, as reported in [2]: namely, we did not include any joint factors in our model in this paper.

In the Genomics application, our goal with our collaborators at Stanford Medicine was to extract mentions of genes that if mutated may cause certain phenotypes (symptoms) linked to Mendelian diseases, for use in a clinical diagnostic setting. The code for this project is online, although it remains partially under development and thus some material from our collaborators is private.¹⁰

In the Pharmacogenomics application, our goal was to extract interactions between genes for use in downstream pharmacogenomics research analyses; full results and system details are reported in [21].

In the Disease Tagging application, which we had our collaborators work on during a set of short hackathons as a user study, the goal was to tag mentions of human diseases in PubMed abstracts. We report results of this hackathon in [12], as well as in our Snorkel tutorial online.

G.1.3 Labeling Functions

In general, we saw two broad types of labeling functions in both prior applications (when they were referred to as “distant supervision rules”) and in our most recent user studies. The first type of labeling function leverages some weak supervision signal, such as an external knowledgebase (as in traditional distant supervision), very similar to the example illustrated in Fig. 1(a). All of the applications studied in this paper used some such labeling function or set of labeling functions.

The second type of labeling function uses simple heuristic patterns as positive or negative signals. For our text extraction examples, these heuristic patterns primarily consisted of regular expressions, also similar to the example pseudocode in Fig. 1(a). Further specific details of both types of labeling functions, as well as others used, can be seen in the linked code repositories and referenced papers.

G.2 Synthetic Experiments

In Fig. 3(a–b), we ran synthetic experiments with labeling functions having constant coverage β = 0.1, and accuracy drawn from α ∼ Uniform(μ_α − 0.25, μ_α + 0.25) where μ_α = 0.75 in the above plots. In both cases we used 1000 normally-drawn features having mean correlation with the true label class of 0.5.

Figure 3.

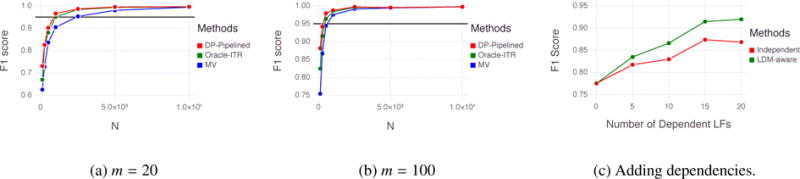
Comparisons of data programming to two oracle methods on synthetic data.

In this case we compare data programming (DP-Pipelined) against two baselines. First, we compare against an if-then-return setup where the ordering is optimal (ITR-Oracle). Second, we compare against simple majority vote (MV).

In Fig. 3(c), we show an experiment where we add dependent labeling functions to a set of m_ind = 50 independent labeling functions, and either provided this dependency structure (LDM-Aware) or did not (Independent). In this case, the independent labeling functions had the same configurations as in (a-b), and the dependent labeling functions corresponded to “fixes” or “reinforces”-type dependent labeling functions.