L-GATOR: Genetic Association Testing for a Longitudinally Measured Quantitative Trait in Samples with Related Individuals

Abstract

In complex-trait mapping, when each subject has multiple measurements of a quantitative trait over time, power for detecting genetic association can be gained by the inclusion of all measurements and not just single time points or averages in the analysis. To increase power and control type 1 error, one should account for dependence among observations for a single individual as well as dependence between observations of related individuals if they are present in the sample. We propose L-GATOR, a retrospective, mixed-effects method for association mapping of longitudinally measured traits in samples with related individuals. L-GATOR allows arbitrary time points for different individuals, incorporates both time-varying and static covariates, and properly addresses various types of dependence. In simulations, we show that L-GATOR outperforms existing prospective methods in terms of both type 1 error and power when there is phenotype model misspecification or missing data. Compared with the previously proposed longGWAS method, L-GATOR was more than ten times faster for association testing in our simulations and almost 100 times faster for parameter estimation. L-GATOR is applicable to essentially arbitrary combinations of related and unrelated individuals, including small families as well as large, complex pedigrees. We apply the method to data from the Framingham Heart Study to identify association between longitudinal systolic blood pressure measurements and genome-wide SNPs. Of the smallest p values, one-third occur in or near genes that have been previously identified as associated with pulse pressure (such as PIK3CG) and systolic and diastolic blood pressure (such as C10orf107), showing that L-GATOR is able to prioritize relevant loci in a genome screen.

Introduction

In some genome-wide association studies (GWASs), phenotype data are measured longitudinally or repeatedly for each individual in the sample. In such studies, association analyses based on single-time-point measurements of the trait, or on individuals’ average trait values, can lose power by not making full use of the available phenotype information.¹ Furthermore, when individuals’ average phenotype values are analyzed, it can be problematic to incorporate dynamic (i.e., time-varying) covariates in an appropriate way. In addition, when related individuals are included in the sample, failure to account for residual correlation among relatives’ phenotypes can lead to inflated type 1 error and reduced power. A statistical analysis that uses all the longitudinal information and properly accounts for relatedness among individuals, as well as for dependence among observations from an individual, has the potential to improve power for detecting genetic association.

For genetic analysis of longitudinal traits, methods that are appropriate for unrelated individuals (i.e., that assume there is no residual phenotypic correlation among individuals) include fGWAS² and MASAL.³ For related individuals, the FBAT-PC-based methods^{4, 5, 6} have been developed, and these can allow covariates and missing phenotype values, but they have stringent requirements on the availability of genotype data on relatives. The longGWAS method¹ also allows covariates and is applicable to a wider range of samples than FBAT-PC, but it is limited in its handling of different time points for different individuals and missing data.

We propose L-GATOR, a retrospective, mixed-model method for genetic association analysis of longitudinal traits in related individuals. L-GATOR can be viewed as an extension, to longitudinal traits, of the MASTOR method⁷ for quantitative traits. Features of L-GATOR include the following: (1) it is applicable to arbitrary combinations of related and unrelated individuals, (2) it allows both static and dynamic covariates to be included in the analysis, (3) it allows different individuals to have different time points, (4) it has correct type 1 error even when the trait model is misspecified, and (5) it improves power by using information on dependence among relatives to make use of observations that have either missing phenotype or missing genotype data. For comparison, we also propose and implement PMALT, a prospective, mixed-model method that is an extension, to longitudinal traits, of the GTAM method⁸ for quantitative traits and that is also closely related to the longGWAS method.¹

Through simulations, we demonstrate that L-GATOR represents an improvement over other methods in terms of type 1 error and power. The proposed methods are applied to a whole-genome analysis of longitudinal systolic blood pressure (SBP) measurements from the Framingham Heart Study (FHS).

Material and Methods

Suppose that in an association study we have phenotype, covariate, and genotype data for a group of m individuals with known pedigree information. The phenotype data are assumed to consist of longitudinal measurements of a quantitative trait. We allow in the analysis both dynamic covariates (e.g., age) and static covariates (e.g., sex). We consider the phenotype and covariate data at a single time point for a given individual to be a “record” for that individual. Each record thus provides a snapshot of the trait and the covariates of an individual at a specified time point. Different individuals are allowed to have different numbers of records and different time points. We can think of records as being nested within individuals and individuals as being nested within families. We assume that the set of individuals is partitioned into families in such a way that if two individuals are in different families, then they are unrelated. (A family is permitted to consist of a single individual if that person is unrelated to anyone else in the sample.) Assume, for simplicity, that the m individuals in the sample are ordered so that individuals within the same family are listed consecutively. Denote the number of records for individual i, $1\le i\le m$, by $n_i$, and denote the total number of records by $n={\sum }_{i=1}^m{n}_i$. We define $\mathbf{t}={\left({\mathbf{t}}_1^T,{\mathbf{t}}_2^T,\cdots ,{\mathbf{t}}_m^T\right)}^T$, where ${\mathbf{t}}_i$ is a vector of length $n_i$ whose j^th entry, $t_{ij}$, is equal to the measurement time of the j^th record on the i^th individual for $1\le j\le n_i$. (In practice, only the time intervals and not the actual times are needed.) We let $\mathbf{Y}$ denote the trait vector (length n) and let $\mathbf{W}$ denote the covariate matrix (size $n\times q$), which is assumed to include an intercept. Here, $\mathbf{Y}$ and the rows of $\mathbf{W}$ are assumed to be arranged in the same order as $\mathbf{t}$, such that all the records for person 1 are listed first, followed by all the records for person 2, and so on. Note that $\mathbf{W}$ can incorporate dynamic covariates such as age. Static covariates in $\mathbf{W}$ retain the same value for all records on a given individual. Table 1 shows an example of the assumed data structure. We define a “complete record” to be a table row that contains no missing values, i.e., it consists of the data of a single individual at a single time point for which the phenotype and covariates are observed without missing values. For example, in Table 1, individual 101 has three complete records, and individual 112 has two complete records. Note that we use the term “complete record” to refer only to phenotype and covariate data and not to genotype data.

Table 1.

Example of Phenotype and Covariate Data

Family	Individual	Record	t	Y	W
					Intercept	Static Covariate	Dynamic Covariate
1	101	1	40.01	4.79	1	1	3.03
1	101	2	42.04	4.71	1	1	3.06
1	101	3	44.06	4.77	1	1	3.04
1	112	1	58.67	4.86	1	0	2.97
1	112	2	60.38	4.93	1	0	2.98
1	31	1	27.38	5.11	1	1	3.29
1	31	2	29.70	5.24	1	1	3.28
1	31	3	31.52	5.17	1	1	3.27
1	31	4	33.27	5.21	1	1	3.31
2	15	1	58.82	4.91	1	0	3.15
2	15	2	60.91	4.86	1	0	3.18
2	15	3	62.71	4.77	1	0	3.21

The first three columns show the hierarchy of family, individual, and record. In columns 4 and 5, $\mathbf{t}$ denotes the measurement time (note that only time intervals and not the times themselves are used in the analysis), and $\mathbf{Y}$ denotes the trait value. The covariate matrix, $\mathbf{W}$, is shown with an intercept column, one static covariate, and one dynamic covariate. In general, $\mathbf{W}$ is assumed to always contain the intercept column, and it could contain any number of additional static and/or dynamic covariates.

For simplicity, we assume that the observed genetic variants are biallelic. (The extension to multiallelic variants is similar to that given in Appendix A of Jakobsdottir and McPeek.⁷) Markers are tested one at a time for association. For a given variant, with alleles arbitrarily labeled 0 and 1, we write the corresponding genotype data as a vector $\mathbf{X}$ (length m) with i^th component

$$X_i=\frac{1}{2}\times \left(\text{the}\text{number}\text{of}\text{alleles}\text{of}\text{type}1\text{in}\text{individual}i\right),1\le i\le m.$$

The vector $\mathbf{X}$ differs from $\mathbf{Y}$ and $\mathbf{W}$ in that it is indexed by individual rather than by record. We define the matrix $\mathbf{B}$ (size $n\times m$) to be a “vertically expanded identity matrix,” i.e.,

$$\mathbf{B}=\begin{array}{c}\left(\begin{array}{c}{B}_1\\ ⋮\\ B_m\end{array}\right)\end{array},$$ (Equation 1)

where, for $1\le i\le m$, $B_i$ is an $n_i\times m$ matrix with every row equal to the i^th row of the $m\times m$ identity matrix, i.e., the $\left(j,k\right)$^th element of $B_i$ is $1_{k=i}$. Then, for example, to expand the genotype data, $\mathbf{X}$, from the individual level to the record level, we can simply write $\mathbf{B}\mathbf{X}$.

We assume known pedigree structure and define the $m\times m$ kinship matrix of the sampled individuals by

$$\mathbf{\Phi }=\left(\begin{array}{cccc}1+h_1& 2{\varphi }_{12}& \cdots & 2{\varphi }_{1m}\\ 2{\varphi }_{12}& 1+h_2& \cdots & 2{\varphi }_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ 2{\varphi }_{1m}& 2{\varphi }_{2m}& \cdots & 1+h_m\end{array}\right),$$

where $h_i$ is the inbreeding coefficient of individual i, and ${\varphi }_{ij}$ is the kinship coefficient between individuals i and $j$, where $1\le i\le m$ and $1\le j\le m$. Matrix $\mathbf{\Phi }$ is block-diagonal such that each diagonal block represents the kinship matrix of a family and the off-diagonal blocks are 0 matrices.

In what follows, we introduce two association testing methods: PMALT (which is a loose acronym for “prospective mixed-model method for association of a longitudinal trait”) and L-GATOR (an acronym for “longitudinal genetic association test on relatives”). PMALT is a prospective method, meaning that the analysis is conditional on $\left(\mathbf{W},\mathbf{X}\right)$ with $\mathbf{Y}$ treated as random, whereas L-GATOR is a retrospective method, meaning that the analysis is conditional on $\left(\mathbf{W},\mathbf{Y}\right)$ with $\mathbf{X}$ treated as random. An important difference between the two is that the PMALT analysis includes only genotyped individuals who have at least one complete record, whereas the L-GATOR analysis can incorporate certain types of partially missing data, as described in the subsection L-GATOR Incorporates Incomplete Data.

PMALT: Missing Values Excluded

The PMALT method for longitudinal quantitative traits can be viewed as an extension of the GTAM method⁸ for non-longitudinal quantitative traits. Like GTAM, PMALT can be formulated as a version of the prospective likelihood score test based on a mixed model for phenotype conditional on genotype and covariates. (This is described in more detail in the following paragraphs.) In PMALT, only individuals with observed genotype data at the SNP being tested and with at least one complete record are included in the analysis. Furthermore, for each genotyped individual, incomplete records are ignored. Notationally, once we have culled the data that will be ignored by PMALT, we could write that in the PMALT analysis, the number of records, $n_i$, for individual i satisfies $n_i\ge 1$ for each $1\le i\le m$, such that the resulting $\mathbf{X},\mathbf{Y}$, and $\mathbf{W}$ are assumed to contain no missing values. The numbers of records and the time points are permitted to differ across individuals. The set of individuals included in the analysis can differ across variants because of missing genotype data for some individuals at some SNPs.

The modeling assumption underlying PMALT is that the trait vector $\mathbf{Y}$ (possibly after suitable transformation of the phenotype and/or covariates) has a multivariate normal distribution conditional on $\mathbf{W}$ and $\mathbf{X}$,

$$\mathbf{Y}|\mathbf{W},\mathbf{X}\sim \text{MVN}\left(\mathit{\mu },\mathbf{\Sigma }\right),$$ (Equation 2)

where the mean, $\mathit{\mu }$, is assumed to be the following linear function of the covariates and genotype data:

$$\mathit{\mu }=\mathbf{W}\mathit{\beta }+\mathbf{B}\mathbf{X}\gamma ,$$ (Equation 3)

where $\mathit{\beta }$ is an unknown length-q vector of fixed effects and γ is an unknown scalar representing the association between the variant and the trait. Additional sources of variation are incorporated in the variance-covariance matrix,

$$\mathbf{\Sigma }={\sigma }_E^2\mathbf{I}+{\sigma }_I^2\mathbf{J}+{\sigma }_A^2\mathbf{K}+{\sigma }_T^2\mathbf{L},$$ (Equation 4)

where ${\sigma }_E^2,{\sigma }_I^2,{\sigma }_A^2$, and ${\sigma }_T^2$ are unknown variance components and $\mathbf{I},\mathbf{J},\mathbf{K},$ and $\mathbf{L}$ are matrices of size $n\times n$. $\mathbf{I},\mathbf{J},$ and $\mathbf{K}$ are known matrices, whereas $\mathbf{L}$ includes two additional unknown parameters. $\mathbf{I}$ is the identity matrix, so ${\sigma }_E^2$ represents variance due to random measurement error at the record level. $\mathbf{J}$ and $\mathbf{L}$ are both block-diagonal such that each diagonal block corresponds to one individual and the off-diagonal blocks are 0 matrices. For the i^th individual, the $n_i\times n_i$ diagonal block ${\mathbf{J}}_i$ is a matrix with every entry equal to 1, so ${\sigma }_I^2$ stands for variance due to non-genetic individual random effects that do not vary over time. For the i^th individual, the $n_i\times n_i$ diagonal block ${\mathbf{L}}_i$ has a ${\left(j,k\right)}^{\text{th}}$ entry given by $\text{exp}\left(-\alpha {\left|t_{ij}-t_{ik}\right|}^c\right)$, where $1\le j\le n_i$, $1\le k\le n_i$, α and c are unknown parameters and $t_{ij}$ and $t_{ik}$ are the j^th and k^th components of the subvector ${\mathbf{t}}_i$ in the vector $\mathbf{t}$, so that $\left|t_{ij}-t_{ik}\right|$ is the absolute difference in measurement times between the j^th and k^th records for individual i. We think of $\mathbf{L}$ as modeling autocorrelation in an individual’s trait measured over time.⁹ Therefore, ${\sigma }_T^2$ represents variance attributable to time-varying individual random effects. Parameters α and c control the time dependence between the trait measurements for an individual. Note that $c=1$ corresponds to a continuous-time analog of the first-order AR covariance. $\mathbf{K}=\mathbf{B}\mathbf{\Phi }{\mathbf{B}}^T$ is the kinship matrix expanded from the individual level to the record level; hence, ${\sigma }_A^2$ stands for variance attributed to additive polygenic random effects. The variance-component model is similar to other polygenic models that have been proposed for linkage analysis and association testing in longitudinal family studies.^{10, 11, 12, 13} In this setting, the covariance matrix $\mathbf{\Sigma }$ depends on six unknown parameters, ${\sigma }_E^2,{\sigma }_I^2,{\sigma }_A^2,{\sigma }_T^2,\alpha ,$ and c. For convenience, we reparametrize the variance components so that one of the parameters is the total residual variance (for an outbred individual), ${\sigma }^2={\sigma }_E^2+{\sigma }_I^2+{\sigma }_A^2+{\sigma }_T^2$, and the others are the narrow-sense heritability, ${\sigma }_A^2/{\sigma }^2$, and the proportions of (residual) variance explained by individual effects, ${\sigma }_I^2/{\sigma }^2$, and by measurement error, ${\sigma }_E^2/{\sigma }^2$. We drop ${\sigma }_T^2/{\sigma }^2$ from the parameterization to avoid redundancy. The vector of unknown parameters that appear in $\mathbf{\Sigma }$ can then be written as $\left({\sigma }^2,\mathit{\tau }\right)$, where we define $\mathit{\tau }=\left({\sigma }_E^2/{\sigma }^2,{\sigma }_I^2/{\sigma }^2,{\sigma }_A^2/{\sigma }^2,\alpha ,c\right)$. We further write

$$\mathbf{\Sigma }={\sigma }^2\mathbf{V}\left(\mathit{\tau }\right),$$ (Equation 5)

$$\text{where}\mathbf{V}\left(\mathit{\tau }\right)\equiv \frac{{\sigma }_E^2}{{\sigma }^2}\mathbf{I}+\frac{{\sigma }_I^2}{{\sigma }^2}\mathbf{J}+\frac{{\sigma }_A^2}{{\sigma }^2}\mathbf{K}+\left(1-\frac{{\sigma }_E^2}{{\sigma }^2}-\frac{{\sigma }_I^2}{{\sigma }^2}-\frac{{\sigma }_A^2}{{\sigma }^2}\right)\mathbf{L}.$$ (Equation 6)

For convenience, we often drop the argument $\mathit{\tau }$ and denote this matrix by $\mathbf{V}$. In the special case when all individuals are outbred, $\mathbf{V}$ is the correlation matrix of $\mathbf{Y}|\mathbf{W},\mathbf{X}$.

To obtain a prospective likelihood score test of the null hypothesis $H_0:$ $\gamma =0$ in the model defined by Equations 2, 3, 4, 5, and 6, one would typically first obtain the null maximum likelihood estimate (MLE) of the nuisance parameter $\left(\mathit{\beta },{\sigma }^2,\mathit{\tau }\right)$, i.e., the MLE of $\left(\mathit{\beta },{\sigma }^2,\mathit{\tau }\right)$ in the model with $\gamma =0$. We denote this null MLE by $\left({\hat{\mathit{\beta }}}_0,{\hat{\sigma }}_0^2,{\hat{\mathit{\tau }}}_0\right)$. (See Appendix A for details on how to obtain the null MLE.) We define the transformed phenotypic residual to be

$$\mathbf{R}\mathbf{Y}={\hat{\mathbf{V}}}_0^{-1}\left(\mathbf{Y}-\mathbf{W}{\hat{\mathit{\beta }}}_0\right),$$ (Equation 7)

where $\mathbf{R}={\hat{\mathbf{V}}}_0^{-1}-{\hat{\mathbf{V}}}_0^{-1}\mathbf{W}{\left({\mathbf{W}}^T{\hat{\mathbf{V}}}_0^{-1}\mathbf{W}\right)}^{-1}{\mathbf{W}}^T{\hat{\mathbf{V}}}_0^{-1}$, ${\hat{\mathbf{V}}}_0=\mathbf{V}\left({\hat{\mathit{\tau }}}_0\right)$, and ${\hat{\mathit{\beta }}}_0={\left({\mathbf{W}}^T{\hat{\mathbf{V}}}_0^{-1}\mathbf{W}\right)}^{-1}{\mathbf{W}}^T{\hat{\mathbf{V}}}_0^{-1}\mathbf{Y}$. The test statistic for the prospective likelihood score test could then be written as

$$S=\frac{{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{Y}}{\sqrt{{\widehat{\text{Var}}}_0\left[{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{Y}|\mathbf{X},\mathbf{W}\right]}}=\frac{{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{Y}}{\sqrt{{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{B}\mathbf{X}{\hat{\sigma }}_0^2}}=\frac{{\left(\mathbf{B}\mathbf{X}\right)}^T{\hat{\mathbf{V}}}_0^{-1}\left(\mathbf{Y}-\mathbf{W}{\hat{\mathit{\beta }}}_0\right)}{\sqrt{{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{B}\mathbf{X}{\hat{\sigma }}_0^2}},$$ (Equation 8)

where ${\hat{\sigma }}_0^2=n^{-1}{\mathbf{Y}}^T\mathbf{R}\mathbf{Y}=n^{-1}{\left(\mathbf{Y}-\mathbf{W}{\hat{\mathit{\beta }}}_0\right)}^T{\hat{\mathbf{V}}}_0^{-1}\left(\mathbf{Y}-\mathbf{W}{\hat{\mathit{\beta }}}_0\right)$ and where we have used the fact that $\mathbf{R}{\hat{\mathbf{V}}}_0\mathbf{R}=\mathbf{R}$ in deriving Equation 8. Under the null hypothesis, S would follow a standard normal distribution asymptotically. The PMALT test statistic is a slight variation on the prospective likelihood score test, given by

$$\text{PMALT}=\frac{{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{Y}}{\sqrt{{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{B}\mathbf{X}{\hat{\sigma }}_Y^2}}=\sqrt{\frac{{\hat{\sigma }}_0^2}{{\hat{\sigma }}_Y^2}}S,$$ (Equation 9)

where ${\hat{\sigma }}_Y^2={\left(n-q-1\right)}^{-1}{\mathbf{Y}}^T\mathbf{Q}\mathbf{Y}$, with $\mathbf{Q}=\mathbf{R}-\mathbf{R}\mathbf{B}\mathbf{X}{\left[{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{B}\mathbf{X}\right]}^{-1}{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}$. Here, ${\hat{\sigma }}_Y^2$ is an estimate of the residual variance of $\mathbf{Y}$ under the alternative model (e.g., as in generalized regression), whereas ${\hat{\sigma }}_0^2$ is an estimate of the residual variance of $\mathbf{Y}$ under the null model. Under the null hypothesis, ${\hat{\sigma }}_0^2/{\hat{\sigma }}_Y^2$ converges in probability to 1, so PMALT and S are asymptotically equivalent under the null hypothesis, and the asymptotic null distribution of PMALT is also standard normal.

Note that the numerator of the PMALT statistic can be written as ${\mathbf{X}}^T\mathbf{A}$, where $\mathbf{A}={\mathbf{B}}^T\mathbf{R}\mathbf{Y}$ is a vector whose i^th entry, $A_i$, is obtained via summation of individual i’s entries of the transformed phenotypic residual vector $\mathbf{R}\mathbf{Y}={\hat{\mathbf{V}}}_0^{-1}\left(\mathbf{Y}-\mathbf{W}{\hat{\mathit{\beta }}}_0\right)$. Thus, $A_i$ is a scalar quantity that encapsulates all the complete records (longitudinal measurements and covariates) for individual i into a single transformed phenotypic residual.

We can obtain a slightly different interpretation of the PMALT test statistic by viewing it as the t-statistic for testing $H_0:\gamma =0$ versus $H_1:\gamma \ne 0$ in the generalized regression model given by

$$\mathbf{Y}=\mathbf{W}\mathit{\beta }+\mathbf{B}\mathbf{X}\gamma +\mathit{ϵ},$$ (Equation 10)

with the assumption that $E\left(\mathit{ϵ}\right)=0$ and $\text{Var}\left(\mathit{ϵ}\right)={\sigma }^2{\hat{\mathbf{V}}}_0$, where ${\hat{\mathbf{V}}}_0$ is treated as fixed and known and $\mathit{\beta }$, γ, and ${\sigma }^2$ are treated as unknown. Let $\hat{\mathit{\beta }}$, $\hat{\gamma }$, and ${\hat{\sigma }}_Y^2$ represent the parameter estimates obtained by generalized regression under this model. Then the PMALT test statistic is the same as the generalized regression t-statistic for testing $H_0:\gamma =0$, which is given by

$$\text{PMALT}=\hat{\gamma }\sqrt{\frac{{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{B}\mathbf{X}}{{\hat{\sigma }}_Y^2}},$$ (Equation 11)

where $\hat{\gamma }={\left[{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{B}\mathbf{X}\right]}^{-1}{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{Y}$, ${\hat{\sigma }}_Y^2$ is as defined above, and the expressions in Equations 9 and 11 are equal.

Note that if the same individuals were genotyped at every tested SNP, then, in the expression for the PMALT test statistic given in Equation 9, $\mathbf{B}$, $\mathbf{R}$, $\mathbf{Y}$, and ${\hat{\sigma }}_Y^2$ would be the same for every SNP, and only the values of $\mathbf{X}$ would change across SNPs. However, if different individuals had missing genotypes at different SNPs, then not only would $\mathbf{B}$, $\mathbf{Y}$, and $\mathbf{X}$ change for every SNP, but, in principle, we would also need to re-estimate ${\hat{\mathit{\tau }}}_0$ at every SNP, in addition to recalculating $\mathbf{R}$ and ${\hat{\sigma }}_Y^2$, which are functions of both ${\hat{\mathit{\tau }}}_0$ and $\mathbf{Y}$. For computational convenience, we only calculate ${\hat{\mathit{\tau }}}_0$ once per genome screen by using a representative set of individuals rather than re-estimating it at every SNP. However, we do recalculate $\mathbf{B}$, $\mathbf{Y}$, $\mathbf{X}$, $\mathbf{R}$, and ${\hat{\sigma }}_Y^2$ at every SNP.

L-GATOR for Complete Data

Unlike PMALT, which is a prospective analysis based on $\mathbf{Y}|\left(\mathbf{X},\mathbf{W}\right)$, L-GATOR is a retrospective analysis based on $\mathbf{X}|\left(\mathbf{Y},\mathbf{W}\right)$. The retrospective framework is particularly useful for incorporating certain types of partially missing data because one can conveniently make use of the known dependence structure among relatives’ genotypes that arises from Mendelian inheritance. (This will be explained in more detail in the next subsection.) Another advantage of the retrospective approach is the robustness of the analysis to misspecification of the phenotype model, in the sense that the type 1 error of the association test will generally be correct even when the phenotype model is misspecified.

For clarity, we first present L-GATOR for the special case of complete data, meaning that only individuals with observed genotype data at the SNP being tested and with at least one complete record are included in the analysis (the same assumptions used in PMALT in the previous subsection). In the complete-data case, we define the L-GATOR test statistic by

$${\text{L}\text{-}\text{GATOR}}_{\text{comp}}=\frac{{\left[{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{Y}\right]}^2}{{\widehat{\text{Var}}}_0\left[{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{Y}|\mathbf{Y},\mathbf{W}\right]}.$$ (Equation 12)

Comparison of Equations 9 and 12 shows that the square of the PMALT statistic and the L-GATOR_comp statistic have the same numerator, whereas their denominators are the null conditional variances of the numerator given $\left(\mathbf{X},\mathbf{W}\right)$ and $\left(\mathbf{Y},\mathbf{W}\right)$, respectively.

In order to give a more specific expression for L-GATOR in the complete-data case and to partially justify an asymptotic ${\chi }_1^2$ null distribution, we first make two modeling assumptions on the distribution of $\mathbf{X}|\left(\mathbf{Y},\mathbf{W}\right)$. The first assumption concerns the null mean:

$$E_0\left(\mathbf{X}|\mathbf{Y},\mathbf{W}\right)={\mathbf{W}}_{\mathbf{s}}\mathit{\eta },$$ (Equation 13)

where ${\mathbf{W}}_{\mathbf{s}}$ is the $m\times q_s$ matrix of static covariate values and $q_s$ is the number of static covariates. The rows of ${\mathbf{W}}_{\mathbf{s}}$ are indexed by individuals, the columns are indexed by the static covariates, and the ${\left(i,j\right)}^{\text{th}}$ element is equal to the value of the j^th static covariate in the i^th individual. The static covariates are the covariates that stay the same for all records of an individual (e.g., sex), whereas dynamic covariates, such as age, change over time. Because the intercept is always included as a static covariate, ${\mathbf{W}}_{\mathbf{s}}$ will always contain at least one column, and $1\le q_s\le q$. In Equation 13, $\mathit{\eta }$ is an unknown column vector of length $q_s$. The interpretation of Equation 13 is that, under the null hypothesis of no association and no linkage between genotype and phenotype, the genotype is permitted to be linearly related to the static covariates. A special case of this condition would be $E_0\left(\mathbf{X}|\mathbf{Y},\mathbf{W}\right)=f\mathbf{1}$—where f is the allele frequency and 1 is a vector of length m, all of whose entries are equal to 1—a case that arises when all the entries of $\mathit{\eta }$ are 0 except for the entry corresponding to the intercept, so that the null mean does not depend on any other static covariates.

To understand why we make the assumption in Equation 13, it is helpful to first understand the relationship between the full covariate matrix $\mathbf{W}$, which has rows indexed by records (and thus has n rows), and the static covariate matrix ${\mathbf{W}}_{\mathbf{s}}$, which has rows indexed by individuals (and thus has m rows). If we use the vertically expanded identity matrix, $\mathbf{B}$, to expand ${\mathbf{W}}_{\mathbf{s}}$ from the individual level to the record level, then the columns of $\mathbf{B}{\mathbf{W}}_{\mathbf{s}}$ are a subset of the columns of $\mathbf{W}$. Because the matrix $\mathbf{R}$ is orthogonal to the column space of $\mathbf{W}$, we have $\mathbf{R}\mathbf{B}{\mathbf{W}}_{\mathbf{s}}=0$. Thus, the assumption of Equation 13 ensures that

$$E_0\left[{\left(\mathbf{B}\mathbf{X}\right)}^T\mathbf{R}\mathbf{Y}|\mathbf{Y},\mathbf{W}\right]=E_0\left[{\mathbf{Y}}^T\mathbf{R}\mathbf{B}\mathbf{X}|\mathbf{Y},\mathbf{W}\right]={\mathbf{Y}}^T\mathbf{R}\mathbf{B}{\mathbf{W}}_{\mathbf{s}}\mathit{\eta }=0.$$ (Equation 14)

In other words, the square root of the numerator of the L-GATOR_comp statistic has mean 0 under the null hypothesis.

The second modeling assumption that we make on the distribution of $\mathbf{X}|\left(\mathbf{Y},\mathbf{W}\right)$ is that

$${\text{Var}}_0\left(\mathbf{X}|\mathbf{Y},\mathbf{W}\right)={\sigma }_X^2\mathbf{\Phi },$$ (Equation 15)

where ${\sigma }_X^2$ is an unknown scalar. This is a version of the standard variance relationship that holds, for example, under Mendelian inheritance in a single population. Here, however, we use the more general parameter ${\sigma }_X^2$ rather than assuming that it equals $0.5f\left(1-f\right)$, which would hold under Hardy-Weinberg equilibrium (HWE). The complete-data L-GATOR-test statistic from Equation 12 can then be equivalently written as

$${\text{L}\text{-}\text{GATOR}}_{\text{comp}}=\frac{{\left({\mathbf{Y}}^T\mathbf{R}\mathbf{B}\mathbf{X}\right)}^2}{{\widehat{\text{Var}}}_0\left({\mathbf{Y}}^T\mathbf{R}\mathbf{B}\mathbf{X}|\mathbf{Y},\mathbf{W}\right)}=\frac{{\left({\mathbf{A}}^T\mathbf{X}\right)}^2}{{\widehat{\text{Var}}}_0\left({\mathbf{A}}^T\mathbf{X}|\mathbf{Y},\mathbf{W}\right)}=\frac{{\left({\mathbf{A}}^T\mathbf{X}\right)}^2}{{\mathbf{A}}^T\mathbf{\Phi }\mathbf{A}{\hat{\sigma }}_X^2},$$ (Equation 16)

where $\mathbf{A}={\mathbf{B}}^T\mathbf{R}\mathbf{Y}$ is the individual-level transformed phenotypic residual vector, defined in the sub-section PMALT: Missing Values Excluded. Furthermore,

$${\hat{\sigma }}_X^2=\frac{1}{m-q_s}{\mathbf{X}}^T\mathbf{U}\mathbf{X}$$ (Equation 17)

is an estimator of the null conditional variance of the genotype of an outbred individual, where we define

$$\mathbf{U}={\mathbf{\Phi }}^{-1}-{\mathbf{\Phi }}^{-1}{\mathbf{W}}_{\mathbf{s}}{\left({\mathbf{W}}_{\mathbf{s}}^T{\mathbf{\Phi }}^{-1}{\mathbf{W}}_{\mathbf{s}}\right)}^{-1}{\mathbf{W}}_{\mathbf{s}}^T{\mathbf{\Phi }}^{-1}.$$ (Equation 18)

The estimator ${\hat{\sigma }}_X^2$ is based on the residual sum of squares for the generalized regression of $\mathbf{X}$ on ${\mathbf{W}}_{\mathbf{s}}$ with conditional covariance matrix proportional to $\mathbf{\Phi }$. If more restrictive assumptions were made, e.g., if Equation 13 were replaced with the assumption $E_0\left(\mathbf{X}|\mathbf{Y},\mathbf{W}\right)=f\mathbf{1}$, then we could replace ${\hat{\sigma }}_X^2$ of Equation 17 with

$${\stackrel{⌣}{\sigma }}_X^2=\frac{\mathbf{1}}{m-\mathbf{1}}{\mathbf{X}}^T{\mathbf{\Phi }}^{-1}\left(\mathbf{X}-\hat{f}\mathbf{1}\right)=\frac{\mathbf{1}}{m-\mathbf{1}}{\mathbf{X}}^{\mathbf{T}}{\mathbf{U}}_1\mathbf{X},$$ (Equation 19)

where $\hat{f}={\left({\mathbf{1}}^T{\mathbf{\Phi }}^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^T{\mathbf{\Phi }}^{-1}\mathbf{X}$ is the best linear unbiased estimator¹⁴ (BLUE) of the allele frequency f for the current variant, and ${\mathbf{U}}_1={\mathbf{\Phi }}^{-1}-{\mathbf{\Phi }}^{-1}\mathbf{1}{\left({\mathbf{1}}^T{\mathbf{\Phi }}^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^T{\mathbf{\Phi }}^{-1}$. If, in addition, we assumed HWE at the variant, we could replace ${\hat{\sigma }}_X^2$ of Equation 17 with the estimator¹⁵

$${\tilde{\sigma }}_X^2=\frac{1}{2}\hat{f}\left(1-\hat{f}\right).$$ (Equation 20)

Under the assumptions in Equations 13 and 15, and with the usual regularity conditions sufficient for a central limit theorem, L-GATOR_comp is asymptotically ${\chi }_1^2$ distributed under the null hypothesis of no association and no linkage.

L-GATOR Incorporates Incomplete Data

One advantage of the retrospective analysis used in L-GATOR is that it provides a natural way to incorporate certain types of partially missing data in order to improve the power of association testing. In contrast, the PMALT analysis ignores data on individuals who have one or more complete records but have missing genotype data at the variant being tested or who have genotype data at the variant being tested but do not have any complete records.

We introduce notation to represent and distinguish different types of incomplete data. Recall that we assume that genetic variants are tested one by one for association with the trait. In what follows, we call the genetic variant currently being tested the “variant of interest.” For a given variant of interest, let P denote the subset of individuals in the sample who have at least one complete record and who satisfy at least one of the following three criteria: (1) they have nonmissing genotype at the variant of interest, (2) they have a relative in the study with nonmissing genotype at the variant of interest, or (3) they are in the same pedigree with an individual who has at least one complete record and either has nonmissing genotype or has a relative with nonmissing genotype at the variant of interest. We let G denote the subset of individuals in the sample with nonmissing genotype at the variant of interest. The PMALT association analysis includes only the individuals in the set $P\cap G$ (i.e., those in P who satisfy criterion 1 above). In contrast, the L-GATOR association analysis is based on the larger set of individuals in $P\cup G$. We also introduce notation, Z, for the set of all individuals who have at least one complete record, where $P\subseteq Z$.

To accommodate partially missing data, we need to redefine the index sets for some of the vectors and matrices defined in the previous two subsections. We let $p=\left|P\right|$ and $g=\left|G\right|$, which are the numbers of phenotyped and genotyped individuals, respectively, who are included in the L-GATOR association analysis for the variant of interest. We assume that all incomplete records have been culled from the dataset, that $n_i$ represents the number of complete records for individual i, and that $n={\sum }_{i\in P}{n}_i$ represents the total number of complete records included in the L-GATOR analysis. We redefine the genotype vector, $\mathbf{X}$, to have length g and be indexed by the set G, and we redefine the vertically expanded identity matrix, $\mathbf{B}$, to be $n\times p$. We define ${\mathbf{\Phi }}_P$, ${\mathbf{\Phi }}_{PG}$, and ${\mathbf{\Phi }}_G$ to be submatrices of $\mathbf{\Phi }$ where, for example, ${\mathbf{\Phi }}_P$ is the $p\times p$ matrix that retains in the $\mathbf{\Phi }$ matrix the rows and columns corresponding to individuals in P, and ${\mathbf{\Phi }}_{PG}$ is the $p\times g$ matrix that retains in the $\mathbf{\Phi }$ matrix the rows corresponding to individuals in P and the columns corresponding to individuals in G. Hence, we rewrite the null conditional variance assumption in Equation 15 as

$${\text{Var}}_0\left(\mathbf{X}|\mathbf{Y},\mathbf{W}\right)={\sigma }_X^2{\mathbf{\Phi }}_G,$$ (Equation 21)

we redefine the expanded kinship matrix ${\mathbf{K}}_{n\times n}$ to be $\mathbf{K}=\mathbf{B}{\mathbf{\Phi }}_P{\mathbf{B}}^T$, and we redefine ${\mathbf{U}}_1$ to be the $g\times g$ matrix ${\mathbf{U}}_1={\mathbf{\Phi }}_G^{-1}-{\mathbf{\Phi }}_G^{-1}\mathbf{1}{\left({\mathbf{1}}^T{\mathbf{\Phi }}_G^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^T{\mathbf{\Phi }}_G^{-1}$. We also redefine the individual-level transformed phenotypic residual vector $\mathbf{A}$ to be $p\times 1$ with $\mathbf{A}={\mathbf{B}}^T\mathbf{R}\mathbf{Y}$.

In the incomplete-data case, the L-GATOR statistic becomes

$$\text{L}\text{-}\text{GATOR}=\frac{{\left({\mathbf{Y}}^T\mathbf{R}\mathbf{B}{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\mathbf{X}\right)}^2}{{\widehat{\text{Var}}}_0\left({\mathbf{Y}}^T\mathbf{R}\mathbf{B}{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\mathbf{X}|\mathbf{Y},\mathbf{W}\right)}=\frac{{\left({\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\mathbf{X}\right)}^2}{{\widehat{\text{Var}}}_0\left({\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\mathbf{X}|\mathbf{Y},\mathbf{W}\right)},$$ (Equation 22)

which we rewrite as

$$\text{L}\text{-}\text{GATOR}=\frac{{\left({\mathbf{A}}^T\hat{\mathbf{X}}\right)}^2}{{\widehat{\text{Var}}}_0\left({\mathbf{A}}^T\hat{\mathbf{X}}|\mathbf{Y},\mathbf{W}\right)}=\frac{{\left({\mathbf{A}}^T\hat{\mathbf{X}}\right)}^2}{{\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1{\mathbf{\Phi }}_{GP}\mathbf{A}{\hat{\sigma }}_X^2},$$ (Equation 23)

where ${\hat{\sigma }}_X^2$ is a consistent estimator of ${\sigma }_X^2$ (discussed below) and where the vector ${\hat{\mathbf{X}}}_{p\times 1}$ is the best linear unbiased predictor¹⁶ (BLUP) of the vector of genotypes for the individuals in set P. Here, the BLUP, $\hat{\mathbf{X}}$, is based on $\mathbf{X}$, the vector of genotypes of the individuals in set G, and the kinship information. Specifically, the BLUP is given by

$$\hat{\mathbf{X}}=\hat{f}\mathbf{1}+{\mathbf{\Phi }}_{PG}{\mathbf{\Phi }}_G^{-1}\left(\mathbf{X}-\hat{f}\mathbf{1}\right)=\left[\mathbf{1}{\left({\mathbf{1}}^T{\mathbf{\Phi }}_G^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^T{\mathbf{\Phi }}_G^{-1}+{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\right]\mathbf{X},$$ (Equation 24)

where $\hat{f}={\left({\mathbf{1}}^T{\mathbf{\Phi }}_G^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^T{\mathbf{\Phi }}_G^{-1}\mathbf{X}$ is the BLUE of allele frequency based on $\mathbf{X}$. Further details can be found in McPeek.¹⁶ The equality of the expressions in Equations 22 and 23 is shown in Appendix B.

In the special case when an individual is in $P\cap G$, so that his or her genotype is observed, then the BLUP of the individual’s genotype is simply equal to the individual’s observed genotype. Thus, in the complete-data case, the numerator, ${\left({\mathbf{A}}^T\hat{\mathbf{X}}\right)}^2$, of L-GATOR in Equation 23 becomes equal to the numerator, ${\left({\mathbf{A}}^T\mathbf{X}\right)}^2$, of L-GATOR_comp in Equation 16. Similarly, in the complete-data case, the denominator, ${\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1{\mathbf{\Phi }}_{GP}\mathbf{A}{\hat{\sigma }}_X^2$, of L-GATOR in Equation 23 becomes equal to the denominator, ${\mathbf{A}}^T\mathbf{\Phi }\mathbf{A}{\hat{\sigma }}_X^2$, of L-GATOR_comp in Equation 16. (See Appendix B for details.)

Possible estimators, ${\hat{\sigma }}_X^2$, of ${\sigma }_X^2$ of Equation 23 include the estimator of Equation 17, where we restrict the estimator to be based only on those individuals who have both genotype and static covariates available (see Appendix B). Alternatively, if we assumed $E_0\left(\mathbf{X}|\mathbf{Y},\mathbf{W}\right)=f\mathbf{1}$, then we could replace ${\hat{\sigma }}_X^2$ of Equation 23 by

$${\stackrel{⌣}{\sigma }}_X^2=\frac{1}{g-1}{\mathbf{X}}^T{\mathbf{U}}_1\mathbf{X},$$ (Equation 25)

as in Thornton and McPeek¹⁷, or we could use Equation 20 if we were also willing to assume HWE.

To obtain an asymptotic ${\chi }_1^2$ distribution for the L-GATOR test statistic under the null hypothesis, in the case of incomplete data, we slightly modify the assumption on the null mean, given in Equation 13 for the complete-data case, to obtain

$$E_0\left(\hat{\mathbf{X}}|\mathbf{Y},\mathbf{W}\right)={\mathbf{W}}_{\mathbf{s}}\mathit{\eta },$$ (Equation 26)

where $\mathbf{X}$ in Equation 13 has been replaced with $\hat{\mathbf{X}}$ in Equation 26. Under the assumptions of Equations 21 and 26 and with the usual regularity conditions sufficient for a central limit theorem, L-GATOR is asymptotically ${\chi }_1^2$ distributed under the null hypothesis of no association and no linkage.

We can define an alternative version of L-GATOR, which we call L-GATOR_alt, in which the BLUP, $\hat{\mathbf{X}}$, depends not only on $\mathbf{X}$ but also on the static covariates (see Appendix C for details). Note that use of L-GATOR_alt would require that all individuals included in the set G also have non-missing values for the static covariates.

L-GATOR can be viewed as a quasi-likelihood score test that generalizes the MASTOR test⁷ for quantitative traits to the context of repeated-measures. Specifically, the expression for L-GATOR in Equation 23 can be seen as a generalization of the MASTOR statistic given in equation 11 of Jakobsdottir and McPeek,⁷ where the quantity $\mathbf{P}\mathbf{Y}$ defined in Jakobsdottir and McPeek for a non-longitudinal quantitative trait is replaced by the more general vector $\mathbf{A}={\mathbf{B}}^T\mathbf{R}\mathbf{Y}$ for a longitudinal quantitative trait and where these two quantities are equal if there is only one time point.

Understanding the Contribution of Partially Missing Data in L-GATOR

If an individual has at least one complete record but has missing genotype data at the current marker, or if the individual has genotype data but no complete records, it is of interest to understand to what extent the data on this individual can still provide information on genotype-phenotype association. One type of information these data can provide is information on nuisance parameters, which indirectly improves inference on association. To be specific, genotyped individuals with no complete records can still provide information on population allele frequencies, and individuals with missing genotype data at the current marker but with at least one complete record can still provide information on the null MLE of the phenotypic nuisance parameter $\left(\mathit{\beta },\mathit{\tau }\right)$ used in L-GATOR. In the current implementation of L-GATOR, the nuisance parameter f is estimated from the data on all individuals in G, the nuisance parameter $\mathit{\tau }$ is estimated from the data on all individuals in Z (i.e., the individuals with at least one complete record), and the nuisance parameter $\mathit{\beta }$ is estimated from the data on all individuals in the set P.

When the sample includes relatives, it is also possible for individuals with at least one complete record but missing genotype data to provide more direct information on genotype-phenotype association if they have relatives whose data give partial information on the missing genotypes. In particular, if an individual has a missing genotype, one or more complete records, and at least one genotyped relative, then the BLUP formulation of L-GATOR in Equation 23 shows that the individual contributes to the association analysis such that the BLUP of their genotype replaces their observed genotype in the numerator (and the additional uncertainty in their genotype is accounted for in the denominator).

Finally, there is another less obvious contribution that can be made by an individual, say individual a, who has at least one complete record, missing genotype data, and no genotyped relatives but is in the same pedigree with an individual, b, who has at least one complete record and either is genotyped at the variant of interest or has a genotyped relative. In that case, b contributes to the association analysis because either an observed genotype or a BLUP for the genotype of b is available, and a can contribute to the transformed phenotypic residual of b provided that ${\left({\hat{\mathbf{V}}}_0^{-1}\right)}_{ij}\ne 0$ for at least one pair $\left(i,j\right)$, where i is a record of individual a and j is a record of individual b. This represents a slight contribution of individual a to the analysis through the transformed phenotypic residual of individual b. For example, consider a parent-offspring trio in which the father has genotype data but no complete records, whereas both the mother and offspring have at least one complete record but missing genotype data. Then, a BLUP of the genotype is available for the offspring, so the BLUP formulation of L-GATOR in Equation 23 makes clear how the offspring’s data contribute to the association analysis. The father’s data provide information for the BLUP of the offspring, whereas the mother’s data can contribute to the observed phenotypic residual of the offspring.

Connection between longGWAS and PMALT

The previously proposed longGWAS method¹ is a prospective, longitudinal analysis based on a mixed-effects model and implemented in R. There is a close connection between the longGWAS and PMALT methods. The main difference between them lies in the parameterization of the correlation between repeated observations on an individual, where this correlation is given in the $\mathbf{L}$ matrix of PMALT and in the $\mathbf{D}$ matrix of longGWAS. In PMALT, the correlation between the j^th and k^th observations of individual i depends only on the length of time, $\left|t_{ij}-t_{ik}\right|$, between the two observations and is given by $\text{exp}\left(-\alpha {\left|t_{ij}-t_{ik}\right|}^c\right)$, which is the $\left(j,k\right)$^th element of the i^th diagonal block of the $\mathbf{L}$ matrix. The entire $\mathbf{L}$ matrix involves only two unknown parameters, α and c, which must be estimated. In contrast, in longGWAS, the correlation between the j^th and k^th observations of individual i depends not simply on the length of time between the two observations but on the actual times themselves and is given by $d_{t_{ij},t_{ik}}$, which is an unknown parameter. Thus, for example, if we were to try to use longGWAS to analyze data from the original cohort of the FHS dataset (see the subsection SBP Data from the Framingham Heart Study for a description) and if we used the age of the individual rounded to the nearest year as the time point and assumed that individuals were tested every 2 years (and never allowed an odd number of years as a time increment), the $\mathbf{D}$ matrix would already involve more than 1,800 unknown parameters that must be estimated, in contrast to two parameters for the $\mathbf{L}$ matrix of PMALT. Because of this, the longGWAS method does not seem well suited to analysis of the FHS data or other similar datasets in which the number of possible distinct time points is large and each individual has observations at only a small subset of the possible time points.

Another difference between the two methods is that longGWAS does not include a component of variance for non-genetic individual random effects that do not vary over time (the term ${\sigma }_I^2\mathbf{J}$ in Equation 4). In addition, in longGWAS, the minor allele frequency (MAF) is imputed for any missing genotype for computational convenience, whereas missing genotypes are excluded in PMALT. The variance estimators used in the two methods are asymptotically equivalent, though not exactly equal in small samples. In datasets in which the number of distinct possible time points is not very large in relation to the number of observations per individual, in which ${\sigma }_I^2$ is also close to 0 and in which there are no missing genotypes, PMALT and longGWAS would be expected to behave very similarly.

Simulation Studies

We performed simulation studies to assess the type 1 error and compare the power of L-GATOR, PMALT, and longGWAS. We also assessed the sensitivity of L-GATOR and PMALT to estimation of the variance-components parameter, $\mathit{\tau }$, from a subset of individuals who are not exactly the same individuals used in the association test. To achieve these goals, we simulated data that included related individuals by using two different trait models and various assumptions about missing genotype and phenotype data, as we now describe.

We simulated two trait models, denoted I and II, both of which have an intercept, static and dynamic covariates, major gene effects, additive polygenic effects, and static and dynamic non-genetic individual effects. The models differ in the major gene effects, such that model I has two unlinked major causal loci that each act dominantly with epistasis between them, whereas model II has four unlinked major causal loci with epistasis between them. For both models, the values of the static covariate were simulated as independent standard normal random variables, one per individual. Each individual was assumed to have five time points with a common difference of 2 years between each consecutive pair of measurement times for an individual. The values of the dynamic covariate were simulated as independent standard normal random variables, five per individual, corresponding to the five time points. Trait model I is given by Equations 2 and 4 with

$$\mathit{\mu }=\mathbf{W}\mathit{\beta }+\mathbf{B}\mathbf{f}\left({\mathbf{X}}_1,{\mathbf{X}}_2\right),$$ (Equation 27)

where the first column of $\mathbf{W}$ contains the intercept, the second column contains the static covariate, and the third column contains the dynamic covariate; $\mathit{\beta }={\left(1,0.6,-0.2\right)}^T$, $\mathit{\tau }={\left(0.4,0.1,0.4,0.04,1.2\right)}^T$, and either ${\sigma }^2=5$ (in the scenarios with no missing genotype data) or ${\sigma }^2=2$ (in the scenarios with some missing genotype data). Here, $\mathbf{B}$ is the vertically expanded identity matrix given in Equation 1, and $\mathbf{f}\left({\mathbf{X}}_1,{\mathbf{X}}_2\right)$ is a vector with i^th element equal to $f\left(X_{1i},X_{2i}\right)$, where $X_{1i}$ and $X_{2i}$ are the genotype values of individual i at causal loci 1 and 2, respectively. Each individual’s genotype at locus i is coded as 0, 0.5, or 1 according to whether the individual carries 0, 1, or 2 copies, respectively, of the variant allele at locus i. The frequency of the variant allele is 0.1 at locus 1 and 0.5 at locus 2. Table 2 gives the values of $f\left(x_1,x_2\right)$ for $\left(x_1,x_2\right)\in {\left\{0,\text{0}.5,1\right\}}^2$. Trait model II is given by Equations 2 and 4 with

$$\mathit{\mu }=\mathbf{W}\mathit{\beta }+\mathbf{B}\mathbf{g}\left({\mathbf{X}}_1,{\mathbf{X}}_2,{\mathbf{X}}_3,{\mathbf{X}}_4\right),$$ (Equation 28)

where $\mathbf{W}$, $\mathit{\beta }$, $\mathbf{B}$, $\mathit{\tau }$, and ${\sigma }^2$ are the same as for trait model I. Here, $\mathbf{g}\left({\mathbf{X}}_1,{\mathbf{X}}_2,{\mathbf{X}}_3,{\mathbf{X}}_4\right)$ is a vector with i^th element equal to $g\left(X_{1i},X_{2i},X_{3i},X_{4i}\right)$, where $X_{1i},X_{2i},X_{3i}$, and $X_{4i}$ are the genotype values of individual i at causal loci 1, 2, 3, and 4, respectively. The frequency of the variant alleles at loci 1, 2, 3, and 4 are 0.1, 0.2, 0.3, and 0.4, respectively. Table 3 gives the values of $g\left(x_1,x_2,x_3,x_4\right)$ for $\left(x_1,x_2,x_3,x_4\right)\in {\left\{0,0.5,1\right\}}^4$.

Table 2.

Genetic Effects, $f\left(x_1,x_2\right)$, for the Two Unlinked Causal Loci of Trait Model I

	x2= 0	x2= 0.5	x2= 1
$x_1=0$	0.04	0.04	0.04
$x_1=0.5$	0.04	0.8	0.8
$x_1=1$	0.04	0.8	0.8

Genotypic effects are given as a function of $\left(x_1,x_2\right)$, where $x_i$ is 0, 0.5, or 1 according to whether the individual has zero, one, or two copies, respectively, of the variant allele at locus i. The frequency of the variant allele is 0.1 at locus 1 and 0.5 at locus 2.

Table 3.

Genetic Effects, $g\left(x_1,x_2,x_3,x_4\right)$, for the Four Unlinked Causal Loci of Trait Model II

(x1, x2)	(x3, x4)
	(0, 0)	(0, 0.5)	(0, 1)	(0.5, 0)	(0.5, 0.5)	(0.5, 1)	(1, 0)	(1, 0.5)	(1, 1)
$\left(0,0\right)$	0.04	0.04	0.04	0.3	0.3	0.3	0.5	0.5	0.5
$\left(0,0.5\right)$	0.04	0.1	0.1	0.3	0.3	0.3	0.5	0.5	0.5
$\left(0,1\right)$	0.04	0.1	0.1	0.3	0.3	0.3	0.5	0.5	0.5
$\left(0.5,0\right)$	0.2	0.2	0.2	1.2	1.2	1.2	1.4	1.4	1.4
$\left(0.5,0.5\right)$	0.2	0.2	0.2	1.2	1.2	1.2	1.4	1.4	1.4
$\left(0.5,1\right)$	0.2	0.2	0.2	1.2	1.2	1.2	1.4	1.4	1.4
$\left(1,0\right)$	0.4	0.4	0.4	1.4	1.4	1.4	1.6	1.6	1.6
$\left(1,0.5\right)$	0.4	0.4	0.4	1.4	1.4	1.4	1.6	1.6	1.6
$\left(1,1\right)$	0.4	0.4	0.4	1.4	1.4	1.4	1.6	1.6	1.6

Genotypic effects are given as a function of $\left(x_1,x_2,x_3,x_4\right)$, where $x_i$ is 0, 0.5, or 1 according to whether the individual has zero, one, or two copies, respectively, of the variant allele at locus i. The frequency of the variant allele is 0.1, 0.2, 0.3, and 0.4 at loci 1, 2, 3, and 4, respectively.

We simulated three different sample configurations and three different ascertainment schemes for a total of nine different sample types, each of which consisted of a choice of sample configuration and a choice of ascertainment scheme. Sample configuration 1 contained 50 outbred, three-generation families, each containing 16 individuals related as in Figure S1. Sample configuration 2 contained 75 families of the type in Figure S1. Sample configuration 3 contained 400 unrelated individuals plus 50 families of the type in Figure S1. For each sample configuration, we allowed three possible ascertainment schemes. Ascertainment scheme a was random ascertainment of families and individuals. In ascertainment scheme b, ascertainment of each family was conditional on its having at least two family members whose time-averaged phenotype values were $>$1.5 SD away from the population mean, whereas unrelated individuals (if any) were sampled randomly from the population. In ascertainment scheme c, ascertainment of each family was conditional on its having at least two family members whose time-averaged phenotype values were $>1$ SD above the population mean, whereas unrelated individuals (if any) were sampled randomly from the population. Then, for example, sample type 2b denoted a sample with configuration 2 and ascertainment type b.

We considered three possible choices of which individuals were genotyped in a given sample: “all” denoted that all sampled individuals were genotyped, “both tails” denoted that only individuals whose time-averaged phenotype value was $>$1.5 SD away from the population mean were genotyped, and “upper tail” denoted that only individuals whose time-averaged phenotype value was $>$1 SD above the population mean were genotyped. We also considered three possible choices of which individuals were phenotyped in a given sample: “all” denoted that all sampled individuals were phenotyped for all records; “missing A” denoted that each sampled individual had a 25% chance of having all phenotype records set to be missing, where this was independent across individuals; and “missing B” denoted that each of the individuals unrelated to anyone else in the sample (if any) had a 50% chance of having all phenotype records set to be missing, where this was independent across individuals, whereas all phenotype records were assumed to be available for all individuals in the sampled families in missing B.

SBP Data from the Framingham Heart Study

The FHS¹⁸ is a long-term, multigenerational study designed for the purpose of identifying risk factors that contribute to cardiovascular disease. Our use of the FHS data was approved by the institutional review board of the Biological Sciences Division of the University of Chicago. We analyzed longitudinal SBP measurements on 14,173 FHS-sampled individuals, 1,475 of whom were apparently unrelated to anyone else in the sample and 12,698 of whom could be divided into 1,537 multigeneration pedigrees. The sampled individuals were divided into three cohorts such that the individuals in cohort 1 (original cohort) had measurements at up to 28 time points, approximately every 2 years; the individuals in cohort 2 (offspring cohort) had up to 8 time points, approximately every 4 years; and the individuals in cohort 3 (third generation) had one time point. The time points for an individual in a given cohort could be somewhat irregularly spaced, and the number of time points could vary across individuals in a cohort due to missing data. We analyzed log(SBP) as a longitudinal quantitative trait. In order to account for possible effects of hypotensive medication usage among sampled individuals, we first adjusted the SBP measurements^{19, 20} by adding a sensible constant (10 mmHg) to measurements that occurred when the corresponding patient was on treatment. In the longitudinal trait model, we included the following nine covariates: sex (1 = male, 0 = female); age (years); age²; log(BMI), where BMI is body mass index (MIM: 606641); log(current smoking), where current smoking was measured as the number of cigarettes per day; smoking history (1 = current or former smoker, 0 = never smoked up to the time of measurement); log(blood glucose), where blood glucose was measured in mg/100 mL; and two cohort indicators to account for generation effects. We excluded 149 records that occurred when the corresponding individuals were under 18 years of age.

Among the sampled individuals, 9,240 were genotyped on the Affymetrix 500K array, and 536 of these were apparently unrelated to anyone else in the sample. As part of our quality-control procedure, we excluded genotyped individuals who met either of the following two criteria: (1) empirical self-kinship coefficient ${\widetilde{\text{Φ}}}_{ii}\ge 0.525$, i.e., empirical inbreeding coefficient ${\tilde{h}}_i\ge 0.05$, or (2) completeness $\le 96\text{\%}$, where completeness is defined as the proportion of markers for which a given individual had genotypes called and where we used the completeness value given in the dbGaP quality-control file. Genotype data on 469 individuals satisfying criterion 1 and 584 individuals satisfying criterion 2 (such that 410 individuals satisfied both criteria) were then filtered out (i.e., set to be missing) for all SNPs. Only SNPs that met all of the following quality-control criteria were included in the analysis: (1) call rate $\ge 96\text{\%}$, (2) Mendelian error rate $\le 2\text{\%}$, and (3) MAF $\ge 1\text{\%}$; for all three of these criteria, we used the values given in the dbGaP quality-control file. We then used PMALT and L-GATOR to test for association between log(SBP) and each of the 369,046 SNPs that met all three of these quality-control criteria. (The analysis of the FHS data was not computationally feasible with longGWAS.)

Results

To assess type 1 error, we simulated under each of the 18 different settings of trait model, missing data, and sample type listed in Table 4, and in each setting, we tested association between the trait and an unlinked and unassociated marker. For each setting, one phenotype replicate was sampled, and empirical type 1 error was calculated on the basis of 50,000 simulated replicates of genotype data for the unlinked and unassociated marker, which in each case had a MAF of 0.2. Columns 5, 7, and 9 of Table 4 give the empirical type 1 error for PMALT, L-GATOR, and longGWAS at nominal level 0.001. From these results, we can see that both PMALT and L-GATOR were correctly calibrated in all the simulation settings, in the sense that none of the empirical type 1 error results were significantly different from the nominal, according to a z-test at level 0.05. In contrast, although longGWAS was correctly calibrated in the scenarios with no missing genotype data, its type 1 error was drastically too large in the “both tails” scenario of missing genotype data and drastically too small in the “upper tail” scenario. This phenomenon was caused by the fact that longGWAS substitutes the MAF for any missing genotypes, which, in these scenarios, results in heterskedasticity that causes the type 1 error to be incorrect.

Table 4.

Empirical Type 1 Error of PMALT, L-GATOR, and Long GWAS at Level 0.001

Genotyped Individuals	Sample Type	Phenotyped Individuals	Trait Model	Empirical Type 1 Error
				PMALT	PMALTZ	L-GATOR	L-GATORP ∩ G	LongGWAS
All	1a	all	I	0.0010	0.0010	0.0011	0.0011	0.0009
All	1a	all	II	0.0010	0.0010	0.0010	0.0010	0.0009
All	2a	missing A	I	0.0012	0.0012	0.0011	0.0011	0.0010
All	2a	missing A	II	0.0010	0.0010	0.0010	0.0010	0.0009
All	3a	missing B	I	0.0012	0.0012	0.0012	0.0012	0.0010
All	3a	missing B	II	0.0009	0.0009	0.0010	0.0010	0.0012
Both tails	1b	all	I	0.0012	0.0200	0.0010	0.0010	0.0673
Both tails	1b	all	II	0.0010	0.0354	0.0008	0.0009	0.1235
Both tails	2b	missing A	I	0.0010	0.0330	0.0008	0.0009	0.1224
Both tails	2b	missing A	II	0.0012	0.0373	0.0009	0.0009	0.0990
Both tails	3b	missing B	I	0.0010	0.0165	0.0009	0.0009	0.0541
Both tails	3b	missing B	II	0.0011	0.0269	0.0011	0.0010	0.0869
Upper tail	1c	all	I	0.0010	0	0.0008	0.0009	0
Upper tail	1c	all	II	0.0010	0	0.0011	0.0012	4 × 10−5
Upper tail	2c	missing A	I	0.0011	0	0.0009	0.0009	0.0004
Upper tail	2c	missing A	II	0.0009	0	0.0008	0.0008	0.0006
Upper tail	3c	missing B	I	0.0010	0	0.0012	0.0011	0.0001
Upper tail	3c	missing B	II	0.0012	0	0.0009	0.0009	0.0003

For each row of the table, the empirical type 1 error values were calculated on the basis of one phenotype replicate and 50,000 simulated genotype replicates. The minor allele frequency of the tested marker is 0.2. Underlined values are those that differ significantly (p value < 0.05) from the nominal level of 0.001 by a z-test.

In addition, we considered the robustness of the type 1 error of PMALT and L-GATOR to estimation of the variance-component parameter, $\mathit{\tau }$, from a slightly different subset of individuals than those included in the association test. Recall that we ordinarily include in the PMALT analysis only those individuals in $P\cap G$, i.e., those who are both genotyped and phenotyped, and this set is used for both estimation of $\mathit{\tau }$ and testing of association. In column 6 of Table 4, we give the type 1 error for PMALT when the variance-component parameter, $\mathit{\tau }$, was instead estimated from the larger set, Z, consisting of all phenotyped individuals, whereas the association test was applied only to the set, $P\cap G$, of individuals who were both phenotyped and genotyped. We refer to this procedure as PMALT_Z. From Table 4, we can see that this small change in the estimation procedure for $\mathit{\tau }$ can, in some settings, lead to drastically incorrect type 1 error, either too liberal or too conservative, depending on the setting. We can apply a similar analysis to L-GATOR. In our default implementation of L-GATOR, we estimated $\mathit{\tau }$ by using the set of all phenotyped individuals, Z. In column 8 of Table 4, we give the type 1 error for L-GATOR when the variance-component parameter, $\mathit{\tau }$, was instead estimated from the smaller set, $P\cap G$, of individuals who were both phenotyped and genotyped, whereas the association test was applied to the larger set, $P\cup G$. We refer to this procedure as ${\text{L}\text{-}\text{GATOR}}_{P\cap G}$. From Table 4, we can see that ${\text{L}\text{-}\text{GATOR}}_{P\cap G}$ was correctly calibrated in all simulation settings, in the sense that none of the empirical type 1 error results were significantly different from the nominal, according to a z-test at level 0.05. Thus, L-GATOR is much more robust than PMALT to changes in how the variance components are estimated. This can be explained by the fact that L-GATOR is a retrospective method, so correct type 1 error does not depend on correct specification of the phenotype model, whereas PMALT is a prospective method, so type 1 error is more sensitive to changes in parameter estimates of the phenotype model. In the simulation settings in which the individuals in Z had a different phenotype distribution overall from those in the subset $P\cap G$, namely the “both tails” and “upper tail” settings, the change in how the parameters were estimated could throw off the type 1 error of PMALT_Z. This suggests that when PMALT is used, the variance components should ideally be estimated from the same set of individuals used in the test for a specific variant.

To assess power, we simulated under each of the 18 different settings of trait model, missing data, and sample type listed in Table 5, and in each setting, we tested association between the trait and causal SNP 1 of the simulated model. For each setting, empirical power was calculated on the basis of 5,000 simulated replicates of the sample genotypes, covariates, and phenotypes. In Table 5, we can see that for settings with nonmissing genotype data (rows 1–6 of Table 5), PMALT and L-GATOR achieved comparable power. This result held even when there was missing phenotype data (rows 3–6 of Table 5), suggesting that the extra information (i.e., genotype data on individuals with missing phenotype) that is used by L-GATOR, but not by P-MALT, in estimation of the nuisance parameter, f, does not have a large effect on power. In contrast, in the settings in which some genotypes were missing (rows 7–18 of Table 5), L-GATOR was always more powerful than PMALT. This extra power resulted from the fact that genotyped relatives provided partial genotype information on the individuals who were phenotyped but had missing genotypes. P-MALT ignores this information, whereas L-GATOR is able to make use of this additional information to increase power for association.

Table 5.

Power Comparison of PMALT and L-GATOR

Genotyped Individuals	Sample Type	Phenotyped Individuals	Trait Model	Power (SE)
				PMALT	L-GATOR
All	1a	all	I	0.84 (0.005)	0.84 (0.005)
All	1a	all	II	0.82 (0.005)	0.82 (0.005)
All	2a	missing A	I	0.89 (0.004)	0.89 (0.004)
All	2a	missing A	II	0.87 (0.005)	0.87 (0.005)
All	3a	missing B	I	0.93 (0.004)	0.93 (0.004)
All	3a	missing B	II	0.90 (0.004)	0.90 (0.004)
Both tails	1b	all	I	0.60 (0.007)	0.73 (0.006)
Both tails	1b	all	II	0.62 (0.007)	0.72 (0.006)
Both tails	2b	missing A	I	0.66 (0.007)	0.81 (0.006)
Both tails	2b	missing A	II	0.69 (0.007)	0.83 (0.005)
Both tails	3b	missing B	I	0.74 (0.006)	0.85 (0.005)
Both tails	3b	missing B	II	0.74 (0.006)	0.84 (0.005)
Upper tail	1c	all	I	0.25 (0.006)	0.37 (0.007)
Upper tail	1c	all	II	0.36 (0.007)	0.46 (0.007)
Upper tail	2c	missing A	I	0.29 (0.006)	0.35 (0.007)
Upper tail	2c	missing A	II	0.34 (0.007)	0.36 (0.007)
Upper tail	3c	missing B	I	0.33 (0.007)	0.37 (0.007)
Upper tail	3c	missing B	II	0.41 (0.007)	0.42 (0.007)

Empirical power at significance level 0.05 was calculated on the basis of 5,000 simulated replicates. The higher power for each simulation setting is underlined.

We also assessed the power of longGWAS in the first six settings listed in Table 5 because these were the only simulation settings in which longGWAS had correct type 1 error. The empirical power of longGWAS was calculated on the basis of only 500 simulated replicates of the sample genotypes, covariates, and phenotypes rather than on 5,000 replicates as for L-GATOR and PMALT because running longGWAS is much slower. In these six settings, the power of longGWAS was not significantly different from that of L-GATOR and PMALT (see Table S1). This verifies our theoretically based expectation that in datasets in which the number of possible time points is not very large in relation to the number of observations per individuals, in which ${\sigma }_I^2$ is not large, and in which there are no missing genotypes, longGWAS would behave similarly to PMALT.

In the analysis of the SBP data (described in the next subsection), we noticed that the estimated value of ${\sigma }_I^2/{\sigma }^2$, the proportion of variance due to non-genetic individual random effects, was quite small. For the case when the true value of ${\sigma }_I^2/{\sigma }^2$ was small to moderate, we explored whether this parameter could be safely removed from the analysis without harming power. To do this, we assessed the power of PMALT and L-GATOR in six settings (see Table S1) under which the analyses were performed with ${\sigma }_I^2$ set to 0 (i.e., removed from the model) even though the simulation settings had ${\sigma }_I^2/{\sigma }^2=0.1$. Comparing the results of Table S1 with those of the first six rows of Table 5, we found that in this case of relatively small ${\sigma }_I^2/{\sigma }^2$, there was no significant difference in power for either PMALT or L-GATOR when ${\sigma }_I^2$ was removed from the model.

Analysis of SBP Data from the Framingham Heart Study

We used both PMALT and L-GATOR to analyze the SBP data from the FHS. We were not able to complete the analysis with the longGWAS method. (In general, longGWAS is not suitable for the analysis of the FHS data or other similar datasets in which the number of possible distinct time points is large and each individual has observations at only a small subset of the possible time points.) For both PMALT and L-GATOR, we first estimated the variance-component parameter, $\mathit{\tau }$, and the covariate effects, $\mathit{\beta }$, under the null on the basis of all individuals with at least one non-missing record; the results are given in Table 6 and Table 7, respectively. In each case, the standard error was calculated as the square root of the corresponding diagonal entry of the inverse Fisher information matrix (see Appendix A for more details). In Tables 6 and 7, two different PMALT analyses are summarized. “PMALT After” refers to the PMALT analysis after the genotypes of all individuals in cohort 1 were set to be missing, whereas “PMALT Before” refers to the PMALT analysis when the genotypes of the individuals in cohort 1 were not set to be missing. The purpose of the PMALT After analysis is described later in this subsection. In Table 7, we see that all covariates except log(current smoking) were significant in the L-GATOR analysis, and all but log(current smoking) and smoking history were significant in the PMALT analyses. In Table 6, we see that the variance due to (non-genetic) individual effects, ${\sigma }_I^2$, appeared to be not significantly different from 0 in any of the three analyses. This presumably reflects the fact that there were three other variance components in the model, so the modeled covariance structure was able to fit the data well without the ${\sigma }_I^2$ term. Parameters α and c control the time dependence across the trait measurements for an individual. Under the model with the values of α and c given in Table 6 (where these values are based on time measured in years), the correlation between the measurements on a single individual at two different time points decayed fairly slowly as a function of the time interval between the measurements. For example, the correlation was 0.93 (PMALT Before), 0.95 (PMALT After), or 0.91 (L-GATOR) for a 2-year span, and the correlation was 0.59 (PMALT Before), 0.61 (PMALT After), or 0.56 (L-GATOR) for a 10-year span. The estimated narrow-sense heritability for the log(SBP) trait in this study ranged from 0.31 to 0.35 for the different analyses.

Table 6.

Estimated Variance Components (Based on L-GATOR and PMALT) for Log(SBP) in the FHS Data

Parameter	Estimate (SE)
	L-GATOR	PMALT Before	PMALT After
${\sigma }^2$	0.017 (2 × 10−4)	0.014 (2 × 10−4)	0.013 (2 × 10−4)
${\sigma }_E^2/{\sigma }^2$	0.254 (0.006)	0.303 (0.008)	0.302 (0.012)
${\sigma }_I^2/{\sigma }^2$	3 × 10−7 (0.02)	4 × 10−7 (0.03)	2 × 10−5 (0.04)
${\sigma }_A^2/{\sigma }^2$	0.35 (0.01)	0.31 (0.02)	0.33 (0.02)
α	0.043 (0.006)	0.031 (0.006)	0.017 (0.007)
c	1.13 (0.07)	1.23 (0.09)	1.47 (0.18)

“PMALT Before” refers to the variance-component estimation results from PMALT before the cohort 1 genotypes were removed from the FHS dataset, whereas “PMALT After” refers to the variance-component estimation results from PMALT after the cohort 1 genotypes were removed from the FHS dataset. The variance-component estimation results for L-GATOR are based on all phenotyped individuals, so they do not change when cohort 1 genotypes are removed. Estimation of α and c is based on years as the unit of measurement for time.

Table 7.

Estimated Covariate Effects (with SEs and p Values) from the PMALT and L-GATOR Analyses of Log(SBP) in the FHS Data

Parameter	PMALT Beforea		PMALT After		L-GATOR
	estimate (SE)	p value	estimate (SE)	p value	estimate (SE)	p value
Intercept	3.98 (0.02)	0	3.78 (0.03)	0	3.96 (0.02)	0
Age	−2.3 × 10−3 (3 × 10−4)	6.6 × 10−17	−3.6 × 10−3 (4 × 10−4)	5.3 × 10−25	−1.0 × 10−3 (2 × 10−4)	2.3 × 10−5
Age2	5.3 × 10−5 (2 × 10−6)	1.8 × 10−98	6.8 × 10−5 (4 × 10−6)	2.3 × 10−79	4.1 × 10−5 (2 × 10−6)	8.9 × 10−77
Sex	0.035 (0.002)	9.7 × 10−58	0.038 (0.002)	2.1 × 10−61	0.025 (0.002)	2.5 × 10−38
log(BMI)	0.242 (0.005)	0	0.231 (0.006)	0	0.265 (0.004)	0
log(current smoking)	4 × 10−4 (6 × 10−4)	0.53	3 × 10−4 (7 × 10−4)	0.62	9 × 10−4 (5 × 10−4)	0.054
Smoking history	−0.005 (.003)	0.051	−0.004 (0.003)	0.15	−0.012 (0.002)	1.7 × 10−8
log(blood glucose)	0.012 (0.003)	2.6 × 10−6	0.053 (0.004)	3.4 × 10−32	0.006 (0.002)	5.6 × 10−4
Cohort 2 indicator	−0.044 (0.003)	1.6 × 10−50	0.036 (0.003)	2.5 × 10−43	−0.076 (0.002)	3.3 × 10−301
Cohort 3 indicator	−0.084 (0.004)	4.2 × 10−119	NA	NA	−0.125 (0.003)	0

SBP measurements are adjusted according to hypotensive medication usage. SBP, BMI, current smoking, and glucose are log transformed. Age is measured in years; sex is coded as 1 = male and 0 = female; BMI is body mass index; current smoking is measured in cigarettes per day; smoking history = 1 if the individual is a current or former smoker and 0 if the individual has never smoked up to the time of measurement; blood glucose is measured in mg/(100 mL); cohort 2 indicator = 1 if the individual is a member of cohort 2 and 0 otherwise, and the same applies for the cohort 3 indicator.

^aSee Table 6 legend.

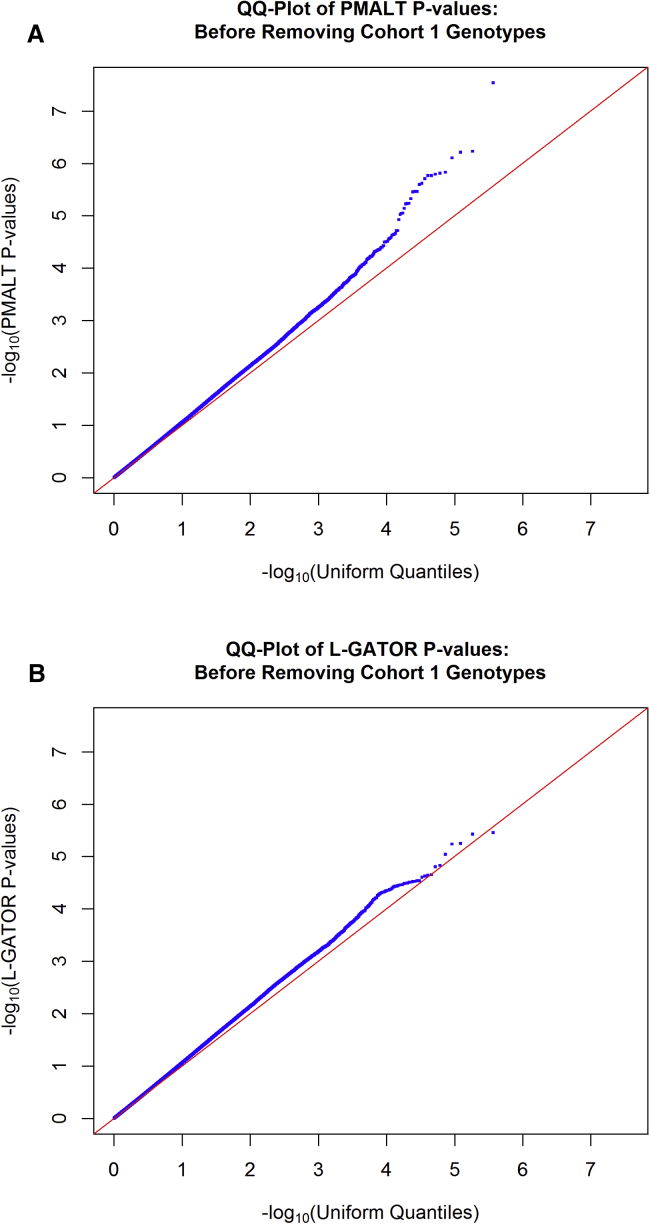
Figure 1 shows the quantile-quantile (Q-Q) plots of the negative ${\text{log}}_{10}$-transformed p values for the PMALT and L-GATOR analyses (before the removal of cohort 1 genotypes). The resulting genomic-control inflation factors were 1.064 (PMALT) and 1.065 (L-GATOR), slightly larger than the threshold of 1.05, which is generally considered benign.²¹ Although the inflation factors suggest that the p values did not show substantial departure from the uniform distribution overall, we observed that the Q-Q plots seemed to lift off the line between 1 and 2 (on the negative ${\text{log}}_{10}$ scale), and we also noticed that the smallest p values seemed noticeably smaller in PMALT than in L-GATOR. This motivated us to perform a further investigation on the quality of the genotype data for the three cohorts. To do this, we went back to the original data before applying our quality-control filters. Figure S2 gives histograms of the completeness values (where completeness is defined as the proportion of markers for which a given individual has genotypes called and where we use the completeness value given in the dbGaP quality-control file) for the individuals in cohort 1 (Figure S2A) and the individuals in cohorts 2 and 3 (Figure S2B). Figure S3 gives histograms of empirical self-kinship coefficients for these two groups. The distributions of completeness and empirical self-kinship coefficient suggest that the original cohort had on average noticeably lower-quality genotype data than the other two cohorts.

Figure 1.

Q-Q Plots of PMALT and L-GATOR p Values for the FHS SBP Data before the Removal of Cohort 1 Genotypes

Q-Q plots of genome-wide p values for association with SBP in the FHS data before the removal of genotypes for cohort 1 are shown. The p values were computed by the PMALT method (A) or the L-GATOR method (B). In each panel, p values for 369,046 genome-wide SNPs are plotted on the negative ${\text{log}}_{10}$ scale.

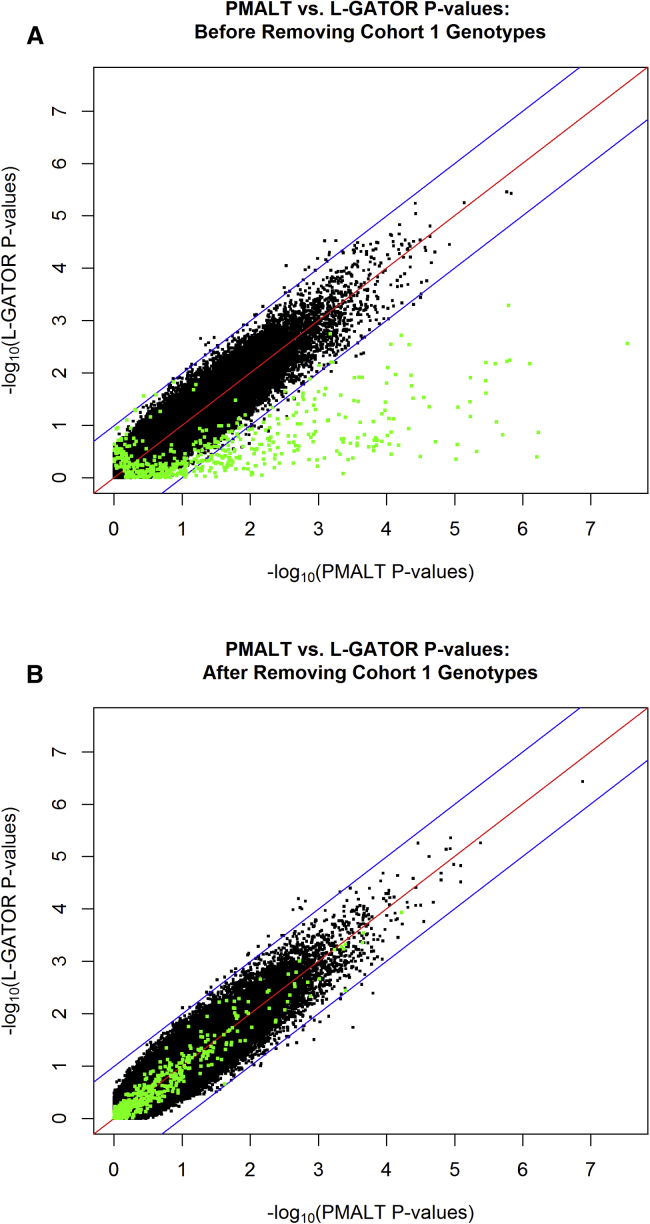
In order to investigate whether lower-quality genotype data in the original cohort were likely to affect the association tests, we tested, for each SNP, whether the allele frequency in cohort 1 was equal to the allele frequency in the combined cohorts 2 and 3. At significance level ${10}^{-10}$, 709 SNPs showed a significant difference in allele frequency between the two groups. Of these 709 SNPs, 170 had already been filtered out on the basis of our original quality-control criteria (call rate, Mendelian error rate, and MAF) and so were not included in the association analysis. Of the remaining 539 SNPs with extremely significant cohort allele-frequency differences, 322 had MAF $<2\text{\%}$. This is not surprising because, for fixed rates of differential genotyping error, SNPs with smaller MAF would be expected to be more sensitive than SNPs with MAF closer to 0.5. Figure 2A shows that the 539 SNPs with extremely significant cohort allele-frequency differences tended to have markedly different association p values between the L-GATOR and PMALT analyses; specifically, many of them had very small p values in PMALT but not in L-GATOR. Among the 539 SNPs with extremely significant cohort allele-frequency differences, $\sim 40\text{\%}$ of them (215 SNPs) had PMALT p values smaller than $1/10$ of their L-GATOR p values (below the lower blue line of 10-fold change on the negative ${\text{log}}_{10}$ scale), whereas only one SNP showed up in the other direction (above the upper blue line of 10-fold change on the negative ${\text{log}}_{10}$ scale). The small p values for PMALT were probably the result of confounding due to different apparent allele frequencies in different generations, which probably resulted from differential genotyping error. To understand why the L-GATOR p values were not also inflated, it is helpful to recall that L-GATOR can be thought of as handling missing genotype data by imputing the BLUP of the missing genotypes (and fully accounting for the error of imputation). For the 539 SNPs with extremely significant cohort allele-frequency differences, we noticed that many individuals with missing genotype data had relatives with highly unlikely genotype configurations, which led to imputation of BLUP values that were “contaminated” by likely genotyping errors in some of the data used for calculating the BLUP. This led to extra noise in the genotypes for the L-GATOR method, which tended to make the p values larger.

Figure 2.

Scatterplots for L-GATOR p Values versus PMALT p Values from the FHS SBP Data before and after the Removal of Cohort 1 Genotypes

The L-GATOR p value of each SNP in the FHS SBP data is plotted against its PMALT p value, where both p values are on the negative ${\text{log}}_{10}$ scale. Shown are the results before (A) and after (B) removal of the genotypes for cohort 1. In each case, the red line represents perfect concordance between the PMALT and L-GATOR p values (ratio of 1 between them), whereas the blue lines represent a 10-fold difference between the PMALT and L-GATOR p values (ratio of 10:1 or 1:10). Shown in green are the SNPs with extremely significant (p value $<{10}^{-10}$) differences in allele frequency between cohort 1 and the other cohorts.

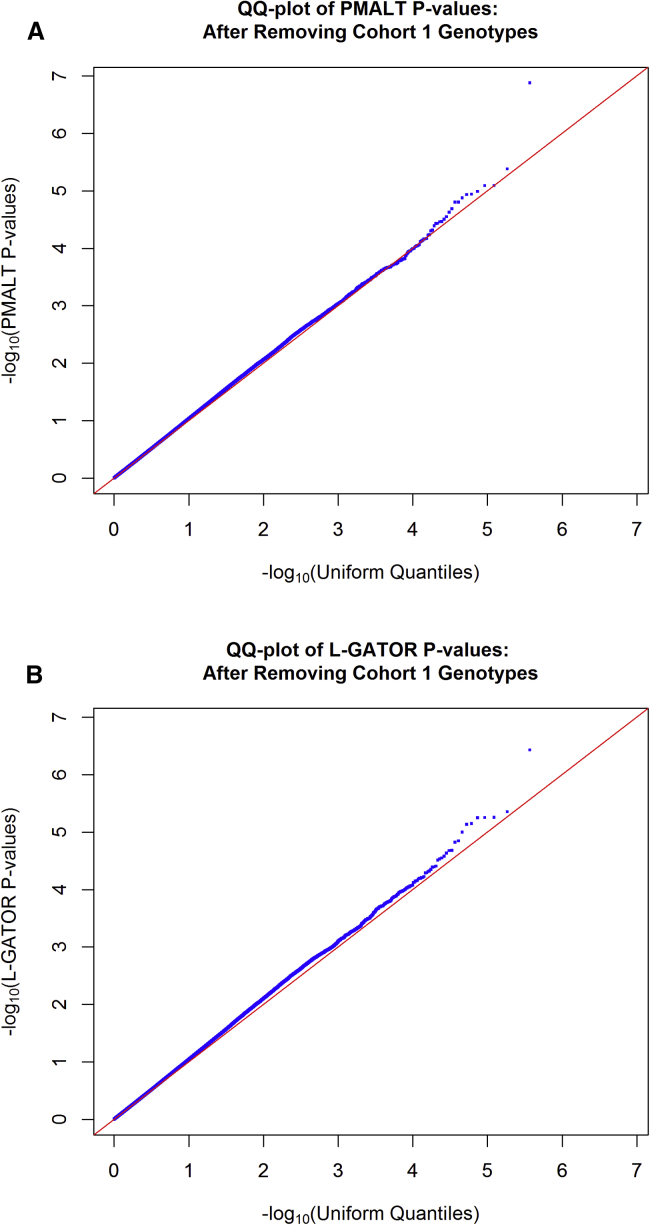
To avoid problems caused by possible lower-quality genotype data in the original cohort, we set the genotype data of the original cohort to be missing for all SNPs and reran the two analyses. Note that for L-GATOR, the estimates of the variance-component parameters under the null hypothesis (Table 6) did not change when the genotype data of cohort 1 were set to be missing because they were estimated based on the set, Z, of individuals with at least one complete record, and this set did not change. Similarly, the L-GATOR estimates of the fixed effects (Table 7) did not change noticeably when the genotype data of cohort 1 were set to be missing because L-GATOR used the set P, which also did not change very much, to estimate these parameters. In contrast, the parameter estimates for PMALT could change substantially because parameter estimation was based on the set $P\cap G$, which changed substantially because G was changed substantially. Both sets of estimates for PMALT are listed in Tables 6 and 7. Figure 3 shows the Q-Q plots of the negative ${\text{log}}_{10}$-transformed p values for the PMALT and L-GATOR analyses after the removal of cohort 1 genotypes. The genomic control inflation factors for the PMALT and L-GATOR analyses after removal of cohort 1 genotypes were 1.028 and 1.041, respectively, which are lower than in the previous analyses. The corresponding scatterplot of PMALT p values versus L-GATOR p values is shown in Figure 2B. We see that after the removal of genotype data for cohort 1, the Q-Q plots look closer to uniform, and the two analyses produce relatively consistent p values.

Figure 3.

Q-Q Plots of PMALT and L-GATOR p Values for the FHS SBP Data after Removal of Cohort 1 Genotypes

Q-Q plots of genome-wide p values for association with SBP in the FHS data after removal of genotypes for cohort 1 are shown. The p values were computed by the PMALT method (A) or the L-GATOR method (B). In each panel, p values for 369,046 genome-wide SNPs are plotted on the negative ${\text{log}}_{10}$ scale.

Table 8 lists the 13 SNPs for which L-GATOR gave a p value $<2.5\times {10}^{-5}$ for association with SBP after removal of the genotype data for the original cohort. Three of these SNPs, $\text{rs}17398575$, $\text{rs}12705390$, and $\text{rs}11760498$, are located at $7\text{q}22$, close to PIK3CG (MIM: 601232), which was identified²² as associated with pulse pressure, the difference between SBP and diastolic blood pressure (DBP), in a meta-analysis of individuals of European ancestry from 35 studies (one of which is the FHS). PIK3CG encodes a protein that belongs to the pi3/pi4-kinase family, and the gene is located in a region previously identified as associated with platelet aggregation²³ and with mean platelet volume, counts, and function.²⁴ SNP $\text{rs}12246717$, located at $10\text{q}21$, is near C10orf107, which was previously reported to be associated with SBP and DBP in meta-analyses of individuals of European ancestry.^{25, 26}

Table 8.

Strongest Association Signals in the FHS SBP Data after Removal of Cohort 1 Genotypes

Chromosomal Region	Nearby Genes	SNP ID	Position	P Value
1q24	BAT2L2, MYOC	rs235891	169,839,888	3.71 × 10−7
		rs235864	169,855,206	5.51 × 10−6
2q14	CNTNAP5	rs13033474	124,653,857	2.06 × 10−5
2q21	TMEM163	rs655472	135,006,691	5.50 × 10−6
		rs666614	135,006,923	5.43 × 10−6
7q22	PIK3CG, FLJ36031	rs17398575	106,196,688	1.04 × 10−5
		rs12705390	106,198,013	1.56 × 10−5
		rs11760498	106,206,208	7.23 × 10−6
10q21	C10orf107	rs12246717	63,129,189	2.11 × 10−5
17q22	C17orf67, NOG	rs227661	52,170,897	7.31 × 10−6
		rs227660	52,171,218	4.41 × 10−6
18p11	RAB31	rs1455587	9,700,554	1.39 × 10−5

SBP-associated SNPs with L-GATOR p value $<2.5\times {10}^{-5}$ are reported on the basis of the FHS data with cohort 1 genotypes removed. Underlined genes have been previously identified as associated with SBP. MIM numbers of genes not mentioned in the text: MYOC (MIM: 601652), CNTNAP5 (MIM: 610519), NOG (MIM: 602991), RAB31 (MIM: 605694).

Our results seem to have little in common with the results of a previous FHS SBP analysis,²⁷ which tested SNPs on the Affymetrix 100K GeneChip for association with either single time-point measurements or long-term averages. The strongest results in the previous study do not appear to have been replicated to date. The previous study had a much smaller sample size and lower SNP density than did our analysis, and the previous study did not make use of longitudinal information, whereas our analysis did. These major differences most likely account for the lack of consistency between the two sets of results.

Assessment of Run Time

We provide freely available software called L-GATOR, which is programmed in C and which can perform both the L-GATOR and PMALT analyses. In Table 9, we compare the run times of L-GATOR and PMALT, using the L-GATOR software with default settings, with that of longGWAS, using the longGWAS R package with default settings, for analysis of sample type 1a of trait model I. These times were obtained with a single processor on a shared machine with 4-core Intel Xeon 3.16 GHz central processing units and 32 GB RAM. From Table 9, we can see that longGWAS took almost 100 times as long as PMALT or L-GATOR for variance-component estimation, which is done once per genome screen, and longGWAS took more than ten times as long per SNP as L-GATOR for association testing.

Table 9.

Comparison of Run Times for PMALT, L-GATOR, and longGWAS

	Time (s)
	PMALT	L-GATOR	longGWAS
Variance-component estimation (once per dataset)	7.778	7.771	743.581
Association testing (per SNP)	0.016	0.028	0.335

Comparison uses sample type 1a of trait model I.

We also give run times for L-GATOR genome-wide analysis of the FHS SBP data. (We were not able to complete the analysis with longGWAS.) The FHS data are computationally challenging because they contain some large families with a large number of repeated measures per individual. For example, there are six families with sizes larger than 100 individuals, and the largest family contains 499 individuals and 3,284 records. To assess the run time, we first performed a genome-wide analysis of the FHS SBP data while excluding the six largest families. In that case, the average run time for L-GATOR was about 0.58 s per SNP for association testing. When all families were included, the computation was five to six times slower as a result of memory allocation and matrix decomposition and inversion for large matrices.

For both the L-GATOR and PMALT analyses, the L-GATOR software calculates ${\hat{\mathit{\tau }}}_0$ just once per genome screen. The slowest step is the calculation, at each marker, of the inverse, ${\hat{\mathbf{V}}}_0^{-1}$, for the PMALT analysis and of both ${\hat{\mathbf{V}}}_0^{-1}$ and ${\mathbf{\Phi }}_G^{-1}$ for the L-GATOR analysis. By default, these inverses are calculated at each marker because the set $P\cap G$ in PMALT and the sets P and G in L-GATOR can vary by marker. For very large datasets, possible approximate approaches, which speed calculation, are to either (1) calculate ${\hat{\mathbf{V}}}_0^{-1}$ just once per genome screen and select the needed rows and columns of ${\hat{\mathbf{V}}}_0^{-1}$ for each SNP or (2) calculate the transformed phenotypic residual vector, ${\hat{\mathbf{V}}}_0^{-1}\left(\mathbf{Y}-\mathbf{W}{\hat{\mathit{\beta }}}_0\right)$, once per genome screen and select the needed entries of it for each SNP. These approaches would be expected to provide good approximations only if the set of individuals with missing genotypes is quite similar across markers (and would be exact if the set of individuals with missing genotypes is the same across markers). Our software gives users the option of using either of these approaches, although the default is to recalculate ${\hat{\mathbf{V}}}_0^{-1}$ for every SNP. The use of either option provides a considerable speed-up, and option 2 is faster than option 1.

Discussion

Longitudinal studies have the potential to provide substantial information for identification of genetic variants and environmental factors that affect complex phenotypes over time. When individuals in the longitudinal study are related, the dependence of genotypes across individuals and dependence of phenotype measurements both across individuals and across time can pose statistical and computational challenges for genetic analysis. In order to make efficient use of the full longitudinal information contained in such data, we propose L-GATOR, a retrospective quasi-likelihood score test for genetic association with a longitudinally measured trait in samples with related individuals. L-GATOR is based on a mixed-effects trait model that (1) incorporates both time-varying and static covariates as fixed effects and (2) uses random effects to model dependence among observations for an individual, including both static and time-varying individual effects, as well as additive genetic effects that model dependence across observations from related individuals. The mixed-effects approach allows the analysis to make full use of the available information on repeated-measurements, for which different individuals are permitted to have different time points and different numbers of observations. In samples with related individuals, the retrospective approach has the advantage of providing a natural and computationally efficient way to incorporate partially missing observations in the analysis in order to increase power while properly accounting for uncertainty and dependence. L-GATOR is applicable and computationally feasible for essentially arbitrary combinations of related and unrelated individuals, including large, complex, inbred pedigrees as well as samples in which small outbred families are combined with unrelated individuals.

In our simulations, L-GATOR was more than ten times faster than the previously proposed prospective method, longGWAS, for association testing and almost 100 times faster for parameter estimation. Furthermore, in the presence of ascertainment or missing data, L-GATOR was able to maintain correct type 1 error, whereas longGWAS was not. In part because of the challenge of using longGWAS in our simulations and data analysis, we also developed PMALT, a prospective method similar to longGWAS but that adopts the longitudinal modeling approach of L-GATOR so that it can take advantage of the computational speed-up. Through simulation, we have demonstrated that, although both L-GATOR and PMALT are correctly calibrated, L-GATOR provides higher power to detect association in samples with ascertainment and partially missing data (missing phenotype or genotype) when related individuals are present in the sample. This is because L-GATOR uses the information on dependence of related individuals to allow individuals with missing genotype or missing phenotype to contribute power to the analysis. Furthermore, we have shown that compared with PMALT, L-GATOR is more robust to misspecification of the phenotype model in that it maintains correct type 1 error even when the variance-component parameter is misspecified. We applied L-GATOR to detect association with SBP in data from the FHS. Among the strongest association signals were four SNPs in or near genes previously reported to be associated with blood pressure (PIK3CG and C10orf107).

From the point of view of analyzing the FHS SBP data, a key aspect of the L-GATOR model is the parametric modeling of correlation among observations from the same individual at different time points, as captured in the $\mathbf{L}$ matrix, which depends on the two parameters α and c. This is essential because of the wide range of ages (time points) in the study and the fact that each individual has observations for at most a small subset of these. In contrast, completely nonparametric modeling of the correlation among observations from the same individual at different time points¹ is impractical in this context. The modeling of additive genetic variance is also essential in this context because of the presence of relatedness in the sample. In contrast, the estimated value of ${\sigma }_I^2/{\sigma }^2$, the proportion of variance due to non-genetic individual random effects, is quite small in the FHS SBP data, indicating that it is not needed in the analysis. In Table S1, we report the power results for L-GATOR and PMALT in six settings when the true value of ${\sigma }_I^2/{\sigma }^2=0.1$ but when the analyses were performed with ${\sigma }_I^2$ set to 0 (i.e., removed from the model). We found that in this case of low to moderate ${\sigma }_I^2/{\sigma }^2$, there was no significant difference in power for either PMALT or L-GATOR when ${\sigma }_I^2$ was removed from the model. The current version of L-GATOR software offers the user the option of removing this variance component from the model.

The L-GATOR method we describe accounts for known relatedness. In addition, it might be of interest to account for further unknown population structure and cryptic relatedness. One possible approach to this is to replace the L-GATOR statistic of Equation 23 with

$$\text{L}\text{-}\text{GATOR}=\frac{{\left({\mathbf{A}}^T\hat{\mathbf{X}}\right)}^2}{{\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\hat{\mathbf{\Psi }}{\mathbf{U}}_1{\mathbf{\Phi }}_{GP}\mathbf{A}{\hat{\sigma }}_X^2},$$ (Equation 29)

where $\hat{\mathbf{\Psi }}$ is an empirical genetic-relatedness matrix calculated from genome-wide data. This has the effect of correcting the variance of the statistic for additional unknown structure. An alternative approach could be to include ancestry-informative vectors as covariates in the model and replace $\hat{\mathbf{\Psi }}$ with a residual empirical genetic-relatedness matrix that is orthogonal to the ancestry-informative vectors. The second approach could be expected to have more power if population structure is substantial.

A general feature of retrospective association testing approaches such as L-GATOR is that the type 1 error is not affected by misspecification of the trait model, and this is confirmed by Table 4. However, power for association can sometimes be affected by trait model misspecification. An example in which power is not significantly affected is given in Table S1. On the other hand, examples in which power is reduced (in the case of a non-longitudinal quantitative trait) can be seen by a comparison of the ASTOR and MASTOR results in rows 1–4 of Table 4 of a previous work⁷. The fact that power for association can sometimes be affected by trait model misspecification motivates our careful development of the mean and variance models for L-GATOR, and it is worth considering how to address possible deviations from that model. For example, the trait model fit by L-GATOR assumes that the genetic effect is constant over time. Other possibilities could include that there is an initial genetic effect that attenuates over time or a genetic effect that does not manifest until late in life. If the true trait model deviated strongly from the assumption of constant genetic effect over time, it could affect power for association. Relatively simple approaches to improving the power in that case could include (1) restricting consideration to an age range over which the genetic effect is believed to be strong and/or (2) extending the model of L-GATOR to allow an interaction between the genetic fixed effect and age.

The L-GATOR method we propose is designed for genetic analysis of longitudinal measurements of a quantitative trait. L-GATOR could certainly also be applied to longitudinal measurements of a binary trait. A drawback would be that the trait model given in (Equation 2), (Equation 3), (Equation 4) would be misspecified for a binary trait because a key feature of binary data is that the variance of a binary random variable with mean μ must be $\mu \left(1-\mu \right)$. This model misspecification could affect the power of the association test for a binary trait (although not the type 1 error). To improve power for longitudinal binary traits, we could consider developing a new method that combines the approach used in L-GATOR with the approaches used in the recent CARAT²⁸ and CERAMIC²⁹ methods for non-longitudinal binary traits to create a hybrid method that would be expected to be more powerful than L-GATOR for longitudinal binary traits.

Published: April 5, 2018

Appendix A

Null MLE and Fisher Information for $\left({\sigma }^2,\mathit{\tau }\right)$

From the log-likelihood function under the null,

$$\ell =-\frac{1}{2}\left[n\log \left(2\pi {\sigma }^2\right)+\text{log}\left|\mathbf{V}\right|+\frac{1}{{\sigma }^2}{\left(\mathbf{Y}-\mathbf{W}\mathit{\beta }\right)}^T{\mathbf{V}}^{-1}\left(\mathbf{Y}-\mathbf{W}\mathit{\beta }\right)\right],$$

we can obtain the null MLE, $\left({\hat{\mathit{\beta }}}_0,{\hat{\sigma }}_0^2,{\hat{\mathit{\tau }}}_0\right)$, of $\left(\mathit{\beta },{\sigma }^2,\mathit{\tau }\right)$ by performing the one-dimensional minimization

$${\hat{\mathit{\tau }}}_0=\underset{\mathit{\tau }}{\text{arg}\text{min}}\left\{\text{log}\left|\mathbf{V}\right|+n\log {\hat{\sigma }}_0^2\left(\mathit{\tau }\right)\right\},$$

where ${\hat{\sigma }}_0^2\left(\mathit{\tau }\right)=\frac{1}{n}{\mathbf{Y}}^T{\mathbf{V}}^{-1}\left[\mathbf{Y}-\mathbf{W}{\hat{\mathit{\beta }}}_0\left(\mathit{\tau }\right)\right]$ and ${\hat{\mathit{\beta }}}_0\left(\mathit{\tau }\right)={\left({\mathbf{W}}^T{\mathbf{V}}^{-1}\mathbf{W}\right)}^{-1}{\mathbf{W}}^T{\mathbf{V}}^{-1}\mathbf{Y}$ are the null MLEs of ${\sigma }^2$ and $\mathit{\beta }$ as functions of $\mathit{\tau }$. We then set ${\hat{\mathit{\beta }}}_0={\hat{\mathit{\beta }}}_0\left({\hat{\mathit{\tau }}}_0\right)$ and ${\hat{\sigma }}_0^2={\hat{\sigma }}_0^2\left({\hat{\mathit{\tau }}}_0\right)$.

To obtain the Fisher information for the parameter vector ${\left({\sigma }^2,\mathit{\tau }\right)}^T$ where $\mathit{\tau }=\left({\tau }_1,{\tau }_2,{\tau }_3,\alpha ,c\right)$ (note that $\mathit{\beta }$ is independent and can be considered separately), let ${\mathbf{\Lambda }}_1=\partial \mathbf{V}/\partial {\tau }_1,{\mathbf{\Lambda }}_2=\partial \mathbf{V}/\partial {\tau }_2,{\mathbf{\Lambda }}_3=\partial \mathbf{V}/\partial {\tau }_3,{\mathbf{\Lambda }}_4=\partial \mathbf{V}/\partial \alpha ,\text{and}{\mathbf{\Lambda }}_5=\partial \mathbf{V}/\partial c$, and the corresponding Fisher information matrix is then

$$\mathcal{I}=\left[\begin{array}{cc}{\mathcal{I}}_{{\sigma }^2}& {\mathcal{I}}_{{\sigma }^2\mathit{\tau }}^T\\ {\mathcal{I}}_{{\sigma }^2\mathit{\tau }}& {\mathcal{I}}_{\mathit{\tau }}\end{array}\right],$$

where ${\mathcal{I}}_{{\sigma }^2}=n/2{\sigma }^4$, ${\mathcal{I}}_{{\sigma }^2\mathit{\tau }}$ is a vector of length 5 with i^th component $\left(1/2{\sigma }^2\right)\text{tr}\left({\mathbf{V}}^{-1}{\mathbf{\Lambda }}_i\right)$ for $1\le i\le 5$, and ${\mathcal{I}}_{\mathit{\tau }}$ is a matrix of size 5 $\times$ 5 with $\left(i,j\right)$^th component $\left(1/2\right)\text{tr}\left({\mathbf{V}}^{-1}{\mathbf{\Lambda }}_i{\mathbf{V}}^{-1}{\mathbf{\Lambda }}_j\right)$ for $1\le i\le 5\text{and}1\le j\le 5$.

Appendix B

Equality of the Expressions in Equations 22 and 23

To obtain equality of the numerators in Equations 22 and 23, it is sufficient to show that

$${\mathbf{A}}^T\hat{\mathbf{X}}={\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\mathbf{X}.$$ (Equation B1)

This follows from the fact that $\mathbf{R}\mathbf{B}1=0$ (because $\mathbf{R}$ is orthogonal to the column space of $\mathbf{W}$, and $\mathbf{B}1$ equals the intercept column of $\mathbf{W}$), and so ${\mathbf{A}}^T\mathbf{1}={\mathbf{Y}}^T\mathbf{R}\mathbf{B}\mathbf{1}=0$. Thus, ${\mathbf{A}}^T\hat{\mathbf{X}}={\mathbf{A}}^T\mathbf{1}{\left({\mathbf{1}}^T{\mathbf{\Phi }}_G^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^T{\mathbf{\Phi }}_{\mathbf{G}}^{-1}\mathbf{X}+{\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\mathbf{X}={\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\mathbf{X}$ because the first term is 0. To obtain equality of the denominators of Equations 22 and 23, we note that a key fact, easily verified, is that

$${\mathbf{U}}_1{\mathbf{\Phi }}_G{\mathbf{U}}_1={\mathbf{U}}_1.$$ (Equation B2)

Combining this with Equation B1, we have

$${\widehat{\text{Var}}}_0\left({\mathbf{A}}^T\hat{\mathbf{X}}|\mathbf{Y},\mathbf{W}\right)={\widehat{\text{Var}}}_0\left({\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1\mathbf{X}\right)={\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1{\mathbf{\Phi }}_G{\mathbf{U}}_1{\mathbf{\Phi }}_{GP}\mathbf{A}{\hat{\sigma }}_X^2={\mathbf{A}}^T{\mathbf{\Phi }}_{PG}{\mathbf{U}}_1{\mathbf{\Phi }}_{GP}\mathbf{A}{\hat{\sigma }}_X^2.$$

Equality of the Denominators in Equations 23 and 16 with Complete Data

With complete data, we have ${\mathbf{\Phi }}_{PG}={\mathbf{\Phi }}_G$, so the denominator of Equation 23 becomes ${\mathbf{A}}^T{\mathbf{\Phi }}_G{\mathbf{U}}_1{\mathbf{\Phi }}_G\mathbf{A}{\hat{\sigma }}_X^2={\mathbf{A}}^T\left({\mathbf{\Phi }}_G-\mathbf{1}{\left({\mathbf{1}}^T{\mathbf{\Phi }}_G^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^T\right)\mathbf{A}{\hat{\sigma }}_X^2={\mathbf{A}}^T{\mathbf{\Phi }}_G\mathbf{A}{\hat{\sigma }}_X^2$ because ${\mathbf{A}}^T\mathbf{1}=0.$

Estimator ${\hat{\sigma }}_X^2$ in Equation 23

Equation 23 gives the form of L-GATOR in the incomplete-data case, which includes ${\hat{\sigma }}_X^2$, an estimator of the null conditional genotypic variance. In the complete-data case, we have an expression for ${\hat{\sigma }}_X^2$ that is given in Equation 17. However, this expression must be modified for the incomplete-data case. Let $\Delta$ denote the set of individuals with genotype and all static covariates available, and let $\delta =|\Delta |$. Then, in the incomplete-data case, we let

$${\hat{\sigma }}_X^2={\left(\delta -q_s\right)}^{-1}{\mathbf{X}}_{\Delta }^T{\mathbf{U}}_{\Delta }{\mathbf{X}}_{\Delta },$$ (Equation B3)

where ${\mathbf{X}}_{\Delta }$ is the genotype vector $\mathbf{X}$ restricted to those individuals in $\Delta$, and ${\mathbf{U}}_{\Delta }={\mathbf{\Phi }}_{\Delta }^{-1}-{\mathbf{\Phi }}_{\Delta }^{-1}{\mathbf{W}}_{\Delta ,s}{\left({\mathbf{W}}_{\Delta ,s}^T{\mathbf{\Phi }}_{\Delta }^{-1}{\mathbf{W}}_{\Delta ,s}\right)}^{-1}{\mathbf{W}}_{\Delta ,s}^T{\mathbf{\Phi }}_{\Delta }^{-1}$, where ${\mathbf{\Phi }}_{\Delta }$ and ${\mathbf{W}}_{\Delta ,s}$ are $\mathbf{\Phi }$ and ${\mathbf{W}}_s$, respectively, restricted to those individuals in $\Delta$.

Appendix C

Extension of L-GATOR to Include Covariates in BLUP for Genotype

If we required all of the individuals in G to have non-missing values for the static covariates, i.e., if we required $G=\Delta$, then we could define an alternative version of L-GATOR, called L-GATOR_alt, where

$${\text{L}\text{-}\text{GATOR}}_{\text{alt}}=\frac{{\left({\mathbf{Y}}^T\mathbf{R}\mathbf{B}{\mathbf{\Phi }}_{P\Delta }{\mathbf{U}}_{\Delta }{\mathbf{X}}_{\Delta }\right)}^2}{{\widehat{\text{Var}}}_0\left({\mathbf{Y}}^T\mathbf{R}\mathbf{B}{\mathbf{\Phi }}_{P\Delta }{\mathbf{U}}_{\Delta }{\mathbf{X}}_{\Delta }|\mathbf{Y},\mathbf{W}\right)}$$

which we rewrite as

$${\text{L}\text{-}\text{GATOR}}_{\text{alt}}=\frac{\left({\mathbf{A}}^T{\hat{\mathbf{X}}}_{\text{alt}}\right)}{{\widehat{\text{Var}}}_0\left({\mathbf{A}}^T{\hat{\mathbf{X}}}_{\text{alt}}|\mathbf{Y},\mathbf{W}\right)}=\frac{\left({\mathbf{A}}^T{\hat{\mathbf{X}}}_{\text{alt}}\right)}{{\mathbf{A}}^T{\mathbf{\Phi }}_{P\Delta }{\mathbf{U}}_{\Delta }{\mathbf{\Phi }}_{\Delta P}\mathbf{A}{\hat{\sigma }}_X^2},$$

where ${\hat{\sigma }}_X^2$ is defined in Equation B3 and where

$${\hat{\mathbf{X}}}_{\text{alt}}={\mathbf{W}}_s\hat{\mathit{\eta }}+{\mathbf{\Phi }}_{P\Delta }{\mathbf{\Phi }}_{\Delta }^{-1}\left(\mathbf{X}-{\mathbf{W}}_{\Delta ,s}\hat{\mathit{\eta }}\right)=\left[{\mathbf{W}}_s{\left({\mathbf{W}}_{\Delta ,s}^T{\mathbf{\Phi }}_{\Delta }^{-1}{\mathbf{W}}_{\Delta ,s}\right)}^{-1}{\mathbf{W}}_{\Delta ,s}^T{\mathbf{\Phi }}_{\Delta }^{-1}+{\mathbf{\Phi }}_{P\Delta }{\mathbf{U}}_{\Delta }\right]{\mathbf{X}}_{\Delta }$$

is a new BLUP that uses not only the available genotypes but also the static covariates to predict the missing genotypes.

L-GATOR_alt belongs to the family of quasi-likelihood score tests in association analysis,¹⁵, ³⁰ and it can be derived as the quasi-likelihood score test of $H_0:\xi =0$ (no association and no linkage) under the retrospective mean model $E\left[{\mathbf{X}}_{\Delta }|\mathbf{W},\mathbf{Y}\right]={\mathit{W}}_{\Delta ,s}\mathit{\eta }+\xi {\mathbf{\Phi }}_{\Delta P}\mathbf{A}$ with the null variance assumption ${\text{Var}}_0\left({\mathbf{X}}_{\Delta }|\mathbf{W},\mathbf{Y}\right)={\sigma }_X^2{\mathbf{\Phi }}_{\Delta }$. Note that validity of the L-GATOR_alt test depends only on the assumptions $E_0\left[{\mathbf{X}}_{\Delta }|\mathbf{W},\mathbf{Y}\right]={\mathit{W}}_{\Delta ,s}\mathit{\eta }$ and ${\text{Var}}_0\left({\mathbf{X}}_{\Delta }|\mathbf{W},\mathbf{Y}\right)={\sigma }_X^2{\mathbf{\Phi }}_{\Delta }$, in addition to the usual regularity conditions needed for a central limit theorem.

Web Resources

• Affymetrix, https://www.affymetrix.com/analysis/netaffx/index.affx

• dbGaP, https://www.ncbi.nlm.nih.gov/gap

• L-GATOR source code, http://www.stat.uchicago.edu/∼mcpeek/software/index.html

• NCBI Gene, http://www.ncbi.nlm.nih.gov/gene

• OMIM, http://www.omim.org/