Integration of Temporal and Spatial Properties of Dynamic Connectivity Networks for Automatic Diagnosis of Brain Disease

Abstract

Functional connectivity networks (FCNs) using resting-state functional magnetic resonance imaging (rs-fMRI) have been applied to the analysis and diagnosis of brain disease, such as Alzheimer’s disease (AD) and its prodrome, i.e., mild cognitive impairment (MCI). Different from conventional studies focusing on static descriptions on functional connectivity (FC) between brain regions in rs-fMRI, recent studies have resorted to dynamic connectivity networks (DCNs) to characterize the dynamic changes of FC, since dynamic changes of FC may indicate changes in macroscopic neural activity patterns in cognitive and behavioral aspects. However, most of the existing studies only investigate the temporal properties of DCNs (e.g., temporal variability of FC between specific brain regions), ignoring the important spatial properties of the network (e.g., spatial variability of FC associated with a specific brain region). Also, emerging evidence on FCNs has suggested that, besides temporal variability, there is significant spatial variability of activity foci over time. Hence, integrating both temporal and spatial properties of DCNs can intuitively promote the performance of connectivity-network-based learning methods. In this paper, we first define a new measure to characterize the spatial variability of DCNs, and then propose a novel learning framework to integrate both temporal and spatial variabilities of DCNs for automatic brain disease diagnosis. Specifically, we first construct DCNs from the rs-fMRI time series at successive non-overlapping time windows. Then, we characterize the spatial variability of a specific brain region by computing the correlation of functional sequences (i.e., the changing profile of FC between a pair of brain regions within all time windows) associated with this region. Furthermore, we extract both temporal variabilities and spatial variabilities from DCNs as features, and integrate them for classification by using manifold regularized multi-task feature learning and multi-kernel learning techniques. Results on 149 subjects with baseline rs-fMRI data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) suggest that our method can not only improve the classification performance in comparison with state-of-the-art methods, but also provide insights into the spatio-temporal interaction patterns of brain activity and their changes in brain disorders.

Graphical abstract

1. Introduction

Alzheimer’s disease (AD) is a chronic neurodegenerative disease that usually starts slowly and gets worse over time. It is the most common cause of dementia among older adults. It is reported that AD accounts for 60 to 80 percent of dementia cases (Burns and Iliffe, 2009). In 2015, there were approximately 29.8 million people worldwide with AD, and causes about 1.9 million death (Vos et al., 2016). Dementia is the loss of cognitive functioning (e.g., thinking, remembering and reasoning) and behavioral abilities, which often causes a severe burden on the patient and caregiver, including social, psychological, physical and economic elements. In developed countries, AD is one of the most financially costly diseases (Bonin-Guillaume et al., 2005). In recent years, many studies have tried to find early biomarkers to evaluate AD risk pre-symptomatically in a rapid and rigorous way. Mild cognitive impairment (MCI), as a prodromal stage of AD, has gained increasing attention, due to its high probability of progression to AD (Reiman et al., 2010). Moreover, an early treatment of MCI may prevent or at least delay the progression of the disease and preserve some cognitive functions of the brain. Therefore, accurate diagnosis of MCI is of great importance.

Functional magnetic resonance imaging (fMRI), as an advanced medical imaging technique, provides a way to quantify the functional interaction of the human cerebrum (Bai et al., 2009). Those interaction patterns can be characterized as functional connectivity network (FCN) with functional connectivity (FC) measuring the temporal correlation between intrinsic BOLD signals in distributed brain regions. Studies on FCNs using resting-state fMRI (rs-fMRI) have shown great potential in understanding the brain’s function in health and disease, and also in diagnosis of brain disease. A number of studies have applied FCNs to the analysis of brain diseases (e.g., AD/MCI (Wang et al., 2013; Bai et al., 2011), schizophrenia (Micheloyannis et al., 2006) and attention deficit hyperactivity disorder (Tian et al., 2006)) using group analysis, and found a series of abnormal connectivities or network properties. For example, reduced functional connectivity between the hippocampus and other regions (Wang et al., 2007; Supekar et al., 2008), and disrupted “small-world characteristics” (Stam et al., 2007; Sanz-Arigita et al., 2010) have been reported in AD/MCI patients. One of the limitations in these studies is that they can not be automatically used to identify patients with brain disease from normal controls (NCs) at the individual level. On the other hand, studies have applied FCNs to the classification of brain diseases (e.g., AD/MCI (Chen et al., 2011; Jie et al., 2014) and schizophrenia (Shen et al., 2010)) by using machine learning. For example, Wee et al. (2012) integrated functional and structural connectivity networks for identification of MCI. Zanin et al. (2012) explored multiple topological features from FCNs for MCI classification. Wen et al. (2017) combined topological properties of FCNs for diagnosis of early tourette syndrome children.

Studies on the FCNs are based on the temporal correlation between distributed brain regions, with an implicit assumption that the FC is constant (i.e. temporal stationary) throughout recording period in rs-fMRI (Sporns, 2011). As a result, the dynamics of brain network are neglected in these studies. In fact, a number of studies demonstrate that the FC exhibits dynamic changes over time (Zhang and Small, 2006; Kiviniemi et al., 2011) that, to some degree, may be of neuronal origin and related to changes in cognitive and vigilance state (Thompson et al., 2013; Chang et al., 2013). Also, increasing evidence has shown that assessing dynamic changes in FCN is critical for a better understanding the fundamental properties of brain networks (Damaraju et al., 2014; Kudela et al., 2017) and the underpinnings of pathology of brain diseases (Hutchison et al., 2013; Zhang et al., 2016). Accordingly, studies have resorted to dynamic connectivity network (DCN) (Hutchison et al., 2013) to characterize the dynamic changes of FC, and investigated the association of dynamic changes of DCNs with brain diseases (Jones et al., 2012; Damaraju et al., 2014; Sakouglu et al., 2010; Starck et al., 2013). Jones et al. (2012) reported differences in the “dwell time” in sub-network configurations of the default mode network between AD patients and NCs, demonstrating rs-fMRI changes in AD patients beyond traditional stationary-based FCNs. Besides, studies have applied DCNs to the classification of MCI (Wee et al., 2016) and schizophrenia (Sakoglu et al., 2009), and achieved better classification performance compared with the conventional (i.e., stationary-based) FCNs.

Currently, most of the existing studies on DCNs focus on two aspects: 1) temporal properties of single FC between specific brain regions (Zalesky et al., 2014; Kucyi and Davis, 2014), and 2) the changing patterns of whole brain network (Allen et al., 2014). The former usually increases the burden of identifying the most informative FCs, while the latter may be less sensitive in identifying local changes in the brain. A recent work (Zhang et al., 2016) investigated the temporal properties of DCNs by defining the temporal variability of FCs associated with a specific brain region, which provides a convenient way to identify brain regions exhibiting significant changes in patients and thus helps to understand the dynamics of DCNs for various brain disease. However, the spatial properties of brain networks (e.g., the spatial variability of FCs associated with a specific brain region) have never been investigated in rs-fMRI studies. Actually, studies have shown that the human brain is intrinsically organized into dynamic and spatio-temporal interaction network (Fox et al., 2005; Sadaghiani and Kleinschmidt, 2013), demonstrating remarkable spatio-temporal variability in its function and structure (Sadaghiani and Kleinschmidt, 2013; Sadaghiani et al., 2010; Neumann et al., 2003). Also, recent evidence on FCNs suggests that, besides temporal variability, there may be significant spatial variability of activity foci over time (Kiviniemi et al., 2011; Birn et al., 2001; Zhang and Small, 2006; Kudela et al., 2017), which is often related to low-frequency physiologic effects (Kiviniemi et al., 2011; Birn et al., 2001). Hence, spatial properties of brain network may convey the important wealth of information and thus help deeper understanding of brain networks and diseases. Intuitively, jointly using temporal and spatial properties of brain networks can further improve the performance of brain disease diagnosis.

In this paper, we first define a new measure to characterize the spatial variability of DCN at a specific brain region. Then, we propose a novel framework to integrate both temporal and spatial properties of DCNs for brain disease classification. Specifically, we first construct dynamic connectivity networks from the rs-fMRI time series at successive, non-overlapping time windows. Then, we characterize the spatial variability of a given brain region by computing the correlation of functional sequences associated with this region. Here the functional sequence is defined as the changing profile of FC between a pair of brain regions within all time windows. Furthermore, we extract both temporal variabilities and the spatial variabilities from constructed dynamic connectivity networks as features, and then exploit a manifold regularized multi-task feature selection (M²FL) method to jointly select the most important region-related features. Finally, we adopt multi-kernel support vector machine (SVM) technique for brain disease classification. The experimental results on 149 subjects with baseline rs-fMRI data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (http://adni.loni.usc.edu/) demonstrate that our method can not only improve the classification performance in comparison with state-of-the-art methods, but also provide insights into the spatio-temporal interaction patterns of the brain activity and their changes in brain disorders.

The main contributions of this paper are three-fold. First, we define a new measure to characterize the spatial variability of DCN at a specific brain region. To the best of our knowledge, this is among the first attempts to characterize the spatial changing properties of DCN at the region level. Second, we develop a novel learning framework to integrate both temporal and spatial variabilities of DCNs for automated brain disease diagnosis based on rs-fMRI data. Finally, we investigate the changing patterns of the temporal variability and spatial variability in MCI patients.

The rest of the paper is organized as follows. In Section 2, we briefly describe the data used in this study, and present the proposed method and learning framework. In Section 3, we introduce experimental settings and results. In Section 4, we present discussions for experimental results, the influence of parameters, and limitation of our method. Finally, we conclude this paper in Section 5.

2. Materials and Method

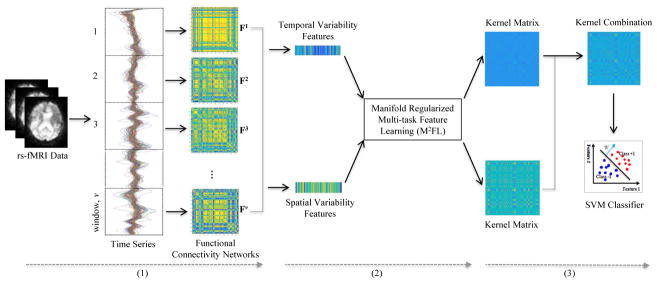
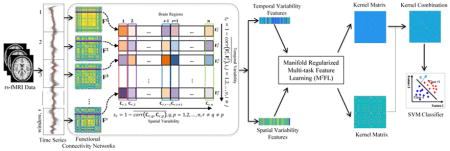
Figure 1 illustrates the proposed framework for brain disease diagnosis, by using both temporal and spatial properties of DCNs. As can be seen from Fig. 1, there have three main steps, including (1) image preprocessing and network construction, (2) feature extraction and selection, and (3) multikernel SVM based classification. In this section, we first introduce the data used in this study, and then present the details of each step in our proposed framework.

Figure 1.

Illustration of the proposed learning framework integrating both temporal and spatial properties of DCNs, including (1) image preprocessing and network construction, (2) feature extraction and selection, and (3) multi-kernel support vector machine (SVM) based classification. Dynamic connectivity networks are first constructed from the rs-fMRI time series by using non-overlapping time window approach. Two sets of features (i.e., the temporal variability features and the spatial variability features) are then extracted from constructed DCNs. Furthermore, a manifold regularized multi-task feature selection (M²FL) method is used to jointly select the most important region-related features. Finally, multi-kernel SVM is used for classification.

2.1. Subjects

In this study, we use a total of 149 subjects, including 50 NCs, 56 early MCI (eMCI) and 43 late MCI (lMCI) subjects, with baseline rs-fMRI data from ADNI database. All rs-fMRI data were acquired on 3.0 Tesla Philips scanners (with varied models/systems) at multiple sites. There is a range (from 2.29mm to 3.31mm) for imaging resolution in X and Y dimensions, with the slice thickness of 3.31mm. TE (echo time) for all subjects is 30 ms and TR (repetition time) is from 2.2 s to 3.1 s. For each subject, there are 140 volumes (time points). The demographic and clinical information of the studied subjects is presented in Table 1.

Table 1.

Characteristics of the studied subjects (MMSE ± Standard Deviation). MMSE: Mini-Mental State Examination.

Group	lMCI	eMCI	NC
Male/Female	26/17	21/35	21/29
Age (Mean ± SD)	72.1 ± 8.2	71.1 ± 6.8	75.0 ± 6.9
MMSE (Mean ± SD)	27.2 ± 2.0	28.1 ± 1.5	28.9 ± 1.6

2.2. Image Preprocessing and Network Construction

Image pre-processing is performed for all rs-fMRI data by using a standard pipeline, including brain skull removal, slice time correction, motion correction, spatial smoothing, and temporal pre-whitening using FSL FEAT software package (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FEAT). Specifically, the acquired rs-fMRI images are corrected for the acquisition time difference among all slices. All images are then aligned to the first volume for motion correction and a brain mask is also created from the first volume. As the head motion has substantial effects on FCN measures (Van Dijk et al., 2012), we have excluded subjects with excessive head motion in our study. That is, any subject with head motion more than 2.0mm in any of the x, y or z direction or more than 2.0° in any of the rotation axis will be removed. We then computed mean motion (Van Dijk et al., 2012), i.e., the mean absolute displacement of each brain volume as compared to the previous volume, estimated from the translation parameters in the x (left/right), y (anterior/posterior), and z (superior/inferior) directions. The average values of mean motion for lMCI, eMCI and NC groups are 0.28, 0.31 and 0.30, respectively. The head-motion profiles were matched for lMCI vs. eMCI groups (with the p-value on mean motion as 0.24) and eMCI vs. NC groups (with the corresponding p-value as 0.51).

As a last step, the global drift removal and band pass filtering between 0.01Hz–0.1Hz are performed using the tool in (Zhu et al., 2012). The preprocessing steps of the T1-weighted MRI data include brain skull removal and also the segmentation of brain tissues into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) by using FSL FAST software package (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FAST). The pre-processed T1 image is then co-registered to the first volume of the pre-processed rs-fMRI data of the same subject, and the BOLD signals in GM are merely extracted and adopted to avoid the relatively high proportion of noise caused by the cardiac and respiratory cycles in WM and ventricle (Van Dijk et al., 2010). Finally, the whole brain of each subject in the rs-fMRI space is parcellated into 116 regions of interest (ROIs), by warping the automated anatomical labeling (AAL) template (Tzourio-Mazoyer et al., 2002) to the rs-fMRI image space of each subject using the FSL FLIRT software package (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FLIRT). For each of the 116 ROIs, the mean rs-fMRI time series was calculated by averaging the GM-masked BOLD signals among all voxels within the specific ROI.

Finally, we construct the DCNs at successive, non-overlapping time windows, as shown in Fig. 1. Specifically, for each subject, we first equally segment all BOLD time series into v non-overlapping time windows. Then, we build a functional connectivity network (i.e., matrix) Fⁱ by computing Pearson correlation coefficient between BOLD signals from a pair of ROIs within the i^th time window, i.e.,

$${\mathbf{F}}^i(r,q)=\frac{\mathit{cov}({\mathbf{S}}_r^i,{\mathbf{S}}_q^i)}{{\sigma }_{{\mathbf{S}}_r^i}{\sigma }_{{\mathbf{S}}_q^i}}$$ (1)

where cov denotes the covariance between two vectors, ${\sigma }_{{\mathbf{S}}_r^i}$ denotes the standard deviation of vector ${\mathbf{S}}_r^i$, and ${\mathbf{S}}_r^i$ and ${\mathbf{S}}_q^i$ represent the BOLD signals of a pair of ROIs r and q within the i^th time window, respectively. Here, Fⁱ(·, ·) represents the element of matrix Fⁱ.

According to Eq.1, Fⁱ(r, q) defines the function connectivity of a pair of ROIs r and q within the i^th time window. Thus, we obtain a set of FCNs with v time windows, i.e., 𝔽 = {F¹, F², …, F^v}.

2.3. Temporal and Spatial Variabilities of DCN

In this section, we first introduce the temporal variability of DCN defined in recent studies (Zhang et al., 2016), and then present our proposed spatial variability of DCN.

Given the set of FCNs, 𝔽 = {F¹, F², …, F^v}, to characterize the time-varying properties of DCN at a specific brain region, Zhang et al. (2016) define the temporal variability of an ROI r as:

$$t_r=1-\frac{1}{v(v-1)}\sum _{i,j=1,i\ne j}^v\mathit{corr}({\mathbf{F}}^i(r,:),{\mathbf{F}}^j(r,:))$$ (2)

where Fⁱ(r, :) = [Fⁱ(r, 1), Fⁱ(r, 2), …, Fⁱ(r, r − 1), Fⁱ(r, r + 1), …, Fⁱ(r, n)]^T denotes the functional architecture of brain region r at the i^th time window, corresponding to the elements of the r^th row of the matrix Fⁱ except element Fⁱ(r, r), n is the number of ROIs of each subject, and corr(Fⁱ(r, :), F^j(r, :)) denotes the correlation coefficient between two functional architectures. The latter part of Eq. (2) computes the average correlation coefficient among all functional architectures of brain region r across different time windows, and thus measures their temporal similarity. Hence, Eq. (2) reflects the temporal variability of functional architectures associated with a given brain region. In this way, it provides a potential approach to analyze the temporal properties of DCN at the region level. However, the spatial variability of DCN at a specific brain region has never been explored in rs-fMRI studies.

In this work, we define a measure to characterize the spatial variability of a given brain region. Specifically, to reflect the changes of FC over time, we first define the changing profile of FC between a pair of specific brain regions within all time windows as the functional sequence. For instance, F^(:)(r, q) = [F¹(r, q), F²(r, q), …, F^v(r, q)]^T represents the functional sequence between brain regions r and q. The spatial variability of an ROI r is defined as:

$$s_r=1-\frac{1}{(n-1)(n-2)}\sum _{p,q=1,p\ne q\ne r}^n\mathit{corr}({\mathbf{F}}^{(:)}(r,q),{\mathbf{F}}^{(:)}(r,p))$$ (3)

where corr(F^(:)(r, q), F^(:)(r, p)) computes the correlation coefficient between two function sequences F^(:)(r, q) and F^(:)(r, p), measuring their similarity. The latter part of Eq. (3) computes the average correlation coefficient among all functional sequences associated with the brain region r across different brain regions, measuring the spatial similarity of all functional sequences associated with the brain region r. Thus, Eq. (3) computes the spatial variability of functional sequences of a given brain region.

Figure 2 illustrates the process of defining the temporal variability and spatial variability of a given brain region r. It is worth noting that, if we combine functional architectures from all time windows into a matrix F_r = [F¹(r, :), F²(r, :), …, F^v(r, :)]^T, then it is easy to show that F_r = [F^(:)(r, 1), F^(:)(r, 2), …, F^(:)(r, r − 1), F^(:)(r, r + 1), …, F^(:)(r, n)], i.e., each functional sequence of brain region r corresponds to one column of matrix F_r, as shown in Fig. 2. Therefore, two kinds of variabilities defined on the specific brain region reflect local changing properties of DCN from two different views. That is, the variability defined in Eq. 2 reflects the time-varying properties of the functional architecture of a particular brain region, while the spatial variability defined in Eq. 3 reflects the space-varying properties of the functional sequence associated with a brain region.

Figure 2.

Illustration of temporal variability and spatial variability of brain region r. For the i^th FCN (i.e., matrix), a functional architecture of brain region r consists of the r^th row elements except for Fⁱ(r, r), i.e., Fⁱ(r, :) = [Fⁱ(r, 1), Fⁱ(r, 2), …, Fⁱ(r, r − 1), Fⁱ(r, r + 1), …, Fⁱ(r, n)]^T. We combine all functional architectures associated with brain region r into a matrix F_r = [F¹(r, :), F²(r, :), …, F^v(r, :)]^T. Each column of F_r is a functional sequence associated with brain region r, e.g., F^(:)(r, q) = [F¹(r, q), F²(r, q), …, F^v(r, q)]^T, and F_r = [F^(:)(r, 1), F^(:)(r, 2), …, F^(:)(r, r − 1), F^(:)(r, r + 1), …, F^(:)(r, n)]. Finally, the temporal variability of brain region r is defined based on the correlation of functional architectures (i.e., rows of matrix F_r) associated with brain region r across different time windows, while, the spatial variability of brain region r is defined based on the correlation of functional sequences (i.e., columns of the matrix F_r) associated with the brain region r.

2.4. Feature Extraction and Selection

For each of those two kinds of variability defined in Eqs. 2 and 3, we extract a set of variabilities from constructed DCNs as features, thus producing two sets of features for each subject. These two kinds of features extracted from DCNs potentially include redundant features for subsequent brain disease classification. Also, two types of features reflect the local properties of DCNs from two different views, which may convey complementary information. To remove some redundant features and preserve the common subset of features (i.e., from the same regions) that are most likely relevant to disease pathology, we further perform feature selection using the manifold regularized multi-task feature learning method proposed in our previous work (Jie et al., 2015), where each task focuses on one type of features. Here, multi-task feature learning is used, since multi-task learning can take advantage of related information among tasks and hence generates good performance (Obozinski et al., 2010; Argyriou et al., 2008).

We denote ${\mathbf{X}}_m={[{\mathbf{x}}_m^1,{\mathbf{x}}_m^2,\dots ,{\mathbf{x}}_m^i,\dots ,{\mathbf{x}}_m^N]}^T(m=1,2)$ as the matrix for totally N training subjects with two kinds of features (i.e., temporal variability features and spatial variability features). Here, ${\mathbf{x}}_1^i={[t_1,t_2,\dots ,t_n]}^T$ represents the vector of temporal variability features extracted from the i^th training subject defined in Eq. 2. ${\mathbf{x}}_2^i={[s_1,s_2,\dots ,s_n]}^T$ represents the vector of spatial variability features defined in Eq. 3. We represent Y = [y¹, y², …, yⁱ, …, y^N] as the response vector of N training subjects, with yⁱ ∈ {+1, −1} corresponding the class label (i.e., patient or normal control) of the i^th training subject. Then, the objective function of M²FL (Jie et al., 2015) can be defined as follows:

$$\underset{\mathbf{W}}{min}\sum _{m=1}^M{\Vert \mathbf{Y}-{\mathbf{X}}_m{\mathbf{w}}_m\Vert }_2^2+\lambda \sum _{m=1}^M{({\mathbf{X}}_m{\mathbf{w}}_m)}^T{\mathbf{L}}_m({\mathbf{X}}_m{\mathbf{w}}_m)+\gamma {\Vert \mathbf{W}\Vert }_{2,1}$$ (4)

where W = [w₁, …, w_M] is the weight matrix, L_m = D_m − S_m denotes the Laplacian matrix on the m^th learning task. S_m is a similarity matrix that defines the similarity on task m across different training subjects, which can be defined as: S_m(i, j) = 1 if the i^th subject and the j^th subject have the same class label, and 0 otherwise. D_m is a diagonal matrix defined as ${\mathbf{D}}_m(i,i)={\sum }_{j=1}^N{\mathbf{S}}_m(i,j)$. M is the number of tasks (M = 2 in this work). In Eq. (4), the first item is a quadratic loss function that measures the fitting degree of data. The second item is a manifold regularized item that preserves the distribution information of the whole data from each task, and thus help induce more discriminative features for classification. The last item is a group-sparsity regularizer Obozinski et al. (2010) defined as ${\Vert \mathbf{W}\Vert }_{2,1}={\sum }_{i=1}^n{\Vert \mathbf{W}(i,:)\Vert }_2$, where W(i, :) denotes the i^th row vector of matrix W, which encourages features to be jointly selected across different tasks. The coefficients λ and γ are the corresponding regularization parameters, balancing the contributions of three items. Their values can be determined via inner cross-validation on the training subjects.

It is worth noting that features with non-zero elements in W will be selected for subsequent classification. For simplicity, in the following, we still use ${\mathbf{x}}_m^i$ to represent a vector of the selected features on the i^th subject from the m^th learning task. Besides, it is easy to show that the problem in Eq. 4 is reduced to the group-sparsity regularized optimization problem in the least absolution shrinkage and selection operator (gLASSO) (Meier et al., 2008), when λ equals to zero.

2.5. Multi-kernel SVM Classification

We use the multi-kernel SVM for classification, since multi-kernel SVM can effectively integrate multiple features (Zhang et al., 2011). Specifically, we first calculate a linear kernel on each set of features selected by M²FL method across different subjects. Therefore, we can get two kernels for two kinds of features. Then, we adopt the following multi-kernel learning technique to combine these two kernels:

$$k({\mathbf{x}}^i,{\mathbf{x}}^j)=\sum _{m=1}^M{\beta }_m{k}_m({\mathbf{x}}_m^i,{\mathbf{x}}_m^j),$$ (5)

where $k_m({\mathbf{x}}_m^i,{\mathbf{x}}_m^j)$ is the kernel over the m^th kind of features (i.e., the temporal variability features or the spatial variability features) across two subjects xⁱ and x^j (the linear kernel is adopted in our experiment), β_m denotes the integrating weight on the m^th feature, with the constraint of ${\sum }_{m=1}^M{\beta }_m=1$. Following (Zhang et al., 2011), we use a coarse-grid search strategy via cross-validation on the training subjects to find the optimal β_m. Once obtaining the optimal β_m, multiple kernels can be combined into a mixed kernel, and thus the standard SVM can be performed for classification.

3. Experiments and Results

In this section, we present our experimental settings, results of brain disease classification and comparison between our proposed method and several state-of-the-art methods.

3.1. Methods for Comparison

We first compare our proposed method with the baseline method (denoted as Baseline) using conventional (i.e., stationary-based) connectivity network. In the baseline method, the functional connectivity network of each subject is first constructed based on Pearson correlation between the whole time series of ROIs, then the local weighted clustering coefficients (Rubinov and Sporns, 2010) are extracted as features for classification. Moreover, we compare our proposed method with two methods using only a single property of DCNs, including 1) the method using only the temporal variability features (denoted as TVF), and 2) the method using only the spatial variability features (denoted as SVF). In those two comparison methods, the temporal variability features defined in Eq. 2 and the spatial variability features defined in Eq. 3 are, respectively, extracted from the constructed DCNs and used independently for classification. It is worth noting that, in all these three comparison methods (i.e., Baseline, TVF and SVF), the widely used LASSO method (Tibshirani, 1996) is applied to feature selection, and a linear SVM classifier with a default parameter (i.e., C = 1) is used for classification.

The proposed method is further compared with two methods that are widely used for combining multiple features in the classification based on brain networks, including the method that simply concatenates two variability features (denoted as CV²F), and the gLASSO-based multi-task method (denoted as gLASSO). In this two methods, two sets of features (i.e., the set of temporal variability features defined in Eq. 2 and the set of spatial variability features defined Eq. 3) are first extracted from our constructed DCNs. In the CV²F method, two sets of features are simply concatenated into a longer feature vector, and then LASSO-based method is used to perform feature selection, following by a linear SVM classifier with a default parameter for classification. In the gLASSO method, we use the group LASSO method (Meier et al., 2008), instead of M²FL method, to perform feature selection, and then use a multi-kernel SVM for classification.

3.2. Experimental Setting

In the experiments, we conduct two classification tasks, i.e., lMCI vs. eMCI classification, and eMCI vs. NC classification, using a leave-one-out (LOO) cross-validation strategy. We evaluate the classification performance by computing the accuracy (i.e., the proportion of subjects that are correctly classified), sensitivity (the proportion of patients that are correctly classified), specificity (the proportion of NCs that are correctly classified), and the area under the receiver operating characteristic (ROC) curve (AUC).

In the process of network construction, to avoid the arbitrary determination of window length (i.e., the number of time points), we construct the DCNs with different v (i.e., v = {5, 6, …, 12}), the corresponding window length is located in the interval (10,30). It is suggested that window sizes around 30–60s (equal to 10–30 time points, in our experiments) produce robust results in image acquisitions, cognitive states and topological properties of brain networks (Jones et al., 2012; Shirer et al., 2012). We compute the average value with all values v as the final temporal/spatial variability feature of the ROI. For each feature extracted from the constructed DCN, we perform normalization by using its mean and standard deviation calculated from all training subjects, and apply these values of the mean and standard to normalize the corresponding feature of each testing subjects.

In the step of feature selection, the values for parameters (e.g., λ and γ) are determined by using another round of LOO cross-validation on the training subjects. Specifically, we vary the values of λ within the range of {2,4,6,8,10,12,14} and the values of γ within the range of {2,4,6,8,10,12,14,16, 18,20,22,24,26,28,30}. The parameter values corresponding to the best performance will be used to predict the testing subjects. The linear SVM classifier is implemented by using LIBSVM toolbox (Chang and Lin, 2011) with a default parameter value (i.e., C = 1). The optimal parameters β_m(m = 1, 2) in multi-kernel SVM method are learned based on another LOO cross-validation on the training subjects via a grid search in the range [0, 1] with a step size of 0.1. It is worth noting that the cross-validation on the training subjects is only used to determine the optimal parameter values, while the outer cross-validation loop is used for evaluating the generalizability of learning models for unknown subjects.

3.3. Classification Performance

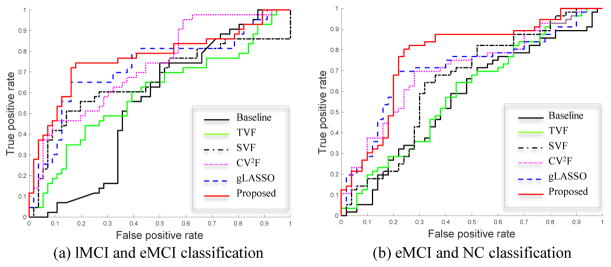
The classification performance achieved by six methods are summarized in Table 2. Also, the average number of features involved in the course of classification is given in Table 2. Figure. 3 provides the ROC curves of the methods. As can be seen from Table 2 and Fig. 3, our proposed method consistently outperforms the comparing methods in both classification tasks. For instance, our proposed method yields the accuracy of 78.8% and 78.3% for lMCI vs. eMCI classification and eMCI vs. NC classification, respectively, while the best accuracies of the competing methods are 74.7% and 73.6%, respectively. Also, our proposed method yields the AUC of 78.3% and 77.1% in both classification tasks, respectively, while the best AUCs of the competing methods are 72.9% and 71.2% in both classification tasks, respectively, indicating the effectiveness of our proposed method in brain disease diagnosis.

Table 2.

Results of six methods on two classification tasks. ACC: ACCuracy; SEN: SENsitivity; SPE: SPEcificity; The number in the bracket (i.e., “(No.)”) denotes the average number of features involved in the course of classification.

Method	lMCI vs. eMCI (%)				eMCI vs. NC (%)
	ACC (No.)	SEN	SPE	AUC	ACC (No.)	SEN	SPE	AUC
Baseline	56.6 (18.6)	55.8	57.1	55.1	59.4 (26.8)	66.1	52.0	56.9
TVF	57.6 (20.8)	48.8	64.3	59.9	60.4 (18.4)	64.3	56.0	59.1
SVF	63.6 (14.3)	60.5	66.1	65.8	63.2 (20.3)	71.4	54.0	64.4
CV2F	64.6 (22.2)	53.5	73.2	72.6	68.9 (41.0)	66.1	72.0	70.5
gLASSO	74.7 (24.4)	65.1	82.1	72.9	73.6 (44.2)	69.6	78.0	71.2
Proposed	78.8 (29.2)	74.4	82.1	78.3	78.3 (46.6)	82.1	74.0	77.1

Figure 3.

ROC curves of six methods on (a) the lMCI vs. eMCI classification, and (b) the of eMCI vs NC classification.

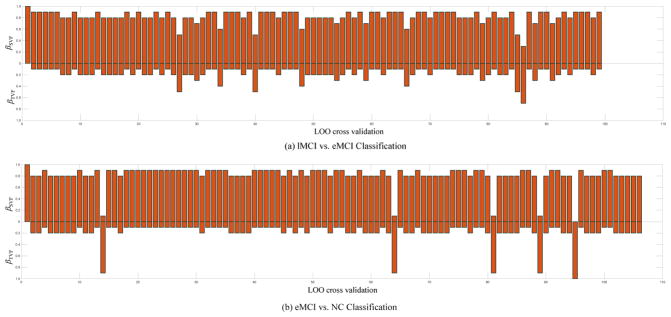
Furthermore, we could observe that, from Table 2 and Fig. 3, the methods combining multiple network properties (i.e., CV²F, gLASSO, and the proposed method) perform better than the methods using any single type of network properties alone (i.e., TVF, and SVF), implying that two these types of variability convey the different-yet-complementary information, and thus should be integrated together for further improving the classification performance. Also, Table 2 and Figure 3 show that the method based on the spatial variability features (i.e., SVF) consistently outperforms the performance of the method using temporal variability features (i.e., TVF). Figure 7 illustrates the weight distribution of these two kinds of network properties at each cross-validation. The results show that the weight value of β_SVF is larger than the weight value of β_TVF in most cases. These results suggest our defined spatial variability can effectively assess dynamic changes in FCN, thus helping better identify patients from normal controls. Besides, Table 2 and Figure. 3 also show that the DCN-based methods (i.e., TVF, SVF, CV²F, gLASSO, and the proposed method) outperform the conventional (stationary-based) connectivity network method (i.e., Baseline), indicating the advantages of the DCN over the conventional FCN.

Figure 7.

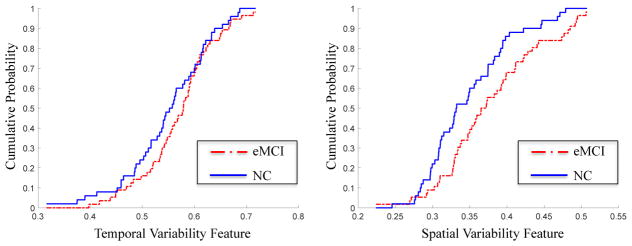
Cumulative-probability distribution of the temporal variability feature (left) and the spatial variability feature (right) in each subject group.

To evaluate the possible overfitting with LOO cross-validation strategy, we perform two groups of additional experiments. In the first group of experiments, we test the performance of our proposed method by using a 5-fold cross validation strategy. Specifically, the set of all subjects is (roughly) equivalently partitioned into five subsets. One subset is selected as the testing data. The remaining four subsets are combined as the training data. This process is repeated five times, and at each time a different subset is treated as the testing data. The results show that our proposed method achieves accuracies of 77.1% and 77.8% in the tasks of lMCI vs. eMCI classification and eMCI vs. NC classification, respectively. In the second group of experiments, we randomly reassign labels to all subjects (i.e., performing a random shuffling for the labels of all subjects), and perform the LOO cross-validation on the new labeled data (also after random shuffling). In the tasks of lMCI vs. eMCI classification and eMCI vs. NC classification, we achieve accuracies of 55.6% and 57.5%, respectively. All these results suggest the efficacy and generalization ability of our proposed method.

3.4. Important Brain Regions

In this subsection, we investigate the important features (corresponding to ROIs) selected by our proposed method in eMCI vs. lMCI classification and eMCI vs. NC classification, respectively. For each classification task, since the selected features are different in each LOO cross-validation fold, we choose features that always occur in all folds of cross-validation as the most important features. Moreover, for each selected feature, the standard t-test is also performed between two subject groups (i.e., patient group and NC group) for evaluating its discriminative power. Table 3 and Table 4 show those important ROIs and their corresponding p-values in two classification tasks, respectively. Figure 5 and Figure 6 plot those important ROIs in the template space.

Table 3.

Important brain regions involved in lMCI vs. eMCI classification. TVF=Temporal Variability Feature, SVF=Spatial Variability Feature. L.=Left, R.=Right.

ROI	p-value (TVF)	p-value (SVF)
L. Superior frontal gyrus (dorsal)	0.508	0.017
L. Orbitofrontal cortex (inferior)	0.030	0.110
R. Orbitofrontal cortex (medial)	0.239	0.009
L. Middle cingulate gyrus	0.037	0.205
R. ParaHippocampal gyrus	0.503	0.044
R. Postcentral gyrus	0.383	0.042
R. Angular gyrus	0.233	0.030
L. Temporal pole (superior)	0.071	0.041
L. Inferior temporal	0.231	0.223
L. lobule X of cerebellar hemisphere (flocculus)	0.462	< 0.001
Lobule I, II of vermis	0.385	0.033
Lobule III of vermis	0.372	0.033

Table 4.

Important brain regions involved in eMCI vs. NC classification. TVF=Temporal Variability Feature, SVF=Spatial Variability Feature, L.=Left, R.=Right.

ROI	p-value (TVF)	p-value (SVF)
L. Middle frontal gyrus	0.087	0.181
R. Orbitofrontal cortex (middle)	0.065	0.001
R. Rolandic operculum	0.438	0.002
L. Superior frontal gyrus (media)	0.054	0.150
R. Orbitofrontal cortex (medial)	0.081	0.025
R. Rectus gyrus	0.192	0.009
L. Posterior cingulate gyrus	0.085	< 0.001
R. Posterior cingulate gyrus	0.001	0.401
L. Hippocampus	0.087	0.023
L. Amygdala	0.031	0.043
L. Inferior occipital gyrus	< 0.001	0.016
R. Precuneus	0.094	0.002
R. Pallidum	0.117	0.006
R. Middle temporal gyrus	0.185	0.093
R. Temporal pole (middle)	0.063	0.010
L. crus II of cerebellar hemisphere	0.245	0.052
R. crus II of cerebellar hemisphere	0.166	0.020
L. Lobule VI of cerebellar hemisphere	0.068	0.030
R. lobule VIIB of cerebellar hemisphere	0.096	0.006
L. lobule IX of cerebellar hemisphere	0.052	0.020

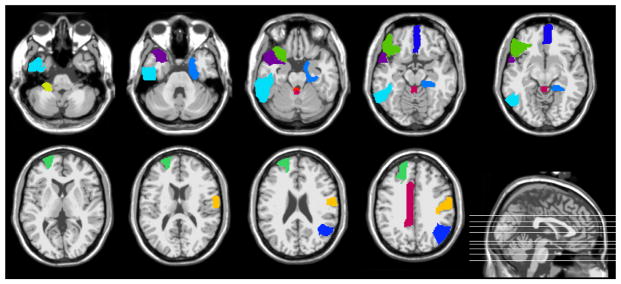
Figure 5.

Import brain regions identified by the proposed method in lMCI vs. eMCI classification.

Figure 6.

Import brain regions identified by the proposed method in eMCI vs. NC classification.

The results show that the important brain regions selected by our proposed method in two classification tasks are consistent with previous studies. For instance, the brain regions detected in the eMCI vs. NC classification, including posterior cingulate gyrus, hippocampus, amygdala, precuneus and temporal pole, have been reported to be useful in discriminating MCI patients from NCs.

On the other hand, from Tables 3 and 4, we can see that p-values of many important features are less than 0.05, indicating good discriminative power of those features. Table 4 also indicates that for eMCI patients, most of the selected brain regions (including Posterior cingulate gyrus, Hippocampus and Amygdala) show significant higher spatial variability when compared with NCs. It is worth noting that most of the selected spatial variability features are more discriminative than the selected temporal variability features, indicating that, compared with temporal variability, there exists more significant spatial variability between patients and NCs. This could partly explain why the method using the spatial variability features (i.e., SVF) can achieve better performance than the method using the temporal variability features (i.e., TVF), as shown in Table 2. Such results further indicate the efficacy of our defined spatial variability in characterizing the dynamics of FCN.

Another interesting observation from Tables 2, 3 and 4 is that more brain regions are involved in the task of eMCI vs. NC classification, compared with those in lMCI vs. eMCI classification This may indicate that, with the disease progression, more functional variability changes are produced in late MCI, thus a small number of brain regions with relatively large changes is sufficient for successful lMCI vs. eMCI classification.

3.5. Analysis of Variability of Whole Brain

In this subsection, we investigate the variability of the whole brain in patients with eMCI and identify the disease-related changes. Specifically, for each kind of variability features, we perform the standard t-test between two groups of subjects, i.e., eMCI subject group and NC subject group, and select brain regions with the significant difference in variability (i.e., the corresponding p-values< 0.05). Table 5 and Table 6 show the obtained results for the two kinds of variability, respectively. For comparison, Tables 5 and 6 also report the average value of the corresponding features for eMCI subject group and NC subject group, respectively.

Table 5.

Brain regions with significant temporal variability and the corresponding average value of features for eMCI subject group and NC subject group. L.=Left, R.=Right.

ROI	eMCI	NC	p-value
L. Superior frontal gyrus (dorsal)	0.522	0.514	0.036
R. Superior frontal gyrus (dorsal)	0.527	0.511	0.017
R. Orbitofrontal cortex (superior)	0.642	0.588	0.021
L. Rectus gyrus	0.624	0.596	0.044
R. Anterior cingulate gyrus	0.588	0.565	0.037
R. Posterior cingulate gyrus	0.576	0.556	0.001
L. Amygdala	0.609	0.595	0.031
L. Inferior occipital gyrus	0.485	0.490	< 0.001
R. Fusiform gyrus	0.557	0.543	0.027
L. Postcentral gyrus	0.532	0.522	0.021
R. Putamen	0.585	0.560	0.011
L. Lobule III of cerebellar hemisphere	0.593	0.574	0.008

Table 6.

Brain regions with significant spatial variability and the corresponding average value of features for eMCI subject group and NC subject group. L.=Left, R.=Right.

ROI: seMCI > sNC	eMCI	NC	p-value
L. Precentral gyrus	0.381	0.346	0.007
R. Precentral gyrus	0.379	0.352	0.002
L. Orbitofrontal cortex (middle)	0.367	0.338	0.011
R. Orbitofrontal cortex (middle)	0.367	0.357	0.001
L. Inferior frontal gyrus (triangular)	0.371	0.341	0.001
R. Rolandic operculum	0.374	0.362	0.002
L. Olfactory	0.358	0.321	0.008
R. Superior frontal gyrus (media)	0.384	0.349	0.010
R. Orbitofrontal cortex (medial)	0.361	0.333	0.025
L. Rectus gyrus	0.383	0.334	0.002
R. Rectus gyrus	0.396	0.342	0.009
R. Anterior cingulate gyrus	0.373	0.343	0.041
L. Posterior cingulate gyrus	0.383	0.352	< 0.001
L. Hippocampus	0.375	0.340	0.023
R. ParaHippocampal gyrus	0.371	0.343	0.039
L. Amygdala	0.356	0.334	0.043
L. Cuneus	0.385	0.359	0.006
L. Middle occipital gyrus	0.372	0.344	0.015
R. Middle occipital gyrus	0.384	0.348	0.046
L. Inferior occipital gyrus	0.393	0.357	0.016
R. Precuneus	0.412	0.380	0.002
R. Paracentral lobule	0.410	0.386	0.023
R. Pallidum	0.374	0.354	0.006
L. Heshl gyrus	0.361	0.334	0.003
R. Heschl gyrus	0.358	0.329	0.047
L. Superior temporal gyrus	0.391	0.363	0.030
L. Temporal pole (superior)	0.371	0.347	0.002
R. Temporal pole (middle)	0.366	0.325	0.010
L. Inferior temporal	0.391	0.348	0.029
R. Inferior temporal	0.400	0.364	0.045
R. crus II of cerebellar hemisphere	0.388	0.323	0.020
L. Lobule VI of cerebellar hemisphere	0.399	0.359	0.030
L. lobule VIIB of cerebellar hemisphere	0.367	0.323	0.003
R. lobule VIIB of cerebellar hemisphere	0.379	0.322	0.006
L. lobule IX of cerebellar hemisphere	0.343	0.292	0.020
Lobule VI of vermis	0.387	0.362	0.007
Lobule VIII of vermis	0.374	0.332	0.007

As we can see from Table 5 and Table 6, most of the brain regions, such as posterior cingulate, rectus gyrus, hippocampus, parahippocampal gyrus, amygdala and temporal pole, have been reported in previous AD/MCI studies (Buckner et al., 2008; Yao et al., 2013; Liu et al., 2012; Fleisher et al., 2009; Smith et al., 2011). Also, Table 5 and Table 6 show that almost all identified brain regions of patients with eMCI exhibit a significant increase in temporal and spatial variability (i.e., only one brain region exhibits decrease in temporal variability), indicating the spatio-temporal changes of FCN in eMCI, which is consistent with previous studies. For instance, studies have reported the abnormal functional connectivity in the brains of AD and MCI patients, including disrupted connectivity in the posterior cingulate and hippocampus (Greicius et al., 2004; Bai et al., 2011), increased connectivity between the frontal lobe and other brain regions (Wang et al., 2007), and altered connectivity of amygdala (Yao et al., 2013). Also, the altered topological patterns of FCNs have been reported, such as the increase of characteristic path length and the impaired functional connectivity between different functional modules in MCI patients (Wang et al., 2013; Liu et al., 2012), and loss in small-world characteristics (i.e., shorter path length and higher degree of clustering) in subjects with MCI and AD (Supekar et al., 2008; Sanz-Arigita et al., 2010). In line with these finding, patients with AD/MCI exhibit increased variability (spatial variability in particular) in these brain regions associated with abnormal activity and connectivity. This is consistent with a recent study (Jones et al., 2012) that demonstrates rs-fMRI changes in AD patients beyond stationary-based connectivity networks.

It is worth noting that 1) many brain regions identified based on the variability are identical to those selected in the course of eMCI vs. NC classification, showing again the efficacy of our proposed method. 2) Compared with temporal variability, more disease-related brain regions are identified in spatial variability, further indicating that patients with eMCI exhibit more significant spatial variability when compared with temporal variability.

Furthermore, we assess the total variability of the whole brain in eMCI patients. Specifically, for each type of variability, we first compute the average value of features for all brain regions in each subject, and then perform the standard t-test between eMCI subject group and NC subject group. Also, we compute the cumulative-probability distribution of each type of variability features in each subject group as illustrated in Fig 7. Here, we calculate the proportion of feature occurred in each subject group as the probability of the corresponding feature. The results show that, compared with NCs, the eMCI patients do not exhibit significant temporal variability (with the corresponding p-value of 0.158), but, have significantly increased spatial variability (with the corresponding p-value of 0.011), suggesting the importance of our defined spatial variability. In addition, Figure 7 shows that, for all subjects, the values of temporal variability features are significantly larger than the values of spatial variability features (the p-value< 7.8e–20), showing that brain network exhibits greater temporal variability when compared with spatial variability.

4. Discussion

Numerous studies suggested that the physiological and psychiatric diseases, such as AD and MCI, exhibit significant changes in dynamic properties (Greicius, 2008; Aerts et al., 2016; Zhang et al., 2016; Córdova-Palomera et al., 2017). Quantification of changed dynamics in brain connectivity network may lead to better understanding of brain disease, and eventually better prognostic indicator or diagnosis. Currently, most studies investigate temporal variability of brain networks. However, few works investigate the spatial variability of brain networks. In this paper, we first define a measure to characterize the spatial variability of DCN, and further develop a novel framework that integrates both temporal and spatial variabilities of DCNs for improving disease diagnosis performance. The dynamic connectivity networks are constructed from the rs-fMRI time series, and then both temporal and the spatial variabilities are extracted from constructed DCNs as features, and further integrated for classification of brain diseases, by using M²FL for feature selection and multi-kernel SVM for classification. The experimental results on 149 subjects from ADNI dataset suggest that our proposed method outperforms several state-of-the-art methods, demonstrating that characterizing and integrating both temporal and spatial properties of brain interaction patterns is effective in boosting the diagnosis performance of brain diseases. It is worth noting that our defined spatial variability can be potentially used for analyzing the fundamental properties of brain network or brain activity, e.g., the underlying relationship between spatial variability of functional sequence of a specific brain region and its structural connectivity and neural activity.

On the other hand, we found that the brain regions detected in the eMCI vs. NC classification by our proposed method are relevant to MCI pathology. For example, brain regions, including posterior cingulate gyrus, hippocampus, precuneus, and middle frontal gyrus, are mostly the components of the default mode network (DMN). Previous studies have suggested that the activity patterns with DMN may be directly related to the pathology of AD (Buckner et al., 2008). Other brain regions include amygdala (Yao et al., 2013; Liu et al., 2012) rectus gyrus (Fleisher et al., 2009), temporal gyrus (Fleisher et al., 2009; Smith et al., 2011), and temporal pole (Wang et al., 2007; Ni et al., 2017). Besides, some regions from the cerebellum were also selected. Previous studies suggested that although the cerebellum might be directly associated with the origin of AD, it contributes to human recognition (Baldaccara et al., 2011) and may provide useful information for AD prognosis (Weis et al., 2004; Wee et al., 2016).

Brain network analysis has revealed changes in functional connectivity or topological organization of the brain in many brain disorders, including AD and MCI (Greicius et al., 2004; Bai et al., 2011; Yao et al., 2013; Liu et al., 2012; Jones et al., 2012). However, the spatio-temporal changing properties of the brain network in MCI have never been investigated. In fact, a number of studies have suggested that resting-state fluctuations reflect a deeper biological principle of organization and are a consequence of the spatio-temporal structure of primate anatomical connectivity (Ghosh et al., 2008). As a result, brain diseases including AD and MCI are expected to be characterized by various disrupted functional configurations (Córdova-Palomera et al., 2017). Of note, the underlying neurobiological mechanisms can be characterized by measuring variation in synchrony among regions over time (Hutchison et al., 2013; Hindriks et al., 2016; Córdova-Palomera et al., 2017). In our work, we define and investigate the spatio-temporal variability of the brain, and identify disease-related changes in eMCI patients which might be related to disrupted functional configurations. For instance, neuropathological studies have found that aging and AD are related to myelin aberrations (Bartzokis, 2004). Also, existing studies have suggested that the changes in the functional configurations are constrained in the case of degradation of myelination (Ghosh et al., 2008; Córdova-Palomera et al., 2017). Therefore, our study may provide important clues to understand the underlying neuropathology of brain diseases and thereby contribute to the development of diagnostic imaging.

4.1. Functional Connectivity Network and Diagnosis of Brain Disease

Conventional stationary-based functional connectivity networks have been applied to the analysis of brain diseases (e.g., AD and MCI). Most studies investigated connectivity or topological properties of brain network by using group analysis approach, and reported a series of disrupted connectivity (Greicius et al., 2004; Bai et al., 2011; Yao et al., 2013) and changing patterns associated with a specific brain disorder (Wang et al., 2013; Liu et al., 2012; Supekar et al., 2008; Sanz-Arigita et al., 2010). These studies provide an important alternative to make use of the network properties to classify the patients with brain disease from NCs. Besides, some works classified AD/MCI by extracting features from FCNs (Chen et al., 2011; Jie et al., 2014; Zanin et al., 2012; Wee et al., 2012) and achieved reasonable results.

Recently, dynamic properties of brain networks have attached increasing attention. A number of studies have investigated the association between dynamic changes in DCN and various brain diseases (Zhang et al., 2016; Filippini et al., 2009). More recently, (Wee et al., 2016) utilized the temporal dynamics of rs-fMRI for early MCI classification. In this work, the dynamic connectivity networks were first estimated from rs-fMRI using the overlapping time window approach, then, the two network measures (i.e., clustering coefficients and characteristic path lengths (Rubinov and Sporns, 2010)) were calculated from each network to extract temporally dynamic patterns for classification. The experiment results on 59 subjects (including 29 eMCI patients and 30 NCs) from the ADNI dataset show that their method yielded an accuracy of 79.7% and an AUC of 79.2%. This is one of the first reports demonstrating the classification performance of DCNs in disease beyond the conventional stationary-based connectivity networks. In contrast to these existing works, our work presents a novel learning framework to integrate both temporal and spatial variabilities from DCNs for brain disease classification, and achieves comparable results.

4.2. Comparison of Different Combining Schemes

To investigate the effect of both combining weights (i.e., the weight of temporal variability features, β_TVF and the weight of spatial variability features, β_SVF) on the classification performance of our proposed method, we test all of their possible values in the range [0, 1] at a step size of 0.1, with the constraint of β_TVF + β_SVF = 1. Figure 8 shows the classification performance, including classification accuracy and AUC value, with respect to different combining weights of these two kinds of variability features. It is worth noting that, for each plot, the vertices of curve, i.e., the leftmost and the rightmost, denote the results of the method using only temporal variability features (i.e., β_TVF = 1) and method using only spatial variability features (i.e., β_SVF = 1), respectively.

Figure 8.

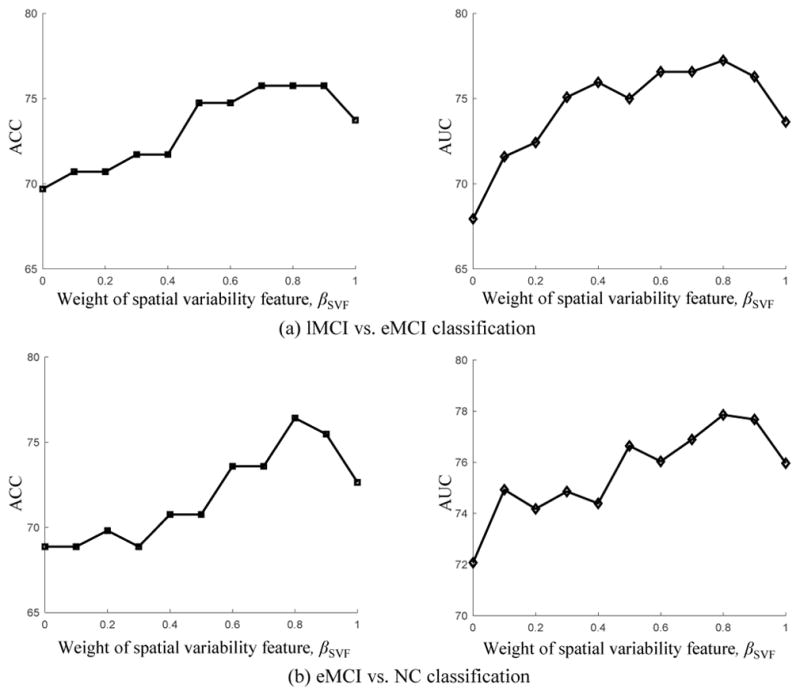
Results achieved by our proposed method with respect to different combining weights of temporal and spatial variability features from DCNs in the classification tasks of (a) lMCI vs. eMCI, and (b) eMCI vs. NC. Note that β_TVF = 1 − β_SVF.

As can be seen from Fig. 8, most of the inner intervals of the curve have larger values (i.e., better classification) than the two vertices, demonstrating the effectiveness of combining these two kinds of network properties for classification. Moreover, the intervals with higher performance mainly lie in the interval of [0.5, 0.9], implying that two kinds of network properties are indispensable to each other for achieving good classification. Also, Figure 8 shows that this method is inferior to our multi-kernel SVM based method as shown in Table 2, indicating that these two kinds of network properties contribute differently and hence should be integrated adaptively for achieving better performance.

4.3. Effect of Feature Learning

Feature learning, which can be considered as the biomarker identification for AD and MCI, is the most commonly used approach for simplifying the data model and thus improving the efficiency of data analysis. In this subsection, we will evaluate the effect of feature learning from three aspects: 1) feature selection with different combinations of parameter values, 2) comparison with different feature selection methods, and 3) without feature selection.

In our proposed classification framework, the M²FL method is adopted to perform the feature selection, where includes two regularization items, i.e., the manifold regularizer and the group-sparsity regularizer. The former is used to induce more discriminative features, while the latter is used to determine the number of selected features. The parameters λ and γ balance the relative contribution of two terms. Therefore, we evaluate the effect of feature learning via investigating the effects of the regularization parameters λ and γ on classification performance of our proposed method. Specifically, we test different values of λ, ranging from 0 to 30 with a step size of 2, and also test the values of γ, ranging from 0 to 14 with a step size of 2. It is worth noting that larger γ value means few features selected for classification, and, when γ = 0, no feature selection step is performed, i.e., all features extracted from DCNs are used for classification. Also, when λ = 0, no manifold regularization item is included, and thus M²FL method will be degraded to a gLASSO-based method Meier et al. (2008).

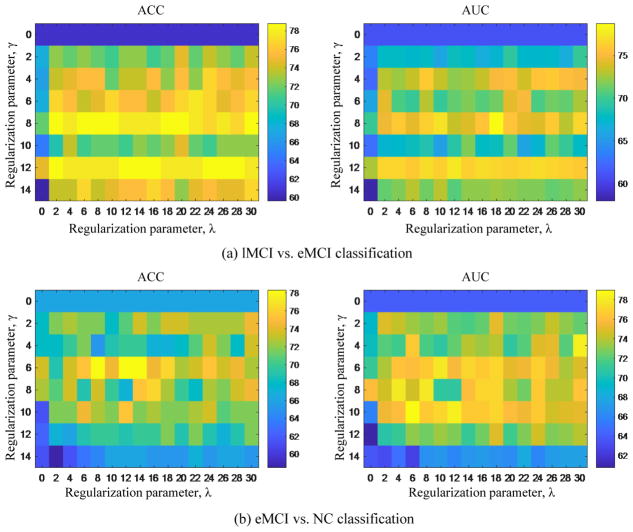
Figure 9 shows the classification results with respect to different combinations of λ and γ values. As can be seen from Fig. 9, the classification performance of our proposed method with respect to different combinations of λ and γ values (i.e., λ > 0 and γ > 0) is consistently better than that of gLASSO-based method (i.e., λ = 0 and γ > 0), indicating the efficacy of our proposed method. Also, Figure 9 shows that the classification performance with feature selection (i.e., γ > 0) is better than the method without feature selection (i.e., γ = 0), suggesting the importance of feature selection for classification. Besides, from Fig. 9, we can also observe that the performance on two classification tasks is largely affected by different γ values, indicating that the importance of determining the optimal γ value. This is reasonable since γ determines the sparsity of M²FL model and thus controls the number of selected features.

Figure 9.

Results achieved by our method with respect to the selections of regularization parameters λ and γ values on (a) the lMCI vs. eMCI classification, and (b) the eMCI vs. NC classification.

To further compare with different feature selection methods, besides the LASSO-based method, we test the performance of t-test method for feature selection in four competing methods (i.e., Baseline, TVF, SVF and CV²F). Specifically, we use a statistical t-test method with the same threshold (i.e., p-value< 0.05) for feature selection in four competing methods, followed by a linear SVM with default parameter for classification. Table 7 gives the obtained results. As we can see from Table 7, these results on both classification tasks are inferior to those of our proposed method (see Table 2), suggesting again the efficacy of our proposed method.

Table 7.

Results of four methods with t-test for feature selection on two classification tasks. ACC: ACCuracy; SEN: SENsitivity; SPE: SPEcificity; The number in the bracket (i.e., “(No.)”) denotes the average number of features involved in the course of classification.

Method	lMCI vs. eMCI (%)				eMCI vs. NC (%)
	ACC (No.)	SEN	SPE	AUC	ACC (No.)	SEN	SPE	AUC
Baseline	55.6 (2.2)	46.5	53.6	55.0	60.4 (9.8)	62.0	58.9	61.6
TVF	58.6 (3.7)	44.2	69.6	58.1	59.4 (12.6)	62.5	56.0	60.1
SVF	62.6 (21.9)	62.8	62.5	61.1	64.2 (37.5)	69.6	58.0	68.3
CV2F	64.7 (25.6)	62.8	66.1	66.0	67.9 (50.1)	68.1	64.3	71.0

In addition, to evaluate the effect of feature selection, we test the classification performance of four competing methods (i.e., baseline, TVF, SVF and CV²F) and the proposed method without feature selection. Since no feature selection step is performed, we directly use all extracted features for classification in these methods. Table 8 gives the obtained results on both classification tasks. As can be seen from Table 8, our proposed method still achieves good performance in comparison with other methods, showing again the efficacy of our proposed method. Besides, we can see from Tables 8 and 2 that the classification results in all methods with feature selection are better than those by methods without feature selection, showing the importance of feature learning for improving classification performance.

Table 8.

Results of five methods without feature selection on two classification tasks. ACC: ACCuracy, SEN: SENsitivity, SPE: SPEcificity. The number in the bracket (i.e., “(No.)”) denotes the number of features involved in the course of classification.

Method	lMCI vs. eMCI (%)				eMCI vs. NC (%)
	ACC (No.)	SEN	SPE	AUC	ACC (No.)	SEN	SPE	AUC
Baseline	45.5 (116)	27.9	58.9	39.9	55.7 (116)	57.1	54.0	55.6
TVF	52.5 (116)	44.2	58.9	52.5	57.6 (116)	60.7	54.0	58.9
SVF	52.5 (116)	46.5	57.1	52.6	60.4 (116)	60.7	60.0	61.3
CV2F	57.6 (232)	41.9	69.6	56.6	63.2 (232)	62.5	64.0	63.1
Proposed	60.6 (232)	48.8	69.6	61.1	66.0 (232)	71.4	60.0	64.1

4.4. Limitations

There are several limitations to be considered in this study. First, the proposed method is based on the spatio-temporal dynamics during the rs-fMRI scan. However, the neurobiological basis and mechanisms for these dynamics are still unclear (Kudela et al., 2017; Zhang et al., 2016), and it is difficult to determine whether those dynamic changes are actually due to neuronal activity or simply a byproduct driven by the noise. Second, in the current study, we construct DCNs by using non-overlapping time window method. It is interesting to utilize different network construction approaches (e.g., the over-lapping sliding window approach (Hindriks et al., 2016), independent component analysis (Chang and Glover, 2010) and time series models (Lindquist et al., 2014)) to further evaluate the proposed method, which will be our future work. In addition, brain parcellation (i.e., the definition of brain regions) is the very basic step for network-based analysis. Different brain parcellations can lead to the brain networks with different connectivity (Zalesky et al., 2010), hence making the brain network exhibit different variability. As the future work, we will evaluate the effects of different brain parcellations for our method.

5. Conclusion

In this paper, we have defined a new measure to characterize the spatial variability of dynamic connectivity networks, and further integrated both temporal and spatial properties of DCNs for brain disease classification. Specifically, we first construct the dynamic connectivity network of each subject from rs-fMRI time series by using non-overlapping time window approach. Then, we characterize the spatial variability of DCN by computing the correlation of functional sequences of a given brain region. Furthermore, we extract both temporal and spatial variabilities from the constructed DCNs as features, and explore a manifold regularized multi-task feature selection method to jointly select the most important features. Finally, a multi-kernel SVM technique is implemented for classification. The results on MCI dataset suggest that our proposed method can not only improve the classification performance of brain diseases, but also provide insights into the spatio-temporal interaction patterns of the brain activity and their changes in brain disorders.

Figure 4.

Weight combination of two kinds of variabilities in each cross-validation for our proposed method on (a) the lMCI vs. eMCI classification (b) the eMCI vs. NC classification. The median values of β_SVF are all 0.8 for the two classification tasks, and the corresponding median values of β_TVF are all 0.2.

Highlights.

• A new measure to characterize the spatial variability of DCN is proposed.

• A novel learning framework to integrate both temporal and spatial variabilities of DCNs is developed.

• Achieving an accuracy of 78.8% and 78.3% for lMCI (late MCI) vs. eMCI (early MCI) classification and eMCI vs. NC (normal control) classification, respectively.

• eMCI patients exhibit significant increased spatial variability.