Summary
Background/Objective
Spatial knowledge of the anatomy of the proximal humerus is critical for effective treatment, particularly in patients affected by fragility fractures. High-resolution peripheral quantitative computed tomography (HR-pQCT) imaging with medical image processing techniques enable three dimensional (3D) analysis of volumetric bone mineral density (vBMD) of bones of different sizes and shapes.
Methods
To elucidate the bony anatomy and to create 3D reference data, we conducted a computerized HR-pQCT-based study in intact postmortem samples of the proximal humerus to highlight the anatomy with particular emphasis on the size, shape, and bone stock distribution pattern.
Fifty-eight defrozen intact humerus samples from 28 female and 30 male donors, who were aged 61–98 years old (mean age ± standard deviation, 80.6 ± 9 years), were scanned in the proximal third using the extended standard HR-pQCT protocol. A 3D statistical bone and averaged bone density models with low, middle, and high total vBMDs were computed. We examined the 3D patterns of size and shape variations using principal component analysis, and the vBMD distributions and variabilities using volume-rendering and virtual bore probing.
Results
The computer models revealed a highly variable bony anatomy in which size was the predominant variation in the first principal component (PC). In the second PC, we observed notable variabilities in the shape of the head and shaft inclination. A distinct 3D pattern of bone stock distribution was detected in which the lowest vBMD values were identified in the medullary cavity, middle values were identified in the central zone, and the highest values were identified in the cortex and humeral head—particularly in the subarticular zones. In the presence of bone loss, the vBMD values were ubiquitously decreased, but the pattern of 3D bone stock distribution was maintained.
Conclusion
The new anatomical 3D data that we acquired will improve the understanding of the normal bony anatomy of the proximal humerus. The extended HR-pQCT protocol and computer models may be used for other skeletal sites and used as 3D reference models that can be applied to systematically improve implant design and anchorage.
Keywords: bone mineral density, fracture, high-resolution peripheral quantitative computed tomography, osteoporosis, proximal humerus, three-dimensional statistical bone model
Introduction
The proximal humerus is an angulated, non-weight-bearing extremity of the long bone in the upper limb and consists of two main anatomical structures: the proximal shaft portion and the humeral head. The humeral head with its caput humeri is inclined toward the medial side; comprises variable amounts of cortical, subarticular, and trabecular bone; and articulates with the glenohumeral joint to reach the scapula. The anatomical neck separates the caput humeri from the greater and lesser tuberosities, which are laterally and anteriorly located, respectively. Below the humeral head is the surgical neck. Cortical bone also exists in the shaft and neck portion that confines the proximal end of the medullary cavity. Traditional methods have been used to describe different morphologic and radiometric features and to characterize variations in the normal anatomy and bony content for implant design features or classification purposes [1], [2], [3], [4].
Proximal humerus fractures occur within this skeletal site and represent a particular type of traumatic injury. Fracture lines and gaps occur in all of the main anatomical structures. Osteosynthesis is highlighted in conditions that involve reduced bone mass and altered bone structure that significantly compromises implant anchorage and consequently the mechanical stability of the bone implant construct. With ageing, the proximal humerus may be notably affected by bone loss and structural decay [5]. Osteoporosis increases the fracture risk and increases the difficulty of surgical repair in patients who have fragility fractures. Fragility fractures of the proximal humerus are low-energy traumas and are particularly concerning because they represent an increasing problem for the health system [6], [7]. Such fractures follow fractures of the femoral neck and distal radius as the third most common type of osteoporotic fracture [8]. Disimpaction of the humeral head creates a void area and may even require bone-grafting procedures [9], [10]. Hence, adequate fracture fixation is of particular concern for elderly patients and severely injured patients who are affected by osteoporosis. Adequate fixation can be achieved by using minimally invasive osteosynthesis, open reduction and plate fixation, intramedullary nailing and primary arthoplasty, or additional bone-grafting procedures [10], [11]. However, operative treatment is associated with a high complication rate, and several risk factors are associated with an increased rate of fixation failure or impaired functional outcomes. Low bone mineral density is one factor [12], [13], [14]. Implant choice, indications for humeral head replacement, osteosynthesis techniques, and additional bone grafting in osteoporotic humeri may differ from the treatment of patients with better bone stock. Several authors have outlined that poor local bone quality must be considered in the decision-making process [11], [15], [16].
The proximal humerus forms a specific treatment site that has variable internal and external anatomies. Understanding the implications for improving fracture management and implant constructs, particularly among elderly patients, requires a thorough anatomical and clinical evaluation. Based on a few anatomical landmarks obtained from the proximal and distal epiphyses, Cretan humeri have undergone sex-related evaluations for forensic medical purposes [17]. However, additional anatomical information about the spatial aspects is required and ought to be viewed in light of the therapeutic implications and morphological variations that have been observed across different individuals.
We conducted the present computational study to elaborate the spatial anatomy of the proximal humerus via investigations of the three-dimensional (3D) shape, size, and bone stock distribution and variation patterns. In contrast to previous computed tomography/quantitative computed tomography (CT/QCT) studies [18], [19], we hypothesized that the 3D anatomical conditions of the proximal humerus would be captured within a single parametric high-resolution peripheral quantitative computed tomography (HR-pQCT)-based computer model. Our objectives were specifically as follows: (1) to analyse the variabilities in size and shape; (2) to compute 3D-averaged bones with low, medium, and high volumetric bone mineral density (vBMD) at high resolution; (3) to examine the bone stock distributions to identify the sites with invariable bone stock; and (4) to demonstrate the differences between high and low bone stock.
Materials and methods
Bone specimens
Fifty-eight unpaired intact fresh frozen humeri were examined. These bones were obtained from 28 female and 30 male donors and comprised three right samples and 55 left samples from individuals aged 61–98 years old. The overall mean age was 80.6 ± 9 years (mean ± standard deviation). The mean age for the female donors was 84.5 ± 7.6 years and the mean age for the male donors was 76.9 ± 8.7 years. Anonymized postmortem humeri were donated for unrelated biomechanical studies from university hospitals in Switzerland and Germany after internal review board approval, and were made available for scanning for the purpose of this project. The specimens were stored at −20°C. All bone specimens were maintained in a vacuum-packed state in polyethylene during the measurements.
Image acquisition
After thawing the bone specimens at room temperature, they were subjected to HR-pQCT scanning. The protocol comprised scanning a maximum length of 16 cm of the proximal extremity using a HR-pQCT scanner (XtremeCT; Scanco Medical, Brüttisellen, Switzerland) with phantom calibration. The machine settings were the following, as described by Popp et al [20] at the distal tibia: the x-ray tube was set at 60 kVp with an effective energy of 40 keV (900 μA) and an image matrix size of 1024 × 1024 at nominal 82 μm isotropic resolution. The scanned volume of interest was defined on the scout view. The HR-pQCT scans were stored in Digital Imaging and Communication in Medicine (DICOM) format. Approximately 1950 slices were acquired from each specimen.
Image processing
The DICOM image data stacks were loaded into Amira software (Amira version 5.4.5; Visualization Science Group, Merignac Cedex, France). Virtual radiograph visualization (i.e., a digitally reconstructed radiograph) was computed and checked before processing to exclude potential unreported alterations such as unidentified bone disease. All samples that were included were free from obvious pathology, as determined by a trained professional. The DICOM records were expressed in Hounsfield units and were converted to vBMD data, based on the linear transformation defined by the machine's calibration. The vBMD values are expressed as milligrams of hydroxyapatite per centimetre cubed (mg HA/cm3). Tissues other than bone were labelled algorithmically, and their values were set to 0. All images of the right proximal humeri were mirrored to the left side, and all data were cropped to the proximal 33% of the full length of each humerus. Standard image segmentation was performed to create 3D computer models of the surfaces of the proximal humeri. Geomagic Studio version 12 software (Geomagic U.S. Corp., Research Triangle Park, NC, USA) processed the images to obtain smooth regular triangular surface structures without holes or triangle intersections.
3D statistical bone modelling
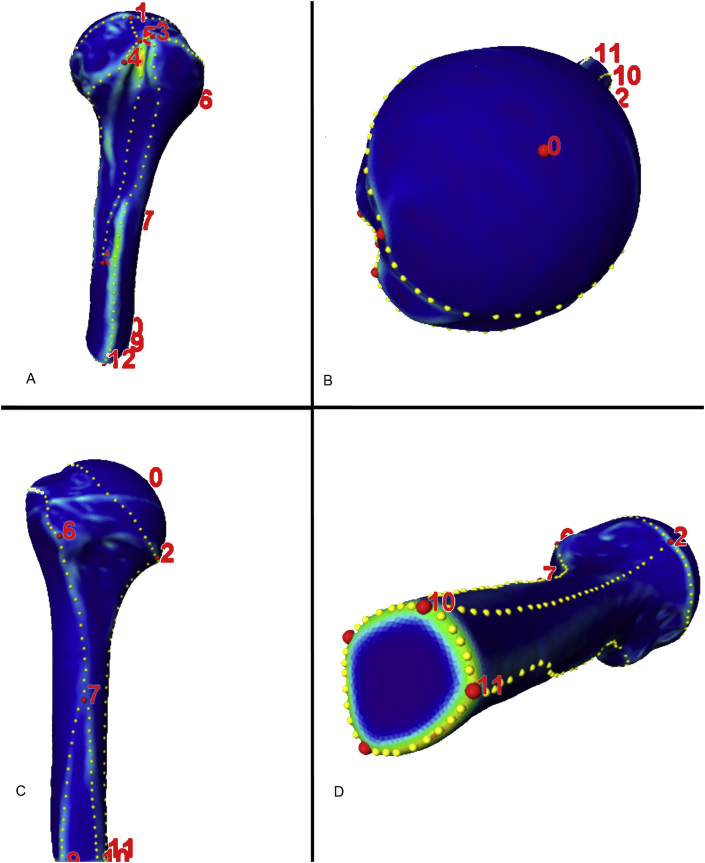
To assess the variations in the shapes and sizes of the proximal humeri, anatomically homologous landmarks and segments were identified on each of the 58 surface models (Figure 1). A representative 3D model was selected and warped to the remaining 3D models using thin plate spline (TPS) transformation. The TPS represents an interpolation-based registration technique that has been adapted by Bookstein [21] for use in morphometrics. It generated anatomically homologous triangular meshed surfaces with identical numbers and locations on the different models that consisted of 10,000 surface points and 19,996 triangles per proximal humerus [22]. All homologous surface-meshed models were aligned using a nonscaled Procrustes fit alignment to generate a mean model and a 3D statistical model of the proximal humerus [23].
Figure 1.
Definitions of anatomically homologous regions within 58 computer models of the proximal humerus. Coloured curvature-grade models were generated and facilitated the manual placement of the anatomically homologous landmarks (red dots). Additional landmarks place the boundaries of anatomically homologous areas. These landmarks were replaced by computing identically numbered equidistant landmarks (yellow dots).
Resampling and grouping of the HR-pQCT scans
Using the Amira software (Visualization Science Group), all HR-pQCT scans were resampled to achieve a 0.164-mm isotropic voxel size. A continuous number series of average vBMDs was calculated from all voxels of the entire proximal humerus to categorize the data into three groups, based on the average vBMD values. The first group had the lowest average vBMDs and consisted of 20 HR-pQCT scans with an average vBMD of 200.4 ± 29.8 mg HA/cm3 and a range of 127.7–242 mg HA/cm3 The second group had medium average vBMDs and consisted of 19 scans with an average vBMD of 265.1 ± 12.2 mg HA/cm3 (range, 245–280.6 mg HA/cm3). The third group consisted of 19 HR-pQCT scans with an average vBMD of 314.2 ± 21.7 mg HA/cm3 (range, 288.2–372.6 mg HA/cm3).
Generating the averaged vBMD models
A regular space grid within the mean surface model of the proximal humerus was computed with an isotropic voxel edge length of 0.164 mm. The reference space grid was warped to the samples via TPS transformation, based on anatomically homologous surface points to obtain a homologous voxel grid structure for all samples, as described by Wagner et al [19]. The volumetric data from all HR-pQCT scans were accordingly reprocessed to obtain identically numbered and located anatomically homologous grid data. All HR-pQCT scans of the group with the highest average vBMDs were elastically transformed into the mean surface model. This procedure resulted in a volumetric dataset with 19,382,673 averaged voxels within the mean surface model of the proximal humerus. This algorithm was repeated for the remaining two HR-pQCT groups. These processes resulted in three distinct models with identical sizes, shapes, and volumes that differed in averaged bone stock, as described by their average vBMD values.
Analysis/visualization
The mean shape was computed by averaging the coordinates of the anatomically homologous surface points, and principal component analysis (PCA) was performed to assess variations in the sizes and shapes in the 3D statistical model of the proximal humerus [19], [22], [23]. Principal component analysis was performed in accordance with the method obtained from statistical shape analysis, which is the main method used to analyse geometrical properties of a given set of shapes by statistical methods [24].
We assessed the 3D bone stock distribution using threshold-based labelling of the vBMD values and 3D volume-rendering visualization (i.e., different vBMD threshold ranges were selected while gradually increasing the upper threshold and maintaining the lower threshold at 0). For proper 3D visualization, we inverted the vBMD values (i.e., the vBMD value of 150 was set to −150). This procedure prevented the trabecular bone from being masked by the dense cortical shell. To quantify the differences between the three categories in the different subregions of the proximal humerus, we measured the vBMDs along a 4-mm diameter virtual bore probe at selected sites of the main structures of the proximal humerus. In addition, the probe volumes of five distinct trabecular sites of the humeral head were analysed.
Results
Computer models
A series of HR-pQCT scans of the proximal humerus were postprocessed using a combination of state-of-the-art 3D medical imaging, image processing, and analysis techniques with a 3D statistical model and averaged vBMD models generated to assess the anatomical variability and bone stock distribution.
Surface variability
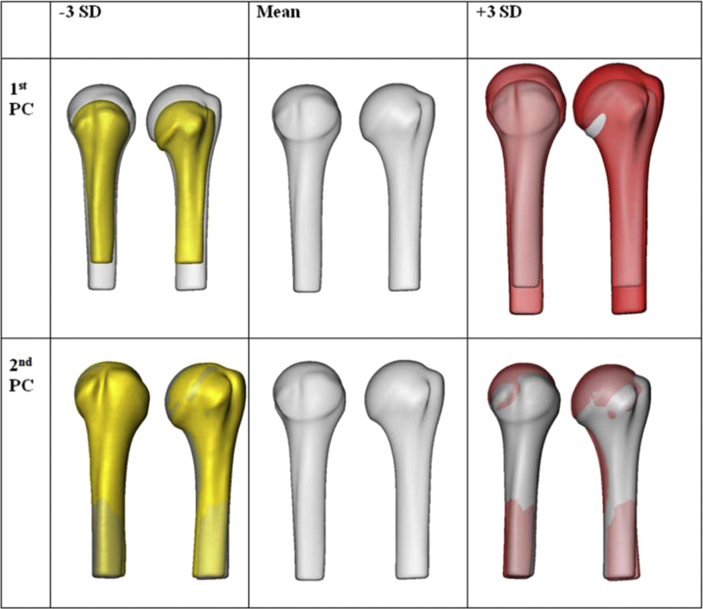
The PCA revealed major size and shape variations. Size was the most variable anatomical pattern, as illustrated in the first PC (Figure 2). The second PC revealed shape variations, which were primarily the result of the variation in the inclination of the humeral head and the shaft portion. The first two PCs covered 65% of the overall anatomical variation. Seventeen PCs were required to account for 95% (i.e., 95.03%).
Figure 2.
The three-dimensional (3D) patterns of the variations of the surface of the proximal humerus, based on principal component (PC) analysis of the (left) anterior view and (right) lateral view. Size variations (i.e., the first PC) dominate over shape variations (i.e., the second PC), as demonstrated in the yellow and red computer models. The mean model is grey. SD = standard deviation.
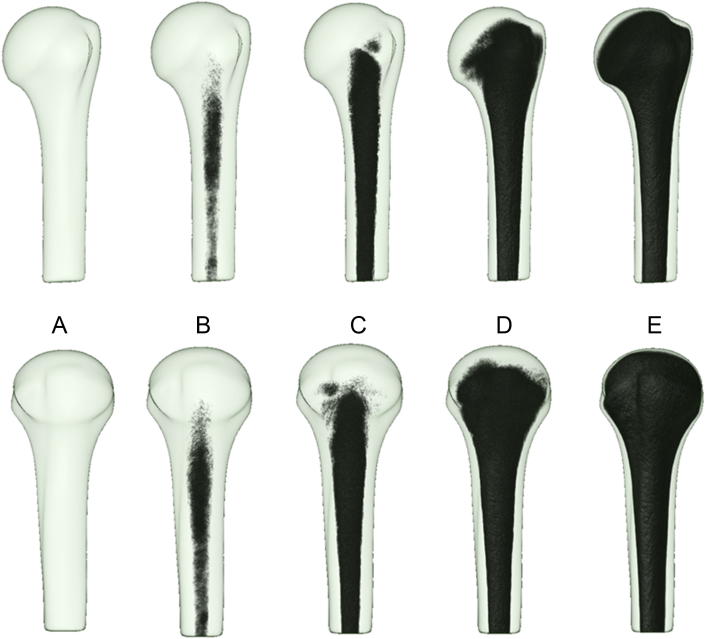
3D bone stock distribution (Figures 3A–E and 4A–C)
Figure 3.
(A–E) The three-dimensional (3D) bone stock distribution of the proximal humerus within semitransparent mean models in the anterior view (top row) and lateral view (bottom row). The 3D bone stock distribution was visualized using the volume-rendering and inversed vBMD values. (B and C) The medullary cavity has the lowest threshold range for vBMD for trabecular bone, and (D) the subarticular bone has the highest threshold range for vBMD for trabecular bone. (E) The 3D aspects of the cortical bone are visible.
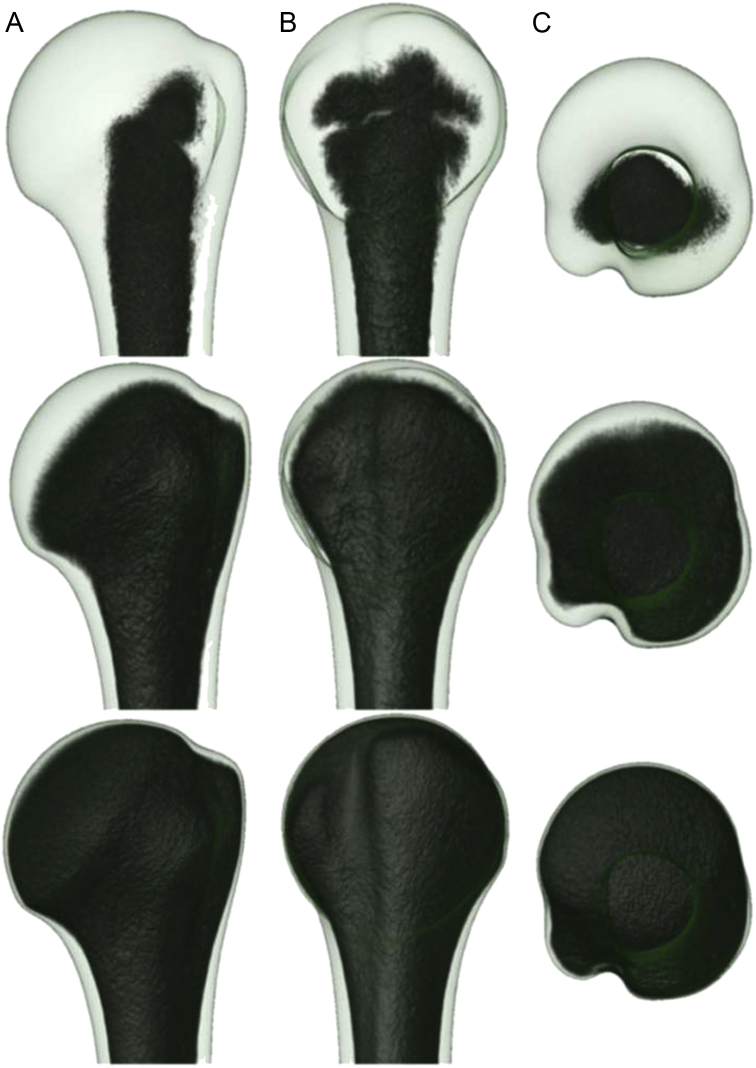
Figure 4.
The three-dimensional (3D) bone stock distribution of the humeral head in (A) the anterior view, (B) the lateral view, and (C) the cranial view at the following three volumetric bone mineral density (vBMD) threshold ranges: 0 to −52 (upper row); 0 to −250 (middle row), and 0 to −500 (lower row). At high vBMD threshold ranges, only the subarticular trabecular bone remain unlabelled, which indicates better bone stock with increasing vBMD values toward the subarticular cortex. The 3D aspects of the cortical shell are presented in the bottom row.
When a low vBMD threshold range of 0 to −6 was selected (Figure 3B) within the 3D averaged vBMD model (i.e., when 3D rendering averaged voxels with only low vBMD values), labelling occurred solely at sites with low bone stock. These sites corresponded to the medullary cavity of the proximal humerus. Other trabecular and cortical regions of the proximal humerus remained unlabelled because they exhibited higher vBMD values. When the threshold range was extended (i.e., when displaying low values and including higher averaged vBMD values), the labelling spread toward the cortical bone of the shaft portion and proximally to the central part of the humeral head (Figure 3C). Additional widening of the threshold range led to 3D labelling of the minor and major tuberosities (Figure 3D and E). Trabecular sites with higher vBMD values were in the humeral head—primarily in the subarticular region—and the maximum values were in the subarticular zones of the humeral head. At a high threshold range (i.e., when visualizing the low and high vBMD values), the proximal shell of the cortical bone remained unlabelled, and the cortical thickness gradually increased to the shaft portion (Figure 3, Figure 4).
Virtual bore probing: variations in the 3D bone stock distribution
The evaluation revealed curves, according to the grouped HR-pQCT images. The curves demonstrate the 3D patterns of the cortical and trabecular bone stocks along given virtual bore probe pathways (Figure 5). The virtual bore probes taken medially to laterally in the shaft portion revealed relatively thick cortical bone and high vBMD peaks of approximately 1000 mg HA/cm3 (Figure 5, left column). The resultant curves from bore probes that were applied in the humeral head are illustrated in Figure 5 (middle and right columns). When probing from the greater tuberosity to the medial humeral head, the corresponding curves increased in length and showed maximum peak vBMDs at the entry and exit points of approximately 500 mg HA/cm3, which corresponded to the cortical bone. The vBMD rapidly decreased in the subcortical zone of the greater tuberosity. This decrease was followed by a central zone that exhibited the lowest vBMD values. A trabecular region with vBMDs steadily increased medially toward the articular surface. When probing the minor tuberosity in the direction toward the posterior humeral head, there was a more equal pattern of low vBMDs with slightly better bone stock. When probing at different articular sites, the peak vBMDs at the entry and exit points were approximately 300 mg HA/cm3 and revealed a more equal vBMD distribution pattern.
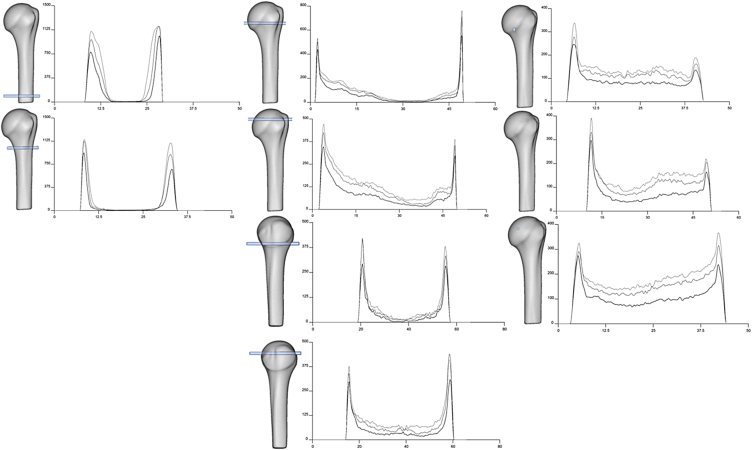
Figure 5.
Virtual bore probing. The mean model of the proximal humerus (grey transparent) in the anterior view (columns 1–3) and lateral view (column 2, lower two images) illustrates the different pathways of the virtual bore probes. The probes measure the volumetric bone mineral density (vBMD) along pathways that were used to create the curves, according to the grouped high-resolution peripheral quantitative computed tomography [y axis: vBMD (mg HA/cm3), x axis: length of the bore probe (cm)]. The first group exhibits the low average vBMD values (black line), the second group exhibits the medium average vBMD values (dark grey line), and the third group exhibits the high average vBMD value (light grey line). The first column displays the anterior view of the mean model and virtual bore probes that were obtained medially to laterally in the shaft zone. The second column illustrates the anterior and lateral views of the mean model and virtual bore probes from the greater and lesser tuberosities. The third column shows the anterior view of the mean model and bore probes from different articular sites.
Probe volumes of the trabecular regions of interest
The probe volumes for the trabecular regions of the humeral head (Figure 6) were calculated by averaging the vBMD values of the contributing voxels of the respective regions of interest (ROI). The highest average vBMD values of 119 mg HA/cm3 were identified in the caput humeri. However, large variations were observed when comparing samples with minimum values with samples with the highest values (30.3 mg HA/cm3 vs. 209.4 mg HA/cm3). Descriptive statistics of the different trabecular sites are presented in Table 1.
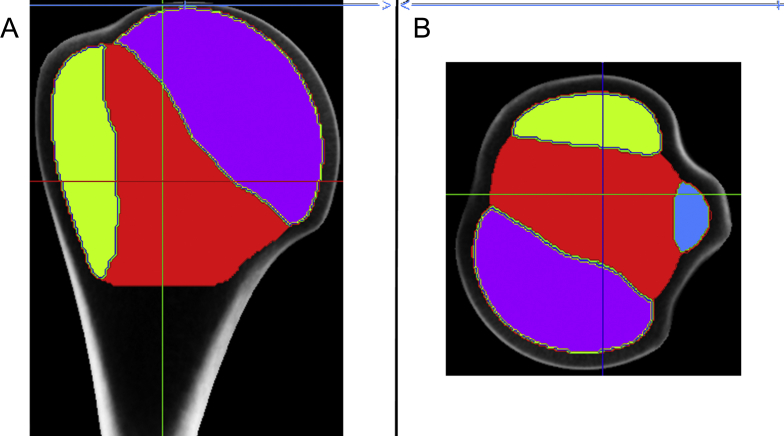
Figure 6.
The probe volumes of the different trabecular sites of the humeral head. Five different probe volumes were manually selected at the greater tuberosity (green), lesser tuberosity (blue), in the centre zone (red), at the articular site (purple), and for the overall humeral head, as illustrated in (A) the frontal and (B) the axial high-resolution peripheral quantitative computed tomography views.
Table 1.
Descriptive statistics of the volumetric bone mineral density [vBMD; expressed as milligrams of hydroxyapatite per centimetre cubed (mg HA/cm3)], which is calculated from the probe volumes of the five trabecular sites of the proximal humerus (as illustrated in Figure 6).
| Mean (mg HA/cm3) | Std (mg HA/cm3) | Min (mg HA/cm3) | Max (mg HA/cm3) | |
|---|---|---|---|---|
| Overall humeral head | 82.3 | 20.8 | 26.0 | 152.4 |
| Articular site (purple) | 119.0 | 23.4 | 30.3 | 209.4 |
| Centre (red) | 41.1 | 19.8 | 17.6 | 93.4 |
| Lesser tuberosity (blue) | 55.0 | 19.8 | 4.4 | 128.4 |
| Greater tuberosity (green) | 56.5 | 18.8 | 15.2 | 141.7 |
The values of the five respective regions are calculated as the mean of all vBMD values of the contributing voxels of high-resolution peripheral quantitative computed tomography. The articular site has the highest mean and maximum values, whereas the centre region has the lowest vBMD.
HA = hydroxyapatite; Max = maximum; Min = minimum; Std = standard deviation.
Discussion
The present computational study was initiated to extend anatomical knowledge because the utilized technique offers the possibility of characterizing an entire treatment site in 3D. Three-dimensional statistical and averaged bone density models of the proximal humerus were established based on HR-pQCT scans, state-of-the-art image processing, and 3D statistical modelling techniques [20], [24], [25]. These models allowed the analyses of bones of different sizes and shapes and thus permitted anatomically homologous regions to be compared [26]. PCA represented a state-of-the-art concept to assess the most important anatomical variations. The first PC was primarily associated with bone length, whereas the second PC was associated with the inclination of the humeral head and the shaft portion. These areas are the most relevant PCs. However, PCA may be too demanding to be applied in daily practice and to draw quantitative conclusions. The interpretation of the PCs with respect to clinical measures may be difficult because they may not necessarily coincide with typical morphologic features such as the bone length or thickness. An extended HR-pQCT protocol was used to assess the bone stock and its variation. A similar technique has previously been described by Wagner et al [19], who applied it to the sacrum, based on computed tomography images of the pelvis. High-resolution peripheral quantitative computed tomography delivers detailed spatial information about the bone stock, based on the vBMD, and at a high resolution. Standard HR-pQCT protocols include scanning and analysis within a given ROI, however, the protocols do not typically account for the entire skeletal region.
We observed computational and numeric difficulties while processing such a large dataset using a standard computer. By using Amira's built-in resampling module, we downsized the HR-pQCT data to a resolution of 0.164 mm, after setting the values for tissues other than bone to 0. The diameter of the virtual bore probe at its entry and exit angles may be additional sources of influence on the measurements. However, the characteristics between the models were not likely altered. In this study, the 3D bone stock distribution was visualized in a volume-rendering mode. Areas of high density are typically less transparent than areas of low density. This behaviour of standard volume rendering is unsuitable for visualizing bony regions with a low bone mass because they are masked by the dense cortical shell. To visualize primarily trabecular bone, we therefore introduced an approach that involved inverting the vBMD values. Varying the upper thresholds permitted the identification and visualization of sites with different bone stock in 3D.
In this study, a mean model of the proximal humerus was established. The 3D statistical bone model revealed largely variable bone shapes and sizes. The averaged bone density models exhibited a distinct 3D pattern of bone stock distribution. We identified and quantified sites of low and relatively high bone stock, irrespective of whether bone loss was present. As expected, the medullary cavity corresponded to the region with the lowest vBMD values. Starting from this site, the trabecular bone became gradually denser toward the cortical bone of the shaft and neck. In the humeral head, the trabecular bone stock was unevenly distributed, as revealed by major regional differences in vBMD. The first zone in which the labelling process was completed—but only at higher vBMD values—was in the greater and lesser tuberosities. The second zone was at the articular site and exhibited vBMD values that steadily increased toward the subarticular region. Therefore, the subarticular zone and the two tuberosities were identified as regions with the best trabecular bone stock. These sites could be clearly distinguished from the central zone within the central humeral head, which exhibited markedly lower vBMD values.
Proximal humerus fractures are low-energy traumas; therefore the centre of the humeral head may coincide with a region that exhibits a higher degree of comminution and thus may be associated with more complex fracture patterns that create a relatively large void area during surgical reconstruction. If such regions exist, they would be particularly affected by bone loss and significantly increase the difficulty of surgical procedures and may even require additional bone grafting.
Fracture fixation requires that the anatomical differences are carefully considered to ensure stable implant fixation to avoid high complication rates. Variations in the anatomy of the proximal humerus may be common. However, such variations may occur for several reasons such as age, sex, individual variations in size and shape, individual bone stock distributions, or specific pathologies. Studies of normal and pathologic conditions may be important prerequisites to understanding the therapeutic implications and selecting treatment strategies that can achieve optimal outcomes. One option may be to assess the pathological status on the affected side and the given anatomical condition on the contralateral side because both anatomies are accessible on preoperative CT or radiographs. Despite advances in preoperative assessment, the paucity of evidence makes it difficult to judge specific cases. The proximal humerus represents a skeletal site for which therapeutic considerations must be made while taking into account variations in individual anatomy, particularly for fragility fractures of the proximal humerus. Hence, a stable osteosynthesis construct may be difficult to obtain because of a complex fracture pattern, low bone quality, and large anatomical variations that may compromise implant fit.
Osteoporosis signifies a growing problem among elderly patients and represents a metabolic disease that leads to altered internal structures due to bone loss and structural decay [27]. The densitometric definition of osteoporosis of the World Health Organization is based on areal BMD, as measured by dual-energy x-ray absorptiometry (DXA) [5]. This procedure subsumes the altered structure as the bone mass per projected area of the standardized skeletal sites (e.g., the lumbar spine and the proximal femur). However, DXA measurements are demanding to perform before shoulder surgery and are not feasible because standardized reference data are not available for this skeletal site. One option may be to predict the bone quality from preoperative radiographs [28] or preoperative CT [16]. In this study, a continuous number series of vBMDs was determined to define three categorical groups because the groups could not be clustered by an alternative criterion such as DXA.
Osteosynthesis of the proximal humerus may depend on the fracture pattern and the individual anatomy, which include factors such as local bone quality. Implants (i.e., the design, type, and number of implant and screws) and the surgical technique have to be adapted to the local anatomical and pathological conditions. The sites of the virtual bore probes were chosen to represent the grouped vBMD values of the two main anatomical structures of the proximal humerus. However, the information could also be used for implant design and optimization.
Several reports that have investigated the bone stock distribution of the proximal humerus. Tingart et al [29] investigated 17 pQCT scans obtained from postmortem specimens and observed significantly higher BMDs in the proximal part of the head than in the distal part. At the articular surface of the proximal part of the head, Tingart and colleagues [31] found significantly higher BMDs in the posterior region than in the anterior region; furthermore, they observed significantly higher BMDs in the posterior region of the greater tuberosity than in the medial region. In a histomorphometric study of 24 postmortem bone specimens by Hepp et al [30], the maximal bone quality and quantity were in the medial and dorsal aspects of the bone, and these authors concluded that screws should be placed in exactly these areas of maximal bone stock. Based on a clinical CT series, Yamada et al [15] reported that the medial side, particularly the articular side, offers more bone tissue than other areas. These investigators also suggest that the bone quality should be defined on a case-by-case basis when treating humeral head fractures in elderly patients, that the site and angle of insertion for fixation should be carefully established, and that the need for grafting to obtain optimal fixation on the lateral side should be considered.
As demonstrated by our virtual bore probes, bone loss was associated with a ubiquitous decrease in bone stock. An osteoporotic humerus and normal humerus may exhibit an identical 3D bone distribution pattern; however, an osteoporotic humerus may exhibit significantly lower vBMD levels. We detected no sites with invariable bone stock. Regions with low BMD values may be predicted as the zones that exhibit greater levels of comminution and thus create larger void areas after disimpaction. Because fragility fractures of the proximal humerus are typically low-energy traumas, the central zones of osteoporotic humeral heads may be associated with greater degrees of comminution that create particularly large void areas, which increase the difficulty of surgical repair.
The cortical bone was not evenly distributed over the proximal humerus in thickness or in the peak vBMD value. Both of these parameters exhibited maximal values in the distal sites and gradual decreases toward and within the epiphysis.
We experienced generalized bone loss that occurs in osteopenia and osteoporosis. These disorders are metabolic problems that are associated with a wide range of effects on the skeletal system. Some show deleterious effects such as increased endocortical resorption, increased cortical porosity, and large decreases in the vBMD, which may be the most important cause of increased skeletal fragility in the elderly, whereas other bones show beneficial effects such as periosteal apposition with outward cortical displacement [33], [34], [32], [31]. Our computer models accordingly revealed that the bone stock was decreased in all sites, whereas the pattern of bone distribution remained virtually unchanged.
Osteosynthesis includes the placement of different types of implants with screws that are positioned through cortical, subcortical, trabecular, and subarticular zones. Alloplastic implants are designed to achieve the best implant purchase and pull-out strengths [35]. The data revealed that the trabecular part, especially the osteoporotic humeral head, is voided. Screw anchorage possibilities are limited within the humeral head.
The following principles could be deducted from this study: a detailed spatial, anatomical knowledge with information about overall morphological variation and local bone quality are essential to optimize the fixation techniques. The subarticular region provides increased vBMD values for trabecular bone and therefore represents the preferred site for screw purchase [36], [37], however, this region is potentially at increased risk of screw perforation into the articular space. The different shape and size patterns of the proximal humerus may require different implant designs and screw positioning. Intramedullary nails, plates with screw holes, and screws may be designed or optimized accordingly. Additional implant fixation may be achieved using augmentation techniques to avoid secondary implant migration.
The limitations of this study include the in vitro approach, the age of the study samples, and the lack of aBMD/DXA reference data for this anatomical region. The interpretation of the PCs may be difficult with regard to typical clinical measures. Despite the new 3D anatomical knowledge we have created, how to predict the local bone quality in clinical settings remains an open question.
The strengths of this study are: (1) the large number of postmortem samples, which permitted grouping; and (2) the computational method, which allowed comparisons of humeri of different sizes and shapes. The extended HR-pQCT protocol permitted the mapping of the entire skeletal site in vBMD in three dimensions. The anatomical knowledge may be novel and may serve as 3D reference data.
In conclusion, we successfully tested our hypothesis and presented a unique computational approach for the spatial assessment and quantification of size and shape variations and bone stock distributions and variations in the proximal humerus. However, no sites with invariable bone stock were detected. Based on the acquisition of HR-pQCT images, information such as shape, size, and bone stock distribution can be captured. These results suggest the existence of large interindividual anatomical variations associated with distinct bone stock distributions and maximum vBMD values in the subarticular bone of the humeral head. In the presence of bone loss, the bone stock was ubiquitously decreased, whereas the 3D bone stock distribution was maintained. Computer bone models with standardized shapes and sizes could be designed with distinct bone distribution patterns. Different computational techniques were required because they were all relevant for highlighting the particular 3D anatomy of the proximal humerus. An application may use computer models with variable shapes, sizes, and bone stock distributions. Such models may also be applied to other skeletal sites and used as benchmarking models or transferred to a finite element environment to assess systematically osteosynthesis constructs.
Conflicts of interest
All contributing authors declare no conflicts of interest.
Funding/support
This research project was supported by AOTrauma of the AO Foundation in Davos, Switzerland (research grant number, Trauma-11-05B).
References
- 1.Neer C.S., 2nd Displaced proximal humeral fractures. I. Classification and evaluation. J Bone Jt Surg Am. 1970;52:1077–1089. [PubMed] [Google Scholar]
- 2.Ruedi T., Murphy W.M. Thieme; Stuttgart-New York: 2000. AO principles of fracture management. [Google Scholar]
- 3.Boileau P., Walch G. The three-dimensional geometry of the proximal humerus. Implications for surgical technique and prosthetic design. J Bone Jt Surg Br. 1997;79:857–865. doi: 10.1302/0301-620x.79b5.7579. [DOI] [PubMed] [Google Scholar]
- 4.Hertel R., Knothe U., Ballmer F.T. Geometry of the proximal humerus and implications for prosthetic design. J Shoulder Elb Surg. 2002;11:331–338. doi: 10.1067/mse.2002.124429. [DOI] [PubMed] [Google Scholar]
- 5.Assessment of fracture risk and its application to screening for postmenopausal osteoporosis. Report of a WHO study group. World Health Organ Tech Rep Ser. 1994;843:1–129. [PubMed] [Google Scholar]
- 6.Dimai H.P., Redlich K., Peretz M., Borgström F., Siebert U., Mahlich J. Economic burden of osteoporotic fractures in Austria. Health Econ Rev. 2012;2:1–10. doi: 10.1186/2191-1991-2-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hernlund E., Svedbom A., Ivergard M., Compston J., Cooper C., Stenmark J. Osteoporosis in the European Union: medical management, epidemiology and economic burden. A report prepared in collaboration with the International Osteoporosis Foundation (IOF) and the European Federation of Pharmaceutical Industry Associations (EFPIA) Arch Osteoporos. 2013;8:1–115. doi: 10.1007/s11657-013-0136-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kanis J.A., Johnell O., Oden A., Johansson H., McCloskey E. FRAX and the assessment of fracture probability in men and women from the UK. Osteoporos Int. 2008;19:385–397. doi: 10.1007/s00198-007-0543-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mascarenhas R., Rusen J., Saltzman B.M., Leiter J., Chahal J., Romeo A.A. Management of humeral and glenoid bone loss in recurrent glenohumeral instability. Adv Orthop. 2014;2014:640952. doi: 10.1155/2014/640952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Euler S.A., Hengg C., Wambacher M., Spiegl U.J., Kralinger F. Allogenic bone grafting for augmentation in two-part proximal humeral fracture fixation in a high-risk patient population. Arch Orthop Trauma Surg. 2015;135:79–87. doi: 10.1007/s00402-014-2128-z. [DOI] [PubMed] [Google Scholar]
- 11.Maier D., Jäger M., Strohm P.C., Südkamp N.P. Treatment of proximal humeral fractures—a review of current concepts enlightened by basic principles. Acta Chir Orthop Traumatol Cech. 2012;79:307–316. [PubMed] [Google Scholar]
- 12.Meier R.A., Messmer P., Regazzoni P., Rothfischer W., Gross T. Unexpected high complication rate following internal fixation of unstable proximal humerus fractures with an angled blade plate. J Orthop Trauma. 2006;20:253–260. doi: 10.1097/00005131-200604000-00004. [DOI] [PubMed] [Google Scholar]
- 13.Südkamp N., Bayer J., Hepp P., Voigt C., Oestern H., Kääb M. Open reduction and internal fixation of proximal humeral fractures with use of the locking proximal humerus plate. Results of a prospective, multicenter, observational study. J Bone Jt Surg Am. 2009;91:1320–1328. doi: 10.2106/JBJS.H.00006. [DOI] [PubMed] [Google Scholar]
- 14.Solberg B.D., Moon C.N., Franco D.P., Paiement G.D. Locked plating of 3- and 4-part proximal humerus fractures in older patients: the effect of initial fracture pattern on outcome. J Orthop Trauma. 2009;23:113–119. doi: 10.1097/BOT.0b013e31819344bf. [DOI] [PubMed] [Google Scholar]
- 15.Yamada M., Briot J., Pedrono A., Sans N., Mansat P., Mansat M. Age- and gender-related distribution of bone tissue of osteoporotic humeral head using computed tomography. J Shoulder Elb Surg. 2007;16:596–602. doi: 10.1016/j.jse.2007.01.006. [DOI] [PubMed] [Google Scholar]
- 16.Krappinger D., Roth T., Gschwentner M., Suckert A., Blauth M., Hengg C. Preoperative assessment of the cancellous bone mineral density of the proximal humerus using CT data. Skelet Radiol. 2012;41:299–304. doi: 10.1007/s00256-011-1174-7. [DOI] [PubMed] [Google Scholar]
- 17.Kranioti E.F., Nathena D., Michalodimitrakis M. Sex estimation of the Cretan humerus: a digital radiometric study. Int J Leg Med. 2011;125:659–667. doi: 10.1007/s00414-010-0470-4. [DOI] [PubMed] [Google Scholar]
- 18.Whitmarsh T., Fritscher K.D., Humbert L., Del Rio Barquero L.M., Roth T., Kammerlander C. A statistical model of shape and bone mineral density distribution of the proximal femur for fracture risk assessment. Med Image Comput Comput Assist Interv. 2011;14:393–400. doi: 10.1007/978-3-642-23629-7_48. [DOI] [PubMed] [Google Scholar]
- 19.Wagner D., Kamer L., Rommens P.M., Sawaguchi T., Richards R.G., Noser H. 3D statistical modeling techniques to investigate the anatomy of the sacrum, its bone mass distribution, and the trans-sacral corridors. J Orthop Res. 2014;32:1543–1548. doi: 10.1002/jor.22667. [DOI] [PubMed] [Google Scholar]
- 20.Popp A.W., Windolf M., Senn C., Tami A., Richards R.G., Brianza S. Prediction of bone strength at the distal tibia by HR-pQCT and DXA. Bone. 2012;50:296–300. doi: 10.1016/j.bone.2011.10.033. [DOI] [PubMed] [Google Scholar]
- 21.Bookstein F.L. Cambridge University Press; Cambridge, UK: 1991/1997. Morphometric tools for landmark data. [Google Scholar]
- 22.Noser H., Hammer B., Kamer L. A method for assessing 3D shape variations of fuzzy regions and its application on human bony orbits. J Digit Imaging. 2010;23:422–429. doi: 10.1007/s10278-009-9187-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kamer L., Noser H., Schramm A., Hammer B. Orbital form analysis: problems with design and positioning of precontoured orbital implants: a serial study using post-processed clinical CT data in unaffected orbits. Int J Oral Maxillofac Surg. 2010;39:666–672. doi: 10.1016/j.ijom.2010.03.005. [DOI] [PubMed] [Google Scholar]
- 24.Dryden I.L., Mardia K.V. John Wiley & Sons; Chichester, UK: 1998. Statistical shape analysis: Wiley series in probability and statistics. [Google Scholar]
- 25.Zollikofer C.P.E., Ponce de Leon M. Wiley-Interscience; New York, NY: 2005. Virtual reconstruction, a primer in computer-assisted paleontology and biomedicine. [Google Scholar]
- 26.Lamecker H., Seebass M., Hege H.C., Deuflhard P.A. 3D statistical shape model of the pelvic bone for segmentation. Proc SPIE–Medical Imaging Image Process. 2004;5370:1341–1351. [Google Scholar]
- 27.NIH Consensus development Panel on osteoporosis prevention, diagnosis, and therapy. Osteoporosis prevention, diagnosis, and therapy. JAMA. 2001;285:785–795. [Google Scholar]
- 28.Mather J, MacDermid JC, Faber KJ, Athwal GS. Proximal humerus cortical bone thickness correlates with bone mineral density and can clinically rule out osteoporosis. J Shoulder Elbow Surg 2013 Jun;22(6):732–738. [DOI] [PubMed]
- 29.Tingart M.J., Bouxsein M.L., Zurakowski D., Warner J.P., Apreleva M. Three-dimensional distribution of bone density in the proximal humerus. Calcif Tissue Int. 2003;73:531–536. doi: 10.1007/s00223-002-0013-9. [DOI] [PubMed] [Google Scholar]
- 30.Hepp P., Lill H., Bail H., Korner J., Niederhagen M., Haas N.P. Where should implants be anchored in the humeral head? Clin Orthop Relat Res. 2003;415:139–147. doi: 10.1097/01.blo.0000092968.12414.a8. [DOI] [PubMed] [Google Scholar]
- 31.Parfitt A.M. Skeletal heterogeneity and the purposes of bone remodeling: implications for the understanding of osteoporosis. In: Marcus R., Feldman D., Kelsey J., editors. Osteoporosis. Academic; San Diego, CA: 1996. pp. 315–339. [Google Scholar]
- 32.Duan Y., Turner C.H., Kim B.T., Seeman E. Sexual dimorphism in vertebral fragility is more the result of gender differences in age-related bone gain than bone loss. J Bone Min Res. 2001;16:2267–2275. doi: 10.1359/jbmr.2001.16.12.2267. [DOI] [PubMed] [Google Scholar]
- 33.Riggs B.L., Melton L.J., 3rd, Robb R.A., Camp J.J., Atkinson E.J., Peterson J.M. Population-based study of age and sex differences in bone volumetric density, size, geometry, and structure at different skeletal sites. J Bone Min Res. 2004;19:1945–1954. doi: 10.1359/JBMR.040916. [DOI] [PubMed] [Google Scholar]
- 34.Zebaze R.M., Ghasem-Zadeh A., Bohte A., Iuliano-Burns S., Mirams M., Price R.I. Intracortical remodelling and porosity in the distal radius and post-mortem femurs of women: a cross-sectional study. Lancet. 2010;375:1729–1736. doi: 10.1016/S0140-6736(10)60320-0. [DOI] [PubMed] [Google Scholar]
- 35.Seebeck J., Goldhahn J., Städele H., Messmer P., Morlock M.M., Schneider E. Effect of cortical thickness and cancellous bone density on the holding strength of internal fixator screws. J Orthop Res. 2004;22:1237–1242. doi: 10.1016/j.orthres.2004.04.001. [DOI] [PubMed] [Google Scholar]
- 36.Schiuma D., Plecko M., Kloub M., Rothstock S., Windolf M., Gueorguiev B. Influence of peri-implant bone quality on implant stability. Med Eng Phys. 2013;35:82–87. doi: 10.1016/j.medengphy.2012.04.001. [DOI] [PubMed] [Google Scholar]
- 37.Brianza S., Röderer G., Schiuma D., Schwyn R., Scola A., Gebhard F. Where do locking screws purchase in the humeral head? Injury. 2012;43:850–855. doi: 10.1016/j.injury.2011.10.028. [DOI] [PubMed] [Google Scholar]