Systems and synthetic biology approaches in understanding biological oscillators

Abstract

Background

Self-sustained oscillations are a ubiquitous and vital phenomenon in living systems. From primitive single-cellular bacteria to the most sophisticated organisms, periodicities have been observed in a broad spectrum of biological processes such as neuron firing, heart beats, cell cycles, circadian rhythms, etc. Defects in these oscillators can cause diseases from insomnia to cancer. Elucidating their fundamental mechanisms is of great significance to diseases, and yet challenging, due to the complexity and diversity of these oscillators.

Results

Approaches in quantitative systems biology and synthetic biology have been most effective by simplifying the systems to contain only the most essential regulators. Here, we will review major progress that has been made in understanding biological oscillators using these approaches. The quantitative systems biology approach allows for identification of the essential components of an oscillator in an endogenous system. The synthetic biology approach makes use of the knowledge to design the simplest, de novo oscillators in both live cells and cell-free systems. These synthetic oscillators are tractable to further detailed analysis and manipulations.

Conclusion

With the recent development of biological and computational tools, both approaches have made significant achievements.

INTRODUCTION

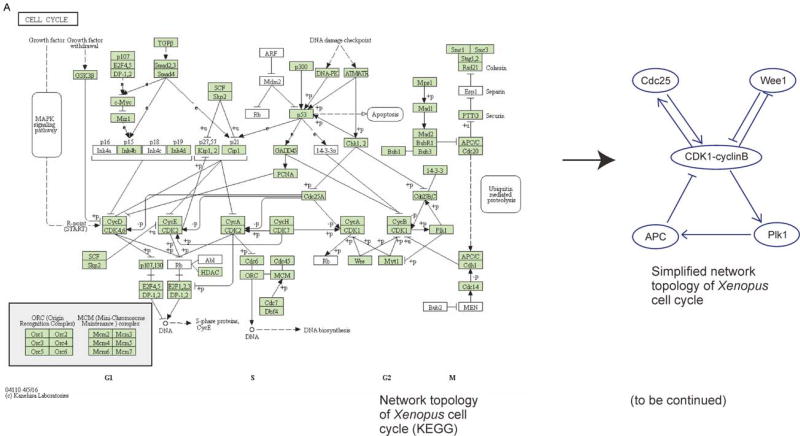
Studies over the past decades have made major progress in identifying genes, proteins, and metabolites that are involved in the rhythmic phenomena. A typical pathway of an oscillator that can be found in databases nowadays is rather complicated. For example, the cell cycle pathway in KEGG (Figure 1A) contains hundreds of molecules.

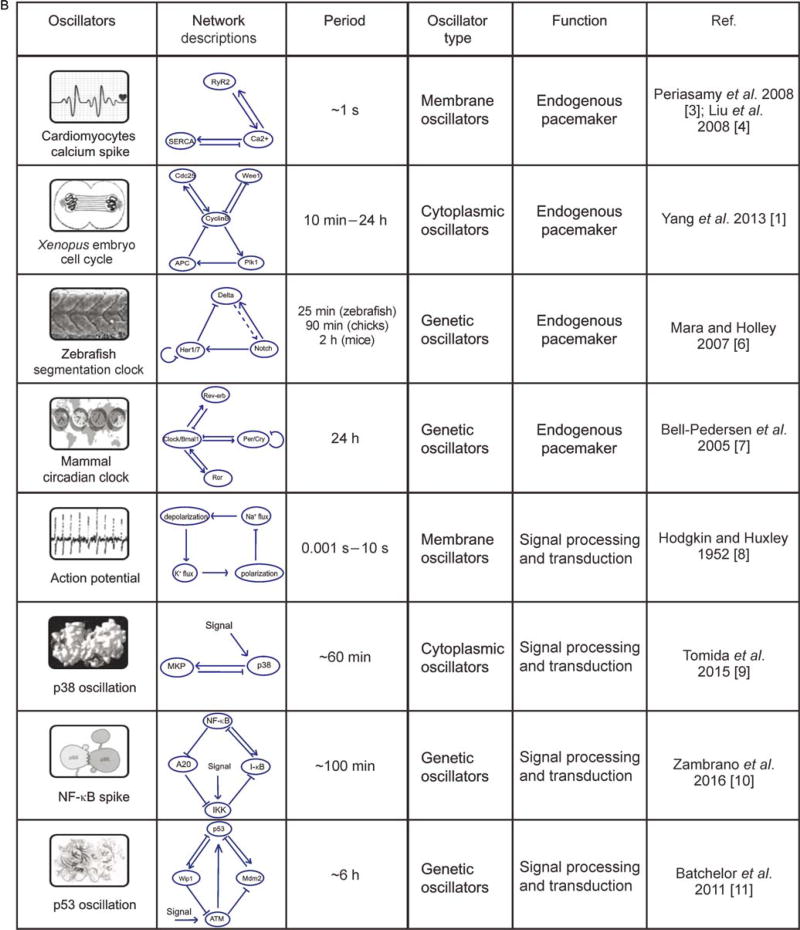
Figure 1. Quantitative studies have revealed core architectures of biological oscillators that are both complicated and diverse.

(A) Left: The cell cycle pathway diagram of Xenopus laevis adopted from Kyoto Encyclopedia of Genes and Genomes (KEGG) database. Right: A simplified version of Xenopus early embryonic cell cycle circuitry that contains only the most essential components [1,2]. (B) Examples of biological oscillators and their network structures. From top to bottom: calcium spikes in cardiomyocytes [3,4], embryonic cell cycles in Xenopus [1,2], segmentation clock in Zebrafish [5,6], and circadian clock in Mammals [7], action potential in neuron [8], p38 oscillations in HeLa cells [9], NF-kB spikes in fibroblasts [10], p53 oscillation in human cell lines [11]. Their periods span orders of magnitude.

Biological oscillators are not only complicated, but also appear to be extremely diverse in their dynamic properties and compositions. From sub-second neural spikes, to daily circadian rhythms, to annual reproduction in plants and animals, the periods of oscillators span orders of magnitudes. Molecules that drive these events are very different from oscillators to oscillators: i) cytoplasmic oscillators, in particular glycolytic oscillators, are formed by protein enzymes and small molecule metabolites that mainly interact within the cytoplasm; ii) membrane oscillators, such as action potentials in neural and cardiac pacemaker cells, are formed by regulatory ion channels restricted to the membrane; iii) genetic oscillators are composed of a set of genes that regulate each other inside cells.

These oscillators perform several functions in general (Figure 1B). Most oscillators function as an endogenous pacemaker. Circadian clocks, for example, exist in almost all organisms on earth and help them adapt to the natural periodicity of the day-night alternations, by orchestrating their intrinsic gene expressions with a period of approximately 24 hours [7,12,13]. Heartbeat [14], respiration [15], and cell cycle [16–18], etc., are other examples in this category. The pacemaker oscillators also play a role in the spatial organization of development. Through an excitable medium, a local oscillatory signal may trigger waves that propagate over a large distance much faster than through pure diffusion [19]. Examples of trigger waves include polar regeneration in Acetabularia [20], cAMP waves in the aggregation and differentiation of Dictyostelium discoideum [21], and mitotic waves recently reconstituted in Xenopus cell-free extracts [22]. Alternatively, in multidimensional or metameric systems, the phase differences among cell-autonomous periodic events in cells as a function of their spatial locations, resulted in another type of wave, called phase wave. These may be exemplified by pattern formation of hypostome in Hydra [23] and periodic tissue morphogenesis of vertebrates [5,24]. In addition to being a pacemaker, oscillators can also generate frequency-modulated signals to regulate their downstream gene expression levels and influence cellular fate decisions [25,26] in an accurate manner through information transduction. Examples of these have been seen in frequency coding of neurons [27] and a number of signal transduction pathways that have oscillatory dynamics, such as NF-kappaB [28], p53 [11,29], p38 [9], Ca signaling [30,31]. These oscillators are flexible in tuning their frequencies.

The question whether a common mechanism is shared by all these seemly different oscillators has stimulated much interest and its answer may allow for a fundamental understanding of such widespread phenomena. However, the high complexity and broad diversity of biological oscillators make it extremely challenging to identify the fundamental mechanisms. To address such difficulty, approaches in systems and synthetic biology have been effective in dissecting or creating an oscillatory circuit and analyzing its functions beyond the molecular level. In this review, we attempt to summarize the major progress in quantitative systems biology and synthetic biology that aim to delineate the mechanisms and understand oscillatory properties at the systems level.

QUANTITATIVE ANALYSIS OF BIOLOGICAL OSCILLATORS IN ENDOGENOUS SYSTEMS

The biological oscillators are amenable to quantitative analysis both in theory and experiments. One of the first characterized biological clocks is the action potential in a giant nerve fibre of Loligo. In their Nobel Prize winning studies, Alan Hodgkin and Andrew Huxley carried out a series of measurements of the nerve cell membrane ionic current under a “voltage clamp” [32–36]. Under certain conditions, the nervous system exhibits an oscillatory behavior, with electrical pulses repeatedly generated in response to a stimulus. To interpret the findings, they developed a set of ordinary differential equations (ODEs) [8] that include multiple voltage-dependent currents of ion (e.g., potassium and sodium) channels, known as the Hodgkin-Huxley model. The model marks the starting point for theoretical biophysics of action potential.

About a decade later, another oscillator is observed in the metabolism pathway glycolysis, which drives repetitive fluctuations of concentrations of metabolites intermediates. This time, the oscillations were not investigated in the membrane of a giant cell, but in a whole cell suspension [37] and a cytosolic cell-free system [38,39] of yeast cells Saccharomyces carlsbergensis. Although these early metabolic assays only captured damped sinusoidal oscillations, theoretical work describing six reaction equations using ODE models for phosphofructokinase and the associated glycolytic intermediates predicted the existence of self-sustained limit-cycle behaviors in glycolytic oscillations [40]. Such limitcycle oscillations were soon observed in a later experiment [41]. Other metabolite oscillations have also been observed in cAMP synthesis [42] and peroxidase-oxidase reactions [43].

The first genetic oscillator in theory was proposed by Brian Goodwin back in 1963 [44], shortly after the model of gene regulation developed by Francois Jacob and Jacques Monod. This classical Goodwin oscillator contains only a single gene whose product represses itself after a sufficient delay, allowing for periodic gene expression to occur. Remarkably, this theoretical work predicts that a genetic circuit is able to generate the limit cycle oscillations, even before any real genetic oscillator is discovered experimentally. The experimental investigations on genetic oscillators lagged behind until the development of genetic engineering techniques in modern molecular biology and the rapidly growing popularity of luminescence and fluorescence microscopy techniques. One of the most characterized genetic oscillators is circadian clock, which has been found in all eukaryotes and some prokaryotes such as cyanobacteria. Circadian clocks endogenously drive cell-autonomous oscillations roughly once per day, so that organisms have the ability to anticipate the time of day. Studies on circadian clocks have been performed on various organisms (Synechococcus [45], Neurospora [46], Drosophila [47], mouse [48] and Arabidopsis [49]).

These studies have successfully combined experimental measurements and mathematical modeling to enable understanding of how each of these biological oscillators functions in great quantitative details. Following these studies, the quantitative approaches have been applied to the discovery and characterization of many more oscillators. For readers interested in a thorough and detailed description of biological oscillators, the classical book and review article by Goldbeter [50,51] are recommended.

Although major progress has been made in understanding relevant components and functions of biological oscillators, challenges for further quantitative analysis of these oscillators in living systems are obvious. One major obstacle is that the core architecture of an oscillator is often embedded in a significantly more complicated network. It also tends to interfere with other pathways or couple with other oscillators [52–54]. These make it hard to isolate the central oscillator circuitry for investigation. Another obstacle is the limited capability of dissecting feedback loops and manipulating oscillatory behaviors in living systems. To address these problems, synthetic biologists create well-defined de novo oscillatory circuitry in a system that is amenable to detailed analysis and accurate control. In the next two sections of this review, we introduce how synthetic biology has become an increasingly important alternative approach that will complement studies in the endogenous system. We will specifically focus on recent development of synthetic oscillators in both live cells and cell-free extracts.

BUILD TO UNDERSTAND — A SYNTHETIC BIOLOGY APPROACH IN THE UNDERSTANDING OF BIOLOGICAL OSCILLATORS

As reflected by Richard Feynman’s 1988 quote “What I cannot create, I do not understand”, synthetic biologists seek to improve understanding of oscillators by making them from scratch. The extensive quantitative studies on various biological clocks have revealed that, although the molecular forms can look vastly different from oscillators to oscillators, their network structures share common features. Notably, most of them seem to reduce down to a core architecture that contains positive plus negative feedback loops. This may support the possibility of building a simple oscillator that contains only the most essential core components. To build such an oscillator, an inevitable question is — what are the minimum requirements for generating sustained oscillations? The answer to this question may also help us identify fundamental mechanisms that are shared by all biological oscillators.

Basic requirements of making oscillators in theory

Ever since the early discoveries of biological oscillations, theorists have started to pursue the answers to such question by building simplest possible models that capture fundamental mechanisms of various oscillatory systems. Here we will mainly focus on the development of ODE models which have the longest history and are one of the most widely used models to describe oscillatory behaviors. Some other method like Boolean model is also useful when dealing with highly complicated networks with few known parameters [55]. Stochastic differential equation models have also been used to reliably explain more complicated biological clock behaviors [56,57]. Right after the discovery of metabolic oscillations, Ilya Prigogine approached three biochemical oscillators of distinct catalytic properties in physicochemical terms by arguing that all these biochemical oscillations are not different than non-equilibrium spatial and temporal self-organization as dissipative structures in chemical systems [58]. This view provides a conceptual framework that supports the later research of unifying all biological oscillators [51].

Throughout the years, efforts have been made in simplifying existing detailed models, the complexity of which may obscure the fundamental design principles underlying the core architecture of an oscillator. In contrast to the complicated models, a model with only the most essential components is more accessible to experimental validation as it requires less parameters to measure to build an accurate model. The original Hodgkin-Huxley investigations of the action potential [8] describes in a detailed manner the voltage-current relationship based on experimental observations, which requires more than twenty parameters. It was simplified in the FitzHugh-Nagumo (FHN) model [59] and later in the Morris-Lecar model [60], where two differential equations describe the system as coupled positive and negative feedback loops. Importantly, despite the simplifications, these models capture the main dynamic responses, and by adding diffusion, the FHN model generates trigger wave propagations as seen in axons [19].

Simple models have also helped postulate the fundamental requirements for designing an oscillator. Since the design of the Goodwin oscillator [44,61], the inhibitory feedback loop and a source of delay in this feedback have been postulated as two required elements for limit cycle oscillations [62]. However, a time-delayed negative feedback could not explain the noise-resistance behavior in circadian rhythms. The activator-repressor oscillator was thus proposed by Barkai and Leibler [63]. It was a two-component gene circuit that contains both an activator and a repressor. In addition to the negative feedback loop formed by the activator activating its own repressor, the activator can also auto-activate itself resulting in a self-positive feedback loop. Remarkably, it turns out later that such “design principle”, i.e., the coupled positive and negative feedback loops, is widely found in biological oscillators. In the 2008 review article, Novak and Tyson have extensively discussed the general requirements for biochemical oscillations [64]. Besides the negative feedback and time delay, sufficient nonlinearity and properly balanced timescales of opposing chemical reactions are also reported to be indispensable. In addition, the positive feedback is helpful to amplify and delay the negative-feedback signal, which makes the oscillator more robust. A computational study has suggested that adding a positive feedback may increase the robustness and frequency range of the system [65]. All together, these computational studies have provided key theoretical bases for creating synthetic oscillators, and experiments have been demanded for verifications.

Pioneering work of making simple oscillators

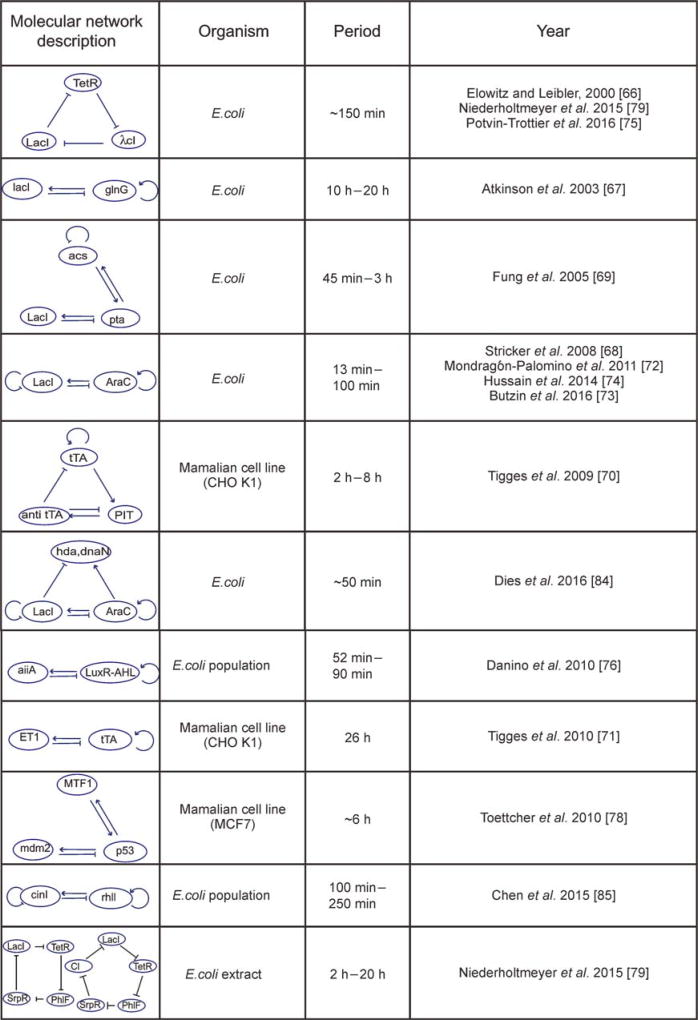
With the development of the genetic engineering tools, creating a de novo designed oscillator in real biological systems becomes possible. A list of well-known synthetic oscillators has been summarized in Figure 2 and will be described in more details below.

Figure 2. Examples of synthetic oscillators.

For each synthetic oscillator, the information such as its molecular network structure, the organism that the oscillator is built in, and the period, has been listed [66–79].

In 2000, Elowitz and Leibler, in a landmark study in synthetic biology, constructed the first genetic oscillator in Escherichia coli cells, named repressilator [66]. In this oscillator, three negative transcriptional regulators, TetR, lcI and LacI, repress each other to form a delayed negative feedback loop. A green fluorescence protein GFP under the control of TetR promoter has been used to report the oscillatory behavior of the system, confirming that a single negative feedback is sufficient for generating oscillations. However, it was not robust, with only 40% of the cells oscillatory. Based on this work, many new oscillators have been proposed aiming for better performance.

In 2003, Atkinson et al. constructed for the first time the activator-repressor genetic oscillator [67], reminiscent of the theoretical clock of Barkai and Leibler [63]. Turbidostat cell cultures of E. coli containing this oscillator achieved synchronized oscillations. However, the oscillations become damped over time, possibly due to a loss of synchrony among cells. Further development in bacteria is made by Stricker et al. [68]. Besides a negative feedback formed by araC and lacI, araC also activates itself and lacI inhibits itself. This time, the oscillator was tested in microfluidic devices using single-cell fluorescence microscopy. Unlike the ensemble measurements, the ability of tracking single cells relieves the requirement of synchronization of cells. Single-cell data has shown that the period of this oscillator can be as short as 13 min and the oscillation is self-sustained and robust.

The first metabolic circuit using glycolytic flux to generate oscillations was designed in E. coli by Fung et al., called metabolator [69]. Like all genetic oscillators at the time, this synthetic metabolic oscillator was designed in bacteria cells. The first synthetic oscillator in mammalian cells was reported by Tigges et al. in 2009 [70]. Using auto-regulated sens-antisense transcription control, they built a molecular network that resembles the typical activator-repressor circuit, where tetracycline-dependent transactivator (tTA) functions as an activator and pristinamycin-dependent transactivator (PIT) a repressor. Further development of this system has led to an oscillator with frequency comparable to that of a circadian clock [71].

These pioneer studies of synthetic oscillators play an important role in testing the minimal design principles postulated by theoretical studies. In a review article, Purcell et al. have focused on several basic in silico designs that have been implemented in synthetic genetic oscillators [80]. The simple synthetic oscillators have also paved the way for further more complicated designs.

Making more complicated synthetic oscillators and their applications

At present, while new designs continue to expand the list of synthetic oscillators, the focus of the research has shifted from making new circuits to improving the existing oscillators with new functions or applications.

First, more features have been added to existing oscillators. By modifying the aforementioned synthetic oscillator with coupled positive- and negative-feedback loops [68], Mondragon-Palomino et al. have built an oscillator that can be entrained by external periodic signals [72]. Butzin et al. [73] further demonstrated that such synthetic oscillators can also be entrained by aperiodic signals, similar to the entrainment of cells in our body by the noisy natural signals. Modifying the same dual-feedback oscillator [68] through a single amino acid mutation to its core repressor, Hussain et al. have built an oscillator with temperature compensation [74]. The temperature compensation, i.e., keeping a constant period over a range of temperatures, is an essential property of circadian clock. In addition, Potvin-Trottier et al. focused on noise resistance and built an improved version of repressilator that can lead to synchrony in bacteria without coupling [75].

Second, the ability to program population-level dynamics and emergent collective behavior has become increasingly interesting in synthetic biology. Using quorum sensing to couple individual genetic oscillators, Danino et al. was able to construct synchronized oscillations at the colony level. In microfluidics devices, they demonstrated a variety of spatiotemporal waves propagating across cellular populations [76]. This work was further developed by Prindle et al. by coupling 12,000 such quorum-sensing synchronized colonies, called “biopixels”, in a macroscopic array, through gas-phase redox signaling. The ability to synchronize a large scale of colonies across the entire array enabled the construction of a low-cost biosensor that can detect heavy metals like arsenic via modulation of the frequency [81]. Chen et al. further extended the monoclonal system to create a synthetic microbial consortium containing two distinct cell types. The “activator” cells and “repressor” cells express orthogonal cell-signaling molecules and can only oscillate when both strains were present [77]. They also showed that certain network topologies of the two-strain circuit exhibited more robust oscillations than others. A recent study has developed a more complicated synthetic microbial community through multiplexed quorum sensing circuits [82]. Although all above-mentioned studies have utilized quorum sensing as a key design to produce population-level dynamics, Marguet et al. were able to construct oscillations in bacterial population density that required no quorum-sensing genes or promoters. Instead, the oscillations arise through the unexpected interplay of the host cell and the density-dependent plasmid amplification that established a population-level negative feedback. This study has highlighted the importance of considering “hidden interactions” between the synthetic circuits and the pre-existing metabolic and regulatory networks in complex host cells [83].

Third, integrating synthetic components into natural biological oscillators can modulate the endogenous oscillator behaviors. By adding MTF1 in the p53 signaling pathway, Toettcher et al. constructed an oscillatory system that is tunable in frequency [78]. In another study, Dies et al. linked the cell division cycle to a dual-feedback oscillator [68] in E. coli, by driving the hda and dnaN genes that inhibit the initiation of chromosomal replication, under the oscillator. In this engineered system, they observed the entrainment between the synthetic oscillator and the cell cycle [84].

Finally, studies have started to introduce synthetic circuits into organisms to enable a new function or application. A recent study has reconstructed the cyanobacterial KaiABC oscillator in E. coli, making this endogenously non-circadian bacterium perform circadian rhythms [85]. This demonstrated that a circadian oscillator is transplantable to a heterologous organism. Moreover, a study engineered a bacterium capable of synchronous lysis at a threshold population density [86]. Introducing the lysis strain in combination with a chemotherapy, the study also demonstrated its clinical significance.

ANALYSIS OF BIOLOGICAL OSCILLATORS USING A CELL FREE SYSTEM

While many oscillators have been created in live bacteria and cell lines, oscillators have also been reconstituted in vitro in well-defined cell-free systems for decades. Comparing to live cells, a cell-free system has several unique advantages. First, a cell-free system usually contains only the most essential components in a test tube, which reduces potential interferences from the complex intracellular and extracellular environment. Second, it is convenient to introduce recombinant plasmids, mRNAs, proteins, as well as small molecules and drugs into the cell-free system, to precisely tune its oscillatory reactions, without worrying about the cytotoxicity, delivery efficiency, cross-talks, etc. Because of such flexibility and specificity of introducing molecules, it is more efficient and less time-consuming to design and test a functional circuit in cell-free systems than in living systems. Remarkably, it makes dissection of the circuits much easier, allowing for obtaining the steady state response function of each dissected reaction, parameters of which are crucial to build models.

In this section, we will specifically review the extensive application of a cell-free extract system [87], as a successful example, that has made major advances in understanding the cell cycle progression [1,22,88–92]. We will then extend this discussion to include a broader spectrum of cell-free systems and oscillators.

The cell free assays have made major contributions to the initial discovery and characterization of the central mitotic regulators. Extracts prepared from eggs of Xenopus laevis have enabled the first purification and in vitro kinase activity characterization of the maturation-promoting factor (MPF), later known as the protein complex cyclin B1-Cdk1 [87,93,94]. Clam oocyte extracts have allowed for the first discovery of anaphase-promoting complex or cyclosome (APC/C) [95], functioning as a E3 ubiquitin ligase. The activation of cyclin B1-Cdk1 drives mitotic entry and activates APC/C-Cdc20, which in turn marks the cyclin B1 for degradation and deactivates Cdk1, resulting in mitotic exit, and completing a core negative feedback loop. Studies making use of cycloheximide-treated interphase Xenopus egg extracts have shown that when adding APC-resistant cyclin mutants into the extracts, the extracts approach a steady state of Cdk1 activity rather than oscillating [87]. This confirms the essential role of the negative-feedback loop in mitotic oscillations.

In theory, a negative feedback alone can generate oscillations. However, additional positive feedback loops through the regulations of Wee1 and Cdc25 are evolutionarily conserved [96,97]. Compromising the positive feedback loops will suppress oscillations in Xenopus egg extracts [91], suggesting that these are essential for sustained embryonic cell cycle oscillations. Together, these studies have identified the core architecture of cell cycles as interlinked positive and negative feedback loops, a commonly occurring motif also found in many other biological oscillators.

In addition to discovering the core architecture, cell-free assays have been combined with theory to dissect the interconnected feedback loops and investigate the function of each leg in isolation, in greater details. Tyson & Novak [98] and Thron [99] first proposed that the Cdk1/Cdc25/Wee1 system functions as a bistable trigger for mitosis. This hypothesis was then examined in quantitative measurements of Xenopus cell-free systems, showing that both Wee1 and Cdc25 respond to Cdk1 in an ultrasensitive (i.e., highly non-linear) manner [90–92,100]. In a rate balance analysis [101], this mirror-image, two-loop structure composed of Cdk1, Cdc25, and Wee1 with ultrasensitive responses makes the system substantially easier to generate a bistable response than otherwise. Bistable switch is a key consequence of positive feedback that delays the negative-feedback signal and prevents the system damped into a stable steady state [64]. Indeed, this has an experimental evidence that short-circuiting positive feedback in cell-free cycling Xenopus extracts makes the cell cycle oscillations damped [91].

Further studies, by integrating real-time fluorescence assays into the cell-free system, have revealed the core negative feedback system to operate as a time-delayed, digital switch, with a time lag of ~15 min between Cdk1 and APC/C-Cdc20 activation and a tremendously high degree of ultrasensitivity [1,2]. A simple, analytically tractable model has been developed to show how the attributes of time delay and ultrasensitivity contribute to the generation of robust, clock-like oscillations. A mechanism centered on the multisite phosphorylation of APC has also been postulated to explain how the ultrasensitivity and time delay are generated.

All together, these studies have proved that cell-free extracts are amenable to quantitative biochemical and synthetic approaches. By reconstituting and analyzing mitotic cycles in cell-free extracts, they have identified the key mechanisms for the mitotic oscillations: negative feedback, sufficient time delay, sufficient “nonlinearity” of the reaction kinetics, positive feedback, all consistent with the general requirements for biochemical oscillations [64].

Cell cycles are not the only study of oscillatory circuit that benefits from detailed quantitative analysis enabled by a simple cell-free system. In a pioneering study, Kondo and colleagues have reconstituted a simplest possible circadian oscillator in vitro using only three proteins: KaiA, KaiB, and KaiC [102]. In the presence of ATP as an energy supply, these three proteins can generate self-sustained oscillations with a period of about 24 hours and that are temperature compensated. Both the 24-hour period and temperature compensation are the defining characteristics of circadian oscillations observed in vivo. Without transcription or translation, this cell-free system has paved the way to examining the kinetic interactions of three Kai proteins in a detailed and quantitative manner [103].

In addition to recreating natural circuits such as cell cycles and circadian clocks, de novo engineered artificial networks have also been increasingly constructed thanks to the recent advances in synthesizing well-defined biopolymers and replicating systems in vitro [104]. These synthetic networks can not only perform various functions such as polymerase chain reaction (PCR) [105], transcription/translation machinery [106–108], bistable switches [109], etc., but can also behave as oscillators, such as DNA-based predator-prey molecular ecosystems [110,111], in vitro transcriptional oscillators [112–116], inorganic chemical reactions such as the Belousov-Zhabotinsky (BZ) reaction [117,118]. The recent development in microfluidics techniques has significantly improved the cell-free system by simplifying the fabrication process or creating high-throughput arrays [119–122].

A broad variety of cell-free systems (e.g., extracts from archea, protozoa, plants, insects, etc.) allowing for in vitro transcription and translation [123] can serve as a powerful platform for synthesizing and examining oscillatory circuits. Besides the well-established Xenopus egg extracts [93], extracts widely prepared from other eukaryotic systems including yeast cells [124], clam oocytes [95], Drosophila embryos [120,121], mammalian cell lines [125,126], have been applied to the investigation of mechanisms underlying cell cycles and metabolic cycles. Prokaryotic cell-free systems such as E. coli cytoplasmic extracts have been developed to provide a highly versatile cell-free platform to construct complex biological systems. These include the protein synthesis using recombinant elements (PURE) system [127], the hybrid bacteriophage — Escherichia coli transcription and translation (TX-TL) system [128], and more recently, the all E. coli TX-TL system [129]. Oscillators built in these prokaryotic cell-free systems, e.g., the in vitro ring oscillators, show similar properties as the transcriptional oscillatory systems built in vivo [79,112]. Recent development in synthetic biology also makes it possible to produce modular oscillators using nucleic acid [130,131] or organic molecules [132]. It is also possible to generate biological trigger waves [22] in cell-free systems when allowing diffusion, similar to the well-known BZ waves.

PERSPECTIVE

Systems and synthetic biology has been a promising approach to delineate an oscillator’s mechanism by building and analyzing the functions at the systems level. An ultimate goal of synthetic biology is to engineer from the bottom-up a complete customized system with desired functions and applications. To build such an oscillatory system, a set of building blocks, which correspond to the functional modules in biological systems, must be available on hand. Using theoretical and experimental approaches, a set of modules of oscillation have been found and verified, including time delayed negative feedbacks and amplified negative feedbacks [133]. However, besides central oscillatory modules, peripheral modifications are also found to be highly conserved among different biological systems [65]. Different approaches have been used to identify functions of these auxiliary topological structures. These include: testing a hypothesis in a few oscillatory structures [65,134–136]; performing evolutionary network search [137,138]; and doing an exhaustive network enumeration [139,140]. Although these studies have made progress in identifying some peripheral modifications that help promote the robustness of an oscillator, the role of many other peripheral modifications remains unclear. Further investigations, both theoretically and experimentally, are needed to understand it.

The development of statistical tools and bioinformatics methods has also been used to push forward progress in system and synthetic biology. A deeper understanding of genomics is a breakthrough in 21st century biology. With the help of functional genome predictions, synthetic biologist can now make much more complicated biological networks to facilitate the understanding of biological system [141]. Development in data science and computational methods is another significant event that helps understanding and designing of biological oscillators. The statistical method like machine learning is used to identify functional proteins in biological systems [142]. Artificial intelligence is also helping the development of smarter cell-free systems that can automatically produce better proteins in parallel [143]. With greater computational power, we can now simulate much more complicated networks in shorter time, which is immensely helpful in theoretical research, but it also means that methods in data science will be widely used to investigate the data produced by high throughput simulations [144].

There are still many opening questions in biological oscillators, the understanding of which will be of both academic and clinical interest. Findings from studying essential biological and synthetic oscillators have been applied in the development of effective drugs for clock-related diseases [145,146] and other medical application [86]. The already established quantitative approaches in systems and synthetic biology will be facilitated by new methods from other fields such as engineering and bioinformatics, which will enable greater achievements in the scientific and medical studies on biological oscillators.

Author summary.

Biological oscillators drive neuron firing, cell cycles, sleep-wake patterns, and many other essential processes in living systems. Quantitative investigation of how biological oscillators are designed can help us better understand and cure diseases. Over the past decades, development of techniques in the field of systems and synthetic biology has paved the way to decipher the mechanisms behind these oscillators. Here we review a series of experimental and theoretical studies in quantitative system and synthetic biology to discuss the progress that has been made in studying biological oscillators.