Kinematics and Kinetics of the Shoe during Human Slips

Abstract

This paper quantified the heel kinematics and kinetics during human slips with the goal of guiding available coefficient of friction (ACOF) testing methods for footwear and flooring. These values were then compared to the testing parameters recommended for measuring shoe-floor ACOF. Kinematic and kinetic data of thirty-nine subjects who experienced a slip incident were pooled from four similar human slipping studies for this secondary analysis. Vertical ground reaction force (VGRF), center of pressure (COP), shoe-floor angle, side-slip angle, sliding speed and contact time were quantified at slip start (SS) and at the time of peak sliding speed (PSS). Statistical comparisons were used to test if any discrepancies exist between the state of slipping foot and current ACOF testing parameters. The main findings were that the VGRF (26.7 %BW, 179.4 N), shoe-floor angle (22.1°) and contact time (0.02 s) at SS were significantly different from the recommended ACOF testing parameters. Instead, the testing parameters are mostly consistent with the state of the shoe at PSS. We argue that changing the footwear testing parameters to conditions at SS is more appropriate for relating ACOF to conditions of actual slips, including lower vertical forces, larger shoe-floor angles and shorter contact duration.

1. Introduction

Slips and falls are among the leading causes of occupational injuries. Slips, trips and falls (STF) lead to over 9 million treated cases in hospital emergency departments (Centers for Disease Control and Prevention, 2017) and more than one-fourth of the non-fatal occupational injuries in 2015 (U.S. Department of Labor- Bureau of Labor Statistics, 2016). A survey among young adults indicated that about half of the falling accidents are caused by slips (Heijnen and Rietdyk, 2016). STF prevention programs often recommend use of slip-resistant footwear to reduce slip risk (Bell et al., 2008).

Mechanical slip-testing devices that measure available coefficient of friction (ACOF) are frequently utilized to assess the slip-resistant performance of footwear and flooring. These devices sometimes attempt to simulate the dynamics of the foot slip in order to achieve “biofidelity” (i.e., similarity between test conditions and shoe dynamics during slipping) since the kinematics and kinetics applied to footwear affect ACOF measurements (Chang et al., 2016). For instance, ACOF measurements are affected by shoe-floor angle (Beschorner et al., 2007; Blanchette and Powers, 2015b), vertical force (Beschorner et al., 2007; Blanchette and Powers, 2015b), horizontal sliding speed (Beschorner et al., 2007; Blanchette and Powers, 2015b; Redfern and Bidanda, 1994) and contact duration (Gronqvist et al., 2003). Prior research has suggested that using test conditions that are more biofidelic improves the ability of ACOF measurements to predict slips (Iraqi et al., 2018). Furthermore, other biomechanical parameters that have not been formally incorporated in ACOF testing may need to be considered to improve biofidelity. For example, the side-slip angle (i.e., direction of heel velocity relative to the footwear orientation in the transverse plane) (Albert et al., 2017) has generally been limited to sliding the footwear specimen along the axis of the shoe (toe-to-heel) during ACOF measurements. This testing parameter may be important since the orientation of tread design affects ACOF (Blanchette and Powers, 2015a; Li and Chen, 2005; Yamaguchi et al., 2017). Another parameter that has not been considered is the location of the center of pressure (COP) for ground reaction forces, which may affect the portion of the tread in contact during ACOF testing. Thus, additional studies that report biomechanics of slipping would contribute knowledge towards developing ACOF measurement methods with improved biofidelity.

Biomechanical studies have reported certain kinematic and kinetic variables during slipping. These variables have been parameterized at times including heel strike (HS) (Chambers et al., 2002; McGorry et al., 2010), slip start (SS) (Albert et al., 2017; Strandberg and Lanshammar, 1981), and peak sliding speed (PSS) (Albert et al., 2017; Lockhart et al., 2003; Moyer et al., 2006; Strandberg and Lanshammar, 1981). These times represent the initial condition of the step, beginning of slip, and most severe portion of the slip, respectively. Table 1 summarizes key biomechanical variables at the times of HS, SS, and PSS reported in previous studies. The reported values are variable within each time and across times. These biomechanical studies serve as an important resource regarding the slipping biomechanics, which can be used to guide ACOF measurement techniques.

Table 1.

Vertical force, shoe-floor angle, sliding speed, contact time, and side-slip angle reported by biomechanical studies at HS, SS and PSS. Values are reported as mean ± standard deviations.

Study	Time points	Vertical force (%BW)	Shoe-floor angle (°)	Sliding speed (m/s)	Contact time from HS (ms)	Side-slip angle (+Medial)	Floor with liquid contaminant
(Strandberg and Lanshammar, 1981)	HS	NA	21.3±5.5	0.67±0.76 Ʊ	NA	NA	NA-soap
	SS	64±16	5.5±5.9	0.15±0.12Ʊ	48 ± 21	NA
(Cham and Redfern, 2002b)	HS	NA	16.8±1.5§, 20.5± 0.9*	1.01±0.20§, 0.62±0.41*	NA	NA	Vinyl with motor oil (10W–40)
	SS	NA	1.5±0.6§, 2.2±1.8*	NA	78.9±9.5§	NA
					65.7±3.5*
	PSS	NA	NA	0.31±0.06§, 0.78±0.16*	121.4±12.4§, 171.4±28.7*	NA
(Chambers et al., 2002)	HS	NA	28.2±3.0	NA	NA	NA	Vinyl with glycerol
	PSS	NA	NA	1.79±0.37	NA	NA
(McGorry et al., 2010)	HS	NA	25.3±5.4	1.10±0.74	NA	NA	Delrin dry, Teflon dry, Teflon with aerosol furniture polish
(Albert et al., 2017)	SS	NA	14.7±6.9	0.27±0.18	NA	66°±54.1	Vinyl with 90% glycerol-10% water solution
	PSS	NA	9.5±7.0	1.72±0.71	NA	3.2±15.9

^Ʊthe average sliding speed have been calculated based on the individual results reported from each subject in the study

^§at forward slipping during slip recovery

^*at forward slipping for slip leading to a fall

NA indicates that this variable was not reported for this study

Gaps in the literature exist regarding the biomechanical state of the foot during slipping. One limitation is that some studies only considered one type of footwear (Albert et al., 2017; Cham and Redfern, 2002b), which might not be generalizable. Other studies have been limited to few participants repeatedly exposed to slippery conditions (Strandberg and Lanshammar, 1981). Data from repeated slips may not represent the dynamics during unexpected human slips since participants alter their gait when anticipating a slippery condition (Cham and Redfern, 2002a). The limitations in the previous biomechanical studies impede the development of test methods that are biofidelic. Thus, additional research on this topic is needed.

The aim of the current study was to quantify biomechanical variables during unexpected human slips to guide biofidelic measurements of ACOF. Additionally, this study will determine if these variables deviate from the ACOF testing parameters recommended by a footwear traction testing standard (ASTM F2913-11, 2011) (Table 2) for variables specified in this testing standard.

Table 2.

ACOF testing parameters recommended by footwear traction testing standards (ASTM F2913-11, 2011; EN ISO 13287, 2012)

ACOF testing parameters	Levels
Vertical force (N)	400, 500
Shoe-floor angle (°)	7
Side-slip angle (°)	0
Sliding speed (m/s)	0.3
Contact time (s)§	0.10–0.30
Contact time (s)*	0.30–0.60
Contaminants§δ	water, detergent aqueous solution, oil
Contaminants*	glycerol aqueous solution, detergent aqueous solution, ethanol aqueous solution

^§ASTM F2913-11

^*EN ISO 13287

^δThe ACOF testing methods specified by ASTM F2913 are reportedly applicable to a wide variety of surface contaminants including but not limited to liquid water, ice, grease and oil.

2. Methods

2.1 Subjects

Kinetic and kinematic data for 39 subjects (18 female; mean age: 22.3±3.3years; mean height: 173.1±8.3cm; mean body mass: 68.3±10.0kg; mean BMI: 22.8±3.2) were extracted from four different human slipping studies performed in the same laboratory (Beschorner et al., 2016; Chambers and Cham, 2007; Iraqi et al., 2018; Jones et al., 2018; Moyer et al., 2006). The exclusion criteria for subject recruitment were any conditions that potentially impede regular gait such as orthopaedic, cardiovascular, neurological and pulmonary abnormalities. The human slipping protocols were authorized by the University of Pittsburgh Institutional Review Board and subjects were provided with informed consent. The inclusion criteria into this post-hoc analysis were: 1. young adults (18–35 years), 2. slips that were preceded by at least three gait trials where their left foot landed clearly on the dry force plate preceding the exposure to liquid-contaminant, and 3. a slip distance of greater than 3cm (Albert et al., 2017; Beschorner et al., 2016; Leamon and Li, 1990). In addition, subjects or liquid-contaminated trials were further excluded during data processing based on the following criteria: 4. subjects’ left foot did not land completely on the liquid-contaminated force plate, 5. if the subject experienced a heel slip in the first liquid-contaminated exposure, then their second exposure was discarded, 6. if the subject’s required coefficient of friction (RCOF) changed more than 16% after exposure to the first liquid-contaminated trial, their second exposure was discarded, and 7. the subject reported that they noticed the liquid contaminant before stepping on it (Iraqi and Beschorner, 2017; Iraqi et al., 2018; Jones et al., 2018). The rationale for criteria 5–7 were that these subjects might be anticipating a slip and could have different gait patterns. These criteria were established a priori (i.e., prior to performing statistical analyses).

2.2 Human Slipping Protocol

Subjects wore a whole-body marker set and donned a safety harness. Subjects were instructed to ambulate across a level vinyl composite tile walkway in a lab space equipped with a motion capture camera system (Vicon, Oxford, UK) and force plates (Bertec 4060A, Columbus, OH). Subjects performed three to five gait trials on the dry walkway where their left foot fully landed on the force plate. Then, the subjects were unexpectedly exposed to a liquid contaminant that was placed on the force plate. Subjects were distracted before each walking trial by facing away from the walkway, listening to music using earphones, and working on a word puzzle. The lights were dimmed to obscure the application of liquid contaminants. After their first unexpected liquid-contaminated exposure, the subjects were assigned to a different pair of footwear, performed 15–20 gait trials on the dry walkway and were exposed to the second unexpected liquid-contaminated trial. Kinematic and kinetic data were sampled at 120Hz and 1080Hz, respectively.

Three types of shoes and two types of boots were included in this analysis. The shoe types included a work shoe (S1), a work shoe labeled as slip-resistant with completely worn tread (S2), and another work shoe labeled as slip-resistant (S3). The two boots had the same collar height and tread design but different outsole material hardness (B1 and B2). The liquid contaminants included diluted glycerol and canola oil (Table 3).

Table 3.

Footwear-floor-contaminant conditions and number of slips (n) for each condition.

Study	Footwear	n	Liquid contaminant	Floor	Footwear style	Tread design	ACOF§ (Iraqi et al., 2018)
(Chambers and Cham, 2007; Moyer et al., 2006)	S1	7	75% glycerol-25% water	Vinyl			0.052 (0.010)
(Iraqi et al., 2018)	S2	10	90% glycerol-10% water	Vinyl			0.032 (0.004)
(Jones et al., 2018)	S3	10	Canola oil	Vinyl			0.120 (0.011)
(Beschorner et al., 2016)	B1	6	50% glycerol-50% water	Vinyl			0.085 (0.005)
(Beschorner et al., 2016)	B2	6	50% glycerol-50% water	Vinyl			0.067 (0.007)

^§The testing parameters for ACOF measurements were 250 N normal force, 17° shoe-floor angle and 0.5 m/s sliding speed.

2.2 Data and Statistical Analysis

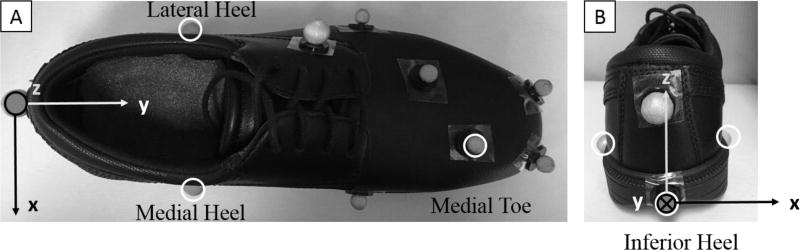
Kinematic and kinetic variables were quantified from the left foot (i.e., slipping foot) and included the vertical component of ground reaction forces (VGRF), COP, shoe-floor angle, side-slip angle, sliding speed and contact time. The COP data were quantified relative to the local coordinate system (LCS) of the heel. A LCS was created for the heel originating at the inferior portion of the calcaneus (inferior heel) and based on markers placed on the medial (medial heel) and lateral (lateral heel) side of the shoe about one third of the footwear length anterior from the heel (Figure 1A and B). The y-axis connected the inferior heel marker to the mid-point of medial and lateral heel markers. The z-axis pointed superiorly and was perpendicular to the plane formed by the three markers. The side-slip angle was defined as the angle between the heel’s y-axis and the velocity vector in the transverse plane of the heel LCS (Figure 1) (Albert et al., 2017). The sliding speed was tracked using the position of the inferior heel marker in the plane parallel to the floor. The shoe-floor angle was calculated using the inferior heel marker and medial toe marker (Albert et al., 2017; Cham and Redfern, 2002b). The shoe-floor angle for static trials was quantified and subtracted from the shoe-floor angles in the gait trials. Position data were filtered using a 4th order low-pass Butterworth filter with a cutoff frequency of 24Hz (Iraqi et al., 2018).

Figure 1.

Reflective markers placed on the footwear from (A) top view and (B) posterior view.

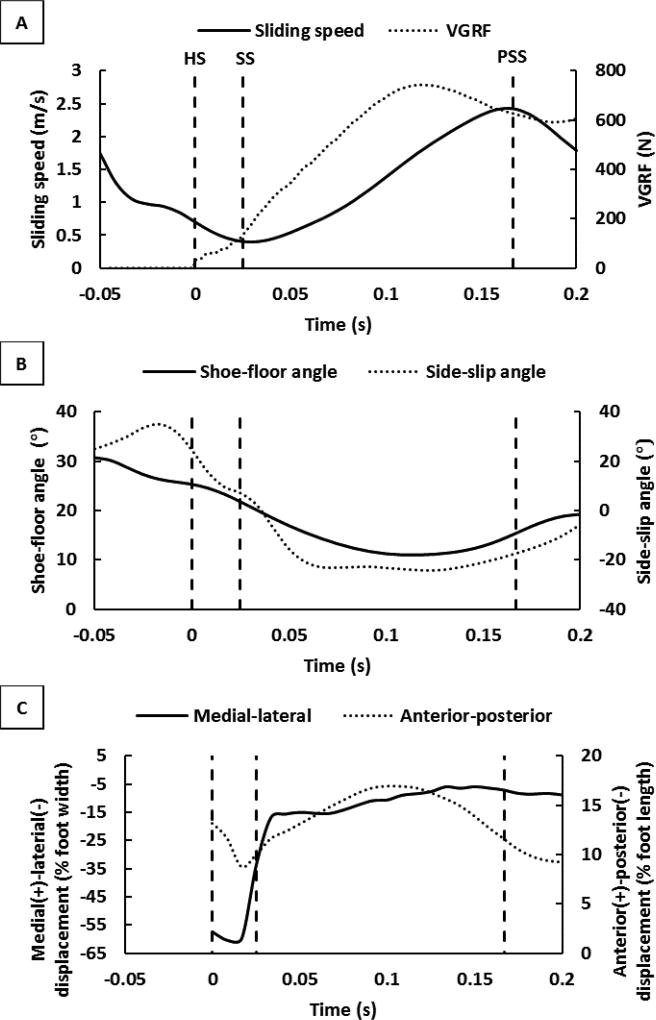
Two time points were used to parameterize the kinematic and kinetic variables: (1) SS; and (2) PSS (Figure 2A–C). The start of slipping (SS) was defined as the first local minimum in the sliding speed (Figure 2A) of the inferior heel marker after HS (Figure 1B) (Albert et al., 2017; Lockhart et al., 2003; Strandberg and Lanshammar, 1981). HS was defined as the instant when VGRF first exceeded 25 N (Figure 2A). The PSS was defined as the first local maximum in heel speed 50ms after HS (Moyer et al., 2006) (Figure 2A). SS was chosen since this represents the moment when ACOF is insufficient to prevent the foot from accelerating. PSS was selected as the moment of greatest slip severity.

Figure 2.

Typical heel dynamics at heel strike (HS), slip start (SS) and peak sliding speed (PSS) from an unexpected liquid-contaminated exposure: (A) sliding speed and VGRF, (B) shoe-floor angle and side-slip angle, and (C) COP. HS occurs at time = 0. SS was defined as the first local minimum after HS in the sliding speed. PSS was defined as the first local maximum in the sliding speed.

The slip distance and RCOF values were quantified to determine the occurrence of a slip in each liquid-contaminated exposure and to assess potential anticipation of a slippery condition, respectively. The resultant slip distances were calculated between the SS and the first local minimum after PSS (Iraqi et al., 2018). The RCOF values were calculated from the three preceding gait trials (on the dry walkway) based on a method by Chang et. al. (Chang et al., 2011).

Statistical analyses were performed to test different statistical model assumptions, to test whether kinematic and kinetic differences exist across the footwear conditions, and to test if any discrepancies exist between the state of slipping foot and ACOF testing parameters (ASTM F2913-11, 2011). A Shapiro-Wilk test was used to test if each kinematic and kinetic variables (response variables) at SS and PSS met the required assumptions for ANOVA of normally distributed residuals. A Levene test was used to test the ANOVA assumption for homoscedasticity across the footwear type. Transformation of the response variables were often successful in achieving homoscedasticity and normally-distributed residuals. In these circumstances, the reciprocal transformation was performed for reporting the mean and confidence intervals. If the ANOVA assumptions were met, a one-way ANOVA was performed to test differences across the footwear type on the response variable at SS and PSS. A Tukey HSD multiple comparison procedure was performed as a post-hoc analysis if a significant effect was found for footwear type. Simultaneous confidence intervals (CI) were calculated using Bonferroni method to test if the ACOF testing parameters (Table 2) used in standard measurement of ACOF by whole-shoe testers (ASTM F2913-11, 2011) were within the 95% CI of the corresponding kinematic and kinetic variables across each footwear type at SS and PSS. If the ANOVA assumptions were not met, non-parametric analyses were performed to test for differences across footwear type (Kruskal-Wallis test); post-hoc analyses when a significant footwear type effect was observed (Steel-Dwass test); and whether the standard measurement value was within the 95% CI (Wilcoxon Signed-Rank test). All statistical analyses were performed using commercial software (JMP® Pro 13.1.0, SAS Institute Inc., Cary, NC, USA) with a significance level of 0.05.

3. Results

Transformations were used to correct for skew and homoscedasticity (positive skew: square root of VGRF and contact time, logarithm of sliding speed; and negative skew: square of contact angle). When transformations were unsuccessful, non-parametric methods were used on data that were not normally distributed including COP_{Anterior-Posterior} (W=0.80, p-value<0.001) at SS, shoe-floor angle (W=0.92, p-value=0.007) at PSS, and COP_{Medial-Lateral} (W=0.91, p-value=0.004) at PSS. Non-parametric methods were also used for contact time at PSS since it had an unequal variance (F_4,34=4.74, p-value=0.004).

3.1 Kinematic variables

The shoe-floor angle across all the subjects were 22.1° (mean) at SS and 11.3° (median) at PSS. The 7° shoe-floor angle suggested by ASTM F2913 was lower than the 95% CI of the mean shoe-floor angle for all of the footwear types at SS (Figure 3A). At PSS, the 7° shoe-floor angle was not significantly different from the median shoe-floor angle for each footwear (Figure 3B). The central tendency of the side-slip angle across all the subjects was primarily in the medial direction at SS (mean=15.6°) and then changed to the lateral direction at PSS (mean=−6.3°). The 0° side-slip angle incorporated in the ASTM F2913 was within the 95% CI of the mean side-slip angle of all the footwear types at SS and PSS (Figure 3C). The average sliding speed across all the subjects was 0.10m/s at SS and 1.87m/s at PSS. The 0.3m/s sliding speed suggested by ASTM F2913 was within the CI of the mean sliding speed of S1 and S2, but was higher than the CI of the mean sliding speed of S3, B1 and B2 at SS (Figure 3D). The 0.3 m/s was significantly lower than PSS across all the footwear types (Figure 3D).

Figure 3.

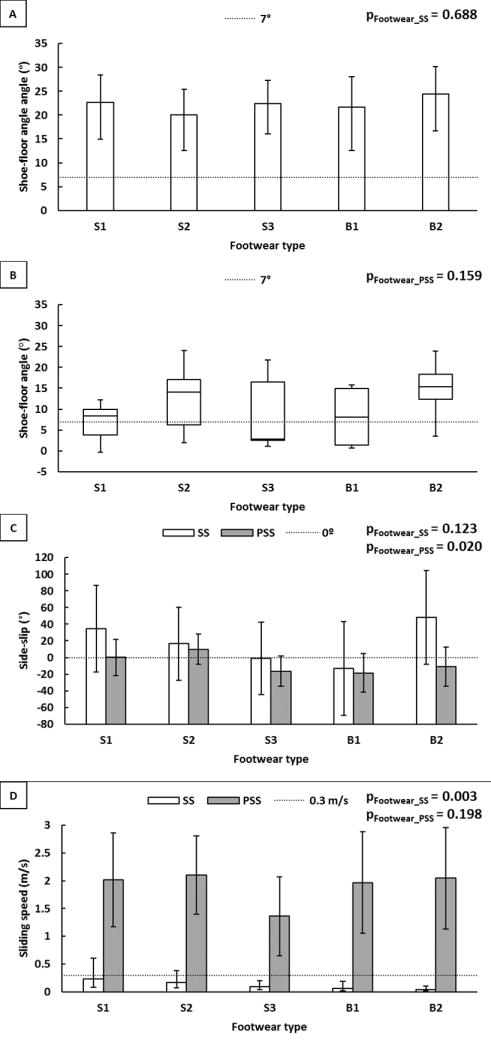
Kinematic variables across different footwear conditions: (A) Shoe-floor angle (°) at SS (The error bars represent 95% CI). (B) Summary statistics (minimum, 1^st quartile, median, 3^rd quartile and maximum) of shoe-floor angle (°) at PSS. (C) side-slip angle (°) at SS and PSS (Positive angles represent a medial angle and negative angles represent a lateral angle) (The error bars represent 95% CI), and (D) Sliding speed (m/s) at SS and PSS (The error bars represent 95% CI).

Among the kinematic variables, the sliding speed at SS and side-slip angle at PSS were significantly different across footwear conditions (Table 4). The post-hoc analysis at SS indicated that the sliding speed for B2 was significantly lower than S1 and S2. The post-hoc analysis at PSS indicated that the side-slip angle for S2 was pointing in medial direction whereas S3 was in lateral direction.

Table 4.

Statistical results for the effect of footwear type on the kinematic and kinetic variables. Significant F, χ² and p-values (p<0.05) have been made bold. Horizontal lines separate the kinematic variables, kinetic variables and contact time.

Biomechanical variables	Time point	F4,34 (p-value)	χ24 (p-value)
Shoe-floor angle	SS	0.57 (0.688)
	PSS		6.59 (0.159)
Side-slip angle	SS	1.96 (0.123)
	PSS	3.38 (0.020)
Sliding speed	SS	4.89 (0.003)
	PSS	1.60 (0.198)
VGRF	SS	2.40 (0.070)
	PSS	1.78 (0.156)
COPMedial-Lateral	SS	2.89 (0.037)
	PSS		8.56 (0.073)
COPAnterior-Posterior	SS		10.42 (0.034)
	PSS	2.64 (0.051)
Contact time	SS	0.99 (0.428)
	PSS		12.88 (0.012)

3.2 Kinetic variables

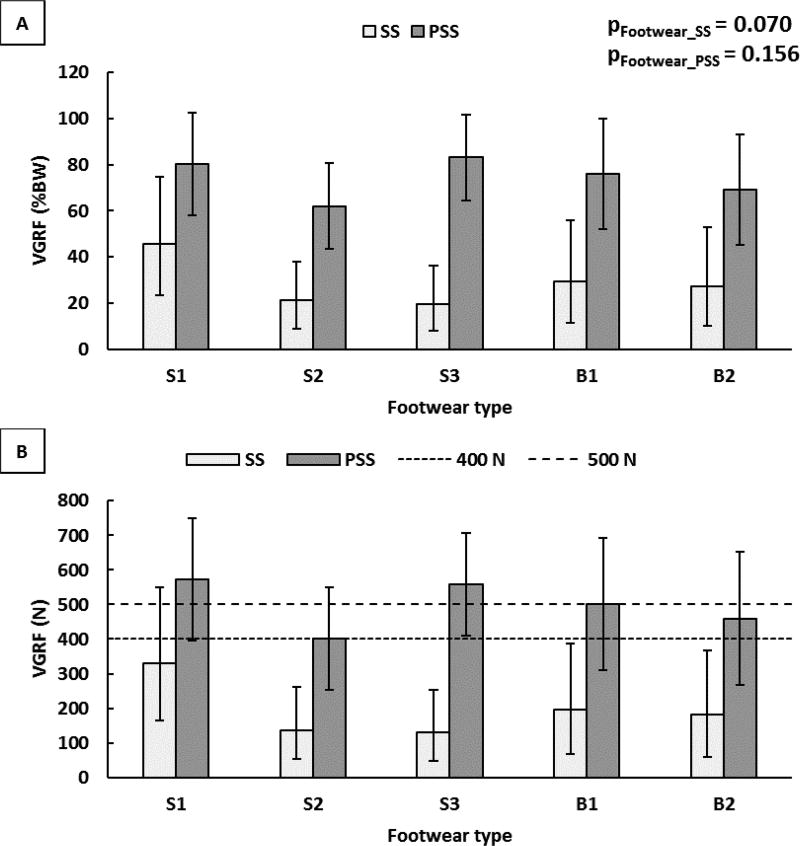
The average VGRF across all the subjects was 26.7%BW (179 N) at SS and 74.0%BW (497N) at PSS. At SS, the 400N and 500N normal force suggested by ASTM were significantly higher than S2, S3, B1 and B2 (Figure 4). However, 400N and 500N were within the CI of S1 at SS. The 400N and 500N were within the CI of the mean VGRF for all the footwear at PSS, except for S3 where the 400N was below the CI (Figure 4B). The average COP_{Medial-Lateral} across all the subjects was primarily in the lateral direction at SS (mean=−30.2% foot width) and PSS (median=−11.6% foot length). The COP_{Anterior-Posterior} across all the subjects was 9.6% foot length at SS (median) and 16.2% foot length at PSS (mean).

Figure 4.

VGRF across different footwear (A) normalized to bodyweight and (B) raw force value at SS and PSS. (The error bars represent 95% CI). Horizontal dashed lines represent the force values included in the ASTM F2913 standard.

The COP_{Medial-Lateral} and COP_{Anterior-Posterior} were significantly different across footwear conditions at SS (Table 4) (Figure 5). The post-hoc analysis at SS indicated that B2 had significantly more lateral COP than S2. At SS, S3 was more anterior than B1.

Figure 5.

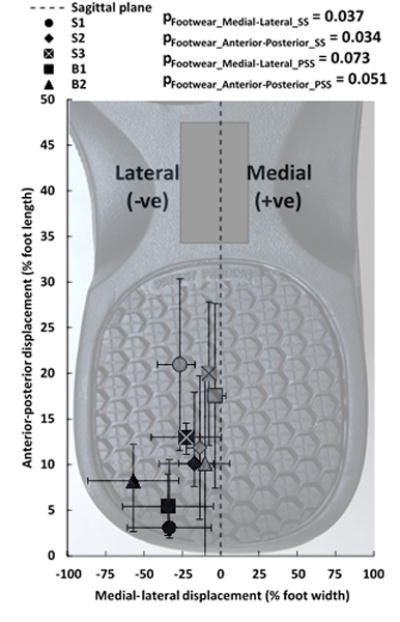
COP (% foot length and width) across different footwear at SS (black) and PSS (gray). The error bars represent 95% CI for COP_{Medial-Lateral} at SS and COP_{Anterior-Posterior} at PSS. The error bars represent IQR for COP_{Anterior-Posterior} at SS and COP_{Medial-Lateral} at PSS.

3.3 Contact time

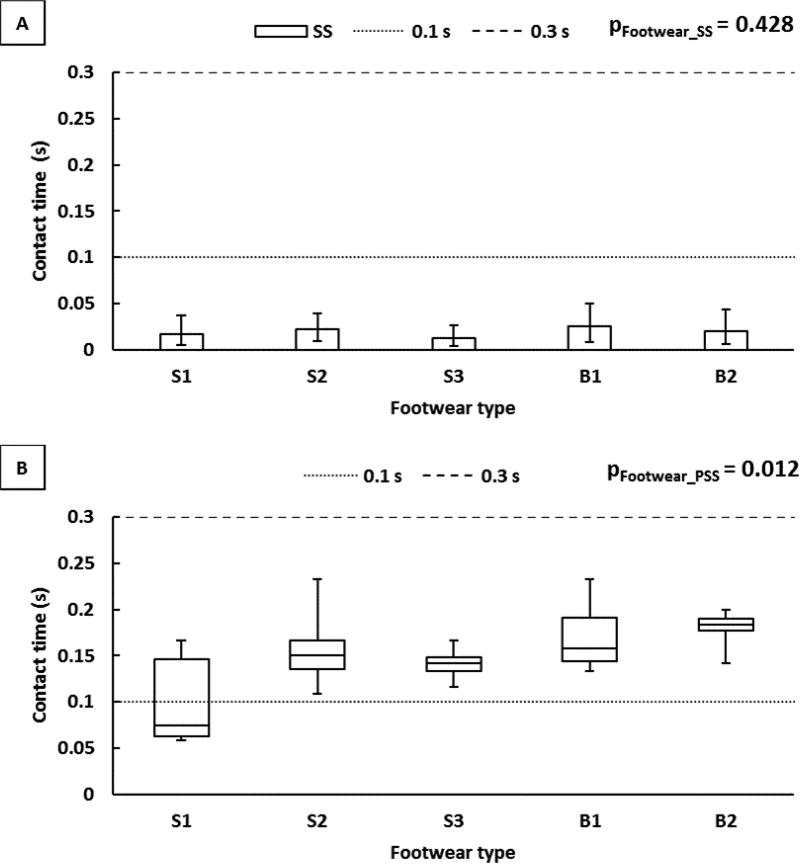
The contact time across all the subjects at SS and PSS were 0.02s (mean) and 0.15s (median), respectively. The contact time was significantly different between footwear types at PSS (Table 4) (Figure 6B). The post-hoc analysis at PSS indicated that the contact time for S3 was significantly shorter than B2. The measurement period of 0.10–0.30s suggested by ASTM F2913 was significantly higher than the contact time for all the footwear type at SS (Figure 6A). The CI for contact time was within the range of 0.10–0.30s for all footwear at PSS.

Figure 6.

(A) Contact time (s) across different footwear at SS. (The error bars represent 95% CI). (B) Box plot including summary statistics (minimum, 1^st quartile, median, 3^rd quartile and maximum) of contact time (s) across different footwear at PSS.

4. Discussion

The main finding of this study was that significant discrepancies exist between the footwear traction testing parameters and the heel dynamics during the onset of slipping. The central tendency of the VGRF, shoe-floor angle and contact time at SS were significantly different from the ACOF testing parameters suggested by ASTM F2913-11 (ASTM F2913-11, 2011). In particular, the average VGRF at SS was less than the typical normal forces (400N to 500N) applied during ACOF testing. In addition, the average shoe-floor angle at SS exceeded the contact angle (7°) used for the ACOF testing methods. The general consensus is that ACOF testing conditions should match the biomechanics of human gait during slipping accidents (Chang et al., 2016; Redfern et al., 2001). Thus, current footwear traction testing methods may become more biofidelic by including lower vertical forces (<400N), larger shoe-floor angles (>7°) and shorter contact duration (<0.10s) to be more consistent with heel dynamics at SS. The biomechanical variables at SS may be more informative with respect to friction that prevents slips, whereas increased friction at PSS might be important to lessen the severity of slip. A few of the biomechanical variables were consistent across footwear conditions while others were more footwear-dependent like the sliding speed at SS and side-slip angle at PSS. Thus, data across multiple designs of footwear should be considered when making determinations of what constitutes biofidelic for these specific variables.

Differences were observed in biomechanical parameters at SS between the current study and previous biomechanics of slipping studies. The average VGRF (26.7%BW) was substantially less than the vertical force of 64% BW (Strandberg and Lanshammar, 1981) and the median shoe-floor angle (22.1°) was significantly higher than the contact angle of 5.5° (Strandberg and Lanshammar, 1981), 1.5° (slip recovery) (Cham and Redfern, 2002b) and 2.2° (slip leading to a fall) (Cham and Redfern, 2002b). In addition, the contact time (0.02s) quantified in this study was shorter than the time of slip start of 0.05s (Strandberg and Lanshammar, 1981), 0.08s (slip recovery) (Cham and Redfern, 2002b) and 0.07s (slip leading to a fall) (Cham and Redfern, 2002b). One explanation for these discrepancies is that one of the studies repeatedly slipped subjects (Strandberg and Lanshammar, 1981). Thus, the kinematic and kinetic parameters reported may have been influenced by anticipation of a slippery condition (Cham and Redfern, 2002a; Chambers et al., 2002). The differences between this study and Cham and Redfern’s (2002b) study might be due to the higher severity of slips (as measured by PSS) in the current study (1.87m/s) compared to 0.31m/s (slip recovery) and 0.78m/s (slip leading to a fall) reported by Cham and Redfern’s (2002b). Another reason for the differences between the current study and the previous studies may be due to different shoe-floor-contaminant combinations (Table 1), which may lead to different levels of slippery conditions. The shoe-floor angle (22.1°) was closer to the value reported by Albert et al. (2017) (14.7°). We should note that Albert et al. (2017) used the same testing condition as S2 but with a different set of subjects. The average sliding speed (0.10m/s) at SS was within the range of sliding speeds observed in other studies, i.e., 0.08–0.32m/s (Strandberg and Lanshammar, 1981) and 0.27m/s (Albert et al., 2017). Moreover, the side-slip angle was primarily pointing to the medial direction during SS, which was consistent with Albert et al. (2017).

The kinematic and kinetic parameters quantified in this study provide insight on the state of the heel during SS. The dynamics of the heel has significant implication on slip-resistance measurements since biomechanical factors affect ACOF (Beschorner et al., 2007). First, the results suggest that lower VGRF (<400N) and higher shoe-floor angles (>7°) should be included in the ACOF testing parameters to achieve higher relevance to the onset of slipping. Inappropriate vertical force and contact angle during ACOF measurements may yield incorrect conclusion about the slip-performance of the footwear since ACOF is sensitive to the biomechanical parameters (Beschorner et al., 2007; Blanchette and Powers, 2015b). For instance, a contact angle of 7° may result in a higher ACOF value compared to 22.1° due to a higher contact area (Moghaddam and Beschorner, 2017), which may provide an incorrect inference about the slip-performance of the footwear. Second, the non-zero value of sliding speed during slip start suggests that ACOF performed by dynamic test methods might be more relevant to the dynamics of heel slip compared to static test methods. The static friction is generally higher than the dynamic friction (Gronqvist et al., 2003), which may overestimate the slip-performance of the footwear. Third, the lateral COP location at slip start may suggest that during ACOF testing a slight inversion angle of the footwear to achieve a lateral COP may need to be considered. This indicates that tread on the lateral portion of the footwear may be more critical than tread on the medial side.

The limitations of this study should be acknowledged. First, the effect of footwear size was not considered in the analyses. Second, the footwear styles were limited to the oxford and boot, therefore the results may not be generalizable to alternative footwear, which have different biomechanical properties during slipping (Chander et al., 2016). Third, this study only included young adults and may not be generalizable to older adults since kinematic and kinetic differences may exists between these age groups during slipping accidents (Moyer et al., 2006).

In summary, the current study suggests that the footwear traction testing methods may not resemble the vertical force, shoe-floor angle, sliding speed and contact duration at SS or the sliding speed at PSS. These variables may need to be adjusted to account for the biomechanics of the foot during slip start and to improve the accuracy of the footwear traction testing methods.

Highlights.

• Biomechanics of heel during slips can guide footwear traction testing standards.

• Kinematics and kinetics of heel were quantified for thirty-nine subjects.

• Biomechanical variables were parameterized at slip start and peak sliding speed.

• Major differences exist between the traction testing parameters and heel dynamics.

• Traction testing parameters may need to be adjusted to achieve biofidelity.