Control-oriented physiological modeling of hemodynamic responses to blood volume perturbation

Abstract

This paper presents a physiological model to reproduce hemodynamic responses to blood volume perturbation. The model consists of three sub-models: a control-theoretic model relating blood volume response to blood volume perturbation; a simple physics-based model relating blood volume to stroke volume and cardiac output; and a phenomenological model relating cardiac output to blood pressure. A unique characteristic of this model is its balance for simplicity and physiological transparency. Initial validity of the model was examined using experimental data collected from 11 animals. The model may serve as a viable basis for the design and evaluation of closed-loop fluid resuscitation controllers.

1. Introduction

Fluid infusion is an essential component of circulatory resuscitation for hypovolemia caused by infection (e.g., sepsis), perioperative and traumatic hemorrhage, neuro-critical care, burns and so forth (Bouglé, Harrois, & Duranteau, 2013; Chatrath, Khetarpal, & Ahuja, 2015; Goodman & Kumar, 2014; Haberal, Sakallioglu Abali, & Karakayali, 2010; Rochwerg et al., 2014). Fluid resuscitation requires titration and retitration of fluid infusion dose to the varying physiological state of a patient. In today’s clinical practice, caregivers are responsible for the continuous titration tasks. As a practical matter, this tedious but life-critical requirement presents a few challenges. First, the choice of target endpoints is heterogeneous and depends on the underlying pathophysiology of the patient and the preference of caregivers (e.g., blood pressure (BP) was shown effective for fluid infusion after uncomplicated hemorrhage in animals (Vaid et al., 2006) while urinary output (UO) was shown effective for burns (Salinas et al., 2008)). Second, caregivers may not effectively perform titration due to, e.g., heavy workload, distractions, and clinical inertia (Oliveira, Garcia, & Nogueira, 2016). Third, caregivers may not make optimal titration due to enormous variability in fluid responses across different patients.

The above limitations naturally suggest the desire for autonomy in fluid resuscitation. In fact, published reports document that autonomous closed-loop control systems for fluid resuscitation may alleviate the caregiver workload while still maintaining the quality of care by reducing the laps and errors associated with therapy adjustments (Michard, 2013; Rinehart, Liu, Alexander, & Cannesson, 2012; Rinehart, 2014; Bighamian, Kim, Reisner, & Hahn, 2016). However, existing work on closed-loop fluid resuscitation is not abundant, if not rare, both in terms of design and evaluation. Most closed-loop fluid resuscitation controllers reported to date are built upon empiric decision rules and gain tuning (Hoskins et al., 2006; Rinehart, Lee, Cannesson, & Dumont, 2013; Salinas et al., 2008; Ying & Sheppard, 1990). This state-of-the-art leaves much room for improving the efficacy and robustness of closed-loop fluid resuscitation controllers via model-based design approaches established in the field of control theory (Ioannou & Sun, 2012; Khalil, 2001; Nise, 2011; Skogestad & Postlethwaite, 2005; Slotine & Li, 1991). In addition, most evaluation studies have resorted to costly and time-consuming animal experiments (Rafie et al., 2004; Chaisson et al., 2003; Elgjo, Traber, Hawkins, & Kramer, 2000). Discussions at the recent Public Workshop on Physiological Closed-Loop Controlled Medical Devices organized by the Food and Drug Administration (FDA) found that computational models may offer time- and cost-efficient means for non-clinical testing (FDA Public Workshop, 2015). Hence, a credible mathematical model that can reproduce hemodynamic responses to blood volume perturbation may open up new opportunities for the design and evaluation of closed-loop fluid resuscitation controllers.

A mathematical model must be equipped with a pair of conflicting attributes to be useful for both design and evaluation of closed-loop control systems. First, it must be simple enough to streamline the design of closed-loop controllers. Second, it must be accurate and transparent, or interpretable, enough to produce legitimate evaluation outcomes. However, existing mathematical models that aim to reproduce hemodynamic responses to blood volume perturbation do not appear to fulfill an adequate balance between these two requirements: one class of black-box models are too empiric to offer viable physiological implications (Lewis, 1986; Mardel et al., 1995; Simpson et al., 1996; Wears & Winton, 1990), whereas the other class of first-principles models are too complex, involving as many as a few thousand parameters (Abram, Hodnett, Summers, Coleman, & Hester, 2007; Kofránek & Rusz, 2010; Pirkle & Gann, 1976; Hedlund, Zaar, Groth, & Arturson, 1988; Arturson, Groth, Hedlund, & Zaar, 1989; Carlson, Kligman, & Gann, 1996), making it inappropriate for the purpose of controller design. Therefore, a pre-requisite for the development of next-generation closed-loop fluid resuscitation controllers is a simple yet accurate and mechanistically transparent mathematical model suited to the design and evaluation of closed-loop fluid resuscitation controllers. Such a model must be able to reproduce a comprehensive list of hemodynamic responses to blood volume perturbation used as clinical endpoints of fluid resuscitation in today’s clinical practice, including blood volume (BV), stroke volume (SV) and cardiac output (CO), BP, and central venous pressure (CVP) (Roche, Miller, & Gan, 2009; Rinehart, Lee, Canales, et al., 2013; Blankenship, Wallace, & Pacifico, 1990; Cannesson, de Backer, & Hofer, 2011; Bighamian, Kim, et al., 2016).

This paper presents a lumped-parameter model to reproduce hemodynamic responses to blood volume perturbation applicable to the design and evaluation of closed-loop fluid resuscitation controllers. A unique characteristic of this model is its balance for simplicity (via abstraction of complex microscopic physiological mechanisms into systems-level feedback control actions) and physiological transparency (via rigorous use of established physiological knowledge). The preliminary validity of the model was examined using experimental data collected from 11 animals. First, a fully individualized model (a model obtained for each animal by estimating all the parameters from the data) was studied. Then, a parametric sensitivity analysis was performed to obtain a well-conditioned model by identifying low-sensitivity model parameters and fixing them at nominal values. Finally, a partially individualized model (a model obtained by estimating only the parameters to be individualized from the data) was studied.

2. Materials and methods

2.1. Lumped-parameter model of hemodynamic responses to blood volume perturbation

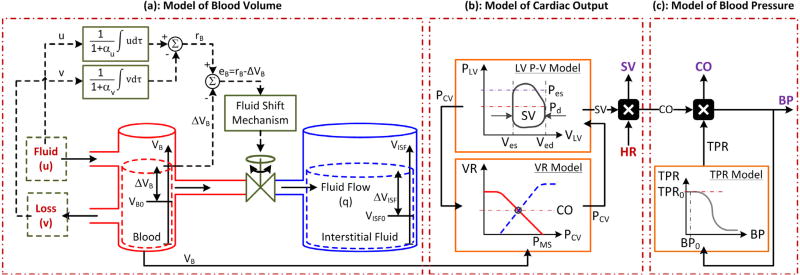
The model consists of three sub-models: (a) a control-theoretic model to relate blood volume perturbation (specifically, hemorrhage and fluid infusion) to blood volume; (b) a simple physics-based model to relate blood volume to stroke volume and cardiac output; and (c) a phenomenological model to relate cardiac output to blood pressure (Fig. 1). Compared to existing models available in the literature, a unique characteristic of this model is its balance for simplicity (via abstraction of complex microscopic physiological mechanisms into systems-level feedback control actions) and physiological transparency (via rigorous use of established physiological knowledge). Details follow.

Fig. 1.

A lumped-parameter model of hemodynamic responses to blood volume perturbation. The model consists of (a) a control-theoretic model to relate blood volume perturbation to blood volume; (b) a simple physics-based model to relate blood volume to stroke volume (SV) and cardiac output (CO); and (c) a phenomenological model to relate cardiac output to blood pressure (BP). (a) The left and right compartments represent intravascular and extravascular volumes, while the flow through the valve represents fluid shift between the two volumes. Fluid infusion (u) and loss (υ; including hemorrhage and urine) act on the intravascular volume to alter blood volume (V_B), which in turn alters interstitial fluid volume (V_ISF). The magnitude of valve opening is a function of the discrepancy between target versus actual changes in blood volume. α_u: fluid gain distribution ratio. α_υ: fluid loss distribution ratio. r_B: target change in blood volume in the steady state. ΔV_B: change in blood volume from V_B0 = V_B(0) (V_B(t) = V_B0 + ΔV_B(t)). ΔV_ISF: change in interstitial fluid volume from V_ISF0 = V_ISF(0) (V_ISF(t) = V_ISF0 + ΔV_ISF(t)). (b) Stroke volume and cardiac output are computed from blood volume by Guyton’s cardiac output-venous return (CO-VR) theory combined with the Frank–Starling mechanism and left ventricular pressure–volume loop theory. HR: heart rate. P_MS: mean systemic pressure. P_CV: central venous pressure. V_LV: left ventricular volume. P_LV: left ventricular pressure. V_ed: left ventricular end diastolic volume. V_es: left ventricular end systolic volume. P_d: diastolic pressure. P_es: end-systolic pressure. (c) Blood pressure is computed from cardiac output via a logistic function model of total peripheral resistance (TPR). BP₀: nominal blood pressure. TPR₀: nominal total peripheral resistance.

2.1.1. Modeling of blood volume response to blood volume perturbation

Fluid in the body is distributed in 3 major compartments: intravascular (blood), extravascular (interstitial fluid), and intracellular (Guyton, Taylor, & Granger, 1975). In the context of critical care, the gain or loss of fluid occurs primarily in the intravascular compartment in the form of hemorrhage, UO, fluid infusion etc., but the perturbation in the intravascular fluid volume thus occurred is dynamically distributed across all 3 major compartments via the inter-compartmental fluid shift (Guyton et al., 1975). In our prior work, a control-theoretic model of BV response to fluid infusion was developed (Bighamian, Reisner, & Hahn, 2016). The basic idea was to formalize established physiological principles underlying fluid volume distribution (that fluid infused into the intravascular compartment is distributed in the intravascular and extravascular compartments to regulate the ratio between their volumetric changes (Guyton et al., 1975)) into a mathematical model by abstracting myriads of complex microscopic fluid shift mechanisms into macroscopic feedback control actions.

Given that the ratio between the intravascular and extravascular volumetric changes is different for fluid loss (hemorrhage) and gain (fluid infusion) due to the compositional differences in the fluids involved in each process (blood lost consists of plasma and red blood cells (RBCs) while infused fluid may consist of electrolyte (crystalloid such as Lactated Ringer’s solution (LR)) and starch (colloid such as Hextend (Hex))), our original model developed primarily for fluid infusion scenarios is not readily applicable to the scenarios in which a patient undergoes both hemorrhage and fluid infusion. In the current work, our original model was extended as follows to address this limitation. Denoting the ratio between the intravascular and extravascular volumetric changes in the steady state in response to fluid gain (fluid infusion) and loss (hemorrhage and urine) as α_u and α_υ, respectively, the desired steady-state change in BV, r_B(t), can be written as follows:

$$r_B(t)=\frac{1}{1+{\alpha }_u}{\int }_0^{t}u(\tau )d\tau -\frac{1}{1+{\alpha }_{\upsilon }}{\int }_0^t\upsilon (\tau )d\tau$$ (1)

where u(t) and υ(t) = υ_H(t) + υ_U(t) denote the rates of fluid gain (infusion) and loss (hemorrhage υ_H(t) and UO υ_U(t)) at time t. At each time t, the inter-compartmental fluid shift is dictated by the discrepancy between the desired (r_B(t)) versus actual (ΔV_B(t)) changes in BV as follows:

$$q(t)=q(e_B(t))=q(r_B(t)-\Delta V_B(t))$$ (2)

Then, applying the conservation of volume to the intravascular compartment in Fig. 1(a) dictates that the rate of change in ΔV_B at time t is given by the resultant sum of the fluid gain u(t), fluid loss υ(t), and the inter-compartmental fluid shift q(t) (see the inflows and outflows associated with the “Blood” bucket):

$$\Delta {\dot{V}}_B(t)=u(t)-\upsilon (t)-q(t)$$ (3)

If the inter-compartmental fluid shift is abstracted into the action of a simple proportional–integral (PI) controller that strives to drive e_B(t) to zero in the steady state (Nise, 2011):

$$q(t)=-K_p{e}_B(t)-K_i{\int }_0^t{e}_B(\tau )d\tau$$ (4)

where K_p and K_i are proportional and integral gains, the dynamics dictating the rate of change in BV can be written as follows by combining (1)–(4):

$$\Delta {\stackrel{⃛}{V}}_B(t)+K_p\Delta {\ddot{V}}_B(t)+K_i\Delta {\dot{V}}_B(t)=[\ddot{u}(t)-\ddot{\upsilon }(t)]+\frac{K_p}{1+{\alpha }_u}\dot{u}(t)-\frac{K_p}{1+{\alpha }_{\upsilon }}\dot{\upsilon }(t)+\frac{K_i}{1+{\alpha }_u}u(t)-\frac{K_i}{1+{\alpha }_{\upsilon }}\upsilon (t)$$ (5)

This model is visualized in Fig. 1(a) as a two-bucket system connected by a bi-directional flow valve, where the buckets represent the intravascular and extravascular compartments, respectively, while the valve represents the resultant action of all the inter-compartmental fluid shift mechanisms.

2.1.2. Modeling of stroke volume and cardiac output responses to blood volume changes

A perturbation in BV entails the corresponding perturbations in SV and CO. The influence of BV on SV and CO can be viewed from 2 complementary standpoints: vascular and ventricular. On one hand, Guyton’s CO-venous return (VR) theory dictates that a perturbation in BV results in perturbations in CO and VR by altering mean systemic pressure (MSP) (Beard & Feigl, 2011) (Fig. 1(b)):

$$\mathit{\text{VR }}(t)=\mathit{\text{CO }}(t)=\frac{P_{\mathit{\text{MS}}}(t)-P_{\mathit{\text{CV}}}(t)}{R_{\mathit{\text{VR}}}}$$ (6)

where P_VC(t) is CVP, R_VR is the resistance to VR, $P_{\mathit{\text{MS}}}=\frac{(V_B-V_{\mathit{\text{BU}}})}{C_S}$ is MSP, V_BU is the unstressed BV, and C_S is the systemic capacitance (Beard & Feigl, 2011; Young, 2010). Expanding P_MS in (6) yields the following relationship between BV, SV, and CO:

$$\mathit{\text{CO }}(t)=\mathit{\text{HR }}(t)·\mathit{\text{SV }}(t)=\frac{1}{R_{\mathit{\text{VR}}}}[\frac{V_B(t)-V_{\mathit{\text{BU}}}}{C_S}-P_{\mathit{\text{CV}}}(t)]=\frac{1}{C_S{R}_{\mathit{\text{VR}}}}{V}_B(t)-\frac{1}{R_{\mathit{\text{VR}}}}{P}_{\mathit{\text{CV}}}(t)-\frac{V_{\mathit{\text{BU}}}}{C_S{R}_{\mathit{\text{VR}}}}$$ (7)

Note that V_B(t) = V_B0 + ΔV_B(t) is the sum of baseline BV V_B0 and its change ΔV_B(t) at time t given by (5). On the other hand, the Frank–Starling mechanism together with the left ventricular (LV) pressure–volume loop theory dictates that a perturbation in BV results in perturbations in SV and CO by altering the LV preload: LV end diastolic volume (LVEDV) (Sagawa, Maughan, Suga, & Sunagawa, 1988) (Fig. 1(b)). First, SV and CO are related to LVEDV V_ed(t) as follows:

$$\mathit{\text{SV }}(t)=\frac{\mathit{\text{CO }}(t)}{\mathit{\text{HR }}(t)}=\frac{E_S}{E_S+E_A}(V_{\mathit{\text{ed}}}(t)-V_0)$$ (8)

where E_S is the LV elastance, E_A is the arterial elastance (defined as the product of HR and total peripheral resistance (TPR)), and V₀ is a constant parameter. Using the LV end-diastolic pressure–volume relationship (Morley et al., 2007; Santamore & Burkhoff, 1991) evaluated at the end of diastole (V_LV(t) = V_ed(t) and P_D(V_LV(t)) = P_ed(t), where P_ed(t) is LV end diastolic pressure (LVEDP)):

$$P_D(V_{\mathit{\text{LV}}}(t))=B[e^{A(V_{\mathit{\text{LV}}}(t)-V_0)}-1]\stackrel{V_{\mathit{\text{LV}}}(t)=V_{\mathit{\text{ed}}}(t)}{\to }{V}_{\mathit{\text{ed}}}(t)-V_0=\frac{1}{A}\text{log }(\frac{1}{B}{P}_{\mathit{\text{ed}}}(t)+1)$$ (9)

where A and B are constant parameters specifying the end-diastolic LV pressure–volume relationship (Morley et al., 2007; Santamore & Burkhoff, 1991). Assuming that LVEDP P_ed(t) is proportional to CVP P_CV(t), P_ed(t) ≈ γP_CV(t) (Uemura et al., 2005), (8) reduces to the following:

$$\mathit{\text{SV }}(t)=\frac{\mathit{\text{CO }}(t)}{\mathit{\text{HR }}(t)}=\frac{E_S}{E_S+E_A}\frac{1}{A}\text{log }(\frac{\gamma }{B}{P}_{\mathit{\text{CV}}}(t)+1)$$ (10)

To obtain a direct relationship between BV and SV, (7) and (10) can be combined to yield the following by canceling CVP P_CV(t):

$$\mathit{\text{SV }}(t)={\theta }_1\text{ log }({\theta }_2·\mathit{\text{HR }}(t)·\mathit{\text{SV }}(t)+{\theta }_3{V}_B(t)+{\theta }_4)$$ (11)

where ${\theta }_1=\frac{E_S}{A(E_S+E_A)},{\theta }_2=-\frac{\gamma R_{\mathit{\text{VR}}}}{B},{\theta }_3=\frac{\gamma }{{\mathit{\text{BC}}}_S}$, and ${\theta }_4=-\frac{\gamma }{B}\frac{V_{\mathit{\text{BU}}}}{C_S}+1$ are the parameters that must be tuned to each individual based on the experimental data. A direct relationship between BV and CO can then be obtained by multiplying HR by (11):

$$\mathit{\text{CO }}(t)=\mathit{\text{HR }}(t)·\mathit{\text{SV }}(t)=\mathit{\text{HR }}(t)·{\theta }_1\text{ log }({\theta }_2·\mathit{\text{CO }}(t)+{\theta }_3{V}_B(t)+{\theta }_4)$$ (12)

In this way, SV and CO responses to blood volume perturbation can be reproduced. In addition, CVP response may also be reproduced from SV or CO either by (7) or (10). This model is visualized in Fig. 1(b).

2.1.3. Modeling of blood pressure response to cardiac output changes

A perturbation in CO entails the corresponding perturbations in BP and TPR. Specifically, a perturbation in CO first results in a proportional change in BP, which is compensated by a decrease in TPR via the arterial autonomic-cardiac regulation (Coleman & Guyton, 1969; Montani & Van Vliet, 2009). Despite its complex first principles nature, it has been suggested that autonomic-cardiac regulation can be abstracted into a sigmoidal relationship reasonably well (Cheng, Ivanova, Fan, & Khoo, 2010; Kawada et al., 2001; Toru Kawada et al., 2004; Magosso, Biavati, & Ursino, 2001; Pruett et al., 2013; Ursino, Antonucci, & Belardinelli, 1994). Hence, the following phenomenological model was used to relate the influence of BP on TPR (it is noted that a multitude of phenomenological sigmodal relationships were considered, and (13) turned out to offer the best ability to fit the experimental data among the models considered):

$$\mathit{\text{TPR }}(t)={\mathit{\text{TPR}}}_0-\frac{\Delta \mathit{\text{TPR}}}{2}\frac{\mathit{\text{sgn }}(\mathit{\text{BP }}(t)-{\mathit{\text{BP}}}_0)\sqrt[3]{|\mathit{\text{BP }}(t)-{\mathit{\text{BP}}}_0|}}{1+\sqrt[3]{|\mathit{\text{BP }}(t)-{\mathit{\text{BP}}}_0|}}$$ (13)

where TPR₀ and BP₀ are TPR and BP at nominal state, respectively, and ΔTPR is the maximal possible change in TPR. Then, the relationship between CO and BP can be given by multiplying (13) by CO:

$$\mathit{\text{BP }}(t)=\mathit{\text{CO }}(t)\times \mathit{\text{TPR }}(t)=\mathit{\text{Co }}(t)\times ({\mathit{\text{TPR}}}_0-\frac{\Delta \mathit{\text{TPR}}}{2}\frac{\mathit{\text{sgn }}(\mathit{\text{BP }}(t)-{\mathit{\text{BP}}}_0)\sqrt[3]{|\mathit{\text{BP }}(t)-{\mathit{\text{BP}}}_0|}}{1+\sqrt[3]{|\mathit{\text{BP }}(t)-{\mathit{\text{BP}}}_0|}})$$ (14)

This model is visualized in Fig. 1(c).

In sum, the mathematical model relating blood volume perturbation to hemodynamic responses of BV, SV, CO, and BP consists of (5), (12), and (14).

2.2. Experimental data

The experimental data used to validate the proposed lumped-parameter model were collected from 11 conscious sheep undergoing intravenous blood volume perturbation in the forms of hemorrhage and fluid infusion. The measurements included the rates of hemorrhage, fluid infusion, and UO as well as BV, CO, BP, and HR. The data collection protocol was approved by the Institutional Animal Care and Use Committee (IACUC) at the University of Texas Medical Branch and is described in detail elsewhere (Rafie et al., 2004).

All 11 animals received LR. 5 of these animals also received Hex. For the 5 animals which received both fluids, LR and Hex experiments were performed separately in a randomized order, with the experiments at least 5 days apart from each other. The duration of study for each fluid in each animal was 180 min. After the baseline data were recorded, an initial hemorrhage (25 mL/kg) was performed over 15 min. Fluid infusion was started 30 min after the start of the hemorrhage and continued for 150 min. Second and third hemorrhage (5 mL/kg) were performed 50 and 70 min after the start of the initial hemorrhage, and each lasted for 5 min. Fluid infusion was performed automatically with a rule-based closed-loop controller described in our prior work (Marques et al., 2017; Rafie et al., 2004; Vaid et al., 2006). In brief, a maximum flow of 100 ml/min (crystalloid) or 30 ml/min (colloid) per 70 kg was set when BP was equal to or lower than 40 mmHg, 80% of the maximum infusion rate was set when BP was between 41 and 44 mmHg, 60% of the maximum infusion rate was set when BP was between 45 and 49 mmHg, 30% of the maximum infusion rate was set when BP was between 50 and 69 mmHg, and 10% maximum infusion rate when BP was between 70 and 89 mmHg. At 90 mmHg and above, there was no infusion rate. In fact, it had previously been found that an effective means to maintain BP at a target level using the decision table algorithm, was to continue to infuse a small volume at a low rate until 10 mmHg above target BP (Marques et al., 2017; Vaid et al., 2006).

In each animal, baseline BV was measured via indocyanine green dye (ICG) (Henschen, Busse, Zisowsky, & Panning, 1993). Hematocrit, defined as the ratio between the red blood cell volume (RBCV) and BV, was measured before and throughout the experiment at 5 to 10 min intervals and was used to measure the fractional change in BV (see (Henschen et al., 1993) for details). Other hemodynamic responses were measured at similar time instants.

2.3. Individualized model evaluation method

The ability of the proposed model to reproduce hemodynamic responses to blood volume perturbation was evaluated. Our primary focus was to investigate if the model could be adapted to each individual animal and reproduce subject-specific hemodynamic responses. First, the model was fitted to the experimental data of each animal (called fully individualized model identification). Second, parametric sensitivity analysis of a generalized model (obtained by averaging the 11 fully individualized models) was performed in order to obtain a well-conditioned model by identifying low-sensitivity model parameters and fixing them at nominal values. Third, the model was fitted to the experimental data of each animal while fixing low-sensitivity model parameters to their nominal values (called partially individualized model identification). Fourth, the performance of the fully and partially individualized models were compared in terms of accuracy and accuracy-complexity trade-off as well as physiological transparency.

2.3.1. Individualized model identification and analysis

The fully individualized model identification was performed via numerical optimization. All sub-models combined, the model involves 10 tunable parameters: 4 in (5) (α_u, α_υ, K_p, K_i); 4 in (12) (θ_i, i = 1 ⋯ 4); and 2 in (14) (TPR₀ and BP₀) after fixing ΔTPR to cover experimentally observed maximal change in TPR in all animals (30 [mmHg·min/l]). Given a set of initial parameter estimates, the model computed BV, CO, and BP responses from the inputted experimental hemorrhage, fluid infusion, UO, and HR data as follows. First, the change in BV was computed from (5). At the same time, the change in RBCV was computed as follows:

$$\Delta V_{\mathit{\text{RBC}}}(t)=-{\int }_0^{t}H(\tau ){\upsilon }_H(\tau )d\tau$$ (15)

where ΔV_RBC(t) is the change in RBCV at time t, υ_H(t) is the fluid loss due to hemorrhage at time t, and H(t) is hematocrit at time t, related to BV and RBCV as follows:

$$H(t)=\frac{V_{B0}H(0)+\Delta V_{\mathit{\text{RBC}}}(t)}{V_{B0}+\Delta V(t)}$$ (16)

Second, CO response was computed by inputting the computed BV and measured HR to (12) and using a root finding algorithm to solve for CO that best satisfies (12) at each time t. Third, BP was computed by inputting the computed CO to (14). The computed BV, CO, and BP responses were compared with the respective experimental data, and the discrepancy between them was minimized by solving the following optimization problem to estimate the optimal set of model parameters:

$$\begin{gathered} {\Omega }^{\ast }=\{{\alpha }_u^{\ast },{\alpha }_{\upsilon }^{\ast },K_p^{\ast },K_i^{\ast },{\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast },{\mathit{\text{TPR}}}_0^{\ast },{\mathit{\text{BP}}}_0^{\ast }\} \\ =\text{arg }\underset{\Omega }{\text{min}}{\Vert \left[\right(\frac{{\check{\Delta V}}_B(t)-\Delta V_B(t|\Omega )}{\overline{{\check{\Delta V}}_B(t)}}\left)\right(\frac{\check{\mathit{\text{CO }}}(t)-\mathit{\text{CO }}(t|\Omega )}{\overline{\check{\mathit{\text{CO }}}(t)}})\times (\frac{\check{\mathit{\text{BP }}}(t)-\mathit{\text{BP }}(t|\Omega )}{\overline{\widehat{\mathit{\text{BP }}}(t)}}\left)\right]\Vert }_2 \end{gathered}$$ (17)

where ${\check{\Delta V}}_B(t),\check{\mathit{\text{CO }}}(t)$, and $\check{\mathit{\text{BP }}}(t)$ are measured BV, CO, and BP responses, while ΔV_B(t|Ω), CO(t|Ω), and BP(t|Ω) are the same hemodynamic variables predicted by the model. $\overline{{\check{\Delta V}}_B(t)},\overline{\check{\mathit{\text{CO }}}(t)}$, and $\overline{\check{\mathit{\text{BP }}}(t)}$ are the same hemodynamic variables averaged over the entire study duration, used to normalize the error magnitudes associated with each hemodynamic variables. The optimization problem (17) was solved using the differential evolution algorithm (Storn & Price, 1997), a derivative-free method suited to solve problems with multimodal and continuous-valued cost functions.

The fully individualized model was analyzed for (i) its ability to reproduce hemodynamic responses in each animal, (ii) accuracy-complexity trade-off via Akaike’s Information Criterion (AIC) (Burnham & Anderson, 2003), and (iii) the relevance of its parameter estimates. First, the models’ ability to reproduce experimental hemodynamic responses was assessed by computing the root-mean-squared errors (RMSEs) between the measured versus model-reproduced BV, hematocrit, SV, CO, and BP responses. Second, the AIC value associated with the model identified for each animal was computed. Third, the physiological relevance of the estimated model parameters was assessed in terms of the following: (i) ${\alpha }_u^{\ast }$ identified for crystalloid (LR) infusion versus colloid (Hex) infusion (colloid contains large molecules, which allows it to be better retained in the intravascular compartment than crystalloid, resulting in smaller ${\alpha }_u^{\ast }$ compared to crystalloid (Bighamian, Reisner, et al., 2016; Hedin & Hahn, 2005)); (ii) measured V_B0 versus V_BU derived from the identified CO model parameters $(V_{\mathit{\text{BU}}}^{\ast }=(1-{\theta }_4^{\ast })/{\theta }_3^{\ast })$; (iii) correlation between measured V_B0 and R_VR derived from the identified CO model parameters ( $C_S^{\ast }{R}_{\mathit{\text{VR}}}^{\ast }=-{\theta }_2^{\ast }/{\theta }_3^{\ast }$; noting that inter-individual variability in systemic compliance $C_S^{\ast }$ is not large (Oren, Grossman, & Frohlich, 1996) and that V_B0 and R_VR are known to exhibit positive correlation (Chirinos et al., 2009), model-derived $C_S^{\ast }{R}_{\mathit{\text{VR}}}^{\ast }$ may be positively correlated to V_B0); and (iv) discrepancy between measured BP and TPR in the steady state versus ${\mathit{\text{BP}}}_0^{\ast }$ and ${\mathit{\text{TPR}}}_0^{\ast }$ (noting from (13) that ${\mathit{\text{BP}}}_0^{\ast }$ and ${\mathit{\text{TPR}}}_0^{\ast }$ indicate nominal BP and TPR, they may be close to experimental values in the steady state in each animal).

2.3.2. Post-hoc parametric sensitivity analysis

The post-hoc parametric sensitivity analysis was conducted using the identified fully individualized models in order to determine high-sensitivity parameters (those having a large influence on the model outputs) and low-sensitivity parameters (those having a small influence on the model outputs), and thereby to (a) understand the identifiability properties of the model (it is noted that analytical identifiability analysis based on, e.g., linear regression analysis (Ljung, 1999) is not feasible due to a subset of the model parameters that are nonlinearly involved) as well as to (b) obtain a well-conditioned model (a model with low parametric variance) by fixing low-sensitivity parameters to their nominal values. Noting that BV, CO, and BP were all used in identifying the model, the parametric sensitivity analysis was performed a{t the sub-model level. That is, the sensitivity of the BV model (5) to $\{{\alpha }_u^{\ast },{\alpha }_{\upsilon }^{\ast },K_p^{\ast },K_i^{\ast }\}$ was examined; the sensitivity of the CO model (12) to $\{{\theta }_1^{\ast },{\theta }_2^{\ast },{\theta }_3^{\ast },{\theta }_4^{\ast }\}$ was examined; and the sensitivity of the BP model (14) to $\{{\mathit{\text{TPR}}}_0^{\ast },{\mathit{\text{BP}}}_0^{\ast }\}$ was examined. Details follow.

Two nominal models were constructed for parametric sensitivity analysis: one nominal model to simulate crystalloid response, equipped with the parameters averaged over all the animals and ${\alpha }_u^{\ast }$ averaged over 11 crystalloid animals, and another nominal model to simulate colloid response, equipped with the parameters averaged over all the animals and ${\alpha }_u^{\ast }$ averaged over 5 colloid animals. To elucidate the parametric sensitivity of the models to both fluid gain and loss, the model was simulated with a hemodynamic perturbation scenario consisting of (i) 30 min of 0.05 ml/kg/min hemorrhage and (ii) 30 min of 0.05 ml/kg/min LR infusion or 0.05/3 ml/kg/min Hex, which were separated by 150 min zero-input period. The data thus acquired were used to compute the parametric sensitivity as follows. First, the control-theoretic BV model (5) was formulated into the following state space model:

$$\dot{\mathbf{x}}(t)=\mathit{f}(\mathbf{x}(t),u(t),\upsilon (t),{\Omega }_{V_B})=𝒜\mathbf{x}(t)+ℬ\left[\begin{array}{c}\hfill u(t)\hfill \\ \hfill \upsilon (t)\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill -K_p\hfill & \hfill K_i\hfill & \hfill \frac{K_p}{(1+{\alpha }_u)}\hfill & \hfill \frac{-K_p}{(1+{\alpha }_{\upsilon })}\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill \frac{1}{(1+{\alpha }_u)}\hfill & \hfill \frac{-1}{(1+{\alpha }_{\upsilon })}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\mathbf{x}(t)+\left[\begin{array}{cc}\hfill 1\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\left[\begin{array}{c}\hfill u(t)\hfill \\ \hfill \upsilon (t)\hfill \end{array}\right],\mathbf{x}(t_0)={\mathbf{x}}_0$$ (18)

$$\Delta V_B(t)=𝒞\mathbf{x}(t)=[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}]\mathbf{x}(t)$$

where x(t) = [ΔV_B(t) ∫ e_B (τ) dτ ∫ u (τ) dτ ∫ υ (τ) dτ]^T, Ω_VB = [α_u α_υ K_p K_i]^T, and 𝒜 and ℬ are the system and input matrices. From (18), the following sensitivity function was constructed (Khalil, 2001):

$${\dot{𝒮}}_{\mathbf{x}}(t)=𝒜{𝒮}_{\mathbf{x}}(t)+\mathscr{H}(t),{𝒮}_{\mathbf{x}}(t_0)=0_{4\times 4}$$ (19)

$${𝒮}_{V_B}(t)=𝒞{𝒮}_{\mathbf{x}}(t)$$

where 𝒮_x(t) is the parametric sensitivity matrix associated with x(t), 𝒮_VB(t) is the parametric sensitivity function associated with BV, and ℋ(t) is given by the Eq. (20) in Box I.

Box I.

$$\mathscr{H}(t)=\frac{\partial \mathit{f}(\mathbf{x}(t),u(t),\upsilon (t),{\Omega }_{V_B})}{\partial {\Omega }_{V_B}}=\left[\begin{array}{cccc}\hfill \frac{-K_p\int u(\tau )d\tau }{{(1+{\alpha }_u)}^2}\hfill & \hfill \frac{K_p\int \upsilon (\tau )d\tau }{{(1+{\alpha }_{\upsilon })}^2}\hfill & \hfill \frac{\int u(\tau )d\tau }{1+{\alpha }_u}-\frac{\int \upsilon (\tau )d\tau }{1+{\alpha }_{\upsilon }}-\Delta V_B(t)\hfill & \hfill \int e_B(\tau )d\tau \hfill \\ \hfill \frac{-\int u(\tau )d\tau }{{(1+{\alpha }_u)}^2}\hfill & \hfill \frac{\int \upsilon (\tau )d\tau }{{(1+{\alpha }_{\upsilon })}^2}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$$ (20)

Second, the sensitivity functions associated with the physics-based CO model (12) and phenomenological BP model (14) were constructed by computing their partial derivatives with respect to the respective model parameters:

$${𝒮}_{\mathit{\text{CO}}}(t)=\left[\begin{array}{c}\hfill \frac{\partial \mathit{\text{CO }}(t)}{\partial {\theta }_1}\hfill \\ \hfill \frac{\partial \mathit{\text{CO }}(t)}{\partial {\theta }_2}\hfill \\ \hfill \frac{\partial \mathit{\text{CO }}(t)}{\partial {\theta }_3}\hfill \\ \hfill \frac{\partial \mathit{\text{CO }}(t)}{\partial {\theta }_4}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \frac{\mathit{\text{HR }}(t)({\theta }_2\mathit{\text{CO }}(t)+{\theta }_3{V}_B(t)+{\theta }_4)\text{ log }({\theta }_2\mathit{\text{CO }}(t)+{\theta }_3{V}_B(t)+{\theta }_4)}{({\theta }_2\mathit{\text{CO }}(t)+{\theta }_3{V}_B(t)+{\theta }_4)-{\theta }_1{\theta }_2\mathit{\text{HR }}(t)}\hfill \\ \hfill \frac{{\theta }_1\mathit{\text{HR }}(t)\mathit{\text{CO}}(t)}{({\theta }_2\mathit{\text{CO }}(t)+{\theta }_3{V}_B(t)+{\theta }_4)-{\theta }_1{\theta }_2\mathit{\text{HR }}(t)}\hfill \\ \hfill \frac{{\theta }_1\mathit{\text{HR }}(t)V_B(t)}{({\theta }_2\mathit{\text{CO }}(t)+{\theta }_3{V}_B(t)+{\theta }_4)-{\theta }_1{\theta }_2\mathit{\text{HR }}(t)}\hfill \\ \hfill \frac{{\theta }_1\mathit{\text{HR }}(t)}{({\theta }_2\mathit{\text{CO }}(t)+{\theta }_3{V}_B(t)+{\theta }_4)-{\theta }_1{\theta }_2\mathit{\text{HR }}(t)}\hfill \end{array}\right]$$ (21)

$${𝒮}_{\mathit{\text{BP}}}(t)=\left[\begin{array}{c}\hfill \frac{\partial \mathit{\text{BP }}(t)}{\partial {\mathit{\text{TPR}}}_0}\hfill \\ \hfill \frac{\partial \mathit{\text{BP }}(t)}{\partial {\mathit{\text{BP}}}_0}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \frac{\mathit{\text{CO}}(t){(1+\sqrt[3]{|\mathit{\text{BP}}(t)-{\mathit{\text{BP}}}_0|})}^2}{{(1+\sqrt[3]{|\mathit{\text{BP}}(t)-{\mathit{\text{BP}}}_0|})}^2+5\mathit{\text{CO}}(t){(|\mathit{\text{BP}}(t)-{\mathit{\text{BP}}}_0|)}^{-2/3}}\hfill \\ \hfill \frac{5\mathit{\text{CO}}(t){(|\mathit{\text{BP}}(t)-{\mathit{\text{BP}}}_0|)}^{-2/3}}{{(1+\sqrt[3]{|\mathit{\text{BP}}(t)-{\mathit{\text{BP}}}_0|})}^2+5\mathit{\text{CO}}(t){(|\mathit{\text{BP}}(t)-{\mathit{\text{BP}}}_0|)}^{-2/3}}\hfill \end{array}\right]$$ (22)

Then, 𝒮V_B(t), 𝒮_CO(t), and 𝒮_BP(t) were numerically computed by solving (19), (21), and (22) simultaneously with (5), (12), and (14) subject to the hemodynamic perturbation scenario described above. Since the model parameter values exhibited diversity in terms of magnitude, the computed 𝒮_VB(t), 𝒮_CO(t), and 𝒮_BP(t) were normalized using the respective nominal parameter values and time series sequences of ΔV_B(t), CO(t), and BP(t). For each sub-model, the magnitudes of the normalized parametric sensitivity functions were compared and low-sensitivity parameter(s) were identified as those whose sensitivity magnitudes are considerably small relative to the sensitivity functions associated with the remaining parameters. Since these parameters do not exert a large influence on the model’s response compared to the remaining parameters, they may not be identified accurately, and therefore, may be fixed at nominal value(s) without making any notable influence on the model’s ability to reproduce the experimental hemodynamic responses.

2.3.3. Partially individualized model identification and analysis

The partially individualized model identification was performed via numerical optimization. The parametric sensitivity analysis showed that K_i and θ₁ could be classified as low-sensitivity parameters (see Results). All sub-models combined, the model involves 8 tunable parameters: 3 in (5) (α_u, α_υ, K_p); 3 in (12) (θ_i, i = 2 ⋯ 4); and 2 in (14) (TPR₀ and BP₀) after fixing K_i and θ₁ to their respective average values across all the animals. The optimization problem was solved as previously described to estimate the optimal set of model parameters for the partially individualized model. Then, the partially individualized model was analyzed in comparison with its fully individualized counterpart for (i) its ability to reproduce hemodynamic responses in each animal, (ii) accuracy-complexity trade-off via AIC, and (iii) the relevance of its parameter estimates.

3. Results

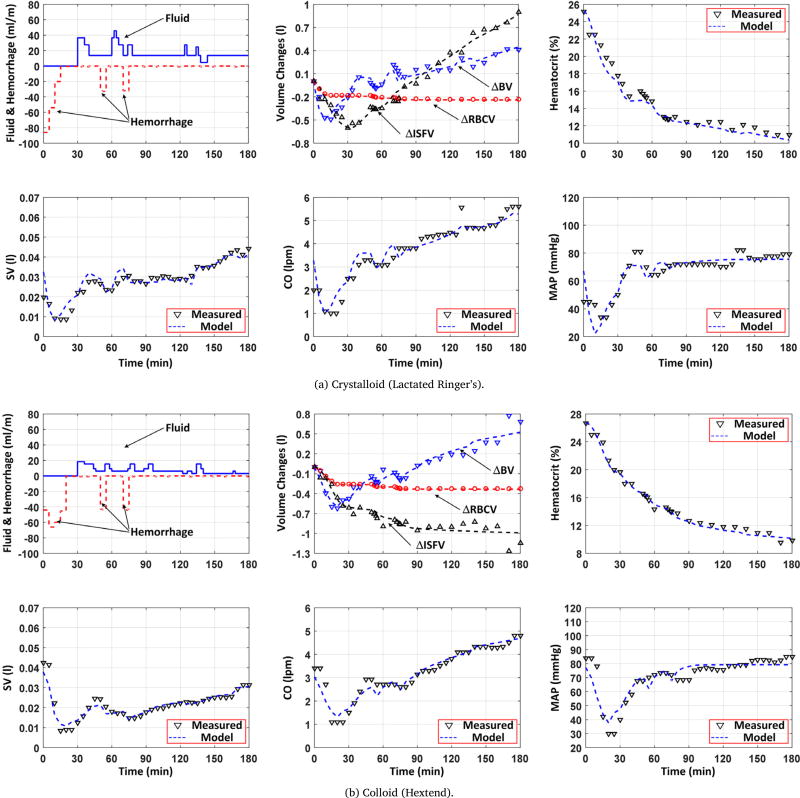
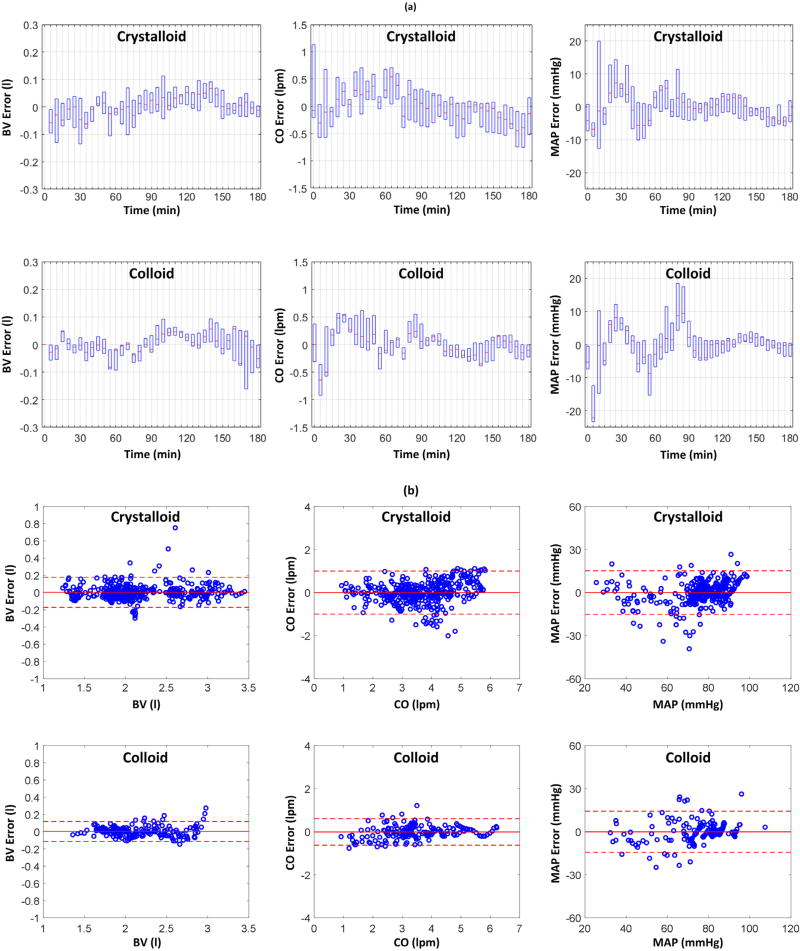
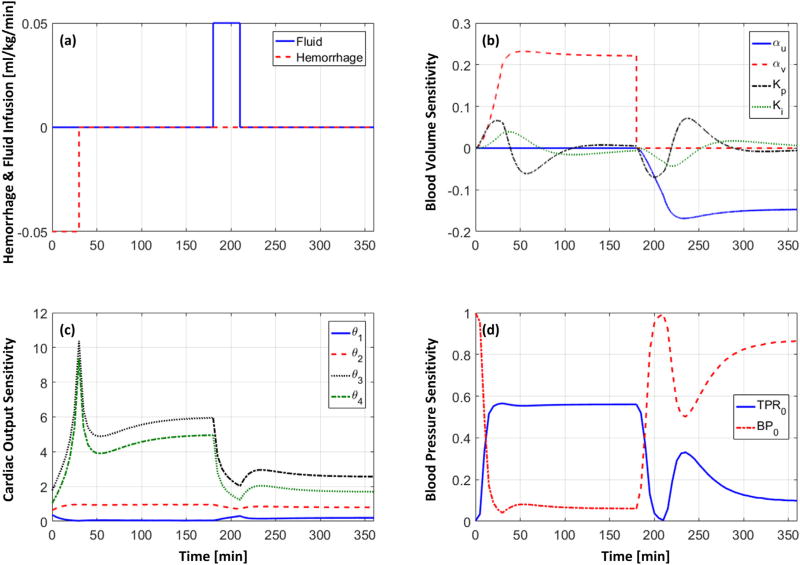
Table 1 shows the RMSEs associated with the fully and partially individualized models in reproducing BV, hematocrit, SV, CO, and BP (mean (SD)). In terms of AIC, partially individualized model outperformed its fully individualized counterpart in 6 (out of 11) animals for LR and in 4 (out of 5) animals for Hex. In sum, the former was superior to the latter, for either LR or Hex or both, in 8 out of 11 animals. Fig. 2 shows a representative example of measured hemodynamic responses to (a) LR and (b) Hex, and the same responses reproduced by the partially individualized model in an animal (the results associated with the fully individualized model were highly comparable and thus are not shown). Fig. 3 shows BV, CO, and BP errors associated with all 11 LR animals and 5 Hex animals, in terms of (a) the error distribution through time (median and IQR) and (b) the Bland–Altman plot. Table 2 summarizes the model parameter values associated with the fully and partially individualized models. Fig. 4 shows the time evolution of normalized parametric sensitivity functions in response to hemorrhage and crystalloid infusion (the results for colloid infusion exhibited the same trend and thus are not shown).

Table 1.

RMSEs associated with the individualized models (mean (SD)). Full: fully individualized model. Partial: partially individualized model.

(a) Crystalloid
Subject	Model	BV error [l]	Hematocrit error [–]	SV error [ml]	CO error [lpm]	BP error [mmHg]
1	Full	0.08	0.76	2.6	0.26	11.4
	Partial	0.09	0.76	2.5	0.25	11.6
2	Full	0.05	0.60	3.8	0.45	8.7
	Partial	0.06	0.60	4.3	0.53	8.2
3	Full	0.05	0.60	3.8	0.31	4.0
	Partial	0.08	0.80	3.9	0.32	3.8
4	Full	0.07	1.30	10.3	0.81	10.4
	Partial	0.07	1.28	10.3	0.81	10.1
5	Full	0.06	0.69	12.6	0.85	6.6
	Partial	0.05	0.68	13.9	0.97	6.9
6	Full	0.06	0.52	3.6	0.47	5.5
	Partial	0.07	0.57	3.3	0.42	5.9
7	Full	0.05	0.71	3.5	0.41	6.6
	Partial	0.06	0.79	3.5	0.41	6.8
8	Full	0.08	0.69	3.3	0.42	5.9
	Partial	0.13	1.13	3.4	0.39	6.1
9	Full	0.21	1.37	3.8	0.62	7.7
	Partial	0.23	1.33	5.1	0.61	9.9
10	Full	0.09	0.67	2.7	0.35	6.5
	Partial	0.11	0.87	3.9	0.48	7.6
11	Full	0.07	0.77	1.9	0.24	8.6
	Partial	0.07	0.75	2.3	0.26	8.5
Mean	Full	0.08 (0.05)	0.79 (0.28)	4.7 (3.4)	0.47 (0.21)	7.5 (2.2)
(SD)	Partial	0.09 (0.05)	0.87 (0.26)	5.1 (3.6)	0.50 (0.23)	7.8 (2.2)
(b) Colloid
Subject	Model	BV error [l]	Hematocrit error [–]	SV error [ml]	CO error [lpm]	BP error [mmHg]
1	Full	0.04	0.49	2.4	0.19	2.1
	Partial	0.05	0.52	3.8	0.32	1.7
2	Full	0.04	0.52	6.4	0.42	9.5
	Partial	0.04	0.52	6.6	0.44	6.8
3	Full	0.05	0.51	4.5	0.36	6.4
	Partial	0.05	0.52	4.6	0.36	6.4
4	Full	0.09	0.52	2.5	0.28	6.9
	Partial	0.09	0.52	2.6	0.28	6.6
5	Full	0.06	0.39	1.7	0.26	9.1
	Partial	0.06	0.43	1.7	0.24	8.8
Mean	Full	0.05 (0.02)	0.49 (0.06)	3.5 (1.9)	0.30 (0.09)	6.8 (3.0)
(SD)	Partial	0.06 (0.02)	0.50 (0.04)	3.8 (1.9)	0.33 (0.08)	6.1 (2.6)

Fig. 2.

Measured versus model-reproduced hemodynamic responses to (a) crystalloid (Lactate Ringer’s) and (b) colloid (Hextend) infusion as well as hemorrhage. BV: blood volume. ISFV: interstitial fluid volume. RBCV: red blood cell volume. SV: stroke volume. CO: cardiac output. MAP: mean arterial blood pressure.

Fig. 3.

Blood volume (BV), cardiac output (CO), and mean arterial pressure (MAP) errors associated with all 11 crystalloid animals and 5 colloid animals. (a) Error distribution in time.

Table 2.

Model parameter values associated with the individualized models (mean (SD)). Full: fully individualized model. Partial: partially individualized model.

	Model	${\alpha }_u^{\ast }$a [·]	${\alpha }_{\upsilon }^{\ast }$ [·]	$K_p^{\ast }$ [min−1]	$K_i^{\ast }$ [min−2]	${\theta }_1^{\ast }$ [ml]	${\theta }_2^{\ast }$ [min/ml]	${\theta }_3^{\ast }$ [ml−1]	${\theta }_4^{\ast }$ [·]	${\mathit{\text{T P R}}}_0^{\ast }$ [mmHg·min/l]	${\mathit{\text{B P}}}_0^{\ast }$ [mmHg]
Crystalloid	Full	2.3 (2.0)	1.1 (0.9)	0.1 (0.1)	17e-4 (1e-3)	12.2 (5.4)	−0.048 (0.046)	0.28 (0.12)	−422 (231)	16.5 (6.12)	82.9 (7.14)
	Partial	1.56 (0.67)	1.09 (0.83)	0.13 (0.10)	31e-4 (0)	13.0 (0)	−0.045 (0.044)	0.27 (0.13)	−421 (246)	17.4 (6.66)	82.2 (7.59)
Colloid	Full	−0.20 (0.26)	0.93 (0.52)	0.15 (0.13)	63e-4 (41e-4)	14.7 (5.46)	−0.063 (0.041)	0.31 (0.12)	−410 (165)	14.7 (3.88)	91.1 (22.4)
	Partial	−0.20 (0.23)	0.90 (0.37)	0.20 (0.11)	31e-4 (0)	13.0 (0)	−0.072 (0.043)	0.32 (0.13)	−442 (228)	17.0 (7.56)	94.5 (31.2)

^aSignificantly different between crystalloid and colloid. (p < 0.05).

Fig. 4.

Time evolution of normalized parametric sensitivity functions (indicating percent change in the hemodynamic responses caused by unit percent perturbation in each parameter from the nominal value) in response to simulated hemorrhage and crystalloid infusion. (a): Hemorrhage and fluid infusion scenario. (b): Sensitivity functions (19) for control-theoretic BV model (5) (𝒮_VB(t)). (c): Sensitivity functions (21) for physics-based CO model (12) (𝒮_CO(t)). (d): Sensitivity functions (22) for phenomenological BP model (14) (𝒮_BP(t)).

4. Discussion

A lumped-parameter model that can reproduce hemodynamic responses to blood volume perturbation was developed, equipped with simplicity to facilitate the design of closed-loop controllers and transparency to allow credible validation and interpretation. Here, the accuracy and physiological relevance properties of the proposed model are elaborated.

4.1. Fully versus partially individualized models

Once tuned to the data associated with individual animals, both fully and partially individualized models could reproduce hemodynamic responses to hemorrhage as well as infusion of crystalloid (LR) and colloid (Hex) fluids accurately, including BV, hematocrit, SV, CO, and BP (Table 1). When root-mean-squared across all the animals, the RMSEs associated with BV, SV, CO, and BP were 1.9 ml/kg and 2.2 ml/kg, 0.12 ml/kg and 0.13 ml/kg, 0.42 lpm and 0.44 lpm, and 7.2 mmHg and 7.3 mmHg, respectively. On the average, these errors amounted to less than 14.4% of the mean value of the corresponding responses in case of crystalloid and less than 11.7% in case of colloid. The goodness of fit observed for BV, ISFV, RBCV, and hematocrit suggests the validity of abstracting the inter-compartmental fluid shift (which involves many complex physiological mechanisms) into a simple closed-loop (PI) control action, while the goodness of fit observed for SV and CO illustrates the appropriateness of minimum-complexity physics-based expression for the relationship between BV versus SV and CO (Fig. 2 and Fig. 3). Overall, the model exhibited remarkable performance in reproducing the experimental hemodynamic responses despite its simple architecture, indicating its potential to offer complementary value to the class of highly complex first-principles models currently available in the field, e.g., (Abram et al., 2007; Kofránek and Rusz, 2010).

Close scrutiny of the fully individualized model showed that the model parameters are physiologically relevant. First, the values of ${\alpha }_u^{\ast }$ associated with crystalloid (LR) infusion versus colloid (Hex) infusion were significantly different (p < 0.05). This observation is consistent with the physiological anticipation: colloid, compared to crystalloid, enhanced BV expansion via reduced fluid shift from BV to ISFV due to the large molecules it contains (Bighamian, Reisner, et al., 2016; Hedin & Hahn, 2005). This finding highlights the potential need for fluid-dependent models in the design and evaluation of closed-loop fluid resuscitation controllers. Second, V_BU derived from the identified CO model parameters $(V_{\mathit{\text{BU}}}^{\ast }=(1-{\theta }_4^{\ast })/{\theta }_3^{\ast })$ was closely correlated with the measured V_B0 (r = 0.87). This observation is consistent with the physiological anticipation that individuals with small (large) V_B0 tend to have small (large) V_BU (Peterson & Bronzino, 2007). Third, R_VR derived from the identified CO model parameters $(C_S^{\ast }{R}_{\mathit{\text{VR}}}^{\ast }=-{\theta }_2^{\ast }/{\theta }_3^{\ast })$ was correlated positively with measured V_B0 (r = 0.59), which is consistent with an earlier finding that R_VR has a tendency to be proportional to V_B0 (Chirinos et al., 2009). Finally, the agreement between ${\mathit{\text{BP}}}_0^{\ast }$ and ${\mathit{\text{TPR}}}_0^{\ast }$ versus their steady-state experimental values in each animal was adequate with average discrepancy of 12.3% for ${\mathit{\text{BP}}}_0^{\ast }$ and 29.3% for ${\mathit{\text{TPR}}}_0^{\ast }$. Overall, these observations indicate that at least a subset of the parameters in the proposed model are physically transparent and physiologically interpretable, which encourages follow-up work on subject-specific estimation of these parameters and its applications to the development of decision-assist and control algorithms as well as in-silico testing tools for investigational closed-loop fluid resuscitation controllers.

Comparing fully and partially individualized models, the RMSEs associated with the former were comparable to those associated with the latter. Specifically, RMSEs for BV (p = 0.24), hematocrit (p = 0.20), SV (p = 0.26), CO (p = 0.50), and BP (p = 0.29) responses were not significantly different. In addition, AIC preferred partially individualized model to fully individualized model in many animals (see Results). The difference in the 8 tunable parameters was minimal and mostly insignificant (p > 0.05 for both LR and Hex, except K_p associated with Hex (p = 0.03)). Further, the physiological relevance of parameters observed for the fully individualized model was preserved in the partially individualized model. Hence, the impact of fixing K_i and θ₁ to their nominal values on the validity and physiological relevance of the model was minimal. Considering that the partially individualized model involves fewer tunable parameters and equivalent RMSEs, it may be claimed that it is equipped with superior accuracy-complexity tradeoff to the fully individualized model.

4.2. Parametric sensitivity

Examining the time evolution of the parametric sensitivity functions offered additional insights as to the relative importance and identifiability properties of the model parameters. First, the time evolution of 𝒮_VB(t) indicates that BV response in the steady state is primarily sensitive to α_u and α_υ while the same response during transients is also influenced by K_p and K_i (Fig. 4(b)). This is plausible in that α_u and α_υ specify steady-state changes in BV and ISFV, whereas K_p and K_i are parameters dictating dynamic inter-compartmental fluid shift. In addition, the amplitudes of the sensitivity functions associated with K_p and K_i are relatively smaller than those associated with α_u and α_υ, suggesting the relative importance of the latter parameters compared to the former parameters. In particular, K_i appears to be the least important parameter in the control-theoretic BV model, suggesting that the inter-compartmental fluid shift may be adequately described by individualizing the proportional control action alone, at least for the data used in this paper. Second, the time evolution of 𝒮_CO(t) indicates that CO response is sensitive to θ₃ and θ₄ relative to θ₁ and θ₂ (Fig. 4(c)). This observation is plausible in that θ₃ and θ₄ are related to BV and unstressed BV, the changes in which directly influences SV and CO. The amplitude of sensitivity functions was in general larger under hemorrhage than fluid infusion (Fig. 4(c); except $\frac{\partial \mathit{\text{CO}}(t)}{\partial {\theta }_1}$ which exhibited the opposite trend), which may be attributed to an increase in the denominator term (θ₂CO(t) + θ₃V_B(t) + θ₄) − θ₁θ₂ HR(t) in 𝒮_CO(t) (21) in response to BV expansion during fluid infusion. In sum, θ₁ appears to be the least important parameter in the physics-based CO model. Third, the time evolution of 𝒮_BP(t) indicates that both TPR₀ and BP₀ make a large influence on BP response (Fig. 4(d)). In particular, noting that (13) is a saturating function in the BP-TPR plane (Fig. 1(c)), perturbing TPR₀ and BP₀ shifts the function (13) in vertical and horizontal directions, respectively. Hence, the function, and thus BP response as well, is more sensitive to TPR₀ than BP₀ when BP is far away from BP₀ (i.e., the saturating ends of the function) while it is more sensitive to BP₀ than TPR₀ when BP is near BP₀. The sensitivity functions in Fig. 4(d) clearly follow this anticipated behaviors: $\frac{\partial \mathit{\text{BP}}(t)}{\partial {\mathit{\text{TPR}}}_0}$ exhibited larger amplitude during hemorrhage (with which BV decreases away from its baseline value) than during fluid infusion (with which BV increases back towards its baseline value), while $\frac{\partial \mathit{\text{BP}}(t)}{\partial {\mathit{\text{BP}}}_0}$ exhibited the opposite behaviors. Though TPR₀ and BP₀ influence BP response in different regimes, their peak amplitudes were quite comparable. Thus, both parameters were regarded as important in reproducing BP response accurately.

4.3. Potential avenues for model improvements

There are a few aspects of the model that may potentially be improved in future work to make it more amenable to the design and evaluation of closed-loop fluid resuscitation controllers, by refining the trade-off between the first-principles and abstract components in the model. First, to make it more amenable to controller design, the nonlinearity originating from the first principles and nonlinear abstract components (e.g., those in Eqs. (12) and (14)) may be removed by the use of linear abstract components with acceptable accuracy, so that the analysis of the model’s structural properties (including identifiability, controllability, and observability) as well as the design of controllers can be streamlined. Second, to make it more suited to controller evaluation, additional first-principles components may be incorporated. For example, one weakness of the current model from controller evaluation standpoint is the assumption that heart rate is available as input to the model. However, an ideal model for controller evaluation must be self-sufficient so that it can generate all the desired hemodynamic responses once fluid gain and loss are inputted. In addition, the current model does not explicitly consider the regulation of unstressed blood volume (Costanzo, 2014), which may be important in certain hemorrhage and fluid resuscitation scenarios. These expansions may be achieved by incorporating autonomic-cardiac regulation and renin–angiotensin–aldosterone functions among others. In this way, judicious balance between first-principles and abstract components in the model may facilitate the creation of an array of physiological models suited to the context of use (i.e., design and evaluation of closed-loop controllers).

4.4. Model-based design and evaluation of closed-loop fluid resuscitation controllers: Prospects

Mathematical models of physiological systems have the potential to contribute to the design and evaluation of closed-loop fluid resuscitation controllers. In the design phase, it enables the control designer to easily acquire insights on system dynamics and influence of each physiological component on the performance of closed-loop controllers via analysis and simulation. This in turn lends confidence to the efficacy of model-based closed-loop controllers by conferring on them sufficient level of performance and robustness against conceivable physiological variability and challenging clinical scenarios, which are hard to achieve with empiric and rule-based controllers designed by iterative trial and error processes. In the evaluation phase, mathematical models can facilitate the evaluation of closed-loop fluid resuscitation controllers in the forms of in-silico and hardware-in-the-loop test methods, similarly to the physiological closed-loop controllers in other domains (e.g., artificial pancreas (Dassau et al., 2009; Kovatchev, Breton, Dalla Man, & Cobelli, 2009)). By leveraging such non-clinical test methods, it is possible to perform rigorous stress testing of closed-loop fluid resuscitation controllers in a wide range of clinical scenarios, enabling the study of the behavior of the closed-loop controllers under worst-case clinical scenarios. Therefore, computational simulations incorporating mathematical models with established validity and utility for pre-clinical evaluation may be used as complementary evidence for the evaluation of closed-loop fluid resuscitation controllers, potentially obviating or reducing time and cost required to conduct a large-scale animal study. From these perspectives, the mathematical model developed in this paper may serve as a viable initial step towards model-based design and evaluation of closed-loop fluid resuscitation controllers.

5. Conclusion

A lumped-parameter model that may be useful in the development and evaluation of closed-loop algorithms for fluid resuscitation in critically ill patients was developed and analyzed. It was demonstrated that the model was equipped with several desired characteristics required for a model to be used as a control design and testing tool, including simplicity, transparency, and accuracy. Moving forward, follow-up efforts are begin made to further investigate and improve the model as well as to translate the model into clinically impactful closed-loop controllers and evaluation tools.