Coupling between an electrostatic network and the Zn²⁺ binding site modulates Hv1 activation

Hv1 proteins form a voltage-gated proton channel that is inhibited by extracellular Zn²⁺. De La Rosa et al find that extracellular Zn²⁺ is octahedrally coordinated by specific protein atoms and that Zn²⁺ occupancy modulates voltage sensor activation in Hv1 by long-range conformational coupling to a conserved intracellular electrostatic network.

Abstract

The voltage sensor (VS) domain in Hv1 proton channels mediates a voltage-dependent and H⁺-selective “aqueous” conductance (G_AQ) that is potently modulated by extracellular Zn²⁺. Although two conserved His residues are required for Zn²⁺ effects on G_AQ gating, the atomic structure of the Zn²⁺ coordination site and mechanism by which extracellular Zn²⁺ stabilizes a closed-state conformation remain unknown. Here we use His mutagenesis to identify residues that increase Zn²⁺ potency and are therefore likely to participate in first solvation shell interactions with Zn²⁺. Experimental Zn²⁺-mapping data were then used to constrain the structure of a new resting-state Hv1 model (Hv1 F). Molecular dynamics (MD) simulations show how protein and water atoms directly contribute to octahedral Zn²⁺ coordination spheres in Zn²⁺-bound and -unbound Hv1 F models. During MD simulations, we observed correlated movements of Zn²⁺-interacting side chains and residues in a highly conserved intracellular Coulombic network (ICN) that contains highly conserved Arg “gating charges” in S4 as well as acidic “counter-charges” in S2 and S3 and is known to control VS activation, suggesting that occupancy of the extracellular Zn²⁺ site is conformationally coupled to reorganization of the ICN. To test this hypothesis, we neutralized an ICN Glu residue (E153) and show that in addition to shifting G_AQ activation to more negative voltages, E153A also decreases Zn²⁺ potency. We speculate that extracellular gating-modifier toxins and other ligands may use a generally similar long-range conformational coupling mechanism to modulate VS activation in related ion channel proteins.

Introduction

Divalent metal ions such as Zn²⁺ commonly function as protein cofactors by directly interacting with oxygen, sulfur, and nitrogen atoms in His, Cys, Glu, and Asp side chains (Stote and Karplus, 1995; Dudev et al., 2003; Laitaoja et al., 2013). Increasing the concentration of extracellular ZnCl₂ causes the apparent open probability (P_OPEN)–voltage relation for the intrinsic (i.e., “aqueous”) H⁺-selective conductance (G_AQ) in native and expressed Hv1 channels to shift positively (Cherny and DeCoursey, 1999; Ramsey et al., 2006; Sasaki et al., 2006; Musset et al., 2010; Takeshita et al., 2014; Qiu et al., 2016). The effect of ZnCl₂ to modulate Hv1 gating is inferred to mean that zinc(II), which is a divalent cation (Zn²⁺) in aqueous solution, stabilizes a closed-channel conformation and therefore attenuates H⁺ current amplitude (Cherny and DeCoursey, 1999; Ramsey et al., 2006; Sasaki et al., 2006; Musset et al., 2010; Takeshita et al., 2014; Qiu et al., 2016). The relatively high concentration of Zn²⁺ in human seminal fluid is hypothesized to prevent spermatozoon activation in the male reproductive tract in vivo by preventing Hv1 channel opening, indicating that Zn²⁺ modulation of G_AQ gating is physiologically meaningful (Lishko and Kirichok, 2010). Although recent studies have provided important insights into the mechanism of Zn²⁺ effects on Hv1 gating (Ramsey et al., 2006; Takeshita et al., 2014; Qiu et al., 2016), essential mechanistic details remain unknown.

The effects of Zn²⁺ and other divalent metal cations on G_AQ gating are concentration dependent (IC₅₀ ≈ 0.2–2 µM) and sensitive to changes in pH_O (apparent pK_a ≈ 6.4), suggesting that one or more His residues are required for Zn²⁺ coordination (Meech and Thomas, 1987; Byerly and Suen, 1989; Cherny and DeCoursey, 1999; Ramsey et al., 2006; Sasaki et al., 2006; Lishko et al., 2010; Musset et al., 2010). The availability of human, mouse, and Ciona intestinalis HVCN1 cDNAs encoding bona fide voltage-gated H⁺ channel proteins (Ramsey et al., 2006; Sasaki et al., 2006) led to the identification of His residues in the predicted S2 helical segment (H140/H^2.40) and S3–S4 linker (H193/H^3.71) in the human Hv1 voltage sensor (VS) domain that are necessary for Zn²⁺ effects on G_AQ gating (Fig. 1 A; Ramsey et al., 2006). The H140A-H193A double mutant is essentially insensitive to submillimolar [Zn²⁺], but single H140A and H193A mutations decrease Zn²⁺ potency only 10- to 30-fold (Ramsey et al., 2006). Hv1 orthologues from C. intestinalis and Coccolithus pelagicus also lack H^3.71 (Fig. 1 A) and exhibit similar Zn²⁺ sensitivity to human Hv1 H193A (Ramsey et al., 2006; Sasaki et al., 2006; Taylor et al., 2011; Qiu et al., 2016), indicating that H^3.71 is not required for the effect of Zn²⁺ on G_AQ gating. Electron density attributed to Zn²⁺ is observed near E^1.58, D^1.62, and H^2.40 in the anomalous difference map of a mouse Hv1-based protein chimera (mHv1cc) x-ray structure solved to 3.45 Å (Takeshita et al., 2014), but the position of H^3.71 is not resolved, and the low overall resolution precludes unambiguous determination of Zn²⁺ coordination sphere geometry or identification of liganded protein and water atoms.

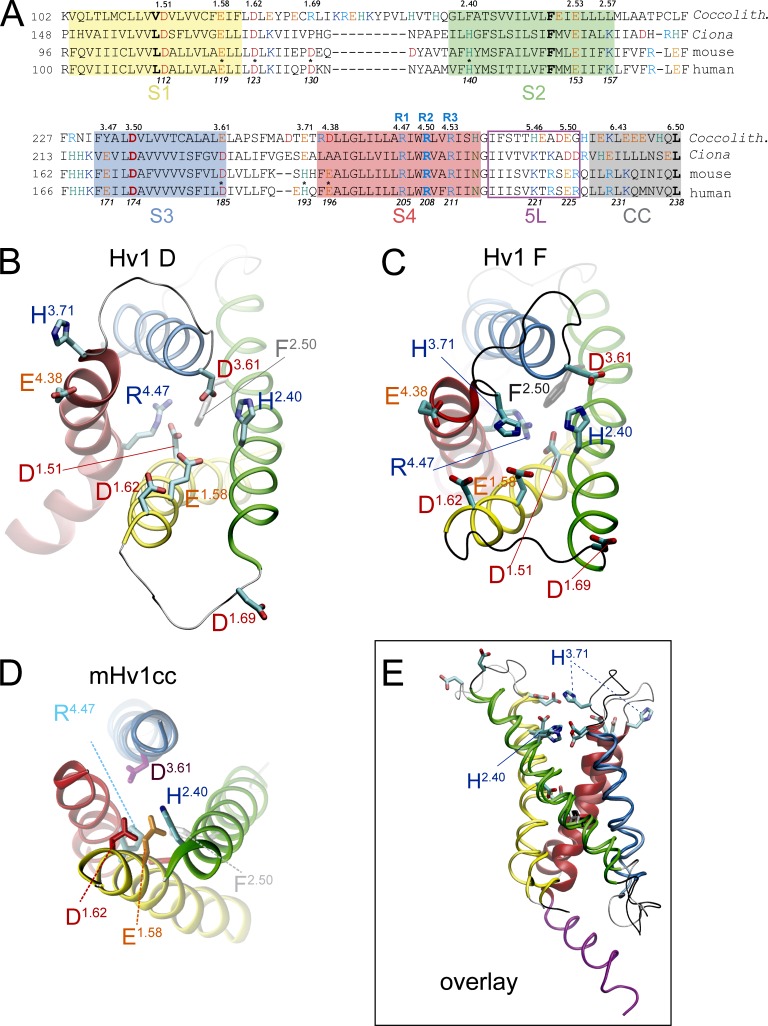
Figure 1.

Model of the extracellular network in putative Hv1 VS domain resting-state model and x-ray structures. (A) Amino acid sequence alignment of the VS domain in C. intestinalis (Ciona), Mus musculus (mouse), C. pelagicus (Coccolith), and Homo sapiens (human) Hv1 proteins. The positions of selected residues in human Hv1 are shown in italics below the sequences, and residue locations in a consensus numbering scheme described previously (Randolph et al., 2016) are shown above the sequences. The positions of R1 (R^4.47), R2 (R^4.50), and R3 (R^4.53) are indicated in blue type. Approximate boundaries of helical segments 1–4 (S1–S4), the C-terminal CC motif, and S4–CC linker helix (5L) are indicated by colored numbers and colored boxes (S1, yellow; S2, green; S3, blue, S4, red; 5L, magenta; CC, gray). Residues are colored type (red, Asp; orange, Glu; aqua, His; blue, Arg or Lys; green, Asn). Asterisks indicate residues that are mutated in this study. (B and C) The positions of candidate extracellular Zn²⁺-coordinating side chains in Hv1 D and Hv1 F are shown in snapshots taken at the beginning (B) or end (C) of respective MD trajectories (Randolph et al., 2016; Fig. 5F). Helical segments are represented as colored ribbons (S1, yellow; S2, green; S3, blue; S4, red; 5L, magenta), loops are shown as silver (Hv1 D) or black (Hv1 F) tubes, and selected residue side chains (labeled) are indicated by colored licorice representations. The distances between C_γ atoms in H140 (H^2.40) and H193 (H^3.71) are 20.32 Å (Hv1 D) and 7.28 Å (Hv1 F). (D) A representation of the mHv1cc x-ray structure (PDB accession no. 3WKV) is shown for comparison to Hv1 D and Hv1 F. (E) A view of Hv1 D (lighter color shades) and Hv1 F (darker color shades) in overlay (structural alignment, MultiSeq STAMP, VMD; Roberts et al., 2006) from within the plane of the membrane illustrates the overall similarity in backbone structure in regions outside the S1–S2 and S3–S4 loops. The S4 and 5L helices are separated by a helical break at G215 (G^4.57).

Although E^1.58 is close to Zn²⁺ in the mHv1cc x-ray structure, single Ser mutations at E115/E^1.58 or D119/D^1.62 do not measurably alter Zn²⁺ sensitivity (Takeshita et al., 2014). Mutation of another phylogenetically conserved acidic side chain (D/E^3.61) that is predicted to be near E^1.58 (Fig. 1 D) alters Zn²⁺ sensitivity in C. intestinalis Hv1. D^1.51 is required for exquisite H⁺ selectivity in Hv1, but the large effects of mutations at this site on G_AQ gating and channel expression (Rada and Leto, 2008; Ramsey et al., 2010; Qiu et al., 2016) could confound the interpretation of D^1.51 mutant effects on Zn²⁺ potency. The differential sensitivity of H⁺ currents and fluorescence signals in Alexa Fluor 488–maleimide–labeled C. intestinalis Hv1 S242C (S^3.70C) mutant channels to extracellular Zn²⁺ may indicate that more than one Hv1 conformational state is capable of binding Zn²⁺ (Qiu et al., 2016), but additional studies are needed to correlate structural changes and fluorescence signal (Randolph et al., 2016) changes with functional readouts such as G_AQ (Randolph et al., 2016) and G_SH (Randolph et al., 2016) gating. Collectively, data presented by Qiu et al. (2016) suggest that E^1.58, H^2.40, and D^3.61 are necessary for Zn²⁺ modulation of H⁺ channel gating in C. intestinalis Hv1. However, putative Zn²⁺-coordinating oxygen atoms in a C. intestinalis Hv1 model structure are 4.2 Å (E^1.58) and 3.7 Å (D^3.61) away from the metal ion (Qiu et al., 2016), which is too far for these ligands to contribute to first solvation shell interactions with Zn²⁺ (Stote and Karplus, 1995; Dudev et al., 2003; Laitaoja et al., 2013). Additional studies are therefore needed to elucidate the atomic structure of the extracellular Zn²⁺ binding sites and to determine how Zn²⁺ occupancy is linked to changes in G_AQ gating.

Materials and methods

Electrophysiology

FlpIn293-TRex cells (Thermo Fisher Scientific) were transfected with cDNAs encoding an N-terminal Venus-tagged human Hv1 fusion protein (Hv1) and subjected to whole-cell voltage clamp electrophysiology 24–48 h later as previously described (Ramsey et al., 2010; Villalba-Galea, 2014; Randolph et al., 2016). Briefly, pipette and bath solutions contained (in mM) ∼80 TMA-MeSO₃, 100 Bis-Tris, and 8 HCl, pH 6.5, at room temperature (∼21°C), 310–320 mOsm. An acidified 1-M stock solution of ZnCl₂ was serially diluted in bath recording solution to the indicated concentrations, and solution changes were accomplished by a gravity-fed superfusion of the bath recording chamber. Cells were superfused for at least 2 min between solution changes to ensure that the superfused [Zn²⁺] had reached steady state. Currents were measured using a model 2400 integrating patch clamp amplifier (A-M Systems) and digitized for storage and analysis using a USB-2551 A/D interface controlled by Lab View software (National Instruments) as described previously (Villalba-Galea, 2014) [REF submitted manuscript]. Signals were low-pass filtered (2 kHz) online and digitally sampled at 20 kHz. Current records were analyzed using Clampfit 9.2 (Molecular Devices), Origin 6.0 (Microcal), and custom software that is available on request (Villalba-Galea, 2014).

Conductance during the applied voltage step (G_STEP) was calculated from the current measured at the end of the voltage step (I_STEP) by G_STEP = I_STEP/V−V_REV, where V_REV is the measured reversal potential of the I_STEP-V relation, as previously described [REF submitted manuscript]. Data were fit to a Boltzmann function of the form

$$G_{STEP}=\frac{\left(G_{STEPmax}\right)-\left(G_{STEPmin}\right)}{1+e^{{\displaystyle \raisebox{1ex}{$V-V_{0.5}$}\!\left/ \!\raisebox{-1ex}{$dx$}\right.}}}+G_{STEPmin},$$ (1)

where V_0.5 is the voltage at which 50% of the maximum G_STEP is reached, dx is a slope factor, and G_STEPmax and G_STEPmin represent the maximum and minimum G_STEP amplitudes, respectively. After subtraction of G_STEPmin, G_STEP data are normalized to the fitted value of G_STEPmax. V_0.5 values in Table 1 represent means ± SEM from n determinations in separate cells; fitted curves and V_0.5 and dx values reported in Figs. 2, 3, 4, and S1 represent Boltzmann fits to the mean data shown in plots.

Table 1. Effects of Hv1 mutations on V_0.5 and Zn²⁺ potency.

Mutations	VSTEP	Fit V0.5	SD	n	Mean τACT @ VSTEP	SEM	n	Mean IC50 @ VSTEP	SEM	pIC50	n	Hill value	SEM
	mV	mV			ms			μM
WT	100	62.4	2.9	5	1,055	262	5	3.8	1.7	−5.44	3	0.81	0.20
H140A (H2.40A)	100	80.1	3.7	3	2,008	1,016	3	38.9	9.4	−4.41	3	0.67	0.07
H193A (H3.71A)	100	58.3	1.7	3	759	261	3	87.8	23.8	−4.06	3	1.04	0.02
H140A-H193A (H2.40A-H3.71A)	100	79.1	5.7	4	1,802	235	4	1,754.4	272.7	−2.76	4	1.57	0.13
E119A (E1.58A)	120	98.5	17.8	4	1,666	553	4	7.55	4.0	−5.16	4	0.80	0.14
E119A-H193A (E1.58A-H3.71A)	100	84.5	2.4	4	1,095	556	4	281.79	79.8	−3.56	3	0.78	0.09
E119H (E1.58H)	100	90.4	2.8	5	625	170	5	0.606	0.06	−6.22	3	1.08	0.40
E119H-H140A (E1.58H-H2.40A)	120	99.1	6.1	6	1,598	356	6	0.60	0.17	−6.23	4	2.09	0.90
E119H-H193A (E1.58H-H3.71A)	100	97.8	2.9	3	1,273	493	3	3.7	1.5	−5.45	3	0.86	0.15
E119H-H140A-H193A (E1.58H-H2.40A-H3.71A)	60	67.9	2.0	4	429	75	4	7.3	3.2	−5.15	3	0.84	0.23
D123H (D1.62H)	80	94.6	1.9	4	857	303	4	4.3	4.9	−5.56	3	0.95	0.20
D123H-H140A (D1.62H-H2.40A)	80	95.8	2.2	5	1,115	254	5	18.0	8.6	−4.78	5	0.58	0.08
D123H-H193A (D1.62H-H3.71A)	80	101.6	1.7	4	760	201	4	36.0	28.1	−4.54	4	1.06	0.14
D130H (D1.69H)	120	87.4	2.0	4	1,788	948	4	3.0	2.9	−5.67	4	0.95	0.35
D130H-H140A (D1.69H-H2.40A)	80	92.0	3.7	5	1,111	413	5	41.5	19.7	−4.42	4	0.58	0.16
D130H-H193A (D1.69H-H3.71A)	120	87.3	2.8	4	1,217	628	4	3.7	2.7	−5.51	3	0.91	0.17
D185H (D3.61H)	120	130.0	4.3	3	886	153	3	4.2	1.5	−5.38	3	0.77	0.15
H140A-D185H (H2.40A-D3.61H)	120	74.2	4.5	4	1,169	386	4	11.2	3.7	−4.96	3	0.81	0.35
D185H-H193A (D3.61H-H3.71A)	80	95.8	7.4	3	1,328	492	3	37.9	35.6	−4.54	3	0.60	0.09
H140A-D185H-H193A (H2.40A-D3.61H-H3.71A)	100	63.9	2.7	3	1,050	277	3	762.3	308.1	−3.15	3	1.05	0.10
E119H-H140A- D185H-H193A (E1.58H-H2.40A-D3.61H-H3.71A)	120	107.4	2.8	3	308	3	3	13.8	8.0	−4.90	3	0.72	0.10
D185A-H193A (D3.61A-H3.71A)	140	104.8	1.8	4	584	113	4	135.1	40.7	−3.88	4	0.62	0.19
E196H (E4.38H)	100	45.0	5.8	4	579	113	4	37.2	46.8	−4.63	4	0.63	0.15
E153A (E2.53A)	40	5.4	2.3	4	306	82	4	241.2	50.1	−3.77	4	0.87	0.16
D112N (D1.51N)	140	120.3	4.8	4	–	–	–	9.5	2.8	−5.03	3	0.76	0.28
D112H (D1.51N)	130	117.4	4.9	3	–	–	–	1,139.3	429.4	−2.96	3	0.56	0.03

Measured V_0.5, τ_ACT, and Zn²⁺ IC₅₀ and pIC₅₀ values for each Hv1 mutant construct in this study are shown. Note that on average, V_STEP = V_0.5 + 12.7 mV (except for E196H, V_STEP >26 mV or ≤3 mV different from V_0.5), indicating that τ_ACT and Zn²⁺ potency (IC₅₀) are determined at similar apparent P_OPEN values. Values for D112N/H were determined from tail current.

Figure 2.

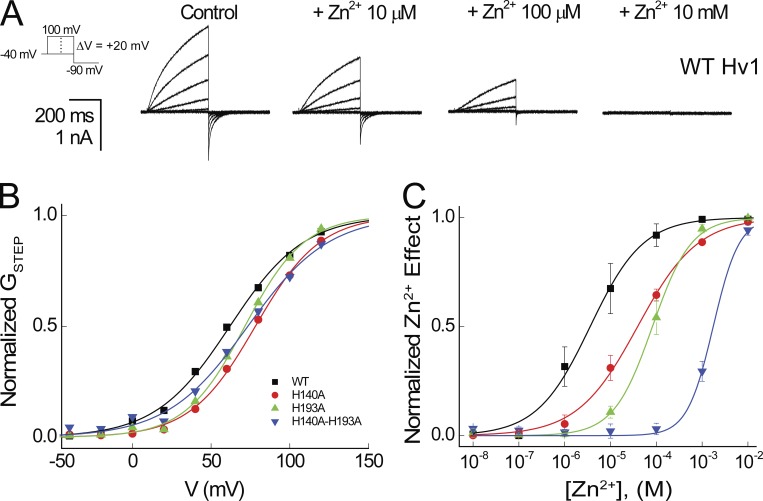
Zn²⁺ sensitivity is altered by mutation of H140/H^2.40 and H193/H^3.71 to Ala. (A) Representative currents elicited by a voltage step protocol (−40 to +100 mV in 20-mV increments followed by a step to −90 mV) indicated in the diagram in the absence (Control) and presence of Zn²⁺ at the indicated concentrations are shown for a cell expressing WT human Hv1. (B) Normalized G_STEP-V relations are shown for the representative cell expressing WT Hv1, H140A, H193A, and H140A-H193A shown above. Colored lines represent fits of the mean data to a Boltzmann function: WT Hv1 (black line, V_0.5 = 61.9 mV, dx = 23.6), H140A (red line, V_0.5 = 78.1 mV, dx = 20.6), H193A (green line, V_0.5 = 71.4 mV, dx = 19.0), and H140A-H193A (blue line, V_0.5 = 73.3 mV, dx = 25.8). (C) Normalized Zn²⁺ concentration responses are shown for the representative cell expressing WT Hv1 (black squares), H140A (red circles), H193A (green triangles), and H140A-H193A (blue triangles) shown above. Data points represent means ± SEM, and colored lines represent fits of the mean data to a Hill function: WT Hv1 (black line, IC₅₀ = 3.6 µM, n_H = 0.8), H140A (red line, IC₅₀ = 39.0 µM, n_H = 0.7), H193A (green line, IC₅₀ = 82.2 µM, n_H = 1.0), and H140A-H193A (blue line, IC₅₀ = 1.743 mM, n_H = 1.5).

Figure 3.

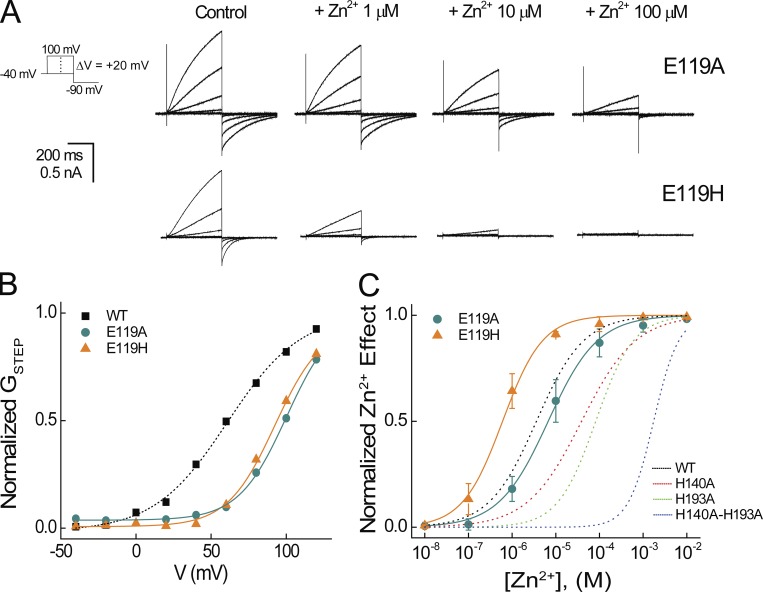
Effects of E119/E^1.58 mutations on potency for Zn²⁺ modulation of Hv1 gating. (A) Representative currents in a cell expressing Hv1 E119A or E119H elicited by the indicated voltage protocol are shown in the absence (Control) or presence of the indicated [Zn²⁺]. (B) Normalized G_STEP-V relations are shown for representative cells expressing WT Hv1 (data from Fig. 2B), E119A, or E119H. Colored lines represent fits of the mean data to a Boltzmann function: WT Hv1 (dashed black line, V_0.5 = 61.9 mV, dx = 23.6), E119A (aqua line, V_0.5 = 98.5 mV, dx = 17.8), and E119H (orange line, V_0.5 = 92.4 mV, dx = 15.8). (C) Normalized Zn²⁺ concentration responses are shown for representative cells expressing E119A or E119H. Colored lines represent fits of the mean data to a Hill function: E119A (solid aqua line, IC₅₀ = 6.7 µM, n_H = 0.8) and E119H (solid orange line, IC₅₀ = 0.60 µM, n_H = 0.9). Dashed lines represent fits to WT Hv1, H140A, H193A, and H140A-H193A data, as shown in Fig. 2. Data points represent means ± SEM.

Figure 4.

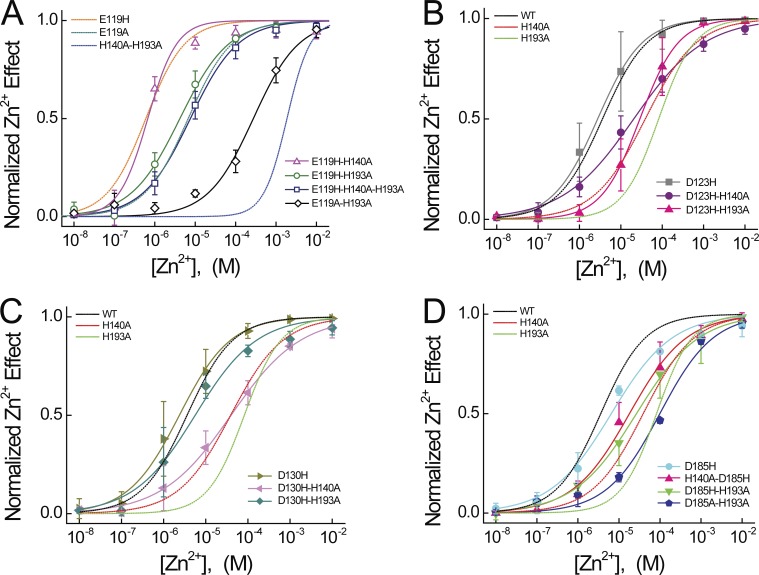
Effects of E119, D123, D130, and D185 mutations on Zn²⁺ potency. (A) Normalized Zn²⁺ concentration responses are shown for E119H-H140A, E119H-H193A, E119H-H140A-H193A, and E119A-H193A. Colored lines represent fits of the mean data to a Hill function: E119H-H140A (solid magenta line, IC₅₀ = 0.67 µM, n_H = 1.2), E119H-H193A (solid green line, IC₅₀ = 4.2 µM, n_H = 0.7), E119H-H140A-H193A (solid navy blue line, IC₅₀ = 7.6 µM, n_H = 0.7), and E119A-H193A (solid black line, IC₅₀ = 273.7 µM, n_H = 0.8). Dashed lines represent fits to Hv1 E119H, E119A, and H140A-H193A, as shown in Fig. 3. (B) Normalized Zn²⁺ concentration responses are shown for D123H, D123H-H140A, and D123H-H193A. Colored lines represent fits of the mean data to a Hill function: D123H (solid gray line, IC₅₀ = 2.5 µM, n_H = 0.8), D123H-H140A (solid purple line, IC₅₀ = 20.5 µM, n_H = 0.5), and D123H-H193A (solid pink line, IC₅₀ = 28.6 µM, n_H = 0.9). In B–D, dashed lines represent fits to WT Hv1, H140A, and H193A data, as shown in Fig. 2. (C) Normalized Zn²⁺ concentration responses are shown for D130H, D130H-H140A, and D130H-H193A. Colored lines represent fits of the mean data to a Hill function: D130H (solid olive line, IC₅₀ = 2.4 µM, n_H = 0.7), D130H-H140A (solid pink line, IC₅₀ = 39.7 µM, n_H = 0.5), and D130H-H193A (solid aqua line, IC₅₀ = 5.6 µM, n_H = 0.6). (D) Normalized Zn²⁺ concentration responses are shown for D185H, H140A-D185H, D185H-H193A, and D185A-H193A. Colored lines represent fits of the mean data to a Hill function: D185H (solid cyan line, IC₅₀ = 6.5 µM, n_H = 0.6), H140A-D185H (solid pink line, IC₅₀ = 18.0 µM, n_H = 0.6), D185H-H193A (solid green line, IC₅₀ = 26.7 µM, n_H = 0.6), and D185A-H193A (solid royal blue line, IC₅₀ = 99.2 µM, n_H = 0.7). Data points represent means ± SEM.

Various mutations tested here have different effects on the position of the G_STEP-V relation; to measure Zn²⁺ effects at similar apparent P_OPEN for all mutants, the value of V_STEP used to activate G_AQ in the presence and absence of Zn²⁺ was varied commensurately with the V_0.5 for that mutant (Fig. S1 and Table 1). The midpoint of Zn²⁺ concentration responses were determined by calculating G_STEP in the absence (G_STEPControl) and presence (G_STEPZn²⁺) of the indicated [Zn²⁺] and normalizing the data to G_STEPControl. Data are plotted as the fractional decrease in G_STEPZn²⁺ [Zn²⁺ effect = 1 − (G_STEPZn²⁺/G_STEPControl)]. Concentration–response curves are fit to a Hill function of the form,

$$Effect=\frac{{[{Zn}^{2+}]}^{n_H}}{I{C}_{50}{}^{n_H}+{[{Zn}^{2+}]}^{n_H} },$$ (2)

where IC₅₀ is the [Zn²⁺] at which 50% effect is reached and n_H is the Hill coefficient. IC₅₀ and n_H values in Table 1 represent means ± SEM from n determinations of Zn²⁺ potency measured in separate cells; fitted curves, IC₅₀ values, and n_H values reported in Figs. 2, 3, 4, and S1 represent Hill fits to the mean data shown in plots. To compare Zn²⁺ effects at equivalent apparent P_OPEN in WT and mutant Hv1 channels, we measured currents elicited by voltage steps to the voltages indicated in Table 1. pIC₅₀ values are calculated as log (IC₅₀); for determination of statistical significance of ΔpIC₅₀s, individual pIC₅₀ values determined from data in n different cells are compared using Student’s unpaired t test with significance set at P < 0.05.

Homology modeling and simulation

The previously described Hv1 D resting-state human Hv1 VS domain model (Randolph et al., 2016) was used as the template for subsequent modeling (Modeller 9.16; Webb and Sali, 2016) to produce a starting structure (Hv1 F) for subsequent MD simulations. We generated 100 models in each of four consecutive rounds of refinement; the best model from each round was selected based on molpdf and DOPE_HR scoring functions (Modeller 9.16) and agreement to experimentally defined structural restraints (Table S1) for continued refinement in the next stage. In the first round of refinement, the x-ray crystal structure of the Hv1 coiled-coil (CC) motif (PDB accession no. 3A2A; Li et al., 2010) was used as a template for residues 226–266 with α-helical restraints applied to S4 residues 197–266. In the second round of refinement, the dopehr_loopmodel feature (Modeller 9.16) was used to remodel the backbone of residues 185–194 and 215–225, and α-helical restraints were applied to 165–184, 216–221, and 223–226. To recapitulate the electrostatic networks determined from whole-cell patch clamp experiments (Ramsey et al., 2010), distance restraints were manually applied to C_α atoms in selected residues (Table S1). The resultant model (preHv1 F) was subjected to a third round of refinement in which dopehr_loopmodel was used to remodel the backbone structure of residues 124–139 (S1–S2 loop) and 184–186 with α-helical restraints applied to residues 132–158 (S2 helix), 165–185 (S3 helix), 216–221 (S4-CC linker helix), and 223–226 (N terminus of CC motif). For the final refinement, dopehr_loopmodel was used to remodel residue ranges 124–139 and 184–186 with α-helical restraints applied to residue ranges 132–158 (S2 helix), 165–184 (S3 helix), 216–221 (S4–CC linker helix), and 223–226 (CC). Additional experimentally derived distance restraints were used to constrain the position of amino acid side chains (Table S1). To focus on the VS domain structure, the C-terminal CC motif structure (residues 227–266) was subsequently removed from the model. In all models, the imidazolium groups of His residues were defined such that N_ε1 is protonated and N_δ1 is deprotonated (HSE).

The final model (Hv1 F) was embedded into a presolvated (12,057 TIP3P waters; Jorgensen et al., 1983), preequilibrated POPC lipid bilayer (163 POPC molecules) in a simulation box of dimensions 88 Å × 92 Å × 93 Å, and POPC lipids occupying overlapping space with protein (any atom–atom distance <0.8 Å or heavy atom–heavy atom distance <1.3 Å) were deleted using the psfgen plugin in VMD 1.9.2 (http://www.ks.uiuc.edu/). The AutoIonize plugin (VMD 1.9.2) was used to add either Na⁺ (34 Na⁺ cations) or Zn²⁺ (34 Zn²⁺ cations; 100 mM) and sufficient Cl⁻ to achieve charge neutrality (Hv1 F + Na⁺ system: 34 Na⁺, 35 Cl⁻, 11,885 waters, 55,718 total atoms; Hv1 F + Zn²⁺ system: 34 Zn²⁺, 69 Cl⁻, 11,954 waters, 55,959 total atoms). A single Zn²⁺ (Hv1 F + Zn²⁺) or Na⁺ (Hv1 F + Na⁺) ion was manually moved into proximity of N_δ1 atoms in H140/H^2.40 and H193/H^3.71 in the Hv1 F model structure to allow for spontaneous metal–protein interactions. Energy minimization was achieved by 5,000 steps of conjugate gradient energy minimization. After successful energy minimization, the POPC lipids were equilibrated around Hv1 F. After a final round of equilibration with harmonic restraints to equilibrate the overall system (harmonic restraints: C_α atoms, 5 kcal/mol/Å), an all-atom MD simulation was performed using the CHARMM36 force field (MacKerell et al., 1998, 2004; Klauda et al., 2010, 2012; Best et al., 2012; Huang et al., 2017; http://mackerell.umaryland.edu/charmm_ff.shtml). To determine equilibration, simulations were assessed for stabilization of RMSD, all energy terms calculated by NAMD 2.9, and periodic boundary condition cell size. Energy minimization and equilibration were simulated using a graphical processing unit (GPU) build of NAMD 2.9. MD simulations were performed using either a GPU build of NAMD 2.9 or a central processing unit build of NAMD 2.10. Tcl forces (NAMD 2.9 or 2.10) were used to keep water out of the membrane during equilibration and MD simulations. Unless otherwise indicated, energy minimization and MD simulations were conducted under standard conditions (temperature, 300°K; pressure, 1 atm; time step, 2 fs; particle mesh Ewald electrostatics grid size, 125 Å × 125 Å × 125 Å; cutoff distance, 12 Å; switching distance, 10 Å; constant temperature control, Langevin dynamics; constant pressure control, Langevin piston).

We then conducted an MD simulation in the presence of Zn²⁺ (Hv1 F + Zn²⁺), but in contrast to our expectations from experimental data (Ramsey et al., 2006), we found that Zn²⁺ does not stably interact with N_δ1 atoms in H140/H^2.40 or H193/H^3.71, resulting in a rapid increase and the distance between these residues during the first 2 ns of the MD trajectory (Fig. 5 F). This result suggests that the geometry of Zn²⁺ coordination by His N_δ1 and carboxylate and/or water oxygen atoms is not sufficiently optimized during model equilibration to yield a stable coordination sphere. To address this limitation, we conducted a second MD simulation (Hv1 F·Zn²⁺) in which harmonic constraints (initially 5 kcal/mol/Å) were applied to bonds between Zn²⁺ and N_δ1 atoms of H140/H^2.40 and H193/H^3.71 to mimic stable first solvation shell interactions between nitrogen atoms and Zn²⁺ (Ramsey et al., 2006). After 50 ns of Hv1 F·Zn²⁺ simulation time, harmonic constraints were decreased to 3 kcal/mol/Å; 20 ns later, harmonic constraints were removed (Fig. 5 G). After removal of N_δ1-Zn²⁺ harmonic constraints, additional MD simulation of the Hv1 F·Zn²⁺ system (130 ns) was conducted identically to the Hv1 F + Zn²⁺ systems. We also introduced H140A or H193A mutations into the Hv1 F model structure and conducted MD simulations (Hv1 F H140A·Zn²⁺ and Hv1 F H193A·Zn²⁺) in which harmonic constraints (5 kcal/mol/Å) were applied to bonds between Zn²⁺ and the N_δ1 atom of H140/H^2.40 (in H193A) or between Zn²⁺ and the N_δ1 atom of H193/H^3.71 (in H140A), respectively (Fig. S4). A third MD simulation (Hv1 F + Na⁺) was conducted in the presence of Na⁺ instead of Zn²⁺ without harmonic constraint between N_δ1 atoms and Na⁺ (Fig. S5 and Tables S2, S3, S4, and S5).

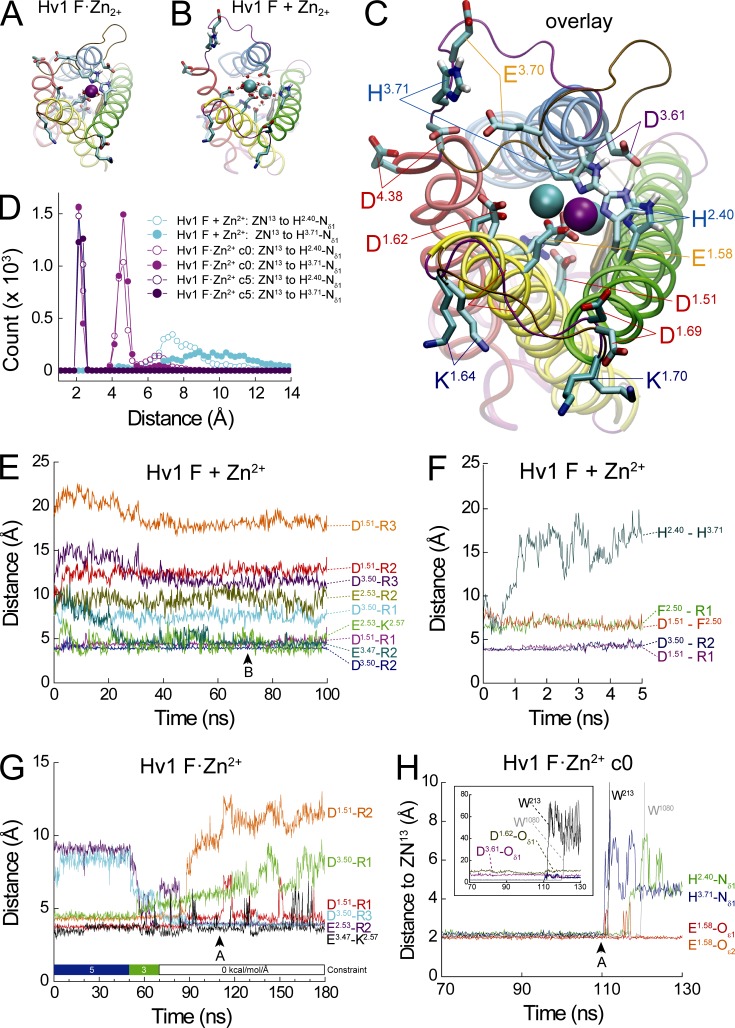
Figure 5.

MD simulations of Zn²⁺-bound (Hv1 F·Zn²⁺) and unbound (Hv1 F + Zn²⁺) Hv1 F model structure. (A–C) Snapshots taken from Hv1 F·Zn²⁺ (A: t = 110 ns; see G and H) and Hv1 F + Zn²⁺ (B: t = 70 ns; see F) MD simulations are shown alone or in overlay (C). Zn²⁺ ions are represented as colored spheres (A: ZN¹³, violet; B: ZN² and ZN¹³, cyan). In A, ZN¹³ is coordinated by H140/H^2.40-N_δ1 and H193/H^3.71-N_δ1, E119/E^1.58-O_ε1 and E119/E^1.58-O_ε2, and two water molecules (W¹⁰⁸⁰ and W²¹³, red/white CPK representations). In B, the first Zn²⁺ solvation shells of ZN² and ZN¹³ are each stably coordinated by six water oxygen atoms that are on average 2.100 ± 0.004 Å and 2.100 ± 0.002 Å (mean ± SD) away from the respective Zn²⁺ ion (Fig. S3); ZN² and ZN¹³ are separated by a mean distance of 6.88 ± 0.68 Å (mean ± SD measured between t = 50–70 ns of Hv1 F + Zn²⁺). In A–C, helices, loop segments, and selected side chains are represented as in Fig. 2; S1–S2 and S3–S4 loop backbones are colored ochre (Hv1 F·Zn²⁺) or magenta (Hv1 F + Zn²⁺). Except for representations of H^2.40 and H^3.71 imidazole groups, hydrogen atoms are omitted for clarity. Water molecules outside the first solvation shells and lipids are not depicted. (D) Distance histograms for ZN¹³ to H^2.40-N_δ1 (open circles) or H^3.71-N_δ1 (filled circles) are calculated for 120 ns (Hv1 F + Zn²⁺, cyan circles; Hv1 F·Zn²⁺ c0, magenta circles) or 50 ns (Hv1 F·Zn²⁺ c5, purple circles) MD trajectories (F and H). First solvation shell interactions (peak at ∼2.1 Å) are not observed in Hv1 F + Zn²⁺, but second shell (∼4.6 Å peak) and third shell (∼6.5 Å peak) are observed in all systems. (E and F) Distances between selected terminal carbon (Arg, Asp, Glu, His, and Phe) or nitrogen (Arg and Lys) atoms during a 100-ns MD simulation of theHv1 F + Zn²⁺ system are plotted in function of simulation time. Atomic distances over the entire (F) or initial 5 ns (G) of the MD trajectory are represented by colored lines. (G) Distances between terminal carbon or nitrogen atoms of selected side chains are plotted in function of Hv1 F·Zn²⁺ MD simulation time. Atomic distances over the entire simulation are represented by colored lines. The Hv1 F·Zn²⁺ system was initially equilibrated with 5 kcal/mol/Å harmonic constraints applied to bonds between ZN¹³ and both H^2.40-N_δ1 and H^3.71-N_δ1 (t = 0–50 ns: c5, blue bar). The harmonic constraints were reduced to 3 kcal/mol/Å for 20 ns (t = 50–70 ns: c3, green bar) and removed for the remaining 110 ns of simulation time (t = 70–180 ns: c0, white bar). (H) Distances between ZN¹³ and selected atoms in its first solvation shell are plotted in function of Hv1 F·Zn²⁺ MD simulation time after relief of harmonic constraints between ZN¹³ and both H^2.40-N_δ1 and H^3.71-N_δ1 (Hv1 F·Zn²⁺_c0, see H). Inset: Atomic distances between ZN¹³ and the indicated atoms with expanded scaling.

Images of atomic structures were rendered using Tachyon ray tracing in VMD 1.9.2 or 1.9.3 (Humphrey et al., 1996; Stone, 1998). Salt bridges (O–N distance cutoff ≤3.2 Å) and H-bonds (donor–acceptor distance ≤3.0 Å; angle cutoff, 20°) in Hv1 F and Hv1 F·Zn²⁺ MD simulation trajectories were identified using plugins in VMD 1.9.2 or 1.9.3 (Humphrey et al., 1996). Model structures were compared after structural alignment using the MultiSeq STAMP structural alignment plugin in VMD 1.9.2 or 1.9.3 (Humphrey et al., 1996; Eargle et al., 2006; Roberts et al., 2006). Atomic distance changes during MD simulation trajectories were measured using VMD 1.9.2 or 1.9.3 (Humphrey et al., 1996) by manually picking selected atoms. To ensure proper treatment of Zn²⁺ by the CHARMM36 force field (MacKerell et al., 1998, 2004; Klauda et al., 2010, 2012; Best et al., 2012), the radial distribution function (RDF) plugin in VMD 1.9.2 (Humphrey et al., 1996) was used to calculate the Zn²⁺ RDF for every frame for the Hv1 F·Zn²⁺ and Hv1 F + Zn²⁺ systems, as illustrated for selected Zn²⁺–ligand interactions during MD simulations (Figs. 6 and S7) that reproduce experimentally observed Zn²⁺ RDFs (Hitoshi et al., 1976; Johansson, 1992; Stote and Karplus, 1995). VMD 1.9.2 (Humphrey et al., 1996) was used to calculate the distance of interactions between Zn²⁺ and H^2.40-N_δ1 or H^3.71-N_δ1 atoms for every frame in Hv1 F·Zn²⁺ and Hv1 F + Zn²⁺ systems. Distance histograms (bin width = 0.25 Å) were constructed using OriginPro 8.1. The Salt Bridges plugin of VMD 1.9.2 (Humphrey et al., 1996) was used to determine the salt bridges for every frame in the Hv1 F·Zn²⁺, Hv1 F + Zn²⁺, and Hv1 F + Na⁺ systems. To determine if changes in salt bridges observed during MD simulations were correlated to distances between Zn²⁺ and H^2.40-N_δ1 or H^3.71-N_δ1, the Pearson’s correlation coefficient (PCC) was calculated using custom Python 2.7 scripts (http://www.python.org). H-bond occupancy was calculated using the VMD 1.9.2 (Humphrey et al., 1996) Hydrogen Bonds plugin over every frame in the Hv1 F·Zn²⁺, Hv1 F + Zn²⁺, and Hv1 F + Na⁺ systems using default settings described previously.

Figure 6.

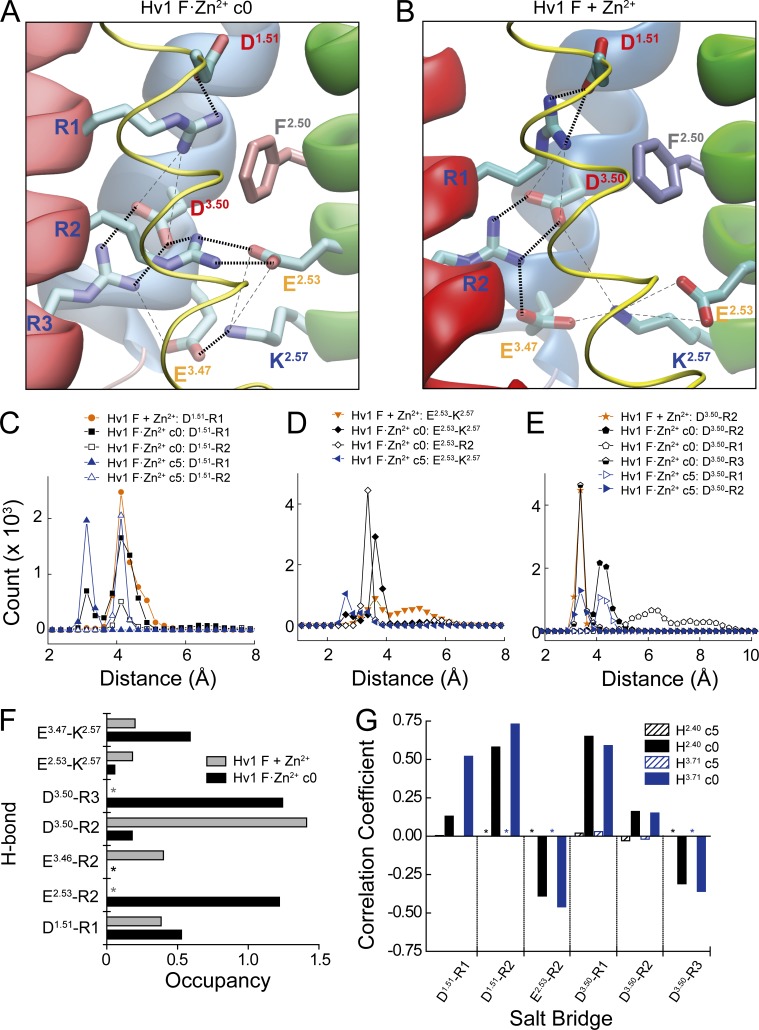
Extracellular Zn²⁺ occupancy is conformationally coupled to reorganization of electrostatic networks that control voltage-dependent gating. (A and B) Coulombic interactions between ionizable side chains in Hv1 F·Zn²⁺ c0 (A, snapshot taken at t = 110 ns; arrowhead A in Fig. 5 H) and Hv1 F + Zn²⁺ (B, snapshot taken at t = 70 ns; arrowhead B in Fig. 5 F) MD simulations are illustrated by dashed lines. Thick black lines represent strong interactions (distance <3.0 Å), and thin gray lines represent weak interactions (distance >3.0 Å). Helices are represented by tubes (S1) or ribbons (S2–S4) colored as in previous figures. In Hv1 F·Zn²⁺ c0 (A), R1–R3 each participate in strong pairwise interactions with acidic side chains (D112/D^1.51-R1, E153/E^2.53-R2, and D174/D^3.50-R3). In Hv1 F + Zn²⁺, R3 and E^2.53 do not participate in a strong Coulombic interaction (B). (C–E) Calculated distances between selected terminal oxygen (Asp, Glu) and nitrogen (Arg) atoms of side chains that participate in salt bridges identified using the VMD 1.9.2 salt bridge plugin are shown for 120 ns (Hv1 F + Zn²⁺ and Hv1 F·Zn²⁺ c0) or 50 ns (Hv1 F·Zn²⁺ c5) MD trajectories (Fig. 5, E–H). Colored symbols and lines represent specific bonds in each MD trajectory. In C–E, distances are binned at 0.25 Å intervals. (F) Relative occupancies of side chain–to–side chain H-bond pairs (distance cutoff <3.0 Å, angle cutoff 20°, VMD 1.9.3 H-bond plugin) calculated during Hv1 F + Zn²⁺ (stippled blue columns) and Hv1 F·Zn²⁺ before (Hv1 F·Zn²⁺ c5, solid black columns) and after (Hv1 F·Zn²⁺ c0, solid gray columns) relief of harmonic constraints. Asterisks indicate that the H-bond does not form during the indicated MD trajectory. (G) PCC calculated for distance changes between atoms in the indicated salt bridges and ZN¹³ to H^2.40-N_δ1 (black columns) or ZN¹³ to H^3.71-N_δ1 (blue columns) during Hv1 F·Zn²⁺ c5 (hashed columns) and Hv1 F·Zn²⁺ c0 (filled columns) MD trajectories. Asterisks indicate that the indicated salt bridge does not form during the MD trajectory. See Table 3 and Fig. S7 D.

Online supplemental material

Fig. S1 shows Zn²⁺ concentration–response curves for E119H at various voltages, scatter plots of pIC₅₀ or τ_ACT values in function of V_0.5, and Zn²⁺ concentration–response curves D112N, D112H, and E153A. Fig. S2 shows a comparison of C. intestinalis Hv1, Hv1 FL, mHv1cc (PDB accession no. 3WKV), and Hv1 D model structures. Fig. S3 shows Zn²⁺ coordination geometries in Hv1 F·Zn²⁺ and Hv1 F + Zn²⁺; water occupancy in Hv1 F·Zn²⁺ c5, Hv1 F·Zn²⁺ c0, and Hv1 F + Zn²⁺; and ZN¹³ to D^1.51-C_δ1 and D^1.51-C_δ1 distance histograms for Hv1 F·Zn²⁺ c5, Hv1 F·Zn²⁺ c0, and Hv1 F + Zn²⁺ MD trajectories. Fig. S4 shows representations and distance plots for Hv1 F·Zn²⁺ H140A and H1933 model MD trajectories. Fig. S5 shows comparisons of Zn²⁺ and Na⁺ positions in snapshots taken from Hv1 F + Zn²⁺ and Hv1 F + Na⁺ MD trajectories and distance plots for selected atoms in the Hv1 F + Na⁺ MD trajectory. Fig. S6 shows plots of distances between selected terminal side-chain atoms in the Hv1 F·Zn²⁺ c0 MD trajectory, snapshots showing differences in Zn²⁺ position before (Hv1 F·Zn²⁺ c5) and after (Hv1 F·Zn²⁺ c0) ZN¹³ dissociation from H^2.40-N_δ1 and H^3.71-N_δ1, and PCC for distance between terminal atoms of selected salt bridge pairs and distance between ZN¹³ and H^2.40-N_δ1 or H^3.71-N_δ1 during Hv1 F·Zn²⁺ c0 and Hv1 F·Zn²⁺ c5 MD trajectories. Fig. S7 shows salt bridge distance plots and amplitude histograms for selected residues in the Hv1 F·Zn²⁺ c0 MD trajectory. Fig. S8 shows distance plots for selected atom pairs during Hv1 F·Zn²⁺ c5, Hv1 F·Zn²⁺ c3, and Hv1 F·Zn²⁺ c0 MD trajectories.

Table S1 shows distance restraints for the last three rounds of Hv1 F model refinement. Table S2 shows mean C_α – C_α distances in Hv1 F + Zn²⁺, Hv1 F·Zn²⁺ c5, Hv1 F·Zn²⁺ c0, and Hv1 F + Na⁺ MD trajectories. Table S3 shows RMSD calculations for Hv1 F + Zn²⁺, Hv1 F·Zn²⁺ c5, Hv1 F·Zn²⁺ c0, and Hv1 F + Na⁺ MD trajectories. Table S4 shows mean salt bridge distances in Hv1 F + Zn²⁺, Hv1 F·Zn²⁺ c5, and Hv1 F·Zn²⁺ c0 MD trajectories. Table S5 shows occupancy of selected H-bonds in Hv1 F + Zn²⁺, Hv1 F·Zn²⁺ c5, Hv1 F·Zn²⁺ c0, and Hv1 F + Na⁺ MD trajectories.

Results

The locations of candidate Zn²⁺-coordinating side chains in a previous resting-state Hv1 model structure (Hv1 D; Randolph et al., 2016) and the mHv1cc crystal structure (Takeshita et al., 2014) are shown in Fig. 1. In Hv1 D, C_γ atoms in H^2.40 and H^3.71 are separated by ∼20 Å (Fig. 1 B), and His nitrogen atoms are therefore too distant to simultaneously substitute for water oxygen atoms in the first solvation shell (distance ≤2.5 Å) of a liganded Zn²⁺ ion (Stote and Karplus, 1995; Dudev et al., 2003; Laitaoja et al., 2013). We remodeled extracellular loops in Hv1 D to generate a new Hv1 resting-state model (Hv1 F) in which the C_γ atoms in H^2.40 and H^3.71 are separated by only 7.3 Å and imidazolium N_δ1 atoms are close enough to potentially participate in first-shell interactions with Zn²⁺ (Fig. 1 C). Except for an added S4–S5 linker helix (5L) in Hv1 F, the positions of backbone atoms in S1–S4 helical segments in Hv1 D and Hv1 F are highly similar, indicating that the remodeling procedure did not substantively alter the overall structure (Fig. 1 E). Over the final 20 ns of Hv1 D and initial 20 ns of Hv1 F + Zn²⁺ MD simulations, the overall backbone RMSD is 4.2 Å, and RMSDs in individual helical segments are 2.5 Å (S1), 3.0 Å (S2), 2.7 Å (S3), and 1.7 Å (S4). Hv1 F thus represents a new candidate Zn²⁺-liganded conformation of the Hv1 VS domain. To identify side chains that are close to the coordinated Zn²⁺ ion, we mutated candidate extracellular residues to Ala or His and measured their effects on the potency of Zn²⁺ to modulate G_AQ gating. If the residue contributes to stabilizing a divalent metal-liganded conformation, Ala mutations should decrease, and His substitutions increase, Zn²⁺ potency. Because mutations may also alter voltage-dependent gating (Ramsey et al., 2010; Randolph et al., 2016), we first determine the midpoint (V_0.5) for voltage-dependent activation of G_AQ from G_STEP-V relations and adjust the voltage used to measure Zn²⁺ sensitivity such that each mutant is tested at similar apparent P_OPEN (Figs. 2 B, 3 B, and S1, and Table 1).

Consistent with a previous study (Ramsey et al., 2006), Zn²⁺ potently modulates G_AQ gating in WT Hv1 (Fig. 2, A and C). H140A and H193A mutations, alone or together, cause only small shifts in V_0.5 (Fig. 2 B), and G_AQ activation kinetics are also similar in WT, H140A, H193A, and H140A-H193A (Table 1), indicating that H^2.40 and H^3.71 do not directly control VS activation gating. As expected (Ramsey et al., 2006), Zn²⁺ potency is markedly decreased in H140A and H193A (H140A: IC₅₀ = 38.9 ± 9.4 µM; H193A: IC₅₀ = 87.8 ± 23.8 µM) compared with WT Hv1 (WT: IC₅₀ = 3.8 ± 1.7 µM), and Zn²⁺ sensitivity in the H140A-H193A double mutant is shifted into the millimolar range (H140A-H193A: IC₅₀ = 1.7 ± 0.3 mM; Fig. 2 C and Table 1). Relative changes in Zn²⁺ potency between selected mutants are reported by ΔpIC₅₀ values: mutations that decrease Zn²⁺ potency yield positive ΔpIC₅₀s (Table 2). For example, H140A-H193A causes a 2.7 log unit decrease in Zn²⁺ potency compared with WT (ΔpIC₅₀ = −2.7; Table 2). E119A also decreases Zn²⁺ potency when engineered into the background of H193A (ΔpIC₅₀ = −0.5; Fig. 4 A and Table 2), consistent with the hypothesis that H^2.40 and E^1.58 might interact to coordinate Zn²⁺ (Takeshita et al., 2014; Qiu et al., 2016). Zn²⁺ potency is also decreased in D112H and E153A, but E119A, D123H, D130H, and E196H do not produce statistically significant changes (Fig. 3 C; Fig. 4, A–D; Fig. S1 E; and Table 2). The inability of His substitutions at D^1.51, D^1.62, D^1.69, and E^4.38 to increase Zn²⁺ sensitivity suggests that the side chains of these residues are likely to be too far away from Zn²⁺ to directly contribute to its coordination sphere. The effect of E153A to reduce Zn²⁺ potency is surprising because this residue is part of the intracellular Coulombic network (ICN) and thus distant the from the extracellular Zn²⁺ coordination site in Hv1 F (E^2.53-C_α and ZN¹³ are separated by 23 Å in Hv1 F; Figs. 1 C and 5 A).

Table 2. Effects of mutations on pIC₅₀ values for Zn²⁺ modulation of Hv1 gating.

Insertion	Mutant 2	Mean pIC50 Mutant 2 (pIC50_2)	Mutant 1	Mean pIC50 Mutant 1 (pIC50_1)	Mean ΔpIC50 = (pIC50_1 - pIC50_2)	t value: t test	p-value: t test
E119H (E1.58H)	E119H-H140A-H193A	−5.15	H140A-H193A	−2.76	2.39	−25.1	1.8 × 10−06*
E119H (E1.58H)	E119H-H140A-D185H-H193A	−4.90	H140A-D185H-H193A	−3.15	1.75	−9.7	0.0005*
E119H (E1.58H)	E119H-H140A	−6.23	H140A	−4.41	1.81	−16.9	7.0 × 10−05*
D130H (D1.69H)	D130H-H193A	−5.51	H193A	−4.06	1.44	−6.6	0.003*
E119H (E1.58H)	E119H-H193A	−5.45	H193A	−4.06	1.38	−10.6	0.0004*
E119H (E1.58H)	E119H	−6.22	WT	−5.44	0.77	−5.7	0.004*
R205H (R1H/ R4.47H)	H140A-D185H-H193A-R205H	−3.68	H140A-D185H-H193A	−3.15	0.54	−4.2	0.013*
D185H (D3.61H)	H140A-D185H	−4.96	H140A	−4.41	0.54	−5.3	0.005*
D185H (D3.61H)	D185H-H193A	−4.61	H193A	−4.06	0.52	−2.0	0.11
D123H (D1.62H)	D123H-H193A	−4.54	H193A	−4.06	0.47	−2.2	0.073
D185H (D3.61H)	H140A-D185H-H193A	−3.15	H140A-H193A	−2.76	0.38	−3.6	0.015*
D123H (D1.62H)	D123H-H140A	−4.78	H140A	−4.41	0.36	−2.5	0.041*
D130H (D1.69H)	D130H	−5.67	WT	−5.44	0.22	−0.80	0.45
D123H (D1.62H)	D123H	−5.56	WT	−5.44	0.11	−0.36	0.73
D130H (D1.69H)	D130H-H140A	−4.42	H140A	−4.41	0.01	−0.05	0.95
D112N (D1.51N)	D112N	−5.03	WT	−5.06	−0.03	0.16	0.87
H193A (H3.71A)	D130H-H193A	−5.51	D130H	−5.67	−0.16	0.52	0.62
D185H (D3.61H)	E119H- H140A-D185H- H193A	−4.90	E119H-H140A-H193A	−5.15	−0.25	1.4	0.21
E119A (E1.58A)	E119A	−5.16	WT	−5.44	−0.28	1.6	0.17
H140A (H2.40A)	H140A-D185H	−4.96	D185H	−5.38	−0.42	3.6	0.021*
E119A (E1.58A)	E119A-H193A	−3.56	H193A	−4.06	−0.50	4.6	0.009*
H193A (H3.71A)	D185H-H193A	−4.54	D185H	−5.38	−0.84	3.5	0.023*
E196H (E4.38H)	E196H	−4.63	WT	−5.06	−0.43	−1.1	0.3
H140A (H2.40A)	H140A	−4.41	WT	−5.44	−1.02	7.0	0.002*
E153A (E2.53A)	E153A	−3.77	WT	−5.06	−1.29	3.3	0.02*
H140A (H2.40A)	H140A-H193A	−2.76	H193A	−4.06	−1.30	24.5	2.1 × 10−6*
H193A (H3.71A)	H193A	−4.06	WT	−5.44	−1.37	9.1	0.0007*
H193A (H3.71A)	H140A-H193A	−2.76	H140A	−4.41	−1.65	24.5	2.1 × 10−6*
H193A (H3.71A)	E119A-H193A	−3.56	E119A	−5.16	−1.60	10.6	0.0001*
D112H (D1.51H)	D112H	−2.96	WT	−5.06	−2.1	10.7	0.001*
H140A-H193A (H2.40A-(H3.71A)	H140A-H193A	−2.76	WT	−5.44	−2.68	23.1	2.7 × 10−6*

Data are ranked by ΔpIC₅₀; positive values indicate an increase in Zn²⁺ potency whereas negative values reflect a loss in potency. Statistically significant (*, P < 0.05 by Student’s unpaired t test) differences in ΔpIC₅₀ values are indicated by asterisks.

Mutations in Hv1 can independently affect Zn²⁺ potency and G_AQ gating. For example, V_0.5 differs by only 11.2 mV in H140A-H193A and E119H-H140A-H193A (Table 1), but Zn²⁺ IC₅₀ increases 2.4-fold (from 1.7 mM in H140A-H193A to 7.3 µM in E119H-H140A-H193A; Tables 1 and 2). The converse is observed in D185H, where V_0.5 shifts positively (+67.6 mV relative to WT Hv1), but Zn²⁺ potency (IC₅₀ = 4.2 µM) is not different from WT (Fig. 4 D and Table 1). In E153A, V_0.5 is shifted −57 mV (Table 1) and Zn²⁺ potency decreases substantially (ΔpIC₅₀ = −1.29; Fig. S1 F and Table 2) compared with WT Hv1 (Tables 1 and 2). A plot of pIC₅₀ versus V_0.5 values for all mutants tested here reveals that the effects of mutations on V_0.5 and pIC₅₀ are poorly correlated (R² = 0.08; Fig. S1 C). The time constant for G_AQ activation is also poorly correlated with V_0.5 (τ_ACT; R² < 0.001; Fig. S1 D). D112H causes V_0.5 to shift +55 mV, consistent with our previous work showing that D^1.51 and D^3.61 likely interact with R1 (R^4.47) to stabilize an activated-state conformation of the Hv1 VS domain (Randolph et al., 2016). However, His substitutions of other extracellular acidic side chains (E^1.58, D^1.62, and D^1.69, but not E^4.38) also shift the G_AQ-V relation positively. The effect of D185H on V_0.5 is also strongly dependent on the mutant background (Table 1). Together, the data suggest that His mutations of extracellular acidic residues may perturb Coulombic interactions that serve to stabilize an activated-state VS conformation. In summary, D^1.51, E^1.58, D^1.62, D^1.69, and D^3.61 mutations produce the same effect on G_AQ gating (positive shift) as extracellular Zn²⁺ (Cherny and DeCoursey, 1999), whereas E^2.53 mutations shift G_AQ gating negatively (Ramsey et al., 2010).

In contrast to E119H, D123H and D130H single mutants do not significantly alter Zn²⁺ potency (Fig. 3 C; Fig. 4, A–C; and Table 2). The lack of effect in D123H is somewhat surprising given that in the mHv1cc x-ray structure, the D^1.62 side chain is close to the putative Zn²⁺ binding site (Fig. 1 D; Takeshita et al., 2014). However, when H^2.40 is neutralized, His substitution at D^1.62 does appear to partially restore Zn²⁺ potency (D123H-H140A vs. H140A: ΔpIC₅₀ = 0.47; Fig. 4 B and Table 2). Consistent with a previous study showing that suggesting that D^1.62 neutralization does not alter Zn²⁺ sensitivity (Takeshita et al., 2014), our data suggest that although this side chain probably does not directly contribute to Zn²⁺ coordination in WT Hv1, it could participate in the coordination sphere in H140A and H193A mutant channels (Fig. S4, B and C). In contrast to D^1.62, introducing His at D^1.69 dramatically increases Zn²⁺ sensitivity the background of H193A (D130H-H193A vs. H193A: ΔpIC₅₀ = 1.44; Fig. 4 C and Table 2). Zn²⁺ is nearly equipotent in D130H-H193A (IC₅₀ = 3.7 ± 2.7 µM; Table 1) and WT Hv1 (IC₅₀ = 3.8 ± 1.7 µM; Table 1). His substitution of D^1.69 suffices for Zn²⁺ coordination in the absence of H^3.71 but not in the absence of H^2.40 (Table 2). We find that several other His mutant combinations do not significantly alter Zn²⁺ potency (Tables 1 and 2), suggesting that the gain-of-function effect depends on local structural features that differ in the various mutant proteins. The observation that WT-like Zn²⁺ potency is measured in E119H-H140A, E119H-H193A, E119H-H140A-H193A, and D130H-H193A suggests that Zn²⁺ coordination spheres are likely to be structurally distinct in various mutant proteins, highlighting a potential limitation of mutagenesis strategies for understanding the mechanism of Zn²⁺ effects in WT Hv1.

Among the mutants tested here, E119H appears to be special in producing a gain-of-function phenotype with respect to Zn²⁺ potency. E119H decreases Zn²⁺ IC₅₀ from 3.8 µM (WT) to 0.6 µM (ΔpIC₅₀ = 0.8; Fig. 3 C and Tables 1 and 2), consistent with studies indicating that this side chain is close to the liganded Zn²⁺ ion (Takeshita et al., 2014; Qiu et al., 2016). The effect of E119H is magnified in the background of H140A and/or H193A mutants; in E119H-H140A-H193A, Zn²⁺ potency increases 2.4 log units (Fig. 4 A and Table 2). Zn²⁺ modulates Hv1 gating more potently in E119H and E119H-H140A mutants than in WT, and five of the six largest positive ΔpIC50s are measured in mutants containing E119H (Fig. 4 A and Table 2). In summary, we find that mutations of both extracellular (E^1.58) and intracellular (E^2.53) acidic residues affect Zn²⁺ potency. One possibility, which we explore later (Fig. 6), is that extracellular Zn²⁺-coordinating and ICN structures are functionally coupled in Hv1, similar to allosteric modulation in G-protein–coupled receptors (GPCRs; Wacker et al., 2017).

To gain insight into the structural basis for Zn²⁺ coordination, we conducted an MD simulation of the Hv1 F model structure. Prior to MD, a Zn²⁺ (ZN¹³) was manually positioned between E^1.58, H^2.40, and H^3.71 to encourage spontaneous coordination by His-N_δ1 and Glu carboxylate oxygen atoms (Figs. 1 C and 5 C). The Hv1 F + Zn²⁺ model is stable during MD simulation (Fig. 5 E), but we do not observe stable first solvation shell coordination of ZN¹³ by E^1.58, H^2.40, or H^3.71 side chains (Fig. 5, D and F). Instead, H^2.40 and H^3.71 migrate to positions that are separated by >15 Å, similar to the Hv1 D template (Figs. 1 B and 5 F). To optimize the geometry of the Zn²⁺ coordination sphere in Hv1 F, we placed harmonic constraints (5 kcal/mol/Å) on ZN¹³ to H140-N_δ1 and ZN¹³ to H193-N_δ1 bonds and ran a separate “constrained” MD simulation (Hv1F·Zn²⁺ c5). As expected, the distance (∼2.1 Å) between ZN¹³ and N_δ1 atoms in H^2.40 and H^3.71 remains stable in Hv1F·Zn²⁺ c5 (Fig. 5, D, G, and H). The Hv1F·Zn²⁺ c5 system also exhibits less backbone dynamic fluctuation than Hv1 F + Zn²⁺, as evidenced by differences in C_α atom RMSD values (Fig. 5 G and Table S3).

As expected for Zn²⁺ in solution (Stote and Karplus, 1995), we observe that ions are persistently coordinated in octahedral geometry during MD simulations. In Hv1F·Zn²⁺ c5, H^2.40-N_δ1, H^3.71-N_δ1, E^1.58-O_ε1, E^1.58-O_ε2, and two water (W²¹³ and W¹⁰⁸⁰) oxygens form a stable His₂-Glu Zn²⁺ coordination sphere, and Zn²⁺ coordination is maintained when His N_δ1-Zn²⁺ harmonic constraints are decreased (3 kcal/mol/Å in Hv1F·Zn²⁺ c3; Fig. 5, D and H; and Fig. S3 A). In the absence of external harmonic constraints (Hv1 F + Zn²⁺), Zn²⁺ ions are octahedrally coordinated by six water oxygens (Figs. 5 B and S3 B). Histograms of Zn²⁺-ligand distances in both Hv1 F + Zn²⁺ and Hv1F·Zn²⁺ simulations show a pattern of peaks that is consistent with the expected RDF for Zn²⁺ interactions (Figs. 5 D and S7 B; Stote and Karplus, 1995). In a control simulation conducted with Na⁺ instead of Zn²⁺ (Hv1 F + Na⁺), we also observe constitutive octahedral coordination of Na⁺ by six waters (Fig. S5). Comparing Hv1 F + Zn²⁺ to Hv1 F + Na⁺ shows that Zn²⁺ and Na⁺ ion stably occupy similar positions in the hydrated extracellular vestibule, but in neither of these systems do we observe proteins atoms engaging in first solvation shell interactions with the metal ion (Fig. S5). Although we observe longer-distance interactions between Zn²⁺ and potential ligand atoms in MD simulations (Figs. 5 D and S7), we do not analyze such interactions further here because the experimental data (Ramsey et al., 2006; Musset et al., 2010; Takeshita et al., 2014; Qiu et al., 2016) indicate that first solvation shell interactions with H^2.40, H^3.71, and E^1.58 are likely to be the main determinants of potent modulation of G_AQ gating by Zn²⁺, potentially explaining why Na⁺ does not substitute for divalent metal cations (Cherny and DeCoursey, 1999; Ramsey et al., 2006; Musset et al., 2010; Takeshita et al., 2014; Qiu et al., 2016). Our results are consistent with MD simulations and x-ray structures of class A GPCRs that are modulated by Na⁺ via interactions with a highly conserved acidic side chain (Katritch et al., 2014).

Importantly, His₂-Glu coordination of ZN¹³ persists for >40 ns after harmonic constraints are removed (Hv1F·Zn²⁺ c0; Fig. 5 H). The lack of spontaneous first solvation shell interactions between Zn²⁺ and H140-N_δ1 or H193-N_δ1 in Hv1 F + Zn²⁺ (Fig. 5 F) is therefore explained by insufficient optimization of ZN¹³ coordination geometry before MD simulation. In contrast to Hv1F·Zn²⁺, the first solvation shells of Zn²⁺ ions are constitutively occupied by six waters in Hv1 F + Zn²⁺ (Fig. S3, A and B). The stability of the His₂-Glu coordination in the absence of externally applied forces directly demonstrates that an empirical force field can be used to simulate Zn²⁺-protein interactions in silico. Furthermore, Zn²⁺ ions consistently interact with protein atoms at discrete distances, consistent with the expectations for the Zn²⁺ RDF (Figs. 5 D, 6 C, and S7; see Materials and methods; Hitoshi et al., 1976; Johansson, 1992; Stote and Karplus, 1995). Although H^2.40-N_δ1 and H^3.71-N_δ1 leave the first solvation shell of ZN¹³ after harmonic constraints are removed, the coordinating nitrogen atoms remain in close proximity (Fig. 5 H) even though local backbone protein structure is thermodynamically stable before and after the ZN¹³ dissociation, as indicated by C_α atom RMSDs at H140 (0.6 Å) and H193 (0.9 Å) calculated for snapshots at t = 70 ns and t = 130 ns of the Hv1F·Zn²⁺ c0 MD trajectory (Fig. 5 H).

Zn²⁺ dissociation from H^2.40 and H^3.71 N_δ1 atoms during Hv1F·Zn²⁺ c0 is correlated with the reorganization of H-bonds and Coulombic interactions (i.e., salt bridges), and changes in protein backbone structure result. Although ZN¹³ remains octahedrally coordinated throughout the Hv1F·Zn²⁺ trajectory, the identities of coordinating ligands change (Fig. 5, G and H). After ∼40 ns, first H^3.71-N_δ1 and later H^2.40-N_δ1 are seen to dissociate from the first solvation shell of ZN¹³; exchange of first-shell waters (W²¹³ and W¹⁰⁸⁰) occurs within 10 ns of the change in H^3.71-N_δ1 coordination (Fig. 5 H). At the end of the Hv1F·Zn²⁺ c0 simulation, ZN¹³ is octahedrally coordinated by E^1.58-O_ε1, E^1.58-O_ε2, and four different water oxygens. ZN¹³ also migrates deeper into the extracellular vestibule, toward D112/D^1.51 and F150/F^2.50 (Fig. S6). The inward migration of Zn²⁺ observed during Hv1F·Zn²⁺ c0 after ZN¹³ dissociates from H^2.40-N_δ1 and H^3.71-N_δ1 is reminiscent of that in a previous study (Qiu et al., 2016). However, D^1.51-O_δ1 does not participate in first-shell interactions with Zn²⁺ in any of our MD simulations. In Hv1 F + Zn²⁺, two hydrated Zn²⁺ ions occupy the extracellular vestibule, close to the location of ZN¹³ in the Hv1F·Zn²⁺ c5 and Hv1F·Zn²⁺ c0 systems (Fig. 5, B and C). In summary, we observe that Zn²⁺ is persistently coordinated in an octahedral geometry by waters and side-chain atoms of E^1.58, H^2.40, and H^3.71.

Comparing structural differences between Hv1F·Zn²⁺ c5, Hv1F·Zn²⁺ c0, and Hv1 F + Zn²⁺ systems provides insight into the possible mechanism by which Zn²⁺ exerts an effect on G_AQ gating. In Hv1F·Zn²⁺ c5, we observe stable Coulombic interactions between terminal atoms of residues that participate in salt bridges, but marked changes in the distances between salt-bridged side chains occur during the Hv1F·Zn²⁺ c3 and Hv1F·Zn²⁺ c0 simulations (Fig. 5 G). For example, the D^3.50-R3 distance decreases by ∼5 Å between Hv1F·Zn²⁺ c0 and c5 (Fig. 5 G), indicating that the salt bridge is substantially strengthened. In contrast, the D^1.51-R2 salt bridge begins to weaken even before ZN¹³ dissociates from H^2.40-N_δ1 and H^3.71-N_δ1 (Fig. 5 G). The D^1.51-R1 interaction remains strong throughout the MD trajectory, resulting in a net movement of the D^1.51-R1 pair away from other residues in the ICN (Fig. 5 G). Together, side chain and backbone movements observed in constrained and unconstrained Hv1F MD simulations indicate that reorganization of Coulombic interactions and Zn²⁺ occupancy of the His₂-Glu coordination sphere exhibit correlated movements that are suggestive of allosteric coupling.

Snapshots taken from Hv1F·Zn²⁺ and Hv1 F + Zn²⁺ also show that although the positions of D^1.51, F^2.50, and other nearby residues are similar, the organization of salt bridges between conserved S4 Arg “gating charge” side chains and acidic “counter charges” in S2 and S3 is characteristically different (Fig. 6, A and B). During the full Hv1F·Zn²⁺ MD simulation, both short- (<4 Å) and longer- (>4 Å) range Coulombic interactions are measured (Fig. 6, C–E; and Fig. S7). For example, stable short-distance salt bridges are observed between E^2.53-R2 and D^3.50-R3 pairs in Hv1F·Zn²⁺ c0 (Fig. 6, A, D, and E; and Fig. S7). However, in Hv1 F + Zn²⁺, E^2.53 and D^3.50 salt bridge partners are swapped, and E^2.53-R3 and D^3.50-R2 now form stable pairs (Fig. 6, B, D, and E). A stable D^1.51-R1 salt bridge is observed in both Hv1F·Zn²⁺ and Hv1 F + Zn²⁺ simulations (Fig. 6, A and B), consistent with experimental data showing that D112 is not necessary for Zn²⁺ interactions (Tables 1 and 2 and Fig. S1 E). Occupancy of H-bonds between donor and acceptor atoms in ICN side chains shows a similar pattern to salt bridges: E^2.53-R2 and D^3.50-R3 H-bonds are common in Hv1F·Zn²⁺ c0 but absent from Hv1 F + Zn²⁺ (Fig. 6 F). In contrast, D^3.50-R2 H-bonds exhibit high occupancy in Hv1 F + Zn²⁺, but are rare in Hv1F·Zn²⁺ c0 (Fig. 6 F). Overall, it appears that the number and strength of interactions between S4 Arg and S2/S3 acidic groups are increased when Zn²⁺ interactions are constrained.

To test the hypothesis that dissociation of ZN¹³ from its coordination site is correlated with changes in ICN salt bridge distances, we measured atomic distances in pairs of interacting groups in the presence (Hv1F·Zn²⁺ c5) and absence (Hv1F·Zn²⁺ c0) of ZN¹³-N_δ1 harmonic constraints. We measured distances between terminal atoms in identified salt-bridged residue pairs and distances between terminal nitrogen and oxygen atoms in each frame of the Hv1F·Zn²⁺ c5 and Hv1F·Zn²⁺ c0 MD trajectories and analyzed covariance and correlations (see Materials and methods). Correlated changes in salt bridge distance and ZN¹³ to H^2.40-N_δ1 or ZN¹³ to H^3.71-N_δ1 distance are reported by PCC for each pair (Table 3). Several interaction pairs exhibit positive or negative PCC values in Hv1F·Zn²⁺ c0 that are not observed in the Hv1F·Zn²⁺ c5 MD simulation (Fig. 6 G, Fig. S6 G, and Table 3). For example, the increase in D^1.51-R2 distance is positively correlated (PCC > 0.5) with an increase in both the ZN¹³ to H^2.40-N_δ1 and ZN¹³ to H^3.71-N_δ1 distances (Fig. 6 G and Table 3), consistent with our observation that the D^1.51-R1 pair moves away from the ICN after ZN¹³ dissociation from H^2.40-N_δ1 and H^3.71-N_δ1 (Fig. 5 G). Also, consistent with previously described changes in ICN architecture (Fig. 6, A–E), we observe a strong negative correlation between the E^2.53-R2 and D^3.50-R3 salt bridge distance and ZN¹³ to H^2.40-N_δ1 and ZN¹³ to H^3.71-N_δ1 distances (Fig. 6 G). In summary, changes in both salt bridge and H-bond networks in the ICN are strongly correlated with changes in Zn²⁺ occupancy of the primary His₂-Glu coordination sphere.

Table 3. Correlation coefficients for distances of Zn²⁺-His-N_δ1 and salt bridge interaction pairs during Hv1 F·Zn²⁺ MD simulations.

Zn2+ interaction	Salt bridge	Constraint	PCC
H140-Nδ1	D112-R205	+	0.004
		−	0.13
H193-Nδ1	D112-R205	+	−0.0002
		−	0.52
H140-Nδ1	D112-R208	+	ND
		−	0.58
H193-Nδ1	D112-R208	+	ND
		−	0.73
H140-Nδ1	E153-R208	+	ND
		−	−0.39
H193-Nδ1	E153-R208	+	ND
		−	−0.46
H140-Nδ1	E153-K157	+	−0.0003
		−	0.32
H193-Nδ1	E153-K157	+	0.003
		−	0.28
H140-Nδ1	E171-K157	+	0.01
		−	0.23
H193-Nδ1	E171-K157	+	−0.01
		−	0.18
H140-Nδ1	E171-R211	+	ND
		−	0.19
H193-Nδ1	E171-R211	+	ND
		−	0.27
H140-Nδ1	E171-K221	+	ND
		−	0.39
H193-Nδ1	E171-K221	+	ND
		−	0.27
H140-Nδ1	D174-R205	+	0.02
		−	0.65
H193-Nδ1	D174-R205	+	0.03
		−	0.59
H140-Nδ1	D174-R208	+	−0.03
		−	0.16
H193-Nδ1	D174-R208	+	−0.02
		−	0.15
H140-Nδ1	D174-R211	+	ND
		−	−0.31
H193-Nδ1	D174-R211	+	ND
		−	−0.36
H140-Nδ1	E225-K221	+	−0.01
		−	0.13
H193-Nδ1	E225-K221	+	0.01
		−	0.04
H140-Nδ1	E225-R226	+	0.01
		−	−0.58
H193-Nδ1	E225-R226	+	0.03
		−	−0.47

PCC calculated for the distance between ZN¹³ and either H140-N_δ1 or H193-N_δ1 and the distance of the indicated salt bridge during Hv1F MD simulations with (c5: +) and without (c0: −) harmonic constraints (5) applied to ZN¹³-H140-N_δ1 and ZN¹³-H193-N_δ1 bonds. ND, not determined due to absence of salt bridge in one of the MD trajectories.

Zn²⁺-dependent changes in Coulombic and H-bond network structures are also reflected by dynamic reorganization of the protein backbone. Changes in the distance between C_α atoms of key side chains are correlated with the relief of ZN¹³-N_δ1 harmonic constraints or dissociation of Zn²⁺ from its coordination site in Hv1F·Zn²⁺ c0 (Fig. S8). For example, D^1.51-C_α moves ∼4 Å closer to D^3.61-C_α and ∼4 Å away from D^3.50 and R2 C_α atoms (Fig. S8 A). D^1.51-C_α also gets ∼6 Å closer to ZN¹³ in Hv1F·Zn²⁺ c0, partly because D^1.51 moves extracellularly (Fig. S8 G) and partly because ZN¹³ moves intracellularly (Fig. S6). Reorganization of the Zn²⁺-liganded E^1.58 side chain also results in an increase in the R1-C_α to E^1.58-C_α distance (Fig. S8 E), whereas the D^1.51-C_α to E^1.58-C_α distance remains almost unchanged in the unconstrained simulations (Fig. S8 A). R1-C_α and R2-C_α atoms move closer to F^2.50-C_α (Fig. S8, E and F), indicating that S4 undergoes a small (2.0–2.5 Å) outward translation during the Hv1F·Zn²⁺ c0 simulation. In contrast to Hv1F·Zn²⁺ c0, C_α atom distances are relatively constant in the Hv1 F + Zn²⁺ (Fig. S8 H) and Hv1 F + Na⁺ control simulations (Fig. S5 G). Changes in backbone structure demonstrate that alterations in the patterns of Coulombic interactions and H-bonds do not merely result from dynamic side-chain switching in structurally similar conformations. Overall, our data demonstrate that side-chain interactions among highly conserved ICN residues are reorganized in a Zn²⁺-dependent fashion. Extracellular Zn²⁺ coordination and voltage-dependent gating therefore appear to be allosterically coupled by long-range conformational rearrangements within the Hv1 VS domain.

Discussion

Here we show that His mutations of extracellular residues in Hv1 are sufficient to confer a gain of function by increasing Zn²⁺ potency effects. Among the mutations tested here, E119H has the most remarkable effect. Substituting His at position E^1.58 lowers the Zn²⁺ IC₅₀ by 0.8 log units, and WT-like Zn²⁺ potency is maintained even in the absence of H^2.40 and H^3.71 (Tables 1 and 2), indicating that E119H fully substitutes for the loss of these His residues. A straightforward interpretation of the experimental data is that an imidazole nitrogen atom in the introduced His side chain of E119H contributes to the Zn²⁺ coordination sphere via a first solvation shell interaction. This interpretation is reinforced by data showing that E119H-H140A-H193A responds to Zn²⁺ equipotently with WT Hv1. The ability of H140A, H193A, and E119H-H140A-H193A mutants (and nonmammalian Hv1 orthologues containing H^3.71 substitutions) argues that the effect of Zn²⁺ to modulate G_AQ gating is unlikely to require a H^2.40- or H^3.71-dependent “metal ion lock” that shifts voltage dependence merely by restricting the mobility of S4.

The relatively potent effects of Zn²⁺ in D123H, D130H, and D185H suggest that additional extracellular acidic side chains can function as Zn²⁺ ligands in Hv1, as previously suggested (Takeshita et al., 2014; Qiu et al., 2016; Fig. 1 and Tables 1 and 2). However, single His mutants at D^1.62, D^1.69, and D^3.61 are insufficient to lower Zn²⁺ IC₅₀ like E119H, and the effects of His substitutions at these positions are strongly sensitive to the mutant background, suggesting that conformational heterogeneity of the Zn²⁺ coordination site structure could account for moderately potent (i.e., IC₅₀ = 10–100 µM) responses in mutant and nonmammalian Hv1 channels (Sasaki et al., 2006; Qiu et al., 2016). The apparent ability of Hv1 to coordinate Zn²⁺ in more than one conformation suggests that unidentified side chains or conformational changes may therefore be necessary for Zn²⁺ coordination in mutant and nonmammalian Hv1 channels, and caution is therefore warranted in the interpretation of neutralizing mutagenesis studies designed to identify metal ion binding sites (Takeshita et al., 2014; Qiu et al., 2016). In contrast to D^1.62, D^1.69, and D^3.61, His substitutions at D^1.51 and E^4.38 decrease Zn²⁺ potency, suggesting that these residues are too distant from the primary coordination site to participate in first solvation shell interactions with the divalent metal cation.

Our experimental data are consistent with previous studies in that they support the hypothesis that H^2.40 and H^3.71 form a stable Zn²⁺ coordination sphere together with E^1.58 (Ramsey et al., 2006; Takeshita et al., 2014; Qiu et al., 2016) and provide valuable spatial constraints for generating a refined structural model of the human Hv1 resting-state VS domain in a Zn²⁺-liganded conformation (Hv1 F). Hv1 F is the only reported Hv1 VS domain structure in which oxygen and nitrogen atoms in E^1.58, H^2.40, and H^3.71 side chains may simultaneously serve as Zn²⁺ ligands (Figs. 1 C, 5 A, S2, and S3 A; Chamberlin et al., 2014; Takeshita et al., 2014; Li et al., 2015; Qiu et al., 2016; Randolph et al., 2016). Optimal Zn²⁺ coordination geometry in Hv1 F is observed after MD simulation in the presence of harmonic constraints between ZN¹³ and H^2.40-N_δ1 and H^3.71-N_δ1 (Fig. 5 G). In the absence of ZN¹³-N_δ1 harmonic constraints, the Hv1 F model structure readily adopts a conformation that is similar to the previously reported (Hv1 D; Randolph et al., 2016) template during MD simulation (Figs. 1 B and 5 F), indicating that Hv1 D represents a reasonable model of the Zn²⁺-free resting-state Hv1 VS domain conformation. The position of R1 is not markedly different in Hv1 D and Hv1 F (Fig. 1 E), demonstrating that the remodeled Hv1 F structure remains compatible with the structural constraints imposed by the resting-state G_SH in R1H mutant Hv1 channels (Randolph et al., 2016).

Additional MD simulations conducted after ZN¹³-N_δ1 harmonic constraints were relieved (Hv1F·Zn²⁺ c0) reveal the structure of a Zn²⁺ coordination site in the Hv1 VS domain in atomic detail. A His₂-Glu coordination sphere is observed during constrained MD simulations (Hv1F·Zn²⁺ c5 and Hv1F·Zn²⁺ c3), and this atomic architecture persists for >40 ns in the absence of externally applied forces (Fig. 5 G). During the Hv1F·Zn²⁺ c0 MD trajectory (t ≈ 110 ns), Zn²⁺ coordination by H^2.40-N_δ1 and H^3.71-N_δ1 is replaced by water oxygen atoms, which is unexpected if the atomic architecture of the first Zn²⁺ solvation shell represents a thermodynamically stable conformation. We speculate that the empirical force field used here may underestimate the strength of electronic interactions between Zn²⁺ and imidazole nitrogen atoms in H140 and H193, allowing water oxygens to substitute for N_δ1 atoms in the first solvation shell during Hv1F·Zn²⁺ c0 and preventing spontaneous coordination during Hv1F + Zn²⁺ MD simulations. Thus, although the backbone structure of the protein near the Zn²⁺ binding site is thermodynamically stable, the atomic architecture of the first Zn²⁺ solvation shell is evidently not, and His₂-Glu coordination of Zn²⁺ does not persist indefinitely under our MD simulation conditions.

The aforementioned result highlights an inherent limitation in the use of an empirical force fields to simulate electronic interactions between Zn²⁺ and His imidazole nitrogen atoms (Stote and Karplus, 1995), and preclude accurate estimation of Zn²⁺-dependent free energy changes or apparent Zn²⁺ affinity from the MD data. On the other hand, Zn²⁺-ligand distance measurements (Figs. 5 D and S7) show that the CHARMM36 force field used here is appropriately parameterized to yield good estimates of coordination spheres involving protein atoms and biologically import transition metal ions, including Zn²⁺, and in this respect our results compare well to results obtained from semiempirical quantum mechanical methods (Yu et al., 2018). As expected for Zn²⁺ in aqueous solution (Burgess, 1978; Stote and Karplus, 1995), we observe that the first Zn²⁺ solvation shell contains six ligand atoms in an octahedral coordination geometry almost exclusively over >400 ns of total MD simulation time. Consistent with the expected Zn²⁺ RDF (Hitoshi et al., 1976; Stote and Karplus, 1995), we also observe second- and third-shell interactions at the expected distances from Zn²⁺ ions (Figs. 5 D and S7 B). In contrast to a previous study in which Zn²⁺ position was constrained using an umbrella sampling protocol (Qiu et al., 2016), we observe that Zn²⁺ interacts exclusively with protein side-chain and water oxygen atoms, suggesting that applying constraints to specific atoms based on experimental data can yield a more refined picture of the metal ion coordination geometry.

The in silico approach used here offers new insights into the structural determinants of Zn²⁺ coordination in Hv1. Although D^1.51 (D160) mutation in C. intestinalis Hv1 alters voltage-dependent fluorescence changes (Qiu et al., 2016), we show that D112N does not decrease and D112H does not increase Zn²⁺ potency (Tables 1 and 2 and Fig. S1 E), and we do not observe first solvation shell interactions between Zn²⁺ and the D^1.51 side chain in any of our MD simulations (Figs. S3 F and S6 F). Hv1 F is distinct from a C. intestinalis Hv1 resting-state model in which Zn²⁺ participates in first solvation shell interactions with a D233/D^3.61 carboxylate oxygen (d = 2.7 Å), the hydroxyl oxygen of S229/S^3.57 (d = 2.1 Å), a backbone oxygen (d = 1.9 Å), and two or three water oxygens at the putative “site 2” (Qiu et al., 2016). Although our experimental and computational results do not support the hypothesis that Zn²⁺ interactions with or near D^1.51 are required for the observed effects on G_AQ gating, we do observe that Zn²⁺ migrates inward toward the previously defined “site 2” after Zn²⁺-N_δ1 harmonic constraints are relieved (Fig. S6, C–E). In our study, Zn²⁺ (or Na⁺) ions that occupy the vicinity of “site 2” (Qiu et al., 2016) do not make first solvation shell interactions with the H^2.40 or H^3.71 side chains that are necessary for micromolar Zn²⁺ sensitivity (Fig. 2; Fig. 3; Fig. S5, A–F; Fig. S6, E and F; and Tables 1 and 2; Ramsey et al., 2006). Additional studies will be needed to determine whether Zn²⁺ affects G_AQ gating by occupying a “deeper” site, closer to D^1.51, in mutants such as E119H-H140A-H193A.

We hypothesize that Hv1F·Zn²⁺ represents a biologically relevant Zn²⁺-liganded Hv1 resting-state structure, and that structural insights revealed in our MD simulations may be generally useful for understanding Zn²⁺ coordination at solvent-accessible sites in metalloproteins. In Hv1F·Zn²⁺ MD simulations, we observe His₂-Glu-(H₂0)₂ (bidentate Glu O_ε1 and O_ε2 in Zn²⁺ first solvation shell) or His₂-Glu-(H₂0)₃ (monodentate Glu O_ε1 or O_ε2 interaction with Zn²⁺) coordination spheres that are distinct from the tetrahedral geometry commonly observed for Zn²⁺ in high resolution in NMR and x-ray structures (Dudev et al., 2003; Laitaoja et al., 2013). Whereas Zn²⁺ binding sites in solution NMR and x-ray structures appear to be relatively inaccessible to bulk solvent (Dudev et al., 2003; Laitaoja et al., 2013), Zn²⁺ and its ligands are located in the highly hydrated VS central crevice in our MD simulations (Fig. S3, C–E). The rapid reversibility and pH_O dependence of Zn²⁺ effects on G_AQ gating strongly argue that the binding site is readily solvent accessible (Cherny and DeCoursey, 1999; Ramsey et al., 2006; Musset et al., 2010; Takeshita et al., 2014; Qiu et al., 2016). Consistent with the solvent accessibility of the coordinated ZN¹³, we directly observe exchange of Zn²⁺ ligands (H^2.40-N_δ1, H^3.71-N_δ1, and W²¹³ and W¹⁰⁸⁰ oxygens) for other water oxygens in the first Zn²⁺ solvation shell in the Hv1F·Zn²⁺ c0 MD trajectory after relieving ZN¹³-N_δ1 harmonic constraints (Fig. 5 H; and Fig. S3, A and B). Together, our experimental and computational data strongly argue that Zn²⁺ interacts with Hv1 residues in a well-hydrated environment, indicating that high apparent affinity and solvent accessibility are not mutually exclusive.

Rather than acting as a cofactor for enzymatic catalysis or to stabilize protein structure, we hypothesize that Zn²⁺ might function analogously to Na⁺ in class A GPCRs, where the metal ion allosterically tunes agonist affinity and effector interactions by biasing receptor conformation (Gerwert et al., 2014; Katritch et al., 2014; Massink et al., 2015). In high-resolution x-ray structures of inactive class A GPCRs (β₂AR, PDB accession no. 4BVN; A₂AR, PDB accession no. 4EIY; δOR, PDB accession no. 4N6H), Na⁺ exhibits trigonal bipyramidal coordination geometry. The spontaneous conversion from octahedral to trigonal bipyramidal coordination seen in microsecond MD simulations of GPCRs (Shang et al., 2014) is consistent with the hypothesis that dynamic changes in the positions of Na⁺ and its coordinating protein atoms are correlated with conformational changes that alter ligand affinity and effector coupling (Gerwert et al., 2014; Katritch et al., 2014). Additional experimental and computational studies are needed to investigate how subtle differences in Zn²⁺ position or coordination geometries influence Hv1 function, and our results provide a foundation for such future work.

Changes in Zn²⁺ occupancy at the primary His₂-Glu coordination site observed during MD simulation are correlated with structural changes in other regions of the Hv1 VS domain, suggesting the existence of structural pathways for long-range allosteric coupling. Prior to the replacement of H^2.40-N_δ1 and H^3.71-N_δ1 in the first solvation shell with water oxygens (at t = 110 ns in Hv1F·Zn²⁺ c0; Fig. 5 H), we find dynamic changes in both side-chain (H-bonds and salt bridges) and backbone structures (Fig. 5, G and H; and Fig. S8, A–G). Additional functional and computational studies will be needed to further examine Zn²⁺-dependent conformational changes and determine the molecular pathways by which energy is transduced in the Hv1 VS domain. Similar to other VS domain proteins (Swartz, 2008; Lacroix et al., 2014), neutralization of ICN residues in Hv1 (i.e., E153A or D174A) causes the position of the G_AQ-V relation in Hv1 to shift negatively (Ramsey et al., 2010; Chamberlin et al., 2014), indicating that these side chains normally help to stabilize a resting-state conformation. Comparing MD simulations of Zn²⁺-liganded and unliganded conformations illustrates that the pattern of Coulombic interactions and H-bonds between highly conserved acidic “counter-charge” residues (E^2.53 and D^3.50) and S4 Arg “gating charge” (R2/R^4.50 and R3/R^4.53) in the ICN are sensitive to Zn²⁺ occupancy (Figs. 6, S6, and S8, and Tables S4 and S5). Although R1 and D^1.51 form a stable pair in both Hv1 F·Zn²⁺ and Hv1 F + Zn²⁺ MD simulations, D^3.50 exhibits an R3/R2 and E^2.53 selectively makes a stable salt bridge with R3 when Zn²⁺ is constrained (Fig. 6). Differences in ICN structure are consistent with the hypothesis that Zn²⁺ occupancy is associated with an overall strengthening of interactions that stabilize a G_AQ-closed, resting-state conformation in Hv1 (Fig. 6 and Tables S4 and S5).

An analysis of coupled salt bridge and Zn²⁺-ligand distance changes in Zn²⁺-constrained (Hv1 F·Zn²⁺ c5) and unconstrained (Hv1 F·Zn²⁺ c0) MD simulations further supports the idea that Zn²⁺ occupancy of the primary extracellular His₂-Glu binding site is allosterically coupled to changes in ICN structure. We therefore hypothesize that MD simulations elaborate a conformational coupling mechanism for Zn²⁺ modulation of G_AQ gating in Hv1. The effect of E^2.53 neutralization to decrease Zn²⁺ potency shows that changes in ICN structure reciprocally alter Zn²⁺ coordination, further supporting the conformational coupling hypothesis. The allosteric interaction between extracellular Zn²⁺ and ICN residues occurs over a long distance: E^2.53-C_α is 19.9 ± 0.3 Å or 24.1 ± 0.6 Å (mean ± SD during 120 ns Hv1 F·Zn²⁺ c0 MD simulation) away from H^2.40-C_α or H^3.71-C_α, respectively. Long-range allosteric coupling provides a structural explanation for a biophysical phenomenon that has remained unexplained since Zn²⁺-dependent modulation of native voltage-gated H⁺ currents was first measured (Thomas and Meech, 1982; Barish and Baud, 1984; Cherny and DeCoursey, 1999). Additional studies are needed to more precisely understand what causes the ICN conformational differences reported here, but we hypothesize that local structural changes at the His₂-Glu site and ICN may be readily propagated to remote sites via relatively subtle changes in side-chain chemistry (i.e., pK_a shifts at ICN side-chain atoms) that alter the strength of H-bonds and Coulombic interactions in an extended electrostatic network. Long-range electrostatic networks have been previously reported for GPCRs (Isom and Dohlman, 2015; Miao et al., 2015). Finally, we speculate that extracellular “gating modifier toxins” may elicit changes in ICN structure to alter VS activation gating in other VS domain proteins (Rogers et al., 1996; Alabi et al., 2007; Milescu et al., 2009; Salari et al., 2016) by a conformational coupling mechanism that is similar to the effect of Zn²⁺ on G_AQ gating in Hv1 postulated here.