Is the gas-phase OH+H₂CO reaction a source of HCO in interstellar cold dark clouds? A kinetic, dynamic and modelling study

Abstract

Chemical kinetics of neutral-neutral gas-phase reactions at ultralow temperatures is a fascinating research subject with important implications on the chemistry of complex organic molecules in the interstellar medium (T∼10-100K). Scarce kinetic information is currently available for this kind of reactions at T<200 K. In this work we use the CRESU (Cinétique de Réaction en Ecoulement Supersonique Uniforme, which means Reaction Kinetics in a Uniform Supersonic Flow) technique to measure for the first time the rate coefficients (k) of the gas-phase OH+H₂CO reaction between 22 and 107 K. k values greatly increase from 2.1×10^-11 cm³ s^-1 at 107 K to 1.2×10^-10 cm³ s^-1 at 22 K. This is also confirmed by quasi-classical trajectories (QCT) at collision energies down to 0.1 meV performed using a new full dimension and ab initio potential energy surface, recently developed which generates highly accurate potential and includes long range dipole-dipole interactions. QCT calculations indicate that at low temperatures HCO is the exclusive product for the OH+H₂CO reaction. In order to revisit the chemistry of HCO in cold dense clouds, k is reasonably extrapolated from the experimental results at 10K (2.6×10^-10 cm³ s^-1). The modeled abundances of HCO are in agreement with the observations in cold dark clouds for an evolving time of 10⁵-10⁶ yrs. The different sources of production of HCO are presented and the uncertainties in the chemical networks discussed. This reaction can be expected to be a competitive process in the chemistry of prestellar cores. The present reaction is shown to account for a few percent of the total HCO production rate. Extensions to photodissociation regions and diffuse clouds environments are also commented.

1. Introduction

Chemistry in dense interstellar molecular clouds occurs typically at 10 K, a low temperature which can be considered to be at the high edge of ultracold chemistry. The formation of Complex Organic Molecules (COMs) in space is a subject of great interest nowadays since these simple molecules are considered to be precursors of biological molecules, and it is important to determine their origin and evolution from dense clouds to protoplanetary disks. Most gas-phase neutral-neutral reactions forming these molecules have barriers and thus require an activation energy which is not available at temperatures of 10 K. Thus, these COMs have been long assumed to be formed onto interstellar ices and then released to gas phase.

Formaldehyde (H₂CO) was the first organic polyatomic molecule observed in the interstellar medium (henceforth ISM) by Snyder et al. in 1969 (Snyder et al. 1969). Since then, it has been detected in a variety of astrophysical environments with different temperature and density conditions, such as diffuse clouds (Liszt et al. 2006), starless cores (Bacmann et al. 2003), protostellar envelopes (Maret et al. 2004), and dense photodissociation regions, PDRs (e.g., (Guzmán et al. 2011), (Leurini et al. 2010)). On cold prestellar cores, the observations of H₂CO led to relative abundances X_H2CO (=N_H2CO/N_H2) in the range (0.5-9)×10^-10 (Bacmann et al. 2003), while in the Horsehead nebula PDR, X_H2CO ~(2-3)×10^-10 (Guzmán et al. 2011). Currently, the abundances of H₂CO modeled by considering pure gas-phase chemistry are well-interpreted for dense cores, while in PDRs the inclusion of surface chemistry and the subsequent photodesorption is needed (Guzmán et al. 2011). Guzmán et al. modeled that the destruction processes of H₂CO in the Horsehead PDR are dominated by photodissociation, while in the dense core they are controlled by reactions with ions (Guzmán et al. 2011). In cold molecular clouds and prestellar cores, where photodissociation is less important, the reaction of H₂CO with radical species, such as hydroxyl (OH) radicals, could play a significant role in the removal of formaldehyde and also in the formation of formyl (HCO) radicals in the gas phase via the exothermic reaction (1):

$${\text{H}}_2\text{CO}+\text{OH}\to \text{HCO}+{\text{H}}_2\text{O}\Delta {\text{H}}_{298}=\text{-}127\text{KJ}{\text{mol}}^{\text{-}1}$$ (1a)

Other thermodynamically accessible channels are:

$${\text{H}}_2\text{CO}+\text{OH}\to \text{HC(O)OH}+\text{H}\Delta {\text{H}}_{298}=\text{-}89\text{KJ}{\text{mol}}^{\text{-}1}$$ (1b)

$${\text{H}}_2\text{CO}+\text{OH}\to \text{CO}+{\text{H}}_2\text{O}+\text{H}\Delta {\text{H}}_{298}=\text{-}63\text{KJ}{\text{mol}}^{\text{-}1}$$ (1c)

Sivakumaran et al. (Sivakumaran et al. 2003) measured the yield of H atoms from reactions (1b) and (1c) to be very low (<4%) at room temperature, implying that HCO formation is the major reaction pathway at this temperature. Although no experimental evidence for the formation of HC(O)OH have been reported, D’Anna et al. (D ’anna et al. 2003) concluded that the addition pathway will be insignificant even at high temperatures, because the barrier for the OH-addition channel (1b) was calculated to be 33.6 kJ mol⁻¹ above that of the H-abstraction reaction. In addition, its pre-exponential factor was found to be 8 times smaller than for reaction (1a). Channel 1c is a high T channel and most likely from “hot” HCO from channel (1a), so it is unlikely as T is lowered. Anticipating what will be described further in the paper, in the present work it has been calculated that channel (1a) is the main reaction pathway at the investigated temperatures (see Section 3). Channel (1c) is considered within the (1a) since it corresponds to very excited HCO which fragmentizes. This channel has been quantified to be less than 3% of the total reaction probability. Channel (1b) has a higher saddle point and can be disregarded at T below room temperature.

HCO is an interesting radical in astrochemistry because it is an important candidate precursor for the formation of O-bearing COMs and prebiotic molecules. For example it is assumed to be at the onset of the formation of glycolaldehyde, CH₂OHCHO, upon ice surfaces via HCO dimerization followed by successive hydrogenations (Woods et al. 2013). It is also a tracer of regions where an active photochemistry induced by far ultraviolet radiation prevails (Gerin et al. 2009). Astronomical observations indicate that HCO is a widespread radical in cold dark clouds (Jiménez-Serra et al. 2004), (Cernicharo et al. 2012), (Bacmann & Faure 2016), where it is present with fractional abundances relative to H₂ of (1.3-17)×10^-11 (see Table 1), while at the edges of molecular clouds, where the gas is exposed to ultraviolet radiation, its abundance is greatly enhanced (Gerin et al. 2009). In the Horsehead Nebula, the abundance of HCO relative to H₂ varies between below 7×10^-11 in the dense shielded core to ∼(1-2)×10^-9 in the PDR (Guzmán et al. 2011), (Gerin et al. 2009). The source of HCO radicals, however, still remains unclear (see e.g., (Gerin et al. 2009), (Bacmann & Faure 2016), (Agúndez et al. 2015)), with various potentially important formation routes, both on the surfaces of dust grains and in the gas phase. In prestellar cores, the role of the reaction between OH and H₂CO in the formation of HCO has been recently investigated (Bacmann & Faure 2016). These authors modeled the HCO abundance employing a rate coefficient for reaction (1a) of 10^-11 cm³ s^-1 which was obtained from experimental literature measurements at 230 K, since no measurements at lower temperatures were available. In both PDRs and cold dark clouds, the reaction between atomic oxygen and CH₂ radicals has been invoked as one potential major route to HCO (Gerin et al. 2009), (Agúndez et al. 2015),

$$\text{O}+{\text{CH}}_2\to \text{HCO}+\text{H},$$ (2)

Other important synthetic pathways to HCO are reactions involving ions, such as the reaction of O and C₂H₄⁺ (reaction 3) or the dissociative recombination of H₂COH⁺ (Bacmann & Faure 2016), (Agúndez et al. 2015):

$$\text{O}+{\text{C}}_2{\text{H}}_4^{+}\to \text{HCO}+{\text{CH}}_3^{+}$$ (3)

$${\text{H}}_2{\text{COH}}^{+}+{\text{e}}^{\text{-}}\to \text{HCO}+\text{H}+\text{H}$$ (4)

Table 1.

Observed Abundances of HCO (Relative to H₂) and H₂CO (Relative to HCO) in Cold Dark Clouds

Source	NHCO/NH2	NH2CO/NHCO	References
B1-b	1.8×10-11	22	(Cernicharo et al. 2012)(Marcelino et al. 2005)
Lupus-1A	1.7×10-10		(Agúndez et al. 2015)
L483	9.0×10-11	19	(Agúndez et al. 2015) (Tafalla et al. 2000)
L1495B	5.6×10-11		(Agúndez et al. 2015)
L1521F	1.3×10-11		(Agúndez et al. 2015)
Serpens South 1a	8.0×10-11		(Agúndez et al. 2015)
L1389	2.0×10-11		(Agúndez et al. 2015)
L1172	1.1×10-10		(Agúndez et al. 2015)
L1251A	1.2×10-10		(Agúndez et al. 2015)
L1512	8.1×10-11	17	(Agúndez et al. 2015) (Young et al. 2004)
L1689B	9.3×10-11	10	(Bacmann et al. 2003)(Bacmann & Faure 2016)
L429	2.1×10-11	9	(Bacmann et al. 2003)(Bacmann & Faure 2016)
L1709A	3.9×10-11	10	(Bacmann et al. 2003)(Bacmann & Faure 2016)
L1517B		7	(Bacmann & Faure 2016)

The kinetic behavior of these reactions, i.e., their rate coefficients and products distribution, is not fully known at low temperatures, making it difficult to precisely evaluate their role in the formation of HCO.

In astrochemical models the T-dependence of k is commonly described by a three-parameter expression:

$$k(T)=\alpha {(T/300\text{K})}^{\beta }\text{exp}(\text{-}\gamma /T){\text{cm}}^3{\text{molecule}}^{\text{-}1}{\text{s}}^{\text{-}1}$$ (5)

Recent experimental work at temperatures in the range 23-140 K have demonstrated that the rate coefficient for the reaction of methanol with the OH radical increases enormously at temperatures below 200 K (Shannon et al. 2013), (Antiñolo et al. 2016). Similar results have also been found for other OH-reactions with COMs, such as acetone, methyl ethyl ketone or ethanol (Shannon et al. 2013), (Shannon et al. 2010) and methyl formate (Jiménez et al. 2016). The surprise for the scientific community is that all these reactions present a reaction barrier, and according to the usual transition state theory (TST), the reaction rate coefficient should decrease when lowering the temperature. These results have enormous implications because they can open new chemical routes in the ISM networks. From a theoretical point of view, it is important to understand the reaction mechanism: how well do we understand the quantum effects? The observed increase in the OH-reactivity at ultra-low temperatures has been theoretically interpreted for methanol by the formation of a long-lived hydrogen-bonded complex which can undergo quantum-mechanical tunneling to form products (Shannon et al. 2013). Even though the temperature dependence of the calculated rate coefficients using the Master Equation Solver for Multi Energy-well Reactions (MESMER) equation is qualitatively correct, the values of k do not match the experimental ones. Thus, tunneling corrections have been included in order to reproduce the experimental rate coefficients. But some controversy remains concerning the possible presence of methanol dimers which may affect the experimental conclusions for the rate coefficient determination for the OH + CH₃OH reaction (Siebrand et al. 2016). Further theoretical and experimental investigations are presently in progress involving our laboratories and our colleagues in Leeds.

For the title reaction, several studies of the stationary ab initio points have been performed using different levels of theory (D ’anna et al. 2003), (Alvarez-Idaboy et al. 2001), (Xu et al. 2006), (Zhao et al. 2007), (Böhnhardt et al. 2010), (Akbar Ali & Barker 2015), showing a small activation barrier either negative or positive (-1 to + 2 kcal/mol) for channel (1a). The reaction rate coefficients, k₁(T), were obtained using TST (D ’anna et al. 2003), (Alvarez-Idaboy et al. 2001), (Xu et al. 2006), (Zhao et al. 2007), (Böhnhardt et al. 2010), (Akbar Ali & Barker 2015), leading to satisfactory results in the temperature range studied (T> 200 K) when tunneling is added. At the lower temperatures studied in this work, it is necessary to perform precise dynamical calculations on the reactive collision, with the proper description of long range interactions and energetics, especially the stationary points of the potential energy surface (PES). Ab initio molecular dynamics methods are therefore prohibitive, not only because of the computing time of a single point, but also because the number of points on each individual trajectory is very high. Thus an analytic fit is required to study the collision dynamics under these conditions.

For the astrochemical community it is crucial to determine the gas phase rate coefficients at low temperatures for many reactions that were until now neglected, but may have an important impact in understanding the formation of COMs in space. Up to now, kinetic parameters for the OH+H₂CO reaction have been reported between 202 and 1670 K, temperatures of interest in the fields of atmospheric chemistry and combustion chemistry (Atkinson et al. 2006) (and references therein). Compilation of these studies show that the rate coefficient k₁(T) has a positive temperature dependence in the 300-1670 K range. More interestingly, a minimum in the rate coefficient seems to be reached between 200 K and 300 K, as in the reactions of OH with aforementioned COMs.

In the present work we have gathered unique abilities of four research groups in order to explore experimentally and theoretically the kinetics and dynamics of the gas-phase OH + H₂CO reaction at very low temperature and analyze its impact on interstellar chemistry. To match these objectives we have (i) measured the rate coefficient at temperatures of the ISM (22-107 K), using the CRESU technique; (ii) developed detailed calculations to gain more knowledge on the dynamical behavior, going beyond the TSTs or analogous, and determined the reactive cross section between 0.1 and 1000 meV, using a high quality potential energy surface to estimate the rate coefficient in the temperature range of the experiment and (iii) evaluated the impact of the obtained temperature dependence of k₁(T) on the formation of HCO in cold interstellar clouds.

The present work constitutes the very first investigation of the kinetics and dynamics of H₂CO with a radical (here OH) at temperatures relevant to cold objects of the ISM.

2. Methods

2.1. Experiments

The CRESU technique and the experimental setup employed have been previously described elsewhere (Antiñolo et al. 2016), (Jiménez et al. 2016), (Jiménez et al. 2015), and then only a brief overview will be given below. A set of five Laval nozzles were used to get the jet temperatures between 22 and 107 K and characterization of the obtained flows was discussed elsewhere (Canosa et al. 2016). The adiabatic gas expansion through the Laval nozzle from the reservoir to the reaction chamber provokes the cooling of the gas and forms a uniform jet in temperature and total gas density over several tens of cm, i.e. over several hundreds of μs hydrodynamic time, t_hydro (supporting information (SI) Appendix, Table S1). OH radicals were generated in the gas jet by pulsed laser photolysis of gaseous H₂O₂ at 248 nm. The time evolution of OH radicals in the presence and absence of H₂CO was monitored by laser induced fluorescence (LIF) ca. 310 nm, which was collected by a filtered photomultiplier tube. The excitation wavelength (282 nm) was delivered from a frequency-doubled dye laser pumped by the second harmonic of a Nd-YAG laser. The analysis of the exponential decays yields the pseudo-first order rate coefficients, k’, which is linearly related to [H₂CO] concentration under pseudo-first order conditions (SI Appendix, Kinetic analysis). Varying the mass flow rate of a diluted mixture containing a well-known quantity of H₂CO and maintaining the OH-precursor concentration constant, k₁(T) was obtained from the slope of the plot of k’ (or k’-k₀) versus [H₂CO] (SI Appendix, Kinetic analysis).

2.2. Quasi-classical trajectory (QCT) simulations

A full dimensional analytical potential energy surface has been developed to treat the reaction dynamics at temperatures below 100 K, as described in a recent publication (Zanchet et al. 2017). The intrinsic reaction coordinate (IRC) diagram shown in Fig. 1 shows the quality of the analytical fit and describes the energy diagram of the reaction. QCT calculations have been performed using an extension of the code miQCT applied to N atoms (Dorta-Urra et al. 2015). The Hamilton equations are integrated using a step adaptive Adams-Bashforth-Moulton Predictor-corrector method (Shampine & Gordon 1975), using the cartesian coordinates of the position vectors of all atoms. The total integral cross section, σ_vj(E), is calculated according to the following equation (Karplus et al. 1965):

$${\sigma }_{\text{vj}}(E)=\pi b_{\text{max}}^2{\text{P}}_{\text{r}}(E)$$ (6)

where b_max is the maximum impact parameter, corresponding to the maximum distance at which trajectories are efficiently deviated to form products and P_r(E) is the reaction probability given by:

$${\text{P}}_{\text{r}}(E)=N_{\text{r}}(E)/N_{\text{tot}}(E)$$ (7)

N_tot(E) is the maximum number of trajectories at collision energy E with b<b_max, while N_r(E) is the number of reactive trajectories leading to products.

Fig. 1.

Intrinsic reaction coordinate (IRC) for the ab initio, RFF and RFF+MB PES’s. The geometries of reactants and products wells and the saddle point are also displayed.

A Monte Carlo sampling of initial conditions is done for each reagent independently (OH and H₂CO). To include the ZPE, an adiabatic switching method is performed (Grozdanov & Sovolev 1982), (Johnson 1987), (Qu & Bowman 2016). In this method, a random selection of initial conditions is done according to analytical normal modes, and then the harmonic potential is adiabatically switched to the real one. Since the energy spreading is rather high, we select a particular trajectory with the closest energy to the anharmonic ground state eigenvalue of each fragment, which is propagated for 100000 steps. In this case, OH and H₂CO are initially set at zero angular momentum, by using the method of Nyman and coworkers (Nyman et al. 1990). Once the internal vibrational distribution is set, the relative orientation of the two fragments is randomly selected. The impact parameter is randomly selected up to a maximum distance b⁰_max at which trajectories are efficiently deviated. This maximum value is given by the capture model (Levine & Bernstein 2001):

$$b_{\text{max}}^{\mathit{0}}=3^{1/2}{(A/2E)}^{1/3},$$ (8)

The initial distance between the two reagents is set to 120 a.u. These long distances are required for the low energies considered here.

In the present system, the long range interaction between the permanent dipole moments (d_X, X=OH and H₂CO) varies as:

$$V(R\to \infty )=\frac{-A}{R^3}$$ (9)

with A= 4 d_OH d_H2CO.

Two different strategies were followed to analyze the collision dynamics:

1) First, the individual cross section for H₂CO and OH in the ground vibrational and rotational states is calculated in the microcanonical ensemble according to Eq. (6). This is done using a grid of collision energies from 0.1 meV to 1000 meV. For each translational energies 10⁵ trajectories were run. Finally the state-dependent rate, k_v=0,j=0(T), is obtained by numerical integration over a Boltzmann distribution. The final rate coefficient k^e_v=0,j=0(T) is obtained multiplying this k_v=0,j=0(T) by the electronic partition function, q_e, described in the Results Section.

2) Second, the thermal rate coefficients, k(T), are obtained from Eq. (10) running 10⁶ trajectories for each temperature in the macrocanonical ensemble, defining initial conditions for thermal rotational distributions of the two reagents:

$$k(T)=q_e{\left(\frac{8kT}{\pi \mu }\right)}^{\frac{1}{2}}\pi b_{\mathit{max}}^2{P}_r(T)$$ (10)

where µ is the reduced mass of the OH + H₂CO system.

2.3. Chemical ISM model

To evaluate the hypothesis that H₂CO could be a precursor of HCO radicals in cold interstellar clouds, we have run a chemical model of a cold dark cloud in which we adopt typical parameters, i.e., a kinetic temperature of 10 K, a volume density of H nuclei of 2×10⁴ cm^-3, a visual extinction of 30 mag, a cosmic-ray ionization rate of H₂ of 1.3×10^-17 s^-1, and the so-called "low-metal" elemental abundances (Agúndez & Wakelam 2013). We have run models using two chemical networks to have an idea of the robustness of the results. Concretely, we have used the network kida.uva.2014 from the KIDA database (Wakelam et al. 2015) and the rate2012 network from the UMIST database (McElroy et al. 2013). In both chemical networks we have implemented the reaction H₂CO + OH → HCO + H₂O with the extrapolated rate coefficient at 10 K obtained in this work (see Section 3.1).

3. Results and Discussion

3.1. Gas-phase kinetics of the OH+H₂CO reaction between 22 and 107 K

The measured rate coefficients k₁(T) have been compiled in Table 2. They have been determined at ca. 22 K using three different Laval nozzles with total He densities ranging from 3.37×10¹⁶ to 1.67×10¹⁷ cm^-3. At ca. 45 K, two Laval nozzles were employed for different gas densities, 6.90×10¹⁵ to 1.02×10¹⁷ cm^-3 (N₂ and N₂/He respectively). All the physical conditions for all Laval nozzles employed are listed in Table S1 of the supporting information (SI) Appendix. In Table 2, k₁(T=22 K) and k₁(T=45 K) are presented at each gas density. As can be seen no pressure dependence of k₁(T=22 K) was observed in the investigated gas density range implying that reaction (1) at these temperatures is either a bimolecular reaction or a three-body process already in the high pressure limit at the lowest gas density. At 45 K a decrease of 27% is observed in k₁ when the gas density is varied by more than one order of magnitude. Within the experimental uncertainties, this decrease is not expected to be originated by a pressure effect. Such an effect on k₁(T) should be more noticeable at even higher temperatures for which the rate coefficient is lower and then separates even more from the high pressure limit of a fall-off curve. In other words, the high-pressure limit would be reached at higher total pressures. At the highest temperatures investigated in this work (107 K), it can be seen that the rate coefficient is similar to that at 89 K (see Table 2) whereas the total density (1.8×10¹⁷ cm^-3) is 3.6 times higher. If the process was termolecular one should expect that k₁ increases with gas density and when the temperature is lowered. Hence we should have found a significant higher value at 89 K than at 107 K, while it was found, within the experimental uncertainties, k₁(89 K)≅k₁(107 K). For all these reasons, it can be argued that reaction (1) is essentially bimolecular in the temperature range of the present work. As shown in Table 2, an increase in k₁(T) is observed when lowering T.

Table 2.

Rate Coefficients for the Gas-Phase Reaction between OH Radical and H₂CO as a Function of Gas Density and Temperature ^a.

T / K	n / 1016 cm-3	k1(T) b / 10-11 cm3 s-1	k1(T) / 10-11 cm3 s-1
21.1 ± 0.6	3.37 ± 0.15	9.1 ± 1.1	10.1 ± 1.0 c
		10.0 ± 1.1
		12.9 ± 1.6
21.7 ± 1.4	16.65 ± 1.61	12.3 ± 1.3	12.3 ± 1.2 c
		12.1 ± 1.6
22.5 ± 0.7	7.43 ± 0.32	11.8 ± 1.5	12.0 ± 1.2 c
		12.0 ± 1.3
36.2 ± 1.2	17.73 ± 0.86		8.62 ± 0.86
45.6 ± 1.4	10.19 ± 0.52	6.59 ± 0.69	6.09 ± 0.76 c
		5.74 ± 0.66
		5.50 ± 0.62
		6.09 ± 0.64
45.5 ± 2.0	0.69 ± 0.08		4.44 ± 0.45
51.6 ± 1.7	4.17 ± 0.35		4.17 ± 0.43
55.4 ± 1.4	3.02 ± 0.23		4.14 ± 0.42
78.2 ± 1.0	2.45 ± 0.08		2.77 ± 0.29
89.5 ± 0.6	18.24 ± 0.33		2.39 ± 0.25
107.0 ± 0.5	4.90 ± 0.06		2.15 ± 0.22

^aUncertainties in T and n are the standard deviation (only statistical)

^bStated uncertainties are the combination of the statistical and systematic (±10%) errors

^cAveraged value of different experiments.

When combining our data with those reported by Sivakumaran et al. (Sivakumaran et al. 2003) at T<300 K the best fit is:

$$k_1(T=22\text{-}300\text{K})=(7.73\pm 1.82)\times {10}^{\text{-}12}{(T/300\text{K})}^{-(1.03\pm 0.09)}{\text{cm}}^3{\text{s}}^{\text{-}1}$$ (11)

where the uncertainties are ±2σ. The relative difference of the calculated k₁(T) from Eq (11) with respect to the experimental values in the 22-107 K ranges from 4% to 21%. In Figure S3 of the supporting information, the confidence interval bands of the fit are depicted at 95% level of confidence in addition to the experimental data and the above mentioned fit. k₁(T) values in the 200-300 K range are predicted by Eq. (11) within an uncertainty of 1-5% for most of the available measurements.

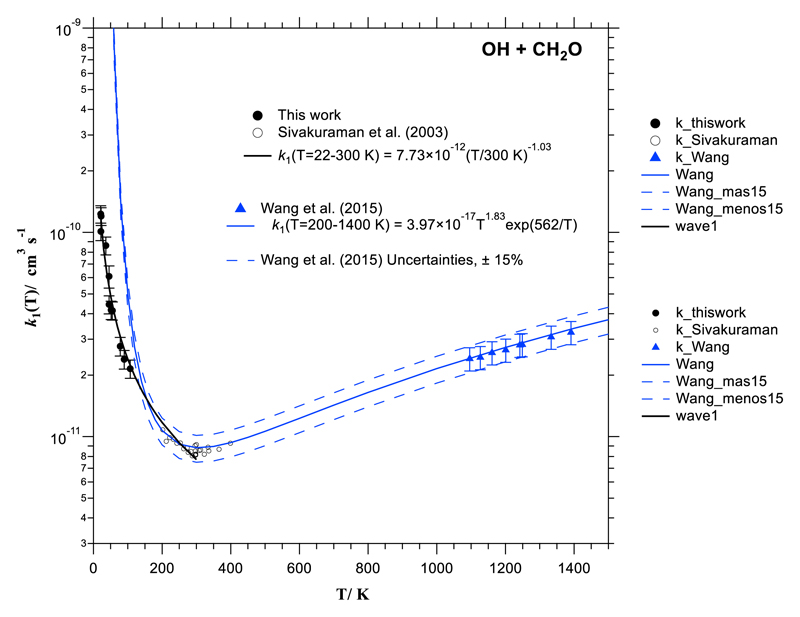
As can be seen in Figure 2, when comparing our results with all the previous kinetic studies on the OH + H₂CO reaction between 200 and 1500 K, a U-shaped curvature is observed in the trend of k₁(T), with a minimum value around 300 K. The three-parameter expression recently proposed by Wang et al. (Wang et al. 2015), which combines their high temperature data with those at lower temperatures from Sivakumaran et al. (Sivakumaran et al. 2003), is displayed by a blue solid line in Fig. 2. This expression represents perfectly experimental data for T > 200 K (within 6-15%) but fails to predict k₁(T) at T < 120 K (difference >50%). For example, the predicted k₁(T=107 K) is almost twice the experimental value. Therefore, we recommend using our expression for k₁(T) below 250 K and Wang's formula above. Our expression has been derived in the range 22 K< T < 250 K. Even though extrapolation can be risky, expression (11) can be used to obtain an estimation of the rate coefficient at 10 K needed for the modeling of HCO and H₂CO abundances in cold interstellar clouds. This leads to a value of (2.60 ± 0.60)×10^-10 cm³ s^-1.

Fig 2.

Temperature dependence of the rate coefficient of OH+H₂CO reaction between 22 and 1400 K. The equation recently proposed by Wang et al. (26) reproduces the light curvature between 200 and 400 K, however it is not consistent with the experimental data below 200 K (see text).

3.2. Dynamics of the OH+H₂CO reaction

The experimental determination of the reaction rate coefficient is done through the disappearance of the OH. One way to check if the measured disappearance of OH corresponds to the formation of HCO product is to perform complete dynamical simulations of the H₂CO+OH → HCO + H₂O reactive collisions. This reaction presents a low barrier of 27 meV, with a zero-point energy (ZPE) of the order of 1 eV (see Figure 1), in agreement with previous studies. If pure transition state theory (TST) is applied, and the reaction coordinate is separated from the orthogonal vibrational modes, the reaction would not happen for collision energies below 27 meV (approx. 300K), and the rates would tend to zero when decreasing temperature, in opposition to the behavior of the experimental results. One way to overcome this difficulty is to introduce tunneling in the TST model, giving rise to different approaches based essentially in the anharmonicity of the potential at the saddle point. These approaches are approximate and the purpose of this work is to carry out full dimension reaction dynamics studies which describe better the reaction mechanism at low temperatures.

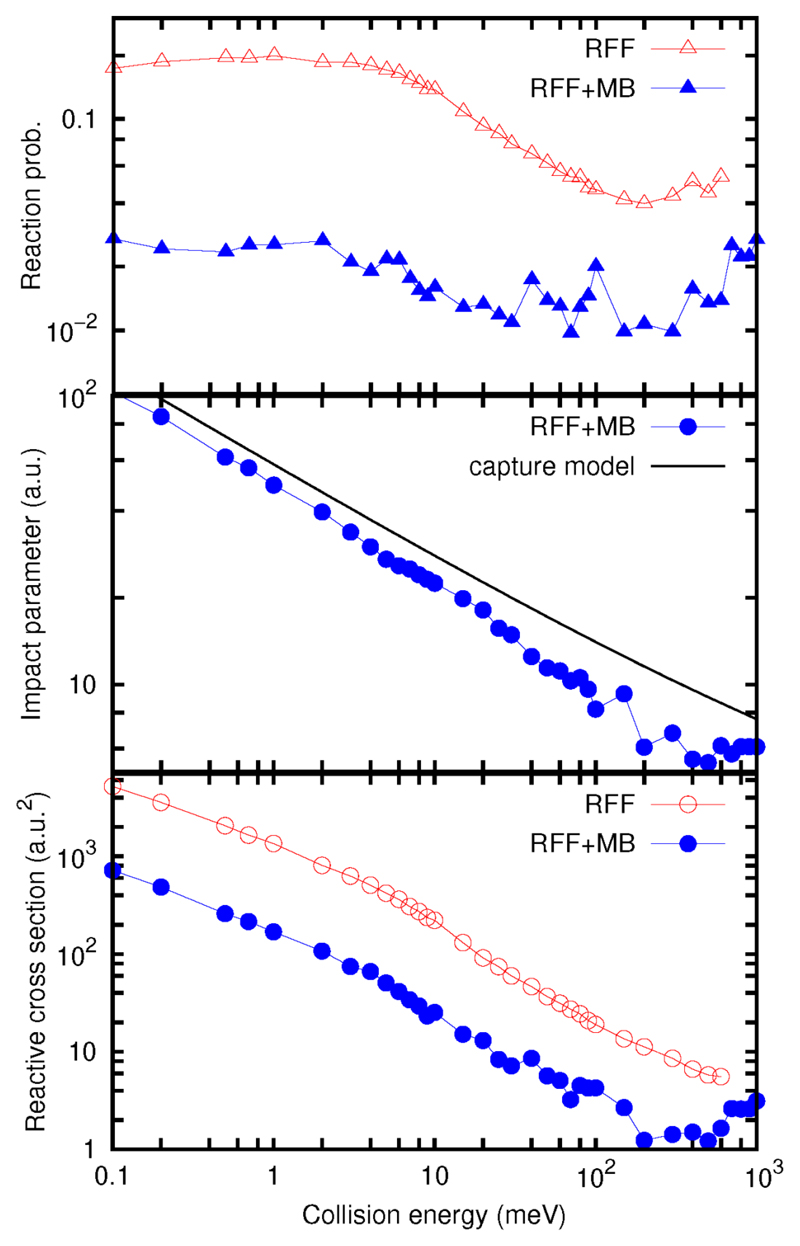
QCT calculations have been done for the H₂CO + OH → HCO + H₂O reaction on the reactive force field (RFF) and the full (RFF+MB, many body) potential energy surfaces (PES) described in Zanchet et al. (2017). These PES’s were developed on purpose, and describe properly the long range interactions and all the energetics, especially the stationary points of the PES. The calculations performed in the microcanonical ensemble, at fixed collision energy, allow a better understanding of the reaction mechanism. The total reaction cross section, σ_v=0,j=0(E), calculated for the ground rotational and vibrational state of the two reactants shows a continuous increase with decreasing collision energy, for both the total RFF+MB and RFF PES’s (see bottom panel of Fig. 3). Clearly the increase of σ_vj is associated to the increase of b_max (middle panel of Fig. 3), while P_r(E) remains nearly constant (top panel of Fig. 3). The increase of the impact parameter is well described by the capture model (Levine & Bernstein 2001) using Eq. (8). The agreement with the one found in the QCT simulations is nearly perfect, until an energy of 100 meV, where the corresponding b_max is of the order of the size of the molecules. This confirms that the potential is able to capture trajectories at low energy with an increasing efficiency as collision energy decreases. This leads to trajectories which are trapped in the OH-H₂CO well during long time, where the dynamics becomes ergodic and chaotic, as recently found in ultracold collisions (Croft & Bohn 2014).

Fig 3.

Top panel: Reactive probabilities P_r(E) as a function of collision energy. Middle panel: impact parameter b_max as a function of collision energy. Bottom panel: Reactive cross section. All the quantities have been calculated with the RFF (red) and the RFF+MB (blue) PES's.

In the top panel of Fig. 3, it is shown that P_r(E) changes smoothly with the collision energy, and does not drop to zero even at 0.1 meV, energy well below the reaction barrier of the two PES’s (of 27 meV). The difference between the reaction cross section found for the two PES’s, RFF and RFF+MB, is explained by the change in the reaction probability, since the impact parameter remains nearly the same for both PES's. This change of the reaction probability is attributed to the many body term introduced in the potential to better describe the calculated ab initio points. The RFF by itself is too isotropic, facilitating the access from the complex to the saddle point, giving rise to an overestimation of the reaction cross section. This fact is corrected by the MB term.

The remaining point to understand is why the reaction probability is non zero at energies below the top of the barrier. Considering the ZPE of reactants, the system has enough total energy to overcome this barrier. If the reactants ZPE remains in the coordinates orthogonal to the reaction coordinate, the reaction could not take place, since there would not be enough energy in the reaction coordinate. Clearly, this is not the case, and there must be couplings between the reaction coordinate and the remaining degrees of freedom, producing an energy transfer which explains the non zero reaction probability even at 0.1 meV of collision energy. Such situation is typical in non-intrinsic reaction coordinate (non-IRC) trajectories (Lourderaj et al. 2008), since they explore large regions of the configuration space, far from the minimum energy path determined by the IRC, where the anharmonicity is larger. The concept of ZPE at the transition state is an approximation based on the separation between the reaction coordinate (in the dissociation continuum) and the orthogonal vibrations. This separation is adequate for trajectories going along the IRC, since the potential can be locally described by a parabolic separable potential. Out of this IRC the potential is no longer separable, and hence the energy can be transferred among the different degrees of freedom. Moreover, the harmonic approximation made to estimate the ZPE at the saddle point is questionable since the PES at the saddle point has a large anharmonicity which tends to reduce the ZPE.

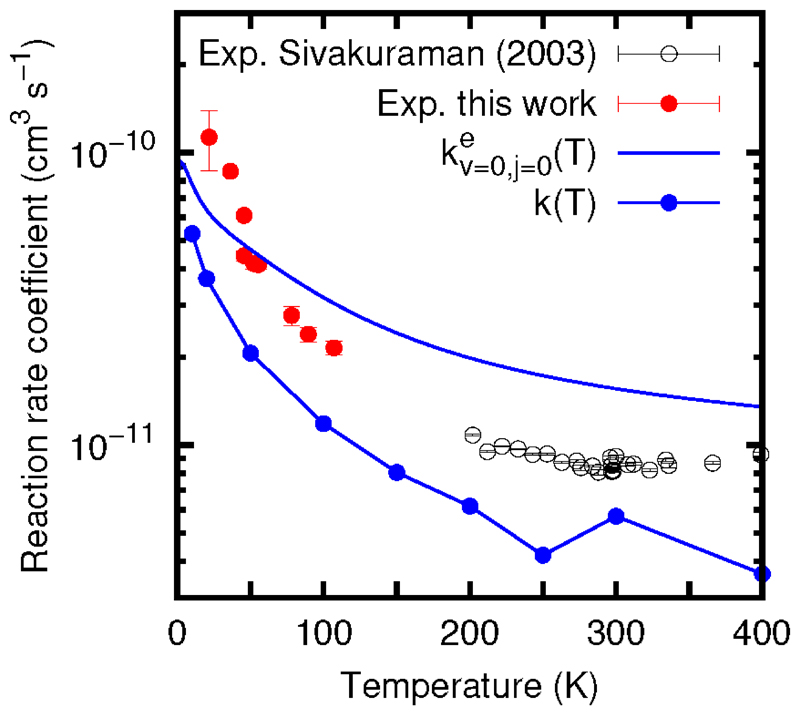
The rate coefficient is calculated by integrating the cross section over a Boltzmann distribution. To account for the spin-orbit splitting of the OH(²Π) states into the F₁(²Π_1/2) and F₂(²Π_3/2), with an energy separation of 200.3 K, the rate coefficient is multiplied by the electronic partition function, q_e = [1+exp(-200.279/T)]^-1. This term arises from the assumption that only the ground spin-orbit state reacts. The rate coefficient thus obtained only corresponds to the ground rotational states of OH and H₂CO, and it is labelled as k^e_v=0,j=0(T) in Fig. 4. In order to compare with the experimental data of this work, also in Fig. 4, we have to consider the rotational populations of the reactants, which vary as a function of temperature. This is done by computing directly the thermal rate coefficient, k(T), in the macrocanonical ensemble according to Eq. (10), which is depicted in Fig. 4. Clearly the computed rate coefficient k(T) is slightly lower than the experimental one, but it shows the same behavior. At T>50 K k(T) is a factor of ca. 2 lower, however the difference between theory and experiments increases somewhat when lowering the temperature. We therefore conclude that the behavior of the simulation is semiquantitatively correct, explaining the experimental results obtained in this work.

Fig 4.

Simulated thermal rate coefficient, k₁(T), and initial-state selected rate coefficient, k^e_v=0,j=0(T), as defined in the text, compared with the experimental results in the 20<T<400 K temperature range.

The quantitative differences may be attributed to two major reasons. First, the reaction probabilities displayed in Fig. 3 depend on the accuracy of the PES. Work is now in progress to improve the current PES. Second, quantum effects are expected to be important at low collision energies, while they are neglected in the present treatment. To analyze the qualitative effect of quantum dynamics we can refer to a similar reaction, OH + F → O + HF, having a similar energy profile, for which the cross section also increases significantly at low energies (Gómez-Carrasco et al. 2004a), (Gómez-Carrasco et al. 2004b), (Gómez-Carrasco et al. 2005). In that triatomic system, exact quantum wave packet calculations were performed, finding that the reaction cross section increases with decreasing collision energy, being always larger than the QCT cross sections. This behavior was interpreted by an indirect mechanism at low energies due to the presence of resonances, both in the quantum and classical simulations. It may be concluded that the QCT approach yielded qualitatively good results, but tends to lead to lower rate coefficients at low temperatures. Similar effects are expected in the H₂CO+OH reaction, and the inclusion of quantum effects may yield to a better agreement with experiments, especially at low temperatures. Quantum effects may be the reason of the increasing difference, and in particular ZPE effects. As the reaction mechanism consists in two steps: the capture to form the complex and the dissociation to either reactants or products. The lifetime of this complex is determined by the number of open channels. This number in the products is already rather large, since the reaction is exothermic. Then the crucial quantity determining the reactivity is the number of open channels in the reactants. For low temperatures, this number reduces to 1, i.e., the ground rovibrational state of the two reactants. This is so in a quantum description. However using a QCT description, there is no quantization. Therefore, the dissociation back to reactants is somehow overestimated, and this probably explains the disagreement between simulations and experiment, especially at low temperatures.

The total rate coefficient corresponds to the rearrangement channel HCO+H₂O. It should be noted, that the products end in highly excited rovibrational states. In the particular case of HCO, with a rather weak bond, it may fragment giving H + CO. Thus the formation of the CO + H + H₂O is included in the present model. However its proportion is rather low, varying between 2 and 4% in the entire temperature range.

3.3. Astrochemical model

In order to evaluate the impact of the titled reaction on the abundances of HCO and H₂CO in cold dark clouds, we performed a chemical model using two different chemical networks, UMIST (McElroy et al. 2013) and KIDA (Wakelam et al. 2015), and set k₁(10 K) to 2.6×10^-10 cm³ s^-1 (value from Eq. (11)).

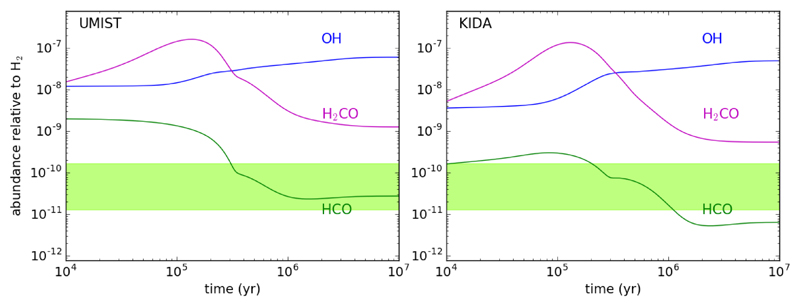
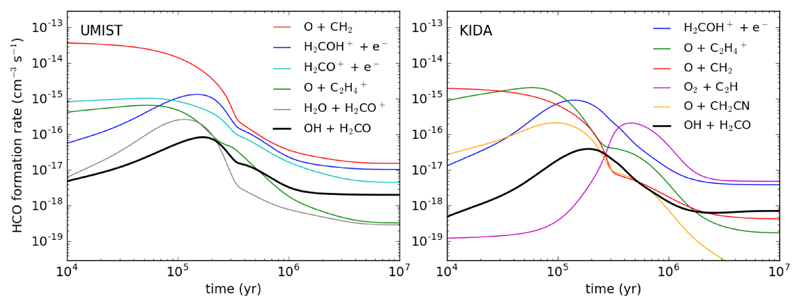
In Fig. 5 we show the calculated fractional abundances of HCO and H₂CO as a function of time using the UMIST and KIDA networks. It is seen that the calculated abundance of HCO at times between 10⁵ and 10⁶ yr is in good agreement with the range of values derived from observations. Even though the reaction between H₂CO and OH is very fast at low temperatures, the chemical model indicates that it accounts for a few percent in the production of HCO, radicals in cold dark clouds. This result is consistently obtained no matter which chemical network is adopted. According to the chemical model, the main HCO-forming routes are reactions involving atomic oxygen (reactions 2 and 3) and the dissociative recombination of the molecular ion H₂COH⁺ (reaction 4). The relative importance between these reactions varies depending on the adopted chemical network. This is illustrated in Fig. 6, where we show the contributions of the five most important HCO-forming reactions as a function of time and compare them with the HCO production rate given by reaction (1). At times between 10⁵ and 10⁶ yr, reaction (2) dominates when the UMIST network is adopted, while if the KIDA network is used the main route to HCO becomes reaction (4).

Fig 5.

Calculated abundances of HCO, H₂CO, and OH in a cold dark cloud as a function of time using the UMIST (left panel) and KIDA (right panel) chemical networks. The horizontal green band indicate the range of HCO abundances observed in cold dark clouds (see Table 1).

Fig 6.

Contribution of the five most important reactions and of reaction (1) to the formation of HCO in a cold dark cloud as a function of time, as calculated with the chemical model using the UMIST (left panel) and KIDA (right panel).

The rate coefficient of the reaction between CH₂ radicals and O atoms has been measured at room temperature (Böhland et al. 1984), although the kinetics has not been studied at low temperature and it is not clear which is the branching ratio of the channel leading to HCO. According to Böhland et al. (Böhland et al. 1984), the HCO radicals formed in the O + CH₂ reaction should contain enough excess energy to dissociate into CO + H. It is therefore uncertain whether reaction (2) is actually an important source of HCO radicals. The UMIST network adopts a rate coefficient of 5×10^-11 cm³ s^-1 estimated in high-temperature experiments while in the KIDA network a smaller value, 2×10^-12 cm³ s^-1, is adopted based on a discussion by Loison et al. (KIDA datasheet 281, (Wakelam et al. 2015)). The importance of reaction (2) strongly depends on its rate coefficient at low T. This explains the big difference between the UMIST and KIDA results shown in Fig. 6. For O + C₂H₄⁺ (reaction 3) and H₂COH⁺ + e^- (reaction 4) the kinetics is better constrained from experiments. For the first reaction, its rate coefficients has been measured to be 2.4×10^-10 cm³s^-1 at room temperature and the branching ratio for the channel yielding HCO has been measured as 45 % (Scott et al. 2000). Since the neutral reactant is non-polar, the rate coefficient should be independent of temperature and thus the value measured at room temperature should pertain at low temperatures as well. Therefore, the value adopted at 10 K in both networks was k₃ = 1.08×10^-10 cm³ s^-1.

The dissociative recombination of H₂COH⁺, as most reactions of this type, is fast at low temperatures, and has been found to preserve the C-O bond in most of the collisions (Hamberg et al. 2007). The branching ratios of the channels leading to H₂CO, HCO, and CO are however not known. However, they are assumed to be equal by KIDA and UMIST networks. The values for k₄ used were 1.10×10^-6 cm³ s^-1 (KIDA) and k₄ = 3.08×10^-6 cm³ s^-1 (UMIST).

The chemistry of HCO radicals in prestellar cores was discussed by Bacmann and Faure (Bacmann & Faure 2016) based on simple steady-state arguments and different assumptions on the main source and sink reactions for HCO. These authors evaluated which HCO abundance would result if this radical is exclusively formed (i) by reaction (1) or (ii) by the dissociative recombination of H₂COH⁺ (reaction (4)), in both cases assuming that the main sink of HCO are reactions of proton transfer from abundant ions which can easily give a proton (e.g., HCO⁺, H3⁺). They concluded that the ionic pathway scenario (reaction (4)) results in HCO abundances that agree with the values derived from observations, while the neutral-neutral reaction OH + H₂CO would need to have a rate coefficient of 4 ×10^-10 cm³ s^-1 to produce HCO in the observed quantities. This is rather close to the value used in the present model extrapolated from our experimental results, k(10 K)=2.6×10^-10 cm³ s^-1. According to the chemical model (see Fig. 6), reaction (1) would need to be more than one order of magnitude faster than indicated by our measurements to compete with other reactions in the synthesis of HCO radicals in cold dense clouds. We however stress that this conclusion is based on a chemical model, which is subject to significant uncertainties because the low-temperature kinetics of most of the reactions included is not precisely known as exemplified earlier with the O + CH₂ reaction for instance.

The formyl radical is particularly abundant in PDRs, where its abundance is enhanced by two orders of magnitude with respect to cold dense clouds (Gerin et al. 2009). It is however not clear how this radical is formed in these environments. Gerin et al. (Gerin et al. 2009) carried out a pure gas-phase model and found that HCO abundances of the order of magnitude of the observed ones can be obtained if HCO is efficiently produced in the photodissociation of H₂CO and in the reaction between CH₂ radicals and O atoms (reaction (2)). These two routes, however, lack the sufficient empirical support and it remains to be seen if alternative HCO-forming routes, as, e.g., reaction (1), would need to be invoked to explain the relatively large abundances of HCO observed in PDRs such as the Horsehead Nebula.

In summary, despite the uncertainties in the rate coefficients and branching ratios of various reactions important for the chemistry of HCO, it seems that, in the present state of knowledge and chemical uncertainties, in cold dense clouds the reaction OH + H₂CO is less efficient than alternative gas-phase routes involving O atoms and the precursor ion H₂COH⁺ in the formation of HCO radicals. It however remains to be explored whether the dramatic enhancement in the reactivity of OH and H₂CO could be responsible for the formation of HCO radicals in other relatively cold interstellar media such as diffuse clouds and PDRs.

4. Conclusions

The rate coefficients for the H₂CO + OH reaction in the gas phase have been determined for the first time at ultralow temperatures (22-107 K) in a CRESU machine. The rate coefficient increases as temperature decreases although a barrier (~ 300 K) is present along the reaction pathway. This behavior is also found in QCT calculations performed on a highly accurate PES, especially developed for this purpose. The experimental finding is explained by two factors. First, the long range dipole-dipole interactions are able to capture trajectories forming an OH-H₂CO long lived complex. Secondly, the dynamics becomes ergodic following trajectories far apart from the minimum energy path or IRC, at which the anharmonicity of the potential is high. In this situation, the reaction coordinate is strongly coupled to the orthogonal vibrations and can exchange energy enough to overcome the barrier.

The impact of the present rate coefficients on interstellar chemistry has been addressed by exploring the potential consequences of this new data on the formation of interstellar HCO. Whereas in cold dark clouds the titled reaction was found to be a minor source of HCO with respect to alternative routes involving O atoms and dissociative recombination of H₂COH⁺, it remains to explore if the OH + H₂CO reaction can provide a significant contribution to the HCO formation in other environments such as PDRs and diffuse clouds.