Optimal Space-time Precoding of Artificial Sensory Feedback through Mutichannel Microstimulation in Bi-directional Brain Machine Interfaces

Abstract

Brain Machine Interfaces (BMIs) aim to restore lost sensorimotor and cognitive function in subjects with severe neurological deficits. In particular, lost somatosensory function may be restored by artificially evoking patterns of neural activity through microstimulation to induce perception of tactile and proprioceptive feedback to the brain about the state of the limb. Despite an early proof of concept that subjects could learn to discriminate a limited vocabulary of intracortical micostimulation (ICMS) patterns that instruct the subject about the state of the limb, the dynamics of a moving limb are unlikely to be perceived by an arbitrarily-selected, discrete set of static microstimulation patterns, raising questions about the generalization and the scalability of this approach.

In this work, we propose a microstimulation protocol intended to activate optimally the ascending somatosensory pathway. The optimization is achieved through a space-time precoder that maximizes the mutual information between the sensory feedback indicating the limb state and the cortical neural response evoked by thalamic microstimulation. Using a simplified multi-input multi-output (MIMO) model of the thalamocortical pathway, we show that this optimal precoder can deliver information more efficiently in the presence of noise compared to suboptimal precoders that do not account for the afferent pathway structure and/or cortical states. These results are expected to enhance the way microstimulation is used to induce somatosensory perception during sensorimotor control of artificial devices or paralyzed limbs.

1. Introduction

Visual and proprioceptive feedback have been shown to play a key role in motor performance during both natural [1] and brain-machine interface (BMI) motor control [2]. Amputated or paralyzed subjects lack the ability to receive continuous tactile and proprioceptive feedback about the state of the limb they control, particularly when reaching to and grasping different objects. A bi-directional BMI system that can reliably deliver proprioceptive information via microstimulation of afferent sensory pathways may therefore improve subject performance in BMI tasks. A number of recent studies have shown that electrical microstimulation can be used as a means of delivering sensory information to the brain in a bi-directional brain interface [3, 4, 5, 6, 7]. The animals not only learned to detect and distinguish distinct spatial and temporal microstimulation patterns during active exploration [3, 4], but also quickly learned to integrate microstimulation cues with natural sensory cues to infer target location during active sensing [5].

These studies, however, have only used a very limited set of spatiotemporal microstimulation patterns to instruct the subject about the state of the brain-actuated device, consequently restricting the amount of information delivered to the brain. Subjects were taught to distinguish between the presence or absence of intracortical microstimulation (ICMS) [3, 5] or between two distinct ICMS patterns [4]. From an information theoretic standpoint, two equally probable stimulation patterns deliver only 1 bit per pattern and only at discrete points in time. Despite the initial success of this proof of concept, the continuous state evolution of a moving limb, whether it be natural [8, 9] or artificial [10], is unlikely to be faithfully represented by an arbitrarily selected, discrete set of microstimulation patterns, raising questions about the generalization and scalability of this approach. The ideal bi-directional brain machine interface should be able to deliver reliably a broad range of spatiotemporal microstimulation patterns in real time to represent the continuously changing state of the limb so that subjects can learn to integrate these continuously delivered microstimulation cues with existing sensory feedbacks during the execution of motor commands.

Our previous work has indicated that the range of spatiotemporal patterns of neural activity that can be evoked through microstimulation is theoretically limited by the neural circuit and the biophysical mechanisms of microstimuation [11, 12]. When viewed as a network, our neural circuit analysis results are consistent with recent biological studies suggesting that neural ensemble spike patterns seem to be drawn from a limited “vocabulary”, sampled narrowly from a repertoire of sensory responses [13, 14, 15, 16]. These suggest that neural systems exhibit spatiotemporal selectivity and that the specific mechanisms that control the spatiotemporal activity patterns observed at the output of a given neural circuit are yet to be revealed. In terms of the biophysics of microstimulation, evidence suggests that electrical microstimulation activates neurons more sparsely and at a greater distance from the electrode tip than previously thought, suggesting axonal - rather than somatic or dendritic - activation [17, 18]. A recent study examined altering the electrical stimulus waveform in order to achieve better spatial specificity in cortex and perhaps similarity to natural stimuli which may increase the number of evocable neural activity patterns and possibly cause artificially evoked perception to feel more natural [19]. Limitations on the range of evocable neural activity patterns may affect the amount of information that could be delivered from the limb to sensory cortex through microstimulation. With a limited range of evocable cortical responses, it becomes desirable to deliver more information using those combinations of spatiotemporal input patterns (e.g. combination of magnitudes and phases of stimulation pulse trains) that can lead to strong system responses that are more robust to biological noise. In other words, if we use spatiotemporal input patterns that are weakly transmitted and potentially perceived by the system such that the resulting cortical response is dominated by background neural noise and the confluence of other - potentially more dominant - sensory and cognitive processes, the brain may not be able to discriminate salient patterns in continuously varying sensory feedback signals. A precoding mechanism that appropriately allocates sensory information among the input plausible spatiotemporal microstimulation patterns based on the efficacy of the system response and the ambient noise level might offer additional advantages. If one considers an ascending sensory pathway as a communication channel, the precoder can be designed to make maximal use of the channel bandwidth.

In this work, we propose a space-time precoder that maximizes the mutual information between the sensory feedback from the brain actuated limb and the artificially evoked cortical neural activity. While the approach we describe here is quite general to apply along any afferent pathway, we propose to use the thalamus as a site for microstimulation while using the cortex as a site for recording the microstimulationevoked activity patterns for a number of reasons. First, the thalamocortical pathway is known to carry tactile and proprioceptive feedback about limb states to cortex [20, 21]. Second, thalamic synchronization has been shown to significantly improve the efficacy of cortical responses [22] and feed-forward inhibition can modulate correlation between neurons in the presence of stimulus evoked activity [23]. These phenomena could produce potentially strong and negative correlations between the firing patterns of neurons. See Tiesinga et al. for an excellent review of some of these mechanisms [24]. Third, thalamic correlation has been shown to impact strongly the cortical state [25]. Fourth, a number of recent studies surveyed briefly below have demonstrated the ability to evoke percepts using thalamic stimulation.

Clinically, electrical stimulation of the thalamus has been proposed as a means of restoring sensory information in patients where sensory neurons have been damaged or connections severed. Thalamic stimulation has been used to evoke responses in both visual cortex [26, 27] and somatosensory cortex [28]. The regions of the thalamus involved in somatosensation have been shown to have a compact somatotopic organization [29, 30]. The study by Heming et al. suggests that percepts evoked by thalamic stimulation could be stable over long time periods [28] and able to evoke close to natural perception - as measured by human subjects’ psychophysical responses - when microstimulation was delivered to the ventrointermedius and the ventrocaudal thalamic nuclei after manual tuning of parameters [31]. Experiences with deep-brain stimulators also suggest that thalamic stimulation should be safe for human subjects and cause minimal tissue damage [32, 33]. Possible sites for electrical stimulation include the ventral posterior medial and ventral posterior lateral nuclei of the thalamus. This makes thalamic stimulation a promising alternative for sensory prostheses. An added advantage is it can alleviate the complexity caused by ICMS artifacts in S1 that may mask neural activity in M1 needed for decoding motor intent [4]. The longer distance between the thalamus and the somatosensory cortex can help reduce stimulation and recording interferences, as simultaneous stimulation and recording within the same brain region could be significantly complicated by electrical stimulation artifacts [34].

The paper is organized as follows: we first describe how the structure of the thalamocortical afferent pathway may inherently limit the information transmitted by means of microstimulation. Next, we fit a linearized model to the thalamocortical circuit and determine the precoder parameters which maximize the information transfer by our system under a power constraint. We then compare the performance of an optimal precoder to that of a suboptimal precoder under the same power constraint and noise level using a simple linear decoder. Our results suggest that this approach performs significantly better than a suboptimal precoder, especially in the presence of noise.

2. Methods

2.1. Thalamo-cortical Networks

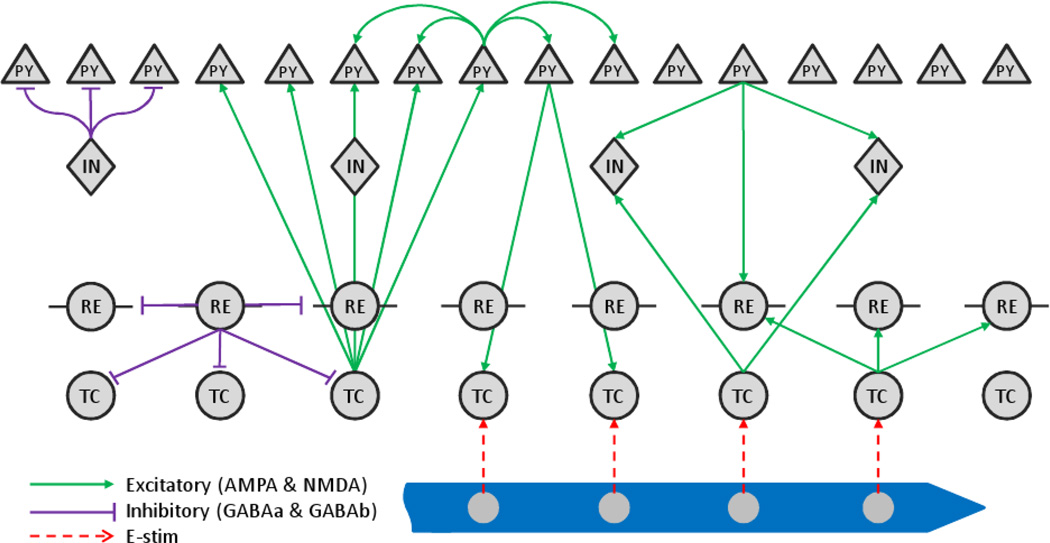
We adopt the thalamo-cortical network model described in [12, 35, 36]. The thalamus consists of a population of inhibitory reticular (RE) neurons and excitatory thalamocortical (TC) neurons, while the cortex model includes a population of excitatory pyramidal cells (PY) and inhibitory interneurons (IN). Figure 1 shows the topology of the thalamo-cortical network. For convenience, we use the instantaneous stimulation frequency that varies continuously over time to model the dynamic stimulation patterns expressed by u. A stimulator is then used to convert the stimulation inputs u to electrical pulse trains that are delivered to TC cells (Figure 2). The instantaneous firing rates of the PY cells are considered to be the outputs, y, of the thalamo-cortical network and are obtained by smoothing the spike trains over a sliding window of length T (T = 200ms). Smoothing over time has the effects of linearizing the input-output relationships and makes a linear model approximation valid over a wider range of firing rates as long as they do not exceed the saturation limits of the PY neurons [12]. Biological studies have indicated that firing rates of neurons may vary linearly with stimuli under certain conditions [37, 38] and a linear-nonlinear cascade model was shown to predict accurately the firing rates of neurons in response to stimuli over a broad range of parameters [39]. In addition, temporal smoothing allows us to investigate the network dynamics over a slower time scale of tens to hundreds of milliseconds, on which our information theoretic analysis will be focused. Typical efferent brain machine interface experiments use time bins ranging from 50 to 300ms [40, 41, 42]. For restoration of somatosensory feedback, it is therefore reasonable to assume a time-scale for sensory information that is close to that of the decoded motor information.

Figure 1.

Topology of the thalamo-cortical network modeling the information transmission in an afferent pathway. PY: cortical pyramidal cells; IN: cortical inhibitory interneurons; RE: inhibitory reticular cells; TC: excitatory thalamocortical cells.

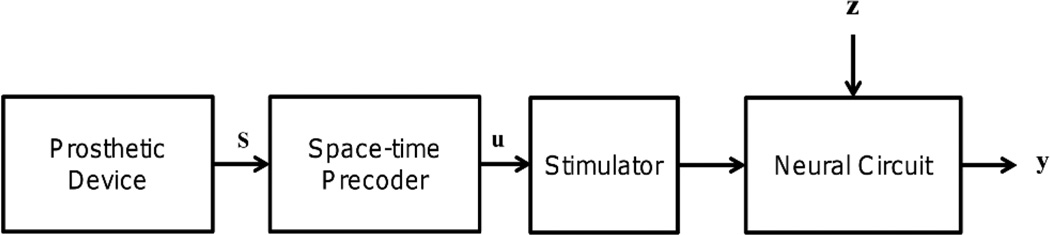
Figure 2.

Space-time precoding of artificial sensory feedback. The space-time precoder provides a continuous time translation between state of the prosthetic device and the stimulator. The variables are as follows: s is the artificial sensory feedback, u is the frequency of stimulation, y is the neuronal response, and z is the noise.

2.2. Space-time Precoding of Artificial Sensory Feedback

As a result of the diversity of cell types and intricate synaptic organization of neocortical circuitry, the biophysics of electrical microstimulation are extremely complex and poorly understood. Recent studies have shown that neural response to electrical currents is not localized as previously thought [17]. A neural circuit under multichannel microstimulation can be reasonably modeled as a Multiple-Input-Multiple-Output (MIMO) system that usually exhibits strong spatial and temporal selectivity [12]. In particular, the stimulation patterns can be selectively amplified or attenuated depending on their spatiotemporal “direction” [11]. Noise from other parallel sensory pathways can interfere anywhere in the neural circuitry being stimulated and contaminate the evoked output over potentially multiple paths and multiple timescales. Consequently, noise can be selectively amplified or attenuated depending on its path of transmission to the output of the circuit and its relevance to the task being executed by the subject.

To optimize the information transmission between the artificial sensory signals measured from the prosthetic device and the artificially evoked responses (see Figure 2), more information should be transmitted along the spatiotemporal directions that have higher Signal to Noise Ratio (SNR). Biophysically speaking, given similar noise levels, the optimal precoder should determine which microstimulation input patterns generate the largest changes in firing rates of cortical neurons. If a microstimulation pattern results in no observed change in cortical activity, the SNR is low and no power should be allocated to that input pattern. On the other hand, if microstimulation does result in a wide range of observed cortical firing rates, the SNR is higher and more power should be allocated to that input pattern. The variability in cortical response strength could be the result of differences in conduction times [43], feedforward inhibition [23], or axonal projection patterns [17] and consequently, optimized input patterns are needed to ensure that sufficiently distinct output patterns can be reliably evoked.

2.3. Precoder Design

We model the thalamocortical pathway under multichannel microstimulation as a discrete time Linear Time Invariant (LTI) MIMO system with M_u stimulation inputs u(n) = [u₁(1), …, u_Mu (n)]^T and M_y measured neural responses y(n) = [y₁(n), …, y_My(n]^T (e.g. firing rates of the recorded neurons) as follows

$$\mathbf{y}(n)=\sum _{k=0}^{\infty }\mathbf{g}(k)\mathbf{u}(n-k)+\mathbf{z}(n)$$ (1)

The impulse response @@@${\{\mathbf{g}(k)\}}_{k=0}^{\infty }$ of the MIMO system contains a sequence of M_y × M_u real matrices. z(n) is a M_y × 1 colored Gaussian random vector with E[z(n] = 0. z(n) is used to model the cumulative effects of unobserved inputs and the unpredicted variations in neural firing. We assume z(n) is uncorrelated with u(n). The stimulation inputs u(n) are generated by precoding the artificial sensory signals s(n) measured from the prosthetic device using a space-time filter @@@${\{\mathbf{f}(k)\}}_{k=0}^{\infty }$, such that

$$\mathbf{u}(n)=\sum _{k=0}^{\infty }\mathbf{f}(k)\mathbf{s}(n-k)$$ (2)

where {f (n)} is a fixed sequence of real M_u × M_s matrices, and s(n) = [s₁(n), …, s_Ms(n)]^T contains M_s artificial sensory signals. These are assumed to be colored Gaussian with E[s(n)] = 0.

Two important considerations in all electrical stimulation experiments are the need to minimize the electrode damage as well as the tissue damage [44]. These are used as constraints on our precoder design. To limit the energy consumption, we also constrain the power of the stimulation inputs u(n). This would be useful when subjects use the prosthesis for extended periods of time and would be an important consideration for clinical use.

With knowledge of the dynamic relationship between the stimulation inputs u(n) and the artificially evoked response y(n) which can be obtained by probing the neural circuit with a variety of stimulation frequencies, the objective is to design a linear filter @@@${\{\mathbf{f}(k)\}}_{k=0}^{\infty }$ to precode the artificial sensory signals s(n) both in space and time, so that the information transmission from the sensory signal s(n) to the evoked response y(n) is optimized under both power and safety constraints on the stimulation inputs u(n).

To this end, we first consider a time segment of duration N (N can be arbitrarily large), and let y_N = [y(N − 1)^T, …, y(0)^T]^T, u_N = [u(N − 1)^T, …, u(0)^T]^T, z_N = [z(N − 1)^T, …, z(0)^T]^T, and s_N = [s(N − 1)^T, …, s(0)^T]^T. For stable {g(k)} and {f (k)}, we can approximately rewrite both (1) and (2) in block matrix form as follows

$${\mathbf{y}}_N={\mathbf{G}}_N{\mathbf{u}}_N+{\mathbf{z}}_N$$ (3)

$${\mathbf{u}}_N={\mathbf{F}}_N{\mathbf{s}}_N$$ (4)

where G_N is given by

$${\mathbf{G}}_N=\left[\begin{array}{ccccc}\hfill \mathbf{g}(0)\hfill & \hfill \mathbf{g}(1)\hfill & \hfill \cdots \hfill & \hfill \mathbf{g}(N-2)\hfill & \hfill \mathbf{g}(N-1)\hfill \\ \hfill 0\hfill & \hfill \mathbf{g}(0)\hfill & \hfill \cdots \hfill & \hfill \mathbf{g}(N-3)\hfill & \hfill \mathbf{g}(N-2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \mathbf{g}(0)\hfill & \hfill \mathbf{g}(1)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \mathbf{g}(0)\hfill \end{array}\right]$$

and F_N is given by

$${\mathbf{F}}_N=\left[\begin{array}{ccccc}\hfill \mathbf{f}(0)\hfill & \hfill \mathbf{f}(1)\hfill & \hfill \cdots \hfill & \hfill \mathbf{f}(N-2)\hfill & \hfill \mathbf{f}(N-1)\hfill \\ \hfill 0\hfill & \hfill \mathbf{f}(0)\hfill & \hfill \cdots \hfill & \hfill \mathbf{f}(N-3)\hfill & \hfill \mathbf{f}(N-2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \mathbf{f}(0)\hfill & \hfill \mathbf{f}(1)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \mathbf{f}(0)\hfill \end{array}\right]$$

Now consider the system from s_N to y_N

$${\mathbf{y}}_N={\mathbf{G}}_N{\mathbf{F}}_N{\mathbf{s}}_N+{\mathbf{z}}_N$$ (5)

Assuming that s_N is independent of z_N, the mutual information between s_N and y_N is

$$I({\mathbf{s}}_N;{\mathbf{y}}_N)=H({\mathbf{y}}_N)-H({\mathbf{y}}_N|{\mathbf{s}}_N)=H({\mathbf{y}}_N)-H({\mathbf{z}}_N)={\text{log}}_2\text{det}({\mathbf{G}}_N{\mathbf{F}}_N{\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}{\mathbf{G}}_N^{*}{\mathrm{\Phi }}_{z_N}^{-1}+\mathbf{I})={\text{log}}_2\text{det}({\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}{\mathbf{G}}_N^{*}{\mathrm{\Phi }}_{z_N}^{-1}{\mathbf{G}}_N{\mathbf{F}}_N+\mathbf{I})={\text{log}}_2\text{det}({\mathbf{G}}_N^{*}{\mathrm{\Phi }}_{z_N}^{-1}{\mathbf{G}}_N{\mathbf{F}}_N{\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}+\mathbf{I})$$

where @@@${\mathrm{\Phi }}_{s_N}=E[{\mathbf{s}}_N{\mathbf{s}}_N^{*}]$, and @@@${\mathrm{\Phi }}_{z_N}=E[{\mathbf{z}}_N{\mathbf{z}}_N^{*}]$ [45]. The optimization problem can thus be formulated as follows

$$\underset{{\{\mathbf{f}(k)\}}_{k=0}^N}{\text{max}}\{\frac{1}{N}I({\mathbf{y}}_N;{\mathbf{s}}_N)\}$$

$$\mathbf{\text{subject to}}:\frac{1}{N}\mathbf{\text{tr}}({\mathbf{F}}_N{\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*})\le P_0$$

$$\mathbf{w}/\mathbf{o}{\lambda }_{\mathit{\text{max}}}({\mathbf{F}}_N{\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*})\le L_0$$ (6)

where tr(·) and λ_max(·) are respectively the matrix trace and the largest singular value. The first constraint limits the average power (the mean of all singular values) and the second constraint limits the peak power (the largest singular value) [46]. The latter constraint imposes upper bounds on the amount of charge injected into the tissue to avoid damage to the tissue and/or the electrode. The information theoretic criterion bears close relationship with that of the Minimum Mean Square Error (MMSE) for a linear decoder when both the precoder and decoder are jointly optimized (See Appendix .1).

2.4. Frequency Domain Formulation of the Information Theoretic Criterion

Unlike the precoding problem formulated in [46] in which the precoding matrix F_N can be arbitrarily chosen, F_N in our problem formulation is in a structured form of a block circulant matrix and is completely decided by @@@${\{\mathbf{f}(k)\}}_{k=0}^{N-1}$. Without any simplifying assumptions on the structure of Φ_sN, the closed-form solution to the problem stated above is not easy to obtain. In addition, as the duration length N can be arbitrarily chosen, the solution, even obtained, would not reveal much about its relationship with the dynamic properties of the transfer function from u to y. To gain more insight into how information should be precoded in order to maximize the information transfer, we reformulated the problem in frequency domain by using the well-known asymptotic properties of the eigenvalue distributions of Toeplitz (and/or block Toeplitz) matrices [47, 48].

By replacing F_N, G_N, Φ_sN and Φ_zN with their block circulant counterparts @@@${\mathbf{F}}_N^c,{\mathbf{G}}_N^c,{\mathrm{\Phi }}_{s_N}^c$ and @@@${\mathrm{\Phi }}_{z_N}^c$ (see Appendix (Appendix .2)), as N → ∞, we have

$$\frac{1}{N}|I({\mathbf{y}}_N;{\mathbf{s}}_N)-{\text{log}}_2\text{det}({\mathbf{G}}_N^c{\mathbf{F}}_N^c{\mathrm{\Phi }}_{s_N}^c{({\mathbf{F}}_N^c)}^{*}{({\mathbf{G}}_N^c)}^{*}{({\mathrm{\Phi }}_{z_N}^c)}^{-1}+\mathbf{I})|\to 0$$

$$\frac{1}{N}|\mathbf{\text{tr}}({\mathbf{F}}_N{\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*})-\mathbf{\text{tr}}({\mathbf{F}}_N^c{\mathrm{\Phi }}_{s_N}^c{({\mathbf{F}}_N^c)}^{*})|\to 0$$

$$|{\lambda }_{\mathit{\text{max}}}({\mathbf{F}}_N{\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*})-{\lambda }_{\mathit{\text{max}}}({\mathbf{F}}_N^c{\mathrm{\Phi }}_{s_N}^c{({\mathbf{F}}_N^c)}^{*})|\to 0$$

Therefore, we can reformulate the optimization problem in the frequency domain as follows (see Appendix .2)

$$\underset{\mathbf{F}(w)}{\text{max}}\{\frac{1}{N}\sum _{w=\frac{2\pi k}{N},k=0}^{N-1}{\text{log}}_2\text{det}({\mathbf{G}}^{*}(w){\mathbf{R}}_z^{-1}(w)\mathbf{G}(w)\mathbf{F}(w){\mathbf{R}}_s(w){\mathbf{F}}^{*}(w)+I_{M_u})\}$$

$$\mathbf{\text{subject to}}:\frac{1}{N}\sum _{w=\frac{2\pi k}{N},k=0}^{N-1}\mathbf{\text{tr}}(\mathbf{F}(w){\mathbf{R}}_s(w){\mathbf{F}}^{*}(w))\le P_0$$

$$\mathbf{w}/\mathbf{o}\underset{w=\frac{2\pi k}{N},k=0,\dots ,N-1}{\text{max}}{\lambda }_{\mathit{\text{max}}}(\mathbf{F}(w){\mathbf{R}}_s(w){\mathbf{F}}^{*}(w))\le L_0$$ (7)

where @@@$\mathbf{G}(w)={\sum }_{k=0}^{\infty }\mathbf{g}(k)e^{-iwk},\mathbf{F}(w)={\sum }_{k=0}^{\infty }\mathbf{f}(k)e^{-iwk}$, E[z(n)z(n − m)*] = r_z(m), −∞ < m < +∞, E[s(n)s(n − m)*] = r_s(m), −∞ < m < +∞, @@@${\mathbf{R}}_z(w)={\sum }_{m=-\infty }^{+\infty }{\mathbf{r}}_z(m)e^{-imw}$, and @@@${\mathbf{R}}_s(w)={\sum }_{m=-\infty }^{+\infty }{\mathbf{r}}_s(m)e^{-imw}$.

For each @@@$w=\frac{2\pi k}{N}$, k = 0. …, N − 1, we compute the singular value decomposition of @@@${\mathbf{G}}^{*}(w){\mathbf{R}}_z^{-1}(w){\mathbf{G}(w)|}_{w=\frac{2\pi k}{N}}=U_k{\mathrm{\Lambda }}_k{U}_k^{*}$, so that the diagonal elements of Λ_k are the M_u singular values λ_k,1 ≥ … ≥ λ_k,Mu ≥ 0 arranged in descending order. Similarly, we compute the singular value decomposition of @@@${{\mathbf{R}}_s(w)|}_{w=\frac{2\pi k}{N}}=V_k{\mathrm{\Sigma }}_k{V}_k^{*}$, k = 0, …, N − 1, so that the diagonal elements of Σ_k are the M_s singular values σ_k,1 ≥ … σ_k,Ms ≥ 0 arranged in descending order.

We will assume for now that the precoding filters have the following frequency response characteristics

$${\mathbf{F}(w)|}_{w=\frac{2\pi k}{N}}=N_k{F}_k{V}_k^{*},k=0,\dots ,N-1$$ (8)

where F_k is of dimension M_u × M_s and (F_k)_i,j = 0, ∀i ≠ j. This form of solution is directly adopted from [49], in which it has been shown to result in no loss of optimality under MMSE criterion. We then substitute into the objective function in (7), and will then have

$$\frac{1}{N}\sum _{k=0}^{N-1}\sum _m^{\text{min}\{M_u,M_s\}}{\text{log}}_2({\lambda }_{k,m}{\sigma }_{k,m}{|{(F_k)}_{m,m}|}^2+1)$$ (9)

Because (9) depends on only the first min{M_u, M_s} singular values, we can thus set |(F_k)_m,m|² = 0, ∀m > min{M_u, M_s} and readapt the constraints as follows

$$\frac{1}{N}\sum _{k=0}^{N-1}\sum _m^{\text{min}\{M_u,M_s\}}{\sigma }_{k,m}{|{(F_k)}_{m,m}|}^2\le P_0$$ (10)

with/without

$$\underset{0\le k\le N-1,1\le m\le \text{min}\{M_u,M_s\}}{\text{max}}\{{\sigma }_{k,m}{|{(F_k)}_{m,m}|}^2\}\le L_0$$ (11)

We will first consider the case of maximizing (9) with a single constraint (10), and then we will extend to the case when both constraints (10) and (11) are present. The first case, the optimal solution for |(F_k)_m,m|², N = 0, …, N − 1, m = 1, …, min{M_u, M_s} is

$${|{(F_k)}_{m,m}|}^2={(\frac{1}{\nu {\sigma }_{k,m}}-\frac{1}{{\lambda }_{k,m}{\sigma }_{k,m}})}^{+}$$ (12)

$$\sum _{k=0}^{N-1}\sum _{m=1}^{\text{min}\{M_u,M_s\}}{\sigma }_{k,m}{|{(F_k)}_{m,m}|}^2=N{P}_0$$

where @@@$\frac{1}{\nu }$ is the design parameter described in [50] which sets the ”water level” over the landscape shaped by @@@$\frac{1}{{\lambda }_{k,m}}$. More water is poured into regionswith large λ_k,m, where λ_k,m is essentially the Signal to Noise Ratio (SNR) of the m^th subchannel after decompostion at frequency @@@$w=\frac{2\pi k}{N}$. Subchannel here is defined as the channel with input in one stimulation direction and output in a direction for a given frequency as determined by singular value decomposition. In addition, the solution (12) only specifies the amplitude of |(F_k)_m,m|² and thus leaves the phase to freely change without affecting the optimality of the solution.

In the case when both constraints have to be satisfied, the optimal solution for |(F_k)_m,m|², N = 0, …, N − 1, m = 1, …, min{M_u, M_s} is

$${|{(F_k)}_{m,m}|}^2=\text{min}\{\frac{L_0}{{\sigma }_{k,m}},{(\frac{1}{\nu {\sigma }_{k,m}}-\frac{1}{{\lambda }_{k,m}{\sigma }_{k,m}})}^{+}\}$$ (13)

$$\sum _{k=0}^{N-1}\sum _{m=1}^{\text{min}\{M_u,M_s\}}{\sigma }_{k,m}{|{(F_k)}_{m,m}|}^2=N\text{min}\{P_0,\text{min}\{M_u,M_s\}{L}_0\}$$

3. Results and Discussion

3.1. Numerical Examples of Space-time Precoding

We randomly selected four out of eight thalamic neurons to stimulate and eight out of sixteen available cortical pyramidal neurons to record from. We chose to use a fraction of the available neurons for stimulation and recording to better resemble a biological experiment where there are uncontrolled inputs and unobserved outputs to the system. The other thalamic neurons still accept random stimulation inputs that serve as sources of noise inputs to the thalamocortical network. A four-input-eight-output linear LTI model is then fitted to the input-output data simulated using the neural circuit described in Section 2.1. Our objective is to transmit four artificial sensory signals acc1, acc2, vel1, and vel2 representing the acceleration and velocity of the limb in 2D space to the measured outputs of the eight cortical pyramidal neurons using the maximally informative criterion under the average power constraint. Behavioral data was collected in the Miller Laboratory of Limb Motor Control (Northwestern University) from a non-human primate performing a serial target pursuit task in which hand velocity and acceleration were sampled using a KINARM (BKIN Technologies, Kingston, Ontario, Canada) at a rate of 1kHz. Both acceleration and velocity were decomposed into two signals representing their respective X and Y components. Figure 3(b) shows the design of optimal space-time precoder using the weighted waterfilling algorithm [50]. The water level 1/ν is the highest in the lowest areas of the two-dimensional landscape formed by 1/λ_k,m, where λ_k,m is the SNR of the m^th subchannel after decomposition at frequency @@@$w=\frac{2\pi k}{N}$ when each stimulation input has unit variance.

Figure 3.

Numerical examples of the design of space-time precoders. The neural circuit under stimulation has four simulation inputs and eight measured outputs. (a) The log of the frequency representation of the input signals after decomposition. (b) Optimal power allocation over frequency and independent channels after decomposition. (c) The space-time precoding filter coefficients from sensory signals s₁(n) and s₂(n) to stimulation inputs u₁(n) and u₂(n). (d) The Effects of precoding on the spread of the evoked spatiotemporal patterns projected along the first and the second principal components. (e) The statistics of the Euclidean distance between the nearest neighbors. The distance between nearest neighbors are 204 ± 56 for the optimal precoder, 192 ± 37 for the suboptimal precoder, and 176 ± 34 for the identity precoder. (f) The distribution of power along the eigenvalues of the system output.

The optimal precoder coefficients from stimulus signals to stimulation inputs are plotted in Figure 3(c). Because the optimization problem formulated in frequency domain does not impose causality constraint on the precoding filter, the coefficients are not necessarily zero for t < 0. To ensure the filter can be implemented in real time, we thus circularly shift the filter coefficients and introduce a delay of several milliseconds similar to what has been done in [38]. Figure 3(d) shows a reduced dimensional representation of the spatiotemporal patterns evoked at the eight output cortical PY neurons. The spatiotemporal patterns generated by the optimal precoder are more dispersed in the principal component domain than those of a suboptimal precoder. The suboptimal precoder was generated by reversing the order of the product σ_k,m|(F_k)_m,m|² according to m for each k = 0, …, N − 1. The newly assigned |(F_k)_m,m|² is then used to calculate the coefficients of the suboptimal precoder based on equation (8). We also examined the case of an identity precoder in which stimulus signals were connected independently to stimulation inputs with coefficients such that it was of equal power to the other precoders. We then computed the nearest neighbor for each output pattern in the principal component domain to further verify that the optimal precoder evoked more evenly dispersed spatiotemporal responses for the eight PY neurons than the suboptimal or identity precoders (Figure 3(e)). Since the suboptimal precoder performed better than the identity precoder, subsequent analysis is presented only for the optimal and suboptimal precoders for the sake of clarity. We also examined the normalized eigenvalues of the principal components for the output patterns for the optimal and suboptimal precoders. If the optimal precoder generates more dispersed output patterns, we would expect the output activity to be more evenly distributed amongst all the principal components. Figure 3(f) shows the normalized eigenvalues for the optimal precoder are indeed more evenly distributed than those of the suboptimal precoder. Encoding information using more scattered spatiotemporal patterns might improve the discriminability of the state of the limb in brain space. In addition, the space-time encoding might also promote rapid and smooth learning of the artificial sensory information by the brain because it is continuously encoded, just as natural stimuli are.

3.2. Effects of Noise

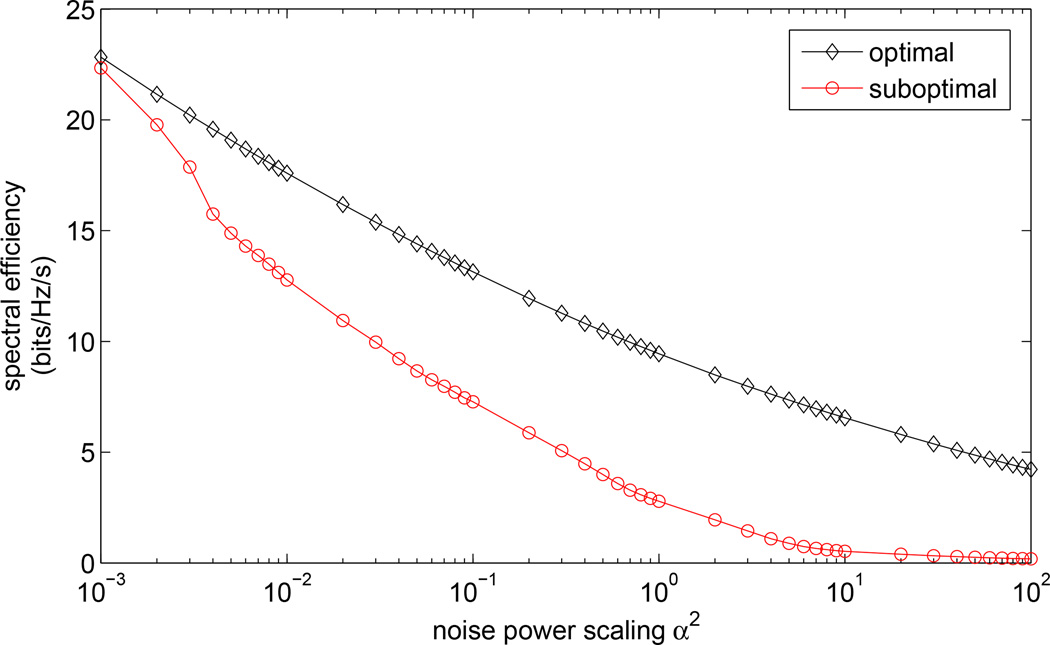
Characterizing the effects of noise on the proposed strategy is crucial for the following reasons: first, the thalamus transmits and process information to and from cortex [51], and was recently shown to have an important role in regulating the asynchronous cortical state [25]. Second, the microstimulation evoked response will undoubtedly interact with ongoing cortical activity representing a myriad of other natural sensory drives and cognitive processes. Third, our mathematical formulation assumes the thalamocortical pathway is modeled as an LTI system, which - despite providing a reasonable approximation to some thalamocortical response phenomena - is rather simplistic. Therefore, it was important to examine the effects of noise in the system on the ability to transmit the desired information to the observed cortical population. Sources of noise here could be the nonlinearities of the circuit, inputs from other brain regions such as the visual cortex, or failure to elicit cortical action potentials. Figure 4 shows the optimal and suboptimal spectral efficiency as we vary the noise power. Spectral efficiency is the information rate divided by the bandwidth of the system and is a way tomeasure how efficiently a system with a fixed bandwidth is being used [52]. The best achievable information rates have an approximately linear relationship with noise power on a logarithmic scale, particularly in low noise power range. At extremely low noise levels, the difference between the optimal and the suboptimal information rates diminishes and the choice of precoding design has little or no effect on the information transfer between the artificial sensory signals and the evoked responses. The advantages of the optimal precoding proposed here become most apparent when the noise levels are relatively high (for a given system function {g(k)}), which further supports the proposed approach since an ideal sensory prosthetic should be robust against high levels of ongoing - perhaps unrelated - neural activity.

Figure 4.

The effects of noise power on achievable information rates. The power constraint P₀ is kept the same for all power scaling factors. Here we define noise power scaling factor, α, as in y = Gu + αz.

3.3. Effects of Space-time Precoding on Decoding Sensory Activity

To test the quality of the cortical representation of the artificial sensory input, we used a linear decoder to quantify our results. If the stimulation patterns were optimally chosen, a decoder should be able to reconstruct the artificial sensory signals that indicate the state of the prosthetic device with high fidelity from the cortical activity. If, however, the stimulation patterns were poorly chosen, the discriminability and consistency of cortical response will suffer and the ability of a decoder to reconstruct the original sensory signals should decrease. A suboptimal precoder might therefore provide weaker proprioceptive feedback that is more contaminated by noise, which has been shown to decrease performance in BMI experiments [2]. The precoder design had a significant impact on the decoding performance. Figure 5 shows the effects of space-time precoding on the decoding performance. The decoder is a simple Wiener FIR filter that is fitted to the data from the eight measured cortical outputs to the four sensory signals as input to the precoder by minimizing the mean squared error. The decoded sensory signals under optimal (left panels) and suboptimal (right panels) precoding are shown in Figure 5(a). Even though the optimal precoder does not necessarily result in smaller mean squared errors for each individual sensory signal, the overall mean squared error from all precoded sensory signals is smaller (see Figure 5(b)). For our test data described above, the decoding results were better with the optimal precoder for both the individual sensory signals as well as the total. The design of the space-time precoder, however, assumes the sensory signals are jointly Gaussian, which may not always be the case. For arbitrary input distributions, one may consider the so-called mercury/waterfilling algorithm [50].

Figure 5.

The effects of space-time precoding on decoding performance. The system has four simulation inputs and eight measured outputs. (a) The decoded sensory signals under optimal (left panels) and suboptimal (right panels) precoding. Total four sensory signals acc1, acc2, vel1, and vel2 are precoded. (b) The mean squared decoding error for each sensory signal and the overall mean squared decoding error for all sensory signals.

3.4. Effects of Input Neuron Selection

We tested the performance of the precoder for different sets of input neurons. Twenty random permutations of four thalamic neurons were tested with a fixed set of eight output cortical neurons. Based on our results from section 3.2, we would expect the optimal precoder to perform at least as well as the suboptimal precoder and potentially much better. Inputs to the system were randomly generated colored gaussian signals which were bandpass filtered. We attempted to recover the original input signals from the cortical unit activity via a simple linear decoder as in section 3.3. The performance of the precoders was assessed by subtracting the sum of the mean square errors of the decoder outputs of the optimal precoder from the suboptimal precoder. The optimal precoder performed better in 70% of the cases and virtually identically in 15% of the cases as shown in Figure 6. In the remaining 15% of cases where the suboptimal precoder performed better, the difference was small, whereas the optimal precoder generally showed larger improvements in performance when superior.

Figure 6.

The differences in performance between the optimal and suboptimal precoders for various selections of input neurons. A unique set of input neurons was randomly selected for trial shown here.

4. Conclusion

It is highly desirable to have a strategy for optimally “writing-in” to the brain when replacing lost natural sensory input with artificial sensation. Designing microstimulation strategies that optimize the choice of stimulation patterns for a given system is crucial to fulfill this goal. By maximally exploiting the information theoretical constraints imposed by the underlying neural circuit under microstimulation, one can maximize the amount of information fedback to the brain in a bi-directional BMI. The use of an information theoretic criterion for system optimization provides a workaround when natural response patterns are unknown as a result of physiological neural damage, or as a result of unknown natural sensory encoding mechanisms. It is our hope that the continuous mapping of sensory information to optimized microstimulation by the precoder presented here would result in cortical spatiotemporal patterns that the subject can quickly learn to associate with a concurrent motor experience. Experiments involving electrical stimulation of peripheral nerves have demonstrated that subjects were able to learn to interpret the sensations generated by the stimulus [7]. By maximizing the distance between microstimulation-evoked spatiotemporal patterns it is expected that this will consequently maximize the discriminability between evoked sensations and aid in this learning. Furthermore, our study showed that optimal precoding makes transmission of information to the brain more robust against noise. We believe this information theoretic approach could be easily adapted to and validated in biological experiments.

Even though we focused on the thalamocortical pathway in the somatosensory system here, the approach could be adapted for other sensory systems. In particular, the approach can be used, for example, to optimize the stimulation patterns along the visual pathway, particularly in the lateral geniculate nucleus (LGN) in vision prosthesis [26, 27]. More sophisticated models of a given afferent pathway may enable further optimization of the approach to fit a wide range of BMI applications.

The physiological effects of direct microstimulation of the cortex are known to be complex and sometimes unpredictable [53]. Direct electrical stimulation of the cortex could affect distal regions of the brain which could have undesirable effects for a sensory prosthetic device. Electrical microstimulation of the thalamus may also affect cortico-cortical signal propagation as a function of stimulation frequency which could potentially have significant implications for our work [54]. A possible direction for future work would be to examine which spatiotemporal microstimulation patterns result in disruption of cortico-cortical signal transmission and avoid them in precoder design. Rather than trying to force the system to conform to preselected putative cortical states that are not measured by current strategies [55], our approach can be understood as a continuous time mapping of artificial sensory signals to the easiest achievable cortical states (in the sense of requiring the least stimulation power to evoke maximally informative cortical neural responses), thereby minimizing tissue and electrode damage and potential side effects that may be caused by lack of stimulation specificity.

Appendix .1

Relationship with Minimum Mean Square Error

Suppose we would like to recover the transmitted signals s_N from the measured response y_N using a decoder matrix D_N, the system then becomes

$${\mathbf{ŝ}}_N={\mathbf{D}}_N{\mathbf{y}}_N={\mathbf{D}}_N{\mathbf{G}}_N{\mathbf{F}}_N{\mathbf{s}}_N+{\mathbf{D}}_N{\mathbf{z}}_N$$ (.1)

We define the Mean Square Error matrix as follows [46]

$$MSE({\mathbf{F}}_N,{\mathbf{D}}_N)=E[({\mathbf{ŝ}}_N-{\mathbf{s}}_N){({\mathbf{ŝ}}_N-{\mathbf{s}}_N)}^{*}]=({\mathbf{D}}_N{\mathbf{G}}_N{\mathbf{F}}_N-\mathbf{I}){\mathrm{\Phi }}_{s_N}{({\mathbf{D}}_N{\mathbf{G}}_N{\mathbf{F}}_N-\mathbf{I})}^{*}+{\mathbf{D}}_N{\mathrm{\Phi }}_{z_N}{\mathbf{D}}_N^{*}$$

Substitute the Wiener receiver that minimizes the cumulative MSE E[(ŝ_N − s_N)*(ŝ_N − s_N)] = tr(MSE(F_N, D_N)), i.e.

$${\mathbf{D}}_{\mathit{\text{Wiener}}}={\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}{\mathbf{G}}_N^{*}{({\mathbf{G}}_N{\mathbf{F}}_N{\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}{\mathbf{G}}_N^{*}+{\mathrm{\Phi }}_{z_N})}^{-1}$$

for D_N in MSE(F_N, D_N), with some algebra we can arrive at

$$MSE({\mathbf{F}}_N,{\mathbf{D}}_{\mathit{\text{Wiener}}})={({\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}{\mathbf{G}}_N^{*}{\mathrm{\Phi }}_{z_N}^{-1}{\mathbf{G}}_N{\mathbf{F}}_N+\mathbf{I})}^{-1}{\mathrm{\Phi }}_{s_N}$$

Given Φ_sN, minimizing det(MSE(F_N, D_Wiener)) becomes equivalent to maximizing det @@@$\text{det}({\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}{\mathbf{G}}_N^{*}{\mathrm{\Phi }}_{z_N}^{-1}{\mathbf{G}}_N{\mathbf{F}}_N+\mathbf{I})$, and thus the mutual information I(y_N; s_N) between s_N and y_N.

Next consider the mutual information I(ŝ_N; s_N) between ŝ_N and s_N, i.e.,

$$I({\mathbf{ŝ}}_N;{\mathbf{s}}_N)=H({\mathbf{ŝ}}_N)-H({\mathbf{ŝ}}_N|{\mathbf{s}}_N)={\text{log}}_2\text{det}({\mathbf{D}}_N{\mathbf{G}}_N{\mathbf{F}}_N{\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}{\mathbf{G}}_N^{*}+{\mathbf{D}}_N{\mathrm{\Phi }}_{z_N}{\mathbf{D}}_N^{*})-{\text{log}}_2\text{det}({\mathbf{D}}_N{\mathrm{\Phi }}_{z_N}{\mathbf{D}}_N^{*})$$

Substitute D_Wiener for D_N in I(ŝ_N; s_N), we arrive at

$$I({\mathbf{ŝ}}_N;{\mathbf{s}}_N)|{\mathbf{D}}_{\mathit{\text{Wiener}}}={\text{log}}_2\text{det}({\mathrm{\Phi }}_{s_N}{\mathbf{F}}_N^{*}{\mathbf{G}}_N^{*}{\mathrm{\Phi }}_{z_N}^{-1}{\mathbf{G}}_N{\mathbf{F}}_N+\mathbf{I})$$

which is exactly the same with I(y_N; s_N). In other words, the optimal Wiener decoder D_Wiener does not result in any information loss.

Appendix .2

Frequency Domain Representation

Construct the block circulant matrices based on G_N and F_N as follows

$${\mathbf{G}}_N^c=\left[\begin{array}{ccccc}\hfill \mathbf{g}(0)\hfill & \hfill \mathbf{g}(1)\hfill & \hfill \cdots \hfill & \hfill \mathbf{g}(N-2)\hfill & \hfill \mathbf{g}(N-1)\hfill \\ \hfill \mathbf{g}(N-1)\hfill & \hfill \mathbf{g}(0)\hfill & \hfill \cdots \hfill & \hfill \mathbf{g}(N-3)\hfill & \hfill \mathbf{g}(N-2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \mathbf{g}(2)\hfill & \hfill \mathbf{g}(3)\hfill & \hfill \cdots \hfill & \hfill \mathbf{g}(0)\hfill & \hfill \mathbf{g}(1)\hfill \\ \hfill \mathbf{g}(1)\hfill & \hfill \mathbf{g}(2)\hfill & \hfill \cdots \hfill & \hfill \mathbf{g}(N-1)\hfill & \hfill \mathbf{g}(0)\hfill \end{array}\right]$$

and

$${\mathbf{F}}_N^c=\left[\begin{array}{ccccc}\hfill \mathbf{f}(0)\hfill & \hfill \mathbf{f}(1)\hfill & \hfill \cdots \hfill & \hfill \mathbf{f}(N-2)\hfill & \hfill \mathbf{f}(N-1)\hfill \\ \hfill \mathbf{f}(N-1)\hfill & \hfill \mathbf{f}(0)\hfill & \hfill \cdots \hfill & \hfill \mathbf{f}(N-3)\hfill & \hfill \mathbf{f}(N-2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \mathbf{g}(2)\hfill & \hfill \mathbf{g}(3)\hfill & \hfill \cdots \hfill & \hfill \mathbf{f}(0)\hfill & \hfill \mathbf{f}(1)\hfill \\ \hfill \mathbf{g}(1)\hfill & \hfill \mathbf{g}(2)\hfill & \hfill \cdots \hfill & \hfill \mathbf{f}(N-1)\hfill & \hfill \mathbf{f}(0)\hfill \end{array}\right]$$

Let F(w) and G(w) denote the discrete time Fourier transform (DTFT) of {f (k)} and {g(k)}, respectively, i.e., @@@$\mathbf{G}(w)={\sum }_{k=0}^{\infty }\mathbf{g}(k)e^{-iwk}$ and @@@$\mathbf{F}(w)={\sum }_{k=0}^{\infty }\mathbf{f}(k)e^{-iwk}$. Then both @@@${\mathbf{F}}_N^c$ and @@@${\mathbf{G}}_N^c$ can be written as follows

$${\mathbf{G}}_N^c=({\mathbf{U}}_N\otimes I_{M_y})\left[\begin{array}{ccc}\hfill \mathbf{G}(0)\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill \mathbf{G}(\frac{2\pi (N-1)}{N})\hfill \end{array}\right]{({\mathbf{U}}_N\otimes I_{M_u})}^{*}$$

$${\mathbf{F}}_N^c=({\mathbf{U}}_N\otimes I_{M_u})\left[\begin{array}{ccc}\hfill \mathbf{F}(0)\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill \mathbf{F}(\frac{2\pi (N-1)}{N})\hfill \end{array}\right]{({\mathbf{U}}_N\otimes I_{M_s})}^{*}$$

where @@@$U_N={(\frac{1}{\sqrt{N}}{e}^{\frac{-i2\pi jk}{N}})}_{j,k=0}^{N-1}$ is the N × N Fourier unitary matrix, and ⊗ is the Kronecker product(or tensor product). Consider covariance matrix Φ_zN, i.e.,

$${\mathrm{\Phi }}_{z_N}=\left[\begin{array}{cccc}\hfill {\mathbf{r}}_z(0)\hfill & \hfill {\mathbf{r}}_z(1)\hfill & \hfill \cdots \hfill & \hfill {\mathbf{r}}_z(N-1)\hfill \\ \hfill {\mathbf{r}}_z(-1)\hfill & \hfill {\mathbf{r}}_z(0)\hfill & \hfill \cdots \hfill & \hfill {\mathbf{r}}_z(N-2)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{r}}_z(-(N-1))\hfill & \hfill {\mathbf{r}}_z(-(N-2))\hfill & \hfill \cdots \hfill & \hfill {\mathbf{r}}_z(0)\hfill \end{array}\right]$$

which is a block Toeplitz matrix. Under conditions specified in [56], it can be shown that the following matrix converges to its inverse @@@${\mathrm{\Phi }}_{z_N}^{-1}$

$${({\mathrm{\Phi }}_{z_N}^c)}^{-1}=(U_N\otimes I_{M_y}){\left[\begin{array}{ccc}\hfill {\mathbf{R}}_z(0)\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathbf{R}}_z(\frac{2\pi (N-1)}{N})\hfill \end{array}\right]}^{-1}{(U_N\otimes I_{M_y})}^{*}$$

where R_z(w) is the DTFT of {r_z(m)}, i.e., where @@@${\mathbf{R}}_z(w)={\sum }_{m=-\infty }^{+\infty }{\mathbf{r}}_z(m)e^{-imw}$. Similarly, @@@${\mathrm{\Phi }}_{s_N}^c$ converges to the covariance matrix Φ_sN

$${\mathrm{\Phi }}_{s_N}^c=(U_N\otimes I_{M_s})\left[\begin{array}{ccc}\hfill {\mathbf{R}}_s(0)\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathbf{R}}_s(\frac{2\pi (N-1)}{N})\hfill \end{array}\right]{(U_N\otimes I_{M_s})}^{*}$$

where R_s(w) is the DTFT of {r_s(m)}, i.e., where @@@${\mathbf{R}}_s(w)={\sum }_{m=-\infty }^{+\infty }{\mathbf{r}}_s(m)e^{-imw}$ .1pm

Substitute G_N, F_N, Φ_zN and Φ_sN with their respective block circulant matrices @@@${\mathbf{G}}_N^c,{\mathbf{F}}_N^c,{\mathrm{\Phi }}_{z_N}^c$ and @@@${\mathrm{\Phi }}_{s_N}^c$, we can dramatically simplify the formula for mutual information as follows

$${\text{log}}_2\text{det}({\mathbf{G}}_N^c{\mathbf{F}}_N^c{\mathrm{\Phi }}_{s_N}^c{({\mathbf{F}}_N^c)}^{*}{({\mathbf{G}}_N^c)}^{*}{({\mathrm{\Phi }}_{z_N}^c)}^{-1}+\mathbf{I})==\sum _{w=\frac{2\pi k}{N},k=0}^{N-1}{\text{log}}_2\text{det}(\mathbf{G}(w)\mathbf{F}(w){\mathbf{R}}_s(w){\mathbf{F}}^{*}(w){\mathbf{G}}^{*}(w){\mathbf{R}}_z^{-1}(w)+I_{M_y})=\sum _{w=\frac{2\pi k}{N},k=0}^{N-1}{\text{log}}_2\text{det}({\mathbf{G}}^{*}(w){\mathbf{R}}_z^{-1}(w)\mathbf{G}(w)\mathbf{F}(w){\mathbf{R}}_s(w){\mathbf{F}}^{*}(w)+I_{M_u})$$

Appendix .3

Alternative Minimum Mean Square Error Criterion

We have shown in Appendix .1 that minimization of the determinant of the mean square error matrix with optimal Wiener decoder, i.e., det (MSE(F_N, D_Wiener)), is equivalent to maximization of the mutual information I(y_N; s_N). A more commonly used alternative, however, is to minimize the trace of the mean square error matrix, i.e., tr (MSE(F_N, D_Wiener)). Following the same procedure used in Appendix .2, we can simplify the problem as follows

$$\text{min}\left\{\frac{1}{N}\sum _{k=0}^{N-1}\sum _m^{\text{min}\{M_u,M_s\}}\frac{{\sigma }_{k,m}}{{\lambda }_{k,m}{\sigma }_{k,m}{|{(F_k)}_{m,m}|}^2+1}\right\}$$ (.2)

such that

$$\frac{1}{N}\sum _{k=0}^{N-1}\sum _{m=1}^{\text{min}\{M_u,M_s\}}{\sigma }_{k,m}{|{(F_k)}_{m,m}|}^2=P_0$$

The closed-form solution is thus

$${|{(F_k)}_{m,m}|}^2={(\sqrt{\frac{1}{\nu {\lambda }_{k,m}{\sigma }_{k,m}}}-\frac{1}{{\lambda }_{k,m}{\sigma }_{k,m}})}^{+}$$ (.3)

where ν is chosen to satisfy the above power constraint.