Evaluation of Approaches to Analyzing Continuous Correlated Eye Data When Sample Size Is Small

Abstract

Purpose

To evaluate the performance of commonly used statistical methods for analyzing continuous correlated eye data when sample size is small.

Methods

We simulated correlated continuous data from two designs: (1) two eyes of a subject in two comparison groups; (2) two eyes of a subject in the same comparison group, under various sample size (5–50), inter-eye correlation (0–0.75) and effect size (0–0.8). Simulated data were analyzed using paired t-test, two sample t-test, Wald test and score test using the generalized estimating equations (GEE) and F-test using linear mixed effects model (LMM). We compared type I error rates and statistical powers, and demonstrated analysis approaches through analyzing two real datasets.

Results

In design 1, paired t-test and LMM perform better than GEE, with nominal type 1 error rate and higher statistical power. In design 2, no test performs uniformly well: two sample t-test (average of two eyes or a random eye) achieves better control of type I error but yields lower statistical power. In both designs, the GEE Wald test inflates type I error rate and GEE score test has lower power.

Conclusion

When sample size is small, some commonly used statistical methods do not perform well. Paired t-test and LMM perform best when two eyes of a subject are in two different comparison groups, and t-test using the average of two eyes performs best when the two eyes are in the same comparison group. When selecting the appropriate analysis approach the study design should be considered.

Introduction

In the preclinical or early phase of clinical investigation of eye diseases, measurements (e.g. visual acuity, intraocular pressure, refractive error) are often taken from both eyes of a small number of subjects.¹ The two eyes of a subject can be either in different treatment groups (e.g. paired design for gene therapy of retinal eye disease^2,3) or in the same treatment group (e.g. systemic dietary supplements for treating eye diseases^2,4,5). Such design usually requires the eye as the unit of analysis,^6,7 and the proper statistical analysis of correlated eye data requires accounting for their inter-eye correlation.^1,8–11 Continuous correlated data from two eyes are commonly analyzed by paired t-test, two sample t-test (using the average value of two eyes or a random eye), or statistical regression models.^8,9,11 The two most commonly used statistical models for correlated eye data are the mixed effects model¹² and the population-average model (i.e. the marginal model) using the generalized estimating equations (GEE) approach.¹³ However, statistical inferences of these models are based on the large-sample approximation. Little is known about their performance in the analysis of continuous correlated eye data when the sample size is small. Furthermore, when using a specific statistical model, there are a variety of options to specify the covariance structures (e.g. unstructured, compound symmetry, independent working correlation) and to select the statistical test (e.g. Wald test, score test). It is uncertain whether using different covariance structure or different statistical tests will provide substantially different results, particularly when the sample size is small.

Motivated by correlated eye data from ophthalmic and vision research, we conducted a simulation study to compare the relative performance of commonly used analysis methods for continuous correlated eye data with small sample size under two designs: (1) two eyes of the same subject are assigned to two different comparison groups; (2) two eyes of a subject are in the same comparison group. We then demonstrated these analysis approaches through analyzing two real datasets from ophthalmic clinical studies. This paper aims to guide the selection of the most appropriate method for analyzing correlated eye data when sample size is small from either of these two study designs.

Methods

We designed our simulation study following the guidelines for the simulation studies in medical statistics.¹⁴ The study adheres to the guidelines of the Declaration of Helsinki. The approval of an Institutional Review Board and the patient consent were not needed for this simulation study.

Simulation settings

We were interested in comparing the mean difference between two comparison groups for the continuous ocular measurements taken from both eyes of a small number of subjects. Thus, we simulated the normally distributed data from bivariate normal distribution with covariance matrices specified corresponding to the study design. We simulated data under various settings of sample size (5, 10, 20, 30, 50), inter-eye correlation (0, 0.25, 0.50, 0.75), and mean difference between two groups for treatment effect (0, 0.4, 0.8).

We simulated data under two designs that are commonly used in ophthalmic and vision research. Design 1 assigns two eyes of a subject to two different treatment or comparison groups (e.g. in paired design, one eye in the treatment group, the fellow eye in the control group). This design is often used for the eye-specific treatment for bilateral eye diseases, e.g. retinal gene therapy of eye disease.^2,3 The treatment effect is quantified by the mean difference of the continuous outcome measure between the treated eye and the untreated fellow eye. For this design, the normally distributed correlated eye data were generated from the following bivariate normal distribution with mean of μ and variance of Σ:

$$\begin{gathered} \mathrm{X}~\text{MVN}(\mathrm{\mu },\mathrm{\sum }), \\ X=\left[\begin{array}{c}{X}_1\\ X_2\end{array}\right],\mathrm{\mu }=\left[\begin{array}{c}D\\ 0\end{array}\right],\mathrm{\sum }=\left[\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right], \end{gathered}$$

where X₁ represents the continuous measurement from the eye assigned to the treated group, X₂ represents the continuous measurement from the fellow eye assigned to the control group, D is the treatment effect, and ρ is the inter-eye correlation.

In design 2, two eyes of the same subject are assigned to the same treatment group (e.g. systemic treatment^4,5) with some subjects in the treated group, while other subjects were in the control group. For this design, the continuous correlated eye data were generated from the following bivariate normal distribution.

$$\begin{gathered} \mathrm{X}~\text{MVN}(\mathrm{\mu },\mathrm{\sum }) \\ X=\left[\begin{array}{c}{X}_1\\ X_2\end{array}\right],\mathrm{\mu }=\left[\begin{array}{c}0\\ 0\end{array}\right]\text{or}\left[\begin{array}{c}D\\ D\end{array}\right],\mathrm{\sum }=\left[\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right], \end{gathered}$$

where X₁, X₂ represent the continuous measurement of the left eye and right eye of the same subject respectively. If the subject is assigned to the treated group, $\mathrm{\mu }=\left[\begin{array}{c}D\\ D\end{array}\right]$, otherwise for a subject in the control group, $\mathrm{\mu }=\left[\begin{array}{c}0\\ 0\end{array}\right]$. D is the 0 treatment effect, and ρ is the inter-eye correlation. We assume equal sample size for the number of subjects in the treated group and control group.

Statistical methods evaluated

Each simulated dataset is analyzed using non-model-based analysis approaches (e.g. two sample t-test, paired t-test) and model-based approaches (e.g. marginal model and mixed effects model). These statistical methods are selected because they are commonly (appropriately or inappropriately) used in ophthalmic and vision research. Evaluating their relative performance under various simulation settings is important to provide practical guidance on choosing the most appropriate approach for analyzing the correlated continuous eye data under each study design.

1. Two sample t-test using each eye data but ignoring the inter-eye correlation. Two sample t-test is commonly used but is not appropriate for analyzing correlated eye data,^8,9 because this method considers each eye as an independent observation, while the measurement from two eyes of the same subject is usually positively correlated.

2. Two sample t-test using averaged value of two eyes. When two eyes of a subject are assigned to the same treatment group (design 2), using the average value of eyes for statistical comparison avoids the need for adjusting for inter-eye correlation. This method is only applied to design 2.

3. Two sample t-test using a randomly selected eye. When two eyes of a subject are assigned to the same treatment group (design 2), often one eye is randomly selected for analysis. This method is only applied to design 2.

4. Paired t-test. When two eyes of a subject are assigned to different treatment groups (design 1), the paired t-test is often used. This method is only applied to design 1.

5. The linear mixed effects model (LMM) with random intercept. The LMM is useful in settings where repeated measurements are made on the same subjects (such as in a longitudinal study), or in settings where measurements are made on clusters of related statistical units (such as two eyes of a subject). The mixed effects model explicitly accounts for the correlations between paired eyes of a subject by adding a random intercept, the intercept is constrained to be the same for the two eyes of a subject, but different across different subjects. The F test of the LMM is used to compare the mean difference between the two treatment groups. This method is applied to both design 1 and 2.

6. The marginal model using the GEE method. Although GEE was initially developed to analyze correlated data from longitudinal repeated measures,¹³ it has been extended to other types of correlated data, including observations from paired eyes.¹⁵ In the GEE approach, a correlation function for inter-eye correlation needs to be selected and a robust estimator of the variance of the regression coefficients, the “sandwich” estimator, is employed. Under large sample theories (i.e. when sample size is large), GEE provides consistent parameter estimates even when the covariance structure is mis-specified. The robust sandwich estimator consistently estimates the covariance matrix of the parameter. In our simulation, the robust sandwich estimator is used to construct the Wald test and the score test. For correlated eye data, two different working correlation structures are considered: the independent working correlation and the compound symmetric (or exchangeable) correlation structure.¹¹ This method is applied to both design 1 and 2.

Evaluation of the relative performance of statistical methods

We performed 2000 simulations for each simulation setting. We analyzed each simulated eye datasets using the above-described statistical methods for comparing the mean difference between the two groups. We calculated empirical type I error rate and statistical power at nominal level of 0.05 for each statistical method under 2000 simulations of each simulation setting. Type I error rate of a statistical method was calculated as the proportion of simulations with p < 0.05 when the difference of treatment effect was specified as 0 (i.e. there was no difference between the two treatment groups). The statistical power was calculated as the proportion of simulations with p < 0.05 when the mean difference between the two groups is greater than 0 (i.e. there is a difference between the two treatment groups).

Data analysis examples

We demonstrated the analysis of small sample data from two ophthalmic studies.

The first example data was used to demonstrate the analysis for small sample size paired data when two eyes are in two comparison groups. We analyzed visual acuity data from 19 patients enrolled from a clinical center for the Complications of Age-related Macular Degeneration Prevention Trial (CAPT).¹⁷ CAPT was a multi-center randomized clinical trial to evaluate whether low-intensity laser treatment for eyes with drusen could prevent vision loss from age-related macular degeneration. The study enrolled 1052 participants aged at least 50 years, visual acuity (VA) 20/40 or better and at least 10 large drusen in each eye. One randomly selected eye was assigned to laser treatment, and the contralateral eye had no treatment. We compared the mean VA change from baseline at Year 6 using the paired t-test, two sample t-test, the Wald test and the score test of GEE, and the F-test of linear mixed effects model. The data from 19 patients can be found in Appendix 1 and the SAS codes for the statistical analyses can be found in Appendix 2.

The second example data was used to illustrate the impact of different analysis approaches on results when two eyes of a subject are in the same comparison group. We analyzed the example data used by Katz.⁷ In this example, intraocular pressures (IOP) were measured from both eyes of 15 subjects of varying ages. The clinical question of interest was to determine whether the mean IOP of younger patients (<60 years old, n = 6) was different from that of older patients (≥60 years old, n = 9). The data from 15 subjects can be found in Appendix 3 and the SAS codes for statistical analyses can be found in Appendix 4.

Each example dataset were analyzed using statistical methods described previously, and their results were compared for means (SE), p-values and 95% confidence intervals for the mean difference.

Software

All simulations were performed in SAS v9.3 (SAS Institute Inc., Cary, NC, USA). The two sample t-test and the paired t-test were performed using the PROC TTEST. The Linear mixed effects model was implemented using PROC MIXED, and GEE tests were performed using the PROC GENMOD.

Results

Design 1: two eyes in different comparison groups

The type I error rates of different statistical methods for design 1 are presented in Table 1. When sample size reached 50, all statistical methods except the two-sample t-test had type I error rates close to 0.05. The paired t-test and the F-test of the LMM method controlled type I error well at nominal level of 0.05 even when sample size was as small as 5 no matter how large the inter-eye correlation was. Since the data were generated from bivariate normal distribution, the paired-test and the F test of the LMM are method equivalent in this case. When there was no inter-eye correlation, the two sample t-test that ignores the inter-eye correlation controlled type I error well, but when there was positive inter-eye correlation, the two sample t-test was very conservative with type I error rate substantially lower than 0.05. With the increase of the inter-eye correlation, the two sample t-test became more conservative. The GEE score test always had a type I error rate lower than nominal level when sample size was small (≤10), while the GEE Wald test always had an inflated type I error when sample size was small (≤30). For both GEE score test and Wald test, the smaller the sample size, the larger the deviations from the nominal error rate of 0.05. We also observed that the results from using the independence working correlation matrix were the same as the results from using compound symmetric working correlation matrix. This is due to the specific design that subjects are independent and all subjects have measurements from two eyes. This phenomenon is also discussed in Diggle and co-authors (2002, p. 61).¹⁶

Table 1.

Type I error rates of the statistical tests in the simulation study at various scenarios for comparing the means between two groups when two eyes of a subject are in two different comparison groups.

ρ	No. of subjects	Type I error ratea
		Two sample t-test	Paired t-test	GEE Wald test	GEE Score test	LMM
0	5	0.056	0.050	0.15	0.028	0.050
	10	0.048	0.052	0.10	0.043	0.052
	20	0.051	0.054	0.080	0.051	0.054
	30	0.051	0.053	0.064	0.052	0.053
	50	0.046	0.050	0.056	0.050	0.050
0.25	5	0.035	0.056	0.15	0.026	0.056
	10	0.026	0.052	0.10	0.040	0.052
	20	0.026	0.054	0.077	0.050	0.054
	30	0.025	0.053	0.067	0.051	0.053
	50	0.023	0.050	0.054	0.049	0.050
0.5	5	0.016	0.054	0.15	0.023	0.054
	10	0.014	0.051	0.10	0.042	0.051
	20	0.007	0.050	0.074	0.047	0.050
	30	0.007	0.049	0.066	0.047	0.049
	50	0.007	0.048	0.060	0.047	0.048
0.75	5	0.003	0.055	0.16	0.025	0.055
	10	0.0005	0.050	0.10	0.041	0.050
	20	0.0005	0.054	0.077	0.051	0.054
	30	0	0.052	0.066	0.050	0.052
	50	0	0.051	0.058	0.050	0.051

^aThe test with type I error rate closest to 0.05 has the best statistical performance.

ρ, Inter-eye correlation; GEE, Generalized estimating equations; LMM, Linear mixed effect model.

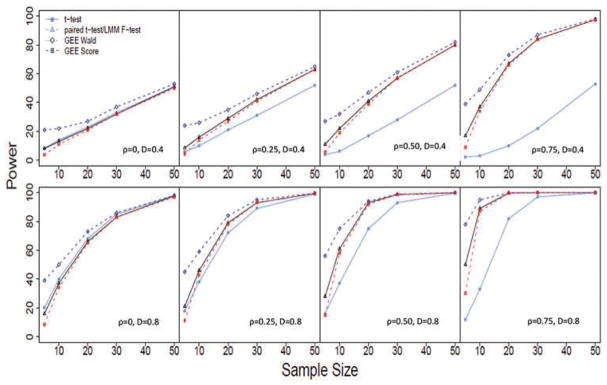
In Figure 1, we present the statistical power of all the methods for detecting effect size of 0.4 and 0.8 at various inter-eye correlations (0, 0.25, 0.50, 0.75) considered for design 1. In all scenarios, the GEE Wald test seemed to have the largest power. However, the GEE Wald test cannot control type I error when sample size is less than 50, thus the power gain was due to the inflated type I error in small samples. When the inter-eye correlation was assumed to be zero, the paired t-test, GEE score test and the F test of LMM all performed similarly well, but when the inter-eye correlation was positive, the two sample t-test that ignored the inter-eye correlation always had the lowest statistical power. The paired t-test and the F-test of the LMM method had higher power than the GEE score test when sample size was 10 or less, and became similar when sample size was 20 or above.

Figure 1.

Statistical power from various statistical analysis approaches evaluated in design 1 (i.e. two eyes of a subject in two different comparison groups) under various levels of inter-eye correlation (ρ), effect size (D) and sample size.

Design 2: two eyes in the same comparison group

The type I error rates of different statistical methods for design 2 are presented in Table 2. The two sample t-test using the average value of two eyes or using a randomly selected eye controlled type I error well at normal level of 0.05 at all levels of inter-eye correlation. When there was positive inter-eye correlation, the two sample t-test that ignored the inter-eye correlation and the F-test of the LMM had substantially inflated type I error, even when the sample size was as large as 50. The GEE Wald test also had inflated type I error, but the inflation was less than the two sample t-test and the LMM method. The type I error rate of the GEE score test was less than the nominal level 0.05 when sample size was 10 or less, but close to 0.05 when sample size was 20 or larger.

Table 2.

Type I error rates of the statistical tests compared in design 2, in the simulation study at various scenarios for comparing the means between two groups when two eyes of a subject are in the same comparison group.

ρ	No. of subjects	Type I error ratea
		Two-sample t-test			GEE Wald	GEE Score	LMM
		Ignore correlation of two eyes	Average of two eyes	Random pick one of the two eyes
0	5	0.058	0.063	0.053	0.17	0.023	0.013
	10	0.053	0.055	0.055	0.097	0.047	0.034
	20	0.053	0.053	0.055	0.072	0.055	0.043
	30	0.055	0.052	0.057	0.071	0.053	0.051
	50	0.042	0.044	0.036	0.055	0.045	0.041
0.25	5	0.095	0.061	0.051	0.17	0.024	0.039
	10	0.083	0.051	0.044	0.096	0.042	0.063
	20	0.080	0.054	0.055	0.076	0.054	0.077
	30	0.081	0.053	0.050	0.072	0.055	0.082
	50	0.073	0.046	0.043	0.057	0.048	0.079
0.5	5	0.13	0.063	0.060	0.17	0.023	0.081
	10	0.11	0.047	0.047	0.089	0.042	0.099
	20	0.11	0.054	0.060	0.077	0.053	0.12
	30	0.11	0.052	0.056	0.068	0.053	0.13
	50	0.098	0.048	0.049	0.058	0.049	0.12
0.75	5	0.17	0.064	0.056	0.17	0.020	0.14
	10	0.14	0.048	0.051	0.090	0.037	0.16
	20	0.14	0.056	0.051	0.075	0.055	0.18
	30	0.14	0.051	0.048	0.066	0.049	0.18
	50	0.12	0.050	0.052	0.056	0.049	0.18

^aThe test with type I error rate closest to 0.05 has the best statistical performance.

ρ, Inter-eye correlation; GEE, Generalized estimating equations; LMM, Linear mixed effect model.

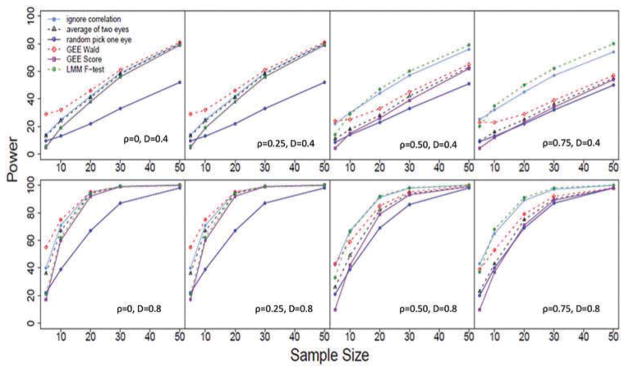
Figure 2 presents the statistical power of all the methods for detecting effect size of 0.4 and 0.8 at various inter-eye correlations considered for design 2. When the sample size was small (<10), the statistical power from GEE score test was lower than the two sample t-test that used average values of two eyes and the two sample t-test that used a randomly selected eye. When sample size became larger (>30), powers of the two sample t-test using average value of two eyes and the GEE score test were similar, and both of them were larger than the two sample t-test using a randomly selected eye, particularly when the inter-eye correlation was small. When the inter-eye correlation was large, the statistical power became similar for the GEE score test, and the two sample t-test using average values of two eyes or using a randomly selected eye. When the inter-eye correlation was low, the analysis that used the randomly selected eye substantially decreased statistical power because only half of the data were used for analysis, and the other half of the data that provided additional information (due to low inter-eye correlation) was not considered.

Figure 2.

Statistical power from various statistical analysis approaches evaluated in design 2 (i.e. two eyes of a subject in the same comparison group) under various levels of inter-eye correlation (ρ), effect size (D) and sample size.

Example 1: comparison of change of visual acuity from baseline from two eyes in two comparison groups

As shown in Table 3, the mean VA loss from baseline was 3.2 letters in treated eyes and 8.2 letters in their contralateral untreated eyes. The difference was statistically significant using paired t-test (p = 0.047), but was not statistically significant from the inappropriate two sample t-test (p = 0.13). The Wald test of GEE provided a smaller p-value (p = 0.03), while the score test of GEE provided a larger p-value (p = 0.051) than the paired t-test. The F-test of linear mixed effects model provided the same p-value as the paired t-test. These results are consistent with findings from our simulation study.

Table 3.

Comparison of change of visual acuity (VA) from baseline between treated eyes and their control eyes of 19 patients at Year 6 using various analysis approaches.

Analysis approaches	Mean VA change (letters) from baseline at Year 6 (SE)		Mean difference in VA change (letters) between treated eye and control eye (95% CI)	p-value
	Treated eye (n = 19 eyes)	Control eye (n = 19 eyes)
Paired t-test	−3.2 (1.7)	−8.2 (2.8)	5.0 (0.07, 10.2)	0.047
Two sample t-test	−3.2 (1.7)	8.2 (2.8)	5.0 (−1.6, 11.6)	0.13
GEE Wald test	−3.2 (1.6)	−8.2 (2.7)	5.0 (0.5, 9.5)	0.03
GEE score test	NA	NA	NA	0.051
LMM	−3.2 (2.3)	−8.2 (2.3)	5.0 (0.07, 9.9)	0.047

SE, standard error; GEE, Generalized estimating equations; LMM, Linear mixed effects model; CI, confidence interval; NA, not available because score test did not provide estimate of the mean and standard error.

Example 2: analysis of intraocular pressure from two eyes in the same comparison group

The correlation of IOP between the paired eyes of 15 subjects is high, with intra-class correlation coefficient of 0.81 (95% CI: 0.54–0.93). The results from various analysis approaches (one eye data only, or both eyes data analyzed without or with adjustment of inter-eye correlation) are shown in Table 4.

Table 4.

Comparison of intraocular pressure between subjects with age <60 years vs. ≥60 years using various analysis approaches.

Analysis approaches	Mean IOP in mmHg (SE)		Mean IOP (mmHg) difference (95% CI)	p-value
	<60 years (n = 6 subjects, 12 eyes)	≥ 60 years (n = 9 subjects, 18 eyes)
One-eye analysis using two sample t-test
Right eye only	18.0 (2.2)	20.0 (1.2)	2.0 (−3.8, 7.8)	0.40
Left eye only	16.0 (1.5)	22.0 (1.7)	6.0 (1.1, 10.9)	0.03
Eye with higher IOP	18.0 (2.2)	22.0 (1.7)	4.0 (−2.2, 10.2)	0.17
Eye with lower IOP	16.0 (1.5)	20.0 (1.2)	4.0 (−0.3, 8.3)	0.06
Randomly selected eye	17.5 (2.4)	21.8 (1.8)	4.3 (−2.4, 11.0)	0.17
Two-eyes analysis
Two sample t-test using average of two eyes	17.0 (1.9)	21.0 (1.4)	4.0 (−1.2, 9.2)	0.11
Two sample t-test using two eyes without adjustment for inter-eye correlation	17.0 (1.3)	21.0 (1.0)	4.0 (−0.5, 7.5)	0.02
GEE Wald test	17.0 (1.7)	21.0 (1.3)	4.0 (−0.2, 8.2)	0.063
GEE score test	NA	NA	NA	0.0986
LMM	17.0 (1.8)	21.0 (1.4)	4.0 (−0.9, 8.9)	0.0996

SE, standard error; IOP, intraocular pressure; GEE, Generalized estimating equations; LMM, Linear mixed effects model; CI, confidence interval; NA, not available because score test did not provide estimate of the mean and standard error.

It is clear that different analysis approaches yield very different results. The comparison using left eye IOP data lead to the mean IOP difference of 6 mmHg, with associated p-value of 0.03, while all other one-eye analyses all yield non-statistically significant difference with p-value ranging from 0.06 (using eye with lower IOP) to 0.40 (using right eye) When the data from both eyes were used, the mean differences between two age groups were all 4 mmHg, but their p-values were very different. The two-eye analysis that ignored the inter-eye correlation provided the smallest and significant p-value of 0.02, while p-values from analyses that accounted for the inter-eye correlation were all not significant (0.06 from GEE Wald test, 0.0986 from GEE score test and 0.0996 from the F-test of linear mixed effects model). The analysis of using the average of two eyes provided the largest p-value (p = 0.11).

Discussion

This article has compared the performance of several commonly used statistical methods for analyzing continuous correlated eye data from small sample-size studies through statistical simulation study and the analyses of real data. The statistical methods covered the model-based analysis including the linear mixed effects model, the marginal model using GEE, and non-model-based analysis such as the paired t-test and the two sample t-test using one eye data or two eyes data. Our simulation results suggested that the performance of these tests depended on the design of the study and the sample size. In the paired design (two eyes in different comparison groups), the linear mixed effects model and the paired t-test worked well even when the sample size is small (<10). When sample size was 20 or larger, the GEE score test performed as well as the linear mixed effects model. When two eyes are in the same comparison group, the linear mixed effects model substantially inflated type I error rate even when the sample size was as large as 50. The two sample t-test using average values of two eyes or using data of one randomly selected eye controlled the type I error at a nominal level of 0.05. However, the two sample t-test using data of randomly selected eyes had lower statistical power than the two sample t-test using the average value of two eyes or the GEE score test, particularly when the inter-eye correlation is low. In both designs, the two sample t-test using individual eye data that ignores the inter-eye correlation cannot achieve nominal type I error rate, under-estimating the type I error when two eyes are in different comparison group, and inflating type I error rate when two eyes are the same comparison groups.

The linear mixed effects model and marginal model are the two commonly used model approaches to account for the inter-eye correlation. Their difference in the model approaches has been discussed in many papers.^11,18,19 The mixed effects model is useful in settings where repeated measurements are made on the same subjects (such as in a longitudinal study), or where measurements are made on clusters of related statistical units (such as two eyes of a subject). When the sample size is small, the performance of the linear mixed effects model varied with the design of the study. In design 1 when two eyes were in two different comparison groups, the linear mixed effects model performed well with nominal type I error controlled, but when the two eyes were in the same comparison group as in design 2, the linear mixed effects model was very conservative when there was no inter-eye correlation, but had substantially inflated type I error when there was inter-eye correlation.

The GEE method has been widely used to model correlated data including correlated eye data.^13,15 When the number of independent clusters is sufficiently large, GEE method has desirable statistical properties which have contributed to its popularity. The regression coefficient estimates from GEE are consistent and asymptotically normal. Their covariance is consistently estimated by the robust sandwich estimate which is robust to the mis-specification of the covariance of the correlated responses. However, when the sample size is small, the GEE score test and Wald test both did not perform well as shown in our simulation study and other simulation studies.^20,21 The GEE Wald test using robust variance estimator always inflates type I error and the GEE score test is always conservative when sample size is small (<20), due to the reason that the robust sandwich variance estimator of GEE does not perform well when sample size is small.^20–22

In ophthalmic and vision research, the non-model-based approach such as the paired t-test or two sample t-test are commonly used by non-statistical researchers who may not be familiar with more complex statistical approaches (e.g. the linear mixed effects model or marginal model). In design 1, when two eyes are in two different comparison groups, the paired t-test performs very well even when the sample size is less than 10, and the two sample t-test that ignores the inter-eye correlation leads to lower statistical power. In design 2, when the two eyes are in the same comparison group, investigators commonly used the average of two eyes or used one eye data (either randomly selected, or using the left eye only, right eye only, or worse eye) to avoid the need of adjusting for inter-eye correlation.^9,23 Such one-eye analysis can help control the type I error well, but lead to the loss of some statistical information and substantially decrease statistical power, particularly when the inter-eye correlation is low. However, these non-model-based analysis approaches are not applicable when the comparison between two comparison groups requires the adjustment of other covariates.

Our two examples of analyzing real data using various analysis approaches highlight the importance of selecting appropriate statistical analysis approach specific to the study design. When sample size is small, different analysis approaches can yield very different study results and inappropriate analysis will lead to invalid conclusions. In the example of comparison of visual acuity between treated eyes and control eyes, the appropriate paired t-test or linear mixed effect model concluded that the VA change from baseline between treated eye and control eye was significantly different (p = 0.047). However, when the inappropriate two sample t-test that ignores the inter-eye correlation or the conservative score test of GEE were used, the significant difference between two groups was missed (p > 0.05). In the example of comparison of IOP between subjects with age <60 years vs. ≥60 years, when the average of two eyes or randomly selected eye was used for comparison, the IOP difference between age groups was not statistically significant (p > 0.10). However, if only data from the left eye were analyzed, or if inter-eye correlation was not considered, the study would incorrectly conclude a significant difference in IOP between younger and older subjects. We did not evaluate the approaches of using left eye only or right eye only in our simulation study because, in theory, their simulation results from the average of many simulated data should be the same as using the random selected eye. However, when analyzing only one real dataset, results from the left eye only or right eye only can be different as demonstrated in the example of analyzing real data.

In contrast to other simulation studies for small clustered data,^20,24 our simulation study is uniquely designed for eye data (i.e. 2 eyes per cluster, and each eye in the same or different comparison group), our simulation results can be directly applied to ophthalmic and vision research. Our study showed that for data from a small sample size study, when two eyes of a subject are in two different comparison groups, the paired t-test or linear mixed effects model should be used. When two eyes of a subject are in the same comparison group, no method has desirable statistical properties (i.e. control of type I error rate, and good statistical power). To be conservative, the two-sample t-test for average of two eyes or score test of GEE may be recommended to use, but these tests may miss the detection of a statistically significant difference. The more favorable statistical property of analyzing eye data from paired design (two eyes of a subject received two different treatments) than the design of assigning two eyes to the same treatment group suggests that the early phase ophthalmic clinical trial with small size may benefit from using this paired design if feasible.

In our simulation study, we only evaluated well-established statistical methods for analyzing continuous correlated data when sample size is small. We did not evaluate the recently developed methods²⁰ that have not been built into statistical software. Our evaluations were in the setting of hypotheses testing, thus the results were summarized as type I error rate and statistical power. Furthermore, our simulation is restricted to normally distributed data, and does not consider repeated measurements within the same eye (over time). Further investigations are needed for the setting when the data do not follow the normal distribution or when the same eye had multiple repeated measurements at the same time point or over time.

In conclusion, this paper evaluated the commonly used statistical approaches for small size eye data through simulation study and real data analysis. Our simulation study suggests that no single statistical method works well across all different settings, emphasizing the importance of selecting the most appropriate method corresponding to a specific design of the study. Our examples of analysis of real data demonstrate that different analysis approaches can yield very different results and inappropriate analysis will lead to invalid conclusions. When the sample size is small (<20), the paired t-test or LMM is most appropriate to use when two eyes of a subject are in two different comparison groups, while the average of two eyes, although not most efficient, is recommended when two eyes of a subject are in the same comparison group.

Appendix 1. Visual acuity from treated eye and control eye of 19 patients

Patient ID	Visual acuity change from baseline at Year 6 (letters)
	Treated eye	Untreated eye
1	11	4
2	−2	−2
3	−9	−12
4	−12	−7
5	−5	−8
6	4	−2
7	−6	−5
8	1	−8
9	2	−10
10	2	−1
11	−22	−24
12	−9	1
13	1	−4
14	−3	4
15	−5	−31
16	0	−16
17	0	6
18	2	−1
19	−11	−40

Appendix 2. SAS codes for analysis of visual acuity data from 19 subjects

/** paired t-test **/
proc ttest data=paired_data;
 paired VAchg_trt*VAchg_con;
run;
/* two sample t-test **/
proc ttest data=model_data;
 var vachg;
 class group;
run;
 /** GEE Wald test **/
proc genmod data=model_data;
 class id group;
 model vachg=group/dist=normal wald;
 repeated subject=ID/type=ind;
 lsmeans group;
 estimate ‘treated vs. control’ group 1 -1;
run;
  /** GEE score test **/
proc genmod data=model_data;
 class id group;
 model vachg=group/dist=normal type3;
 repeated subject=ID/type=ind;
run;
  /** Linear mixed effects model **/
proc mixed data=model_data noclprint;
 class id group;
 model vachg=group/s CL;
 random intercept /sub=id type=cs;
 lsmeans group;
 estimate ‘treated vs. control’ group 1 -1/CL;
run;

Appendix 3. Intraocular pressure taken from two eyes of 15 subjects with age <60 years or ≥60 years

Patient ID	<60 years		Patient ID	≥60 years
	Right eye	Left eye		Right eye	Left eye
1	19	18	7	19	21
2	21	19	8	15	16
3	14	13	9	23	24
4	13	12	10	19	19
5	27	21	11	21	22
6	14	13	12	14	15
			13	23	31
			14	22	26
			15	24	24

Appendix 4. SAS codes for analysis of IOP data from 15 subjects

  /** two-sample t-test of right eye IOP **/
  proc ttest data=IOPdata;
   class group;
   var re;
  run;
   /** two-sample t-test of left eye IOP **/
  proc ttest data=IOPdata;
   class group;
   var le;
  run;
  /** two-sample t-test of average IOP of two eyes **/
  proc ttest data=IOPdata;
   class group;
   var avg_IOP;
  run;
  /** two-sample t-test of eye with higher IOP **/
  proc ttest data=IOPdata;
   class group;
   var max_IOP;
  run;
  /** two-sample t-test of eye with lower IOP **/
  proc ttest data=IOPdata;
   class group;
   var min_IOP;
  run;
  /** two-sample t-test of IOP from randomly selected eye **/
  proc ttest data=IOPdata;
   class group;
   var random_IOP;
  run;
   /* two sample t-test of IOP from two Eyes without accounting for inter-eye correlation **/
  proc ttest data=IOPeye;
   class group;
   var IOP;
  run;
    /** GEE Wald test **/
  proc genmod data=IOPeye;
   class id group;
   model IOP=group/dist=normal Wald;
   repeated subject=ID/type=ind;
   lsmeans group;
   estimate ‘>=60 vs. <60’ group -1 1;
  run;
    /** GEE score test **/
  proc genmod data=IOPeye;
   class id group;
   model IOP=group/dist=normal type3;
   repeated subject=ID/type=ind;
  run;
   /** Linear mixed effects model **/
  proc mixed data=IOPeye noclprint;
   class id group;
   model IOP=group/s CL;
   random intercept /sub=id type=cs;
   lsmeans group;
   estimate ‘>=60 vs. <60’ group -1 1;
  run;