Longitudinal Modeling of Glaucoma Progression Using 2-Dimensional Continuous-Time Hidden Markov Model

Abstract

We propose a 2D continuous-time Hidden Markov Model (2D CT-HMM) for glaucoma progression modeling given longitudinal structural and functional measurements. CT-HMM is suitable for modeling longitudinal medical data consisting of visits at arbitrary times, and 2D state structure is more appropriate for glaucoma since the time courses of functional and structural degeneration are usually different. The learned model not only corroborates the clinical findings that structural degeneration is more evident than functional degeneration in early glaucoma and the opposite is observed in more advanced stages, but also reveals the exact stages where the trend reverses. A method to detect time segments of fast progression is also proposed. Our results show that this detector can effectively identify patients with rapid degeneration. The model and the derived detector can be of clinical value for glaucoma monitoring.

1 Introduction

Glaucoma is an optic neuropathy characterized by progressive loss of retinal ganglion cells and damage of optic nerve. If left untreated, glaucoma may cause irreversible visual field deficits and even blindness [1]. Glaucoma has been called the “silent thief of sight” because the loss of vision often occurs gradually without patients’ awareness until the disease has advanced significantly. It is estimated that over 2.2 million Americans have glaucoma but only half of those know they have it [2]. This large undiagnosed population is mainly due to unnoticeable symptoms of early glaucoma and the difficulty of consistently screening the entire population. In the U.S., more than 120,000 people are blind from glaucoma [3]. Worldwide, glaucoma is the second-leading cause of blindness after cataracts [4].

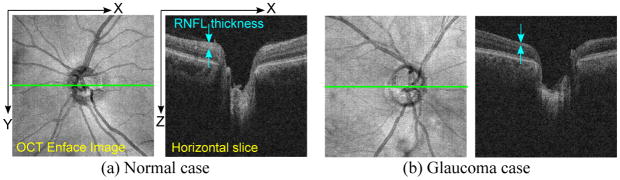
Since the visual field cannot typically be recovered, early identification of glaucoma and its progression, and delivery of appropriate treatment are critical to retard the deterioration and preserve sight. Clinically, several techniques for structural and functional measurement are often utilized for glaucoma monitoring. For example, 3D optical coherence tomography (3D-OCT) is used to examine the optic nerve head [5] (Fig. 1), and psychophysical techniques, such as automated perimetry, are applied to assess the status of the visual field [1].

Fig. 1.

Examples of OCT Images of optic nerve head. The OCT enface (left image) is a 2D image generated by projecting the 3D-OCT volume along the z (depth) axis. The horizontal slice (right image) corresponds to the green line in the enface. In the glaucoma case (b), the retinal nerve fiber layer (RNFL), the topmost layer of the retina that looks bright in OCT images, is apparently thinner than the normal case (a).

Clinical practice has shown that the identification of glaucoma progression is often challenging for the following reasons. First, glaucoma is a slowly progressing disease, and it is difficult to discriminate between true disease-related changes and natural age-related degeneration, in the face of measurement variability and noise. Second, the rate of functional and structural progression among subjects can be highly variable, and thus it is hard to establish one rule of thumb for progression detection. Third, it is observed that structural and functional changes often occur at different times over the disease course. Some subjects can experience substantial structural loss before any evidence of visual field deficits emerges [5]. Due to these difficulties, there is no widely accepted standard for establishing glaucoma progression considering both types of changes.

There are clinical strategies to determine glaucoma progression, usually through subjective assessment or statistical analysis of measurements collected over time [1][5]. The statistical approaches can be divided into event-based and trend-based methods. In event analysis, progression is identified when a follow-up measurement exceeds a pre-established threshold of change from baseline visit. In trend analysis, the behavior of a parameter over time is monitored, using methods such as linear regression. In current clinical practice, the above statistical analysis is generally applied separately for each measurement. There is a lack of methods that take into account all types of measurements to determine the true disease course for glaucoma progression assessment.

In this paper, we propose to combine longitudinal structural and functional measurements and use 2D CT-HMM to decode the underlying true disease stages. We use two hidden state dimensions, one is structural and the other is functional, to model the disease status. The motivation for using CT-HMM is as follows. Since many chronic diseases have a natural interpretation in terms of staged progression [6][7], the discrete state is thus suitable. Furthermore, since patients are often monitored at irregular intervals, a continuous-time model, rather than discrete-time (DT) [8], is more appropriate for medical data [6]. While 1D DT-HMM [9], 1D CT-HMM [10], and 1D event-based disease staging system [11] have been investigated, to our knowledge, we are the first to propose the 2D CT-HMM for disease progression modeling.

This paper makes three contributions: (1) Introduce a 2D CT-HMM model for progression modeling, which can more accurately capture the underlying disease stages. (2) Demonstrate an application of fast progression detection using the model. This detector can identify time segments of fast progression, and is potentially valuable in clinics. (3) A large dataset is used to estimate the model. Our results can be useful in understanding glaucoma progression.

2 Approach

2.1 Formulation of Continuous-Time Hidden Markov Model

The formulation of CT-HMM is as follows [6]. Suppose we have longitudinal data from multiple individuals. The data for individual i has n_i visits, consisting of irregularly spaced visiting times (t_i1, …, t_ini), and corresponding observational data (o_i1, …, o_ini). The hidden states for the data are denoted as (s_i1, …, s_ni) where each state is from a discrete set S. The observation o is generated conditionally on the hidden state s based on the data emission probability p(o|s).

The hidden states evolve with time as an unobserved Markov process. The next state to which an individual enters from a specific state, and the time that this transition occurs, are governed by a set of transition intensities, q_rs, for each pair of states r and s. Each intensity represents the instantaneous risk of moving from state r to s, and is defined as q_rs = lim_δt≈0 p(S(t + δt) = s|S(t) = r)/δt where S(t) represents the state at time t. These intensities form a matrix Q, called instantaneous transition intensity matrix, whose rows are defined to sum to zero, with the diagonal entries set to q_rr = −Σ_s≠r q_rs. The average sojourn time (a single period of occupancy) in state r is given by −1/q_rr. The probability that the next move from state r to s is −q_rs/q_rr, for r ≠ s.

The transition probability matrix with time parameter t is denoted as P(t), and is computed by taking the matrix exponential of Q: P(t) = e^tQ. The (r, s) entry of P(t), denoted as p_rs(t), is the probability of being in state s at instant (t₀ + t) in the future, given that the state at time t₀ is r. Note that p_rs(t) can be non zero when there is a path from state r to s in the model even if q_rs is 0.

The model can be fit to longitudinal data by maximizing the data likelihood. We will explain our method for parameter estimation in Section 2.3.

2.2 2D State Structure for Glaucoma Progression Modeling

To define the 2D state structure, since the glaucomatous damage is typically irreversible, we assume that the degeneration can only increase with time. We also restrict instantaneous transitions to pairs of adjacent states (i.e. cannot skip over a state). The three allowed transitions (to the right, down, diagonal) from each state and the resulting model are illustrated in Fig. 2(a).

Fig. 2.

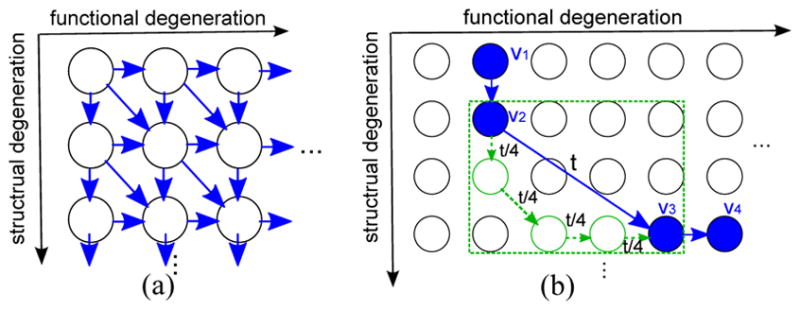
(a) The 2D state structure for glaucoma progression. The blue arrows are the allowed instantaneous transition (q_rs ≥ 0). (b) An example of hidden state decoding. The blue path represents the decoded states for the longitudinal data. The green path represents a possible inner state path between the two non-adjacent states for visit 2 and 3. The duration t between visits 2 and 3 is uniformly distributed across the intermediate states to obtain a coarse explanation of progression.

We now explain our state definition. Among the available measurements, one structural and one functional measurement are selected for state definition. These choices defines the two state space dimensions illustrated in Fig. 2(a). Each state can then be thought of as having a specified range of these two primary parameters. The visiting data are then dispatched to the corresponding states for initializing the parameters of data emission probability p(o|s), where multivariate Gaussian distribution is assumed.

2.3 Algorithm for Parameter Estimation

For parameter estimation in CT-HMM, often a numerical method, such as gradient descent, is applied directly to maximize the data likelihood [6]. The data likelihood is often calculated by summing the probability of all possible hidden state paths. It has been noted that there is no widely accepted efficient algorithm for CT-HMM parameter estimation [12], mainly due to the more complex formulation compared to DT-HMM. The lack of efficient algorithms has limited CT-HMM to applications where either the number of states involved is low (e.g. a 3-state disease model [10]), or the amount of allowed transitions is limited.

To efficiently estimate the parameters for our large-scale model, we assume that if the decoded states for two consecutive visits are instantly-adjacent (i.e. have a q_rs link), then the state transition takes place exactly at the visiting time of the second visit. This assumption is valid when the duration between consecutive visits is not long. We then use a hard EM algorithm, which is conceptually similar to the Viterbi-Training (or called the segmental K-means algorithm) for discrete-time HMM [13], for efficient parameter estimation.

In this formulation, we consider the optimization problem max_S f(S,O|λ), which is called state-optimized likelihood in [13], for iterative update of the model parameter λ. In E-step, given the current λ, we aim to find a single best state path S^* (hence the name hard) for each data sequence O = o₁, …o_n with visiting time T = t₁, …t_n by Viterbi decoding [8]:

$$p(S^{\ast },O\mid \lambda )={\mathit{max}}_{S^{\ast }=s_1,\dots ,s_n}\{\pi (s_1)p(o_1\mid s_1)\prod _{k=2}^{n}p(o_k\mid s_k)P_{s_{k-1},s_k}(t_k-t_{k-1})\}$$

where π(s) is the initial state probability, p(o|s) is the data emission probability, and P_r,s(t) is the entry of transition probability matrix P(t) computed from Q.

In the decoded state sequence S^*, there can be two consecutive decoded states r, s that are not instantly-adjacent (i.e. q_rs is 0). This can happen when the time gap between the two visits is long or very rapid degeneration occurs. In this case, we would like to also utilize this transition information to help estimate the q_ij parameters, where i,j are intermediate states in the path between state r and s. We determine the most probable inner path S_rs between r and s, by requiring that intermediate states are distinct and adjacent, and the duration t between the two visits is divided uniformly into each intermediate state (an example is illustrated in Fig. 2(b)). This can be formulated as:

$$p(S_{rs}\mid \lambda )={\mathit{max}}_{S_{rs}=s_1,\dots s_l,l\in l_{rs},s_i\ne s_j,1\le i\le j\le l}\prod _{u=1}^{l-1}{P}_{s_u,s_{u+1}}(\frac{t}{l})$$

where l_rs is the set of all possible lengths of distinct state paths between state r, s. This best inner path S_rs can also be efficiently found using Viterbi allgorithm.

In M-step, we update the model parameters as follows. Let N_rs denote the number of transitions from states r to s, and T_r represent the total time staying at state r from all data, computed from the results in E-step. It has been proved in [12] that if the state transitions are assumed to happen at the visiting times, then the optimized value for Q matrix entries are : q_rs = N_rs/T_r for r ≠ s, and q_rr = −Σ_r≠s q_rs. We then do iterative update of the model parameters by alternating the E-step and M-step until a fixed point is reached.

2.4 Application: Detect State Transitions with Fast Progression

By using the learned model, we can construct a detector to find state transitions within a data sequence which have faster progression than the average model. First, the Viterbi algorithm is applied to find the hidden state sequence for longitudinal data. Then, the transition link list can be derived from the states, each with its own duration t. For example, if the state sequence is 4 → 4 → 7 → 7 → 7 → 9, then the transition link list is 4(t = t₃ − t₁) → 7(t = t₆ − t₃) → 9. For each link from state s_a to s_b with a duration t, we compute P(t) and derive s^* = argmax_s P_sa,s(t), which is the most probable next state from state s_a after duration t, according to the average model. We can then check if the end-state s_b of the patient’s link is structurally and/or functionally worse than s^*. If so, then a structural and/or functional faster progression is detected. Note that in practice, we ignore the first link for detection, since there is an unknown duration in the first state before the first visit. The proposed detector analyzes the decoded state sequence and state duration by segments, which can thus detect local fast changes, and can be potentially useful in clinical applications.

3 Experimental Results

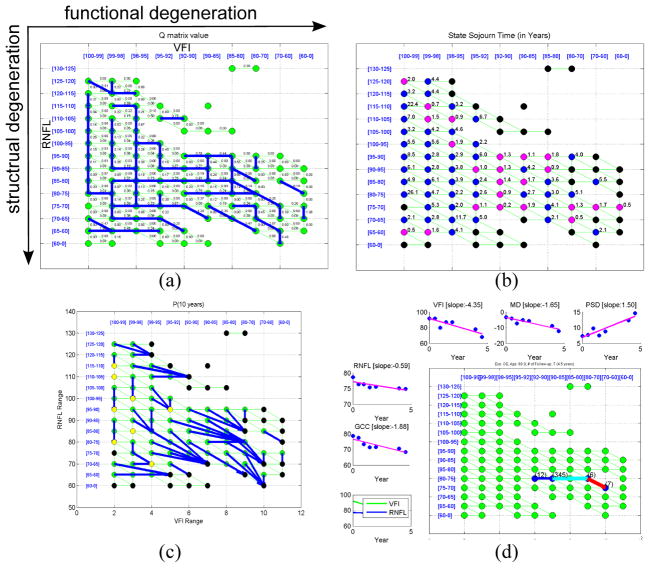
We collected a dataset of 372 eyes with glaucoma or glaucoma suspect (highly likely to have glaucoma but show no visual field defect at the base visit), with a total of 1618 visits traced with an average history of 3.1 ± 0.9 years. The functional measurements used in this study are the visual field index (VFI), mean deviation (MD), and pattern standard deviation (PSD) of the visual field test from automated perimetry. The structural measurements utilized are the average thickness of retinal nerve fiber layer (RNFL) from 3D-OCT optic disc images, and the average thickness of ganglion cell complex (GCC) from 3D-OCT macular images, both are automatically extracted by 3D-OCT machines (RTVue-100 by Optovue). We use VFI and RNFL as the primary index for 2D state definition. VFI range [100-99-98-95-92-90-85-80-70-60-0] and RNFL range [130-125-120-…-60-0] are used to define the states, which are specified empirically based on the available data (see Fig. 3(a) for details).

Fig. 3.

(a) Visualization of the estimated Q matrix. The strongest degeneration links (with largest q_rs for each state r) are shown in blue. Each q_rs value is shown along its link. (b) The state sojourn time of each state. Magenta state: ≤ 2 years, blue: > 2 years, black : lack of transition data. (c) Visualization of P(t) matrix with t = 10 years. For each state r, the most probable next state after 10 years (s^* = argmax_s P_r,s(t)) is shown by a blue link. Yellow state: next state is itself. (d) An example of the Viteribi state decoding result (thick path), and the detected fast progression links (light blue: functional fast, red: both structural and functional fast) from an eye with 7 visits. Data for each measurement type is also shown with linear regression slope.

We now analyze the estimated Q matrix. In Fig. 3(a), the strongest instantaneous transition from each state is illustrated by a blue link. There are several L shape patterns in the top-left area, which reveals that structural degeneration has higher tendency than functional degeneration in the early stages. However, when the disease status reaches the corner of L, the trend starts to reverse. We can find a few long horizontal lines when structural values are in the middle and low range. This implies that more rapid functional changes may occur at these states while structural loss slows down. When structural and/or functional values are low, there are more diagonal links. This tells us that at more advanced disease stages, degeneration in both dimensions tend to happen together.

In Fig. 3(b), the state sojourn time (−1/q_rr) is shown. States with magenta color represent a sojourn time of less than 2 years, which are mostly in the bottom-right area, where more severe stages reside. In Fig. 3(c), the behavior of P(t) matrix with t set to 10 years is illustrated, where the most probable next state from each state after t years is shown by the blue link. The results show that there is more rapid degeneration when disease is in more advanced status. From Fig. 3(b)(c), it is found that that some results are not smooth, which is likely due to the lack of sufficient data and over-fitting in some states.

We then evaluate the method for detecting local fast progression. This detector can partition eyes to four groups: eyes with both structural (S) and functional (F) fast progression, eyes with only S, only F, and the others (relatively stable). In Table 1, the mean slopes of each parameter from each group are shown. We found that for each group of S and/or F fast progression, there is slope of associated parameters significantly different (t-test, p=0.05) from the corresponding slope in the relatively stable group. This tells that the method can effectively identify patients of fast degeneration. One example is shown in Fig. 3(d).

Table 1.

The mean and standard deviation of the slopes of each measurement type for different eye-groups classified by the fast progression detector. Numbers shown in bold face are the ones that are significantly different from the corresponding entry in group “others” by student-t test(p = 0.05).

		Function (F)			Structure (S)
Class	Count	VFI Slope	MD Slope	PSD Slope	RNFL Slope	GCC Slope
Both S,F prog	16	−1.95 ± 1.51	−0.67 ± 0.52	0.68 ± 0.71	−2.03 ± 1.72	−0.60 ± 2.27
Only S prog	24	0.02 ± 0.38	−0.12 ± 0.45	0.00 ± 0.13	−2.04 ± 1.56	−1.64 ± 0.75
Only F prog	16	−1.05 ± 0.91	−0.51 ± 0.28	0.41 ± 0.55	−0.65 ± 1.17	−1.19 ± 1.68
Others	316	0.06 ± 1.69	−0.03 ± 0.62	−0.02 ± 0.37	−0.38 ± 2.16	−0.63 ± 1.77

4 Conclusion

In this paper, we propose to use 2D CT-HMM to statistically characterize patterns of glaucoma progression. Longitudinal measurements are considered together to decode the underlying disease stages along structural and functional dimensions, which can help clinicians capture a patient’s severity in a global and intuitive way. By interpreting the estimated average model, we have gained insight into glaucoma progression. The results not only corroborate clinical findings that structural degeneration usually precedes functional degeneration at early stages and the trend reverses later, but also reveal the exact states where the reverse occurs. A method to detect time segments of local fast progression is also proposed. This method provides an alternative way to detect patients whose progression is faster than the population average, which is potentially useful in clinics. Our results suggest that the 2D CT-HMM model could be profitably applied to other longitudinal medical data.