A Critical Comparison of 3D Experiments and Simulations of Tricalcium Silicate Hydration

Abstract

Advances in nano-computed X-ray tomography (nCT), nano X-ray fluorescence spectrometry (nXRF), and high-performance computing have enabled the first direct comparison between observations of three-dimensional nanoscale microstructure evolution during cement hydration and computer simulations of the same microstructure using HydratiCA. nCT observations of a collection of triclinic tricalcium silicate (Ca₃SiO₅) particles reacting in a calcium hydroxide solution are reported and compared to simulations that duplicate, as nearly as possible, the thermal and chemical conditions of those experiments. Particular points of comparison are the time dependence of the solid phase volume fractions, spatial distributions, and morphologies. Comparisons made at 7 h of reaction indicate that the simulated and observed volumes of Ca₃SiO₅ consumed by hydration agree to within the measurement uncertainty. The location of simulated hydration product is qualitatively consistent with the observations, but the outer envelope of hydration product observed by nCT encloses more than twice the volume of hydration product in the simulations at the same time. Simultaneous nXRF measurements of the same observation volume imply calcium and silicon concentrations within the observed hydration product envelope that are consistent with Ca(OH)₂ embedded in a sparse network of calcium silicate hydrate (C−S−H) that contains about 70 % occluded porosity in addition to the amount usually accounted as gel porosity. An anomalously large volume of Ca(OH)₂ near the particles is observed both in the experiments and in the simulations, and can be explained as originating from the hydration of additional particles outside the field of view. Possible origins of the unusually large amount of observed occluded porosity are discussed.

1. Introduction

This paper describes a detailed, point-by-point comparison of computer simulations with experimental observations of the developing 3D microstructure of a small collection of tricalcium silicate (Ca₃SiO₅) particles as they react in an aqueous solution of calcium hydroxide. “Point-by-point” means here that the simulated and observed microstructures will be compared in terms not only of the total volumes of each phase, but also of how those phases are distributed in space at a resolution of 500 nm. The system under consideration was chosen as a reasonably simple and well-defined analog of portland cement binders in concrete. Tricalcium silicate (Ca₃SiO₅), stabilized in its monoclinic polymorph by impurities such as aluminum or magnesium, is the majority mineral component of portland cement and is known to be the major determinant of early reaction rates and strength gain in concrete binders, at least during the first day. The primary solid product of reaction between Ca₃SiO₅ and water, calcium silicate hydrate gel (C−S−H),¹ is the most complex material, both structurally and chemically, that forms in concrete binders. Therefore, the reaction of even a small cluster of Ca₃SiO₅ particles in water can provide useful insights about microstructure development and strength gain in concrete.

Such a 3D comparison has not been possible until recently. Models of cement microstructure development, with varying levels of rigor, have existed for about three decades [1–8]. Simulated microstructures using these models have often been compared to macroscopic indicators of hydration rates [3–5, 7, 8]. Sometimes they are also compared with 2D micrographs of actual hydrated cement paste microstructure either qualitatively [2, 4] or by statistically analyzing the spatial distribution of the solid phases or capillary porosity using radial distribution functions or autocorrelation functions [8–10]. However, 2D micrographs are typically acquired only after interrupting hydration by solvent exchange or drying, and under the high vacuum conditions of a scanning electron microscope (SEM) These conditions may alter the microstructure considerably compared to that in a fully saturated system, especially the C−S−H [11–13], although a recent report showed that solvent exchange with isopropyl alcohol followed by supercritical drying, which should exert no drying stresses on the structure, yield C−S−H morphologies observed by SEM that are at least qualitatively like those obtained by normal solvent exchange and drying [14]. In contrast, the advent of nanoscale X-ray computed tomography (nCT) has made it possible to examine the 3D microstructure of porous cementitious media with a spatial resolution on the order of tens of nanometers, and coupling tomography with nanoscale X-ray fluorescence spectrometry (nXRF) has enabled the mapping of the elemental concentrations with about the same spatial resolution [15]. Several papers published in the last few years [15–18] have shown the rich 3D data that can be acquired and analyzed with these methods, which make it possible for the first time to make true 3D microstructure comparisons with microstructure-based computer models of cement hydration.

Among the microstructure models available for the purpose, this paper uses the kinetic cellular automaton model called HydratiCA [10, 19]. The choice was made because HydratiCA models the 3D microstructure evolution according to locally calculated kinetics of reactions, including nucleation kinetics and nonlinear rates of dissolution and growth, as a function of the local thermodynamic driving force for those reactions. HydratiCA therefore invokes fewer assumptions about the overall mechanisms of cement hydration than do other models [2, 4, 6, 8, 20], and the assumptions it does make are the values of thermodynamic, structural, and kinetic properties of substances that, at least in principle, can be measured in the laboratory.

Quantitative comparisons between experiment and simulation at the microstructure scale provide an exceptionally stringent test of this kind of model. The great majority of hydration model interpretation and testing [2, 4, 6, 7, 21–26] has been based on the quality of parameter fitting to observed macroscopic measurements of hydration progress such as isothermal calorimetry, chemical shrinkage, or bound water. This kind of testing involves the implicit yet untested assumption that the underlying model captures all the important physical and chemical mechanisms that are involved in the process. However, the danger of that approach is that almost equally good fits can be made to such macroscopic data with different models that are based on different sets of kinetic mechanisms [26, 27]. In contrast, comparisons based on the detailed microstructural evolution trajectory can quickly reveal if incorrect or incomplete mechanisms are being assumed based on the amount and spatial distribution of the phases in the microstructure as a function of time. HydratiCA attempts to model our current mechanistic understanding of hydration with as much detail as we have available. The point of comparing HydratiCA-simulated microstructure development with experimental observation in this paper is not to demonstrate that the model works well, but to reveal gaps in our current understanding of the mechanisms of hydration.

2. Materials and Methods

The experimental data reported in this paper have been published in a previous paper with full details on the procedures used [18]. A brief summary of the procedure is provided here.

2.1. Tricalcium silicate powder

A triclinic Ca₃SiO₅ powder^1,2 was used for the hydration study. Table 1 shows the elemental composition of the powder as measured by inductively coupled plasma optical emission spectroscopy (ICP-OES), together with the specific surface area measured by multipoint BET nitrogen adsorption isotherms. Quantitative X-ray powder diffraction (XRD) indicates that the powder is composed almost entirely of triclinic (T3) Ca₃SiO₅, with approximately 1.5 % by mass of CaO.

Table 1.

Elemental composition and BET specific surface area of the Ca₃SiO₅ powder. Three replicate measurements of each element concentration were made and typically had a range of 2 in the least significant digit. The uncertainty in the surface area is reported as ± one standard deviation±of three replicates.

ICP Elemental Analysis	Al	Ca	Mg	Si	Sr
(mole %)	< 0.2	74.8	< 0.002	25	0.0018
BET surface area (m2 kg−1)	1216 ± 3

The particle size distribution (PSD) was estimated by automated scanning electron microscopy (ASEM) using 4000 individual dispersed particles. About 95 % of the particles had an average diameter between 1 μm and 7.5 μm.

2.2. Specimen preparation

Specimens were prepared by attaching several of the powder particles, with a total mass of about 1.57 ng, to the tip of a tungsten needle with a rapid-curing epoxy,³ as illustrated in Fig. 1. An inverted plastic cone was tightly affixed to the needle to hold the solution. Approximately 2 mg of additional Ca₃SiO₅ powder was glued with the same epoxy to the side of the needle to make the average water:cement mass ratio (w/c) be 5.0 after 10 μL was added to the cone.

Figure 1.

Experimental setup for nCT experiments.

The whole assembly was placed in an ultrahigh-purity N₂ environment to avoid carbonation. An initial nCT scan of the dry particle-needle configuration was made with the cup in the lowest position. Afterward, the prescribed volume of 15 mmol L⁻¹ calcium hydroxide solution was added to the cone to submerge the particles. The whole assembly was maintained at (25 ± 1) °C throughout the experiment. The dilute calcium hydroxide solution was used instead of pure deonized water to intentionally reduce the otherwise very rapid rate of Ca₃SiO₅ dissolution that occurs on first con tact with water [28, 29]. The particles remained submerged for 7 h, after which the seal was removed and hydration arrested by solvent exchange with 99 % isopropyl alcohol (IPA) for 5 min. IPA was used because it has been shown previously to cause no observable differences in the C−S−H morphology or other aspects of the microstructure of hydrated specimens [18].

2.3. nCT

All nCT measurements were made in the Hard X-ray Nanoprobe at Sector 26 in a shared space between the Advanced Photon Source (APS) and the Center for NanoScale Materials (CNM) at Argonne National Laboratory. More information on the instrument and the settings used for this study can be found in Hu et al. [18]. The sample was scanned once at each of a large number of incidence angles to produce a collection of two-dimensional radiographs, from which a single digitized three-dimensional tomograph was reconstructed. The reconstruction technique used mosaic tomography to post-align partially overlapping radiographs, using Stanford TXM-Wizard software [30]. Full details of the reconstruction method, including its specific application to these data, are beyond the scope of this paper but are provided elsewhere [31]. The final segmented tomograph is rendered as a three-dimensional array of voxels at a resolution of 15.6 nm per voxel.

Quantitative volume data for each phase can be obtained from nCT by separating the tomograph into regions of different components based on grayscale values, as described fully in Reference [31]. The nanometric length scale of the nCT data make it highly susceptible to small translations or rotations that can occur due to thermal expansion or stage positioning errors. These shifts can be accommodated by aligning the data from separate scans using the tungsten needle or gold nanoparticle as a registration marker (see Fig. 1). The alignment procedure has been automated with a computer algorithm that finds a rigid-body translation and rotation needed to match the scans [31].

2.4. nXRF

Emitted characteristic X-ray fluorescence radiation was detected with a four-element silicon drift energy dispersive detector [15, 32]. Fluorescence spectra were analyzed using the software package MAPS [33]. Fitting and quantification of the fluorescence data were performed using thin film standards (National Bureau of Standards, Standard Reference Materials 1832 and 1833). Further details on the analysis of nXRF data for this system are provided elsewhere [15, 18, 31].

3. Computer Simulations

3.1. Model description

The computer simulations reported here were performed using a kinetic cellular automaton model, called HydratiCA, developed at the National Institute of Standards and Technology (NIST), which tracks 3D microstructure evolution in aqueous suspensions by coupled transport and reactions. Full details of the model algorithms and verification are given elsewhere [10, 19], so only a brief synopsis will be provided here.

Stoichiometric solid phases (e.g., Ca(OH)₂, Ca₃SiO₅), water, and aqueous solute species (e.g., Ca²⁺, OH⁻) are defined as separate chemical components. Each material component is discretized into cells, each cell corresponding to a prescribed number of moles of that component. The initial microstructure of cement particles and water is mapped onto a cubic lattice by assigning cell occupations numbers for each component at each site. Chemical and structural changes are simulated by iterating over small time steps during which independent reaction and transport processes occur. The probability, pt, of a cell executing a random walk to a neighboring site is determined by that cell’s local diffusivity, D, the time increment, Δt, and the lattice site spacing, λ:

$$p_t=\frac{D\mathrm{\Delta }t}{{\lambda }^2}$$ (1)

Based on published mobilities of ions at infinite dilution [34] and the fact that the solutions used in this system are dilute, with ionic strengths not exceeding 0.1 mol L⁻¹, species released by Ca₃SiO₅ dissolution should be able to diffuse, on average, a distance of 50 μm within 1 s and 100 μm within 3 s [19]. Consequently, for numerical efficiency in this and several other studies of HydratiCA on small systems [19, 35, 36], diffusion rates through the aqueous solution are assumed to be so high compared to the rates of all other processes that the solution is perfectly mixed. This assumption is also supported by the likelihood that locally generated heat of dissolution at the Ca₃SiO₅ particle surfaces will promote convective mixing of the liquid near the particles.

Following the procedure developed by Karapiperis [37], the probability of a unit reaction happening in a time step Δt depends on its rate constant and on the cell occupation number of each reactant.

Table 2 lists the material components used in the simulations and their assumed thermophysical properties, including their molar volumes, molar mass, and, for mobile species, their mobility at infinite dilution. In addition, Table 3 gives the values used to characterize the rates of the various reactions that are assumed to occur among these components during Ca₃SiO₅ hydration. Based on prior measurements of solution composition during supposed “pure” dissolution (i.e., under conditions designed to prevent the precipitation of C−S−H) [28, 38, 39], Ca₃SiO₅ is assumed to dissolve congruently in water according to the reaction

$${\text{Ca}}_3{\text{SiO}}_5+4{\mathrm{H}}_2\mathrm{O}\rightleftharpoons 3{\text{Ca}}^{2+}(\text{aq})+{\mathrm{H}}_3{\text{SiO}}_4^{-}(\text{aq})+5{\text{OH}}^{-}(\text{aq})$$ (2)

with an apparent solubility product K.

Table 2.

Properties of material components used in the simulations. V_m is the molar volume, M is the molar mass, σ is the bulk electrical conductivity through the given solid phase, σ_o is the electrical conductivity of the bulk aqueous solution, and D is the ion diffusion coefficient of an ion in the solution at infinite dilution. η and ϕ_max are parameters determining the efficacy of C–S–H phases in blocking the access of Ca₃SiO₅ to water and are described further in Eq. (6). Unless otherwise indicated, the values in the table are taken from Reference [36].

Component	Vm/10−6 m3 mol−1	M/kg mol−1	σ/σo (a)	D(b)/10−9 m2 s−1	η(c)	ϕmax (c)
H2O	18.1	0.018 02	1.0
Ca3SiO5	72.4	0.228 33	0.0
C2S3H12(d)	633.6	0.5086	0.7		0.75(e)	0.2
C5S3H12(d)	747.2	0.6768	0.7		0.50	1.0
Ca(OH)2	33.1	0.074 09	0.0
Ca2+		0.040 08		0.79
CaOH+		0.057 09		0.71
${\mathrm{H}}_2{\text{SiO}}_4^{2-}$		0.094 10		0.70
${\mathrm{H}}_3{\text{SiO}}_4^{-}$		0.095 10		0.70
OH−		0.017 00		5.28

^(a)Relative conductivity (i.e., the conductivity divided by that in the bulk solution).

^(b)Ion mobility at infinite dilution.

^(c)See Eq. (6) for the meaning of these terms for coverage of Ca₃SiO₅.

^(d)Stoichiometric components of an ideal solid solution model for C−S−H [47].

^(e)Reduced from 0.9 based on more simulation studies conducted after Reference [36] at different lattice spacings.

Table 3.

Stoichiometry and assumed thermodynamic and kinetic parameters for simulated reactions. Except where noted, the collection of reactions and the parameter values are taken from Reference [36] and references therein. The reactions and solubilities for C–S–H are based on a newer solid solution model in Reference [47], and the kinetic parameter values were chosen to give approximately the same rates of nucleation and growth as simulated in Reference [36].

Reaction	k+/μmol m−n s−1(a)	ln K	$I_0^B/{\mathrm{m}}^{-n}{\mathrm{s}}^{-1}$ (a)	q/K3
${\text{Ca}}_3{\text{SiO}}_5+4{\mathrm{H}}_2\mathrm{O}\rightleftharpoons 3{\text{Ca}}^{2+}+{\mathrm{H}}_3{\text{SiO}}_4^{-}+5{\text{OH}}^{-}$	112.5(b)	−39.0(b)
${\mathrm{C}}_2{\mathrm{S}}_3{\mathrm{H}}_{12}\rightleftharpoons 2{\text{Ca}}^{2+}+3{\mathrm{H}}_3{\text{SiO}}_4^{-}+{\text{OH}}^{-}+7{\mathrm{H}}_2\mathrm{O}$	1.5 × 10−7	−37.43	1.1 × 1027(b)	2.0 × 109(b)
${\mathrm{C}}_5{\mathrm{S}}_3{\mathrm{H}}_{12}\rightleftharpoons 5{\text{Ca}}^{2+}+3{\mathrm{H}}_3{\text{SiO}}_4^{-}+7{\text{OH}}^{-}+4{\mathrm{H}}_2\mathrm{O}$	1.5 × 10−7	−80.43	7.3 × 1026(c)	1.7 × 1010(c)
$\text{Ca}{(\text{OH})}_2\rightleftharpoons {\text{Ca}}^{2+}+2{\text{OH}}^{-}$	7.2	−11.97	7.35 × 1026(d)	2.5 × 109(d)
${\text{CaOH}}^{\text{+}}\rightleftharpoons {\text{Ca}}^{2+}+{\text{OH}}^{-}$	6 × 105	−2.81
${\mathrm{H}}_3{\text{SiO}}_4^{-}+{\text{OH}}^{-}\rightleftharpoons {\mathrm{H}}_2{\text{SiO}}_4^{2-}+{\mathrm{H}}_2\mathrm{O}$	1.5 107	1.91

^(a)n = 2 or 3 for heterogeneous or homogeneous processes, respectively.

^(b)Based on linear regression of measurements in Ref. [28].

^(c),(d)Heterogeneous nucleation on Ca₃SiO₅ and C−S−H, respectively.

The nonlinear molar dissolution rate is described by

$$\frac{d{N}_{{\text{Ca}}_3{\text{SiO}}_5}}{dt}=-k_{{\text{Ca}}_3{\text{SiO}}_5}{A}_{\text{eff}}\left(1-\exp \left[-{\left(\frac{\ln K-\ln Q}{s}\right)}^r\right]\right)$$ (3)

where $k_{{\text{Ca}}_3{\text{SiO}}_5}$ is the dissolution rate constant in pure water, approximated from the experimental data [28] as 112.5 μmol m⁻² s⁻¹ and A_eff is the reacting Ca₃SiO₅ surface area, which may be less than the actual Ca₃SiO₅ surface area due to coverage by hydration product. An earlier regression analysis using measurements obtained over a wide range of undersaturations [28] yielded $k_{{\text{Ca}}_3{\text{SiO}}_5}$ = 125 μmol m⁻² s⁻¹, ln K = −41.1 s = 21.05, and r = 3.73 [36]. The activity product, Q, is defined for reaction (2) by

$$Q=\frac{{\left\{{\text{Ca}}^{2+}\right\}}^3\{{\mathrm{H}}_3{\text{SiO}}_4^{-}\}{\left\{{\text{OH}}^{-}\right\}}^5}{{\left\{{\mathrm{H}}_2\mathrm{O}\right\}}^4}$$ (4)

At the low ionic strengths of these experiments, the activity of water should equal the mole fraction of water according to Raoult’s law. The form of the rate law used in Eq. (3) is empirical, but has the satisyfing property that it collapses to the standard rate law for an elementary reaction (i.e., if the order is equal to the molecularity) when r, s → 1:

$$\frac{dC}{dt}=-ck\left(1-\frac{Q}{K}\right)$$ (5)

where C is the molar concentration of a reactant in an elementary reaction, c is the molar stoichiometric coefficient for that reactant, k is the absolute forward rate constant, and K is the equilibrium constant. Therefore, the same general form as Eq. (3) can embrace a wide range of rate behavior.

For reasons given more fully in the Discussion, a small cluster of Ca₃SiO₅ particles is likely too small of a sample to exhibit the bulk mean dissolution rate behavior upon which the parameters ln K, r, and s were obtained earlier. Because of this and the inherent variability in mineral dissolution rates, also taken up more fully in the Discussion, three of the regression parameters were modified in this study to k = 112.5 μmol m⁻² s⁻¹, ln K = −39.0 and s = 20.05. The effect of these modifications on the rate law function is shown in Fig. 2 along with the experimental data upon which the earlier regression was based. These modifications still give a reasonable fit to the prior measurements and have the advantage of yielding a better agreement with the observed total volume of Ca₃SiO₅ after 7 h of hydration, as will be shown in the Results.

Figure 2.

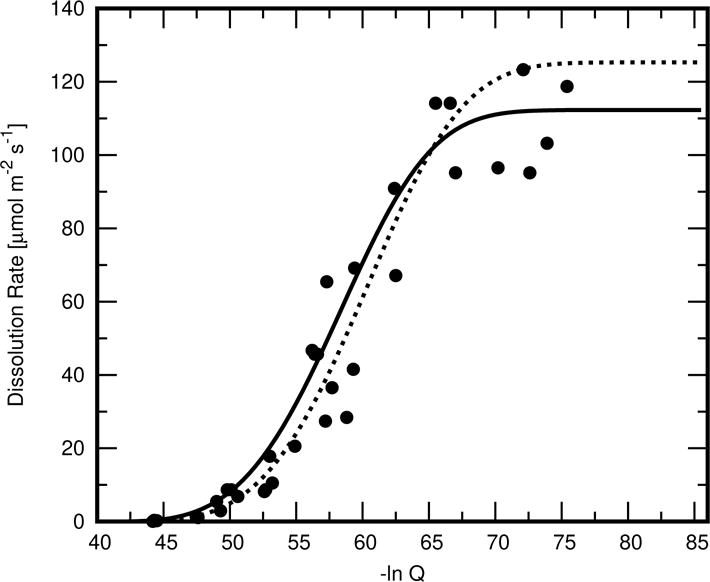
Assumed rate law for Ca₃SiO₅ dissolution as a function of its activity product in solution (solid curve), compared to the one obtained in Ref. [36] (dashed curve) by nonlinear regression to experimental data reported in Ref. [28] (individual points).

The effective Ca₃SiO₅ surface area at a lattice site is defined in HydratiCA as

$$\frac{A_{\text{eff}}}{A}=1-\eta min{\left(1,\frac{{\varphi }_{\text{CSH}}}{{\varphi }_{max}}\right)}^{2/3}$$ (6)

where A is the physical surface area of Ca₃SiO₅, η is the “opacity” of the product layer that forms on the surface (a measure of how effectively a unit area of coverage can inhibit dissolution), ϕ_CSH is the volume fraction of the lattice site occupied by C−S−H, and ϕ_max is the site volume fraction at which the surface is considered to be completely covered with a layer having opacity η. Phases with a low contact angle on Ca₃SiO₅, or those that grow essentially in 2D along the surface, will have relatively lower values of ϕ_max. The use of A_eff is necessitated by the fact that any lattice-based model cannot resolve the microstructure on a scale smaller than a single lattice site, which for these simulations is 1 μm. Drawing from a recent modeling study that assumed the same mechanisms, the values chosen for these opacity parameters, as well as the other physical parameters for all components used in the simulations, are given in Table 2. The Discussion section briefly takes up the question of whether these values are justified in light of the unusual morphology of the hydration product that were observed in this experiment.

In the context of the colloidal model of C−S−H [40, 41], an individual globule of C−S−H produced by Ca₃SiO₅ hydration for 28 d has been reported to have the composition C_1.7SH_1.8 in the saturated state and saturated density of 2604 kg m⁻³ [42, 43], which would correspond to a molar volume ${\overline{V}}_{\mathrm{C}-\mathrm{S}-\mathrm{H}}$ of about 7.2 × 10⁻⁵ m³. HydratiCA does not attempt to explicitly model these individual globules, but considers a fundamental growth unit of C−S−H to include several clusters of these globules together with saturated intercluster pores. The intercluster porosity is assumed to be 70 % by volume and saturated with aqueous solution [44]. The water in the porosity is assumed to be available for further reactions, except for 2.2 formula units of physically adsorbed water per formula unit of SiO₂ in C−S−H [36].

Of equal importance in this study, solution equilibria measurements indicate that during C₃S hydration at early times, a plot of the solution’s Si concentration against its Ca concentration generally lies on the upper of two curves (often called Curve B) first identified by Jennings [45] and later refined by Chen [46]. The composition of C−S−H is modeled here as an ideal solid solution [47] (i.e., assuming zero enthalpy of mixing) with two stoichiometric end members. Generalized regression [48] of that two-component model to published data for Curve B was used to estimate the composition and solubilities of the model end members, which are C₂S₃H₁₂ and C₅S₃H₁₂. The molar volumes, $\overline{V}$, of these components, given in Table 2, were calculated by linear extrapolation from known values of other calcium silicate hydrate compositions [36, 43]. The formula unit volumes needed in Eqs. (7) and (8) are found by dividing the appropriate molar volume by Avogadro’s number.

Table 3 shows the collection of reactions that were used in the simulations, along with the assumed equilibrium constants, reaction rate constants, and nucleation parameters. Nucleation rates of C−S−H and Ca(OH)₂ are assumed to follow classical nucleation theory, with C−S−H and Ca(OH)₂ nucleating heterogeneously on the surface of the cement grain and on C−S−H, respectively. The rate of formation of C−S−H nuclei (m⁻² s⁻¹) is given by [36, 49]

$$I_{\text{het}}=I_0^B{O}_V^B\exp \left[-\frac{q}{{\ln }^2\beta }\right]$$ (7)

where I_het is the nucleation rate, $O_V^B$ is the area of Ca₃SiO₅ per unit volume available for nucleation, and β is the saturation index of the end member that is nucleating, that is, its activity product divided by its solubility product. The other pre-exponential factor is $I_0^B=D/{\Omega }^{4/3}$, where D is the diffusivity in solution of an attaching formula unit and Ω is the formula unit volume of the solid. Finally, the factor q in the exponential argument of Eq. (7) is given by

$$q=\frac{16\pi {\gamma }_{\text{CL}}^3{\Omega }^{2}f(\theta )}{3k_{\mathrm{B}}^3{T}^3}$$ (8)

where γ_CL is the C−S−H interfacial energy with the solution, k B is Boltzmann’s constant, θ is the contact angle between the crystal and the substrate, and

$$f(\theta )=[2+\cos (\theta )]{\sin }^4(\theta /2)$$ (9)

The interfacial energies of the end members CSH(I) and CSH(II) have not been directly measured, but were recently estimated [36], based on a solubility relationship proposed by Söhnel [50], to be 84.0 mJ m⁻² and 77.6 mJ m⁻², respectively.

Equilibrium constants for speciation reactions and for Ca(OH)₂ dissolution at 25 °C were taken from the Nagra/PSI thermochemical database [51], which did not report uncertainties in these values. The rate constants for these solution reactions have been chosen to be sufficiently great to ensure that departures from speciation equilibrium are erased, to within 1 % in the concentration of any species, in 0.1 s or less. The dissolution rate constant for Ca(OH)₂ at 25 °C is estimated in Table 3 from the one extant report of solution composition changes in a particulate suspension [52]. Uncertainties in the solution data and solid surface area were not reported in that study.

Reaction data for C−S−H are more challenging to obtain because of the wide variety of results in numerous published studies of solubility [46, 53–58], and the lack of data on C−S−H growth rates. Nonlinear regression of the C−S−H ideal solid solution model with the two end members given in Table 2 provides nearly as good an agreement with published solubility data as other solid solution models, and the solubility constants given in Table 3 are those that yield the minimum sum of squared residuals (SSR) for those compositions, as described fully in Reference [47]. The rate constants and form of the rate law for C−S−H growth,

$$\frac{d{N}_{\text{CSH}}}{dt}=k_{\text{CSH}}{A}_{\text{CSH}}{({\beta }_{\text{Tot}}-1)}^3$$ (10)

are those shown to provide the closest agreement to recent experimental measurements of C−S−H growth on calcite crystals [44]. In Eq. (10), k_CSH is the rate constant given in Table 3 and is assumed to be the same for both end members, A_CSH is the surface area, and β_Tot is the total saturation of the solid solution, which is the driving force for the growth of the most favorable composition of the solid solution as a function of the aqueous solution composition, as described fully elsewhere [47].

The sensitivity of simulation results to some of the input parameters in Table 3 has been discussed in other papers [36, 47]. A more complete sensitivity analysis is a subject for future work.

3.2. Implementation

Each lattice site in HydratiCA is occupied by numbers of cells of differing types, each of which represents a discrete number of formula units of a particular material component or phase. Periodic boundary conditions are used on the four vertical sides of the system. The additional 2 mg of Ca₃SiO₅ powder placed below the needle tip in the experimental setup was simulated by using non-periodic boundaries at the top and bottom of the system and adding one additional layer of Ca₃SiO₅ lattice sites below the needle. The total volume of the system was chosen to match the average water/cement mass ratio w/c = 5.0 used in the experiment. However, the volumes of Ca₃SiO₅ and hydration products located below the needle tip were not included in the volume totals for solids in either the experiments or the simulations. This was done primarily to keep the computational domain at a feasible size for the simulations and because the primary objective of the study is to focus on the microstructure of the isolated cluster arrangement above the needle. The main impact of excluding the additional material below the needle is that any significant migration of material between the two regions can be inferred only indirectly when comparing the simulations and experiments. This issue will be revisited in more detail in the Results and Discussion sections.

The algorithms used to compute changes in a site’s cell occupation numbers require information only from the site and its nearest and next-nearest neighbor sites. This localization of the algorithms leads to a natural parallel decomposition of the simulation, by which the lattice is partitioned into sublattices, each of which is assigned to a separate computational process. Each process uses one CPU processor. A process owns each of the lattice sites of the sublattice it is assigned, and the owner of a lattice site is responsible for all of the computations needed to update that lattice site during each time step of the simulation. Therefore, lattice sites that are on the surface of a sublattice must gather data from neighboring lattice sites that are owned by other processes. This updating is accomplished by surrounding each sublattice with a layer of “ghost” lattice sites that are images of the actual lattice sites owned by adjacent processes. In the simulations reported here, the lattice was decomposed into orthorhombic sublattices that were as close to the same size and as close to cubic as possible for the lattice shape and number of processes, in an effort to minimize the number of ghost lattice sites. Inter-process communication is handled using MPI (Message Passing Interface), the dominant communications protocol used in high-performance parallel computing [59]. The simulations were performed using the Stampede supercomputer at the University of Texas, a resource of the Extreme Science and Engineering Discovery Environment (XSEDE) [60].

4. Results

4.1. Evolution and Morphology of Solids

Figure 3 shows the tomograph acquired experimentally for the initial particle configuration on the tungsten needle before the aqueous solution was introduced, together with the tomograph acquired after 7 h of reaction in the calcium hydroxide solution. Comparison of the two tomographs shows that dissolution of Ca₃SiO₅ particles happens nonuniformly, as previously observed for similar particle cluster systems by Hu et al. [18]. Although most of the particles have eroded to some extent, a few particles, and isolated regions of other particles, have dissolved more extensively. An example is the area in contact with the needle and the middle region, where the original hole between particles has opened significantly. Other regions show considerably less dissolution, such as the top right particle. Even more striking is the nonuniform distribution of hydration product surrounding the Ca₃SiO₅ particles after 7 h of hydration. A relatively thin layer of product, approximately 1 μm thick, is visible to the left, while more voluminous regions are evident in the lower left, right, and especially the upper right portions of the figure. These larger regions are between 5 μm and 10 μm thick. Though not indicated in the figure, these regions seem to have a large fraction of Ca(OH)₂ [18]. The thickest regions of hydration product are often in the vicinity of regions with relatively less dissolution of the nearest Ca₃SiO₅ particles.

Figure 3.

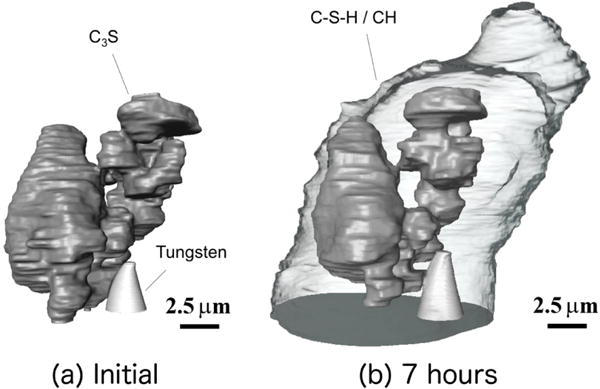
Experimentally acquired tomographs. (a) Initial particle configuration on tungsten needle; (b) after 7 h of reaction in an aqueous solution with initial calcium hydroxide concentration of 15 mmol L⁻¹. Ca₃SiO₅ particles are dark gray, the tungsten needle is light gray, and the hydration products are shown as transparent.

For comparison purposes, each lattice site in the model should ideally be mapped to a single voxel of the initial tomograph. However, the tomographs in Fig. 3 are resolved at 15.6 nm per voxel, so a direct mapping of voxels to lattice sites would generate a computational mesh with approximately 10⁹ sites. Such a large number of lattice sites cannot be feasibly accommodated, so the experimental system of voxels was coarse-grained to a resolution of 500 nm per voxel. The volume-averaged grayscale value of the voxels in each subset was determined. Based on this average grayscale value, the corresponding coarse-grained voxel was thresholded by tagging each voxel with an identification number value of 0 (empty), 100 (partially filled with Ca₃SiO₅, the remaining volume being solution) or 255 (filled with Ca₃SiO₅). The resulting coarse-grained tomograph, with a resolution of 500 nm per voxel, is shown to the left in Fig. 4; it retains the relative phase volume fractions and topology of the original tomograph. Each voxel of this coarser tomograph was mapped to a lattice site in a 51 × 51 × 37 computational mesh to simulate hydration at 25 °C under saturated conditions using HydratiCA. The simulated microstructures after 7 h is shown to the right in Fig. 4. The entire product region is shown in the middle image as a transparent gray envelope to better reveal the remaining Ca₃SiO₅ cluster. The Ca(OH)₂ precipitates are shown in light green in the right image, with C−S−H remaining transparent. These images show that the hydration products nucleate on the surfaces of the Ca₃SiO₅ particles and grow outward, which is in qualitative agreement with the experimental observations in Fig. 3. C−S−H nucleates rapidly on Ca₃SiO₅, which consumes the driving force for further nucleation in less than 60 s, as shown in Section 4.2. Its final nucleation density is 6 μm⁻². Ca(OH)₂ nucleates on this C−S−H after about 17 min, while the C−S−H is still contained within a thin layer around the particles, and continues to nucleate for 5 min after that. A total of 104 Ca(OH)₂ nuclei have formed before the driving force for nucleation becomes too low. (see Section 4.2). These Ca(OH)₂ embryos coalesce extensively as they continue to grow, so only one, or at most two, large domains are visible after 7 h.

Figure 4.

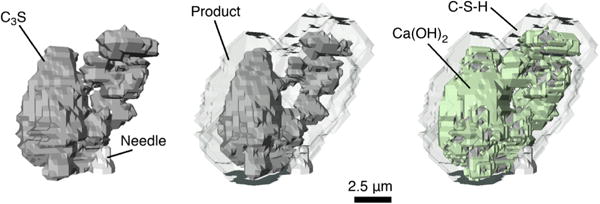
Simulated microstructure of the initial system shown in Fig. 3, coarse-grained to a voxel size of 500 nm (left), and at 7 h of simulated hydration (center and right). The center image shows the entire volume of simulated hydration product as transparent gray; the image on the right shows C–S–H as transparent gray and Ca(OH)₂ as light green. Each image shows the Ca₃SiO₅ as dark gray and the supporting needle as light gray.

The simulated microstructure in Fig. 4 is qualitatively consistent with the nCT observations in Fig. 3. However, the total volume of simulated hydration product (middle image of Fig. 4) is considerably less than the experiments indicate. Furthermore, the experiments show that the products are distributed asymmetrically about the particle, with considerably more being observed at the top and right side of the cluster; the simulations produce a more even distribution of product.

Figure 5 shows the simulated time dependence of the volume of Ca₃SiO₅, C−S−H, and Ca(OH)₂ over 10 h of hydration. The figure also shows the volume of Ca₃SiO₅ measured at 0 h and 7 h as solid circles, and indicates that the simulated rate of Ca₃SiO₅ dissolution is consistent with the observed volume of Ca₃SiO₅ consumed over the same time period.

Figure 5.

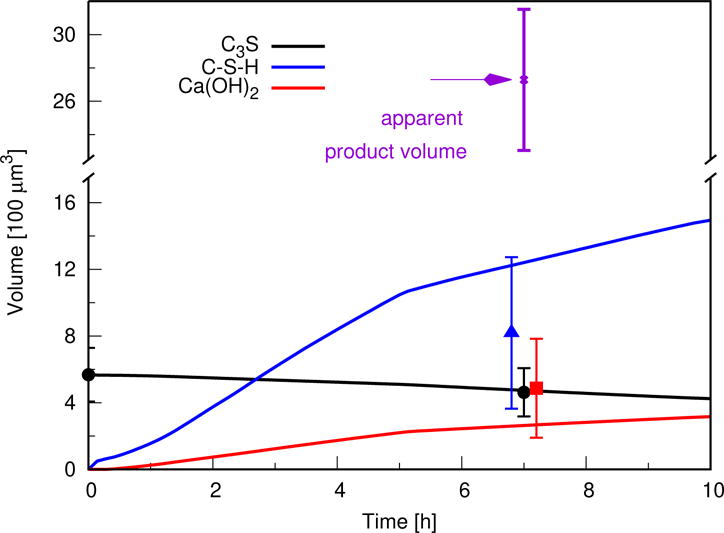
Simulated time dependence of solid product volumes. Solid curves are simulation results. The apparent solid product volume observed by nCT is shown as an “x”. Solid marks indicate estimated true solid volumes of each solid phase, based on voxel counting, for Ca₃SiO₅, and by coupling the apparent product volume with measured molar densities of calcium and silicon using nXRF for C–S–H and Ca(OH)₂. Experimental measurements for C–S–H and Ca(OH)₂ are offset slightly in time for ease of viewing error bars. Error bars for measured Ca₃SiO₅ volumes give the range of possible values based on uncertainty in the voxel gray values at the particle boundaries, and error bars for other measurements give the propagated uncertainty based on the relative standard uncertainty in the molar density values of calcium and silicon measured by nXRF

For comparison, the measured volume of the product region at 7 h is also indicated in the plot. The apparent volume of product is more than twice the combined simulated volumes of C−S−H and Ca(OH)₂ at the same time. At least some of the observed extra volume of product may be caused by a larger amount of fine porosity within the growing C−S−H than the 70 % assumed in the model, as will now be shown by combining the nCT data with analysis of the nXRF measurements of the same system.

Fig. 6 shows the nXRF data obtained on the system, showing the relative calcium and silicon concentrations [18]. The quantitative analysis of the nXRF data was restricted to a region within 3 μm along the left boundary of the product region where the product is closest to the detector, because signal absorption is related to the path length through the material before reaching the detector. Prior work suggested that < 25 % of the Si and 5 % of the Ca X-rays should be absorbed in that region closest to the detector [61].

Figure 6.

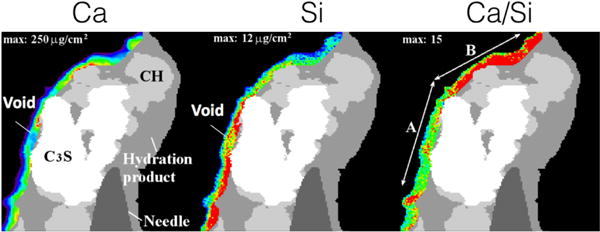
Element maps for calcium and silicon obtained by nXRF after 7 h of hydration. The image on the right shows the relative Ca/Si molar ratio. The most reliable quantitative analysis of elemental concentrations within the hydration product is made using the left-most region nearest to the detector. The thermal color scheme indicates regions of lower concentrations in blue and the highest concentrations in red.

nXRF data fused with nCT data, an analysis technique called “nano-Tomography Assisted Chemical Correlation” (nTACCo) [15], can provide an estimate of the mass density of calcium and silicon in the hydration product region shown in Fig. 6. The nXRF signal is collected over the entire depth of the solid intersected by the X-ray beam, giving mass concentrations per unit cross-sectional area rather than per unit volume [18]. For purposes of rough estimation here, the solid intersection depth in the same region is assumed to be (6 ± 2) μm based on the nCT reconstruction in the same region. With that additional assumption, the region highlighted in Fig. 6 has volume averaged mass densities ρ_Ca = (255 ± 105) kg m⁻³ and ρ_Si = (18 ± 9) kg m⁻³. This corresponds to molar densitiesn Ca = (6362 ± 2620) mol m⁻³ andn Si = (641 ± 320) mol m⁻³, respectively [18]. If one assumes that (1) all the Si in the product is part of C−S−H that itself has a molar Ca/Si ratio of x, and (2) the only solid phases in the product region are C−S−H and Ca(OH)₂, then

$$n_{\mathrm{C}-\mathrm{S}-\mathrm{H}}=n_{\text{Si}}=(641\pm 320)\text{mol}{\mathrm{m}}^{-3}$$ (11)

$$n_{\text{Ca}{(\text{OH})}_2}=n_{\text{Ca}}-x{n}_{\mathrm{C}-\mathrm{S}-\mathrm{H}}$$ (12)

where x is the Ca/Si molar ratio of C−S−H, the composition of which has been normalized by the number of SiO₂ formula units for convenience. If x = 1, which is at the low end of the range of values reported in the literature, then substituting Eq. (11) into Eq. (12) yields n Ca(OH)₂ = (5721 ± 2940) mol m⁻³ Likewise, if x = 2, which is at the high end of the range of values reported in the literature, then n Ca(OH)₂ = (5080 ± 2940) mol m⁻³. Therefore, at least within the ≈ 3 μm thick region of hydration product highlighed in Fig. 6, the effect of C−S−H composition on the inferred amount of Ca(OH)₂ is small compared to the uncertainty in the composition measurements. For that reason, the rest of this analysis will simply assume the value of Ca/Si predicted by the simulation at 7 h of hydration, x = 1.667. That assumption is also reasonably close to the value of x = 1.7 that seems to be most often cited in the literature [42, 43]. In that case, the nXRF measurements imply that the number of moles of Ca(OH)₂ per unit volume of product is n Ca(OH)₂ = (5297 ± 2990) mol m⁻³. In terms of mole fractions, X, of solids in the product region, these molar densities correspond to X C−S−H = 0.11 ± 0.05 and X Ca(OH)₂ = 0.89 ± 0.05. The implied molar ratio of Ca(OH)₂ to C−S−H is 8 ± 4, which is considerably greater than the value of about 1.34 that would be produced solely by reaction of Ca₃SiO₅ if the Ca/Si molar ratio of C−S−H is 1.667.

The molar densities just estimated can be combined with the total solid volume of hydration product above the needle measured by nCT to obtain an estimated number of moles of Ca(OH)₂ and C−S−H at 7 h of hydration. Table 4 compares these values both with the simulated number of moles and with the moles that would be required by the net hydration reaction, assuming that x = 1.667,

$${\text{Ca}}_3{\text{SiO}}_5+5{\mathrm{H}}_2\mathrm{O}\to {\left(\text{CaO}\right)}_{\mathrm{x}}\cdot \left({\text{SiO}}_2\right)\cdot {\left({\mathrm{H}}_2\mathrm{O}\right)}_4+\left(3-x\right)\text{Ca}{\left(\text{OH}\right)}_2$$ (13)

Table 4.

Measured changes in number of moles of each solid phase in Fig. 3 after 7 h of hydration, compared with predictions from simulations and with the values expected from net reaction (13) based on the measured amount of Ca₃SiO₅ dissolved.

Component	ΔN inferred from Measurement [pmol]	ΔN inferred from ΔN Reaction (13) [pmol](a)	simulated [pmol]
Ca3SiO5	−1.46 ± 0.50	–	1.326
C−S−H	1.7 ± 0.6	1.46 ± 0.50	−1.957
Ca(OH)2	14 ± 10	1.95 ± 0.90	7.950

^(a)Based on the measured number of moles of Ca₃SiO₅ dissolved in the second column. This assumes x = 1.667 in Reaction (13), which is the Ca/Si ratio predicted by the simulation at 7 h.

From these data, one may also estimate the volume fraction of fine occluded porosity that is evidently contained in the product region. Using a C−S−H molar volume of ${\overline{V}}_{\mathrm{C}-\mathrm{S}-\mathrm{H}}=1.94\times {10}^{-}{\mathrm{m}}^3$, which is augmented relative to the published value [42] by the assumed 70 % of intercluster pores as already described, the Si molar density measured by nXRF implies that the fraction of the solid product region occupied by C−S−H, including its saturated gel pores, is

$${\varphi }_{\mathrm{C}-\mathrm{S}-\mathrm{H}}=n_{\mathrm{C}-\mathrm{S}-\mathrm{H}}{\overline{V}}_{\mathrm{C}-\mathrm{S}-\mathrm{H}}=0.124\pm 0.062$$

Likewise, the volume fraction of Ca(OH)₂ in the product region can be estimated as the product of its molar density in the product and its molar volume

$${\varphi }_{\text{Ca}{\left(\text{OH}\right)}_2}=n_{\text{Ca}{\left(\text{OH}\right)}_2}{\overline{V}}_{\text{Ca}{\left(\text{OH}\right)}_2}=0.18\pm 0.10$$

Therefore, assuming no other solid components in the region of hydration product, the total volume fraction of solids in that region is estimated to be only 0.30 ± 0.16; the remaining 70 % of the product region is occluded porosity that is not already accounted as C−S−H gel porosity.

Based on the foregoing analysis, the best estimates of C−S−H and Ca(OH)₂ volumes in the product region at 7 h are shown in Fig. 5 as a filled triangle and a filled square, respectively.

4.2. Aqueous Solution

The composition of the aqueous solution was not monitored as part of the nCT experiments, but understanding of the simulation results can be enhanced by considering its predictions of the solution composition. Figure 7 shows as a solid curve the evolution in the total silicate concentration and total calcium concentration. The individual points on this plot are measurements made by different laboratories as compiled and plotted by Jennings as Curve B [45], which is typically observed during early-age hydration of Ca₃SiO₅; additional measurements made at higher calcium concentrations by Bellmann [62] are also shown. Within the first 0.3 s of hydration, the solution composition lies along the data for Curve B, both before and after the precipitation of Ca(OH)₂.

Figure 7.

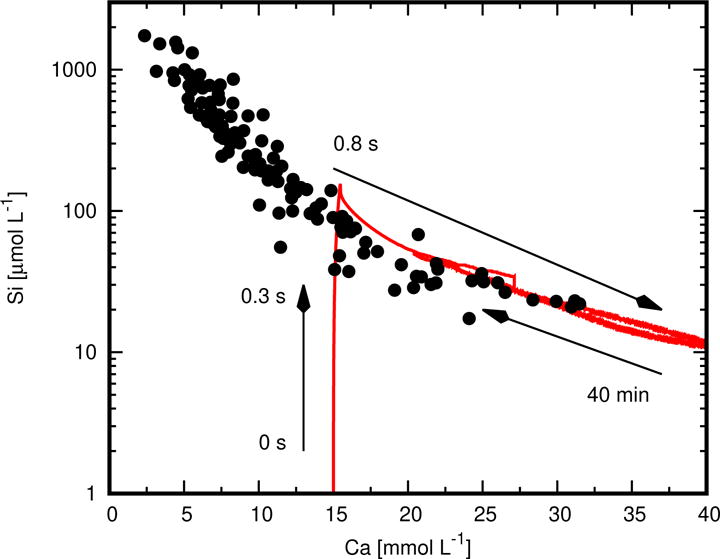
Simulated changes in total silicate and calcium concentrations of the aqueous solution (solid curve). Individual points are measurements made by different laboratories as plotted by Jennings as Curve B [45], together with more recent measurements made by Bellmann [62] at higher calcium concentrations.

The composition and solubility of the solid solution end members for C−S−H (Table 3) were set by assuming that it is in equilibrium with solutions lying along Curve B [48]. Therefore, the fact that the simulated solution remains close to Curve B implies that C−S−H attains and stays close to equilibrium with the solution. In turn, this implies that Ca₃SiO₅ dissolution controls the rate of hydration over this time scale. In support of this interpretation, Fig. 8 shows the total saturation of C−S−H (Eq. (10)) [47] and the saturation index (i.e., ratio of activity product to solubility product) of Ca₃SiO₅. The total saturation with respect to C−S−H rapidly spikes to nearly β_T = 7 at the beginning of the simulation, but then quickly decreases to β_T < 2 within 0.5 s as C−S−H nucleates and grows. From about one second until the end of the simulation, β_T ≈ 1.3, which is close to the equilibrium condition of β_T = 1. The saturation index of Ca₃SiO₅, in contrast, spends most of the simulation at values less than 0.1.

Figure 8.

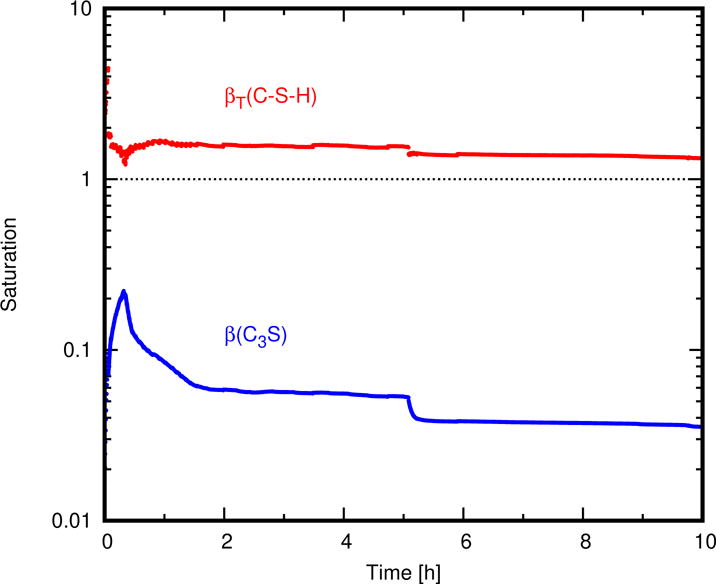
Simulated time dependence of the solution’s saturation with respect to C–S–H and to Ca(OH)₂. The saturation of Ca(OH)₂ is given in terms of its saturation index, β ≡ Q/K, and the saturation of the C–S–H solid solution is given in terms of its total saturation, which is the sum of the saturation indices of its two end members.

An earlier simulation study by Bullard and Scherer [36] suggested that the solution of a hydrating Ca₃SiO₅ paste could be significantly undersaturated with respect to C−S−H, so that neither C−S−H nor Ca₃SiO₅ could be near equilibrium throughout the early stages of hydration. However, that previous study used a discrete mixing model of C−S−H composition instead of the more thermodynamically realistic solid solution model [47] used here, and it also assumed component solubilities for C−S−H that were much lower than the ones used here, more closely approximating Jennings Curve A [45] than Curve B. These two results are therefore not inconsistent, but hinge on the assumption of whether the solubility of C−S−H forming at early times more closely resembles that indicated by Curve B or Curve A [45]. This topic is taken up again in the Discussion.

5. Discussion

The similarities and, more importantly, differences between the experimental observations and the simulation provide insights into those aspects of hydration and microstructure development that can be understood–or at least captured–in terms of the the model’s assumptions and those that are not yet well understood. Those aspects that the model does not adequately simulate can be used to sketch a road map for further research.

5.1. Ca₃SiO₅ Dissolution

Mounting experimental evidence indicates that dissolution rates of numerous minerals [63–68], including rapidly dissolving ones such as gypsum [69] and cubic tricalcium aluminate [70], can vary from point to point on the surface at constant under-saturation by a factor of ten or more, being strongly influenced by the local density and type of surface defects such as dislocation outcroppings, stacking faults, and grain boundaries. Dissolution rates for these minerals, and most probably for Ca₃SiO₅ [17, 18], are therefore more properly characterized by a statistical distribution than by a single rate.

The rates reported by Nicoleau [28] for dissolution of a dilute suspension of Ca₃SiO₅ particles should, therefore, be understood as a statistical average over all exposed surfaces on all the particles in the suspension. Even these average values exhibit considerable scatter, as indicated in Fig. 2. In addition, very few rate measurements were reported at the highest activity products where the dissolution rate is low. Unfortunately, the solution in a hydrating Ca₃SiO₅ system spends all but the first few seconds of its time at those higher activity products. A variation by as little as 0.5 μmol m⁻² s⁻¹ in this region has major implications for the hydration rate. For example, changing the dissolution rate law from the solid curve to the dashed curve in Fig. 2 reduces the degree of hydration at 7 h from 18 % to < 3 %. Besides these uncertainties, a small cluster of only several particles, such as that examined in this paper, is not a large statistical sampling and cannot be expected a priori to dissolve, even on average, at the mean rate for the same undersaturation that otherwise would be observed in a much larger sample.

In the absence of more detailed characterization of the local dissolution rates of the particle cluster, we have chosen to retain the form of the average rate law, Eq. (3), applied uniformly across the exposed Ca₃SiO₅ surface. However, in light of the foregoing discussion, the parameters of the rate law have been modified slightly as shown in Fig. 2, still providing a good agreement with the experimental dissolution data while enabling a better match to the measured net volume of Ca₃SiO₅ lost by the cluster after 7 h of hydration. Therefore, a mean rate law consistent with prior measurements in the literature appears to be adequate for characterizing the dissolution in this system. However, hydration models could benefit greatly from more experimental research on the statistical distribution of Ca₃SiO₅ dissolution rates as a function of undersaturation, and on how those rates are potentially influenced by other dissolved components in solution, such as aluminates and sulfates, that are present in portland cement.

5.2. Hydration Product ftantity

Setting aside for the moment the large amounts of occluded porosity in the region of hydration product, the simulated moles of C−S−H and Ca(OH)₂ at 7 h are 15 % greater and 43 % less, respectively, than observed in the experiment (Table 4). However, the discrepancies in the moles of Ca₃SiO₅ and each of the two hydration products are all within the propagated uncertainties in the measurements. More importantly, both the experiment and simulation exhibit greater amounts of Ca(OH)₂ than can be justified by mass balance when reaction (13) is applied only to the particle cluster at the needle tip. The anomalously high Ca(OH)₂ content is likely caused by hydration of the Ca₃SiO₅ below the field of view. As described in Section 3.1, these simulations assume that ions in solution are homogeneously mixed because the diffusion coefficients are fast enough for diffusion to homogenize the solution within 1 s over the length scales of this simulation [19, 34]. However, a homogeneous distribution of solution components can still lead to an uneven distribution of C−S−H and Ca(OH)₂ products. Recall that an extra layer of Ca₃SiO₅ was placed below the particle cluster in the simulations, which was necessary to mimic the additional Ca₃SiO₅ particles glued to the needle in the nCT experiment. However, this Ca₃SiO₅ layer has only 30 % of the surface area in the simulated system. Therefore, C−S−H nucleation will happen preferentially where the Ca₃SiO₅ surface area is higher, and so more of it will nucleate and grow on the particle cluster than on the layer below. As greater C−S−H surface area forms around the cluster, Ca(OH)₂ will preferentially nucleate and grow there as well. The driving force for growth is constant everywhere because the solution is mixed, so the only variations in product growth are caused by local differences in their surface areas. Only small heterogeneities in surface area are present near the start of hydration, but they are increasingly magnified with time.

Is the use in the simulations of an extra layer of Ca₃SiO₅ below the field of view an adequate way to handle the experimental reality? In the experiments, the powder particles below the field of view are partially embedded in the epoxy that was used to affix them to the needle. Those particles are also arranged more compactly and have significantly more interior porosity than the cluster. It is therefore difficult to determine the exposed surface area of that powder region that can readily exchange dissolved material with the cluster above. If one assumes that only the exterior surface of the powder mass can exchange dissolved material with the cluster, then the simulated and experimental surface area below the needle may not differ by a great amount. However, if the “communicable” surface area of these particles is significantly greater than assumed in the simulations, or if partially dissolved small particles migrate up to the cluster by convection, then the total amount of hydration product could be considerably greater than in the simulations. But the moles of C−S−H and Ca(OH)₂ formed in the simulations and experiments do not differ by more than the measurement uncertainty, so the simulated Ca₃SiO₅ layer below the needle tip is probably sufficient to capture the major effects of the extra material used in the experiments.

5.3. Hydration Product Morphology and Distribution

5.3.1. C−S−H porosity

The most striking observation from the experiments is the large amount of occluded porosity, about 70 %, that evidently is contained within the hydration product in addition to C–S–H gel porosity. Evidence of this porosity is found in the product texture observed in nCT slices, an example of which is shown in the upper left of Fig. 9. More quantitatively, one can calibrate the observed gray values in the nCT data to the absorption of Ca₃SiO₅ and of air, from which an estimate of the density variations in the hydration product can be made. The lower plot in Fig. 9 shows the gray value of the product regions as a function of distance from the Ca₃SiO₅ surface. This plot indicates a uniform decrease in density (or increase in porosity) away from the Ca₃SiO₅ surface. The effect is pronounced enough that the outer third of the product region has an apparent density approaching that of air. This is clear evidence of a high volume of porosity within the product region.

Figure 9.

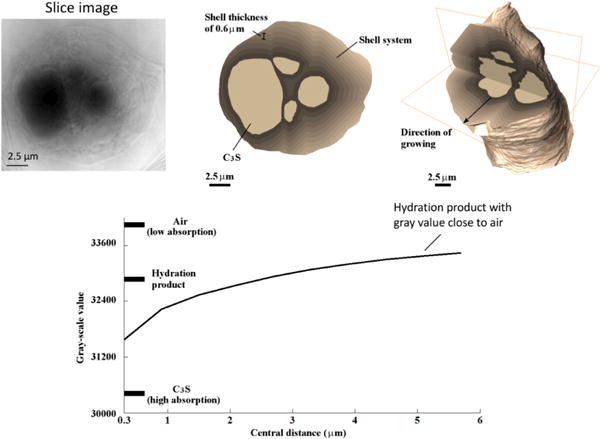
Evidence of large volumes of occluded porosity within the hydration product region can be observed in the texture of the nCT slice shown in the upper left. Calibration of gray values for Ca₃SiO₅ and for air outside the product region can be used to calculate relative average densities in the product region as a function of distance from the Ca₃SiO₅ surface, shown in the plot at the bottom, which indicates that the product becomes progressively less dense with distance and approaches values close to that of air in the outer regions of the product.

The large volume of solution surrounding the small collection of particles might encourage a different growth mode more reminiscent of diffusion limited aggregation [71], which could easily produce sparse networks of material containing a large internal porosity. This kind of morphology would be seen only rarely in denser pastes [72] where convection is absent and the available space for growth; the product could begin to densify at earlier times by intergrowth of additional C−S−H after the free space is exhausted. HydratiCA currently assumes that all solids grow as densely as possible. For C−S−H this assumption means that its gel porosity is an intrinsic part of its internal structure, but that it grows as compactly as possible while retaining that gel porosity. However, this study suggests that such an assumption is not realistic, at least not for C−S−H and probably not for other poorly ordered gel phases.

Gottapu and Biernacki [20] have developed a single particle model of hydration in which C−S−H is assumed to grow rapidly as a “proto-product” with an apparent density of 440 kg m⁻³ that later is assumed to densify more slowly to a maximum density of 2200 kg m⁻³. The molar volume of C₅S₃H₁₂ in Table 2–which includes its gel porosity–corresponds to a density of 910 kg m⁻³, slightly more than twice that of the low-density form used by Gottapu and Biernacki. Had the molar volume been doubled here to coincide with their low-density form, the simulated volume of C−S−H at 7 h (1248 μm³) would have been approximately doubled. When combined with the simulated volume of Ca(OH)₂ (265 μm³), the total apparent volume of hydration product would coincide with the nCT observations (2729 μm³) to within its measurement uncertainty.

The assumed molar volume of C−S−H end members used in the this simulation could be modified to better agree with the low-density form proposed by Gottapu and Biernacki [20], which also had been proposed earlier by Bishnoi and Scrivener [7]. This would immediately produce a closer agreement with the observed product volume in the experiment. However, this low density of C−S−H is probably not a material property but instead is a consequence of its growth mechanism. Therefore, it seems more appropriate to work in the future on a more physically and chemically rigorous growth model for C−S−H that would naturally produce low-density material followed by a gradual in-filling of the occluded porosity as suggested by Fig. 9. Such a growth model, if properly formulated, would also be able to predict the influence on growth morphology of various solution components that have been observed to influence C−S−H growth [73–75]. Unifying the chemistry and physics of C−S−H growth and morphology at this length scale will require more research.

5.3.2. C−S−H distribution

Aside from the low apparent density of C−S−H, the hydration product region observed by nCT is asymmetrically distributed around the original particle cluster, while the simulations produce a more evenly distributed envelope of product around the cluster. Evidently, the simulations fail to capture some physical mechanism causing this asymmetry. One possible explanation is that the Ca₃SiO₅ particles below the field of view are unevenly distributed around the needle, and that their dissolution causes stronger upward convective flow of material on the right side than on the left. The simulation assumed that material dissolved from below the needle is homogeneously mixed throughout the solution, so it was unable to produce such an asymmetric mass transport either by advection or diffusion. In fact, simulating diffusion or advection by HydratiCA currently is accomplished by a biased random walk [76] that, for ions with mobilities in water as great as Ca²⁺ and OH^−, requires exceedingly small time steps on the order of 10⁻⁵ s. The simulation shown here would have taken approximately three months to complete, which was not feasible with our current computational resources (but may be possible in the future as computational power continues to increase).

A second possible explanation for the asymmetric product distribution is that there are a greater density of low-energy nucleation sites for C−S−H on the right and upper portions of the particle cluster. Fig. 3 indicates that Ca₃SiO₅ dissolution happened preferentially in those areas, which suggests that the surfaces may have had higher energy defects to drive that dissolution. According to the derivation leading to Eqs. (8 and (9, for the nucleation rate, the free energy change for forming C−S−H nuclei at those higher-energy sites would be greater than on lower-energy surface sites. Nucleation rates should therefore be greater at high-energy defects than at other surface sites. However, to capture this effect in the simulations would require knowing in advance the distribution and relative energy density of surface defects on the Ca₃SiO₅ particle cluster. This information not available from the experimental characterization methods used here.

Regardless of the origin of the observed asymmetric distribution of product, the effect likely would be less pronounced in a typical cement paste because (a) the free space for growth between particles would be so much less and (b) the much greater number and even spatial distribution of Ca₃SiO₅ particles would ameliorate most inhomogeneities in dissolved material sources and favorable nucleation sites.

5.3.3. C−S−H composition

The experimental solution composition measurements cataloged by Jennings for “Curve B” were all obtained by sampling the solution during hydration of some form of Ca₃SiO₅ for no more than a few days [45, 77], although at least one set of measurements under nominally the same conditions, reported by Brown et al. [56] lied along Curve A. The latter study used colorimetry without treating the solution with a dilute acid, so some additional precipitation could have occurred in the solution to drive it toward Curve A after the Ca₃SiO₅ was removed. With the exception of that study, however, all other data along Curve A, or at least well below Curve B, were reported for experiments during which C−S−H was equilibrated with the solution for much longer periods of time, up to several months [46, 53, 54, 78]. If, as in this simulation, one uses Curve B to define the solubility of C−S−H during hydration at early times, then the dissolution of Ca₃SiO₅ controls the rate of hydration. However, if Curve A defines the C−S−H solubility then neither dissolution nor C−S−H growth fully control the hydration rate [36]. Given the preponderance of data that Curve B characterizes the solution at least until after the main hydration rate peak in the acceleration period, this study has assumed C−S−H end members and solubilities that will generate Curve B. The simulations could have included the possibility of formation of the other C−S−H solid solution that eventually produces Curve A [47] but did not because of computational efficiency and because the majority of prior experimental evidence suggests that Curve A is obtained only at considerably longer times than those simulated here.

5.3.4. Ca(OH)₂ distribution

Turning from the overall appearance of the hydration product region, the simulation predicts for Ca(OH)₂ a fairly large mass that is near and rather evenly distributed about the Ca₃SiO₅ particle cluster. In contrast, Fig. 6 indicates a few higher-density regions in light gray within the product envelope that are probably individual large grains of Ca(OH)₂ [18]. Portlandite is often observed as relatively few large masses even in denser pastes of Ca₃SiO₅ [79], so the current observation of few but large Ca(OH)₂ domains is unlikely to be an artifact of the isolated cluster arrangement. The model assumes classical heterogeneous nucleation rate theory, and there is no experimental evidence that Ca(OH)₂ nucleation is nonclassical. The nucleation work used for Ca(OH)₂ (see Table 3) was estimated from multiple comparisons of HydratiCA simulations to experimental solution composition data during Ca₃SiO₅ hydration, nearly all of which show that the total calcium in solution reaches a maximum concentration of 35 mmol L⁻¹ to 40 mmol L⁻¹ [35, 36, 39, 56]. Those comparisons were made under the assumption that nucleation first begins in that concentration range but then also happens at a fast enough rate to reduce the calcium concentration at a rate tht is also consistent with those experimental data. The values in Table 3 are also in close agreement with the theoretically computed values using the best estimates of the parameters used in Eq. (8).

The current experimental data, however, suggest that the nucleation rate might be considerably lower than in the simulations. Two reasons why the Ca(OH)₂ distribution may be too homogeneous in the simulation are that either the nucleation work is incorrect or the catalog of surfaces on which Ca(OH)₂ can nucleate is incomplete. C−S−H was chosen as a favorable Ca(OH)₂ substrate in the model because C−S−H itself has Ca(OH)₂-like layers separated by silicate chains. Ca(OH)₂ is allowed to nucleate elsewhere, but the assumed nucleation work on other surfaces is set high enough that it does not happen in the simulations. However, other types of surfaces may be present, at much lower concentrations, where Ca(OH)₂ could nucleate. For example, statistical variations in C−S−H growth structure may produce a few microscopic regions that are relatively rich in Ca(OH)₂ layers and relatively denuded of silicate chains, at which Ca(OH)₂ could more readily nucleate. Once again, however, an effect like this would be exceedingly difficult to confirm with existing experimental characterization methods, and without that kind of confirmation the only available course is to alter either the nucleation work or the pre-exponential factor in Eq. (7), and perhaps the growth rate constant for Ca(OH)₂, in such a way that fewer supercritical nuclei are produced before growth rates become sufficiently high to reduce the driving force for nucleation below the maximum supersaturation range. Such alterations could only remain consistent with previous experimental measurements [39, 56] if they do not also greatly change the typical simulated calcium concentration time dependence in solution. Trial-and-error parameter modifications are undesirable, though, since the parameters are tied to material properties and physical mechanisms, and could be avoided with the aid of fundamental Ca(OH)₂ nucleation rate measurements in well-characterized supersaturated solutions with a variety of substrate materials.

6. Conclusions

nCT and nXRF observations of a collection of tricalcium silicate (Ca₃SiO₅) particles reacting in a calcium hydroxide solution were used as a test of HydratiCA simulations that model, as nearly as possible, the thermal and chemical conditions of those experiments. At the 7 h point of comparison, the simulated and observed moles of Ca₃SiO₅, C−S−H, and Ca(OH)₂ agree to within the measurement uncertainty, although both indicate that the moles of hydration product–especially Ca(OH)₂ exceed the amount that can form by hydration of the particle cluster alone. The additional hydration products arrive by migration of ions produced by dissolution of Ca₃SiO₅ below the observation volume.

Measurements of calcium and silicon concentration within a thin sample of the hydration product nearest to the nXRF detector suggest that that region comprises approximately 12 % C−S−H and 18 % Ca(OH)₂, with the remaining 70 % being occluded porosity that is not already part of the gel porosity. This low-density growth morphology is particularly noticeable in these experiments because of the large volume of solution into which growth can easily penetrate, and has approximately the same apparent density as that assumed by Gottapu and Biernacki to rapidly form at early times as low-density “proto-product” which densifies more slowly at later times [20]. However, more research is needed to elucidate the physics and chemistry of C−S−H growth at length scales of 10 nm to 500 nm so that microstructure models can be endowed with more realistic C−S−H growth mechanisms that can account for free volume of growth and solution composition. Ultimately, a new random aggregation and densification model that unifies the physics and chemistry should emerge from that work.

A more careful refinement of Ca(OH)₂ nucleation and growth parameters must also be undertaken, with the aid of controlled experimental observations, to bring the simulation into better agreement with microstructure observations, here and in typical Ca₃SiO₅ pastes, that Ca(OH)₂ usually forms fewer but larger masses than observed in this simulation. In fact, more direct microscopic measurements of nucleation rates and growth rates (not fits to phenomenological equations) of all the common products of portland cement hydration are probably the most important missing data that will be required to improve the predictive capability and microstructure fidelity of computer models of hydration in the future.