Prediction of protein-DNA interactions of transcription factors linking proteomics and transcriptomics data

Graphical abstract

Highlights

• •Selection of ChIP-seq subsets to compare TF site prediction methods is proposed.
• •MATCH is the best method to find sites in genomic sequences for majority of TFs.
• •Partial-AUC is most appropriate for comparing TF site prediction methods.
• •TF sites help to find causative links between proteomics and transcriptomics.

Abstract

We compared positional weight matrix-based prediction methods for transcription factor (TF) binding sites using selected fraction of ChIP-seq data with the help of partial AUC measure (limited to false positive rate 0.1, that is the most relevant for the application of the TF search in the genome scale). Comparison of three prediction methods—additive, multiplicative and information-vector based (MATCH) showed an advantage of the MATCH method for majority of transcription factors tested. We demonstrated that application of TF site identifying methods can help to connect the proteomics and phosphoproteomics world of signaling networks to gene regulation and transcriptomics world.

1. Introduction

Transcription factors (TFs) are proteins of crucial importance for regulation of all processes in human and other organisms. A rigorous classification of human transcription factors was published recently [1], summarizing many years of proteomics research attempting to understand the molecular mechanisms of functioning of transcription factors through their binding to DNA target sites and consecutive regulation of transcription of all genes in the human genome.

The poor correlation between proteomics and transcriptomics data is extensively discussed in proteomics literature [2]. Lack of such correlation making it extremely difficult to use high throughput and easy to generate transcriptomics data in understanding many cellular mechanisms acting mostly on protein level. Dynamic changes of abundance of proteins as well as changes of the status of their posttranslational modifications (such as phosphorylation of many regulatory proteins, including transcription factors) govern many biological processes. Direct measurements of such proteins and their modifications (often related to their activity) with the help of proteomics methods is very tedious, expensive and not always possible at all, often due to the lack of enough biological material necessary for proteomics and phosphoproteomics experiments.

Activity of such important proteins as transcription factors (TFs) can be estimated by their ability to bind DNA at their specific binding sites in genomes. TFs are often triggered in the cells by specific posttranslational modifications (phosphorylation), that enable TFs to bind to their specific sites at DNA. So, by measuring such interactions of TFs with DNA we can deduce activity status of these proteins. Such DNA-binding assay experiments can be combined sometimes with proteomics experiments measuring specific phosphorylation events that can give a lot of information to the researchers about exact mechanisms of acting of this class of proteins. Multiple cascades of phosphorylation and de-phosphorilation events happening in the cell signal transduction system leading to the activation of considered transcription factors. Therefore phosphoproteome data can be also combined with prediction of signal transduction pathways upstream of transcription factors to discover causative mechanism of acting of such transcription factors under particular signaling triggering cells to differentiation or to other cellular fate.

Since its introduction in 2007 [3], ChIP-Seq has become the most powerful experimental technique for genome-wide study of interactions between TFs and DNA. As a rule, a single ChIP-Seq experiment generates millions of short DNA reads. Then the sequenced reads are aligned (mapped) to a reference genome, and the TF-binding regions are identified by applying a peak detection algorithm (or peak finder) to the resulting set of tags (aligned reads). Until now a number of peak detection algorithms have been proposed, in particular, MACS (Model-based Analysis of ChIP-Seq) [4] and SISSRs (Site Identification from Short Sequence Reads) [5]. The reproducibility of nine peak detection algorithms including MACS and SISSRs was studied in [6] on two repeated ChIP-seq experiments for CTCF. It was inferred that MACS is one of the highest reproducible algorithm, while SISSRs is the least reproducible. This conclusion was made with the help of correspondence profiles fitted by a copula model.

A comparative analysis of nine peak detection algorithms including MACS and SISSRs was performed in [7]. This comparison demonstrated that biological conclusions could change dramatically when the same raw ChIP-Seq dataset was processed using different algorithms. The results also indicated that the optimal choice of algorithm depends heavily on the selected dataset. Eleven different peak detection algorithms including MACS and SISSRs were also compared on common data sets [8]. This study offered a variety of ways to assess the performance of each algorithm and addressed the question how to select the most suitable among several available methods. In general, one can conclude that currently it is impossible to choose the most reliable and well-validated algorithm for peak detection.

The ChIP-Seq approach was designed as an experimental tool for identifying TF-binding regions in genome. Unfortunately, some TF-binding regions do not represent genuine TF-binding sites because of, at least, the following three reasons. First, peak detection algorithms can produce much wider TF-binding regions (500–2000 bp or longer) than actual TF-binding sites (5–15 bp). Second, some TF-binding regions are spurious due to the false positive rates of methods for read mapping and peak detection. Third, an unknown fraction of TF-binding regions should not contain the TF-binding sites because of tethered binding [9]. In this case, transcription factor bound to a DNA fragment not because it recognized its site, but because it bound (due to protein–protein interaction) to another transcription factor that, in turn, bound to DNA.

In the 30 years since the PWM approach was introduced [10], it has become the most common and widely used for the computational analysis of TF-binding sites, see [11] for a review. A number of methods for the prediction of TF-binding sites have been developed within this approach. In particular, PWM algorithms were implemented in the computational tools such as MATCH [12], MatInspector [13], MATRIX SEARCH [14], ANN-Spec [15] and MEME [16]. There are several repositories that accumulate many matrices for the representation of TF-binding sites, in particular, TRANSFAC [17], JASPAR [18], Factorbook [19], UniPROBE [20] and HOCOMOCO [21]. Usually these matrices were derived from experimentally identified TF-binding sites (or regions) obtained by gel-shift analysis, SELEX, plasmid construction assays, ChIP-Seq, universal protein binding microarray technology (PBM), and other experimental techniques. The majority of those PWMs are represented as position frequency matrices.

In general, the Receiver Operating Characteristic (ROC) curve has long been used in signal detection theory [22], [23]. It is a good way of visualizing the correspondence between sensitivity and false positive rate of a detection method. The area under the ROC curve, known as the AUC, is currently considered the standard measure to assess the accuracy of prediction methods, including those for the prediction of TF-binding sites. Currently it is common practice to reduce a comparison of different prediction methods to a comparison of the corresponding AUCs [24], [25], [26]. It is important to note that it is necessary to have a representative sample of genuine TF-binding sites in order to evaluate the sensitivities of the comparable methods. Unfortunately, the direct use of the TF-binding region sets for sensitivity estimation does not seem advisable because of the reasons mentioned above (including tethered binding).

We have developed an approach for reliable comparison of TFBS prediction methods under the condition that an unknown fraction of the ChIP-Seq data does not contain genuine TF-binding sites. In this article we have performed a comparative analysis of three existing PWM based methods, namely the common additive, common multiplicative methods, and the method that uses an information vector. We also vary two peak detection algorithms, MACS and SISSR. This analysis was carried out on 266 sets of human TF-binding regions from GTRD (Gene Transcription Regulation Database; http://wiki.biouml.org/index.php/GTRD) and a collection of non-redundant matrices from TRANSFAC (rel.2012.4). The analysis has revealed that all three methods perform rather similarly on the same sets of data. For the majority of PWMs the additive method gave slightly higher AUC values compared to the other two methods. Still both multiplicative and information vector based methods showed higher AUC values for some of the PWMs of the library. A comparison of the methods using partial AUC measure, which compare methods inside of their applicability domain, revealed that the information vector based method often outperforms other site search methods in the area of low false positive rate, whereas methods that don’t use information vector are better for the area of parameter giving a low false negative rate. It is interesting to see that the general results obtained are invariant with respect to choice of peak detection algorithm despite dissimilarities between MACS and SISSRs that were revealed in this work.

Finally, to demonstrate the utility of the TF site prediction methods for proteomics research we combined the TF site analysis with phosphoproteomics and transcriptomics (RNA-seq) data (from PRIDE database) from the recently published experiment of treatment of MCF7 cell line with retinoic acid (RA) [27]. Promoters of differentially expressed genes (from RNA-seq analysis) were analyzed for TF-site frequency using the MATCH method following the approach published earlier [28]. Revealed overrepresented TF-sites indicate to us those transcription factors that are potentially activated (usually through phosphorylation of specific positions in the proteins) in the given cells under stimulation of the cells by RA. Next, we demonstrated that the revealed by this analysis transcription factors are connected to the network of signal transduction cascades identified by phosphoproteomics analysis of the cytoplasmic and nuclear fractions of those cells.

Therefor we can conclude that the methods of computational prediction of protein-DNA interactions of transcription factors that are described in this paper help researchers to find the missing link between the transcriptomics and proteomics (phosphoproteomics) data.

2. Materials and methods

2.1. Data

Human TF-binding region sets that were used in this study are stored in the GTRD database. GTRD collected raw ChIP-Seq data (sequenced reads) from literature, Gene Expression Omnibus (GEO), [29], Sequence Read Archive (SRA) [30], and the ENCODE project (http://www.nature.com/nature/journal/v489/n7414/full/nature11247.html). Currently GTRD contains 1450 human raw ChIP-Seq data sets, and the ChIP-Seq controls (such as input DNA or IgG) are available for 1291 (89%) sets. The sequenced reads were aligned to the reference genome (build 37) using Bowtie release 1.1.1 [31], and the sets of the TF-binding regions were generated independently with the help of two peak detection algorithms, MACS release 1.4.2 and SISSRs version 1.4.

The transcriptomic and phosphoproteomic data of the experiment of treatment of MCF7 cell line with retinoic acid (RA) [27] were extracted from following data repositories: e RNA-seq data are available from the GEO institutional Data Access: http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE81814. The mass spectrometry proteomics data are available in PRIDE database with the dataset identifier PXD004357.

2.2. The ROC curves and AUCs as basis of comparison

According to common practice, the areas under the ROC curves are used in order to compare the site models. In turn, each ROC curve represents the correspondence between sensitivity of the model and false positive rate. In general, it is necessary to have a representative sample of genuine TF-binding sites in order to calculate the sensitivity. ChIP-seq derived TF-binding regions can be used for this purpose. It is assumed that TF-binding regions revealed by ChIP-seq experiments contain genuine TF-binding sites. Therefore the sensitivity was computed as a relative number of the TF-binding regions containing one or more TF-binding sites predicted. The false positive rate was computed on the basis of artificially generated sequences with the help of 10-fold permutations of nucleotides in each TF-binding region. The false positive rate was determined then as the relative number of such artificially generated sequences containing one or more TF-binding sites predicted. For AUC calculation we used the sets of the TF-binding regions that are stored in GTRD.

2.3. Scheme of site model comparison

According to common practice, the comparison of site models is reduced to a comparison of AUCs. In turn, AUCs are calculated on the sets of the TF-binding regions. However, the direct use of the full sets of TF-binding region for the AUCs calculation does not seem advisable because some TF-binding regions can be “empty”, i.e. they do not contain genuine TF-binding sites. To model such a situation we introduced a parameter τ, which defines a percentage of TF-binding regions that are not “empty” and contain at least one genuine TF-binding site. The following scheme of site model comparison takes into account the assumption about the existence of empty TF-binding regions.

First, we prepare the sets of TF-regions in such a way that all regions had the same length. If the TF-binding regions are longer then 200 bp, we redefine them as regions of the lengths 200 bp with the centers in summits of distributions of the number of matched reads. If the TF-binding regions are shorter then 200 bp, we extend them to the total length 200 bp adding respective flanks.

In the next step, each site model predicts its so-called ‘best site’ in every modified TF-binding region. The ‘best site’ of the given site model is defined as the fragment of the TF-binding region where the site model obtained the maximal score among all scores calculated for every possible fragments of the TF-binding region. Then, for each site model, a top list of the τ percent (τ is given) of the ‘best sites’ with the highest scores is constructed and the so-called τ-union of the ‘best sites’ is composed as a union of all such top lists for all three site models considered in the study. Then, the so-called the τ-union of the TF-binding regions is defined as the merged union of such TF-binding regions that contained at least one ‘best site’ from τ-union of the ‘best sites’. Finally, the ROC curves are generated on the τ-union of the TF-binding regions and the corresponding AUC values are calculated.

2.4. Implementation

The proposed approach for comparing the TF site prediction methods was implemented with the help of the open source BioUML platform (http://biouml.org/). We have created the following Java modules:

• 1.‘ROC curves for best sites union’
• 2.‘Summary on AUCs’
• 3.‘Peak finders comparison’
• 4.‘Locations of best sites’

The ‘ROC curves for best sites union’ module generates the ROC curves and calculates the corresponding AUCs for the user-selected set of site models when the value of parameter τ (1 ≤ τ ≤ 100) and the set of the TF-binding regions are specified. The user interface allows for selecting the site model (additive model, multiplicative model or information vector based model, see Site model section above for details). The resulting ROC curves and corresponding AUCs are computed by the java modules and are stored within a user-specified folder in the platform.

The ‘Summary on AUCs’ tool performs a comparative analysis of site models when the value of the parameter τ is pre-specified. Initially all appropriate AUC values calculated by the ‘ROC curves for best sites union’ tool are read in all available tables. Then a comparison of AUC values is performed with the help of the non-parametrical Friedman and Wilcoxon signed rank tests [32]. In the case of the Friedman test, a chi-squared distribution with (k-1) degrees of freedom is used for assessing the statistical significance of the difference between AUCs, where k denotes the number of site models. In the case of the Wilcoxon test, the significances of the differences are assessed with the help of normal approximations of the test statistics. Probability densities of differences between paired AUCs are estimated by the kernel density estimator [33] with Epanechnikov kernel and are plotted for the user.

The ‘Peak finders comparison’ tool performs a comparative analysis of two peak detection algorithms. To compare two peak detection algorithms, this tool carries out a comparative analysis of the matched sets of the TF-binding regions, where the numbers and mean lengths of the TF-binding regions are analyzed independently with the help of the Wilcoxon signed rank test. The statistical significances are assessed on the base of normal approximations of the test statistics. Additionally, the impact of the ChIP-Seq controls (such as input DNA or IgG) on the performance of peak detection algorithms is analyzed. Probability densities of the numbers and mean lengths of the TF-binding regions are estimated by the kernel density estimator with Epanechnikov kernel and are plotted for user.

The ‘Locations of best sites’ tool estimates and plots the probability density of the ‘best site’ locations along the TF-binding regions around the so-called summits where a summit is determined by MACS as the precise binding location within a given TF-binding region. The probability density is estimated by the kernel density estimator with Epanechnikov kernel.

2.5. Three site models available for comparative analysis

Currently, three site models that represent PWM approach are available for comparative analysis. For a given TF they share the same position frequency matrix MAT  = (m_ij), i = {A,C,G,T}, j = 1,…,l but produce diverse scores for a fixed DNA fragment S  = (s₁,…,s_l). In other words, the models represent different scoring algorithms.

2.5.1. Additive model

This model calculates the common additive score x defined by the formula

x = x(MAT)  = Σ_{j = 1,…,l} score(j),

where the values score(j), j = 1,…,l, are determined as follows:

score(j)  = {m_Aj, if s_j = A; m_Cj, if s_j = C; m_Gj, if s_j = G; m_Tj, if s_j = T}.

2.5.2. Multiplicative model

For a fragment S this model calculates the common multiplicative score x_m

x_m = ∏_{j = 1,…,l} score(j).

This model can be converted to an equivalent additive model by taking the logarithms of matrix elements, i.e.

x_ln = Σ_{j = 1,…,l} score*(j),

where the values score*(j), j = 1,…,l, are determined as follows:

score*(j)  = {ln(m_Aj), if s_j = A; ln(m_Cj), if s_j = C; ln(m_Gj), if s_j = G; ln(m_Tj) if s_j = T}.

In order to avoid taking a logarithm of zero we preliminarily found minimal a non-zero element of matrix MAT. Then we replaced all zero values of MAT by this value and re-normed all changed columns of MAT in such a way that the sum of frequencies in each changed column was equal to unit.

2.5.3. Information vector-based model (MATCH model)

This model is determined by the popular PWM method MATCH for TF-binding site prediction. This model calculates the so-called matrix similarity score mSS defined in [12]. Actually, this model is a common additive model, which uses a transformed matrix instead of an initial matrix, where each column of the transformed matrix was determined with the help of weighting the corresponding initial column by information content. More specifically, the j-th column of the weight matrix is equal (up to the constant (–Min/(Max-Min))) to the product of the j-th column of the frequency matrix and the value I(j)/(Max-Min), j = 1,…,l, where I(j), Min, and Max were defined in [12].

2.6. Software availability

The site search algorithms described in this paper are available for free in BioUML/geneXplain platform. The anonymous access to the platform is available here:

http://gtrd.biouml.org/bioumlweb/#anonymous=true

Individualized access to the platform with secure space for your data is available for free upon registration at the URL:

http://www.genexplain.com/genexplain-platform-registration

3. Results

3.1. Selection of τ-union parameter

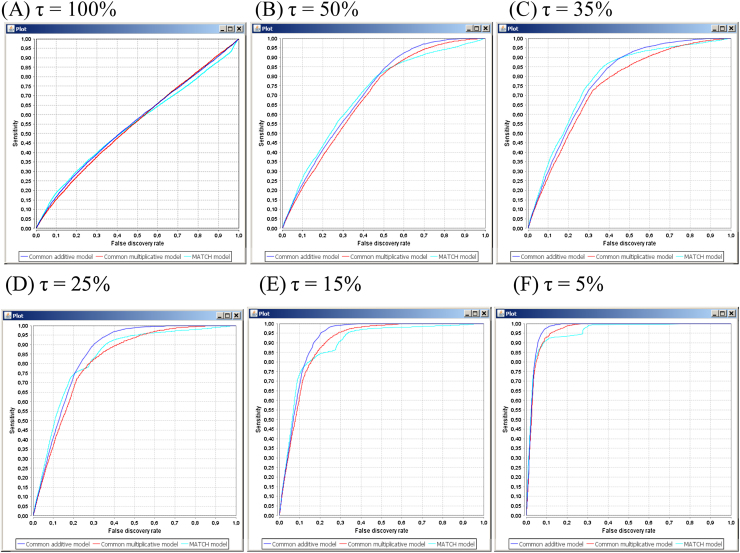
The key step of the proposed scheme of AUCs calculation is the construction of the τ-union of the TF-binding regions, where the percentage τ is a free parameter. In general, the following relationship exists between τ values and the shapes of the ROC curves: the smaller the percentage τ, the more convex the ROC curve is, and the higher the AUC values are. Thus, for small values of τ (5–15%) the ROC curves, as a rule, are strongly convex, while the shapes of the ROC curves became approximately linear when τ tends to 100%. An example is shown in Fig. 1, where the ROC curves were generated on the YY1-binding regions (processed by MACS). In turn the corresponding values of AUCs are close to 0.5 when τ tends to 100%, while these values are close to 1.0 when τ tends to 5%, see Table 1.

Fig. 1.

The ROC curves obtained for different values of τ on the YY1-binding regions that were generated by MACS peak detection algorithm. Dark blue lines correspond to the additive model, red lines to the multiplicative model, and light blue lines to the information vector based model (MATCH model).

Table 1.

AUCs calculated for different values of τ on the YY1-binding regions that were generated by MACS peak detection algorithm.

	Site model			Percentage of regions that are classified as “empty”
Percentage, τ	Information vector based model	Multiplicative model	Additive model
100	0.548	0.550	0.555	0
50	0.707	0.694	0.716	37.5
35	0.782	0.744	0.778	51.5
25	0.835	0.817	0.852	65.4
15	0.892	0.899	0.918	78.8
5	0.956	0.963	0.972	92.9

It is important to note that the shown relationship between τ and the shape of the ROC curve can be interpreted as follows. According to the definition of the τ-union of TF-binding regions, it consists of those TF-binding regions that contain the ‘best sites’ with the highest scores. In other words, the TF-binding regions that contain TF sites with the smallest scores only are removed from further analysis (so-called “empty” regions). Obviously, the higher the percentage τ, the smaller the number of regions that are classified as empty, see also the first and the last columns of Table 1.

3.2. Comparative analysis of three site models

We performed a comparative analysis of the following three site models that represent the PWM approach: additive model, multiplicative model and information vector based model (MATCH model). For this analysis we have selected 266 TFs that have got matrices in TRANSFAC (release 2012.4) and human TF-binding region sets in GTRD. It is important to note that we did not consider matrices derived for TF families. For example, despite the availability of the USF1-binding region set in GTRD, we did not include it in the analysis, because there is no appropriate matrix for the USF1-binding sites in TRANSFAC that contains the matrices V$USF_01, V$USF_02, V$USF_C, V$USF_Q6 and V$USF_Q6_01 derived for the sites of the USF family.

A comparative analysis was performed independently on 265 sets of TF-binding regions generated by MACS, and on 263 sets generated by SISSRs. In the case of SISSRs we excluded 2 sets from our analysis because of their small sizes (<200). TF-binding regions produced by MACS and SISSRs were trimmed or enlarged to 200 bp according to the procedure described in the Method Section.

For the first comparative analysis we have considered the following five values of τ: 100%, 35%, 25%, 15% and 5%. We computed AUC values for each of three site models applied to each of the TF-binding region set with five values of τ. Next, we compared results generated by three site models with the help of the Friedman test which compares distributions of generated AUC values by applying the site models to all analyzed PWMs. We used a Chi-squared distribution with two degrees of freedom for assessing the significance of differences between three site models (see Table 2). As one can see from the result of this comparison, the three site models produce statistically significantly different results. This difference increases with the increase of τ. Therefore it is important to understand which site model is the method of choice in the further analysis of biological data.

Table 2.

Comparison of three site models with the help of Friedman test using two peak detection algorithms. P-value show the statistical significance of the value of the Friedman test statistic showing global difference of the distributions of AUCs for 265 (for MACS) and 263 (for SISSRs) TF-binding ChIP-seq data.

Peak detection algorithm	Percentage τ	Friedman test statistic	p-value
MACS	100	17.556	1.541 × 10−4
	35	108.076	<10−12
	25	139.908	<10−12
	15	163.188	<10−12
	5	218.362	<10−12
SISSRs	100	15.165	5.093×10−4
	35	51.732	5.843×10−12
	25	91.103	<10−12
	15	92.104	<10−12
	5	106.150	<10−12

As the next step, we performed a more detailed comparative analysis of the generated ROC curves and AUC values in order to understand which site models are preferable for each of the PWMs and under which conditions. Here, we choose a value of τ equal to 25%, since most of the site models give reasonably high values of AUC for all of the PWMs (0.7–0.9).

A more detailed consideration of computed ROC curves for each PWM shows that, in fact, the actual difference of AUC values for different matrices is relatively small. This conclusion is invariant with respect to the choice of peak detection algorithm. So, with a few exceptions, we can say that although the general difference of the performance of all three site models for all PWMs altogether is statistically significant, the absolute values of the differences of AUC for each individual PWM are quite small. In Table A1 in the Appendix (see Supplementary data), we provide all values of AUC. We also indicate which site model gives better AUC for each PWM. Also, we annotate this table with the name of the TF antibody which was used in each ChIP-seq experiment, the cell line, the classification of TF according to their DNA binding domain using the classification of human transcription factors [1]. We also computed and presented in the table the total and average entropy and the length of each PWM.

Next, we computed several partial-AUC values for each of the PWMs. This means that we summed up the areas under the ROC curve for particular ranges of FP and FN values only. The reason of computing a partial AUC is well described previously [34], [35]. Such a partial-AUC attempts to estimate the performance of the recognition method in the area of true positive and false positive rates that are actually applied in the data analysis in the majority of cases. We considered the two most frequent use cases of the application of site recognition models. The first one corresponds to values of false positive rates equal or lower then 0.1. It applies to all potential searches of TF binding sites in full genomes, or at least in relatively long genomic regions. It is reasonable to assume that in such an application of the site search method it makes no sense to allow for false positive rate higher then 0.1 (which means on average one site prediction in every tenth position). Normally much lower false positive rates are used in such genome scanning methods to minimize potential huge noise. The second use case corresponds to the values of true positive rate higher or equal to 0.8. It applies to those rather rare use cases when one should not miss practically any of the true sites irrespectively of how many false positives it also finds. Such site searches are applied in cases of analysis of relatively short genome regions (e.g. one individual promoter or enhancer), with consideration of further validation of all found sites by independent experimental or computational methods (for instance, by cross-species comparison [36] or by analysis of site combinations [37]).

We compared the performance of three site models using three measures—AUC, partial-AUC_TP0.8 (which corresponds to the area under the ROC curve of true positive rates higher or equal to 0.8) and partial-AUC_FP0.1 (which corresponds to the area under the ROC curve of false positive rates lower or equal to 0.1) (see Table 3). It is interesting to see that depending on the measure we get rather different results. In case of the application of full AUC, the highest value is provided by the additive site model method for most of the PWMs. The partial-AUC_FP0.1 however gives a completely different picture. For most of the PWMs, the highest values are provided by the information-vector based site model method (MATCH method). Application of partial-AUC_TP0.8 gives a very similar result to the full AUC.

Table 3.

Results of comparison of three site model methods applied to the TRANSFAC PWMs on respective ChIP-seq data sets. Three measures of site recognition methods were applied—full AUC and two partial-AUCs. We computed the number of PWMs that gives maximal value of the measure (full AUC or partial-AUC) for the given site model. The last row gives the number of PWMs when all three methods produced equal values for the respective measure. In bold we indicate a method that gives the highest number of PWMs with maximal AUC_FP0.1 criteria.

A) MACS
Site model method.	Number of PWMs with maximal AUC	Number of PWMs with maximal partial AUC_TP0.8	Number of PWMs with maximal partial AUC_FP0.1
Additive	152	154	40
Multiplicative	61	58	92
MATCH	42	43	113
All three methods give the same AUC value	10	10	20

B) SISSRs
Method name	Number of PWMs with maximal AUC	Number of PWMs with maximal partial AUC_TP0.8	Number of PWMs with maximal partial AUC_FP0.1
Additive	138	134	45
Multiplicative	62	65	85
MATCH	52	53	107
All three methods give the same AUC value	11	11	26

3.3. Application of TF site prediction models to link transcriptomics and phosphoproteomics data

In order to demonstrate the usefulness of the described TF site prediction methods for proteomics research we jointly analyzed phosphoproteomics (from PRIDE database) and transcriptomics (RNA-seq) data from recently published experiment of treatment of MCF7 cell line with retinoic acid (RA) [27]. Since the change of expression of the genes measured by transcriptomics upon treatment by RA must be clearly dependent on the changes of activity of transcription factors we, first of all, analyzed promoters of differentially expressed genes for TF-site frequency using the MATCH method following the approach published earlier [28]. Here we used MATCH models described in the current paper as most specific for the given type of analysis of multiple promoter sequences. Revealed overrepresented TF-sites in promoters of differentially expressed genes in comparison to the promoters of genes with no change of expression indicated to us those transcription factors that are potentially activated or inhibited (usually through phosphorylation of specific positions in their protein sequence) in the given cells under stimulation of the cells by RA. (see Table 3).

In the next step we applied graph algorithms described earlier [28] in order to identify potential common regulators of the activity of predicted set of transcription factors in the signaling network of the cells under study. Statistical significance of such common regulators is confirmed by random shuffling of the input TF lists. Among such common regulators we expect to find protein kinases and other components of signal transduction cascades that can phosphorylate multiple transcription factors or other intermediate signaling molecules and therefore play a role as such common regulators of the activity of the set of TFs under study. In turn, an indicator of activity of such protein kinases often could be their phosphorylation status which is measured in the phosphoproteomics experiments. So, we were interested to find links between the signal transduction proteins detected by phosphoproteomics measurements in the cytoplasm or in the nucleus of the cells and the TFs predicted by our promoter analysis. Indeed, we confirmed such links between identified common regulators and phosphoproteomics measurements. (see Table 4). One can see that almost all found common regulators (9 out of 11) have been identified by the phosphoroteomics experiment (Table 5).

Table 4.

Transcription factors found by the combined analysis of transcriptomics and phosphoprotyomics data. With the help of MATCH algorithm we identified overrepresented TF binding sites in promoters of differentially expressed genes (DEG) (from transcriptomics data). TRANSPAC PWM—name of the position weight matrix from TRANSFAC database which was used by MATCH; Yes-No ratio—the ratio of TF site frequency in promoters of DEG compared to the promoters of non-changed genes; p-value—statistical significance of the Yes-No ratio; Phospho Cytoplasm/Nucleus—detection of the phosphorypation of the TF in cytoplasm or in nucleus of the cells (p- phosphorylation was detected, p-up—phosphorylation was found increased upon treatment by RA, p-dn—decreased by RA).

Gene symbol	TF name	TRANSFAC PWM	Yes-No ratio	P-value	UniProt ID	Phospho Cytoplasm	Phospho Nucleus	Gene description
RELA	RelA-p65	V$RELA_Q6	1.22	2.78E-04	Q04206	p	p	v-rel reticuloendotheliosis viral oncogene homolog A (avian)
RXRA	RXR-alpha	V$DR4_Q2	1.34	8.36E-15	P19793	p	p	retinoid X receptor, alpha
SP1	Sp1	V$SP1_Q6_01	2.37	1.36E-85	P08047	p	p-dn	Sp1 transcription factor
CTCF	ctcf	V$CTCF_01	1.71	1.75E-16	P49711	p	p	CCCTC-binding factor (zinc finger protein)
RXRB	RXR-beta	V$DR4_Q2	1.34	8.36E-15	P28702	p	p	retinoid X receptor, beta
TRIM28	RNF96	V$RNF96_01	2.54	6.71E-43	Q13263	p-up	p-dn	tripartite motif containing 28
NFYC	NF-YC	V$NFY_Q3	1.67	1.16E-04	Q13952	p	p	nuclear transcription factor Y, gamma
SP3	Sp3	V$SP1_Q6_01	2.37	1.36E-85	Q02447	p	p	Sp3 transcription factor
RREB1	RREB-1	V$RREB1_01	1.33	1.28E-12	Q92766	p	p-dn	ras responsive element binding protein 1
NR2F2	COUP-TF2	V$DR4_Q2	1.34	8.36E-15	P24468	p	p	nuclear receptor subfamily 2, group F, member 2
KLF4	GKLF	V$GKLF_Q4	1.63	4.06E-135	O43474	p	p-dn	Kruppel-like factor 4 (gut)
PATZ1	PATZ	V$MAZR_01	2.14	1.90E-11	Q9HBE1	p	p	POZ (BTB) and AT hook containing zinc finger 1

Table 5.

Statistically significant common regulators found by the graph algorithm of the geneXplain platform (www.genexplain.com) by searching upstream of TFs listed in Table 5 in the signal transduction network of TRANSPATH database [38]. TF-reached—number of TFs (out of 12 from Table 5) that are reached in the network downstream from the respective common regulator; Score—score of the common regulator calculated on the basis of the number of reached TFs and topology of the network [28]; FDR and Z-score are calculated by multiple randomization of input set of TFs [28].(FDR <0.05 AND Z-Score > 1.0 AND TF-reached > 7).

TRANSPATH ID	Name of common regulator	TF reached	Score	FDR	Z-Score	Phospho Cytoplasm	Phospho Nucleus
MO000056714	HDAC1	8	0.623	0.036	1.031	p-up	p-up
MO000257368	SUSP1	8	0.555	0.031	1.354	p	p-dn
MO000103308	CKI-gamma1	8	0.530	0.035	1.093
MO000019363	RelA-p65	7	0.484	0.030	1.679	p	P
MO000132731	PP4C	7	0.445	0.047	1.068	p	P
MO000140900	ing4	8	0.434	0.050	1.613
MO000272358	ctcf{sumo}	7	0.390	0.035	1.455	p	P
MO000284804	RNF96{p}	7	0.341	0.047	1.590	p-up	p-dn
MO000107711	RXR-alpha{sumo}	8	0.337	0.033	1.549	p	P
MO000272357	ctcf{sumo}	7	0.275	0.049	1.564	p	P
MO000284833	RNF96{pS473}{pS824}	7	0.250	0.040	1.833	p-up	p-dn

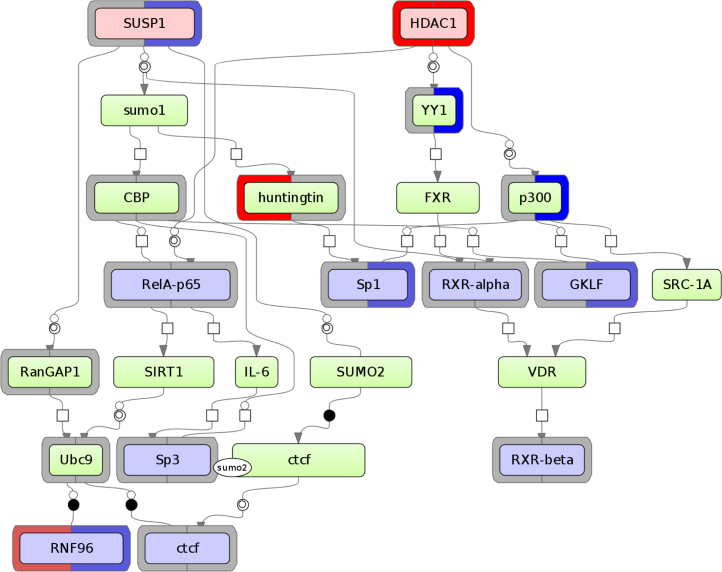
On Fig. 2. we show the diagram that connects two most significant common regulators (light red nodes at the top of the diagram) and TFs (light blue nodes in the middle and at the bottom of the diagram) whose sites found overrepresented in the promoters of differentially expressed genes. With red, blue and gray decoration of several nodes in the diagram we annotate the phosphorylation of the respective proteins detected in the phosphoproteomics experiment. The left part of the decoration circle corresponds to the protein phosporialytion observed in the cytoplasm of the cells and the right side corresponds to the protein phosphorylation observed in the nucleus. The red color corresponds to the increased level of phosphorialtion after treatment of cells by RA, blue color corresponds to decreased level and gray—the same level of phosphorylation of these proteins after the RA treatment.

Fig. 2.

Signal transduction diagram that connects two most significant common regulators (light red nodes at the top of the diagram) and TFs (light blue nodes in the middle and at the bottom of the diagram) whose sites found overrepresented in the promoters of differentially expressed genes. Red, blue and gray decoration of the odes in the diagram annotates the phosphorylation of the respective proteins detected in the phosphoproteomics experiment. The left part of the decoration circle corresponds to the protein phosporialytion observed in the cytoplasm of the cells and the right side corresponds to the protein phosphorylation observed in the nucleus. The red color of the decoration corresponds to the increased level of phosphorialtion after treatment of cells by RA, blue color corresponds to decreased level and gray – the same level of phosphorylation of these proteins after the RA treatment.

We can show here that such important signaling proteins as “histone deacetylase 1 (HDAC1)”, whose level of phosphorylation is rapidly increasing after treatment of the cells by RA, and “SUMO-1-specific protease 1 (SUSP1)”, whose level of phosphorylation is high and stable in the cytoplasm and decreasing in the nucleus, are involved in this cellular system in triggering signal transduction pathways towards activity of particular transcription factors. Among them there are the number of important transcription factors such as RelA, Sp-1, RXR, CTCF, GKLF, RNF96 that are characterized by the high and often changing level of phosphorylation in cytoplasm and especially important, in nucleus and evidently as a result of such signal transduction cascade changing their activity during RA treatment and consequently up-regulating expression of their target genes. It was also interesting to see that HDAC1 was actually one of the top proteins whose phosphorylation status most significantly increased after RA treatment (11 additional phosphopeptides detected in nucleus after the treatment by RA). And it was also independently identified as the top common regulator in our analysis.

Therefor we can conclude that the methods of computational prediction of protein-DNA interactions of transcription factors that are described in this paper help researchers to find the missing link between the transcriptomics and proteomics (phosphoproteomics) data.

4. Discussion

Currently the AUC values are considered the standard measures to assess the predictive abilities of site models. Certainly, for an accurate calculation of precise AUCs it is necessary to have representative samples of genuine TF-binding sites. Available TF-binding regions from ChIP-seq experiments processed by peak calling algorithms provide a good resource for such computations. But the direct use of the raw initial sets of the TF-binding regions for the AUC calculations is not reasonable because many of the TF-binding regions can be “empty” (not actually containing genuine TF-binding sites) mainly due to various experimental and data pre-processing uncertainties discussed above. Indeed, it turned out that when taking full sets of ChIP-seq TF-regions for the majority of the selected TFs, the values of the computed AUCs of all applied PWM-based methods were close to 0.5 (see Table A2 Supplementary data), and the shapes of the ROC curves were approximately linear (see, for instance, Figure A3 Supplementary data).

It becomes clear that such sets of sequences are not directly suitable as an ideal set for the comparison of different TF-site recognition algorithms. In this paper we have suggested the τ-union approach for selecting subsets of TF-binding regions suitable for the sheer purpose of comparing the performance of different site models to each other. Of course this does not guarantee the selection of all true TF-binding sites out of the initial sets of TF-binding regions. This method just provides a platform for a relatively unbiased comparison of different methods for TF-site recognition.

Certainly, the construction of the τ-union of the TF-binding regions is just one of several possible ways to compose refined sets of TF-binding regions that can be used for site model comparison. One of the alternative ways to compose refined sets is to select the most “reliable” TF-binding regions according to external characteristics obtained in the ChIP-seq data preprocessing. We demonstrated (see Appendix 4.4 Supplementary data) that the use of such external characteristics coming from the peak detection algorithm, as ‘FDR’, ‘Fold enrichment’, ‘Tag number’, ‘Score’ and ‘p-value’, does not actually provide suitable platform for comparing TF site prediction methods.

As has been described in detail in the Method Section, the τ-union approach allows for preparing subsets of TF-binding regions that contain an unbiased mixture of DNA motifs for TF-binding sites as they are recognized by different PWM site models. This way we create a good platform for comparing different site models to each other using the same set of sequences, which makes such a comparison most objective and unbiased. At the same time, such a comparison is done on the basis of natural genomic sequences, experimentally shown to be bound by the given transcription factors (directly or indirectly), rather then on the basis of some artificially prepared sequences as has been done elsewhere. This provides a higher reliability of such a comparison of methods and a better basis for choosing the method for a real analysis of genomic sequences.

The final comparison of PWM site models was done on the τ-union sets of TF-binding regions with a relatively low value of τ equal of 25%. This means that only about 25% of TF binding regions obtained from the ChIP-seq experiments were used for such a comparison. Our choice of this value was based on the average values obtained of the AUCs for most of the PWM site models (see Table A1 in the Appendix Supplementary data), which were mainly above 0.7 (with some small exceptions); this is considered to be a borderline for relatively good quality for a diagnostic test [39].

The use of the AUC value for comparing the precision of different recognition methods and diagnostics tests is well accepted in the machine learning community [39], and is widely used for comparison of various bioinformatics methods including TF site recognition methods [40]. However, this practice has recently been questioned [41], [42]. Certain important parameters should be carefully taken into account when applying AUC for comparison of different recognition methods. When comparing two methods by their ROC curves problems arise when the interest does not lie in the entire range of false-positive rates. Often in bioinformatics and other applications it is more useful to look at a specific region of the ROC curve rather than at the whole curve. To overcome these difficulties the approach of computing partial AUC has been proposed earlier [34], [35]. In this approach one focuses for instance on the low false positive rates only, which is often of prime interest for population or genome screening tests, and calculates the value of “partial AUC” by calculating the area under the ROC curve only in the respective part of the curve [34], [35].

In our work we applied two partial AUCs that correspond to two of the most frequently used cases of applying TF-site recognition methods. In the first case, we compute the area under the ROC curve only in the region of false positive rates from 0.0 to 0.1. In this way we focus our attention on the cases of TF binding sites searches in full genomes or at least in relatively long genomic regions. We assume that in such applications of full genome screening it makes no sense to allow false positive rate higher then 0.1. Otherwise the results will be flooded with millions of false positive hits and will become useless in practical applications. In the second use case we focus our attention on the alternative part of the scale when the values of true positive rate should be higher of equal to 0.8. Such use cases correspond to the TF-site analysis in relatively short genome regions (e.g. in an individual promoter or enhancer) when one should minimize the loss of real sites. We implemented two measures of partial AUC—“partial AUC_FP0.1” and “partial AUC_TP0.8”, respectively.

Using these partial AUC measures as well as traditional full AUC we compared the efficiency of three different PWM-based site models for recognition of binding sites for more then 260 different human transcription factors. Such a full-scale comparison has not been done so far. Our results provide a basis for the choice of the TF site identification methods for various future applications.

In order to find a rationale for the higher performance of a certain PWM-based site model for recognition of sites for different transcription factors we compared the results of AUC calculations with various characteristics of transcription factors and their respective PWMs. In Table A1 in the Appendix (see Supplementary data) we summarized several characteristics, including: TF classification index [1], name of the TF antibody and cell line used in the respective ChIP-seq experiments, the length of PWM, mean and sum entropy of the PWM. Our attempts to find any correlation between those characteristics and the performance of one of the tested TF-site model failed. For instance, no significant difference was found while comparing the average entropy of those PWMs that showed superior results for “additive site model” with the average entropy of PWMs showing superior results for the “site model based on information vector”. Also, it was interesting to observe that even for very similar transcription factors belonging to one family, different family members can display absolutely different preferences to one or another TF site model. For instance, the FOX family of transcription factors is characterized by very similar PWMs. Although for most of the family members the highest values of full AUC correspond to the additive site model, for the factor FoxM1 the highest value was achieved by the multiplicative site model, and for the factor FoxO4 it was taken by the site model based on information vector.

Generally the application of the full AUC measure gives the highest values for the “additive site model method” for most of the tested PWMs. Still our results show that for the actual most frequent applications of the PWM method, e.g. in the use cases of searches of TF sites in long genomic sequences, the supreme method is the site model which is based on information vector (which is implemented in the popular MATCH algorithm [12]), since it gives the higher values of the respective partial AUC.

Therefore, in this paper we successfully applied a novel unified method for comparing different approaches of computing TF site models based on PWM.

Finally, to demonstrate the utility of the TF site prediction methods for proteomics research we combined the TF site analysis with phosphoproteomics and transcriptomics data. We analysed promoters of the differentially expressed genes (from RNA-seq) using the MATCH site prediction method and predicted those transcription factors that are potentially activated in these cells. Next, using graph analysis algorithm we connected these transcription factors to the network of signal transduction cascades identified by phosphoproteomics analysis of the cytoplasmic and nuclear fractions of those cells. This example of analysis of two “-omics” datasets allowed us to conclude that the methods of computational prediction of protein-DNA interactions of transcription factors that are described in this paper can indeed help researchers to find the missing link between the transcriptomics and proteomics (phosphoproteomics) data.

We hope that our results will contribute to an improvement of efficiency in the application of computational methods for understanding the molecular mechanisms of functioning of such an important group of proteins as transcription factors and will contribute to the growing field of proteomics research.

Conflict of interest

None.

Appendix A. Supplementary data

The following are Supplementary data to this article: