Temporal Dynamics Assessment of Spatial Overlap Pattern of Functional Brain Networks Reveals Novel Functional Architecture of Cerebral Cortex

Abstract

Objective

Various studies in the brain mapping field have demonstrated that there exist multiple concurrent functional networks that are spatially overlapped and interacting with each other during specific task performance to jointly realize the total brain function. Assessing such spatial overlap patterns of functional networks (SOPFNs) based on fMRI has thus received increasing interest for brain function studies. However, there are still two crucial issues to be addressed. First, the SOPFNs are assessed over the entire fMRI scan assuming the temporal stationarity, while possibly time-dependent dynamics of the SOPFNs is not sufficiently explored. Second, the SOPFNs are assessed within individual subjects, while group-wise consistency of the SOPFNs is largely unknown.

Methods

To address the two issues, we propose a novel computational framework of group-wise sparse representation of whole-brain fMRI temporal segments to assess the temporal dynamic spatial patterns of SOPFNs that are consistent across different subjects.

Results

Experimental results based on the recently publicly released Human Connectome Project grayordinate task fMRI data demonstrate that meaningful SOPFNs exhibiting dynamic spatial patterns across different time periods are effectively and robustly identified based on the reconstructed concurrent functional networks via the proposed framework. Specifically, those SOPFNs locate significantly more on gyral regions than on sulcal regions across different time periods.

Conclusion

These results reveal novel functional architecture of cortical gyri and sulci.

Significance

Moreover, these results help better understand functional dynamics mechanisms of cerebral cortex in the future.

I. Introduction

There have been significant interests in the brain mapping field to study brain function using in-vivo neuroimaging techniques such as functional magnetic resonance imaging (fMRI) [1]–[3]. Specifically, task fMRI (tfMRI) records functional brain activities during a specific task performance [1]–[3]. Based on tfMRI data and associated data processing and analysis approaches, tremendous efforts have been devoted to identify brain regions and networks that are activated and functionally involved during a specific task performance [1]–[4]. Recently, a variety of studies (e.g., [5]–[11]) have reported an interesting finding that during a specific task performance, there exist concurrent functional networks (including both task-evoked and intrinsic connectivity functional networks), each of which locates across specific neuroanatomical areas on the human cerebral cortex. Importantly, these concurrent functional networks are spatially overlapped and interacting with each other. Those overlapped (common) brain regions among multiple concurrent functional networks, which are formally defined as spatial overlap patterns of functional networks (SOPFNs) in this paper (an example illustration of the SOPFNs is in Fig. 1a), have been demonstrated particularly important for the total brain function realization (e.g., [8], [12]–[16]). For example, our recent work [8] successfully performs a novel computational framework of sparse representation of whole-brain fMRI signals to infer a comprehensive collection of concurrent functional networks in the whole brain and to assess the SOPFNs of those multiple concurrent functional networks, and coins ‘Holistic Atlases of Functional Networks and Interactions’ [8]. Moreover, the studies in the neuroscience field (e.g., [12]–[16]) also demonstrate that there are certain brain regions (i.e., SOPFNs) that are involved in multiple concurrent neural processes/functional networks during a specific task performance, and that exhibit strong functional diversity. In short, assessing the SOPFNs has received increasing interest for brain function studies.

Fig. 1.

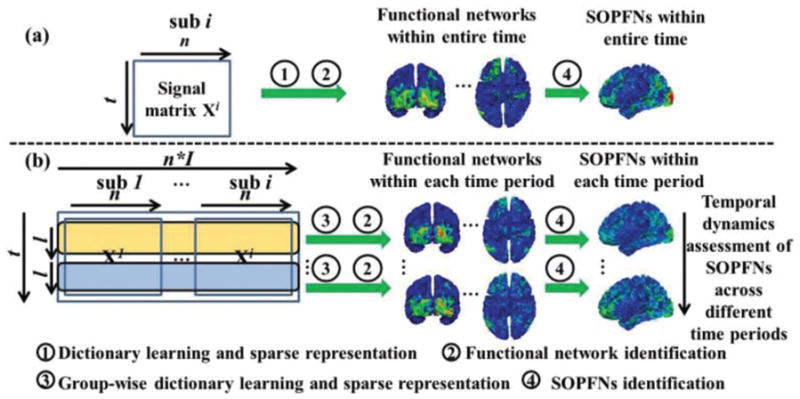
SOPFNs assessment in (a) previous studies and (b) our proposed framework. There are n tfMRI signals for each individual subject. Each signal has t total time points. In (b), there are I subjects in total. Each temporal segment (time period) has unified l time points. The four steps labeled as 1 to 4 are detailed in Section II.

Although significant achievements have been done for SOPFNs analysis in previous studies (e.g., [8], [11]–[16]), there are still two crucial issues to be addressed (to the best of our knowledge) as illustrated in Fig. 1. First, the multiple concurrent functional networks and associated SOPFNs are merely assessed based on the entire fMRI scan data assuming the temporal stationarity (Fig. 1a), while possibly time-dependent dynamics of the spatial patterns of functional networks and associated SOPFNs has not been sufficiently explored yet. The assumption of temporal stationarity of the functional networks and SOPFNs’ spatial patterns might be problematic since neuroscience studies [17] have suggested that the function of the brain is dynamic both spatially and temporally. That is, the dynamically changing functional interactions between different cortical regions mediate the moment-by-moment functional switching in the brain [17]. As shown in Fig. 1b, there is considerable variability of the spatial patterns of the same corresponding functional networks identified across different time periods, suggesting the different involvement of certain regions in the corresponding functional networks across different time periods. As a consequence, there is also considerable variability of the spatial patterns of associated SOPFNs across different time periods (Fig. 1b). Essentially, previous studies (e.g., [8]) under the temporal stationary assumption would merely identify the functional networks and associated SOPFNs from the entire time length (Fig. 1a), and ignore the considerable spatial pattern variability of those corresponding networks and associated SOPFNs across different time periods (Fig. 1b), making it incapable of assessing the temporal dynamic spatial patterns of the SOPFNs precisely. Second, the multiple concurrent functional networks and associated SOPFNs are assessed within individual subjects and the averaged SOPFNs across different subjects are analyzed afterwards in previous studies (Fig. 1a). Although effective in analyzing the consistent SOPFNs across different subjects, other effective computational methodologies can be introduced to obtain accurate spatial locations of the functional networks and associated SOPFNs which are group-wise consistent across individual subjects (Fig. 1b).

To address the above-mentioned two issues, in this paper, we propose a novel computational framework of group-wise sparse representation of whole-brain fMRI temporal segments to assess the temporal dynamic spatial patterns of SOPFNs that are consistent across different subjects (as illustrated in Fig. 1b). Our technical contributions in this paper are two-fold: 1) Instead of merely identifying temporal stationary concurrent functional networks and associated one SOPFN based on entire fMRI scan data (Fig. 1a), we adopt the widely-used sliding time window approach (e.g., [18]–[21]) to divide the entire tfMRI signals into consecutive temporal segments, to identify the concurrent functional networks and associated SOPFNs separately based on each of the temporal segments, and to assess temporal dynamic spatial patterns of the SOPFNs across different temporal segments (Fig. 1b). 2) Instead of identifying functional networks and associated SOPFNs within individual subjects (Fig. 1a), we propose a novel group-wise sparse representation of specific corresponding temporal segments across individual subjects via an effective online dictionary learning algorithm [22] to obtain the group-wise consistent functional networks and associated SOPFNs within each specific temporal segment (time period) (Fig. 1b). In brief, the rationales of adopting sparse representation approach to identify functional networks and associated SOPFNs are as follows. Since a brain region might be involved in multiple concurrent neural processes (e.g., [12]–[16]), its associated tfMRI signal could be composed of various components. Moreover, recent studies have successfully adopted dictionary learning and sparse representation framework to identify functional networks based on the assumption that each fMRI signal is linearly and sparsely composed of dictionary components (e.g., [7]–[11], [23]–[25]). The most crucial characteristics of sparse representation approach compared with other decomposition approaches, e.g., independent component analysis [26], is that sparse representation does not have explicit assumption that temporal patterns of different components are statistically maximal independent [27].

Our other contributions in this paper are as follows. First, for the first time in the brain mapping field (as far as we know), we assess the temporal dynamic spatial distribution difference of SOPFNs across different time periods between cortical gyral and sulcal regions. The rationales are as follows. The human cortical folding, which is highly convoluted as convex gyri and concave sulci, is one of the most crucial features of cerebral cortex [28]. Recent studies from both micro- and macro-scale have reported that there are structural and functional differences between gyri and sulci [11], [29]–[34]. Especially, our recent work [11] has demonstrated that the task-based heterogeneous functional regions (i.e., the regions that are activated during multiple tasks conditions and are involved in multiple task-evoked systems during a specific task performance) which are identified based on entire tfMRI scan data (assuming temporal stationarity) have significant spatial pattern distribution difference between cortical gyri and sulci. This has inspired us to explore the possible temporal dynamic spatial pattern distribution difference of the SOPFNs across different time periods between cortical gyral and sulcal regions in this paper, which might help shed light on understanding functional architecture and dynamics mechanisms of cerebral cortex in the future. Second, we apply the proposed computational framework on the recently publicly released high-quality Human Connectome Project (HCP) grayordinate tfMRI data [35]–[37]. The HCP grayordinate tfMRI data in the standard MNI152 space not only has both high spatial and temporal resolution, but also maintains the correspondence established across individual subjects, making our results relatively reliable and reproducible for other labs and studies.

II. Materials and Methods

A. Dataset and Preprocessing

There are seven different tfMRI datasets including emotion, gambling, language, motor, relational, social, and working memory in the HCP (Q1 release) [35]–[37]. The seven tasks together are designed for comprehensive and systematic mapping of core functional nodes and functional networks across a wide range of cerebral cortex [36]. The detailed task designs of the seven datasets are referred to [36]. There are 64 subjects in total and each subject has the seven tfMRI scans. The major tfMRI acquisition parameters are 220 mm/52°/0.72 s/33.1 ms of FOV/flip angle/TR/TE, 90×104×72 by dimension, 2.0 mm isotropic voxels [36]. Pre-processing of the tfMRI data is referred to [37]. Specifically, we adopt the pre-processed tfMRI data in standard grayordinate space [37]. In the standard MNI152 space, gray matter is modeled as cortical surface vertices and subcortical voxels which termed as ‘grayordinate’. All subjects have the same number (64984) of ‘grayordinates’ (cortical surface vertices) in the standard space [37]. Each grayordinate has the anatomical information that belongs to gyri/sulci [37]. Those grayordinates as well as the associated tfMRI signals not only have both high spatial and temporal resolution, but also have reasonably precise correspondence across individual subjects [37], thus benefiting the group-wise sparse representation of corresponding temporal segments across individual subjects, and assessment of temporal dynamic spatial patterns of group-wise consistent SOPFNs as well as the spatial pattern distribution of SOPFNs on gyral/sulcal regions in this paper.

B. TfMRI Temporal Segments Extraction

In our proposed framework, we first extract a series of consecutive temporal segments of whole-brain tfMRI signals for each individual subject and each of the seven tfMRI datasets, respectively. Specifically, as illustrated in Fig. 2, for subject i, the tfMRI signals of whole-brain grayordinates are extracted [37], [11], normalized to zero mean and standard deviation of 1 [22], and aggregated into a signal matrix Xⁱ ∈ ℝ^t×n with t time points and n grayordinates (Fig. 2a). Then, the sliding time window approach, which has been widely and effectively applied for functional brain temporal dynamics analysis (e.g., [18]–[21]), is adopted and defined in Eq. (1) to segment Xⁱ into a series of consecutive temporal segments X^i,w_j ∈ ℝ^l×n within the time window w_j which starts at time point t_j and has unified window length (number of time points) l:

$${\mathbf{X}}^{i,w_j}=\left\{{\mathbf{x}}^{i,q}\mid t_j\le q<t_j+l,t_j=1,\mathrm{..},(t-l+1)\right\}$$ (1)

where x^i,q is the vector of values of q-th row of Xⁱ at time point q. In total, there are (t − l + 1) corresponding temporal segments (time windows) for each individual subject and each of the seven tfMRI datasets. We choose the value of window length l=20 via experimental results similar as in [18], [19] based on the criterion that l should be both smaller than any of the task paradigm design (Fig. 2c) and large enough to reflect brain response [18], [19]. More details about the parameter selection of l are in Supplemental materials.

Fig. 2.

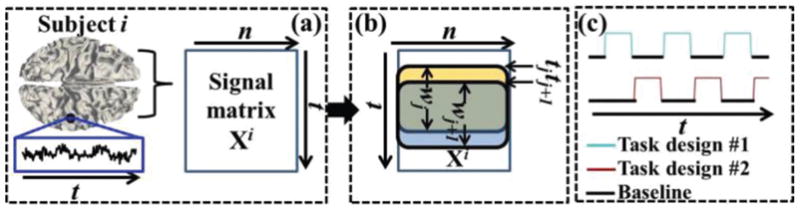
tfMRI temporal segments extraction. (a): The cortical surface and whole-brain tfMRI signal matrix Xⁱ of subject i. The tfMRI signal of an example grayordinate is shown and highlighted by the blue frame. (b): Examples of extracted two consecutive temporal segments within time windows w_j and w_j+1 (highlighted by yellow and blue frames, respectively). The first one starts at time point t_j and the second one starts at time point t_j+1. (c): Example of tfMRI emotion task paradigm. The blocks of the two task designs are interleaved during the entire fMRI scan time t. Window length l is smaller than the length of any of the blocks of the two task designs.

C. Group-wise Sparse Coding of TfMRI Temporal Segments

Once we obtain the tfMRI temporal segments, the next step is to perform group-wise dictionary learning and sparse coding of each corresponding tfMRI temporal segments across a group of subjects to obtain a comprehensive collection of group-wise consistent dictionary components within each temporal segment (time period). The dictionary learning and sparse representation framework has been demonstrated efficient and effective in both characterizing the low-dimensional structure of tfMRI data and identifying the multiple concurrent functional brain networks based on tfMRI data (e.g., [7]–[11], [23]–[25], [38]). As illustrated in Fig. 3a, the conventional sparse representation framework in previous studies (e.g., [7]–[11], [23]–[25], [38]) is merely performed on each individual subject. That is, for a specific temporal segment X^i,w_j ∈ ℝ^l×n of an individual subject i at time window w_j, X^i,w_j is represented as an over-complete dictionary matrix D^i,w_j ∈ ℝ^l×m (m is the dictionary size, m > l and m ≪ n) and a sparse coefficient weight matrix α^i,w_j ∈ ℝ^m×n (Fig. 3a) via an effective online dictionary learning algorithm [22]. Specifically, the temporal segment vector ${\mathbf{x}}_k^{i,w_j}(k=1,\dots n)$ in k-th column of X^i,w_j is approximately represented as ${\mathbf{x}}_k^{i,w_j}={\mathbf{D}}^{i,w_j}\times {\mathbf{\alpha }}_k^{i,w_j}$, where ${\mathbf{\alpha }}_k^{i,w_j}(k=1,\dots n)$ is the k-th column of α^i,w_j corresponding to the sparse coefficient weight vector of ${\mathbf{x}}_k^{i,w_j}$. Note that from brain science perspective, each dictionary component ${\mathbf{d}}_k^{i,w_j}$ in k-th column of D^i,w_j represents the temporal activity of k-th functional network component, and corresponding ${\mathbf{\alpha }}_k^{i,w_j}(k=1,\dots m)$ in k-th row of α^i,w_j can be mapped back to the cortical surface to obtain the spatial pattern of k-th functional network component (Fig. 3b). However, as the conventional sparse representation framework is performed on each individual subject, the group-wise consistency of the reconstructed functional network components across different subjects is not well guaranteed.

Fig. 3.

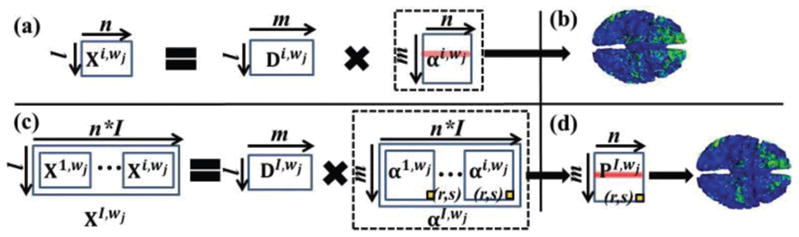
(a) Conventional sparse representation of a specific temporal segment of an individual subject. (c) The proposed group-wise sparse representation of specific corresponding temporal segments across all subjects. (b): The spatial pattern of an example reconstructed functional network via mapping a specific row (highlighted by red) of α^i,w_j back onto the cortical surface based on conventional sparse representation. (d): The spatial pattern of an example group-wise consistent reconstructed functional network via mapping a specific row (highlighted by red) of P^I,w_j back onto the cortical surface based on the proposed group-wise sparse representation.

To solve this problem, in this work, we adopt a novel group-wise dictionary learning and sparse representation framework based on our recent work [38] to reconstruct group-wise consistent functional networks within each time window. As illustrated in Fig. 3c, considering a group of I subjects at time window w_j, the corresponding temporal segments [X^1,w_j,..,X^i,w_j] of all subjects are arranged into a big matrix X^l,w_j ∈ ℝ^l×(n×I). X^I,w_j is then represented as an over-complete dictionary matrix D^I,w_j ∈ ℝ^l×m (m > l and m ≪ (n×I)) and a sparse coefficient weight matrix α^I,w_j ∈ ℝ^m×(n×I) using the online dictionary learning algorithm [22]. D^I,w_j and α^I,w_j are calculated as follows. An empirical cost function of X^I,w_j considering the average loss of regression to all temporal segments ${\mathbf{x}}_k^{i,w_j}(k=1,\dots (n\times I))$ is defined in Eq. (2).

$$f_{n\times I}\left({\mathbf{D}}^{I,w_j}\right)=\frac{1}{n\times I}\sum _{k=1}^{n\times I}\underset{{\mathbf{\alpha }}_k^{I,w_j}\in {ℝ}^m}{min}\frac{1}{2}{\Vert {\mathbf{x}}_k^{I,w_j}-{\mathbf{D}}^{I,w_j}{\mathbf{\alpha }}_k^{I,w_j}\Vert }_2^2+\lambda \Vert {\mathbf{\alpha }}_k^{I,w_j}\Vert$$ (2)

where l₁-norm regularization and parameter λ are adopted to trade-off the regression residual and sparsity level of ${\mathbf{\alpha }}_k^{I,w_j}$, respectively. To make the coefficients in α^I,w_j comparable, there is a constraint for ${\mathbf{d}}_k^{I,w_j}(k=1,\dots m)$ in k-th column of D^I,w_j as defined in Eq. (3).

$$C=\left\{{\mathbf{D}}^{I,w_j}\in {ℝ}^{l\times m}s.t.\forall k=1,\dots m,{({\mathbf{d}}_k^{I,w_j})}^T{\mathbf{d}}_k^{I,w_j}\le 1\right\}$$ (3)

The whole problem in Eq. (2) is then rewritten as a matrix factorization problem in Eq. (4) and solved by effective online dictionary learning algorithm and associated publicly released toolbox [22] to learn the dictionary D^I,w_j. More details are in [22].

$$\underset{{\mathbf{D}}^{I,w_j}\in C,{\mathbf{\alpha }}^{I,w_j}\in {ℝ}^{m\times (n\times I)}}{min}\frac{1}{2}{\Vert {\mathbf{x}}^{I,w_j}-{\mathbf{D}}^{I,w_j}{\mathbf{\alpha }}^{I,w_j}\Vert }_F^2+\lambda {\Vert \mathbf{\alpha }\Vert }_{1,1}$$ (4)

Once D^I,w_j is learned and fixed, α^I,w_j is calculated as an l₁-regularized linear least-squares problem [22]. The values of two major parameters dictionary size m and regularization parameter λ in Eq. (4) are experimentally determined (m=50 and λ =1.5) based on the criterion of consistency of reconstructed functional networks across subject groups [7], [8]. More details about the parameter selection are in Supplemental materials.

As shown in Fig. 3d, in order to obtain the group-wise consistent spatial patterns of reconstructed functional networks across a group of subjects, we calculate the common sparse coefficient weight matrix P^I,w_j ∈ ℝ^m×n based on the learned α^I,w_j ∈ ℝ^m×(n×I) as follows. First, since the dictionary learning and sparse representation framework maintains the organization of all temporal segments across I subjects in the input X^I,w_j, the learned α^I,w_j also preserves the spatial information of temporal segments across I subjects. We therefore decompose α^I,w_j into I sub-matrices [α^1,w_j,..,α^i,w_j ∈ ℝ^m×n] corresponding to I subjects (Fig. 3c). The element (r,s) in each sub-matrix stores the corresponding coefficient value of the s-th grayordinate to the r-th dictionary in D^I,w_j for each subject. Second, since we aim to obtain the common coefficient values which are non-zero across different subjects based on the sparse matrices [α^1,w_j,..,α^i,w_j ∈ ℝ^m×n], we perform t-test of the null hypothesis (r, s) = 0 for (r, s) across I subjects [38] to obtain the common sparse coefficient weight matrix P^I,w_j ∈ ℝ^m×n (Fig. 3d), in which element (r, s) stores the p-value representing statistically coefficient value of the s-th grayordinate to the r-th dictionary across all I subjects. Third, we transform all the values in P^I,w_j from p-value to z-score just for visualization facilitation [38]. Note that larger z-score indicates smaller p-value. Moreover, we only keep the values in P^I,w_j that are larger than 1.65 (corresponding to p-value that is smaller than 0.05) and set all other values that are smaller than 1.65 to 0 [38]. More details about the statistical measurements and corrections are referred to [38]. Finally, ${\mathbf{p}}_k^{I,w_j}(k=1,\dots m)$ in k-th row of P^I,w_j is mapped back to the cortical surface to obtain the group-wise consistent spatial pattern of k-th functional network component at time window w_j (Fig. 3d).

D. Identification of Group-wise Consistent Functional Networks and Associated SOPFNs within Different Time Windows

Once we obtain the spatial patterns of all functional network components, the next step is to identify those meaningful group-wise consistent concurrent functional networks based on current brain science knowledge within different time windows. We adopt the similar methods in [7]–[11], [38] to characterize and identify both task-evoked and intrinsic connectivity functional networks within different time windows. Specifically, we adopt the traditional general linear model (GLM)-derived activation maps as the task-evoked networks templates, and the intrinsic connectivity network (ICN) templates provided in [39] as references. The spatial pattern similarity is then defined as the spatial pattern overlap rate R

$$R(S,T)=\frac{\mid S\cap T\mid }{\mid T\mid }$$ (5)

where S and T are cortical spatial maps of a network component and a task-evoke/intrinsic network template, respectively. Note that S and T are converted from continuous values to discrete labels (values smaller than 0 are labeled as 0, and others are labeled as 1). For each network template, the top five network components with highest spatial pattern similarity defined in Eq. (5) are recorded. A group of experts visually inspect all top five network components to ensure the robustness of the identification via Eq. (5) and to finally determine one network component with highest spatial similarity with the network template as the corresponding group-wise consistent task-evoked/intrinsic network at a specific time window [7]–[11], [38]. Note that the identified functional networks based on the proposed group-wise sparse representation are independent of GLM or ICA approaches. In order to characterize and interpret those meaningful functional networks based on current brain science knowledge, we just utilize the traditional GLM-derived activation maps as the task-evoked networks templates, and the ICA-derived ICN templates as references to characterize those meaningful functional networks. It should also be noted that since we aim to assess the temporal dynamics of spatial patterns of SOPFNs based on identified corresponding functional networks across all time windows, we adopt a relatively strict criterion to only keep those functional networks that are successfully identified across all time windows (i.e., spatial pattern overlap rate R of a corresponding functional network is larger than 0.2 [8] across all time windows) while with potential spatial pattern variability. It is possible that certain functional networks disrupt at specific time windows while recover again at other time windows. The dynamics assessment of the spatial patterns of such functional networks would be another interesting work in the future.

The identification of SOPFNs is straightforward. It is defined as the set of all common cortical vertices (grayordinates) g_i involved in the spatial patterns of all identified concurrent functional networks at a specific time window w_j in Eq. (6).

$${\mathit{SOPFN}}_{w_j}=\forall g_{i}s.t.g_i\mathit{belongs}to\mathit{all}\mathit{networks}at{w}_j$$ (6)

Since each grayordinate g_i has gyri/sulci information [35]–[37], those grayordinates of SOPFNs are counted for gyri and sulci, respectively, and thus the spatial pattern distribution of SOPFNs on cortical gyral/sulcal regions at a specific time window can be assessed. Finally, the temporal dynamic spatial patterns of the SOPFNs as well as the temporal dynamic spatial pattern distribution on gyri/sulci are assessed based on the identified SOPFNs across different time windows.

III. Results

For each of the seven tfMRI datasets, we equally divided all 64 subjects into two groups (32 each) and applied the proposed framework on each of the two subject groups to test the stability and reproducibility of our framework, and to verify the reliability and meaningfulness of identified temporal dynamic spatial patterns of SOPFNs as well as the temporal dynamic spatial pattern distribution difference of SOPFNs on gyri/sulci. Three parts of experimental results are reported in the following, respectively.

A. Concurrent Group-wise Consistent Functional Networks across Different Time Windows

We identified concurrent group-wise consistent functional networks which exist across all time windows based on each of the seven tfMRI datasets. Fig. 4 shows the spatial maps of identified functional networks in one subject group of emotion tfMRI data. Two networks (Fig. 4b–4c) that exist across all time windows are identified in emotion tfMRI data based on the proposed relatively strict criterion since the major aim of this paper is to assess the dynamic spatial patterns of SOPFNs across all time windows based on the functional networks. Specifically, the first network (Fig. 4b) mainly locates at the visual cortex and has reasonable spatial pattern similarity with the GLM-derived spatial pattern, thus can be viewed as the task-evoked network. The second network (Fig. 4c) mainly locates at medial prefrontal gyrus, bilateral supramarginal gyrus, and anterior/posterior cingulate cortex, and is widely known as the default mode network (DMN) [39]. We can see that for each of the two networks across different time windows, albeit similar in overall spatial pattern, there is considerable variability of the spatial patterns across different time windows compared with the spatial pattern merely identified from the entire time length using sparse representation and GLM/ICN template. Quantitatively, the spatial pattern overlap rate R (Eq. (5)) across different time windows is 0.69±0.10 and 0.36±0.06 for the two networks, respectively. This finding is consistent between the two subject groups. More results of the reproducibility studies and the other six tfMRI datasets are in Supplemental Figs. 1–2 and Supplemental Table II.

Fig. 4.

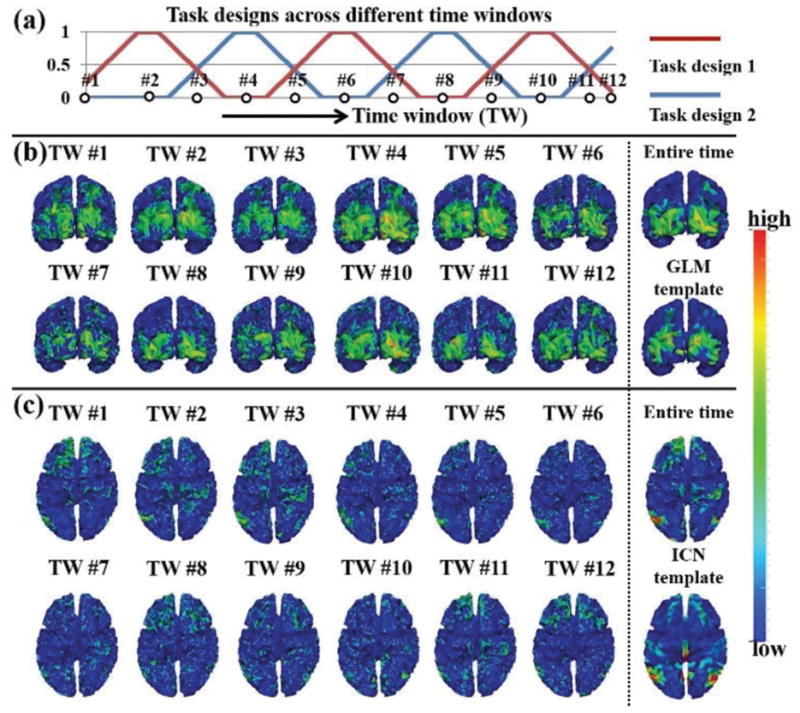
Concurrent group-wise consistent functional networks across different time windows in one subject group of emotion tfMRI data. (a) Task design curves across time windows of emotion tfMRI data. The horizontal axis is the time window and the vertical axis is the task design value. Twelve example time windows are shown. There are two task design curves in emotion tfMRI data. For each time window, if the task design value is non-zero in both two curves, there are both two tasks performed in the time window. If the task design value is non-zero in only one task design curve, there is only the corresponding task performed in the time window. Note that the task design curves are not convoluted with hemodynamic response function for a better visualization. (b) The spatial patterns of task-evoked functional networks identified within the twelve example time windows. The corresponding networks identified from entire time length via sparse representation and GLM are also shown. (c) The spatial patterns of default mode networks (DMN) identified within the same twelve example time windows. The corresponding networks identified from entire time length via sparse representation and the DMN template [39] are also shown. (b) and (c) are color-coded by the z-scores values as illustrated in Section II C.

In short, the spatial pattern variability for the same functional network across different time windows suggests the time-dependent dynamics of spatial patterns of networks due to the different involvement of specific brain regions in the corresponding networks across different time windows [17]. It is also the premise to identify the spatial patterns of SOPFNs within each time window and to assess the temporal dynamic spatial patterns of SOPFNs across all time windows as detailed in the next section.

B. Temporal Dynamic Spatial Patterns of SOPFNs across Different Time Windows

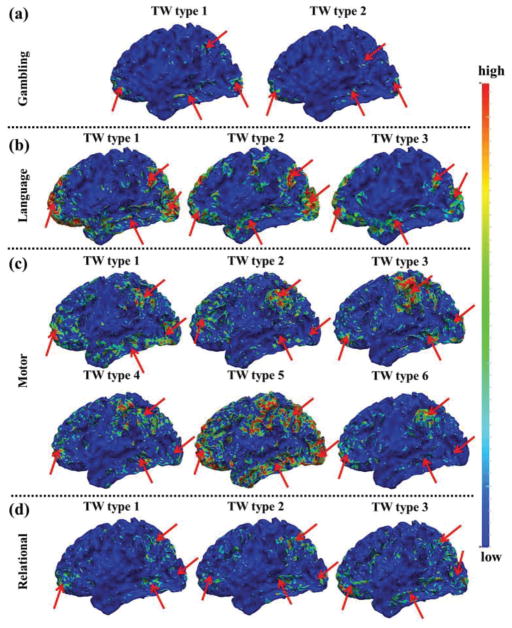
We assessed the SOPFN based on the identified concurrent functional networks within each time window using Eq. (6). Then the regularity and variability of spatial patterns of SOPFNs across different time windows were examined and compared. Fig. 5 shows the spatial maps of SOPFNs in emotion tfMRI data. We can see that there is considerable spatial pattern variability of SOPFNs across different time windows in Supplemental Fig. 5. We further categorized all time windows into three types as illustrated in Fig. 5a. Specifically, time window type 1 only involves task design 1, time window type 2 only involves task design 2, and time window type 3 involves both two task designs. The mean spatial patterns of SOPFNs of time windows within each of the three time window types are shown in Fig. 5b. We can see that there are reasonably certain common spatial patterns of SOPFNs (with relatively higher density as highlighted by red arrows) located at the bilateral parietal/temporal/frontal lobe and visual association cortices across the three time window types and across two subject groups. Moreover, such common spatial patterns of SOPFNs are also relatively consistent across the other six tasks as illustrated in Fig. 6. More results are in Supplemental Fig. 3. This finding is in agreement with previous studies reporting that frontal and parietal lobes include multiple-demand patterns associated with diverse cognitive demands [12], [16], and that visual association cortex is a heterogeneous collection of visual areas and is involved in higher level of processing [40].

Fig. 5.

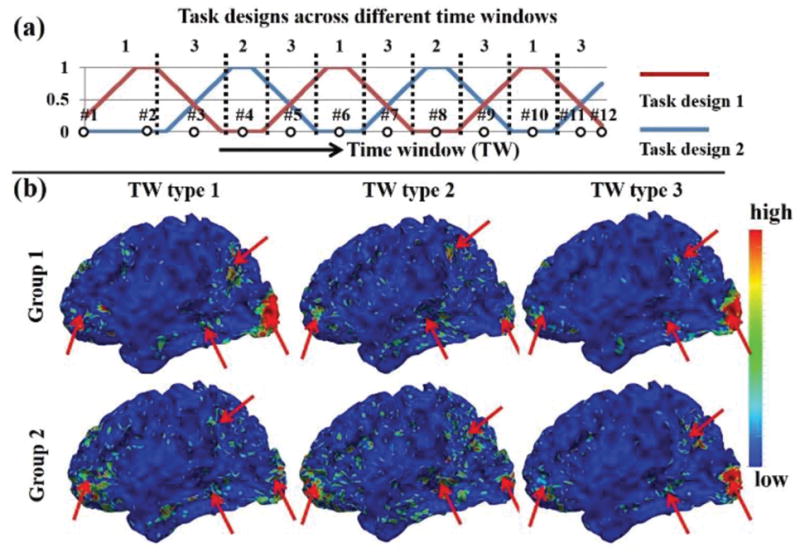
Temporal dynamic spatial patterns of SOPFNs across different time windows based on emotion tfMRI data. (a) Task design curves across time windows. The horizontal axis is the time window and the vertical axis is the task design value. The same twelve example time windows as in Fig. 4 are shown. There are three time window types as shown and divided by black dashed lines. Note that the task design curves are not convoluted with hemodynamic response function for a better visualization. (b) The mean spatial patterns of SOPFNs of time windows within each of the three time window types in each of the two subject groups. The common spatial patterns of SOPFNs with relatively higher density are highlighted by red arrows; (b) are color-coded by the z-scores representing SOPFNs values as illustrated in Section II C.

Fig. 6.

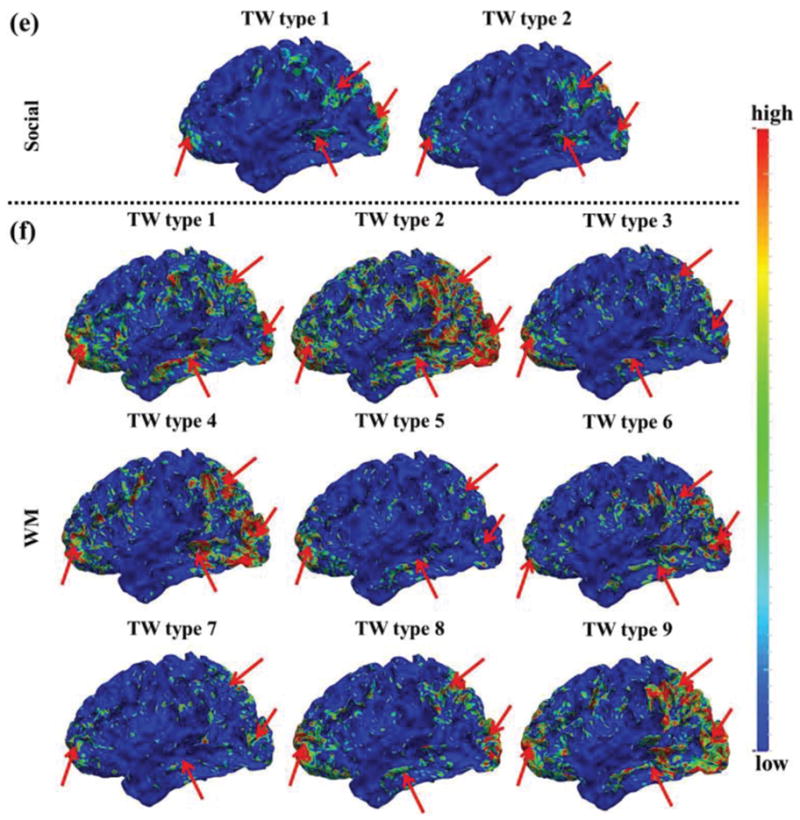
The mean spatial patterns of SOPFNs of time windows within each of the different time window types in one subject group of the other four tfMRI datasets in (a)-(f), respectively. The common spatial patterns of SOPFNs with relatively higher density across different time window types and different tasks are highlighted by red arrows. TW represents time window. (a)-(f) are color-coded by the z-scores as illustrated in Section II C. The detailed time window types of each task are in Supplemental Fig. 3.

More interestingly, we can see the considerable spatial pattern variability of SOPFNs across different time window types (Fig. 5b and Fig. 6) in terms of pattern density in the common regions (bilateral parietal/temporal/frontal lobe and visual association cortices) from visual inspection, indicating the possible time-dependent dynamics of spatial patterns of SOPFNs. This phenomenon is not explored in previous studies which assume the temporal stationarity (e.g., [8], [12], [16], [40]). Quantitatively, we defined and assessed the ‘overlap percentage’ (ratio of vertex number of overlapped region to the total vertex number of concurrent functional networks) of SOPFNs within each time window. We first performed the one-way ANOVA across all three TW types, then performed three pair-wise t-test comparison between any two of the three TW types as post-hoc multiple comparisons, and finally performed correction for multiple comparisons (Bonferroni correction) for the post-hoc tests. Table I demonstrates that the mean overlap percentage is statistically significantly large in time window type 1, small in time window type 2, and moderate in time window type 3 (involving both two task designs). This result is consistent across the two subject groups. Specific significant overlap percentage differences are also found in the other six tasks as demonstrated in Supplemental Table III. In short, there is both regularity and variability of the identified temporal dynamic spatial patterns of SOPFNs across different time windows. Specifically, the spatial patterns of SOPFNs have reasonable common regions across different time windows (in agreement with previous studies assuming temporal stationarity) while with temporal dynamic spatial patterns in terms of significantly different overlap percentage across different time windows.

Table I.

Overlap percentage (mean±std) of the three time window (TW) types and the statistical comparison across different time window types in emotion task.

Overlap percentage	TW type 1	TW type 2	TW type 3
Group 1	0.12±0.16	0.05±0.01	0.07±0.03
Group 2	0.09±0.05	0.06±0.02	0.07±0.03

t-test		type 1 > type 2	type 1 > type 3	type 3 > type 2
Group 1	tstat	2.070	2.871	2.029
	df	62	128	118
	corrected p-value	0.043	0.007	0.043
Group 2	tstat	2.557	1.778	1.866
	df	62	128	118
	corrected p-value	0.020	0.065	0.065

Bold and underlined values indicate p-values smaller than 0.05. tstat: t-statistic; df: degree of freedom.

C. Temporal Dynamic Spatial Pattern Distribution Difference of SOPFNs between Gyral and Sulcal Regions

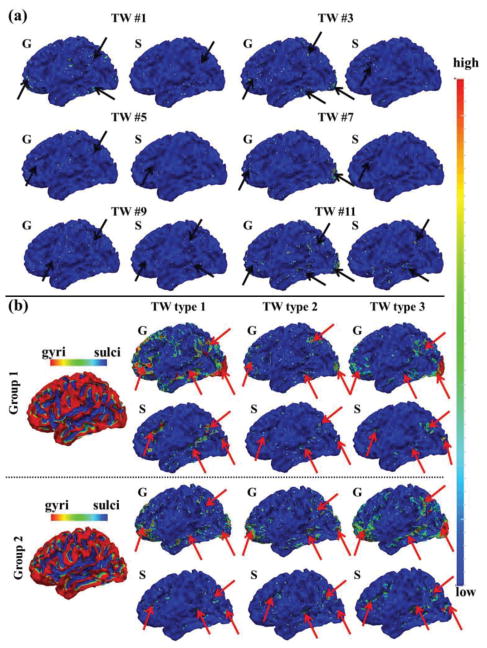
To further explore the temporal dynamics of spatial patterns of SOPFNs across different time windows, we assessed the spatial pattern distribution of identified SOPFN on gyral/sulcal regions within each time window, and investigated the possible temporal dynamics of spatial pattern distribution of SOPFNs on gyral/sulcal regions across different time windows. Fig. 7 shows the spatial pattern distributions of SOPFNs on gyral/sulcal regions in emotion tfMRI data. We can see that there is considerable spatial pattern distribution variability of SOPFNs on gyral and sulcal regions across different time windows as highlighted by black arrows in Fig. 7a. We further assessed the mean spatial pattern distributions of SOPFNs of time windows within each of the three time window types on gyral/sulcal regions as illustrated in Fig. 7b. We can see that similar as the results in Figs.5–6, there are reasonably certain common spatial pattern distributions of SOPFNs (with relatively higher density as highlighted by red arrows) at both gyral and sulcal regions of the bilateral parietal/temporal/frontal lobe and visual association cortices across the three time window types and across two subject groups. Such common spatial patterns of SOPFNs on gyral and sulcal regions are also relatively consistent across the other six tasks as shown in Fig. 8. More results are in Supplemental Fig. 4.

Fig. 7.

Temporal dynamic spatial pattern distributions of SOPFNs on gyral (G)/sulcal (S) regions in emotion tfMRI data. (a) Spatial pattern distributions of SOPFNs on gyral/sulcal regions in six example time windows (Fig. 5a). The major regions are highlighted by black arrows. (b) The mean spatial pattern distributions of SOPFNs across time windows within each of the three time window types on gyral/sulcal regions in each of the two subject groups. The common spatial patterns of SOPFNs on gyral/sulcal regions with relatively higher density are highlighted by red arrows. Note that the surfaces illustrating the SOPFNs in (a)-(b) are color-coded by the z-scores as illustrated in Section II C. The two surfaces in (a)-(b) illustrating the gyri/sulci are color-coded by the principal curvature value with gyri has higher principal curvature.

Fig. 8.

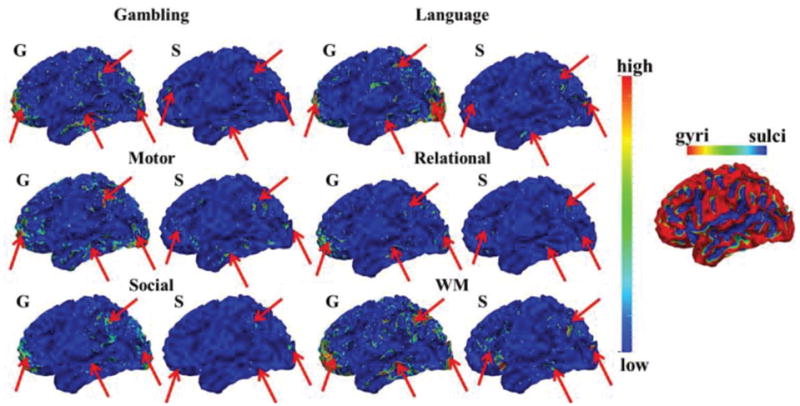
The mean spatial pattern distributions of SOPFNs across time windows within one example time window type on gyral/sulcal regions in one subject group of the other six tfMRI datasets. The common spatial patterns of SOPFNs with relatively higher density across different tasks are highlighted by red arrows. Note that the surfaces illustrating the SOPFNs are color-coded by the z-scores as illustrated in Section II C. The one example surface illustrating the gyri/sulci is color-coded by the principal curvature value with gyri has higher principal curvature.

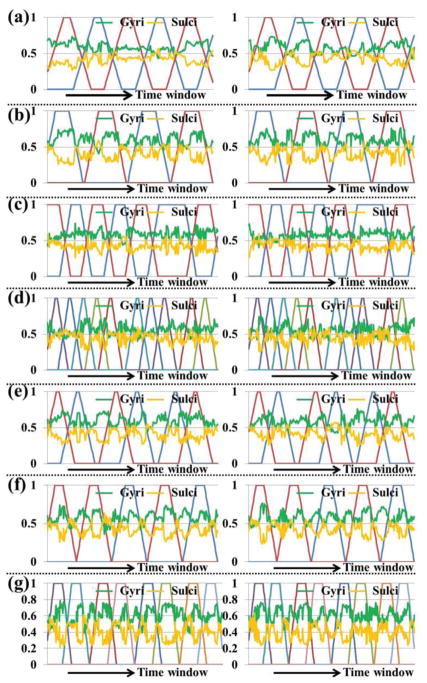
More interestingly, from visual inspection, we can see the considerable spatial pattern distribution variability of SOPFNs on gyral/sulcal regions across different time window types (Fig. 7b and Fig. 8) in terms of pattern density on gyral/sulcal regions of the common regions (bilateral parietal/temporal/frontal lobe and visual association cortices), indicating the possible time-dependent dynamics of spatial pattern distributions of SOPFNs on gyral/sulcal regions. This finding is not explored in previous studies assuming the temporal stationarity (e.g., [8], [12], [16], [40]). Quantitatively, we calculated the distribution percentage of SOPFNs on gyral/sulcal regions within each time window and reported the results in Table II and Fig. 9. We first performed the one-way ANOVA for the distribution percentage between gyri and sulci, and then performed corrections for multiple comparisons. The distribution percentage on gyral regions is statistically significantly larger than that on sulcal regions across all time windows (p<0.05). The mean ratio of distribution percentage on gyri vs that on sulci across all time windows is reported in Table II. Moreover, as illustrated in Fig. 9, it is interesting that there are considerable peaks/valleys for the distribution percentage value on gyri/sulci during the specific time window type across the entire scan, indicating the temporal dynamics of spatial pattern distributions of SOPFNs on gyral/sulcal regions across different time windows. In short, there is both regularity and variability of the spatial pattern distributions of time-dependent SOPFNs on gyral/sulcal regions. Specifically, the spatial pattern distributions of SOPFNs on gyral/sulcal regions have reasonable common regions across different time windows (in agreement with previous studies assuming temporal stationarity) while with temporal dynamics in terms of significantly larger distribution percentage on gyral regions than that on sulcal regions as well as interesting peaks/valleys alternations across different time windows.

Table II.

Mean ratio of distribution percentage on gyri vs that on sulci across all time windows in two subject groups of seven tasks.

	Emotion	Gambling	Language	Motor
Group 1	1.47	1.60	1.46	1.32
Group 2	1.45	1.55	1.38	1.33
	Rational	Social	WM
Group 1	1.59	1.46	1.67
Group 2	1.49	1.47	1.66

Fig. 9.

The temporal dynamic distribution percentage of SOPFNs on gyri (green curve) and sulci (orange curve) across all time windows in the two groups of the seven tasks shown in (a)-(g), respectively. In each sub-figure, the horizontal axis is the time window and the vertical axis is the distribution percentage value. The details of task design curves (represented by different colors) are in Supplemental Fig. 2. Note that the task design curves are not convoluted with hemodynamic response function for a better visualization. Note that at a specific time window, the sum of percentage values of gyri and sulci equals 1.

It should be noted that the identified temporal dynamic spatial patterns of SOPFNs (Figs. 5–6) and the temporal dynamic spatial pattern distributions of SOPFNs on gyral/sulcal regions (Figs. 7–9) are reasonably consistent across the two subject groups and across all seven tfMRI datasets, and in agreement with previous neuroscience studies as detailed above, which is a reasonable verification of reliability and meaningfulness of the reported findings.

IV. Discussion

We identified two major functional networks (task-evoked and DMN) that are consistently exist in all time windows during the scan. Our explanations are as follows. During the task fMRI scan, it is straightforward that the task-evoked networks are consistently activated under specific task stimulus during the whole scanning period. The DMN, which is the most studied ICN, has been demonstrated fundamental for brain functions and existing in both task fMRI and resting state fMRI data. It is therefore reasonable that the DMN has been identified in every time window during the whole scan in this paper. In short, the identified consistent task-evoked network and DMN during the whole scan while with considerable spatial pattern variability in this paper are reasonable from neuroscience perspective. For the other ICNs (including resting state networks and the set of functionally connected brain networks in either resting state or task), to the best of our knowledge, previous studies focus on the exploration of those ICNs in the whole scan period, while the dynamics of those ICNs (e.g., if consistently exist or show dynamics across different time windows) during the scan period is largely unknown. That is also one of the motivations and novelties of this paper to investigate the dynamics of the functional networks as well as SOPFNs. Based the proposed framework in this paper, we identified the most confident two networks (task-evoked and DMN) that consistently exist across all time windows using a relatively strict criterion. This finding is reproducible across two subject groups and seven task fMRI datasets. Given the lack of ground truth in brain mapping, the reproducibility is a reasonable verification of reliability and meaningfulness of the reported findings. In the future, we can investigate the dynamics of those ICNs which are not identified based on the relatively strict criterion in this paper, i.e., different involvement of sub-regions during different time windows within the same ICN, which might be another interesting work for ICN dynamics analysis. This will also lend more evidence for understanding functional brain dynamics mechanism from the neuroscience perspective.

We reported significant spatial pattern distribution difference of SOPFNs between cortical gyri and sulci across time windows. The justification of the findings are two-fold. First, these findings (Section III C) are reproducible between two different subject groups and consistent across seven different task fMRI datasets. Given the lack of ground truth in brain mapping, the reproducibility and consistency across different subjects and datasets is a reasonable justification of the reported significant SOPFN difference between cortical gyri and sulci across time windows. Second, the findings in this paper and our previous works [11, 34] can be mutually supported. Specifically, [11] has demonstrated that under temporal stationarity assumption, the SOPFNs mainly locate on bilateral parietal/temporal/frontal lobe and visual association cortices across different subjects and datasets. Moreover, the SOPFNs locate significantly more on gyri than sulci under temporal stationarity in the whole scan period. In this paper, the analysis of temporal dynamics of SOPFNs also shows that SOPFNs mainly locate on the same regions (bilateral parietal/temporal/frontal lobe and visual association cortices) across different subjects and datasets which is in agreement with [11] but with considerable spatial pattern distribution variability across different time windows considering the temporal dynamics. Moreover, in general, the distribution of SOPFNs locates more on gyri than sulci across different time windows which is also in agreement with [11] but with considerable peaks/valleys for the distribution percentage value on gyri/sulci across different window types. This paper extends the cortical architecture exploration (in terms of SOPFN distribution analysis on gyri/sulci) from temporal stationary [11] to temporal dynamics, indicating that gyri might participate more in those spatially overlapped and interacting concurrent functional networks (neural processes) than sulci under temporal dynamics. Moreover, [34] has demonstrated that the resting state functional connectivity is strong between gyral-gyral regions, weak between sulcal-sulcal regions, and moderate between gyral-sulcal regions, indicating that ‘gyri are functional connection centers (hubs) that exchange information among remote structurally-connected gyri and neighboring sulci, while sulci serve as local functional units that communicate directly with their neighboring gyri and indirectly with other cortical regions through gyri’ [34]. This paper and [11, 34] all indicate that there is significantly functional difference between gyri and sulci in terms of SOPFN distribution (this paper and [11]) or functional connectivity [34]. Moreover, they all indicate and are mutually supported that gyri might participate more in cortical functional processing than sulci in terms of significantly more distribution of SOPFNs (this paper and [11]) or strong functional connectivity [34], while sulci also serve crucial roles in cortical functional processing. In short, this paper reveals a novel functional architecture of cortical gyri and sulci in terms of significantly more distribution of SOPFNs on gyri than on sulci in a temporal dynamics way, and can lend further support evidence to and are mutually supported by our previous studies [11, 34].

The verification of true dynamic functional connectivity analysis using proper statistical test is fundamental and crucial, and has received significant attentions in the brain mapping field. For example, it is fundamental to any dynamic functional connectivity model that if fluctuations are due to statistical uncertainty or due to true changes in population measures [41]. In this paper, we focused on the computational framework for temporal dynamics assessment of SOPFNs in this work. We argue that the reproducibility across different subjects and datasets under proper statistical test is a reasonable validation of the reported dynamics of SOPFNs on gyri and sulci. There are certain issues to be further investigated. For example, why are there peaks/valleys for the distribution percentage value of SOPFNs on gyri/sulci during the specific time windows in Fig. 9? Fully understanding of the unsolved concerns relating to the mechanisms of functional dynamics of cerebral cortex may need more evidence and clues from micro- or macro-scale analysis of brain structure and function in the future.

V. Conclusion

We proposed a novel computational framework of group-wise sparse representation of whole-brain fMRI temporal segments to assess temporal dynamics of spatial patterns of SOPFNs which are consistent across different subjects. Experimental results demonstrate that the distribution percentage of identified SOPFNs on gyral regions is statistically larger than that on sulcal regions across all time windows. These results suggest the possible functional difference between gyri and sulci, and provide a foundation to better understand functional brain dynamics in the future.

Our future work is as follows. First, we will investigate the temporal dynamic spatial pattern distribution of SOPFNs on gyral/sulcal regions in a finer scale based on our recent developed A-DICCCOL system [42] consisting of more than five hundred consistent cortical landmarks with gyral/sulcal and structural fiber connection pattern correspondence across individual subjects. Second, we will apply the proposed framework on resting state fMRI data (e.g., the recently publicly released datasets HCP including 900 subjects, Fcon1000, etc.) to explore the temporal dynamics of spatial patterns of SOPFNs in ‘resting state’. Third, we will apply the proposed framework on disease datasets such as Alzheimer Disease, Autism, schizophrenia, etc. to explore the possible regularity and variability of temporal dynamics of spatial patterns of SOPFNs between specific disease and normal controls, which can be potentially adopted as disease specific biomarkers.