MHD Flow of Sodium Alginate-Based Casson Type Nanofluid Passing Through A Porous Medium With Newtonian Heating

Abstract

Casson nanofluid, unsteady flow over an isothermal vertical plate with Newtonian heating (NH) is investigated. Sodium alginate (base fluid)is taken as counter example of Casson fluid. MHD and porosity effects are considered. Effects of thermal radiation along with heat generation are examined. Sodium alginate with Silver, Titanium oxide, Copper and Aluminum oxide are added as nano particles. Initial value problem with physical boundary condition is solved by using Laplace transform method. Exact results are obtained for temperature and velocity fields. Skin-friction and Nusselt number are calculated. The obtained results are analyzed graphically for emerging flow parameters and discussed. It is bring into being that temperature and velocity profile are decreasing with increasing nano particles volume fraction.

Introduction

The fluid is a particular kind of matter which have no fixed shape and deforms easily due to external pressure¹. Fluids are mainly of two type’s i.e Newtonian and non-Newtonian. Non-Newtonian fluids have numerous industrial applications^2,3. Furthermore, its application with magnetohydrodynamic (MHD) flow in a porous medium can widely be seen in irrigation problem, biological system, petroleum, textile, polymer industries. More investigations have been published on numerous aspects of MHD non-Newtonian fluid passes over a porous medium^4–7. The entropy analysis for nanofluid with different type of nano particles and water type base fluid for unsteady MHD flow was studied by⁸. The impact of magnetic field on free convection of nanofluid in a porous medium is presented by⁹. The effects of heat transfer on MHD nanofluid in a porous semi annulus has investigated by¹⁰ using numerical methods. Sheikholeslami et al.¹¹ examined the influence of free convection in a semi annulus enclosure for ferrofluid flow in the presence of magnetic source with the consideration of thermal radiation. The observation of non-uniform magnetic field and variable magnetic field on forced convection heat is investigated by^12,13. The observation of MHD on fluid flow with heat transfer is studded by^14–16. Recently^17,18 investigated the nanofluid transportation in a in the presence of magnetic source and porous cavity using CuO nano particles. The influence of external magnetic field for nanofluid as water is a base fluid of free convection flow is studied in¹⁹. Sheikholeslami and Ganji²⁰ have investigated the effect of convective heat transfer for the nanofluid by semi analytical and numerical approaches. The same author has also investigated the influence of heat transfer for nanofluid between parallel plates in²¹. The influence of Lorentz forces and convection nanofluid flow is investigated by^22–24. Dissimilar types of nano particles with water based fluid are studied by^25,26. The influence of melting heat for nanofluid is studied by²⁷. The transportation of nanofluid in porous media is investigated by²⁸. The influence of magnetic field for nanofluid with entropy generation is analysed by^29–31.

Nanotechnology is that kind of technology which provides the materials with size less than $100$ nm called nanomaterials. On the basis of the structure and their properties, nanomaterials are divided into four categories³². Carbon based nano materials, metal based nano materials, Dendrimers and composite. The terminology of nanofluid was first investigated by Choi³³. He defined that the fluids occupying the sizes of particles less than 100 nm is called nanofluid. The categorieswith different attitude of nano particles are particle material, Base fluid, size and concentration, of the nanofluid. Suspend these nano particles into any type of conventional fluid like oil, water, ethylene glycol to make nanofluids. The reason why nano size particles are preferred over micro size particles has been explained by³⁴. Nano particles over micro particles, good improvement have seen in thermo physical properties. Nanofluids have various applications such as in air conditioning cooling, automotive, power plant cooling, improving diesel generator efficiency etc.³⁵. Usually water, ethylene glycol are utilized as heat transfer base fluids. Different substances are used for the production of nanoparticles, which are generally divided into metallic i.e. copper³⁶, metal-oxide i.e. CuO³⁷, chalcogenides sulphides, selenides and telluride’s, mentioned³⁸ and different particles, such like carbon nanotubes³⁹. In literature the size of one particle is in between 20 nm⁴⁰ and 100 nm⁴¹.

Casson fluid model was first presented by Casson in 1959. Casson fluids in tubes was first studied by Oka⁴². Examples of Casson fluids are honey, blood, soup, jelly, stuffs, slurries, artificial fibers etc. Cassonnanofluid flow with Newtonian heatingpresented by⁴³. Sarojamma et al.⁴⁴ investigated Casson nanofluid past over perpendicular cylinder in the occurrence of a transverse magnetic field with internal heat generation or absorption.

Khalid et al.⁴⁵ examined unsteady MHD Casson fluid withfree convection flow in a porous medium. Bhattacharyya et al.⁴⁶ studied systematically magnetohydrodynamic Casson fluid flow over a stretching shrinking sheet with wall mass transfer. Arthur et al.⁴⁷ studied Casson fluid flow in excess of a perpendicular porous surface, chemical reaction in the existence of magnetic field. Recently, Fetecau et al.⁴⁸ has investigated fractional nanofluids for natural convection flow over an isothermal perpendicular plate with thermal radiation. Hussanan et al.⁴⁹ investigates the unsteady heat transfer flow of a non-Newtonian Casson fluid over an oscillating perpendicular plate with Newtonian heating. Recently, Imran et al.⁵⁰ analyzed the effect of Newtonian heating with slip condition on MHD flow of Casson fluid. MHD flow of Casson fluid with heat transfer and Newtonian heating is analyzed by Hussanan et al.⁵¹. The effect of Newtonian heating for nanofluid is recently investigated by^43,52. But no work is done until now on heat transfer enhancement in Sodium alginate fluid with additional effects of NH, MHD, porosity, heat generation, and thermal radiation. Silver (Ag), Titanium oxide (TiO₂), Copper (Cu) and Aluminum oxide (Al₂O₃) are nano particles suspended in base fluid. Problem is solved and interpreted graphically with some conclusions.

Mathematical Modeling and solution of the Problem

Sodium alginate with Silver (Ag), Titanium oxide (TiO₂), Copper (Cu) and Aluminum oxide (Al₂O₃) nano particles is considered. Heat transfer, thermal radiation and heat generation are taken. Unsteady flow is over an infinite vertical plate (ξ > 0) embedded in a saturated porous medium. MHD effect with uniform magnetic field B of strength B₀ and small magnetic Reynolds number. Initially both the plate and fluid are at rest with constant temperature Θ_∞. At time t = 0⁺ the plate originates oscillation in its plane ξ = 0 according to condition

$$u=UH\left(t\right)\cos (\omega t)i;\mathrm{or}\mathrm{u}=U\sin \left(\omega t\right)i;t>0$$ 1

After some time, plate temperature is raised to Θ_w. The fluid is electrically conducting. Therefore, by Maxwell equations

$$\mathrm{div}\mathbf{B}=\mathbf{0},\mathrm{Curl}\mathbf{E}=\mathbf{-}\frac{\partial \mathbf{B}}{\partial t},\mathrm{Curl}\mathbf{B}={\mu }_e\mathbf{J}.$$ 2

By using Ohm’s law

$$\mathbf{J}={\sigma }_{nf}\left(\mathbf{E}\mathbf{+}\mathbf{V}\mathbf{\times }\mathbf{B}\right),$$ 3

The quantities ρ_nf, μ_e and σ are assumed constants. Magnetic field B is normal to V. The Reynolds number is so small that flow is laminar. Hence,

$$\frac{1}{{\rho }_{nf}}\mathbf{J}\times \mathbf{B}=\frac{{\sigma }_{nf}}{{\rho }_{nf}}\left[\left(\mathbf{V}\times {\mathbf{B}}_0\right)\times {\mathbf{B}}_0\right]=-\frac{{\sigma }_{nf}{B}_0^2\mathbf{V}}{{\rho }_{nf}}.$$ 4

Equation for an incompressible Casson fluid flow^53–55

$$\tau ={\tau }_0+\mu {\gamma }^{•}$$ 5

Or

$${\tau }_{ab}=\{\begin{array}{cc}2\left({\mu }_{\eta }+\frac{p_{\lambda }}{\sqrt{2\pi }}\right)e_{ab},& \pi >{\pi }_c\\ 2\left({\mu }_{\eta }+\frac{p_{\lambda }}{\sqrt{2{\pi }_c}}\right)e_{ab},& \pi >{\pi }_c\end{array},$$ 6

where π = e_abe_ab and e_ab is the (a, b)^ah factor of the deformation rate, π is represent the product of the factor of deformation rate with itself, π_c is represent the critical value of this product based on the non-Newtonian model, μ_η is represent the plastic dynamic viscosity of the non- Newtonian fluid and P_λ is yield stress of fluid. Under these conditions alongside with the assumption that the viscous dissipation term in the energy equation is neglected, we get the following system⁵⁶:

$${\rho }_{nf}\left(u_t\right)=\left(1+\frac{1}{\gamma }\right){\mu }_{nf}\left(u_{\xi \xi }\right)-\left({\sigma }_{nf}{B}_0^2+\left(1+\frac{1}{\gamma }\right)\frac{{\mu }_{nf}\psi }{k}\right)u+g{\left(\rho \beta \right)}_{nf}\left[\mathrm{\Theta }-{\mathrm{\Theta }}_{\infty }\right];t,\xi >0,$$ 7

$${\left(\rho c_p\right)}_{nf}{\mathrm{\Theta }}_t=k_{nf}\left(1+\frac{16{\sigma }^{⁎}{\mathrm{\Theta }}_{\infty }^3}{3k_{nf}{k}^{⁎}}\right)T_{\xi \xi }+Q_0\left(\mathrm{\Theta }-{\mathrm{\Theta }}_{\infty }\right);\xi ,t>0,$$ 8

$$\begin{array}{l}u=0,\mathrm{\Theta }={\mathrm{\Theta }}_{\infty };\xi \ge 0,t<0\\ u=UH(t)\cos (\omega t)\mathrm{or}u=U\sin (\omega t),\frac{\partial \mathrm{\Theta }}{\partial \xi }=-h_s\mathrm{\Theta };t\ge 0,\xi =0\\ u\to 0,\mathrm{\Theta }\to {\mathrm{\Theta }}_{\infty }\mathrm{as}\xi \to \infty \end{array}\},$$ 9

where k^* is absorption coefficient and σ^* is Stefan-Boltzmann constant. Where Q₀ is the heat generation term, ρ_nf is the density of nanofluids, μ_nf is the dynamic viscosity, u is the fluid velocity in the $x$-axis perpendicular direction, γ is the Casson fluid parameter, ψ(0 < ψ < 1), K > 0, ψ is the porous medium and K is the permeability of porous medium, h_s is a constant heat transfer coefficient, Θ_w is the constant plate temperature (Θ_w < Θ_∞, Θ_w > Θ_∞ due to the cooled or heated plate, respectively), g is the acceleration due to gravity, and β_nf is the thermal expansion coefficient of the nanofluid.

Expressions for (ρc_p)_nf, (ρβ)_nf, μ_nf, ρ_nf, σ_nf, k_nf are given by²⁴:

$$\begin{array}{lll}\hfill {\rho }_{nf}& \hfill =\hfill & (1-\phi ){\rho }_f+\phi {\rho }_s,{\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\phi \right)}^{2.5}},\sigma =\frac{{\sigma }_f}{{\sigma }_s},\hfill \\ \hfill {\left(\rho \beta \right)}_{nf}& \hfill =\hfill & \left(1-\phi \right){\left(\rho \beta \right)}_f+\phi {\left(\rho \beta \right)}_s,{\left(\rho c_p\right)}_{nf}=(1-\phi ){\left(\rho c_p\right)}_f+\phi {\left(\rho c_p\right)}_s,\hfill \\ \hfill k_{nf}& \hfill =\hfill & k_f\left(\frac{k_s+2k_f-2\phi (k_f-k_s)}{k_s+2k_f+\phi (k_f-k_s)}\right),{\sigma }_{nf}={\sigma }_f\left(1+\frac{3\left(\sigma -1\right)\phi }{\left(\sigma +2\right)-\left(\sigma -1\right)\phi }\right),\hfill \end{array}$$ 10

where ϕ the volume fraction of nano particles, ρ_f and ρ_s is represent the density of base fluid and particle respectively, and c_p is specific heat on constant pressure. k_nf, k_f, and k_s are the thermal conductivities of the nanofluid, the base-fluid, and the solid particles, respectively. The expressions of Eq. (10) are classified to nano particles⁵⁷. For supplementary nano particles with unlike thermal conductivity, dynamic viscosity, see to Table 1^58–60.

Table 1.

Thermophysical properties of nanofluids^58–60.

	ρ (kgm−3)	cp (kg−1k−1)	k (Wm−1k−1)	β × 10−5 (k−1)
C6H9NaO7(SA)	989	4175	0.613	0.99
Al 2 O 3	3970	765	40	0.85
Cu	8933	385	401	1.67
TiO 2	4250	686.2	8.9528	0.9
Ag	10500	235	429	1.89

the dimensionless variables are⁵⁶,

$$\left[u^{⁎}=\frac{u}{U_0},{\xi }^{⁎}=\frac{U_0}{\nu }\xi ,t^{⁎}=\frac{{U_0}^2}{\nu }t,\mathit{\theta }=\frac{\mathrm{\Theta }-{\mathrm{\Theta }}_{\infty }}{{\mathrm{\Theta }}_w-{\mathrm{\Theta }}_{\infty }}\right],$$ 11

Into Eqs (7–9), we get

$$u_t=c_2{u}_{\xi \xi }-Hu+G{r}_0\mathit{\theta }t,\xi >0,$$ 12

$${\mathit{\theta }}_t=c_4{\mathit{\theta }}_{\xi \xi }+c_5\mathit{\theta };\xi ,t>0$$ 13

$$\begin{array}{l}u=0,\mathit{\theta }=0;\xi \ge 0,t<0\\ u=H(t)\cos (\omega t)\mathrm{or}u=\sin (\omega t),{\mathit{\theta }}_{\xi }=-\lambda \left(1+\mathit{\theta }\right);t\ge 0,\xi =0\\ u\to 0,\mathit{\theta }\to 0\mathrm{as}\xi \to \infty \end{array}\}$$ 14

where

$$\begin{array}{lll}\hfill {\varphi }_1& \hfill =\hfill & {\left(1-\phi \right)}^{2.5}\left[1-\phi +\phi \left(\frac{{\rho }_s}{{\rho }_f}\right)\right],c_1=1+\frac{3\left(\sigma -1\right)\phi }{\left(\sigma +2\right)-\left(\sigma -1\right)\phi },c_2=\left(1+\frac{1}{\gamma }\right)\frac{1}{{\varphi }_1},\hfill \\ \hfill c_3& \hfill =\hfill & 1-\phi +\phi \frac{{\left(\rho c_p\right)}_s}{{\left(\rho c_p\right)}_f},c_4=\frac{{\lambda }_{nf}\left(1+N{r}_0\right)}{\nu \mathrm{Pr}{c}_3},c_5=\frac{\nu Q_0}{U_0^2{k}_f},{\lambda }_{nf}=\frac{k_{nf}}{k_f},\hfill \\ \hfill M& \hfill =\hfill & \frac{c_1{\sigma }_f\nu B_0^2}{{\rho }_f{U}_0^2},Gr=\frac{\nu g{\left(\rho \beta \right)}_f}{U_0^3{\rho }_f}{(\mathrm{\Theta }}_w-{\mathrm{\Theta }}_{\infty }),\frac{1}{K}=\frac{{\nu }_f^2\psi }{k{U}_0^2},H=\frac{M}{{\varphi }_2}+\frac{c_2}{{\varphi }_{1}K},\hfill \\ \hfill {\varphi }_2& \hfill =\hfill & 1-\phi +\phi \frac{{\rho }_s}{{\rho }_f},Nr=\frac{16{\sigma }^{⁎}{\mathrm{\Theta }}_{\infty }^3}{3k_f{k}^{⁎}},\mathrm{Pr}\frac{{\left(\rho c_p\right)}_f}{k_f},\lambda =\frac{h_s\nu }{U_0},G{r}_0=\frac{{\varphi }_3}{{\varphi }_2}\frac{\nu g{\left(\rho \beta \right)}_f}{U_0^3{\rho }_f}{(\mathrm{\Theta }}_w-{\mathrm{\Theta }}_{\infty })\hfill \\ \hfill {\varphi }_3& \hfill =\hfill & 1-\phi +\phi \frac{{\left(\rho \beta \right)}_s}{{\left(\rho \beta \right)}_f},N{r}_0=\frac{{\lambda }_{nf}}{k_{nf}}\frac{16{\sigma }^{⁎}{\mathrm{\Theta }}_{\infty }^3}{3k_f{k}^{⁎}}\hfill \end{array}$$

where $\frac{1}{K}$ is permeability of pours medium, M is the magnetic parameter, Gr is thermal Grashof number, Pr is Prandtl number, Nr is radiation parameter, and λ is Newtonian heating parameter.

Laplace Transform Solution

Laplace transforms of Eqs (12, 13) gives:

$$c_2\overline{u_{\xi \xi }}-\left(q+H\right)\overline{u}=-G{r}_0\overline{\mathit{\theta }},$$ 15

$$c_4\overline{{\mathit{\theta }}_{\xi \xi }}-\left(q-c_5\right)\overline{\mathit{\theta }}=0,$$ 16

$$\left[\begin{array}{l}\overline{u}=0,\overline{\mathit{\theta }}=0;\xi \ge 0,q<0\\ \overline{u}=\frac{\omega }{q^2+{\omega }^2},{\overline{\mathit{\theta }}}_{\xi }=-\lambda \left(\frac{1}{q}+\overline{\mathit{\theta }}\right);q\ge 0,\xi =0\\ \overline{u}\to 0,\overline{\mathit{\theta }}\to 0\mathrm{as}\xi \to \infty \end{array}\right]$$ 17

Eq. (16) using Eq. (17) gives:

$$\overline{\theta }\left(\xi ,q\right)=\frac{1}{q}\left(\frac{\lambda \sqrt{c_4}}{\sqrt{q-c_5}-\lambda \sqrt{c_4}}\right)e^{-\xi \frac{\sqrt{q-c_5}}{\sqrt{c_4}}}.$$ 18

After taking the inverse Laplace of Eq. (18):

$$\mathit{\theta }\left(\xi ,t\right)=\frac{1}{2}\lambda \sqrt{c_4}{e}^{-\xi \sqrt{\frac{-c_5}{c_4}}}{\int }_0^t\left[\begin{array}{l}{e}^{c_5(t-\tau )}\left\{\frac{1}{\sqrt{\pi }\sqrt{t-\tau }}+\lambda \sqrt{c_4}{e}^{{c_6}^2(t-\tau )}erfc\left(-\lambda \sqrt{c_4}\sqrt{t-\tau }\right)\right\}⁎\\ \left\{2-erfc\left(\frac{2\sqrt{-c_5{c}_4}\tau -\xi }{2\sqrt{c_4\tau }}\right)+{\mathrm{e}}^{2y\sqrt{\frac{-c5}{c4}}}erfc\left(\frac{2\sqrt{-c_5{c}_4}\tau +\xi }{2\sqrt{c_4\tau }}\right)\right\}\end{array}\right]d\tau .$$ 19

Solution of Eq. (15) is:

$$\overline{u}\left(\xi ,q\right)=\left[\overline{u_a}\left(\xi ,q\right)+\overline{u_b}\left(\xi ,q\right)+\overline{u_c}\left(\xi ,q\right)+\overline{u_d}\left(\xi ,q\right)\right].$$ 20

Arranging Eq. (20) as:

$$\begin{array}{lll}\hfill \overline{u_a}\left(\xi ,q\right)& \hfill =\hfill & \frac{\omega }{q^2+{\omega }^2}{e}^{-\xi \frac{\sqrt{q+H}}{\sqrt{c_2}}},\hfill \\ \hfill \overline{u_b}\left(\xi ,q\right)& \hfill =\hfill & \frac{A}{q}\left(e^{-\xi \frac{\sqrt{q-c_5}}{\sqrt{c_4}}}-e^{-\xi \frac{\sqrt{q+H}}{\sqrt{c_2}}}\right),\hfill \\ \hfill \overline{u_c}\left(\xi ,q\right)& \hfill =\hfill & \frac{B_1}{q+\frac{c_7}{c_6}}\left(e^{-\xi \frac{\sqrt{q-c_5}}{\sqrt{c_4}}}-e^{-\xi \frac{\sqrt{q+H}}{\sqrt{c_2}}}\right),\hfill \\ \hfill \overline{u_d}\left(\xi ,q\right)& \hfill =\hfill & \frac{C}{\sqrt{q-c_5}-\lambda \sqrt{c_4}}\left(e^{-\xi \frac{\sqrt{q-c_5}}{\sqrt{c_4}}}-e^{-\xi \frac{\sqrt{q+H}}{\sqrt{c_2}}}\right),\hfill \end{array}$$ 21

where

$$\begin{array}{lll}\hfill A& \hfill =\hfill & \frac{c_8}{c_7\left(\sqrt{c_5}-\lambda \sqrt{c_4}\right)},B=\frac{c_8{c}_6}{c_7\left(\lambda \sqrt{c_4}-\sqrt{\frac{c_7}{c_6}-c_5}\right)},C=\frac{c_8}{{\lambda }^2{c}_4+c_5\left\{c_6\left({\lambda }^2{c}_4+c_5\right)+c_7\right\}},\hfill \\ \hfill B_1& \hfill =\hfill & \frac{B}{c_6},c_6=c_4-c_2,c_7=c_{4}H+c_2{c}_5,c_8=c_{4}G{r}_0\lambda \sqrt{c_4},\hfill \end{array}$$

Upon inversion:

$$u\left(\xi ,t\right)=\left[u_a\left(\xi ,t\right)+u_b\left(\xi ,t\right)+u_c\left(\xi ,t\right)+u_d\left(\xi ,t\right)\right],$$ 22

where

$$\begin{array}{lll}\hfill u_a\left(\xi ,t\right)& \hfill =\hfill & \frac{1}{4\mathrm{i}}{\mathrm{e}}^{\mathrm{i}tw}[{\mathrm{e}}^{-\xi \sqrt{\frac{H+\mathrm{i}w}{c_2}}}erfc\left\{\frac{\xi }{2\sqrt{c_{2}t}}-\sqrt{t\left(H+\mathrm{i}w\right)}\right\}\hfill \\ \hfill & \hfill & +{\mathrm{e}}^{\xi \sqrt{\frac{H+\mathrm{i}w}{c_2}}}erfc\left\{\frac{\xi }{2\sqrt{c_{2}t}}+\sqrt{t\left(H+\mathrm{i}w\right)}\right\}]\hfill \\ \hfill & \hfill & -\frac{1}{4\mathrm{i}}{\mathrm{e}}^{-itw}[{\mathrm{e}}^{-\xi \sqrt{\frac{H-\mathrm{i}w}{c_2}}}erfc\left\{\frac{\xi }{2\sqrt{c_{2}t}}-\sqrt{t\left(H-\mathrm{i}w\right)}\right\}\hfill \\ \hfill & \hfill & +{\mathrm{e}}^{\xi \sqrt{\frac{H-\mathrm{i}w}{c_2}}}erfc\left\{\frac{\xi }{2\sqrt{c_{2}t}}+\sqrt{t\left(H-\mathrm{i}w\right)}\right\}]\hfill \end{array},$$ 23

$$u_b\left(\xi ,t\right)=\frac{1}{2}A\left\{\begin{array}{l}{\mathrm{e}}^{-\sqrt{-\frac{c_5}{c_4}}\xi }\left(2-erfc\left[\frac{2\sqrt{-c_4{c}_5}t-\xi }{2\sqrt{c_{4}t}}\right]+{\mathrm{e}}^{2\sqrt{-\frac{c_5}{c_4}}\xi }erfc\left[\frac{2\sqrt{-c_4{c}_5}t+\xi }{2\sqrt{c_{4}t}}\right]\right)\\ -{\mathrm{e}}^{-\sqrt{\frac{H}{c_2}}\xi }\left(2-erfc\left[\frac{2\sqrt{c_{2}H}t-\xi }{2\sqrt{c_{2}t}}\right]+{\mathrm{e}}^{2\sqrt{\frac{H}{c_2}}\xi }erfc\left[\frac{2\sqrt{c_{2}H}t+\xi }{2\sqrt{c_{2}t}}\right]\right)\end{array}\right\},$$ 24

$$u_c\left(\xi ,t\right)=\frac{B_1{e}^{\frac{c_7}{c_6}}}{2}\left\{\begin{array}{l}{e}^{-\xi i\frac{\sqrt{c_5+\frac{c_7}{c_6}}}{\sqrt{c_4}}}erfc\left(\frac{\xi }{2\sqrt{t}\sqrt{c_4}}-i\sqrt{\left(c_5+\frac{c_7}{c_6}\right)t}\right)+e^{\xi i\frac{\sqrt{c_5+\frac{c_7}{c_6}}}{\sqrt{c_4}}}erfc\left(\frac{\xi }{2\sqrt{t}\sqrt{c_4}}+i\sqrt{\left(c_5+\frac{c_7}{c_6}\right)t}\right)\\ -e^{-\xi \frac{\sqrt{H-\frac{c_7}{c_6}}}{\sqrt{c_2}}}erfc\left(\frac{\xi }{2\sqrt{t}\sqrt{c_2}}-\sqrt{\left(H-\frac{c_7}{c_6}\right)t}\right)-e^{\xi \frac{\sqrt{H-\frac{c_7}{c_6}}}{\sqrt{c_2}}}erfc\left(\frac{\xi }{2\sqrt{t}\sqrt{c_2}}+\sqrt{\left(H-\frac{c_7}{c_6}\right)t}\right)\end{array}\right\},$$ 25

$$\begin{array}{lll}\hfill u_d\left(\xi ,t\right)& \hfill =\hfill & \frac{\xi C}{2\sqrt{c_4}\sqrt{\pi }}{\int }_0^t\left\{{\mathrm{e}}^{c_5\left(t-\tau \right)}\left(\frac{1}{\sqrt{\pi }\sqrt{t-\tau }}+c_6{\mathrm{e}}^{{c_6}^2\left(t-\tau \right)}erfc\left[-c_6\sqrt{t-\tau }\right]\right)⁎\frac{{\mathrm{e}}^{c_5\tau -\frac{{\xi }^2}{4c_4\tau }}}{{\tau }^{3/2}}\right\}d\tau \hfill \\ \hfill & \hfill & -\frac{\xi C}{2\sqrt{c_2}\sqrt{\pi }}{\int }_0^t\left\{{\mathrm{e}}^{c_5\left(t-\tau \right)}\left(\frac{1}{\sqrt{\pi }\sqrt{t-\tau }}+c_6{\mathrm{e}}^{{c_6}^2\left(t-\tau \right)}erfc\left[-c_6\sqrt{t-\tau }\right]\right)⁎\frac{{\mathrm{e}}^{-H\tau -\frac{{\xi }^2}{4c_2\tau }}}{{\tau }^{3/2}}\right\}d\tau .\hfill \end{array}$$ 26

Particular Cases

In order to link our found solutions with published literature, the following particular cases are examined by taking some parameters absent.

Making Gr = γ = 0 and Re = 1 in Eq. (22), reduces to:

$$\begin{array}{lll}\hfill u\left(\xi ,t\right)& \hfill =\hfill & \frac{1}{4\mathrm{i}}{\mathrm{e}}^{\mathrm{i}tw}[{\mathrm{e}}^{-\xi \sqrt{H+\mathrm{i}w}}erfc\left\{\frac{\xi }{2\sqrt{t}}-\sqrt{t\left(H+\mathrm{i}w\right)}\right\}\hfill \\ \hfill & \hfill & +{\mathrm{e}}^{\xi \sqrt{H+\mathrm{i}w}}erfc\left\{\frac{\xi }{2\sqrt{t}}+\sqrt{t\left(H+\mathrm{i}w\right)}\right\}]\hfill \\ \hfill & \hfill & -\frac{1}{4\mathrm{i}}{\mathrm{e}}^{-itw}[{\mathrm{e}}^{-\xi \sqrt{H-\mathrm{i}w}}erfc\left\{\frac{\xi }{2\sqrt{t}}-\sqrt{t\left(H-\mathrm{i}w\right)}\right\}\hfill \\ \hfill & \hfill & +{\mathrm{e}}^{\xi \sqrt{H-\mathrm{i}w}}erfc\left\{\frac{\xi }{2\sqrt{t}}+\sqrt{t\left(H-\mathrm{i}w\right)}\right\}],\hfill \end{array}$$ 27

which is identical to results of ⁶¹, Eq. (24).

Taking $M=\frac{1}{k}=0$ in the above relation, we get:

$$\begin{array}{lll}\hfill u\left(\xi ,t\right)& \hfill =\hfill & \frac{1}{4\mathrm{i}}{\mathrm{e}}^{\mathrm{i}tw}\left[{\mathrm{e}}^{-\xi \sqrt{\mathrm{i}w}}erfc\left\{\frac{\xi }{2\sqrt{t}}-\sqrt{\mathrm{i}wt}\right\}{+e}^{\xi \sqrt{\mathrm{i}w}}erfc\left\{\frac{\xi }{2\sqrt{t}}+\sqrt{\mathrm{i}wt}\right\}\right]\hfill \\ \hfill & \hfill & -\frac{1}{4\mathrm{i}}{\mathrm{e}}^{-itw}\left[{\mathrm{e}}^{-\xi \sqrt{\mathrm{i}w}}erfc\left\{\frac{\xi }{2\sqrt{t}}-\sqrt{-\mathrm{i}wt}\right\}{+e}^{\xi \sqrt{\mathrm{i}w}}erfc\left\{\frac{\xi }{2\sqrt{t}}+\sqrt{-iwt}\right\}\right]\hfill \end{array},$$ 28

Which is in accordance with⁶¹, Eq. (25).

Taking $Gr=M=\frac{1}{k}=\frac{1}{\gamma }=0$, in Eq. (22), it moderates to:

$$\begin{array}{lll}\hfill u\left(\xi ,t\right)& \hfill =\hfill & \frac{1}{4\mathrm{i}}{\mathrm{e}}^{\mathrm{i}tw}\left[{\mathrm{e}}^{-\xi \sqrt{\mathrm{Rei}w}}erfc\left\{\frac{\xi \sqrt{\mathrm{Re}}}{2\sqrt{t}}-\sqrt{\mathrm{i}wt}\right\}{+e}^{\xi \sqrt{\mathrm{Rei}w}}erfc\left\{\frac{\xi \sqrt{\mathrm{Re}}}{2\sqrt{t}}+\sqrt{\mathrm{i}wt}\right\}\right]\hfill \\ \hfill & \hfill & -\frac{1}{4\mathrm{i}}{\mathrm{e}}^{-itw}\left[{\mathrm{e}}^{-\xi \sqrt{-\mathrm{Rei}w}}erfc\left\{\frac{\xi \sqrt{\mathrm{Re}}}{2\sqrt{t}}-\sqrt{-\mathrm{i}wt}\right\}{+e}^{\xi \sqrt{-\mathrm{Rei}w}}erfc\left\{\frac{\xi \sqrt{\mathrm{Re}}}{2\sqrt{t}}+\sqrt{-\mathrm{i}wt}\right\}\right]\hfill \end{array},$$ 29

Identical to⁵⁸, Eq. (35).

Skin friction and Nusselt Number

$$C_f=\frac{1}{{\left(1-\phi \right)}^{2.5}}\left(1+\frac{1}{\gamma }\right){\frac{\partial u\left(\xi ,t\right)}{\partial \xi }|}_{\xi =0},$$ 30

$$\begin{array}{lll}\hfill C_f& \hfill =\hfill & \frac{1}{2}{\mathrm{ie}}^{-\mathrm{i}tw}\frac{1}{{\left(1-\phi \right)}^{2.5}}\left(1+\frac{1}{\gamma }\right)\hfill \\ \hfill & \hfill & \times \left[\begin{array}{l}{1-e}^{2\mathrm{i}tw}-\frac{{\mathrm{e}}^{-t\left(H-\mathrm{i}w\right)}}{\sqrt{c_{2}t}\sqrt{\pi }}-\sqrt{\frac{H-\mathrm{i}w}{c_2}}erf\left[\sqrt{t\left(H-\mathrm{i}w\right)}\right]\\ +{\mathrm{e}}^{2\mathrm{i}tw}\left\{\frac{{\mathrm{e}}^{-t\left(H+\mathrm{i}w\right)}}{\sqrt{c_{2}t}\sqrt{\pi }}+\sqrt{\frac{H+\mathrm{i}w}{c_2}}erf\left[\sqrt{t\left(H-\mathrm{i}w\right)}\right]\right\}\end{array}\right]\hfill \\ \hfill & \hfill & -A\left\{\frac{{\mathrm{e}}^{-Ht}}{\sqrt{c_{2}t}\sqrt{\pi }}+\sqrt{\frac{H}{c_2}}erfc\left(\sqrt{Ht}\right)\right\}\hfill \\ \hfill & \hfill & -B_1{e}^{\frac{c_7}{c_6}}\left\{\frac{{\mathrm{e}}^{\left(c_5+\frac{c_7}{c_6}\right)t}}{\sqrt{c_{4}t}\sqrt{\pi }}+i\frac{\sqrt{c_5+\frac{c_7}{c_6}}}{\sqrt{c_4}}-\frac{{\mathrm{e}}^{-\left(H-\frac{c_7}{c_6}\right)t}}{\sqrt{c_{2}t}\sqrt{\pi }}-\frac{\sqrt{H-\frac{c_7}{c_6}}}{\sqrt{c_2}}\right\}\hfill \\ \hfill & \hfill & +\left(\frac{C}{2\sqrt{c_4}\sqrt{\pi }}-\frac{C}{2\sqrt{c_2}\sqrt{\pi }}\right)\hfill \\ \hfill & \hfill & \times {\int }_0^t\left\{\frac{{\mathrm{e}}^{c_5\left(t-\tau \right)}}{{\tau }^{3/2}}\left(\frac{1}{\sqrt{\pi }\sqrt{t-\tau }}+c_6{\mathrm{e}}^{{c_6}^2\left(t-\tau \right)}erfc\left[-c_6\sqrt{t-\tau }\right]\right)\right\}d\tau .\hfill \end{array}$$ 31

$$Nu=-{\lambda }_{nf}{\frac{\partial \theta \left(\xi ,t\right)}{\partial \xi }|}_{\xi =0},$$ 32

$$Nu=-\frac{1}{2}{\lambda }_{nf}\lambda \sqrt{c_4}{\int }_0^t\left[\begin{array}{l}{e}^{c_5(t-\tau )}\left\{\frac{1}{\sqrt{\pi }\sqrt{t-\tau }}+\lambda \sqrt{c_4}{e}^{{c_6}^2(t-\tau )}erfc\left(-\lambda \sqrt{c_4}\sqrt{t-\tau }\right)\right\}\\ ⁎\left\{2-erfc\left(\sqrt{-c_5\tau }\right)\right\}\end{array}\right]d\tau .$$ 33

Discussion

In this section different parameters including γ, ϕ, Gr, M, K, Pr, Nr Figs 2–11 are plotted. Geometry of problem is shown in Fig. 1. The influence of γ on u(y, t) which shows oscillatory behavior increasing first then decreasing is highlighted in Fig. 2.

Figure 2.

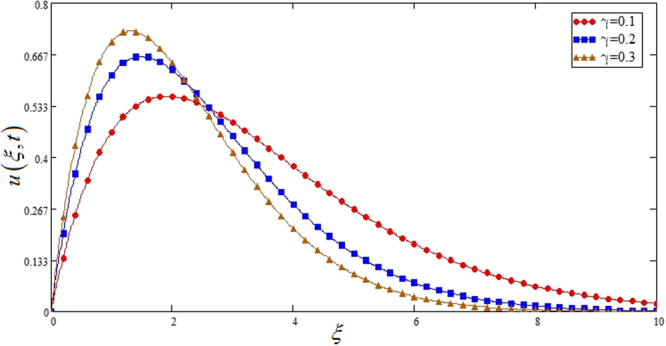
Effects of Casson fluid parameter γ on the velocity profile of Sodium alginate based Casson nanofluid when Pr = 0.7, Gr = 2 and φ = 0.04.

Figure 11.

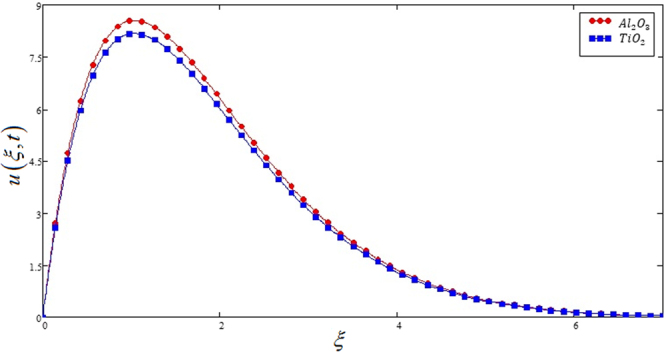
Comparison of velocities profiles of Al₂O₃ and TiO₃ for Casson nanofluids when Pr = 0.71, Gr = 10, Nr = 2, φ = 0.04 and t = 1.

Figure 1.

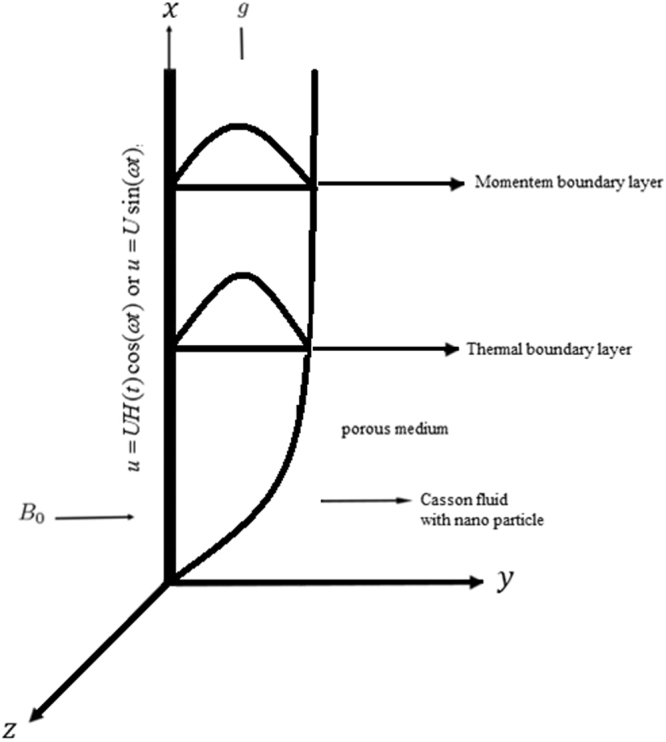
Geometry of the flow.

Figures 3 and 4 show effects of ϕ on u(ξ, t) and θ(ξ, t).φ is take in between 0 ≤ ϕ ≤ 0.04 due to sedimentation when the range goes above from 0.08. It is observed in both cases if the nano particles volume fraction ϕ is increased it leads to the decreasing of temperature and velocity profile.

Figure 3.

Effects of nano particles volume fraction parameter φ on the velocity profile of Sodium alginate based nano fluid when Gr = 0.2, Nr = 0.2 and t = 1.

Figure 4.

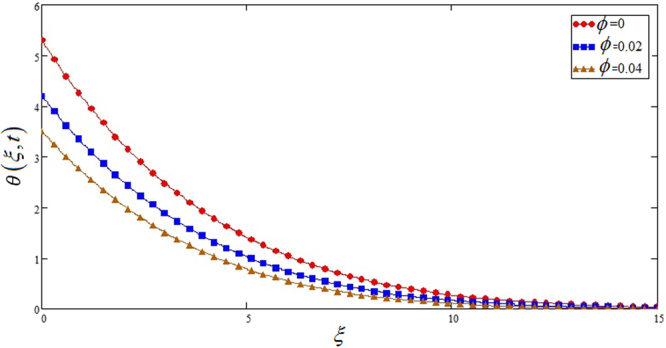
Effects of nano particles volume fraction parameter φ on the temperature profile of Sodium alginate based nano fluid when Pr = 5 and t = 1.

Figure 5 highlights the effect of Gr for Sodium alginate -based, Casson nanofluids on velocity profile. It is found that with increasing Gr, velocity increases. Because increasing effect in Gr, due to increase of buoyancy forces and decrease of viscous forces. Figure 6 the effect of M = 0, 1, 2 on the velocity profile. u(ξ, t) decreases due to increasing dragging force. M = 0, shows absence of MHD. Figure 7 shows K effect of on u(ξ, t). Velocity decrease due to decreasing friction. Figure 8 highlights that profile of velocity is increased with increasing radiation parameter Nr. The effect is studied for TiO₂ nano particle.

Figure 5.

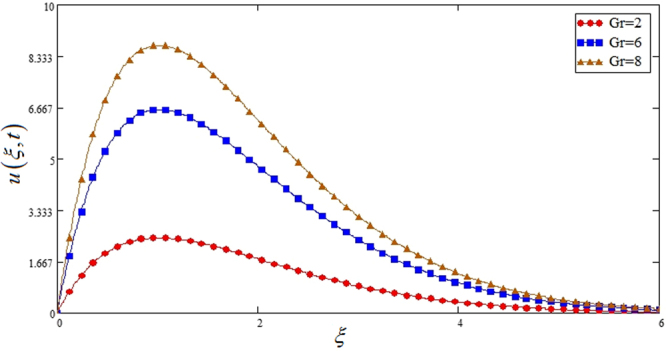
Effects of thermal Grashof number Gr on the velocity profile of Sodium alginate based Casson nano fluid when Pr = 0.7, Nr = 2, φ = 0.04 and t = 1.

Figure 6.

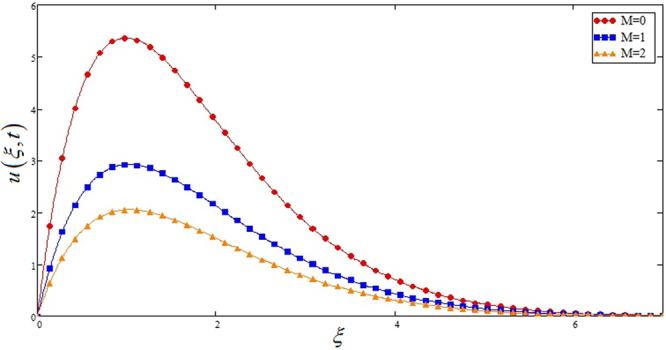
Effects of magnetic parameter M on the velocity profile of Sodium alginate based Casson nano fluid when Pr = 0.7, Nr = 2, Gr = 10, k = 2 and t = 1.

Figure 7.

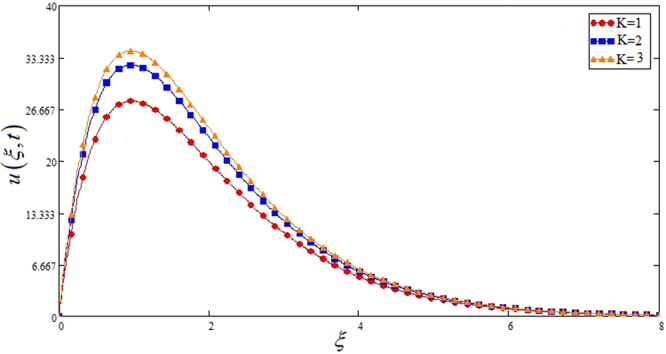
Effects of permeability of porous medium k on the velocity profile of Sodium alginate based nano fluid when Pr = 10, Gr = 10, Nr = 8, φ = 0.04 and t = 1.

Figure 8.

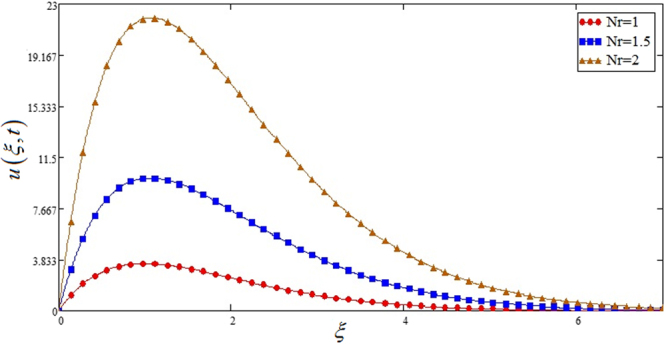
Effects of radiation parameter Nr for TiO₂ on the velocity profile of Sodium alginate based nano fluid when Pr = 0.7, Gr = 8, φ = 0.04 and t = 1.

The impact of two different types of nano particles (Al₂O₃ Sodium alginate -based Casson nanofluid and Ag-Sodium alginate -based nanofluid) on profile of velocity is studied in Fig. 9. The profile of velocity is greater for Al₂O₃ Sodium alginate -based Casson nanofluid and lower profile velocity for Ag-Sodium alginate -based nanofluid is observed.

Figure 9.

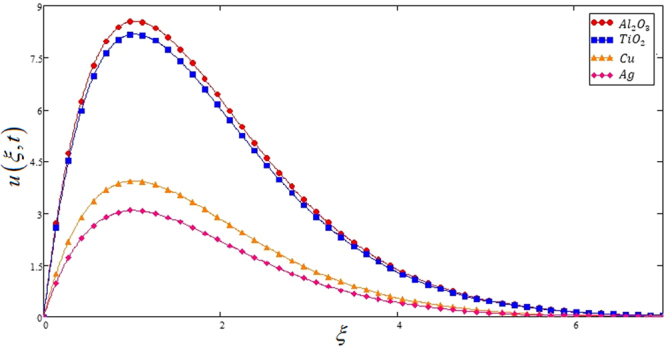
Comparison of velocities profiles for different types of nano particles for Casson nanofluids when Pr = 0.71, Gr = 10, Nr = 2, φ = 0.04 and t = 1.

Figure 10 highlights the comparison of both (Cu Sodium alginate -based Casson nanofluid and Ag-Sodium alginate -based nanofluid) on u(ξ, t). Velocity of Ag-Sodium alginate -based nanofluid is lower than copper Sodium alginate -based nanofluid. This shows that Cu nano particles have more thermal diffusivity compare to Ag which is physically true. Furthermore, the same comparison is study for Al₂O₃ and TiO₂ models in Fig. 11, which shows that Aluminum oxide Al₂O₃ nano particles have high thermal diffusivity as compare to Titanium oxide TiO₂.

Figure 10.

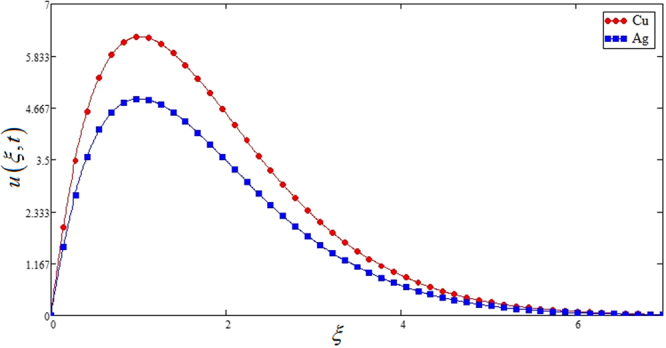
Comparison of velocities profiles of Cu and Ag Casson nanofluids when Pr = 0.71, Gr = 10, Nr = 2, φ = 0.04 and t = 1.

Conclusion

The following remarks are concluded from this work:

• u(ξ, t) decreases as γ increases

• Temperature and velocity profile are decreasing with increasing nano particles volume

  Fraction ϕ.

• Al₂O₃ nanofluid has higher velocity from TiO₂ nanofluid and Cu nanofluid has higher velocity from Ag nanofluid.

• The pours medium K and MHD Μ show opposite behavior.

Author Contributions

A.K. and I.K. designed the study; D.K. and F.K. conducted the experiments with technical assistance from F.A. and M.I.D.K. analyzed the data and wrote the paper; A.K., I.K. and M.I. provided general assistance. All authors have read and approved the final submission.

Competing Interests

The authors declare no competing interests.