Lexical Predictability during Natural Reading: Effects of Surprisal and Entropy Reduction

Abstract

What are the effects of word-by-word predictability on sentence processing times during the natural reading of a text? Although information-complexity metrics such as surprisal and entropy reduction have been useful in addressing this question, these metrics tend to be estimated using computational language models, which require some degree of commitment to a particular theory of language processing. Taking a different approach, the current study implemented a large-scale cumulative cloze task to collect word-by-word predictability data for 40 passages and compute surprisal and entropy reduction values in a theory-neutral manner. A separate group of participants read the same texts while their eye movements were recorded. Results showed that increases in surprisal and entropy reduction were both associated with increases in reading times. Further, these effects did not depend on the global difficulty of the text. The findings suggest that surprisal and entropy reduction independently contribute to variation in reading times, as these metrics seem to capture different aspects of lexical predictability.

1. Introduction

The predictability of a word in context is known to be one of the most important factors affecting the targeting of saccades and duration of fixations during reading (for reviews, see Clifton et al., 2016; Rayner, 1998; Staub, 2015). Although this basic finding is virtually undisputed, there is considerably less agreement regarding how best to conceptualize lexical predictability in a way that is ecologically valid and nuanced, as compared to the stark contrasts that tend to be employed in experimental investigations. The earliest work on this topic demonstrated effects of lexical predictability using experimental manipulations as in (1) that capitalize on systematic differences in cloze probability (Taylor, 1953), or the proportion of participants who provide a particular target word as a completion of an initial sentence stem. Many eyetracking experiments have demonstrated robust effects of predictability in contexts like these, such that predictable words (e.g., cake in 1a) are skipped more often and elicit shorter fixation durations when they are fixated compared to less predictable words (e.g., pies in 1b) (e.g., Balota, Pollatsek, & Rayner, 1985; Choi, Lowder, Ferreira, Swaab, & Henderson, 2017; Drieghe, Rayner, & Pollatsek, 2005; Ehrlich & Rayner, 1981; Rayner & Well, 1996).

• (1a)Since the wedding was today, the baker rushed the wedding cake to the reception.
• (1b)Since the wedding was today, the baker rushed the wedding pies to the reception.

Experimental results using comparisons like these have been extremely useful in developing models of eye-movement control during reading (e.g., Engbert, Nuthmann, Richter, & Kliegl, 2005; Reichle, Rayner, & Pollatsek, 2003). Beyond the eyetracking domain, cloze probability has been shown to reliably modulate the brain’s response to lexical predictability, as evidenced by reduced amplitude of the N400 event-related potential (ERP) component for predictable versus unpredictable words (e.g., Federmeier & Kutas, 1999; Kutas & Hillyard, 1984). In addition, one of the reasons this approach is so popular stems from its face validity—that is, the cloze task is intuitively appealing as a method for quantifying predictability because the cloze probabilities for each target word are derived from samples of participants whose explicit task is to guess the next word of the sentence.

At a theoretical level, questions about lexical predictability factor into a broader trend in cognitive science that casts prediction as a core explanatory principle of information processing (Clark, 2013). Under such a predictive processing framework, the brain uses relevant contextual knowledge to preactivate features of an upcoming stimulus or event before it is perceived, which leads to processing facilitation when the perception matches the prediction, or error-driven learning when the two do not match. Indeed, this view has become quite popular in the sentence-processing literature, with a growing body of evidence now suggesting that language comprehenders can rapidly generate predictions about upcoming input—from lower levels of sublexical and lexical representations up to higher levels of representation associated with event structures and schematic knowledge (see Kuperberg & Jaeger, 2016, for a recent review).

Although results from cloze experiments are sometimes taken as evidence supporting the predictive nature of human sentence processing, it is important to note the drawbacks of this task as it is typically used that limit its generalizability. A cloze task normally includes a single target word per sentence in which the researcher’s goal is to obtain a high cloze and low cloze completion for each item. As a result, these sentences tend to be highly constraining by design, to maximize the chances that a highly predictable completion will be produced (Ferreira & Lowder, 2016). This strategy is designed to ensure that a predictability effect will be observed between the high cloze and low cloze conditions in the main experiment. As a result, artificially constraining sentences that have been constructed to create strong predictions cannot be viewed as compelling evidence for the existence of an inherently predictive language processing system.

Moving away from the traditional cloze task, Luke and Christianson (2016) recently reported a large-scale study in which cloze values were obtained for every word across several multi-sentence texts. Values from this cumulative cloze task were then used to model eyetracking data to better understand the relationships between lexical prediction and online processing. Their results showed a facilitative effect of cloze probability on processing times—a relationship that emerged across the full range of cloze values and affected early and later eye-movement measures. Further, Luke and Christianson conducted a careful analysis of instances of misprediction (i.e., instances in which a word other than the target word was strongly predicted). Their results showed no evidence of a processing cost for these cases of misprediction, but rather some evidence that processing was facilitated when a given target word has a more expected competitor. These results suggest that prediction during reading occurs in a graded fashion, rather than the strict all-or-none process that often characterizes lexical prediction.

In addition to the cloze approach, we have recently seen the development of computational models of sentence processing that aim to quantify predictability for every word of a sentence probabilistically. This approach combines foundational work from information theory (Shannon, 1948) with more recent advances in computational language modeling to generate estimates of information complexity at each word of the sentence that can then be related to online sentence processing measures (Hale, 2001; Levy, 2008). The most common of these metrics is surprisal, defined as the negative log probability of a word, given its preceding context: surprisal(w_i) = −log P(w_i|w₁…w_i−1). As such, surprisal measures the relative unexpectedness of a word in context. In addition, sophisticated computational language models make it simple to estimate surprisal values for any input sentence, thus making it possible to investigate word-by-word predictability for sentences that are not artificially constraining. Using this approach, many studies have now demonstrated a relationship between surprisal and online sentence processing measures. For example, higher surprisal values have been shown to be associated with longer reading times (Boston, Hale, Kliegl, Patil, & Vasishth, 2008; Demberg & Keller, 2008; Smith & Levy, 2013), larger N400 amplitudes in ERP research (Frank, Otten, Galli, & Vigliocco, 2015), and increased activation in several language-related brain areas as measured by functional MRI (Brennan, Stabler, Van Wagenen, Luh, & Hale, 2016; Henderson, Choi, Lowder, & Ferreira, 2016; Willems, Frank, Nijhof, Hagoort, & van den Bosch, 2016).

A different information complexity metric that has received less attention in the sentence-processing literature is entropy, a measure designed to quantify the degree of uncertainty about what is being communicated as a sentence unfolds¹. The entropy H of the probability distribution over X is represented as a function of the probabilities of the various possible outcomes:

$$H(X)=-\sum _{x\in X}P(x){\text{log}}_{2}P(x)$$

Thus, higher entropy is associated with more uncertainty about the value of x, such that entropy is maximal when all possible values of x have the same probability, and entropy is zero when there is 100% certainty about the value of x.

Importantly though, entropy fluctuates as we encounter each new word, with incoming words affecting expectations regarding what will come next. This observation led Hale (2003, 2006, 2011) to propose entropy reduction as a key complexity metric to represent the amount of information gained at each word. So, if entropy at word w_i is represented as H_i, then entropy reduction at w_i is computed as H_i − H_i−1. The fundamental idea is that if entropy is reduced from one word to the next, then communicative uncertainty has been reduced, and the comprehender has done information-processing work. In contrast, cases in which entropy increases from one word to the next are represented as zero, under the assumption that an increase in uncertainty should not affect processing. The important claim is that surprisal and entropy reduction capture unique aspects of information complexity and, as such, should both serve as useful metrics for quantifying word-by-word predictability during incremental sentence processing (Hale, 2016).

Although some have expressed skepticism regarding the usefulness of entropy reduction as a complexity metric (Levy, Fedorenko, & Gibson, 2013; Levy & Gibson, 2013), there is growing evidence suggesting that entropy reduction is in fact a significant predictor of sentence processing times. Indeed, several studies have now shown that greater surprisal and greater entropy reduction independently contribute to increased reading times (Frank, 2013; Linzen & Jaeger, 2016; Wu, Bachrach, Cardenas, & Schuler, 2010). Two methodological points about this previous work are worth noting though. First, all three of these studies used self-paced reading as their dependent measure. Although self-paced reading is a commonly used approach in psycholinguistic research, it does not accurately reflect the normal reading process, as it tends to be rather slow, prone to strategic processing, and prohibits the reader from gaining parafoveal preview information or regressing to previous portions of the text. Second, all three of these studies estimated their measures of surprisal and entropy reduction using some form of statistical language model, including a recurrent neural network model (Frank, 2013), an algorithmic parser operating within a probabilistic context-free grammar (Linzen & Jaeger, 2016), and a hierarchical hidden Markov model (Wu et al., 2010).

Indeed, most of the previous work aimed at relating metrics like surprisal and entropy reduction to human sentence processing data estimate these metrics using computational sentence parsers or some other type of statistical language model. As noted above, this approach has an advantage over the traditional cloze task in that values can be estimated for every word in the sentence, allowing researchers to study naturalistic sentences as opposed to sentences designed to be artificially constraining. However, this approach also has several limitations. First, there are a number of technical choices to make when selecting a computational language model, and these choices require some degree of commitment to a theory of language. For example, the researcher has to choose whether to estimate language statistics using a computational sentence parser or a connectionist model. If using a parser, there are additional choices to make regarding what sort of grammar the parser will assume, as well as what parsing algorithm will be implemented. These choices carry with them implicit assumptions about the nature of human language processing that researchers may not want to commit to. Second, any language model must first be trained on a corpus of language, and this raises additional questions regarding what constitutes an appropriate training corpus and how large that corpus must be before the model can perform adequately. It is not uncommon for language models to be trained on a corpus of only about one million words—far smaller than the vast amount of language experience adult humans have. Finally, computational language models tend to assume that the sentences they take as their input are independent from one another. This makes it problematic to derive accurate metrics for words appearing in connected texts, in which the sentences within the text refer to information from previous sentences.

The goal of the current study was to examine the contributions of surprisal and entropy reduction to word-by-word reading times. Our approach differs from previous treatments of this topic in two important ways. First, we used eyetracking as our measure of online sentence processing. In contrast to the slow, unnatural button-press responses required in self-paced reading, the use of eyetracking allows participants to read text naturally, which includes access to parafoveal preview information and the ability to regress to previous portions of the text that are denied in self-paced reading. In addition, eyetracking provides a much more dynamic measure of reading, including rich information about the time course of processing from early stages of word recognition to later stages of text integration. Second, we derived our measures of surprisal and entropy reduction from a cumulative cloze task rather than a computational language model. In the cumulative cloze task (see also Luke & Christianson, 2016), participants are given the first word of a paragraph and are instructed to guess what they think the most likely second word is. The second word is then revealed, and the task is to guess the third word, and so on. This approach has a number of advantages over both the traditional cloze task and the estimation of complexity metrics from computational language models. First, we can use human predictability data at each word of a text to compute surprisal and entropy reduction in a completely theory-neutral manner without having to assume a grammar, implement a parsing algorithm, or choose a training corpus. Second, this approach allows us to use naturalistic sentences as opposed to the artificially constraining sentences that tend to be used in experiments employing the traditional cloze task. This avoids the concern that participants might notice something unusual about the sentences and adapt to the task or develop explicit processing strategies. Finally, this approach allows us to collect accurate word-by-word predictability data for sentences appearing in connected, meaningful discourse as opposed to sentences in isolation.

In the current study, values of surprisal and entropy reduction for whole paragraphs of text were derived from a large sample of participants who completed the cumulative cloze task. These paragraphs were then read by another sample of participants whose eye movements were recorded. In selecting our materials, we chose paragraphs that represented a wide range of difficulty levels, from easy texts appropriate for children to difficult texts appropriate for college-educated adults. We selected paragraphs representing a wide range of text difficulties to test the hypothesis that variability in surprisal and entropy reduction might have different effects on reading times depending on the global difficulty level of the text. One possibility is that the relationship between word-by-word complexity metrics and reading times may become stronger as texts become more challenging, perhaps reflecting the lower frequency of the words and sentential contexts encountered. Another possibility is that the effects will become weaker, perhaps because more difficult text makes prediction harder, leading readers to give up on the prediction strategy. Finally, the relationship between surprisal and entropy reduction on reading times might be unaffected by text difficulty, suggesting that their effects are not specific to easy or hard texts, but instead hold across a wide range of difficulty levels.

2. Method

2.1 Cumulative cloze task

2.1.1 Participants

A total of 1,600 participants were recruited through Amazon’s Mechanical Turk. Individuals were eligible to participate if they reported that they were 18 years of age or older, indicated that English was their native language, and their IP address registered as being within the United States.

2.1.2 Materials

Forty short passages of text were adapted from standardized reading comprehension tests: the Gray Oral Reading Tests—Fifth Edition (GORT) (Wiederholt & Bryant, 2012) and the Gray Silent Reading Tests (GSRT) (Wiederholt & Blalock, 2000). The GORT and GSRT were chosen because they include passages of text that represent a wide range of difficulty levels. Texts were trimmed to be between 46 and 77 words long. As an objective measure of global text difficulty, we calculated the Flesch-Kincaid grade level of each paragraph (Kincaid, Fishburne, Rogers, & Chissom, 1975), which is computed from the average length of sentences and average number of syllables per word in the text. The score is meant to correspond roughly with the number of years of education required to understand the text. The 40 passages used in the current study had Flesch-Kincaid grade levels ranging from 1.80 to 17.46 (mean = 10.38). Across all texts, there were 1,152 unique words with 2,405 word tokens.

2.1.3 Procedure

After agreeing to participate, participants were redirected to an online survey. The instructions read: “In this task, you will be predicting the upcoming words of a paragraph. You will be given the first word of a paragraph, and your task is to predict what you think the next word most likely is. Type your prediction into the box, and then click the button to advance to the next screen. You will then see what the actual next word of the paragraph is, and you should again make a prediction about what you think the next word is most likely to be. You will do this for the entire paragraph.” After advancing past this initial instruction screen, participants saw the first word of a paragraph with a response box below it. At the top of this page, and on every subsequent page, was an abbreviated set of instructions, reminding participants to “Guess the most likely next word based on the words you have seen so far.” Participants typed their guess into the box and advanced to the next screen, at which point they saw the first two words of the paragraph with a response box below it. This continued for the entire paragraph such that participants entered predictions for all words of the paragraph except for the first word. Participants could not advance to the next page until entering a response in the box, nor could they go back to their previous responses.

Forty participants were randomly assigned to each of the 40 paragraphs, which resulted in there being an equal number of cloze responses for each word across all texts.

2.2 Eyetracking task

2.2.1 Participants

Thirty-two students at the University of California, Davis participated in exchange for course credit. They all reported normal or corrected-to-normal vision and indicated that English was their native language.

2.2.2 Materials

Target passages for the eyetracking task were the same 40 passages used in the cumulative cloze task, with all words clearly visible.

2.2.3 Procedure

Eye movements were recorded with an EyeLink 1000 Plus system (SR Research). Viewing was binocular, but only the right eye was tracked, at a sampling rate of 1,000 Hz. A chinrest was used to minimize head movement. The eyetracker was calibrated at the beginning of each session and recalibrated throughout the session as needed. At the start of each trial, a fixation point was presented near the upper left corner of the screen, marking the place where the first word of the paragraph would appear. Once gaze was steady on this point, the experimenter presented the paragraph. After reading the paragraph, the participant pressed a button on a handheld console, which caused the paragraph to disappear and a true-false comprehension question to appear in its place. Participants pressed one button to answer “true,” and a different button to answer “false.” Mean comprehension-question accuracy was 92%. After the participant answered the question, the fixation point for the next trial appeared.

Participants were first presented with two filler paragraphs that were not analyzed. After this warm-up block, the 40 target passages were presented randomly.

2.3 Analysis

Predictions in the cumulative cloze task were compared to the actual target words to compute a cloze probability score for every word. We then computed the negative log of each cloze probability to convert these scores to surprisal values. Cloze probabilities of zero cannot be converted to a logarithmic scale. Accordingly, we made an a priori decision to replace these values with half the value of the lowest nonzero cloze value before converting them to surprisal values (i.e., the lowest nonzero cloze value possible in this study was .025, and so cloze values of zero were converted to .0125). To compute entropy reduction, we first tabulated the distribution of guesses at each word about the upcoming word and then used these values to compute entropy according to the standard formula (see above). Entropy reduction was computed as the difference in entropy between the current word and the previous word. Cases where entropy increased from w_i−1 to w_i were coded as zero, in keeping with a central proposal of the entropy reduction hypothesis that increases in uncertainty do not affect processing (Hale, 2006).

For the eyetracking data, fixations were excluded from the analysis if they were shorter than 60 ms, longer than 1,200 ms, if they occurred during a track loss, or if they were immediately preceded or followed by a blink. In total, 12.4% of all fixations were excluded from the analysis. In addition, we removed the first and last words of each paragraph from the analysis, as well as proper nouns. For all remaining words, we computed four standard eye-movement measures that reflect a range of processing stages (Rayner, 1998). First-fixation duration is the duration of the initial, first-pass fixation on a word, regardless of whether there are subsequent first-pass fixations on the word. Single-fixation duration is the duration of the initial, first-pass fixation on a word, provided that the word received only one first-pass fixation. These two measures are thought to reflect the earliest stages of word recognition, including processes of perceptual encoding and initial lexical access. Gaze duration is the sum of all first-pass fixations on the word and is believed to index later stages of lexical access and the beginning stages of semantic integration. Regression-path duration is the sum of all fixations beginning with the initial fixation on a word and ending when gaze is directed away from the region to the right. Thus, regression-path duration includes time spent rereading earlier parts of the sentence before the reader is ready to move to the right of the current word. Regression-path duration is generally thought to reflect processes related to higher-level text integration difficulty.

The data were analyzed using linear mixed-effects regression models in the lme4 package (Bates, Maechler, & Bolker, 2012) in R. Separate models were constructed for each reading-time measure. Each of these models included fixed effects of log-transformed word frequency (SUBTLEXus database; Brysbaert & New, 2009), word length, the Flesch-Kincaid grade level of the paragraph in which the word appeared (i.e., text difficulty), surprisal, entropy reduction, and the interactions between surprisal and text difficulty as well as entropy reduction and text difficulty. All predictors were mean-centered. The random-effects structures included random intercepts for subject, word, and paragraph, as well as by-subject random slopes for all fixed effects. Random slopes for the interaction terms were removed from the models because the models would not converge otherwise. Statistical significance was computed using the lmerTest package (Kuznetsova, Brockhoff, & Christensen, 2013) in R.

3. Results

We observed a moderate, positive correlation between surprisal and entropy reduction (r = .29, p < .001). This relationship is depicted in Fig. 1. Results of the reading-time analyses are presented in Table 1. Consistent with previous findings, we observed robust effects of word frequency and word length on all reading-time measures, such that increases in word frequency were associated with decreased reading times, whereas increases in word length were associated with increased reading times. Beyond the word-level effects of frequency and length, we also observed a significant main effect of text difficulty in all reading-time measures, such that increases in text difficulty were associated with increased reading times.

Fig. 1.

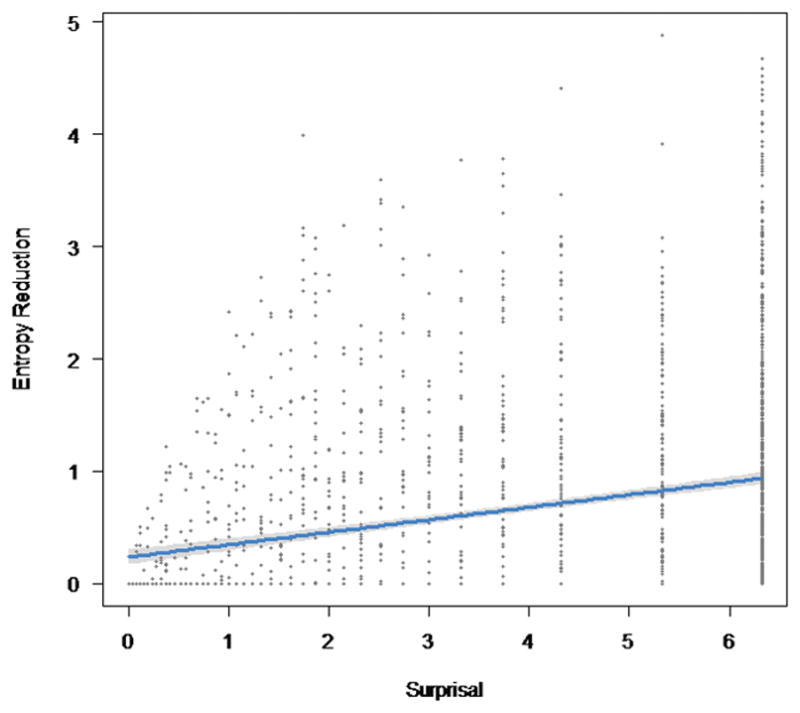
Relationship between surprisal and entropy reduction.

Table 1.

Results of mixed effects analyses

Parameters	FFD			SFD			GZD			RPD
	b	SE	t	b	SE	t	b	SE	t	b	SE	t
(Intercept)	218.34	1.07	204.79	221.43	1.22	181.68	255.93	1.83	139.58	346.05	5.00	69.22
Frequency	−6.08	1.73	−3.51	−5.82	1.95	−2.98	−15.47	3.77	−4.10	−22.19	5.70	−3.89
Length	4.52	1.38	3.27	7.46	1.65	4.52	32.39	2.15	15.09	44.49	5.38	8.27
Text Difficulty	2.70	0.96	2.82	3.15	0.99	3.17	4.06	1.64	2.47	10.12	4.78	2.12
Surprisal	5.01	0.82	6.08	5.36	0.93	5.78	8.18	1.29	6.36	11.72	2.92	4.01
Entropy Reduction	1.91	0.73	2.60	2.23	0.78	2.84	1.03	1.27	0.81	−0.06	2.77	−0.02
Surprisal x Text Difficulty	−1.03	0.59	−1.75	−0.66	0.63	−1.04	0.87	0.93	0.93	2.86	2.22	1.29
Entropy Reduction x Text Difficulty	−0.24	0.66	−0.36	−0.64	0.71	−0.90	−2.03	1.09	−1.87	1.35	2.47	0.55

Note. FFD = first fixation duration; SFD = single fixation duration; GZD = gaze duration; RPD = regression-path duration; statistically significant effects are indicated in boldface

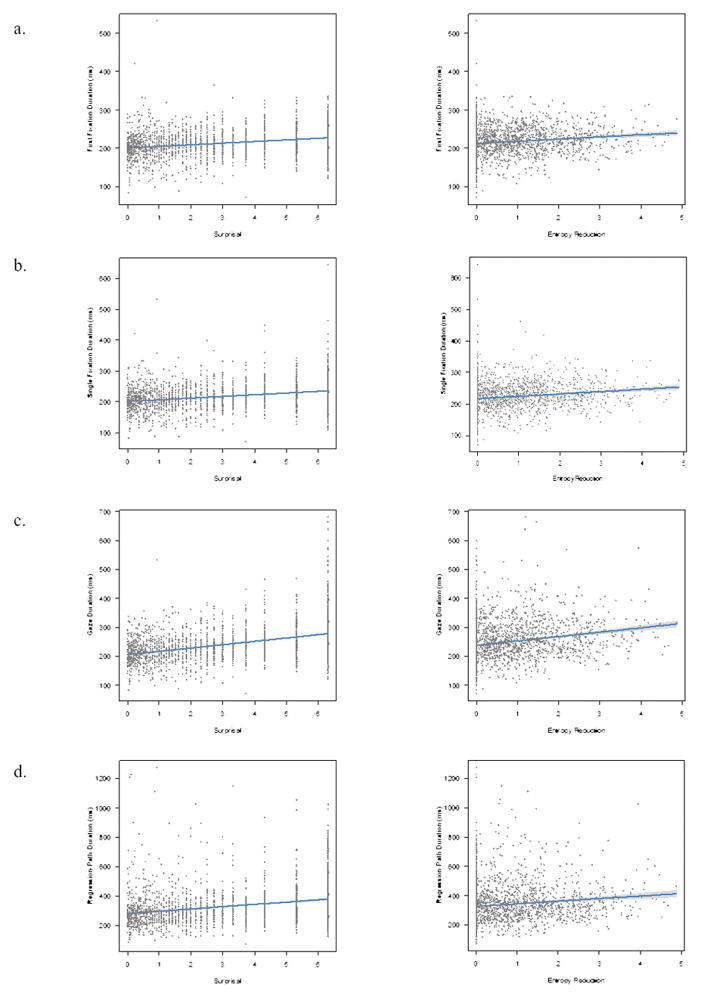
Crucially, we also observed significant effects of surprisal and entropy reduction². The effect of surprisal was significant across the eye-movement record, such that increases in surprisal were associated with increased reading times in all reading-time measures. In contrast, the effect of entropy reduction was only significant in the early measures of first fixation duration and single fixation duration, such that increases in entropy reduction were associated with increased reading times. The effect of entropy reduction was not significant in the later measures of gaze duration and regression-path duration. Fig. 2 plots the relationships between surprisal and entropy reduction and each of the four reading-time measures. Finally, there were no significant interactions between surprisal and text difficulty, nor entropy reduction and text difficulty in any reading-time measure. This lack of an interaction between complexity metrics and text difficulty held despite finding a significant positive relationship between average surprisal value and text difficulty (r = .72, p < .001), as well as a similar trend for a positive relationship between average entropy reduction and text difficulty, although this latter effect was not significant (r = .26, p = .11).

Fig. 2.

Relationships between surprisal (left) and entropy reduction (right) on first fixation duration (a), single fixation duration (b), gaze duration (c), and regression-path duration (d).

As mentioned above, we made an a priori decision to replace cloze values of zero with half the value of the lowest nonzero cloze value before converting them to surprisal values (i.e., cloze = .0125). To ensure that our core findings did not depend on this decision, we conducted three sets of supplemental analyses in which all models were rerun treating values of zero cloze differently in each model. Specifically, Supplemental Model 1 treated zero cloze as being equal to the lowest nonzero cloze value (i.e., cloze = .025). Supplemental Model 2 used values that were two times lower than the values used in our original model (i.e., cloze = .00625), and Supplemental Model 3 used values that were four times lower than the values used in our original model (i.e., cloze = .003125). For all models, the effects of surprisal and entropy reduction on reading times were the same as the results reported here—that is, effects of surprisal emerged in all eyetracking measures, whereas effects of entropy reduction emerged in first fixation duration and single fixation duration. Some of the models also produced evidence of interactive effects between complexity metrics and text difficulty. In Supplemental Models 2 and 3, there was an interaction between entropy reduction and text difficulty for gaze duration. In Supplemental Model 3, there was an interaction between surprisal and text difficulty for first fixation duration. These effects were all fairly weak, but the pattern for all interactions was such that there tended to be stronger effects of the complexity metric for easier rather than more difficult texts. The results of these models are available as supplementary material.

To assess collinearity in our models, we computed variance inflation factors (VIFs) for each predictor in each model³. All VIFs were less than 2, which is well below the recommended limit of 10 (Cohen, Cohen, West, & Aiken, 2003). To further probe the relative contributions of surprisal and entropy reduction, we conducted exploratory analyses in which our primary models from Table 1 were rerun, once with entropy reduction removed, and again with surprisal removed. The results of these analyses are presented as supplementary materials. The patterns of effects presented in Table 1 were unchanged by these modifications. That is, the effect of surprisal was significant across the eye-movement record even when entropy reduction was left out of the model, and the effect of entropy reduction was significant in first fixation duration and single fixation duration when surprisal was left out of the model.

4. Discussion

The current work replicates previous findings demonstrating that surprisal and entropy reduction both contribute to variation in reading times (Frank, 2013; Linzen & Jaeger, 2016; Wu et al., 2010). Importantly, however, our approach extends these findings in several important ways. First, our use of eyetracking as a measure of sentence processing allowed us to examine the time course of these effects during natural reading while avoiding the unnatural button-press responses associated with self-paced reading. Our results indicate that whereas increases in surprisal are associated with increases in reading times across the eyetracking record, increases in entropy reduction were only associated with increases in first fixation duration and single fixation duration. This pattern seems to suggest that readers experience a longer-lasting processing slowdown when a word in the text is unexpected, compared to when a word reduces uncertainty. Although the effect of entropy reduction was not significant in measures reflecting later stages of processing, the overall pattern nevertheless seems consistent with the pattern observed in earlier measures (see Fig. 2). The fact that the effect of entropy reduction was not statistically significant in these later measures of processing suggests that variability in gaze duration and regression-path duration are better accounted for by other factors. Taken together, the dissociation of surprisal and entropy reduction on early versus later measures of processing has implications for models of eye-movement control during reading (e.g., Engbert et al., 2005; Reichle et al., 2003), which aim to explain the time course over which different linguistic properties of words influence the decision of when to move the eyes. Although complexity metrics like surprisal and entropy reduction have not yet been incorporated into these models, the dissociation in time course of processing reported here suggests that this may be a useful implementation.

In addition to testing for main effects of surprisal and entropy reduction, we also examined whether these measures would show different effects in easy versus more challenging paragraphs. Although we observed main effects of text difficulty in all reading-time measures, there was no indication that this factor interacted with surprisal or entropy reduction, suggesting that surprisal and entropy reduction effects are not limited to either the easiest or most difficult texts, but instead that these effects generalize across a range of paragraph difficulty levels⁴. The lack of a significant interaction suggests that our participants employed similar processes of linguistic prediction across texts that were very easy, as well as texts that were much more challenging. Thus, even though the more challenging texts contained infrequent words and longer, more complex sentences, readers nonetheless showed similar responses to words that were relatively higher in surprisal or entropy reduction, regardless of the broader linguistic context. An interesting question for future research might involve examining how individual differences among readers in various measures of linguistic or cognitive performance could modulate the relationships among global text difficulty and word-by-word complexity metrics on reading times.

Whereas previous work has tended to estimate information complexity metrics from computational sentence parsers and other types of statistical language models, we estimated surprisal and entropy reduction using human predictability data in a cumulative cloze task. This approach has a number of advantages in that it allows us to compute complexity metrics in a completely theory-neutral manner, it allows us to use naturalistic sentences as opposed to the artificially constraining sentences that are common in studies using the traditional cloze method, and it allows us to study sentences in connected texts, as opposed to sentences in isolation. Recent work by Luke and Christianson (2016) has also used the cumulative cloze task to assess the relationship between lexical predictability and eye-movement measures. Our finding that surprisal had robust effects across the range of eye-movement measures replicates their findings. Although Luke and Christianson also reported several additional results, including cases of misprediction, they did not conduct analyses of entropy reduction. Our finding that surprisal and entropy reduction independently contribute to eye-movement measures during reading serves as a further extension of the cumulative cloze task to address important questions about the nature of prediction during language processing.

One potential downside of using the cumulative cloze procedure to estimate complexity metrics is that it limits the scope over which entropy reduction can be calculated. Hale’s (2003, 2006, 2011) proposal and its implementation in computational models conceptualizes entropy as the comprehender’s degree of uncertainty regarding all possible upcoming sentence structures, derived over multiple parse trees. In contrast, the nature of the cumulative cloze task used here necessitates that entropy reduction be calculated over next-word entropy as opposed to full entropy, given that participants only predicted the single next word of the sentence. This implementation of entropy reduction may explain why the effect of this metric on reading times was rather small, compared to the larger effects that were observed for surprisal (see Table 1). Nevertheless, we believe our measure of entropy reduction in the current study acts as a useful approximation of the sort of entropy reduction measure proposed by Hale. That is, even though we do not have access to participants’ predictions about the entire upcoming sentence, their guesses about the next word still reflect important information about how they think the sentence is unfolding. Specifically, as the current sentence representation becomes clearer, the range of potential options for the next word should narrow, leading to reduction in entropy.

It is also important to note that the current findings cannot distinguish confidently between theoretical accounts based on preactivation of a specific word before the reader encounters it, as opposed to accounts that instead attribute “prediction” effects to facilitated integration of a word with its preceding context. However, a strong version of either of these frameworks seems implausible in light of these findings. The notion that readers engage in robust, all-or-none prediction of a single word seems unlikely, given that subtle variations in surprisal had significant effects on reading times, even for words at the high end of the spectrum (i.e., words with the lowest cloze values that were rarely predicted). Likewise, a strict integration account seems unlikely, given that effects of surprisal and entropy reduction emerged in first fixation duration and single fixation duration—measures that are thought to reflect the earliest stages of perceptual encoding and lexical access. Thus, the results are most readily consistent with the view recently put forth by Staub (2015) arguing that predictability effects in reading emerge from diffuse preactivation of sets of likely words in a pattern of graded activation (see also Ferreira & Lowder, 2016; Frisson, Harvey, & Staub, 2017; Huettig & Mani, 2016; Kuperberg & Jaeger, 2016; Luke & Christianson, 2016). Such a view may place serious constraints on the extent to which prediction can be viewed as the “engine” that drives cognition (Clark, 2013).

Importantly, the current study serves to link information complexity metrics to mechanistic accounts of cognition in a more naturalistic way. Metrics such as surprisal and entropy reduction are useful in that they can be generated word-by-word according to the specifications of a language model, which can then be related to behavioral or neural processing data to assess the viability of that model (Armeni, Willems, & Frank, 2017; Brennan, 2016; Hale, 2016). As noted above though, these metrics tend to be estimated using computational parsers or other statistical language models. Computational language models are associated with several drawbacks, one of the most serious being that they tend to assume that the sentences they take as their input are independent from one another. This limits the extent to which algorithmically derived information complexity metrics can be applied to connected, naturalistic language. In contrast, a major benefit of the cumulative cloze task used here is that it allows us to derive surprisal and entropy reduction for each word across multi-sentence, connected texts using human judgments. Thus, the combination of human predictability data across more naturalistic texts advances the goal of bridging information theory and online measures of language processing.

In sum, these results demonstrate that effects of lexical predictability on reading times are not limited to strongly predictable versus unpredictable words that tend to appear in experiments using the traditional cloze task. Instead, the cumulative cloze task used here, combined with analyses of data from normal reading in which every word is a potential data point, provides a much more accurate assessment of predictability effects in sentence processing, extending beyond the domain of artificially constraining stimuli. Further, the results demonstrate independent contributions of surprisal and entropy reduction to explaining variability in reading times, providing additional evidence that these information complexity metrics capture unique aspects of lexical predictability.