Understanding the Functional Roles of Multiple Extracellular Domains in Cell Adhesion Molecules with a Coarse-Grained Model

Abstract

Intercellular contacts in multicellular organisms are maintained by membrane receptors called cell adhesion molecules (CAMs) which are expressed on cell surfaces. One interesting feature of CAMs is that almost all of their extracellular regions contain repeating copies of structural domains. It is not clear why so many extracellular domains need to be evolved through natural selection. We tackled this problem by computational modeling. A generic model of CAMs was constructed based on domain organization of neuronal cell adhesion molecule (NrCAM), which is engaged in maintaining neuron-neuron adhesion in central nervous system. By placing these models on a cell-cell interface, we developed a Monte-Carlo simulation algorithm which incorporates both molecular factors including conformational changes of CAMs and cellular factor including fluctuations of plasma membranes to approach the physical process of CAM-mediated adhesion. We found that the presence of multiple domains at the extracellular region of a CAM plays a positive role in regulating its trans-interaction with other CAMs from opposite side of cell surfaces. The trans-interaction can further be facilitated by the intramolecular contacts between different extracellular domains of a CAM. Finally, if more than one CAM is introduced on each side of cell surfaces, the lateral binding (cis-interactions) between these CAMs will positively correlate with their trans-interactions only within a small energetic range, suggesting that cell adhesion is an elaborately designed process in which both trans and cis interactions are fine-tuned collectively by natural selection. In short, this study deepens our general understanding of the molecular mechanisms of cell adhesion.

Graphical Abstract

1. Introduction

Cells form dynamic contacts with each other, so that they can process complicated information from external stimuli or make mechanical responses to surrounding environments in a collective and synergetic way^1–4. These intercellular contacts are maintained by molecular interactions between membrane-receptors expressed on cell surface. These receptors, called cell adhesion molecules (CAMs), usually contain a long extracellular region which facilitates intercellular binding, a single-pass transmembrane domain, and a short cytoplasmic tail involved in downstream cell signaling⁵. They play versatile roles in many biological processes, such as tissue morphogenesis during embryonic development^{6, 7}, invasion of tumor cells during cancer metastasis^{8, 9}, and regulation of synaptic contacts in neural circuits^{2, 10, 11}. CAMs are constituted of multiple protein families, including cadherin¹², selectin¹³, membrane receptors from the immunoglobulin (Ig) superfamily, etc^{14, 15}. A common feature of these CAMs is that their extracellular regions normally contain multiple copies of different domains^16–18. For instance, there are five ectodomains in the type-I classic cadherin¹⁹, while there are 10 Ig-like domains and 6 Fibronectin domains in the extracellular region of the Down syndrome cell adhesion molecule (DSCAM)¹⁰. However, among all these domains, only a few are directly involved in the trans-dimerization of CAMs from opposite sides of cellular interfaces²⁰. It is not clear why so many extracellular domains need to be evolved through natural selection. It has been observed that some CAMs can form intra-molecular interactions between their extracellular domains²¹, while the intermolecular interactions between domains of different CAMs from the same cell surface are proposed to trigger molecular clustering during adhesion²². Overall, the molecular mechanism of CAM’s multiple extracellular domains in cell adhesion is still far from being well-understood.

The specific cellular function of each individual CAM domain in the membrane environment is difficult to verify. Isothermal Titration Calorimetry (ITC)²³ and surface plasma resonance (SPR)²⁴ are the traditional methods used to measure the dynamic binding properties between CAMs. However, in order to determine which part of a CAM is responsible for binding, only partial segments of the molecule’s extracellular region are generally used for the experiments, instead of its entire ectodomains²⁵. Moreover, these methods isolate the interacting components from their usual biological surrounding in order to permit a more convenient analysis which cannot be done within the organism. Therefore, the behavior of CAMs which are tethered on cell surfaces cannot be properly evaluated. On the other hand, in vitro cell-based experiments such as cell aggregation assays are able to estimate the adhesive properties of a CAM’s entire extracellular region in its membrane environment²⁶. However, due to limitations of these cell-based experiments, it is difficult to provide further quantitative details about the binding between CAMs at single molecule level. Computational modeling possesses unique advantages that permit one to test conditions that may currently be difficult to attain experimentally and add a valuable dimension to understand the functions of CAMs. Databases have been built to facilitate bioinformatics studies of CAMs in specific protein families or in certain organisms²⁷. Additionally, molecule-based simulation techniques such as all-atom molecular dynamic simulations have been used to study the dynamic properties of specific adhesive receptors^28–35. These studies depended on structural information of individual proteins. It is currently difficult to reach the timescale in which two CAMs dimerize at cellular interfaces. In contrast to the molecule-based methods, there is a variety of computational modeling approaches, such as partial differentiation equations (PDE) and lattice-based simulations, aiming to describe how collective behaviors of CAMs lead to spatial patterning at cellular interfaces^36–45. Due to the low resolution of these models, molecular details of CAMs are rarely included. Computational models which incorporate both cellular environments and structural details of CAMs are therefore highly needed.

In this article, we introduce a mesoscale simulation method to study the functions of multiple extracellular CAM domains during the process of adhesion. A generic model of CAMs was constructed based on the domain organization of neuronal cell adhesion molecule (NrCAM), which is engaged in maintaining neuron-neuron adhesion in central nervous system⁴⁶. The structure of each extracellular domain in the CAM model was derived by homology modeling. Two consecutive structural domains are connected by a flexible linker. The entire modeled CAM was anchored on a two-dimensional (2D) surface. By placing multiple CAMs on two surfaces which face each other, this coarse-grained model allowed us to imitate the physical process of binding between CAMs at cellular interfaces using a Monte-Carlo algorithm. In the Monte-Carlo simulation, the position of the molecule was randomly changed by translational movements on the 2D surface. The orientation of the molecule was randomly changed by rotation along the axis perpendicular to the cell surface. The conformational variations of each molecule could be further implemented by changing the bond angle and dihedral of residues at flexible linkers. Using this simulation method, the roles of specific extracellular domains in the binding process can be tested by designing different binding scenarios in simulations. We found that the presence of multiple domains in the extracellular region of a CAM plays a positive role in regulating its trans-interaction with other CAMs from opposite side of cell surfaces. The trans-interaction can further be facilitated by the intramolecular contacts between different extracellular domains of a CAM. Finally, we show that if more than one CAM was introduced on each side of cell surfaces, the lateral binding (cis-interactions) between these CAMs interfered with their trans-interactions. In summary, this study deepens our general understanding of the molecular mechanisms of cell adhesion. The coarse-grained model and simulation methods presented in this work can be applied to other specific molecular systems.

2. Model and Methods

2.1. Construction of the structural model of full-length extracellular region of CAM

In order to appreciate the necessity of multiple domains in CAMs and understand their functions during cell adhesion, full-length extracellular region for any CAM model needs to be considered. Instead of focusing on one specific CAM system, here we chose to build a generic model to enable a broader investigation of CAMs across different families. This generic CAM model follows the domain organization of NrCAM as a template. We used the sequence of NrCAM from Homo sapiens (UniProt ID: Q92823) to construct the three-dimensional structure of the CAM model. Specifically, the extracellular region of our constructed model contains 1,111 residues. It is divided into six consecutive Ig domains¹⁵ from the N-terminal side, followed by five fibronectin (FN) domains⁴⁷ at the C-terminal side (Fig 1a). The reasons for choosing NrCAM as a test system were: 1) both Ig domain and fibronectin domain are among the largest domain families and most frequently observed in CAMs, and 2) eleven extracellular domains corresponds to a moderate size for CAMs. Therefore, this selected molecule is a good representative for all CAMs, and its size is well-suited for modeling and simulations.

Figure 1.

Our test model of a generic cell adhesion molecule contains six Ig domains at the N-terminal side, followed by five FN domains at the C-terminal side (a). The structure of this CAM model was constructed (b) using coordinates of each extracellular domain derived from homology modeling with domains connected by a flexible linker. The conformation of a linker is defined by the bond angles and dihedrals among consecutive Cα atoms (c). A coarse-grained Monte-Carlo algorithm was further developed to simulate the interactions between CAMs at the cellular interfaces, in which two CAM molecules are initially placed face to face at random positions at the interface (d).

Only two NMR structures of a single extracellular domain are currently available for this protein⁴⁸. Therefore, in order to build the structural model for the entire extracellular region, we first carried out structural modeling for all eleven extracellular domains. SPARKS-X was used to generate the structural coordinates of each domain individually. SPARKS-X is a web server of protein tertiary structural prediction which uses template-based modeling methods⁴⁹. Given a query protein sequence with unknown structure, the method predicts the structure of the query by matching the one-dimensional structural profiles predicted from the query sequence with the actual structural properties in a template library of native proteins. The structural profiles include secondary structure, backbone torsion angles and solvent accessible surface areas. The benchmark test results indicate that SPARKS-X is one of the best single-method fold recognition servers. We uploaded the sequence of each domain to the server separately to build the three-dimensional atomic model. The detailed information for all domains is listed in Table 1. Consequently, the predicted structural models were downloaded from the server. The atomic coordinates of all eleven domains can be found in the Supplemental Material. The atomic coordinates of each domain were then coarse-grained by a Cα representation. Given the Cα coordinates of all eleven extracellular domains, they were assembled by modeling the linker regions which connect every two consecutive domains. The C_α-based backbone of a domain linker consists of N-1 virtual bonds, in which N is the number of amino acids in the corresponding linker region. Each virtual bond is connected by two consecutive C_α atoms. Given the fixed distance of each virtual bond (3.8 Ångström), the conformation of a linker that contains N C_α atoms is thus defined by 2N variables. Each C_α atom corresponds to two parameters: a bond angle θ_i describing the packing of two consecutive virtual bonds and a dihedral angle φ_i describing the torsional rotations of each virtual bond (Fig 1c)⁵⁰. The CAM model was started from an initial extended conformation for all its domain linker regions, in which all bond angles in the linkers equal 120° and all dihedrals equal 180°. The coarse-grained model (C_α coordinates) of the full-length extracellular region of the CAM model with extended linkers can be found in the Supplemental Material. In the following simulation section (2.2), the variables of bond angles and dihedrals at linker regions were randomly changed to model the flexibility of the CAM model, as described later. One conformation of the complete structural model with all eleven extracellular domains connected by extended linkers is shown in Fig 1b.

Table 1.

The detailed information for all domains of our tested CAM model.

Domain number	Index of beginning residue	Index of end residue	Number of residues	Domain ID
1	46	134	89	Ig-like domain 1
2	141	235	95	Ig-like domain 2
3	267	356	90	Ig-like domain 3
4	361	448	88	Ig-like domain 4
5	454	541	88	Ig-like domain 5
6	545	632	88	Ig-like domain 6
7	649	744	96	Fibronectin domain 1
8	746	843	98	Fibronectin domain 2
9	848	950	103	Fibronectin domain 3
10	954	1051	98	Fibronectin domain 4
11	1064	1156	93	Fibronectin domain 5

It is worth mentioning that we are not aiming to predict the accurate structure of NrCAM in this study. It was only used as a template of a generic model of CAMs. Therefore, it is not consequential if the conformations at domain linker regions were not accurately modeled. By introducing a Monte-Carlo simulation algorithm, we assume that large conformational fluctuations exist at each domain linker region, which leads to the high flexibility of CAM molecules on cell surfaces. Moreover, different scenario can be designed based on this generic CAM model to test the functional role of each CAM domain, such as changing the number of domains in the extracellular region and adding different types of intramolecular or intermolecular interactions during the process of cell adhesion. Detailed testing results can be found in the Results section.

2.2. Coarse-grained Monte-Carlo simulations of CAM interaction at cell interfaces

A coarse-grained Monte-Carlo algorithm was used to simulate the interactions between CAMs in the native environment of cellular interfaces. The simulation box of the cellular interface consisted of two parallel surfaces of 10nm×10nm membranes. The initial perpendicular distance between two surfaces was 80nm. This distance was changed later in the simulations to reflect the membrane distance fluctuations during the encounter between two cells. The simulation is initiated at a conformation in which two CAM molecules, whose structures were constructed by the process described in 2.1, are placed face to face at the cellular interface in random positions (Fig 1d). The simulations include a series of iterative Monte-Carlo steps. In each step, a series of random movements were performed on each molecule. More specifically, a translational movement along the two-dimensional surface was carried out for each molecule. The movement was taken along a random direction with random amplitudes (within 1nm). Periodic boundary condition was applied to the system. Therefore, if such lateral movement drove the molecule to move outside of the predefined two-dimensional box, this molecule would consequentially appear at the other side of the box. Random rotational movements were performed following the translational movements. The molecule was assigned to rotate along the axis perpendicular to the cell surface. The amplitude was randomly taken within the range of ±10°.

After translational and rotational movements, we further changed the distance between the two membrane surfaces. The purpose of this movement was to take into account the effect of distance fluctuation between membranes. The distance between two surfaces in the simulation had to be smaller than 160nm, which corresponded to twice the end-to-end distance of the CAM model in its fully extended conformation. This was done in order to guarantee the simulation efficiency that CAM molecules are able to form interactions. The intra-molecular conformation of each CAM was further randomly modified after the change of membrane distance. We randomly disturbed the local conformations of domain linker regions so as to change the orientations of two consecutive domains, while the intra-domain conformations were fixed. In each simulation step, we randomly picked a Cα atom located in any domain linker region, and the packing angle and dihedral of selected Cα atom were randomly changed. Based on previous statistical studies on protein database⁵¹, the packing angles were changed from 60 degree to 180 degree, and dihedrals were change from −180 to 180 degrees. At the end of each Monte-Carlo step, following all random movements, the probability of dimerization between molecules was inspected for the newly generated conformation. The conformations which contained intra-molecular and inter-molecular geometric clashes or collisions with both membrane surfaces were rejected.

Because there is no structural information on the binding interface of tested CAM, under different simulation scenarios we could assign specific domains as binding domains which are assumed to contain interfaces to bind the other molecule. We used the distance between binding domains of two molecules as the criterion for dimerization. Specifically, the distance was calculated between the centers of mass of two binding domains. In each simulation step along the Monte-Carlo trajectory, the distance between two binding domains was calculated for the new conformation. If the distance was less than 5nm, which is approximately twice the radius of an extracellular domain, we assumed that these two CAMs form a trans-dimer. When two CAMs form a trans-dimer, the total free energy of the system is decreased by ΔG_trans, where ΔG_trans is the binding affinity of trans-dimerization. The value of the binding affinity in our simulation is obtained from the range between 2 and 10kT. The binding affinity of homogeneous interaction between two NrCAM proteins has not been measured experimentally due to the fact that there are multiple domains in extracellular region of NrCAM and it is not known which domains are involved in the homogeneous interaction. On the other hand, computational calculation or theoretic estimation of binding affinity for a protein complex with unknown 3D structure is extremely difficult. Given the structure of protein complexes, computational efforts were mainly focused on predicting the relative changes of binding affinity due to mutations⁵². Nevertheless, previous studies on other systems of cell adhesion molecules suggest that membrane proteins whose extracellular domains belonging to Ig superfamily interact with generally low affinities⁵³. For instance, the dissociation constant (K_d) of binding between CD28 and CD80 is 20μM54, corresponding to the binding affinity of 10kT. The binding of costimulatory receptors CD4 and CD8 is even weaker (K_d > 200μM)⁵⁵. The corresponding binding affinity is weaker than 8kT. Therefore, it is reasonable to set the test range of binding affinities in our simulations between 2 and 10kT. Further increase in affinity would lead to saturation of the system due to the limitation of our simulation length, as shown in 3.3. Finally, the acceptance of the new conformation after each simulation step was determined by the Metropolis criteria⁵⁶ with the probability:

$$p~exp\left(\frac{G_{\mathit{Tot}}^0-G_{\mathit{Tot}}}{T}\right)$$ (1)

In equation (1), G⁰_Tot and G_Tot are total free energies of the system under old (before the simulation step) and new (after the simulation step) conformations. Only the binding free energy was considered in the simulation systems. Given a certain conformation, if the distance between interacting domains of two CAMs is less than 5nm, a trans-dimer is formed. The total free energy of this conformation is ΔG_trans. Otherwise, the total binding free energy of two monomers equals 0. The new conformation is kept if the simulation step is accepted, otherwise the system returns back to the old conformation. The above process is iterated along the simulation trajectory until it was possible to count how many times dimers can be formed along the whole process. Such rate serves as the quantitative variable to compare the preference of dimer formation in different simulation scenarios.

To simulate the system that contains lateral (cis) interaction between CAMs from the same cell surfaces, four CAMs were included in the cellular interface. They were placed oppositely on the two membrane surfaces, with two monomers on each side. A larger size of simulation box (20nm×20nm) was applied. All Monte-Carlo movements were the same in this new simulation. In addition to the trans-dimers formed by CAMs from opposite sides, two CAMs from the same surface had a chance to form a cis-dimer. We predefined specific domains as cis binding domains. If the distance between these cis binding domains was less than 5nm, we assumed that two CAMs formed a cis-dimer. After two CAMs formed a cis-dimer, the total free energy of the system would be decreased by ΔG_cis, in which ΔG_cis is the binding affinity of a cis-dimerization. The formations of bother trans and cis dimers were traced along the simulation trajectories of this system. The total binding free energy for a given conformation along simulation was calculated as G_Tot=N_trans× ΔG_trans+ N_cis× ΔG_cis, in which (N_trans=0, 1, or 2) and (N_cis=0, 1, or 2) are numbers of trans and cis dimers formed in the system. The calculated total free energy was used to determine the acceptance of the new conformation based on the Metropolis criteria (equation (1)).

3. Results

3.1. The effect of the number of domains on trans-dimerization of CAMs

It is a common observation that many CAMs contain multiple extracellular domains. Previous experiments further showed that insertion of additional domains to the original CAMs changed theeir adhesion efficiency⁵⁷. This indicates that extracellular domains, although they might not be directly involved in the binding to their protein ligands, still play important roles in regulating cell adhesion. Therefore, we started our computational experiments by evaluating the impact of the number of domains on trans-dimerization of CAMs at cell interfaces. We first tested the binding between two CAMs with their full-length extracellular regions. Two full-length CAM models were first positioned face to face randomly at the cellular interface as an initial conformation. The perpendicular distance between two surfaces D in the initial conformation was 80nm (Fig 2a). The configuration of the simulation system was then changed by the Monte-Carlo algorithm, as described in the Model and Methods. In Monte-Carlo simulations, we allowed variations of inter-membrane distance to imitate the initial encounter of two cells. In the first test, the horizontal levels of both membrane surfaces were fluctuated within the range ΔD of 30nm (Fig 2a). Therefore, the minimal distance between two surfaces D_min was 20nm, and the maximal distance D_max was 140nm (Fig 2a). Furthermore, as observed in many different types of CAMs, such as classic cadherin, the outmost N-terminal domain is usually involved in trans-dimerization. Therefore, we assumed that the N-terminal domain is the binding domain. If the distance between the N-terminal domains of two CAM in the simulation is less than 5nm, a trans-dimer will be formed. The binding affinity between two CAMs ΔG_trans was set to 4kT in the simulations to stabilize the formed trans-dimer. The value was taken from the range between 2 and 10kT, as described in 2.2. This weak affinity ensured the fast dissociation of a CAM trans-dimer, so that trans-dimerization can form multiple times along a simulation trajectory within a computationally feasible time and the simulation results were statistically meaningful.

Figure 2.

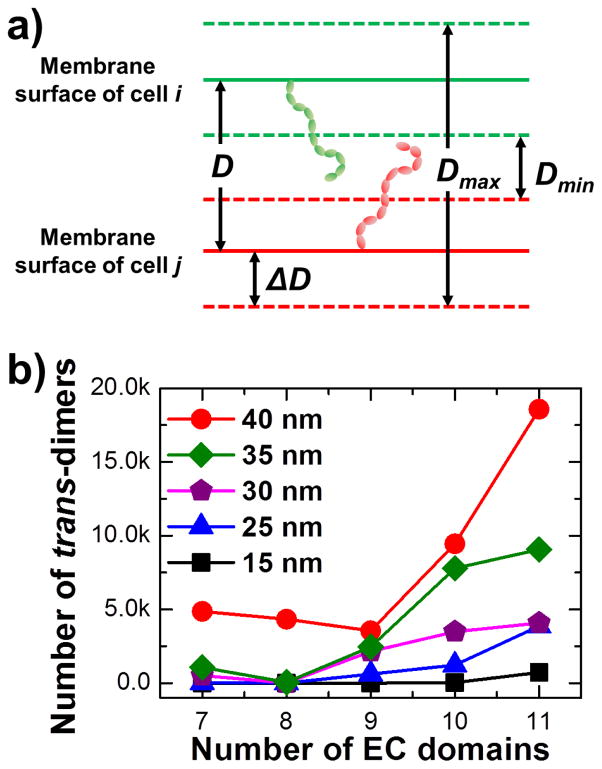
The inter-membrane distance D can fluctuate. The perpendicular distance between two cell surfaces was changed between D_min and D_max within the range of ΔD (a). We tested the relation between domain numbers of tested CAM models and the number of trans-dimers formed along simulations under different ranges of inter-membrane fluctuations (b). We show that CAMs with more extracellular domains are more likely to bind to each other, while larger scale membrane fluctuations facilitate this process.

We generated 10 simulation trajectories in the first test. Each trajectory contained 1×10⁵ Monte-Carlo steps. As a result, we found 4069 trans-dimers among all the simulation trajectories. After the test of a full-length CAM model, we further simulated the trans-dimerization of CAM with different numbers of extracellular domains. Specifically, we first removed one membrane-bound C-terminal domain from the original CAM model. The resulting models with 10 extracellular domains were then positioned face to face randomly at the cellular interface. Following the same Monte-Carlo procedure and the same simulation parameters, 3486 trans-dimers were derived from the 10 simulation trajectories. Additionally, we removed more extracellular domains from the C-terminus. Consequently, when the same simulations were carried out for CAMs in which two, three and four consecutive domains were removed from the C-terminus, we found 2150, 3 and 510 trans-dimers formed, respectively. Fig 2b shows the relation between domain numbers of tested CAM models and the number of trans-dimers formed in simulations. The purple pentagons in the figure correspond to the condition where membrane fluctuations are within the range of 30nm. These results indicate that CAMs with more extracellular domains are more likely to form trans-dimers.

In order to systematically evaluate how domain numbers of CAMs affect their binding under different conditions of cell adhesion, we further carried out simulations in which membrane surfaces underwent random fluctuations within different ranges. As a result, we found that less trans-dimers were formed if membrane surfaces fluctuated within smaller ranges. For instance, blue triangles and black squares in Fig 2b are simulations in which their membrane fluctuations were within 25 and 15nm, respectively. Compared with 30nm fluctuations, less trans-dimers were observed in simulations of all different domain numbers. In contrast, more trans-dimers were formed if membrane surfaces underwent higher degrees of fluctuations. For instance, red circles and green diamonds in Fig 2b are simulations in which their membrane fluctuations are within 40 and 35nm, respectively. Compared with 30nm fluctuations, far more trans-dimers were observed in simulations of all different domain numbers. It is worth mentioning that 40nm is the largest fluctuation for the system, in which the minimal distance between two surfaces is 0nm and the maximal distance between two surfaces is 160nm, twice the end-to-end distance of the CAM model in its fully extended conformation. Interestingly, although CAMs under higher degrees of membrane fluctuations tend to form more trans-dimers, simulations with all different levels of fluctuation showed the same behavior which is that CAMs with more extracellular domains dimerize with each other more easily.

Therefore, our computational results illustrate the functions of CAM trans-dimerization which are undertaken by the multiple extracellular domains of these molecules, and further provide insights into their role in cell adhesion. We showed that CAMs with more extracellular domains are more likely to bind to each other. This is due to the fact that more domain linker regions in these CAMs provide larger numbers of degrees of freedom. Consequently, higher levels of flexibility lead to larger conformational entropy which favors dimerization of CAMs with more extracellular domains. It is worth mentioning that the larger entropy of monomers does not necessarily lead to the larger entropy loss after dimerization, because dimers of CAM with more extracellular domains also contain much more possible conformations than dimers with less extracellular domains. There is larger conformational entropy in the dimers with more extracellular domains. In another words, CAMs with more extracellular domains are more likely to stay flexible after trans-dimerization. Therefore, the larger conformational entropy, and thus the lower free energy in monomers, provides more possible orientations which will make the encounter with each other more likely. Moreover, larger scale membrane fluctuations facilitate dimerization of CAMs at cellular interfaces. In other words, CAMs form trans-dimers more easily when the membrane surfaces undergo large-scale fluctuations. This highlights the importance of trans-dimerization between CAMs at the initial stage of cell adhesion in which the interface between two cells has not been stabilized. Taken together, out study suggests that trans-dimerization between CAMs is the driving force which initializes cell adhesion, while multiple domains of these molecules play regulatory roles during this process.

3.2. The function of intramolecular interactions in trans-dimerization of CAMs

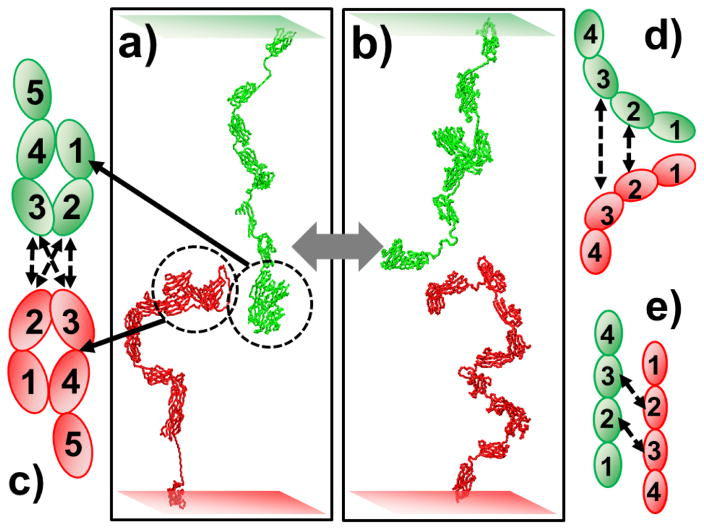
In many molecular systems of cell adhesion, multiple extracellular domains are not linearly extended, but folded into relatively compact conformations which are stabilized by their inter-domain interactions. For instance, the first four N-terminal Ig domains in the L1 family protein neurofascin form a horseshoe-like structure in which large surfaces with hydrophobic patches are involved in the intramolecular binding interfaces between domain 1 and 4 (Fig 3c)⁵⁸. A similar domain spatial arrangement also exists in recently reported crystal structures of CAM sidekick (Sdk) 1 and 2⁵⁹. The Ig 1–4 structural units in both L1 and Sdk contain binding interfaces for trans-dimerization, indicating the generality of using intra-molecular domain-domain interactions as a mean of regulation for cell adhesion. In order to understand the functions of this intramolecular binding in CAM trans-dimerization, we added constraints between domain 1 and domain 4 in our CAM model. Specifically, starting from an initial extended conformation, the distance of centers of mass between domain 1 and domain 4 was minimized through a simulated annealing algorithm. This was attained by randomly changing the packing angle and dihedral of three loop regions from domain 1 to domain 4, until these two domains formed physical contacts. The derived horseshoe conformation for Ig 1–4 of our CAM model is highlighted by dashed circles in Fig 3a. In the following Monte-Carlo simulations, this conformation of Ig 1–4 was fixed to maintain the intramolecular constraint between domain 1 and domain 4.

Figure 3.

We added constraints between domain one and domain four into our CAM model to understand the function of this intramolecular interaction in CAM trans-dimerization (a). The horseshoe conformation from domain one to domain four is shown in (c). In the control simulation, the conformations from domain one to domain four can be freely changed (b). All other simulation parameters and the Monte-Carlo procedure remained unchanged. Our simulations show that homogeneous domain interactions (d) are geometrically less accessible than heterogeneous interactions (e) during the trans-dimerization between CAMs when these two molecules are at opposite sides of the cellular interface.

Consequently, two CAM models with the horseshoe conformation for their first four domains were positioned face to face randomly at the cellular interface as an initial conformation of the Monte-Carlo simulations (Fig 3a). The horizontal levels of both membrane surfaces were fluctuated in the simulations within the range of 25nm. Based on previous experimental evidence that trans-dimerization interfaces are located in the Ig 1–4 structural unit, we assumed that domain 2 and 3 are the binding domains. Two binding scenarios were further tested. In the first scenario, homogeneous domain interactions were considered, in which domain 2 in one CAM interacts with domain 2 in the other CAM and domain 3 interacts with domain 3 (Fig 3c). In the second scenario, heterogeneous domain interactions were considered, in which domain 2 in one CAM interacts with domain 3 in the other CAM (Fig 3c). The binding affinity between two domains was set to 4kT. The value is taken from the range between 2 and 10kT, as described in 2.2. Therefore, the total affinity between two CAMs would be 8kT if both binding domains in one CAM formed interactions with their corresponding partners in the other CAM. We generated 10 simulation trajectories in the first test. Each trajectory contained 1×10⁵ Monte-Carlo steps. Two criteria were used to determine the binding status between two CAMs. In the first criterion, the distances of both binding domains between two CAMs had to be less than 5nm. In the second criterion, the formation of a trans-dimer would be counted if either one of the two binding domains was in contact with its partner. The simulation results are shown as striped bars in Fig 4. The numbers of trans-dimers counted by the first criterion were plotted in Fig 4a and Fig 4b, while the numbers counted using the second criterion are plotted in Fig 4c and Fig 4d. The results following the first simulation scenario are presented in Fig 4a and Fig 4d, while the results from the second scenario are presented in Fig 4b and Fig 4d. Not surprisingly, the figure shows that the number of trans-dimers counted by the second criterion is much larger than the stricter first criterion. The figure further suggests that heterogeneous domain interactions (scenario II) can lead to more frequent trans-dimerization than homogeneous domain interactions (scenario I) under both binding criteria.

Figure 4.

In (a), trans-dimers are formed when domain 2 in one CAM interacts with domain 2 in the other CAM and domain 3 interacts with domain 3 (heterogeneous binding scenario), while the distances of both binding domains between two CAMs have to be less than 5nm. In (b), trans-dimers are formed when domain 2 in one CAM interacts with domain 3 in the other CAM (homogeneous binding scenario), while the same binding criterion was applied. In (c), trans-dimers are formed along the heterogeneous binding scenario, while the distance of at least one pair of binding domains between two CAMs needs to be less than 5nm. Finally, in (d), trans-dimers are formed along the homogeneous binding scenario, while the distance of at least one pair of binding domains between two CAMs needs to be less than 5nm. The simulations of the horseshoe model are plotted by striped bars, while the control simulations are plotted by black bars. The figure suggests that when the binding unit of a trans-dimer is located in more than one domain of a CAM, the inter-domain constraints can facilitate the dimerization between two molecules.

In order to estimate the effect that was brought by the intramolecular constraint, control simulations were carried out in which the intramolecular constraint between domain 1 and domain 4 was removed. In these control tests, the conformations of linker regions within the Ig 1–4 unit could be freely changed (Fig 3b). All other simulation parameters and the Monte-Carlo procedure remained unchanged. The simulation results of this control system are plotted as black bars in Fig 4. The figure clearly shows that much less trans-dimers were formed, when there was no intramolecular constraint within the Ig 1–4 unit. Specifically, when the unit of Ig 1–4 was fixed in the horseshoe conformation, 6734 trans-dimers were found by the first criterion under the homogeneous binding scenario (striped bar of Fig 4a). Using the same criterion and the same binding scenario, only 213 trans-dimers were formed if the inter-domain constraint was relieved (black bar of Fig 4a). Similar results were derived when the other criterion and simulation scenario were used, as shown in Fig 4b, Fig 4c and Fig 4d. These results indicate that the intramolecular interactions between different domains of a CAM, especially when these domains contain binding interfaces with other molecules, play a positive role in mediating the adhesion between CAMs. We therefore suggest that when the binding unit of a trans-dimer is located in more than one domain of a CAM, the inter-domain constraints stabilize the conformational fluctuations within different domains of the unit. This in turn facilitates the dimerization between two molecules when they are in the spatial proximity. It is worth mentioning that our simulation results from the last section (3.1) suggested that reduction in number of domain linkers would have a negative effect on binding. In this section, however, we show that reduction of domain linker number by formation of the horseshoe conformation can actually enhance binding. We indicate that these two results are not contradictory. The simulation result from 3.1 is based on the assumption that the binding interfaces are located in one domain. In the horseshoe model studied in this section, we made the prerequisite that the binding interfaces of a trans-dimer are located in more than one domain of a CAM. Therefore, here we suggest that if the binding interfaces are located in more than one extracellular domain, the introduction of inter-domain constraints, e.g. formation of horseshoe conformation, can stabilize the conformational fluctuations within different domains. This in turn facilitates the dimerization between two molecules when they are in spatial proximity.

Moreover, our results suggest that the heterogeneous domain interactions are more favorable than the homogeneous interactions to trigger trans-dimerization, if the dimerization interfaces are distributed in multiple domains of a CAM. For instance, when there was no constraint between domain 1 and domain 2, 213 trans-dimers were found through the homogeneous interactions scenario using the first criterion (black bar of Fig 4a). While the second criterion was applied, 1551 dimers were found (black bar of Fig 4c). In contrast, under the heterogeneous scenario, these numbers increased to 743 for the first criterion (black bar of Fig 4b) and 2506 for the second criterion (black bar of Fig 4d). This results from the fact that heterogeneous domain interactions (Fig 3e) are geometrically more accessible than homogeneous interactions (Fig 3d) during the trans-dimerization between CAMs when these two molecules are on opposite sides of the cellular interface. This is consistent with a number of examples in which similar patterns of heterogeneous domain binding between a dimer were observed in the crystal structure of different CAM systems, including protocadherin⁶⁰ and receptor protein tyrosine phosphatase (RPTP)⁶¹.

3.3. The interplay between trans and cis interactions during CAM clustering

As more and more CAM structural data accumulated, it was found that the extracellular regions in most of these systems simultaneously contain both trans and cis binding interfaces^62–65. While trans-interactions link CAMs from neighboring cells, cis-interactions link CAMs from the same cell. The combination of trans and cis interactions lead to the assembly of CAMs into high-order structures during adhesion. For instance, a 2D clustering model derived from the three-domain structure of neural cell adhesion molecules (NCAM) was proposed when two different types of interfaces were observed in the crystal structure. Using both interfaces, NCAM was able to promote the assembly by forming an ordered 2D molecular “zipper” and remodeling of various signaling complexes⁶⁶. Beyond these structural evidences, however, little is understood about the dynamic properties of CAM assembly. The coupling between trans and cis interactions in CAM-mediated clustering has been studied computationally at different scales. These studies either didn’t include enough structural information, or only focused on specific molecular systems. In order to explore the general principles of CAM clustering, we added lateral cis-interaction between our tested CAM models into the Monte-Carlo simulations.

Specifically, both trans and cis interactions were included in the model systems (Fig 5a). As described in Model and Methods 2.2, four CAM models were placed oppositely at the interface of a 20nm×20nm area, with two molecules placed on each side. CAMs have probability to form either trans-interaction or cis-interaction, according to the distance criterion. Following our test results in 3.2, the internal degrees of freedom from domain 1 to domain 4 of all four CAMs were fixed into the horseshoe conformation to facilitate trans-interactions. The binding sites of trans-interaction were distributed in domain 2 and 3, so that a trans-dimer would be formed if domain 2 in one CAM interacts with domain 2 in the other CAM and domain 3 interacts with domain 3. We further assumed that lateral binding interfaces were located in domain 9, based on the common observations that cis-interactions occur more frequently between domains at membrane-proximal regions¹⁴. At most, these four-molecular systems can form two trans-interactions and two cis-interaction, as illustrated in Fig 5a. To systematically test the interplay between trans and cis interactions, different values were assigned to the binding affinities of these two interactions. In the Monte-Carlo simulations, the horizontal levels of both membrane surfaces were initially fluctuated within the range of 25nm. However, the inter-membrane distance was fixed later in the simulations, if there was at least one trans-dimer formed in the system which indicated the stabilization of the cellular interface. Moreover, if two CAMs formed a complex (either a trans-dimer or a cis-dimer) in simulations, the complex would move together (both translationally and rotationally) on membrane surfaces. Finally, 10 trajectories were carried out for each simulation. Each trajectory contained 1×10⁵ Monte-Carlo steps.

Figure 5.

To explore the general principles of CAM-mediated clustering, four CAM models were placed opposite from one another at the interface of area size 20nm×20nm, and both trans and cis interactions are included in the model systems (a). The formation of trans-dimers without cis-binding was first tested. Different values of binding affinity that ranged from 2 to 10kT were used. Under the Metropolis simulation scheme, we obtained the linear correlation between the binding affinity and the logarithmic scale of trans-dimer counts (b). However, when the binding affinity reached 10kT, the number of trans-dimers formed in the system was saturated. This resulted from the limitation of our simulation length.

We first tested the formation of trans-dimers in this simulation system without cis-binding. Different values of binding affinity ranging from 2 to 10kT were used. The simulation results are shown in Fig 5b. The linear correlation between the binding affinity and the logarithmic scale of trans-dimer counts indicates that the number of dimers in the system grew exponentially when trans-interactions became stronger. This is consistent with the Metropolis simulation scheme in which the system reaches detailed balance among different free energy states. The figure also shows that the system was saturated when the binding affinity reached 10kT. This resulted from the limitation of our simulation length, considering there were 10⁶ Monte-Carlo steps for each test. The cis-interactions were restored in the next stage. We found that different numbers of trans-dimers were formed if different affinities of cis-interactions were used in the system, even under the same affinity of trans-interactions. For instance, 303 trans-dimers were found when ΔG_trans equals 2kT and ΔG_cis equals 0kT. In contrast, when ΔG_cis equals 8kT, the simulation of the same ΔG_trans led to 439 trans-dimers. In order to quantitatively evaluate the effect of cis-interactions under different affinities of trans-interactions, we calculated the ratio between N(trans) and N₀(trans), in which N(trans) is the number of trans-dimers under given cis-affinity and N₀(trans) is the number of trans-dimers when cis-affinity equals 0. Therefore, the ratio is 1.45 (439/303) for the example in which ΔG_trans equals 2kT and ΔG_cis equals 8kT.

Fig 6 shows the calculated ratios of N(trans)/N₀(trans) under different combinations of trans and cis binding affinities. The ratios whose values are larger than 1 indicate a positive cooperativity in which the presence of cis-interactions can strengthen the trans-interactions. As suggested by our previous results, the positive cooperativity between trans and cis interactions is a premise for clustering of CAMs. Fig 6 suggests a negative correlation between the trans and cis binding affinities in order to reach the positive cooperativity. Moreover, this positive cooperativity only exists within a small range, depending on the values of both trans and cis interactions. For instance, when trans affinity is low (2kT), cis-interactions need to be strong (8kT) to trigger clustering (Fig 6d). When trans-interactions become stronger, the affinities of cis-interactions which result in positive cooperativity become lower. When trans affinity equals 4kT, cis affinity equals 6kT to trigger clustering (Fig 6c). When trans affinity equals 6kT, cis affinity equals 4kT to trigger clustering (Fig 6b). The presence of cis-interaction cannot lead to positive cooperativity when trans-interactions become stronger (Fig 6a). Our simulation results therefore suggest that the CAM-mediated clustering at cellular interface is an elaborately designed process in which both trans and cis interactions are fine-tuned collectively within a small energetic range by natural selection.

Figure 6.

The ratios of N(trans)/N₀(trans) under different combinations of trans and cis binding affinities were calculated. The N(trans) is the number of trans-dimers under given cis-affinity, and N₀(trans) is the number of trans-dimers when cis-affinity equals 0. The ratios are plotted under different values of cis binding affinity, when trans binding affinity equals 8kT (a), 6kT (b), 4kT (c) and 2kT (d). The figure indicates that there is a negative correlation between the trans and cis binding affinities in order to reach the positive cooperativity, in which the presence of cis-interactions can strengthen the trans-interactions.

4. Discussion

CAMs are membrane receptors which mediate intercellular interactions in multicellular organisms. They are essential elements of many important physiological and pathological processes in human body. For instance, CAMs in the Ig superfamily or selectin family play a major role in inflammatory responses by regulating the adhesion between leukocytes and endothelial cells⁶⁷. One interesting feature of these CAMs is that their almost all of extracellular regions contain repeats of structural domains. How each domain in these membrane-tethered CAMs causes impacts on cell adhesion is difficult to test by traditional experimental methods at molecular level. We tackled this problem by computational modeling. Using NrCAM as template, a coarse-grained structure that contains eleven extracellular domains was built as a hypothetical model of a cell adhesion molecule. Different numbers of the CAM model were disposed in such a way as to mimic the surfaces of neighboring cells. Stochastic simulations which incorporated both molecular factors including conformational changes of CAMs and cellular factor including membrane fluctuations were further applied to resemble the molecular adhesion at cellular interfaces. By introducing variations into the simulations, such as changing the number of domains, adding intramolecular or intermolecular constraints between domains, the functional roles of CAM’s different domains could be specifically evaluated. Our computational results suggest that cell adhesion does not simply correspond to molecular interactions between CAMs through their binding interfaces, but that it is regulated by a number of additional mechanisms in which the multiple domains of CAMs at their extracellular region are an indispensable determinant. This study therefore throws light on the complexity of cell adhesion by linking the structural details of CAMs to their cellular environments with a new coarse-grained model.

However, some issues in the study have not been fully considered due to the coarse-grained nature of the model and the simplification made in the simulations. For instance, the description of intermolecular binding in the simulations is not specific enough. We used the distance between interacting domains as the criterion of binding and an arbitrary affinity to determine the strength of binding. Fortunately, this simplified and nonspecific description will not cause too much negative impacts, as long as the same binding criteria and affinity are consistently used in different simulation scenarios. The major variations in the simulation outputs resulted from the difference in simulation setup, while the uncertainties due to the lack of accurate binding description were cancelled out between different systems and therefore could be neglected. As a matter of fact, the attempt of using a broad definition of binding allowed us to carry out a more generic test without any structural and energetic bias on binding. Secondly, the flexibility of domain linker in our test system needed to be tested. In our Monte-Carlo simulation, we randomly changed the conformation of domain linkers by assuming they are highly flexible. The basis of this assumption is the fact that the linkers of NrCAM are much longer than normal CAMs. For instance, the average length of linker regions of type-I cadherin (UniProt ID P12830) among its five extracellular domains is 2 amino acids. For protocadherin (Uniprot ID Q9Y5F3), the average length of linker regions among its first five extracellular domains is 3 amino acids. On the other hand, for our test system, the average length of linker regions among its eleven extracellular domains is 9 amino acids. Longer domain linkers indicate higher degrees of flexibility. For instance, the hinge flexibility of long domain linkers in neural cell adhesion molecules (NCAM) was discovered by micropipette manipulation⁶⁸. The final issue is related to the algorithmic detail of the method. A Metropolis-based Monte-Carlo algorithm is used in the current method to simulate the binding of CAMs. The Metropolis algorithm is not able to study the kinetic properties of molecular binding. This study is thus mainly focused on how changes of CAM’s extracellular domain organization modulate the stability and other thermodynamic properties of binding. In order to facilitate the study of binding kinetics, current Metropolis algorithm can be replaced by the specific kinetic Monte-Carlo simulation algorithm that we previously developed^{69, 70}.

Consequently, upon future improvements, the model can be applied to provide insights into many specific biological systems related to cell adhesion. Practically, the same procedure used in this study for the generic CAM model can be applied to the protein in a specific adhesion system. More specifically, the structure of each domain in the protein would first be built either based on experimental data or by computational predictions. The coarse-grained model of the entire extracellular region can be constructed by modeling the domain linkers. Finally, numbers of protein models would be placed at the cellular interface. The diffusions, trans and cis interactions of these molecules would be simulated by the Monte-Carlo algorithm described in the paper. Using this method, many different systems can be studied. One example is NCAM. The crystal structures of NCAM reveal multiple trans and cis binding interfaces in their extracellular domains⁷¹. This specific structural information, together with experimentally derived binding constants, can be used to simulate the clustering of NCAM at cellular interfaces and study how the presence of multiple extracellular domains affects the process of clustering. Overall, the method developed here not only broadens our knowledge on the general principles of cell adhesion, but will also become an efficient computational tool to study binding of membrane receptors in their cellular environments.

Research Highlights.

• One interesting feature of cell adhesion molecules is that their extracellular regions almost all contain repeating copies of structural domains.

• We used computational simulations to understand why such many extracellular domains need to be evolved through natural selection.

• We found that when two cells form a contact, they can be linked more easily by molecules that contain more extracellular domains.

• Domains can further be organized together, either within one molecule or between two molecules from the same cell to regulate the process of cell adhesion.

• Our study demonstrated the functional importance of multiple domains in cell adhesion molecules.

• The binding between subunits in a complex can be synergistically strengthened during assembly.