An Enhanced Visualization Method to Aid Behavioral Trajectory Pattern Recognition Infrastructure for Big Longitudinal Data

Abstract

Big longitudinal data provide more reliable information for decision making and are common in all kinds of fields. Trajectory pattern recognition is in an urgent need to discover important structures for such data. Developing better and more computationally-efficient visualization tool is crucial to guide this technique. This paper proposes an enhanced projection pursuit (EPP) method to better project and visualize the structures (e.g. clusters) of big high-dimensional (HD) longitudinal data on a lower-dimensional plane. Unlike classic PP methods potentially useful for longitudinal data, EPP is built upon nonlinear mapping algorithms to compute its stress (error) function by balancing the paired weights for between and within structure stress while preserving original structure membership in the high-dimensional space. Specifically, EPP solves an NP hard optimization problem by integrating gradual optimization and non-linear mapping algorithms, and automates the searching of an optimal number of iterations to display a stable structure for varying sample sizes and dimensions. Using publicized UCI and real longitudinal clinical trial datasets as well as simulation, EPP demonstrates its better performance in visualizing big HD longitudinal data.

1 Introduction

Building up the infrastructure for big data visualization is a challenge but an urgent need [1], [2]. Big longitudinal data are generated every day from all kinds of fields in industry, business, government and research institutes [3]–[15]. Discovering useful information from heterogeneous data requires trajectory pattern recognition techniques [16]–[22]. However, developing visualization tools is crucial to guide this technique, which can facilitate the discovery, presentation and interpretation of important structures buried in complex high-dimensional data. Projection Pursuit (PP) is a classical technique to data visualization, first introduced by Friedman and Tukey in 1974 for exploratory analysis of multivariate data [23]. The basic idea of PP is to design and numerically optimize a projection index function to locate interesting projections from high- to low-dimensional space. From these interesting projections, revealed structures such as clusters could be analyzed [24]–[27]. PP is based on the assumption that redundancy exists in the data and the major characteristics are concentrated into clusters. For example, principle components analysis is one of the typical PP methods, widely used for dimension reduction by removing uninteresting directions of variations [23], [26], [28]–[39] and now often used as an initialization before high dimensional data mapping and clustering [26], [40]–[45].

In the present study, our newly developed PP method is compared to two typical PP methods: Andrews Curves and Grand Tour, as all three methods are potentially useful for big longitudinal data visualization where high dimensionality (HD) and repeated measures for each dimension are common. Section II introduces the involvement of Andrews Curves and Grand Tour; Section III discusses the EPP function and algorithms; Section IV includes the comparison of EPP with other methods using real datasets; Section V evaluates EPP with simulated and artificial data; Section VI concludes this study.

2 Andrews Curves and Grand Tour

Proposed in 1972, Andrews Curve has been widely utilized in many disciplines such as biology, neurology, sociology and semiconductor manufacturing. The algorithm of Andrews Curve was designed to project high dimensional data onto a predefined Fourier series [46], and if any structures exist, they may be visible via Andrews Curves. Briefly, for each case X = {x₁, x₂, …, x_d}, which is a vector of measurements, we define a series ( $\frac{1}{\sqrt{2}}$, sin(s), cos(s), sin(2s), cos(2s), …), then the Andrews Curve is calculated as

$$f_x(s)=\frac{x_1}{\sqrt{2}}+x_2\text{ sin}(s)+x_3\text{ cos}(s)+x_4\text{ sin}(2s)+\dots ,$$ (1)

for −π < s < π. Each case may be viewed as a curve between −π and π, and structures may be viewed as different clusters of curves. Since 1972, several variants of the Andrews Curve have been proposed. Andrews himself also proposed to use different integers to generalize f_x(s),

$$f_x(s)=x_1\text{ sin}(n_{1}s)+x_2\text{ cos}(n_{1}s)+x_3\text{ sin}(n_{2}s)+x_4\text{ cos}(n_{2}s)+\dots .$$ (2)

By testing n₁ = 2, n₂ = 4, n₃ = 8, …, the author concluded that Equation (2) is more space filling (ie., a curve whose range contains the entire 2-dimensional unit square, or the mapping is continuous) than Equation (1) but more difficult to interpret when used for visual inspection [46]. A three-dimensional Andrews plot was suggested by Khattree and Naik [47],

$$\sqrt{2}{f}_x(s)=x_1+x_2[\text{sin}(s)+\text{cos}(s)]+x_3[\text{sin}(s)-\text{cos}(s)]+x_4[\text{sin}(2s)+\text{cos}(2s)]+\dots .$$ (3)

As every projection point is exposed to a sine function and a cosine function, the advantage in Equation (3) is that the trigonometric terms do not simultaneously vanish at any given s, which establishes an interesting relation between the Andrews Curve and the eigenvectors of a symmetric positive definite circular covariance matrix.

Different from Andrews Curve, Grand Tour proposed by Asimov [48] and Buja [49] in 1985 is an interactive visualization technique. The basic idea is to rotate the projected plane from all angles and search the interesting structures [50]–[56]. However, these methods were not ideal in terms of intensive computation, computer storage, and projection recovery turns out to be difficult. Motivated by Andrews Curve, Wegman and Shen [57] suggested an algorithm for computing an approximate two-dimensional grand tour, called pseudo grand tour which means that the tour does not visit all possible orientations of a projection plane. The method has recognized advantages, such as easy calculation, time efficiency in visiting any regions with different plane orientations, and easy recovery of projection. Briefly, assuming d is an even number without loss of generality [57], let a₁(s) be

$$\sqrt{\frac{2}{d}}(\text{sin}({\lambda }_{1}s),\text{cos}({\lambda }_{1}s),\dots ,\text{sin}({\lambda }_{d/2}s),\text{cos}({\lambda }_{d/2}s)),$$ (4)

and a₂(s) be

$$\sqrt{\frac{2}{d}}(\text{cos}({\lambda }_{1}s),-\text{sin}({\lambda }_{1}s),\dots ,\text{cos}({\lambda }_{d/2}s),-\text{sin}({\lambda }_{d/2}s)),$$ (5)

where λ_i has irrational values. a₁(s) and a₂(s) have the following properties,

$${\Vert {\mathbf{a}}_{\mathbf{1}}(\mathbf{s})\Vert }_2^2=\frac{2}{d}\sum _{j=1}^{d/2}({\text{sin}}^2({\lambda }_{j}s)+{\text{cos}}^2({\lambda }_{j}s))=1,$$ (6)

$${\Vert {\mathbf{a}}_{\mathbf{2}}(\mathbf{s})\Vert }_2^2=\frac{2}{d}\sum _{j=1}^{d/2}({\text{cos}}^2({\lambda }_{j}s)+{(-\text{sin})}^2({\lambda }_{j}s))=1,$$

and

$$\langle {\mathbf{a}}_{\mathbf{1}}(\mathbf{s}),{\mathbf{a}}_{\mathbf{2}}(\mathbf{s})\rangle =\frac{2}{d}\sum _{j=1}^{d/2}(\text{sin}({\lambda }_{j}s)\text{cos}({\lambda }_{j}s)-\text{cos}({\lambda }_{j}s)\text{sin}({\lambda }_{j}s))=0,$$ (7)

where 〈·〉 is the inner product of two vectors a₁(s) and a₂(s). Then, the projections of data points on the plane formed by the two basic vectors are

$$f_{x_i}(s)=(X_{i_1}^{\prime },X_{i_2}^{\prime }),i=1,2,\dots ,N,$$ (8)

in which

$$X_{i_1}^{\prime }=\sum _{k=1}^d{x}_k{a}_{1k},$$ (9)

$$X_{i_2}^{\prime }=\sum _{k=1}^d{x}_k{a}_{2k}.$$

According to (6), a₁(s) and a₂(s) form an orthonormal basis for a two dimensional plane. Because of the dependence between sin(·) and cos(·), this two-dimensional plane is not quite space filling. However, the algorithm based on (8) is much computationally convenient. By taking the inner product as in (7), a [a₁(s), a₂(s)] plane is constructed on which the high dimensional data are projected.

Different from Andrews Curve and Pseudo Grand Tour, our new enhanced projection pursuit (EPP) method was built upon Sammon Mapping, assuming not all big longitudinal data fit trigonometric functions or transformation. Sammon mapping has been one of the most successful nonlinear multidimensional scaling methods [58], [59] proposed by Sammon in 1969 [60]. It is highly effective and robust to hyper-spherical and hyper-ellipsoidal clusters [60]. The idea is to minimize the error (called “stress”) between the distances of projected points and the distances of the original data points by moving around projected data points on lower dimensional space (mostly 2-dimenstional place) to best represent those in high-dimensional space. Since its advent, much effort concentrated on improving the optimization algorithm [61]–[65] but rarely on modifying Sammon’s Stress function [64].

Our proposed EPP modified Sammon Stress Function by balancing two weights for between and within cluster errors, respectively, in order to better segment and visualize structures (e.g., clusters) on a projected two-dimensional plane while preserving their cluster membership in high-dimensional space. To this end, we developed a nonlinear algorithm to compute EPP stress. Besides, our EPP was developed to automate the searching and finding of the optimal number of iterations to display a stable structure, for varying sample sizes and dimensions. Our goal is to aid the trajectory pattern recognition of longitudinal data. To evaluate the performance of EPP, one big publicized data set and two real longitudinal random controlled trials (RCT) datasets including a large web-delivered trial data were used to compare EPP with Andrews Curve and Pseudo Grand Tour. Simulated big longitudinal data sets based on RCT data parameters were used to evaluate EPP performance at varying conditions.

3 Enhanced Projection Pursuit (EPP)

In longitudinal data analyses, repeated measures for each dimension result in inevitable high-dimensionality. Built upon Sammon Mapping [60], we proposed an Enhanced Projection Pursuit method (EPP) where the Sammon stress becomes a special case of EPP stress when there is only one cluster and the weights of within and between cluster stresses are equal. EPP is used to aid trajectory pattern recognition for such longitudinal data. The key idea of EPP is to balance the weights of between and within cluster variations in order to achieve better visualization, thus aid pattern recognition for high dimensional (HD) longitudinal data. Table 1 summarizes the notations used hereafter. First, we define our data size and high dimensional space.

TABLE 1.

Notations

Symbols	Definitions
X	a vector of measurements
Xi,Xj	The i-th and j-th cases
Xi′,Xj′	The projections in a 2D space
s	angle, 0 < s < π
λ	Linearly independent over the rational
a1 (s), a2 (s)	Orthonormal basis for a 2D plane
N	Number of cases
T	Sample times
d	Number of dimensional
p	Number of components
Dij	Distance between Xi′ and Xj′
$D_{\mathit{\text{ij}}}^{\ast }$	Distance between Xi and Xj
S	Stress
ci	Cluster label of case i
k	The optimal number of clusters
D̅	Average distance
ℓ	Total data size
α	Weight of the within-cluster stress
β	Weight of the between-cluster stress
SEPP	Total EPP stress
fx	Low-dimensional projections of data
ℓ	Size of the simulated data

Definition 1

let N be the number of cases (e.g., subjects, data points, etc.), X_i, 1 ≤ i ≤ N be a vector of d variables {x₁, x₂, …, x_d}, each X_i be repeatedly measured with t times, then the data has dt dimensional space and the entire data size is ℓ = N dt. e.g, with N cases, X_i is a dt dimensional vector {x₁₁, x₁₂, …, x_1t, x₂₁, x₂₂, …, x_2t, …, x_d1, x_d2, …, x_dt}.

Then, the projection of the big longitudinal data from high-dimensional space onto a two-dimensional plane is defined as follows:

Definition 2

To project big HD longitudinal data onto a two dimensional plane and similar to [60], let the distance between any two vectors of X_i and X_j in the dt high dimensional space be defined by $D_{\mathit{\text{ij}}}^{\ast },D_{\mathit{\text{ij}}}^{\ast }={\Vert {\mathit{X}}_i-{\mathit{X}}_j\Vert }_2$, where ‖·‖₂ is the Euclidean norm.

Based on Definition 1 and 2, randomly choose an initial two-dimensional space for the N vectors of X′ and compute all the two dimensional distances D_ij, 1 ≤ i, j ≤ N, i ≠ j. The Sammon Stress [60] is calculated as:

$$S_{\mathit{\text{sam}}}=\frac{1}{\sum _{i<j}{D}_{\mathit{\text{ij}}}^{\ast }}\sum _{i<j}\frac{{(D_{\mathit{\text{ij}}}^{\ast }-D_{\mathit{\text{ij}}})}^2}{D_{\mathit{\text{ij}}}^{\ast }}.$$ (10)

Different from Equation (10), the Stress of EPP stress function S_EPP is expressed as the weighted sum of the within-cluster stress S_{EPP_w} and between-cluster stress S_{EPP_b},

$$S_{\mathit{\text{EPP}}}=\alpha S_{\mathit{\text{EPP}}\_w}+\beta S_{\mathit{\text{EPP}}\_b}$$ (11)

Algorithm 1(a).

Main EPP Algorithm

Input: longitudinal data Xi, i = 1, 2, …, N, cluster labels ci, 0 ≤ i ≤ N, and a range of stress error bound ε, maximum iteration number, lmax, weight change step δ
Output: α, β, fx and SEPP
1:	Initialize X′ by PCA
2:	Set initial values for SEPP0→ ∞, l = 0, m = 0, α0 and β0 (α0, β0 > 0, α0 + β0 = 1)
3:	for l = 0 to lmax do
4:	$f_{x_l}=\underset{f_x}{\text{arg min }}{S}_{\mathit{\text{EPP}}}({\alpha }_l,{\beta }_l,f_x)$
5:	SEPPl= SEPP (αl+1, βl+1, fxl)
6:	while αl, βl > 0, αl + βl = 1 do
7:	if SEPP (αl + δ, βl−δ, fxl) < SEPP (αl, βl, fxl) then
8:	αl+1 = αl+1 + δ, βl+1 = βl+1 − δ
9:	else
10:	if SEPP (αl − δ, βl + δ, fxl) < SEPP (αl, βl, fxl) then
11:	αl+1 = αl+1 − δ, βl+1 = βl+1 + δ
12:	else
13:	break
14:	end if
15:	end if
16:	end while
17:	if |SEPPl − SEPPl−1| ≤ ε then
18:	break
19:	end if
20:	end for

in which

$$\{\begin{array}{c}{S}_{\mathit{\text{EPP}}\_w}=\frac{1}{\sum _{i<j}{D}_{\mathit{\text{ij}}}^{\ast }}\sum _{i<j,c_i=c_j}\frac{{(D_{\mathit{\text{ij}}}^{\ast }-D_{w_{\mathit{\text{ij}}}})}^2}{D_{\mathit{\text{ij}}}^{\ast }}\hfill \\ S_{\mathit{\text{EPP}}\_b}=\frac{1}{\sum _{i<j}{D}_{\mathit{\text{ij}}}^{\ast }}\sum _{i<j,c_i\ne c_j}\frac{{(D_{\mathit{\text{ij}}}^{\ast }-D_{b_{\mathit{\text{ij}}}})}^2}{D_{\mathit{\text{ij}}}^{\ast }}\hfill \end{array}$$ (12)

where $\frac{1}{\sum _{i<j}{D}_{\mathit{\text{ij}}}^{\ast }}$ is a constant for a given big HD longitudinal data, $\sum _{i<j,c_i=c_j}\frac{{(D_{\mathit{\text{ij}}}^{\ast }-D_{w_{\mathit{\text{ij}}}})}^2}{D_{\mathit{\text{ij}}}^{\ast }}$ and $\sum _{i<j,c_i\ne c_j}\frac{{(D_{\mathit{\text{ij}}}^{\ast }-D_{b_{\mathit{\text{ij}}}})}^2}{D_{\mathit{\text{ij}}}^{\ast }}$ are the within-cluster and between-cluster stress, respectively, D_wij is the within cluster Euclidean distance between case i and j if they are in the same cluster, and D_bij is the between cluster Euclidean distance between case i and j if they belong to different clusters; α and β are the weights of the within-cluster stress and between-cluster stress, respectively, a, β > 0 and α + β = 1. Note again that the Sammon stress is a special case of EPP stress when there is only one cluster, c_i = 1, i = 1, 2, …, N and the weights of within cluster and between cluster stresses are equal, α = β.

EPP algorithm aims to obtain an interesting two-dimensional projection of the original high dimensional data that minimizes its stress function. The optimization problem is expressed as

$$\begin{array}{cc}\text{minimize}\hfill & \alpha S_{\mathit{\text{EPP}}\_w}+\beta S_{\mathit{\text{EPP}}\_b}\hfill \\ \text{subject to}\hfill & \alpha ,\beta >0,\alpha +\beta =1.\hfill \end{array}$$ (13)

Definition 3

To minimize S_EPP (α, β, f_x) where f_x stands for the projections of D_wij and D_bij, the gradual approximation algorithm works as: Given a fixed pair of α and β, update the values of f_x where S_EPP has the minimum value, that is, keep updating α and β until there are no changes according to (12).

$$\{\begin{array}{c}\alpha =\alpha +\delta ,\beta =\beta -\delta ,\text{if }{S}_{\mathit{\text{EPP}}}(\alpha +\delta ,\beta -\delta ,f_x)<S_{\mathit{\text{EPP}}}\hfill \\ \alpha =\alpha -\delta ,\beta =\beta +\delta ,\text{if }{S}_{\mathit{\text{EPP}}}(\alpha -\delta ,\beta +\delta ,f_x)<S_{\mathit{\text{EPP}}}\hfill \\ \alpha =\alpha ,\beta =\beta ,\text{otherwise}\hfill \end{array}$$ (14)

The main EPP algorithm is shown in Algorithm 1(a). The embedded gradual approximation algorithm is displayed in Algorithm 1(b) to minimize S_EPP given α and β; the values of f_x were retained when S_EPP has the minimum value. Specifically, the EPP algorithm initialize X′ based on the results from PCA; update f_x according to Algorithm 1(b) based on Equation (15), calculate the EPP stress and update α and β, with a weight change step δ based on Equation (14). If the difference between two consecutive stress values is less than the threshold ε, the algorithm stops. Repeat this process until reaching the maximum iteration number, l_max.

$$f_{x_l}=\underset{f_x}{\text{arg min }}{S}_{\mathit{\text{EPP}}}({\alpha }_l,{\beta }_l,f_x).$$ (15)

Algorithm 1(b).

Algorithm for Updating f_x

Input: Projections X′, α and β, error bound ε, maximum iteration number mmax, SEPP(0) → ∞
Output: SEPP(m+1) and fx(m+1)
1:	for m = 0 to mmax do
2:	fx(m+1) = fx(m) − τ · Δ(m)
3:	SEPP(m+1) = SEPP (α, β, fx(m+1))
4:	if |SEPP(m+1) − SEPP(m)| ≤ ε then
5:	break
6:	end if
7:	end for

Note that in Algorithm 1(b) when updating f_x, f_x^(m) are the projections of the data on the two-dimensional space at the m-th iteration, τ is the iteration step size which is set at 0.3 or 0.4 according to [60], ${\mathrm{\Delta }}^{(m)}=\frac{\partial {S_{\mathit{\text{EPP}}}}^{(m)}}{\partial {f_x}^{(m)}}/\left|\frac{{\partial }^2{S_{\mathit{\text{EPP}}}}^{(m)}}{\partial {({f_x}^{(m)})}^2}\right|$ and $w=\frac{-2}{\sum _{i<j}{D}_{\mathit{\text{ij}}}^{\ast }}$ is a constant. Then the first-order derivative with respect to f_x is shown in Equation (16) and the second-order derivative is expressed in Equation (17).

Unlike nonlinear mapping algorithm [60], the EPP algorithm further automates the searching and finds the optimal number of iterations to display a stable structure by learning the change of S_EPP in two consecutive iterations at a range of varying error bounds, sample size and the number of dimensions.

4 EPP Performance in Case Studies

Our EPP method was tested on 3 real datasets, including one publicized [66] and two random controlled trial (RCT) datasets [43], [67]–[69]. These data features are summarized in Table 2.

TABLE 2.

Real Data Description

Name	Waveform	TDTA	QuitPrimo
Cases(N)	5000	109	1320
Components(p)	21	5	3
Time points(t)	1	4	6
Total data size(ℓ)	105,000	2,180	23,760
Clusters(c)	3	3	4

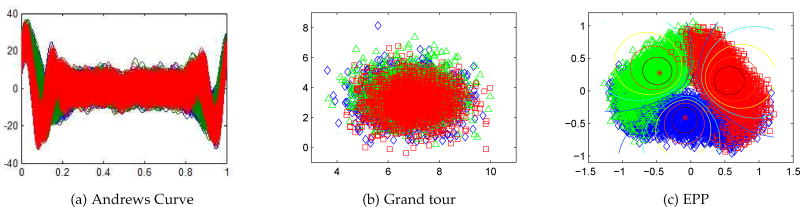
The Waveform data were generated by a clustering data generator described in [70] and published by [66], [70]. It consists of 5000 cases, each with 21 attributes (ℓ = 105, 000). There are 3 clusters of waves identified for testing algorithms. Figure 1 shows the performance of the three PP methods for waveform datasets. Clearly, Andrews Curve and grand tour were unable to visualize the three classes while the EPP demonstrated its projection power in visualizing the 3-cluster structure.

Fig. 1.

Projection Pursuit of Waveform data using Andrews Curve, grand tour and proposed EPP

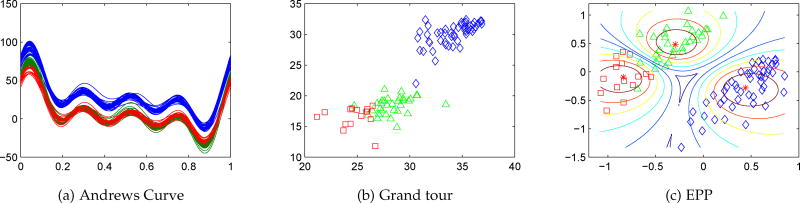
TDTA data were collected from a longitudinal culturally-tailored smoking cessation intervention for 109 Asian American smokers (ℓ = 2, 180). It contains three identified culturally-adaptive response patterns [43]. This intervention used three components: Cognitive behavioral therapy, cultural tailoring, and nicotine replacement therapy. The first two were measured by scores on Perceived Risks and Benefits, Family and Peer Norms, and Self-efficacy scales. Each scale has four repeated measures, total 20 attributes, of which only Perceived Benefits and Family Norms were used using our multiple imputation based fuzzy clustering method discussed elsewhere [71]–[73]. As shown in Figure 2, two of the three clusters projected by Andrews Curve was completely overlapped, while Grand Tour seems to perform as good as EPP for this longitudinal dataset. The parameters of TDTA data are shown in Table 3 and Table 4.

Fig. 2.

Projection Pursuit of TDTA data using Andrews Curve, grand tour and proposed EPP

TABLE 3.

Mean values of TDTA Data

		t1	t2	t3	t4
Benefits	C1	133	128	127	127
	C2	138	127	133	134
	C3	113	112	115	112
Family Norm	C1	116	116	113	111
	C2	116	115	114	115
	C3	101	102	100	99

TABLE 4.

Standard Deviation of TDTA Data

		t1	t2	t3	t4
Benefits	C1	13.89	21.15	17.35	22.60
	C2	14.88	25.80	16.21	14.54
	C3	26.38	16.11	16.59	19.95
Family Norm	C1	9.94	7.19	9.88	12.20
	C2	7.22	7.98	9.14	9.63
	C3	12.96	10.81	12.17	9.47

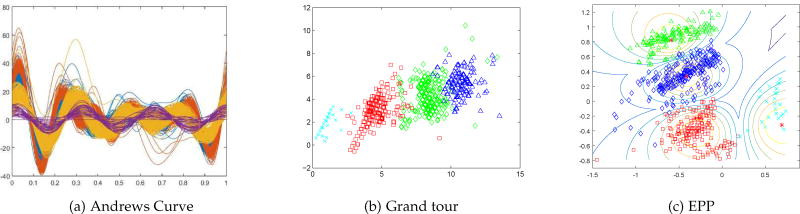
QuitPrimo dataset includes 1320 cases (ℓ = 23, 760) with missing values about 8.4%. This study aims to evaluate an integrated informatics solution to increase access to web-delivered smoking cessation support. The data is collected via an online referral portal about three components: 1) My Mail, 2) Online Community, 3) Our Advice. Each of the first three component has 6 monthly values measured during 6 months. Figure 3 again showcases the strength of EPP over the other two methods for this big longitudinal dataset. Projected four patterns were overlapped using Andrews Curve while and the blue and green patterns were overlapped to a noticeable degree using the Grand Tour. Table 5 and 6 show the mean values and standard deviations of QuitPrimo dataset, respectively.

$$\frac{\partial {S_{\mathit{\text{EPP}}}}^{(m)}}{\partial {f_x}^{(m)}}=\{\begin{array}{c}w\sum _{j=1,j\ne p}^N\left[\frac{D_j^{\ast }-D_{w_j}}{D_j^{\ast }{D}_{w_j}}\right]({f_x}^{(m)}-{X_j}^{\prime (m)})\text{if }{c}_p=c_j,\hfill \\ w\sum _{j=1,j\ne p}^N\left[\frac{D_j^{\ast }-D_{b_j}}{D_j^{\ast }{D}_{b_j}}\right]({f_x}^{(m)}-{X_j}^{\prime (m)})\text{if }{c}_p\ne c_j.\hfill \end{array}$$ (16)

$$\frac{{\partial }^2{S_{\mathit{\text{EPP}}}}^{(m)}}{\partial {\left({f_x}^{(m)}\right)}^2}=\{\begin{array}{c}w\sum _{j=1,j\ne p}^N\frac{1}{D_j^{\ast }{D}_{w_j}}[(D_j^{\ast }-D_{w_j})-\frac{{({f_x}^{(m)}-{X_j}^{\prime (m)})}^2}{D_{w_j}}(1+\frac{D_j^{\ast }-D_{w_j}}{D_{w_j}}\left)\right]\text{if }{c}_p=c_j,\hfill \\ w\sum _{j=1,j\ne p}^N\frac{1}{D_j^{\ast }{D}_{b_j}}[(D_j^{\ast }-D_{b_j})-\frac{{({f_x}^{(m)}-{X_j}^{\prime (m)})}^2}{D_{b_j}}(1+\frac{D_j^{\ast }-D_{b_j}}{D_{b_j}}\left)\right]\text{if }{c}_p\ne c_j.\hfill \end{array}$$ (17)

Fig. 3.

Projection Pursuit of QuitPrimo data using Andrews Curve, grand tour and proposed EPP

TABLE 5.

Mean values of QuitPrimo Data

		t1	t2	t3	t4	t5	t6
MM	C1	0.747	0.154	0.017	0.025	0.006	0.000
	C2	1.091	0.465	0.139	0.080	0.139	0.043
	C3	0.047	0.000	0.000	0.000	0.000	0.000
	C4	0.659	0.157	0.003	0.000	0.000	0.000
OA	C1	5.708	8.601	8.736	6.902	3.997	3.638
	C2	5.708	8.601	8.736	6.902	3.997	3.638
	C3	0.888	0.100	0.000	0.000	0.000	0.000
	C4	6.345	8.686	5.857	1.213	0.007	0.000
OC	C1	0.284	0.020	0.006	0.006	0.003	0.006
	C2	0.455	0.080	0.011	0.021	0.021	0.000
	C3	0.006	0.000	0.000	0.000	0.000	0.000
	C4	0.275	0.031	0.014	0.000	0.000	0.000

TABLE 6.

Standard Deviation of QuitPrimo Data

		t1	t2	t3	t4	t5	t6
MM	C1	1.718	1.124	0.237	0.339	0.106	0.000
	C2	1.595	2.437	0.979	0.732	1.079	0.462
	C3	0.384	0.000	0.000	0.000	0.000	0.000
	C4	1.972	1.246	0.059	0.000	0.000	0.000
OA	C1	1.972	1.246	0.059	0.000	0.000	0.000
	C2	2.431	0.875	0.893	1.394	1.172	1.484
	C3	2.249	0.457	0.000	0.000	0.000	0.000
	C4	2.490	1.067	3.384	1.797	0.083	0.000
OC	C1	2.490	1.067	3.384	1.797	0.083	0.000
	C2	0.996	0.463	0.103	0.178	0.206	0.000
	C3	0.078	0.000	0.000	0.000	0.000	0.000
	C4	0.783	0.194	0.186	0.000	0.000	0.000

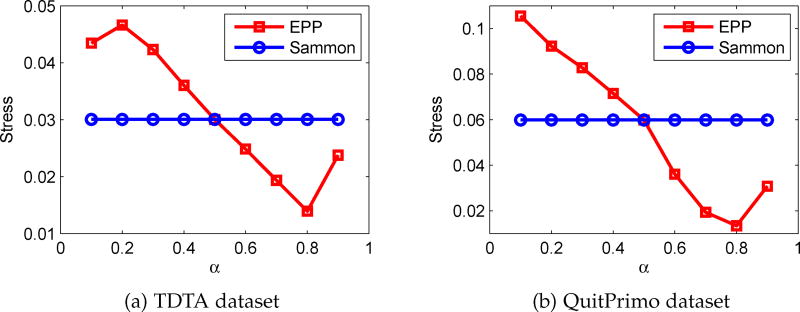
The optimal pairs, α and β, for included real longitudinal datasets TDTA and QuitPrimo given f_x can be detected by the following steps. Initialize a pair of values, e.g., (0.5,0.5), and calculate the stress of the proposed EPP method by Equation (10) and (11). Increase α and decrease β, or vice versa, by a boundary parameter δ, e.g., δ = 0.1, to obtain a new stress value. Updating α and β until the stress values no longer decease, we can obtain the optimal weights α and β for the within and between cluster stresses. As shown in Figure 4(a) and Figure 4(b), the optimal weights of (0.8, 0.2) were founded for TDTA and QuitPrimo data, respectively.

Fig. 4.

Finding an optimal pair of weights that balance the between and within stresses for TDTA and QuitPrimo using EPP (blue line is reference line from Sammon’s Stress)

5 EPP Performance Using Simulated Longitudinal Data

The proposed EPP was also evaluated using simulated data. First, simulated longitudinal data were generated using parameters from the two real datasets, TDTA and QuitPrimo. The data generation procedure is described as follows:

1. Fit the multivariate normal distribution to TDTA and the zero-inflated Poisson mixture distribution to the QuitPrimo web trial data [71], respectively, and learn the parameters such as cluster mean vectors and standard deviations, the results are shown in Table 3, 4, 5 and 6;

2. Set the number of cases of each cluster according to the proportion of each cluster (Table 7);

3. Generate data for each cluster based on the model parameters from (1) and cluster size (2).

4. Randomize data from (3) to generate a complete dataset;

5. Repeat (1–4) and generate datasets with varying sample sizes, N is in {100, 200, 300, 500, 1000, 5000}, d_TDTA = 20, d_QuitPrimo = 18, and ℓ_TDTA = {2000, 4000, 6000, 10000, 20000, 100000}, ℓ_QuitPrimo = {1800, 3600, 4800, 9000, 18000, 36000}.

TABLE 7.

Cluster Information for TDTA and QuitPrimo

	cluster	1	2	3	4
TDTA	# of cases	50	31	16	-
	proportions	0.52	0.32	0.16	-
QuitPrimo	# of cases	356	187	490	287
	proportions	0.27	0.14	0.37	0.22

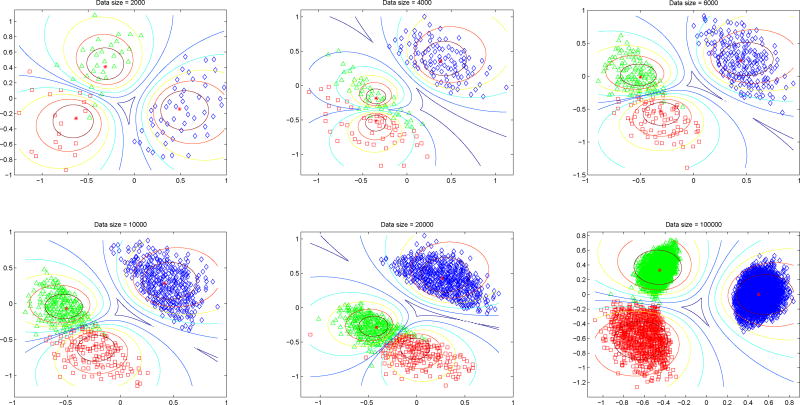
Figure 5 displays the EPP projection based on the TDTA parameters using different sample sizes. From N = 100 to N = 5000, the clusters are clearly projected. With smaller sample sizes, the data points are more spread within the cluster. The red and green clusters are closer to each other compared to the blue cluster.

Fig. 5.

EPP for simulated longitudinal data using TDTA parameters and ℓ is from 2000 to 100000

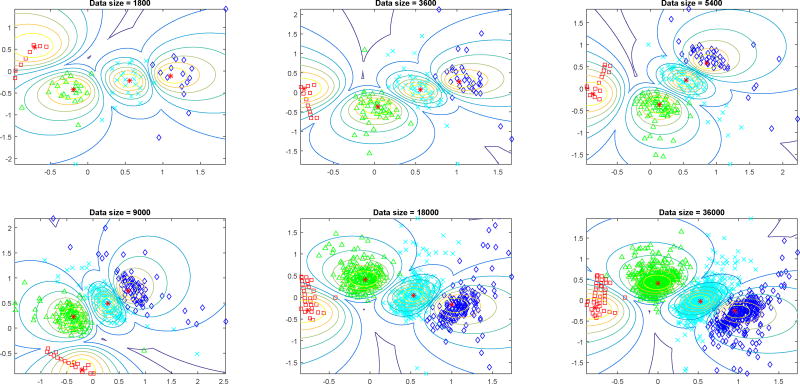
Based on the QuitPrimo parameters, EPP again clearly projected the four clusters across a range of data size ℓ. The blue cluster is always far apart from the red cluster; the other three clusters always touch each other as shown in Figure 6.

Fig. 6.

EPP for simulated longitudinal data using QuitPrimo parameters and from 1800 to 36000

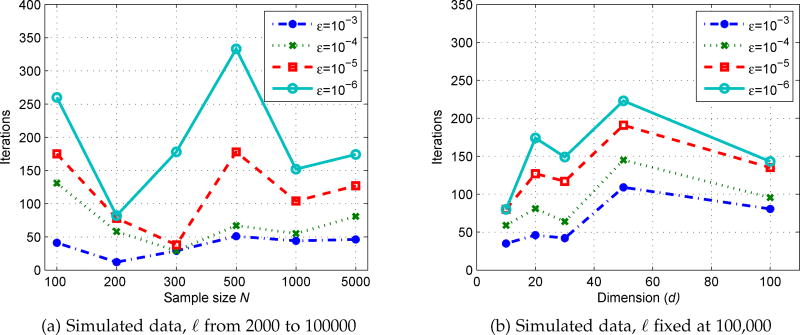
Using the same simulated data sets, the optimal number of iterations were tested for the proposed EPP method using a different number of sample sizes or dimensions. In Figure 7 (a), the number of dimensions was fixed at 20, and the data sizes ℓ were varied from 2,000 to 100,000. In Figure 7 (b), the data sizes ℓ was fixed at 100,000, and the number of dimensions d were varied from 2 to 100. For all conditions, the change between iterations (ε) was varied from 10⁻³ to 10⁻⁶.

Fig. 7.

The optimal number of iterations for EPP at different number of sample sizes or dimensions for simulated data

The findings indicate that across different sample sizes or dimensions or the change of stresses between iterations (ε), the optimal number of iteration seem to be always below 350.

Furthermore, using the same data generation procedure, an artificial longitudinal dataset was generated with standardized mean and variance-covariance matrices to evaluate the EPP performance. The mean vector was set as 0.2, 0.5, and 0.8 for three clusters [74], [75], the correlation matrix (standardized variance-covariance matrix) was set with 1 at the diagonal and other matrix elements were randomly selected from {0.1, 0.3, 0.5} [74], [75]. The data size was varied from 1,000 to 500,000 and dimensions were changed from 10 to 100. The different colored planes stand for the four settings for the change of stresses between iterations (ε), 10⁻³, 10⁻⁴, 10⁻⁵, and 10⁻⁶. As shown in Figure 8, the optimal number of iterations seem to be always below 500 across different sample sizes, dimensions and error bounds (ε) for the change between iterations. Using 500 iterations could be an empirical rule for setting the iterations for EPP. Overall, in terms of computational time, EPP cost 11 and 22 seconds for projecting real TDTA and QuitPrimo data while up to 9 minutes assuming the worst scenario of N = 20,000 and dt = 100.

Fig. 8.

The optimal number of iterations for EPP algorithm for the artificial longitudinal data with varied sample sizes, dimensions and error bounds (ε) for the change between iterations

6 Conclusion

Pattern visualization is a challenging field. A robust projection pursuit method could enormously ease pattern recognition. Our enhanced projection pursuit (EPP), a variant of classic Sammon Mapping, balances the weights of between and within cluster variations and better project big high dimensional longitudinal data onto two-dimensional plane using nonlinear mapping algorithms. Compared to classical Andrews Curve and Grand Tour, our EPP method seems to perform consistently well and was more robust to such data. Different from the two methods, EPP was not built upon trigonometric functions as not all longitudinal datasets follow this assumption, especially those longitudinal random controlled trial (RCT) or observational data [40]–[45], [67], [74], [76]. Using the publicized UCI dataset, real longitudinal RCT datasets and a number of simulated big longitudinal data, EPP showcases its clear and better projection power with respect to high-dimensionality, sample sizes and error bounds for the change between iterations with satisfactory computational costs. Embedding EPP into different trajectory pattern recognition systems and further reducing computational time for bigger data would be future tasks. Testing EPP on more big longitudinal data could further warrant its robustness.

Biographies

Hua Fang is an Associate Professor in the Department of Computer and Information Science, Department of Mathematics, University of Massachusetts Dartmouth, 285 Old Westport Rd, Dartmouth, MA, 02747; Department of Quantitative Health Sciences, University of Massachusetts Medical School, Worcester, MA, 01605; Division of Biostatistics and Health Services Research, Department of Quantitative Health Sciences, University of Massachusetts Medical School. Dr. Fang’s research interests include computational statistics, research design, statistical modeling and analyses in clinical and translational research. She is interested in developing novel methods and applying emerging robust techniques to enable and improve the studies that can have broad impact on the treatment or prevention of human disease.

Zhaoyang Zhang received the B.S. degree in science and the M. S. degree in electrical engineering from Xidian University, Xian, China, in 2007 and 2010, respectively. He is currently pursuing his Ph.D. degree in the College of Engineering, University of Massachusetts, Dartmouth, MA, USA. His current research interests include wireless healthcare, wireless body area networks, big data and cyber-physical systems.