Phantom-based field maps for gradient nonlinearity correction in diffusion imaging

Abstract

Gradient coils in magnetic resonance imaging do not produce perfectly linear gradient fields. For diffusion imaging, the field nonlinearities cause the amplitude and direction of the applied diffusion gradients to vary over the field of view. This leads to site- and scan-specific systematic errors in estimated diffusion parameters such as diffusivity and anisotropy, reducing reliability especially in studies that take place over multiple sites. These errors can be substantially reduced if the actual scanner-specific gradient coil magnetic fields are known. The nonlinearity of the coil fields is measured by scanner manufacturers and used internally for geometric corrections, but obtaining and using the information for a specific scanner may be impractical for many sites that operate without special-purpose local engineering and research support. We have implemented an empirical field-mapping procedure using a large phantom combined with a solid harmonic approximation to the coil fields that is simple to perform and apply. Here we describe the accuracy and precision of the approach in reproducing manufacturer gold standard field maps and in reducing spatially varying errors in quantitative diffusion imaging for a specific scanner. Before correction, median B value error ranged from 33 – 41 relative to manufacturer specification at 100 mm from isocenter; correction reduced this to 0 – 4. On-axis spatial variation in the estimated mean diffusivity of an isotropic phantom was 2.2% – 4.1% within 60 mm of isocenter before correction, 0.5% – 1.6% after. Expected fractional anisotropy in the phantom was 0; highest estimated fractional anisotropy within 60 mm of isocenter was reduced from 0.024 to 0.012 in the phase encoding direction (48% reduction) and from 0.020 to 0.006 in the frequency encoding direction (72% reduction).

1. INTRODUCTION

Multi-site studies are becoming more common as necessary sample sizes for imaging studies increase. For MRI diffusion imaging to provide reliable quantitative measurements across sites and scanners, a number of confounding site effects must be managed. One in particular is the error introduced by neglecting to account for the scanner-specific nonlinearity of the gradient fields, which leads to spatial variation in the amplitude and direction of the applied diffusion gradients. Empirically, this has been an important source of error in multi-site studies ^{Malyarenko 2016}.

Various estimates of the coil field nonlinearities have been applied to improve accuracy within and across sites ^{Tan 2013, Newitt 2015, Malkyarenko 2014a,b}. The spatial derivatives of the gradient fields can be used to more accurately compute the gradients that are actually obtained during imaging ^{Bammer 2003}, which is becoming a standard practice ^{e.g. Sotiropoulos 2013, Glasser 2013}. Here we implement and evaluate a procedure for the latter approach that uses an empirical field map derived from a brief phantom scan.

2. METHODS AND DATA

We measured the magnetic field produced by each gradient coil using a large oil-filled phantom as described in previous work ^{Rogers 2017a,b}. Solid harmonic basis functions were then fit to the measured field, and the fitted field was used to estimate the actually achieved diffusion gradient directions and b-values on a voxel-wise basis. These values were used to fit a diffusion tensor model to data from an isotropic aqueous phantom. We measured diffusivity and fractional anisotropy before and after adjustment and compared.

2.1 Gradient coil field measurements

Scanning was performed on a 3 Tesla MRI system. The gradient field mapping phantom was a synthetic oil in a polypropylene container 290 mm diameter, 500 mm height, holding 24 liters. The phantom was placed at scanner isocenter and imaged with a dual echo EPI-based field mapping sequence. Four field maps were acquired, one each with shim field set to 0.05 mT/m on each axis X, Y, Z plus a final image with gradient coil shim fields set to zero. Each used a 384 mm field of view with 4 mm isotropic voxel size. Total scan time was approximately 5 minutes. Gradient coil fields were estimated by substracting the zero-shim field map from each coil’s respective 0.05 mT/m field map (Figure 1). Field maps were acquired on 29 dates over the course of a year.

Figure 1.

field mapping phantom. Left, photograph. Center, MR image. Right, X gradient coil field map at isocenter.

We modeled each coil’s field as a sum of solid harmonics ^{Tough 1977, Caola 1978, Bammer 2003} to 7th order, excluding even order terms due to the coils’ physical symmetry. These basis functions were fit to the field measurements with robust least squares, using all voxels within a 270 mm diameter sphere at isocenter. The result was an analytically differentiable estimate of the true magnetic field produced by each gradient coil. This fitting procedure was performed on the field maps from individual scans; on the average field map derived from all scans; and on the scanner manufacturer’s estimate of the coil fields as measured during manufacturing and installation.

2.2 Estimating achieved b-values and gradient directions

A spatially varying tensor L relates the achieved gradient to the intended gradient, where B_i is the gradient field for the ith coil Bammer 2003:

$$\mathbf{L}=\left[\begin{array}{ccc}\frac{\partial B_x}{\partial x}& \frac{\partial B_y}{\partial x}& \frac{\partial B_z}{\partial x}\\ \frac{\partial B_x}{\partial y}& \frac{\partial B_y}{\partial x}& \frac{\partial B_z}{\partial y}\\ \frac{\partial B_x}{\partial z}& \frac{\partial B_y}{\partial z}& \frac{\partial B_z}{\partial z}\end{array}\right]$$

This tensor may be computed analytically from the solid harmonic approximation to the measured field, then evaluated at spatial locations of interest. In the common situation where the scanner reports the intended gradient direction and amplitude but the full b-matrix ^{Mattiello 1994, Mattiello 1997, Alger 2012} is not known, an approximate correction to adjust the intended gradient G for the coil nonlinearity is ^{Tan 2013}

$${\mathit{G}}^{\prime }=\mathbf{L}\mathit{G}$$

This estimate of the achieved gradient can then be expressed as the product of an adjusted scalar b-value and a unit vector, G′ = b′g′, which is spatially varying but otherwise may be used in any desired way for further processing of the diffusion images.

2.3 Diffusion imaging of isotropic aqueous phantom

A phantom containing an aqueous solution of polyvinylpyrrolidone ^{Pierpaoli 2009} was scanned with a 16-direction diffusion weighted imaging sequence with b=1500. Each direction was acquired in both + and − polarities to permit correction for cross term effects between the diffusion and the imaging gradients ^{Wu 2007}. Additionally, the entire scan was repeated with images acquired using the opposite phase encoding direction. Finally, diffusion weighted images were adjusted for eddy current effects ^{Andersson 2016} and geometric distortion ^{Andersson 2003} using the FSL software suite ^{Jenkinson 2012}. The diffusion tensor model was then fit at each voxel using, first, the standard assumption of b=1500; and second, the nonlinearity-corrected b-values and gradient vectors described above.

3. RESULTS

Before correction, median B value error ranged from 33–41 relative to manufacturer specification at 100 mm from isocenter; correction reduced this to 0–4. On-axis spatial variation in the estimated mean diffusivity of an isotropic phantom was 2.2% – 4.1% within 60 mm of isocenter before correction, 0.5% – 1.6% after. Expected fractional anisotropy in the phantom was 0; highest estimated fractional anisotropy within 60 mm of isocenter was reduced from 0.024 to 0.012 in the phase encoding direction (48% reduction) and from 0.020 to 0.006 in the frequency encoding direction (72% reduction).

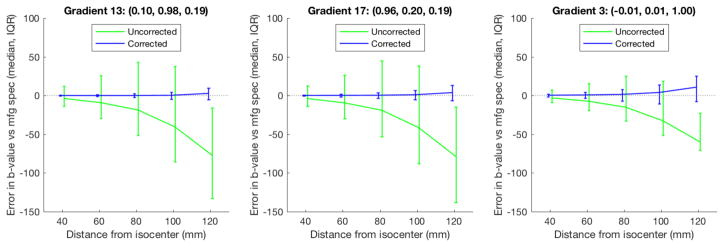
3.1 Spatial variation in b-value

Achieved b-values varied substantially from the specified value of 1500 at greater distances from isocenter (Figure 2, green). For instance, at 100 mm from isocenter where brain tissue is likely to be placed in practice for many scans, achieved b-values for half the voxels were 2.7% or more away from specified for one of the diffusion gradient directions (Figure 2, left panel). The discrepancy between assumed and achieved b-value was considerably reduced by applying the empirical field map based adjustment (Figure 2, blue).

Figure 2.

achieved b-values. Gradient field nonlinearity correction using the individual field maps (blue) substantially reduced errors in assumed b-values compared to no correction (green). Intended b-value was 1500. Errors are with reference to the manufacturer specified gradient coil fields.

3.2 Spatial variation in estimated diffusivity

Without accounting for gradient coil nonlinearity, the estimated diffusivity of the isotropic phantom in a 120 mm field of view varied spatially by up to 2.2% – 4.1% from the value at isocenter (Figure 3, green). Applying the correction based on the average empirical field map reduced this variation to 0.5% – 1.6% and substantially improved the homogeneity of the estimate over space (Figure 3, blue). Even the corrections based on a single five-minute field map scan provided significant improvements in all cases (Figure 3, cyan).

Figure 3.

estimated diffusivity. Gradient field nonlinearity correction (red, blue, cyan) substantially reduced spatial hetereogeneity in estimated diffusivity of an isotropic phantom compared to standard assumptions (green).

Similarly, before correction the estimated fractional anisotropy of the isotropic phantom ranged from 0.006 to 0.024 in a 120 mm field of view (figure 4, green). After correction, the estimate was much more accurate, reaching only 0.013 in the worst case, at the edge of the field of view in the phase-encoding direction near the susceptibility artifact introduced by a small air bubble in the phantom (Figure 4, blue and cyan).

Figure 4.

fractional anisotropy. Gradient field nonlinearity correction (red, blue, cyan) substantially improved the accuracy of estimated fractional anisotropy of an isotropic phantom compared to standard assumptions (green).

4. DISCUSSION

Nonlinearities in the achieved gradient fields on the studied scanner led to b-value errors of 2.7% and higher, and spatial variations of up to 4.1% in estimated diffusivity, within fields of view that are typical for brain imaging. This confirms similar findings by others ^{Malyarenko 2016, Bammer 2003, Newitt 2015}. These errors are large enough to cause important inaccuracies when measuring quantitative diffusion parameters. In single-site studies, the typical variation in head position from one person to another is enough to produce errors in estimated parameters. Multi-site studies will have increased errors due to differences in the physical properties of the gradient coils. The use of empirical field maps to measure the coil nonlinearities reduced these errors substantially. The method is quick and straightforward, can be applied retroactively, and does not require specialized engineering knowledge or access to scanner internals.