Secure genome-wide association analysis using multiparty computation

Abstract

Most sequenced genomes are currently stored in strict access-controlled repositories^1–3. Free access to these data could improve the power of genome-wide association studies (GWAS) to identify disease-causing genetic variants and may aid in the discovery of new drug targets^4,5. However, concerns over genetic data privacy^6–9 may deter individuals from contributing their genomes to scientific studies¹⁰ and in many cases, prevent researchers from sharing data with the scientific community¹¹. Although several cryptographic techniques for secure data analysis exist^12–14, none scales to computationally intensive analyses, such as GWAS. Here we describe an end-to-end protocol for large-scale genome-wide analysis that facilitates quality control and population stratification correction in 9K, 13K, and 23K individuals while maintaining the confidentiality of underlying genotypes and phenotypes. We show the protocol could feasibly scale to a million individuals. This approach may help to make currently restricted data available to the scientific community and could potentially enable ‘secure genome crowdsourcing,’ allowing individuals to contribute their genomes to a study without compromising their privacy.

GWAS aim to identify genetic variants that are statistically correlated with phenotypes of interest (e.g., disease). Analyzing large numbers of individuals is critical for detecting weak, yet important, genetic signals, such as rare variants or those with small effect sizes^4,5. However, privacy concerns^6–9 have stymied these large-scale studies by discouraging individuals and institutions from sharing their genomes^10,11 and necessitating strict access-control policies for the amassed data sets, which limit their utility.

Modern cryptography could potentially enable what we refer to as ‘secure genome crowdsourcing,’ where the input data for population-based studies like GWAS are massively pooled from private individuals or individual entities while hiding the sensitive information (i.e., genotypes and phenotypes) from any entity other than the original data owners. For example, secure multiparty computation (MPC) frameworks¹² enable researchers to collaboratively perform analyses over securely shared data without having direct access to the underlying input. The confidentiality of input data guaranteed by such frameworks would greatly encourage genomic data sharing. Moreover, unlike the current practice of entrusting a single entity (e.g., a biobank^1–3) with the raw data, a breach or corruption of a single party—an increasingly probable event in an era where companies’ sensitive user data are routinely leaked in bulk—no longer compromises the privacy of study participants. However, existing proposals for securely performing GWAS based on cryptographic tools like MPC^15–21 are too limited to enable secure genome crowdsourcing in practice; they either consider vastly simplified versions of the task or require infeasible amounts of computational resources for data sets with a large number of individuals (e.g., many years of computation or petabytes of data). For example, recent work by Jagadeesh et al.²², which introduces privacy-preserving rare variant analysis based on a type of MPC technique known as garbled circuits¹⁴, is limited to simple Boolean operations and is not applicable to large-scale GWAS, as noted in their work.

A major computational bottleneck for secure GWAS is identifying, and correcting for, population structure, which can cause spurious associations that reflect inter-population differences, rather than true biological signal²³. A widely used procedure for accounting for such confounding is to use principal component analysis (PCA) to capture broad patterns of genetic variation in the data²⁴. The top principal components, which are thought to be representative of population-level differences among individuals, are included as covariates in the subsequent association tests to correct for bias. However, performing PCA on very large matrices is challenging for secure computation and, to our knowledge, has not been successfully addressed. This barrier is mainly due to the iterative nature of PCA, which greatly increases the communication cost and overall complexity of the computation. In addition, PCA requires computing over fractional values with sufficient precision. This introduces non-trivial overhead to most existing cryptographic frameworks which are inherently restricted to integer operations. Supporting computations over fractional values not only increases the size of the data representation, but also increases the complexity of the basic underlying operations, such as multiplication and division.

Here, we present the first secure, practically feasible MPC protocol for GWAS that includes both quality control and population stratification correction (Online Methods). An overview of our pipeline is provided in Figure 1. Our protocol has two types of entities: study participants (SPs) and computing parties (CPs). SPs refer to private individuals, institutions, or intermediary data custodians that own the genomes and phenotypes to be collectively analyzed for the study. CPs consist of three independent parties with appropriate computing resources (CP₀, CP₁, and CP₂) that cooperatively carry out the GWAS computation. We envision academic research groups, consortia, or relevant government agencies (e.g., the US National Institutes of Health (NIH); Bethesda, MD) to have these roles. At the beginning of our protocol, each SP securely shares their data with CP₁ and CP₂ using a cryptographic technique called ‘secret sharing’²⁵. Next, CP₁ and CP₂ jointly execute an interactive protocol to perform GWAS over the secret shares without learning any information about the underlying data. During this step, precomputed values from CP₀, which are independent of the data from the SPs, are used to greatly speed up the process. Importantly, CP₀ does not see the input and is involved only during preprocessing. Lastly, CP₁ and CP₂ combine their results to reconstruct the final GWAS statistics and publish them. A complete protocol description is provided in Supplementary Notes 1–9.

Figure 1. Overview of our secure GWAS pipeline.

Study participants (private individuals or institutes) secretly share their genotypes and phenotypes with computing parties (research groups or government agencies), denoted CP₁ and CP₂, who jointly carry out our secure GWAS protocol to obtain association statistics without revealing the underlying data to any party involved. An auxiliary computing party (CP₀) performs input-independent precomputation to greatly speed up the main computation.

Notably, the total communication complexity of our protocol (i.e., the total amount of data transferred between the CPs) scales linearly in the number of individuals (n) and the number of variants (m) for both the precomputation and the main computation phases after initial data sharing (Supplementary Note 9). In contrast, directly applying state-of-the-art MPC frameworks^26–28 leads to quadratic complexity with large multiplicative constants, which is vastly impractical when both n and m are close to a million. This is primarily because existing frameworks strictly adhere to a modular execution of the computation purely expressed in terms of elementary additions and multiplications.

We introduce several key technical tools that overcome these limitations and improve the efficiency of existing approaches. First, we generalize a core MPC technique known as ‘Beaver multiplication triples’, which was initially developed for secure multiplication, to efficiently evaluate arithmetic circuits (Supplementary Note 3). Our generalized method enables efficient protocols for not only matrix multiplication, but also exponentiation and iterative algorithms with extensive data reuse patterns, all of which feature prominently in secure GWAS. Second, we employ cryptographic pseudorandom generators (PRGs) to greatly reduce the overall communication cost (Supplementary Note 7); when a CP needs to obtain a sequence of random numbers sampled by another CP, which constitutes a significant portion of our protocol, both parties simply derive the numbers from the shared PRG non-interactively. Third, we leverage random projection techniques²⁹, which have been shown to be effective for other genomic analyses³⁰, to reduce the task of performing PCA on the large genotype matrix (in population stratification analysis) to factoring a small constant-sized matrix (Supplementary Note 9). Lastly, we restructure the GWAS computation such that each intermediate result (which requires the CPs to communicate a message of the same size) scales linearly with the input dimensions (n and m) (Supplementary Note 9).

We apply our secure GWAS protocol to three GWAS data sets accessed through the National Center for Biotechnology Information (NCBI; Bethesda, MD) dbGaP (Online Methods): a lung cancer data set (n = 9,178), a bladder cancer data set (n = 13,060), and an age-related macular degeneration (AMD) data set (n = 22,683). With the goal of emulating standard GWAS pipelines, we incorporate common quality control filters for genotype missing rate, heterozygosity rate, minor allele frequency, and departure from Hardy-Weinberg equilibrium. We also correct for population stratification using the top principal components as in the original studies. Note that all our operations are performed securely without revealing any of the underlying data to the CPs; only the individual data providers (i.e., SPs) have access to their own raw data.

Our secure GWAS protocol accurately recapitulates the ground truth association scores we obtained based on the plaintext data (Supplementary Fig. 1). Moreover, our top results (Table 1) closely match what was presented in the original publications, despite our limited access to the original data sets and minor differences in the analysis. For example, our secure analysis of the lung cancer data identifies the two strongest associations, rs2736100 (Bonferroni-adjusted p-value = 7.99×10⁻²⁰) and rs7086803 (adjusted p = 6.16×10⁻¹²), which were also the top two findings in the original study. The third strongest (non-redundant) association rs4600802 (Supplementary Table 1) was also previously implicated for lung cancer in a published GWAS³¹. For the AMD data set, we securely identified 262 significantly-associated loci (adjusted p < 0.001), all of which are located in 9 of the 34 AMD-associated regions that were previously reported in the original study. Our results for bladder cancer were not as consistent with the prior report (while still being accurate), which we attribute to the fact that only two thirds of the original data set were available. Nevertheless, our top association for bladder cancer, rs4862110 (adjusted p = 8.79×10⁻²⁹), has been previously implicated in Wegener`s granulomatosis³², which is reported to increase the risk for bladder cancer³³. Overall, our results demonstrate the accuracy of our secure GWAS protocol in realistic scenarios.

Table 1. Our secure GWAS protocol accurately identifies SNPs with significant disease associations while protecting privacy.

We securely performed GWAS on published data sets for lung cancer (n = 9,098 after quality control), bladder cancer (n = 10,678), and age-related macular degeneration (AMD; n = 20,679). Top two significant associations for each disease identified by our protocol are shown (disregarding redundant nearby hits). Ground truth association statistics are calculated based on the plaintext data. P-values are obtained via the Cochran-Armitage trend test (one-sided) and adjusted for multiple testing via Bonferroni correction. For AMD, p-values were smaller than machine precision and thus could not be precisely determined. Our protocol infers biologically meaningful discoveries from GWAS data sets without compromising the privacy of the underlying data. We additionally provide the top 20 associations for each data set in Supplementary Tables 1–3.

Data set	Top association	Genomic position	Gene name	Cochran- Armitage statistic		Secure GWAS p-value (adjusted)
				Secure GWAS	Ground truth
Lung cancer	rs2736100	chr5:1339516	TERT	0.01194	0.01201	7.9924E-20
	rs7086803	chr10:114488466	VTI1A	0.00799	0.00796	6.1631E-12
Bladder cancer	rs4862110	chr4:183988023	DCTD	0.01403	0.01449	8.7899E-29
	rs11245742	chr11:50478883	-	0.01031	0.01101	4.0381E-20
AMD	rs3750847	chr10:124215421	ARMS2 HTRA1	0.09296	0.09297	<1E-300
	rs3766405	chr1:196695161	CFH	0.07441	0.07440	<1E-300

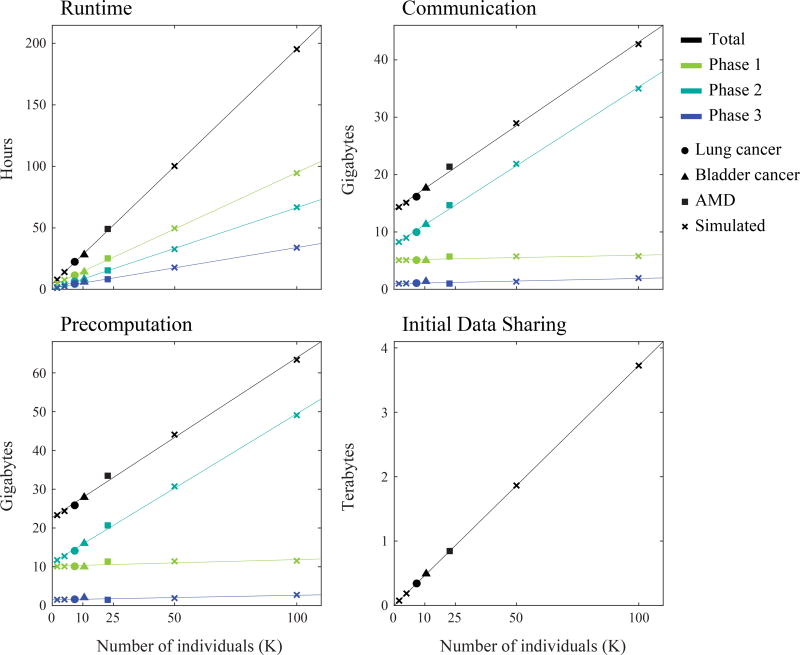
In addition to obtaining accurate association statistics, our secure GWAS protocol achieves a practical runtime of under 3 days for all three data sets (Fig. 2). To assess the scalability of our framework, we measure several key metrics (Online Methods), which include runtime, communication bandwidth, the size of the precomputed data, and the size of the initial data sharing. Our metrics show a clear linear dependence on the number of individuals in the data set, even for up to 100K individuals (Fig. 2). Through extrapolation, we show that our approach requires 80 days of computation for a data set with a million individuals and 500K single nucleotide polymorphisms (SNPs), which is well within the practical realm. Further improvements are possible using parallel computation. As a point of reference, the average access request processing time for controlled-access genomic data by the NIH Data Access Committee was 80 days in 2009–2010, although this was claimed to be reduced to 14 days in 2016 (https://osp.od.nih.gov/scientific-sharing/). Note that secure GWAS obviates the need for such an access control procedure as the data remain private throughout the study.

Figure 2. Our secure GWAS protocol achieves practical runtimes, and all of our scalability metrics follow a linear trend.

We quantified runtime, communication bandwidth, the size of the precomputed data, and the size of the initial data sharing (Online Methods) for the lung cancer, bladder cancer, and AMD data sets as well as simulated data sets of varying sizes obtained by subsampling the lung cancer data set (for 2K and 5K individuals) or duplicating the AMD data set (for 50K and 100K individuals). Since the number of SNPs differ between the data sets, we normalized all measurements to 500K SNPs for comparison, assuming a linear dependence on the number of SNPs. Lines show the best linear fit for each group. Note that the observed linear trends are not perfect due to the fraction of individuals or SNPs passing quality control being different across different data sets. Overall, our protocol achieves practical runtimes, and all of our performance measures scale linearly with the number of individuals. Phase 1: Quality control procedure. Phase 2: Population stratification analysis (PCA). Phase 3: Association tests.

Other metrics also demonstrate reasonable scaling; for a million individuals and 500K SNPs, the size of the initial data sharing is 36 TB (~40 MB data upload for each SP), a total of 435 GB of precomputed data is transferred from CP₀ to CP₁ or CP₂, and the total communication between CP₁ and CP₂ during the main computation is 306 GB. Our experiments were performed with co-located servers, which have low network latencies. Yet even with a coast-to-coast setup in the United States (with an approximate transfer rate of 5 MB per second), the expected increase in runtime is at most a day, due to the fact that the total communication in our protocol is relatively small. Furthermore, if the CPs wish to use a commercial cloud computing platform like Amazon EC2 for executing our protocol, the estimated monetary cost for a million-individual GWAS is a few thousand US dollars (Online Methods), even when the CPs are located on opposite coasts of the United States.

Our protocol is secure in the standard semi-honest (honest-but-curious) security model, where all parties are assumed to faithfully follow the prescribed protocol, but are free to inspect and analyze any portion of the data they observe to gain additional information about the underlying private input. Under this model, our GWAS protocol guarantees that the CPs do not learn any information about the raw genotypes or phenotypes other than what can be inferred from the published results, which include association statistics and the quality control output. We additionally require that the CPs do not collude with one another because they can reconstruct the input by combining their individual shares. We emphasize that this is already a substantial improvement over the current paradigm of entrusting a single entity to handle the raw data.

Notably, our framework can be extended in several different ways to achieve even stronger security guarantees (Supplementary Note 10). First, in the online phase of the GWAS computation, we can relax the no-collusion requirement by introducing additional CPs. If CP₀ and at least one other CP are honest and do not collude with other parties, security holds even if all of the other parties collude. Note that CP₀ is needed only during precomputation and never handles the private inputs provided by the study participants. Introducing additional CPs for the online phase does not substantially increase the total computation time because the parties perform their local computations concurrently. On the other hand, the total communication increases linearly in the number of parties. Based on our benchmarks, the network communication is only a small fraction of the overall runtime, so we believe that this is unlikely to notably reduce the scalability of our protocol. Next, if we require security against malicious parties (who may deviate from the protocol description) during the online computation, we can take the approach by SPDZ²⁷ and include a message authentication code (MAC) with each message. At the end of the protocol execution, the MAC is verified to ensure that each step of the online computation was performed according to the protocol specification. This approach roughly doubles both the total computation and communication of the protocol, but provides security against malicious CPs. We expect practitioners to decide the precise tradeoff between security and performance based on the specific details of the study.

Alternative cryptographic frameworks for secure computation, such as homomorphic encryption¹³ or garbled circuits¹⁴, currently impose an overwhelming computational burden—many years of computation or petabytes of communication at the scale of a million genomes (Supplementary Note 11)—and are therefore not viable for large-scale GWAS. Solutions based on trusted hardware (e.g., Intel Software Guard Extensions) provide another alternative to using cryptographic tools. However, this technology is still in its infancy and susceptible to numerous side-channel attacks^34,35 (e.g., cache timing attacks, page-fault attacks, branch shadowing attacks) that limit its effectiveness for large-scale, privacy-sensitive computations, such as GWAS. A major advantage of our cryptographic approach is that it provides security guarantees without relying on additional trust assumptions about any particular computing platform or hardware vendor.

Although in this work we focused primarily on a common GWAS setup based on Cochran-Armitage (CA) trend tests (Online Methods), our contributions readily generalize to other statistical analyses. In particular, we can extend our framework to support logistic regression analysis for assessing the effect size (odds ratio) of a SNP in case-control studies (Supplementary Note 12). A significant challenge in performing logistic regression is the need for iterative numeric optimization methods, which greatly increase the computational overhead of the secure computation. While our current techniques do not yield a practical runtime for a genome-wide application of logistic regression, our methods do achieve a secure and practical protocol if we restrict our attention to computing the odds ratios for a few hundred SNPs (Supplementary Fig. 2). This suggests an alternative two-step approach which may suffice for many real scenarios. In the first step, our main GWAS protocol (based on CA) is used to identify a small number of significantly associated SNPs, and then, in the second step, logistic regression is applied to compute their odds ratios.

Our work is complementary to existing literature on differential privacy techniques in biomedicine^36,37, whose aim is to control the privacy leak in the published results of a study. While the amount of sensitive information revealed by GWAS results will become increasingly smaller as the size of the GWAS data sets grow to a million genomes and beyond, it is worth noting that any existing differential privacy mechanism, such as controlled perturbation of output, can be used in conjunction with our protocol as a post-processing step.

Given the ever-increasing cost-effectiveness and commercialization of genome sequencing, we are entering the age where individuals may take ownership of their own personal genomes, and institutions and hospitals may build their own private genomic databases. Our work provides a blueprint for how modern cryptographic techniques can be used to securely analyze the unprecedented amounts of genomic data being generated and to prevent privacy concerns from negatively impacting on scientific discovery.

Online Methods

Secret sharing review

Secret sharing²⁵ allows multiple parties to collectively represent a private value that can be revealed if a certain number of parties (e.g., all of them) combine their information, but remains hidden otherwise. To illustrate, imagine an integer x that represents the genotype of an individual at a specific genomic locus. The value of x can be secret-shared with two researchers Alice and Bob by giving Alice a random number r and Bob x − r modulo a prime q, which perfectly hides x if r is uniformly chosen from the integers modulo q. While the information about x is encoded in the two shares without loss, either Alice or Bob alone does not learn anything about x. Using this technique, private individuals can freely contribute their genomes to the computing parties in our GWAS protocol, without giving anyone access to the raw data.

Secure multiparty computation review

Multiparty computation (MPC) techniques based on secret sharing¹² enable indirect, privacy-preserving computation over the hidden input. For example, secure addition of two secret-shared numbers x and y can be performed by having both Alice and Bob add their individual shares for x and y. The new shares represent a secret sharing of x + y, which is the desired computation result. Secure building block protocols for more complicated operations (e.g., multiplication, division) are similarly defined, albeit with more advanced techniques that require certain messages (a sequence of numbers) to be exchanged between Alice and Bob. By composing these protocols, arbitrary computation over the private input—even GWAS—can be carried out while keeping the input data private throughout.

Our MPC techniques for scaling secure GWAS

The key technical hurdle in applying secure MPC in practice has been its lack of scalability. The cost of communication between Alice and Bob quickly becomes impractical as the size of the input data grows and the desired computation becomes more complex. In particular, principal component analysis (PCA) is a standard procedure for GWAS that incurs an overwhelming communication burden for a large input matrix (e.g., a million in each dimension). To achieve a scalable MPC protocol for GWAS, we introduce various techniques, including improved MPC building blocks that minimize redundant computation (Supplementary Note 3), compression of messages via pseudorandom generators (Supplementary Note 7), and more efficient protocol design for GWAS (Supplementary Note 9). The resulting framework scales secure GWAS to a million genomes. Formal descriptions of secret sharing-based MPC as well as our techniques for achieving scalability are provided in Supplementary Notes 1–9.

Data preprocessing

For the lung cancer data set, the combined data across seven study groups consisted of 612,794 autosomal SNPs over 9,178 individuals (5,088 cases and 4,090 controls). The study cohort was divided into five age groups: < 40, 40–50, 50–60, 60–70, and > 70. We used binary membership vectors for age and study group as additional covariates for the association tests (10 linearly-independent features). To generate smaller data sets for scalability analysis, we randomly subsampled the individuals to obtain data sets with 2K and 5K individuals. For the bladder cancer data set, we combined the intersecting SNPs from two releases (phg000132.v2 and phg000532.v1) to obtain a data set of 566,620 autosomal SNPs over 13,060 individuals (6,211 cases and 6,849 controls). A total of 14 linearly-independent covariates included the membership to six study groups, nine age groups, and sex. For the AMD data set, we obtained the portion of data approved for general research use and classified individuals with geographic atrophy (GA), choroidal neovascularization (CNV), or mixed GA/CNV as case subjects and excluded intermediate AMD patients from the analysis, following the original analysis. This resulted in a data set of 508,740 autosomal SNPs over 22,683 individuals (9,648 cases and 13,035 controls). We used data source (blood or cell culture) and membership to 10 age groups as covariate information (10 linearly-independent features).

GWAS details

Following the original lung cancer study³⁸, we incorporated the following filters for quality control: genotype missing rate per individual < 0.05 and per SNP < 0.1, individual heterozygosity rate > 0.25 and < 0.30, minor allele frequency > 0.1, and Hardy-Weinberg equilibrium test chi-squared statistic < 28.3740 (p-value < 10⁻⁷). We used the same set of filters for the bladder cancer and AMD data sets except for the heterozygosity filter, which we excluded due to the distribution of heterozygosity rates being considerably different in these data sets. After quality control, our data consisted of 9,098 individuals and 378,492 SNPs for lung cancer, 10,678 individuals and 389,868 SNPs for bladder cancer, and 20,679 individuals and 221,295 SNPs for AMD.

For population stratification analysis, we chose a subset of SNPs with low levels of linkage disequilibrium by imposing a minimum pairwise distance threshold of 100 Kb, which resulted in 23,724 loci for lung cancer data, 23,894 loci for bladder cancer data, and 22,866 loci for AMD data. Genomic positions of the SNPs in the data are considered public, since they do not contain any private information. Therefore, this filtering step is performed on non-encrypted values. The genotypes of each SNP are standardized before PCA is performed using the same approach as previous work²⁴. We perform this standardization indirectly (i.e., computation results are adjusted after the fact) in order to avoid the size of precomputed data being quadratic in the genotype matrix dimensions (Supplementary Note 9). We kept the top five principal components for the subsequent analysis.

We used the Cochran-Armitage trend test (one-sided) to assess the association between each SNP and the disease status. In the presence of covariates (e.g., top principal components and age/study group memberships), the desired test statistic is equivalent to the squared Pearson correlation coefficient between the genotype and phenotype vectors, where the subspace defined by the covariates are projected out from both vectors before computing the correlation. The resulting correlations are revealed as the final output of our secure protocol along with the quality control results. Note that the mapping between test statistics and statistical significance (p-values) does not reveal any additional information about the input and thus is performed on non-encrypted data.

Scalability metrics

To assess the scalability of our protocol, we measured the following four quantities in our experiments: runtime, communication bandwidth, the size of the precomputed data, and the size of the initial data sharing. The runtime measurements capture just the main computation phase after the initial data sharing phase. This is because the initial transfer is heavily dependent upon the study setup (given the distributed nature of data ownership). While in practice, CP₀ would perform the precomputation prior to the online computation, we allowed CP₀ to compute and send precomputed values on-the-fly to simplify our experimental setup. As such, our reported runtimes also include the precomputation costs, which are small compared to the main computation. We also give the total size of the initial data, which consists of a genotype vector, disease status, and covariate phenotypes collected from each study participant. Initial data sharing includes: (i) distributed data transfer from each SP to CP₁ or CP₂ and (ii) an equal-sized data exchange between CP₁ and CP₂ (Supplementary Note 9). Since the exchange between CP₁ and CP₂ during this procedure can be coalesced into a single batch transfer, we note that physically shipping hard drives can serve as an alternative to online data transfer at the scale of tens of terabytes (when working with millions of genomes). Next, communication bandwidth refers to the total amount of data exchanged between CP₁ and CP₂ during the main computation phase. Finally, the size of precomputed data is the amount of data transferred from CP₀ to either CP₁ or CP₂ during the precomputation phase.

Hardware environment for benchmark experiments

The hardware systems used for our experiments are as follows:

• CP₁: 3.47 GHz Intel Xeon X5690 CPU with 176 GB RAM

• CP₂: 3.33 GHz Intel Xeon X5680 CPU with 96 GB RAM

• CP₀ and SP: 3.47 GHz Intel Xeon X5690 CPU with 48 GB RAM

Since SP only participates in the initial data transfer, the same server could be used for both parties for benchmarking purposes. Our memory usage was well below the full capacity (tens of GBs) and is expected to remain similar for larger data sets, as our protocol loads only a small number of individuals’ data into memory at a time in a streaming fashion. The required storage capacity of our protocol is determined by the size of initial data sharing; our CPs had access to a storage unit with >50 TB of space, which is notably sufficient for even a million-individual data set. All three servers were co-located with an average communication speed of 106 MB per second. The impact of using a long-distance setup is discussed in the main text. We utilized the thread-boosting feature of NTL with 20 cores on each machine, which is used only for speeding up large matrix multiplications in our computation.

Estimating monetary cost for cloud computing services

We estimated the monetary cost of running our protocol on Amazon EC2 using AWS Simple Monthly Calculator (https://calculator.s3.amazonaws.com/index.html). Requesting two “c4.4×large” instances (16 cores with 30 GB memory) on US-East (Virginia) and US-West-2 (Oregon) with 125 GB/month inter-region data transfer costs $3900 total for three months (accessed 12/02/2017) and is sufficient for a million-individual GWAS. Even the initial data transfer of 36 TB between CP₁ and CP₂, which may be better carried out by physically shipping hard drives, increases the cost by only $800.

A life sciences Reporting Summary is available.

Code availability

Our secure MPC protocol is implemented in C++ based on the number theory package NTL version 10.3.0 (http://www.shoup.net/ntl/) for finite field operations. Our code can be downloaded from http://secure-gwas.csail.mit.edu and is also available as Supplementary Code.

Data availability

We obtained three case-control GWAS data sets for lung cancer³⁸ (accession: phs000716.v1.p1), bladder cancer³⁹ (phs000346.v2.p2), and age-related macular degeneration⁴⁰ (AMD; phs001039.v1.p1) via dbGaP Authorized Access⁴¹.