Abstract
Possible links between adhesive properties and the pre-sliding (static) friction response of cartilage are not fully understood in the literature. The aims of this study are to investigate the relation between adhesion and relaxation time in articular cartilage, and the effect of relaxation-dependent adhesion on the pre-sliding response of cartilage. Adhesion tests were performed to evaluate the work of adhesion of cartilage at different relaxation times. Friction tests were conducted to identify the pre-sliding friction response of cartilage at relaxation times corresponding to adhesion tests. The pre-sliding friction response of cartilage was systematically linked to the work of adhesion and contact conditions by a slip-based failure model. It was found that the work of adhesion increases with relaxation time. Also, the work of adhesion is linearly correlated to the resistance to slip-based failure. In addition, as the work of adhesion increases, the adhered (stick) area at the moment of failure increases, and the propagation rate of the annular slip (crack) area towards its centre increases. These findings offer a mechanistic explanation of the pre-sliding friction behaviour and stick–slip response of soft hydrated interfaces such as articular cartilage and hydrogels. In addition, the linear correlation between adhesion and threshold to slip-based failure enables estimation of the adhesive strength of such interfaces directly from the pre-sliding friction response (e.g. shear wave elastography).
Keywords: pre-sliding response, relaxation time, work of adhesion, interfacial failure, stick–slip contrast, cartilage
1. Introduction
Articular cartilage is a biological tissue that cushions and lubricates the interfaces between the tips of long bones in mammals. Articular cartilage is composed of two phases: a fluid phase (water and electrolytes, 65–80% of its wet weight) and a solid phase (collagen fibrils, proteoglycans, chondrocytes and other glycoproteins) [1,2]. The interaction of the solid matrix (collagen fibrils and proteoglycans) and the pressurized fluid effectively distributes loads experienced in daily life activities [3,4]. The exceptional lubrication property of cartilage protects it from severe wear and friction. Excellent mechanical and tribological properties of cartilage make it last over the lifetime of most people. These fascinating characteristics of cartilage have inspired researchers to investigate its mechanics and mimic its behaviour with soft hydrated materials [5].
Numerous studies have investigated the tribological characteristics of cartilage in a sliding (kinetic) friction regime. Many lubrication mechanisms such as hydrodynamic [6], boundary [7,8], weeping [9], boosted [10], biphasic self-generating [11], elastohydrodynamic [12] and biphasic boundary [13,14] lubrications have been proposed for articular cartilage. Previous studies reported that the pressurization of interstitial fluid has a pronounced effect on cartilage lubrication [4,15,16]; the pressurized fluid sustains the applied contact load and effectively slides the contact area over the solid matrix with a low friction coefficient. In particular, Caligaris & Ateshian [15] suggested that the coefficient of friction under stationary contact increases with time, while the coefficient of friction under migrating contact stays at a low value for long durations. They explained that the low coefficient under migrating contact is because the contact area migrates faster than the diffusion rate of interstitial fluid, so that the fluid does not have enough time to flow away from the contact, resulting in the sustained pressurization of interstitial fluid under the contact [15]. Also, they showed that the pressurization of interstitial fluid is much more effective than boundary lubrication [15]. Park et al. [17] performed friction tests on cartilage using atomic force microscopy (AFM) and showed that the absence of the pressurized fluid due to a small contact area increases the coefficient of friction.
While tribological properties of cartilage in the sliding (kinetic) friction regime have been extensively studied, the pre-sliding (static) friction response of cartilage has drawn less attention. Although a few studies reported that the static friction coefficient of cartilage increases with an increase in the contact dwelling duration before sliding [13,18,19], the underlying mechanisms and mechanics of the pre-sliding response were not addressed. A previous study on the wear of articular cartilage in sliding conditions showed that cartilage exhibits severe wear under a stick (static)–slip (kinetic) friction regime rather than under a sliding (kinetic) friction regime [20]. Also, articular cartilage often encounters pre-sliding friction during daily joint movements when joint movements change from a static state to a dynamic state. This evidence suggests that a systematic understanding of the pre-sliding (stick, static) regime is needed to understand wear damage and fill the gaps in our knowledge. A recent paper found that the pre-sliding friction response of hydrogels is significantly affected by poro-elasticity-driven adhesion [21]. Hydrogels and cartilage have similarities in that their matrices are surrounded by fluid, which inspired us to investigate if the work of adhesion is a parameter governing the pre-sliding friction response of cartilage. To the best of our knowledge, the pre-sliding friction response of cartilage itself is not well known, and the effect of relaxation-driven adhesion on the pre-sliding friction response of cartilage has not been studied in the literature.
The pre-sliding friction response of cartilage can be systematically estimated by using a mechanics-based model. As various studies on the pre-sliding friction responses of materials have shown, model-based analysis provides a better understanding of mechanisms [22,23]. In this study, we will employ a mechanics-based model to link relaxation-driven adhesion to the pre-sliding friction response of cartilage. The model we use is a hybrid model previously applied to elastomers and gels. In particular, the stick-to-slip transitions in the pre-sliding response are modelled after Savkoor's model, which was originally proposed and applied to elastomers [24,25]. Unloading of the contact after slip-based failure is modelled after the ‘naive modelling’ approach of Brochard-Wyart & de Gennes [26]. That model was originally employed to explain the stick–slip processes observed in soft materials. Savkoor's model is useful to account for adhesive interactions during the pre-sliding response. The model proposed by Brochard-Wyart and de Gennes helps to explain the stable failure propagation over the contact and transitioning to fully sliding. A combination of those two models is referred to as the ‘slip-based failure model’ in this paper.
The aims of this study are to investigate the relation between adhesion and relaxation time in articular cartilage, and to investigate the effect of relaxation-dependent adhesion on the pre-sliding friction response of cartilage. Adhesion tests were performed to evaluate the work of adhesion of cartilage at different relaxation times. Friction tests were conducted to identify the pre-sliding friction response of cartilage at relaxation times corresponding to adhesion tests. Finally, the experimental pre-sliding friction response of cartilage was systematically correlated to the slip-based failure model to establish a quantitative correlation between the work of adhesion and the resistance of cartilage to frictional loading. Section 2 explains the experimental methods and the slip-based failure model. The experimental methods include sample preparation, adhesion tests and pre-sliding friction tests. A brief overview of a slip-based failure model is provided, and the process of applying the model to experimental pre-sliding data is described. Section 3 lists the results of adhesion and pre-sliding friction tests, and the results of fitting the slip-based failure model to the pre-sliding friction response. Section 4 discusses the physical meaning of the results, followed by conclusions in §5.
2. Material and methods
2.1. Sample preparation
Three full-thickness cartilage samples (N = 3) were harvested from the patellae of three porcine joints (5–6 months old). Cylindrical samples were obtained with a 6 mm diameter coring tool and a scalpel, and their subchondral bones were trimmed using a microtome. The back surface of each sample near the deep zone was attached to a Petri dish using an instant adhesive (Super Bonder 495; Loctite, Ontario, Canada). Samples were kept hydrated during preparation in Dulbecco's phosphate-buffered saline (DPBS) with protease inhibitors, and allowed to relax for about an hour to reach equilibrium before testing. Mechanical testing was performed at five different locations (n = 5) on each of the three cartilage samples (N = 3). The average and standard deviation of material properties were calculated based on Nn = 15.
2.2. Adhesion test
Adhesion tests on the articular surface of hydrated cartilage were performed to investigate the effect of relaxation time on the work of adhesion. Tests were conducted on a Bruker TI950 TriboIndenter (Hysitron Inc., MN) using a sapphire spherical indenter with a radius of 1 mm. A constant normal displacement of 60 µm was instantaneously applied with a velocity of 100 µm s−1, held until a set relaxation time and removed with a velocity of 100 µm s−1 (figure 1a). At this constant displacement, the contact area was small compared with the probe radius, and thus elastic (Hertzian) contact assumptions prevailed. The relaxation (hold) time, trelax, was an independent variable, and 0, 5, 10, 20, 50, 100 and 200 s were used. The pull-off force, Fpull-off, was defined as the maximum negative force of a load–displacement curve. The work of adhesion was calculated through two different methods. The first method was based on the Johnson–Kendall–Roberts (JKR) contact model [27], and the work of adhesion is estimated from measured values of Fpull-off,
| 2.1 |
where R is the radius of the indenter. The average and standard deviation of the work of adhesion per each relaxation time were calculated with 15 measured values (Nn = 15). The second method was based on the normalized relaxation curve, where γi and γf are the work of adhesion at the unrelaxed and fully relaxed states, as in [21],
| 2.2 |
where Fn,i(t), Fn,f(t) and Fn(t) are the normal loads at the initial (trelax = 0 s) and final (trelax = 200 s) relaxation curve and arbitrary time, respectively. Here, γi and γf were the work of adhesion at trelax = 0 s and trelax = 200 s from equation (2.1), respectively. The normalized relaxation curve was obtained by taking the average of 15 relaxation curves from trelax = 200 s. Eventually, the measured (equation (2.1)) and predicted (equation (2.2)) adhesion were compared to check which one can suitably explain the pre-sliding friction response of cartilage. A previous study explained the pre-sliding friction response of hydrogels with relaxation curve-based adhesion [21].
Figure 1.
(a) Normal displacement profile of adhesion tests. (b) Normal and lateral displacement profiles of friction tests. All tests were conducted under displacement control. The profiles were plotted by using one of the experimental results, showing the displacements were controlled well.
2.3. Friction tests
Friction tests were performed to examine the influence of relaxation-dependent adhesion on the pre-sliding friction response of articular cartilage. The same instrument and indenter used in the adhesion tests were used for the friction tests. A normal displacement of 60 µm was applied with a velocity of 100 µm s−1 and maintained until the end of each test. A tangential displacement of 250 µm at a sliding velocity of 100 µm s−1 was applied after set relaxation (hold) times, trelax, that corresponded to the relaxation times used in the adhesion tests. The relatively slow tangential sliding was chosen intentionally to ensure that frictional interactions stem from elastic deformation, and not from hydrated lubrication [28,29]. The normal and tangential displacement profiles are shown in figure 1b. Reported values from the friction tests were calculated with 15 measured values (Nn = 15).
2.4. Slip-based interfacial failure model
2.4.1. Brief overview of the slip-based failure model
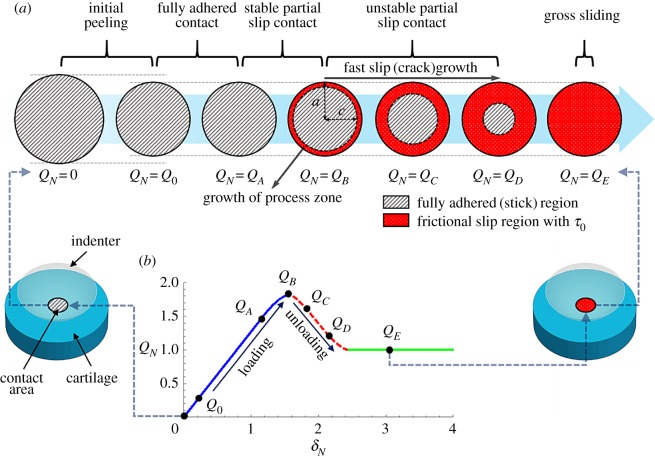
The slip-based failure model addresses fracture-like failure induced in a spherical contact under combined normal and tangential loading, Q, and adhesive interactions (figure 2). First, normal loading creates a circular contact area that is larger than the Hertzian contact area due to adhesion, illustrated as QN = 0. A quick peeling occurs upon application of a tangential force, QN = Q0, and the contact area reduces to the Hertzian contact area to balance out the applied normal load, referred to as initial peeling. After that point, the contact area remains fully adhered until a critical load, QN = QA, referred to as fully adhered contact. As QN increases from QA to QB, the singular tangential tractions at the edge of that contact area yield a critical stress intensity factor, and debonding slightly occurs towards the centre of the contact area. The debonded portion of the contact area undergoes frictional slip with constant tangential traction, τ0, while the central portion of the contact area remains fully adhered, referred to as stable partial slip contact. τ0 is the residual strength of the physically and/or chemically adsorbed layers at the interface, and is assumed to be independent of normal tractions (see [30,31] for experimental evidence). After the critical point where QN becomes maximum, QN = QB, the frictional slip zone grows quickly and unstably towards the centre of the contact area, referred to as unstable partial slip contact. Gross sliding eventually commences after the frictional slip zone extends over the whole contact area, illustrated as QN = QE. We employ stable growth of the slip zone size to analyse displacement-controlled experiments. The following sections (§§2.4.2–2.4.4) introduce how each stage of the model is mathematically expressed in a normalized form, which is directly used to fit the experimental pre-sliding friction response. The electronic supplementary material consists of the derivation of the normalized forms. Section 2.4.5 provides the application process of the model to the experimental results with a schematic diagram.
Figure 2.
(a) Evolution of the stick (dashed-grey) and slip zones (dotted-red) over the projected contact area during tangential loading. (b) Normalized tangential force versus displacement with critical points (QO: end of initial peeling; QA: onset of stable partial slip (failure); QB: onset of unstable partial slip; QC: rapid slip (crack-like failure) growth, QD: moment before the onset of gross sliding; QE: gross sliding). The shear traction distribution over the contact radius at points QA, QB, QC and QD is shown in the electronic supplementary material, figure S1.
2.4.2. Fully adhered contact (Q0 – QA)
Under fully adhered contact (figure 2), the tangential displacement, δ, is linked to Q linearly as follows:
| 2.3 |
where a is the contact radius of the fully adhered contact, and νi and Gi are Poisson's ratio and the shear modulus of the ith contacting material. The normalized form of the tangential force, QN, and the tangential displacement, δN, are defined as follows:
| 2.4 |
and
| 2.5 |
where QS = τ0πa2 is the tangential force when the whole of the contact area slips (gross sliding). Then the relationship between QN and δN in the fully adhered contact is established by substituting equation (2.4) and equation (2.5) into equation (2.3) as follows:
| 2.6 |
2.4.3. Stable partial slip (QA – QB)
After the onset of the stable partial slip (QN = QA) (figure 2), the normalized forms of the tangential force, QN, and the tangential displacement, δN, are defined as follows:
| 2.7 |
and
| 2.8 |
where is the ratio of the critical to sliding tangential forces (referred to as stick–slip contrast) and is the normalized radius of the fully adhered (stick) contact area (figure 1).
2.4.4. Unstable partial slip (QB—before gross sliding)
In the regime of the unstable partial slip (figure 2), to meet the constraints in a set-up with displacement control, the relative tangential velocity of the contacting interfaces, , is assumed to scale linearly with the extension rate of the annual frictional slip zone, . Then its normalized form, , can be expressed as follows:
| 2.9 |
where κ is a scaling constant. The normalized tangential displacement during the unstable partial slip, δN, can be eventually expressed as follows:
| 2.10 |
where is the normalized tangential displacement at QN = QB, χc is the normalized radius of the fully adhered (stick) contact area at QN = QB (see equation (S20), electronic supplementary material) and is the normalized radius of the stick contact area during unloading. The normalized tangential force, QN, is assumed to attain the same value corresponding to the stable partial slip (equation (2.7)) with χun instead of χ. Note that kinematic constraints localized at the interface might exhibit nonlinear correlation to the crack-tip velocities. The linear correlation offered here should be treated as a first-order approximation. In addition, a similar linear relation between the imposed displacement rates and crack-tip velocities is used by Brochard-Wyart and de Gennes to explain the linear decohesion observed experimentally on soft PDMS-on-glass contacts [32]. The physical arguments behind this linear correlation will be revisited in the Discussion.
2.4.5. Application of the slip-based failure model
This section briefly explains the application of the model to the experimental results with a schematic diagram in figure 3. The results of pre-sliding friction tests are re-plotted as normalized forms, δN,exp − QN,exp ( figure 3). The initial portion of the normalized friction result is fitted to the model (fully adhered contact) by adjusting the parameter λ (equation (2.6)). The following portion of the normalized friction result is fitted to the model (stable partial slip contact) by adjusting the parameter Θ, determining χ from δN,exp = δN, and calculating QN from the determined χ (equation (2.7)). The unloading portion of the normalized friction result is fitted to the model (unstable partial slip) by adjusting a fitting parameter of κ, determining χun from δN,exp = δN and calculating QN from the determined χun (equation (2.7)). The effect of parameters Θ and κ on the model is illustrated in the electronic supplementary material, figure S2.
Figure 3.
Schematic diagram of applying the slip-based failure model to pre-sliding friction results. In the stable and unstable partial slips, QN is calculated by substituting χ and χun into the corresponding equations above. χc is determined by using equation (S20) in the electronic supplementary material.
3. Results
3.1. Work of adhesion of cartilage
The relaxation (hold) time had a pronounced effect on the work of adhesion of cartilage. Figure 4a shows the representative results of the adhesion tests at different relaxation times. The pull-off force increased with an increase in relaxation time. The measured pull-off force is converted to the work of adhesion through equation (2.1) (figure 4b). The work of adhesion increased quickly at the beginning of the relaxation process and gradually settled to a steady value after trelax = 50 s. The minimum work of adhesion was 0.27 ± 0.07 J m−2 at trelax = 0 s. The maximum work of adhesion was 5.33 ± 0.96 J m−2 at trelax = 200 s, which was about 20 times greater than the value at trelax = 0.
Figure 4.
(a) Representative results of adhesion tests; (b) work of adhesion as a function of relaxation time. The work of adhesion from equation (2.1) is obtained based on the measured values from the adhesion tests. The work of adhesion from equation (2.2) is predicted based on the normalized relaxation curve. The standard deviations were connected using modified Bezier curves.
In addition to the directly measured work of adhesion, the work of adhesion as estimated by the normalized relaxation curve with γi and γf is also shown in figure 4b. The normalized relaxation curve for that estimation was taken from the average of 15 relaxation responses at trelax = 200 s. γi and γf were from the measured work of adhesion at trelax = 0 s (0.27 ± 0.07 J m−2) and trelax = 200 s (5.33 ± 0.96 J m−2), respectively. Finally, the predicted work of adhesion was obtained by substituting these values into equation (2.2) (figure 4b). Although the measured and predicted adhesion results had similar trends, they were not in complete agreement.
3.2. Pre-sliding friction response of cartilage
The pre-sliding friction response of cartilage strongly depended on the relaxation (hold) time, as did the work of adhesion. The ratios of the tangential to normal loads, measured on cartilage after predefined relaxation times, are presented in figure 5a as a function of the tangential displacement. This ratio is referred to as the coefficient of friction in classical terms. Note that, except for trelax = 0 s, a normal load during friction tests does not change significantly, and thus the ratio shown resembles a tangential load. As the relaxation time increased, the pre-sliding friction increased to a peak value, and then gradually decreased and transitioned to sliding friction values. As for trelax = 200 s, the coefficient of friction at the peak (0.93 ± 0.07) was four times larger than the coefficient of friction (0.25 ± 0.02) in the sliding regime. By contrast, when the relaxation time was relatively short (e.g. trelax = 0 s), the pre-sliding friction response showed a smooth transition to a gross sliding regime.
Figure 5.
(a) Representative results of pre-sliding friction tests; (b) curve fitting of friction tests.
3.3. Application of the slip-based failure model
The results of the pre-sliding friction tests were normalized, and then the normalized results were fitted to the slip-based failure model (figures 3 and 5b). Specifically, the loading, peak friction and unloading portions of the pre-sliding friction response were fitted to the model by adjusting fitting parameters (figure 3). The results from trelax = 0 s were omitted from the fitting because the friction response did not show the peak friction. Representative normalized experimental curves fitted to the slip-based models are shown in figure 5b. In the case of trelax = 5 s, the slip-based failure model predicted the overall pre-sliding friction response from the loading portion to the unloading portion. However, as the relaxation time increased, the model significantly deviated in the extended unloading portion (about 20 < δN) even though it still well simulated the loading, peak friction and initial unloading portions of the pre-sliding friction response.
The linear loading portion of the pre-sliding friction response was influenced by the relaxation time, and the influence was well captured by the model (fully adhered contact, figure 3) with a properly selected value of λ. λ rapidly decreased in a relatively short relaxation time (trelax < 20 s) and became stable (trelax > 20 s) (figure 6a). Shear moduli were calculated based on the determined λ (figure 6b). The shear modulus showed an increasing trend as the relaxation time increased. It ranged from 6.29 ± 3.01 MPa at trelax = 5 s to 13.28 ± 4.63 MPa at trelax = 200 s (16.01 ± 5.92 MPa at trelax = 100 s). These results were consistent with the moduli calculated using the load–displacement curves measured in the adhesion tests (see the electronic supplementary material).
Figure 6.
Results of (a,c,d) fitting parameters and (b) shear modulus. Shear moduli were calculated by substituting the determined λ into equation (2.3), and Poisson's ratio of 0.25 was used. The standard deviations were connected using modified Bezier curves.
The degree of peak friction and the critical adhered (stick) area depended on the relaxation time, and they were quantitatively evaluated by using the model (stable partial slip; figure 3) with related parameters. The value of the peak friction, also called the stick–slip contrast, was quantified by a fitting parameter of Θ. Θ rapidly increased in a relatively short relaxation time (trelax < 50 s) and gradually reached a plateau (trelax > 50 s) (figure 6c). The minimum value was 0.95 ± 0.07 at trelax = 5 s, and the maximum value was 3.89 ± 0.59 at trelax = 200 s. The normalized radius of the critical adhered area, χc, was estimated by substituting the determined Θ into equation (S20) (see the electronic supplementary material). χc increased from 0.8 at trelax = 5 s to 0.98 at trelax = 200 s. The relationship between Θ and χc is presented in the electronic supplementary material, figure S3.
The unloading portion of the pre-sliding friction response changed depending on the relaxation time, and the change was estimated by the model (unstable partial slip, figure 3) with the linear coupling parameter of κ. Please note that κ reported here was estimated by fitting the initial unloading portion (about 20 < δN) because the experiments for long relaxation times exhibited nonlinear unloading after the initial unloading regime. κ showed a sharp decrease before trelax = 50 s and gradually became steady towards trelax = 200 s (figure 6d). The maximum value was 48.8 ± 15.65 at trelax = 0 s, and the minimum value was 14.43 ± 6.81 at trelax = 200 s.
The stick–slip contrast, Θ, showed a strong linear correlation with the work of adhesion, γ. Figure 7 presents Θ as a function of γ. The correlation between γ and Θ was quantitatively estimated by performing curve fitting with linear regression. As a result, the strong linear correlation was found to be Θ = −0.14 + 0.79γ with R2 > 0.99. Note that this curve fit has no applicability when Θ is less than about 1. γ and other parameters also showed linear correlations (R2 = 0.79 for λ and R2 = 0.84 for κ, as shown in the electronic supplementary material, figure S4), but they were not as strong as the linear correlation between Θ and γ.
Figure 7.

Correlation of the work of adhesion, γ, with the stick–slip contrast, Θ (R2 = 0.99). The graph shows that the resistance to the slip-based failure over the contact linearly increases with an increase in the work of adhesion.
4. Discussion
4.1. Relaxation-dependent adhesion of cartilage
The work of adhesion of cartilage, γ, was found to be relaxation dependent, and this was probably due to the combination of the poro-elasticity-driven suction effect, the formation of adhesive bridges within the contact area and the relaxation-driven geometric changes around the contact edges. The correlation between the work of adhesion and the relaxation time is consistent with the previous study on the hydrogel-on-glass contact [21]. The study reported that the adhesion is due to the poro-elasticity-driven suction effect under the indentation probe, arising from the imbalance of osmotic pressure. As hydrogel and cartilage have structural similarities (fibrous solid matrix swollen by fluids), it is expected that poro-elasticity-driven suction contributes to the adhesion of cartilage. The osmotic pressure is closely related to the degree of dehydration localized under the probe. The degree of localized dehydration can be linked to the relaxation response. Following this, the work of adhesion was predicted by substituting the normalized experimental relaxation curves in equation (2.2). Although the predicted adhesion showed a trend similar to the measured adhesion (equation (2.1)), there was a slight difference between them. A plausible reason for the slight difference might be the progressive formation of adhesive bridges between the spherical indenter and the cartilage constituents (e.g. collagen fibrils, hyaluronic acid and glycosaminoglycans (GAGs)) as reported in [20], resulting in the increase in the real contact area. Another possible mechanism linking adhesion and the time-dependent response of cartilage is changes in the shape of contact edges (crack) during relaxation (or creep). As shown by Greenwood & Johnson [33], loading and unloading rates of a contact will influence the shape of contact edges in a viscoelastic material. The relaxation-induced geometric changes will have a regularizing effect on the otherwise singular stresses at the contact edges, and thus increase the apparent work of adhesion measurements. Using this argument, a direct link between the time-dependent constitutive response and the work of adhesion can be constructed. The governing mechanisms of the adhesion of cartilage are beyond the scope of our work, but a similar dependence of the adhesion of cartilage on the relaxation time was successfully found on multiple locations on multiple samples (Nn = 15). The origins of the adhesion could be clearly determined by carefully controlling loading/unloading rates and using selectively modified samples (e.g. collagen digested, GAGs digested and dehydrated cartilage) and chemically treated probes. Finally, the work of adhesion measured here is compared with that calculated using a rigid punch solution (v = 0.25 assumed) [34] and published results [35]; the adhesion force during shearing under zero normal load was originally reported from the intercept of a linear regression line for the friction versus normal load data [35]. The calculated value is of the order of 0.1–1.6 J m−2, and is consistent with the range of our measurement (0.2–6.3 J m−2).
4.2. Pre-sliding friction response of cartilage with the slip-based failure model
The good agreement between the linear loading portion of the pre-sliding friction response and the fully adhered contact model provides a mechanics-based validation of the fully adhered contact and a confirmation of the relaxation-dependent shear modulus. In other words, the indenter was completely adhered to cartilage during the initial phase of tangential loading. Given that the cartilage is more compliant than the probe and transducer assembly, the tangential stiffness deduced from this initial adhered response can be attributed totally to deformations over cartilage. The shear moduli calculated from the tangential stiffness for trelax ≤ 10 s cases are consistent with the range of previously reported values (mouse: 0.10–6.12 MPa [36]; bovine: 1.51 ± 0.37 MPa [37]; porcine: 0.36 MPa (converted from the elastic modulus by assuming v = 0.5) [38]). However, the shear moduli estimated for longer relaxation times are higher than the reported values. Although the higher values in our tests might be attributed to the sample species and test regions, the degree of water exudation in the cartilage–probe interface is probably the major reason. This is partially proved by the trend of the shear modulus (or λ) matching that of the relaxation curve and the consistency between moduli obtained from the adhesion and friction tests (see the electronic supplementary material). A previous study also reported that the relaxation and dehydration of cartilage can significantly increase its modulus [39]. Consequently, the relaxation-dependent shear modulus suggests that the modulus of cartilage increases along with its progressive dehydration induced by the localized pressure gradient. Furthermore, the correlation between the shear modulus and dehydration supports that poro-elasticity-driven suction occurs in the cartilage–probe interface as it is induced by localized dehydration, resulting in the imbalance of osmotic pressure.
The stick–slip contrast and the normalized radius of the critical stick area at failure are relaxation dependent. The stable partial slip of the pre-sliding friction response was well captured by the parameters, Θ and χc, of the model. The increasing trend of Θ with relaxation time shows that the resistance to the slip-based failure over the contact exponentially increases with the relaxation time. This indicates that a larger tangential force is required to initiate the peeling of the fully adhered contact area as the relaxation time increases. The increases in Θ and χc suggest that the fully adhered (stick) contact formed in the linear loading portion is better maintained with increases in the stick–slip contrast and the relaxation time, indicating less of an annular slip area (i.e. fracture process zone). As χc ranged between 0.8 and 0.98, the small-scale failure assumption is valid for the set of experiments analysed.
The strong linear correlation between Θ and γ shows that the relaxation-dependent work of adhesion of cartilage dominantly governs its resistance to tangential loading and slip-based failure. The higher work of adhesion could mean that the poro-elasticity-driven suction and adhesive bridges become stronger over time. Therefore, a higher tangential load is required to break the adhesion (stick) formed by them. Such increased adhesion could induce severe damage on cartilage as observed in [20]. Other studies on the contact interfaces of soft materials support our findings. A hydrogel–glass interface showed that the poro-elasticity-driven suction effect resists the lateral sliding of a probe [21]. Lubricated elastomer contacts showed that the break-loose friction increases with the time of stationary contact because the real contact area increases with the progression of fluid squeeze-out and de-wetting [40]. In addition, earlier studies showed that the contact interfaces between identical soft materials (hydrogel-on-hydrogel [41] and cartilage-on-cartilage [20]) exhibit a similar stick–slip trend simulated by the slip-based failure studied here. Therefore, the slip-based failure model has the potential to explain the mechanics of cohesive contacts between soft materials.
The linear correlation between the maximum tangential load and adhesion is in line with the initially adhered contact and adhesion-controlled failure assumptions employed in the model. Accordingly, the critical energy release rates in our pre-sliding tests should scale as . Specifically, in a mode II loading, , and because the contact radius and sliding friction force in our tests were approximately the same for all cases, . As extracted from the contact stiffness, the equivalent shear modulus increases nearly 2.1-fold from trelax = 5 s to trelax = 200 s in our experiments. Assuming similar variation occurs in the equivalent Young's modulus of the contact, E*, the energy release rate is expected to increase eightfold from trelax = 5 s to trelax = 200 s. This increase is not too different from the fourfold increase in the work of adhesion. Note that mode-mixing and dissipative interactions during the pre-sliding tests could contribute to the apparent energy release rates estimated, and lead to this slight mismatch between the increases in energy release rates and the work of adhesion [24,42,43]. The critical stick areas at the onset of slip-based failure are estimated to be large in comparison with the peeled area (see electronic supplementary material, figure S3). Therefore, brittle failure with negligible mode-mixing is a plausible assumption applicable to the experiments [24]. Dissipative interactions between the probe and cartilage samples are expected to be more prominent in pre-sliding than in adhesion tests. This is because loading and unloading rates during adhesion tests are much higher than 2.5 s sliding durations in pre-sliding tests. Within longer durations, larger portions of the mechanical work will be expended to dissipative processes such as relaxation and diffusion in the tissue. Therefore, the apparent energy release rates estimated will be higher than the work of adhesion. This trend is in line with the previous results of peeling tests from Maugis & Barquins [43]; polyurethane strips were peeled from glass at different peel angles, and they reported that measured energy release rates were higher than the actual work of adhesion. The contribution of dissipative interactions can be independently verified by additional experiments with a range of sliding velocities. However, increasing sliding velocities could trigger rehydration and hydrodynamic interactions at the probe–cartilage interfaces [28,29]. The authors are currently exploring options to decouple those mechanisms, and their effects on the pre-sliding response. Nevertheless, the strong linear correlation between Θ and γ () found in this paper suggests the possibility of predicting the relaxation-dependent work of adhesion from the pre-sliding friction response of cartilage-like hydrated materials, and provides the physical basis and predictive capability to in vivo diagnostic techniques for biomedical interfaces (e.g. shear wave elastography [44]).
The decrease in the linear scaling parameter, κ, with the relaxation time shows that the annular slip area extends faster towards the centre of the contact in the relaxed state. Although the unstable partial slip model with κ provided valuable insight into the extension rate of the slip area in the initial unloading portions (δN < 20), it failed to predict the extension behaviour in the latter unloading portions from relatively long relaxation times (figure 5b). This failure suggests that higher stick–slip contrast induces a nonlinear relationship between the relative tangential velocity of the contacting interfaces and the extension rate of the annular slip area. Note that Brochard-Wyart & de Gennes [26] also used a linear scaling between the imposed displacement rates and crack-tip velocities as , where ϵ0 is the threshold strain beyond which slip-based failure over the contact commences. Moreover, they showed that crack-tip velocities remained relatively constant throughout the peeling process. Even under those crude assumptions, their model successfully captured experimentally observed stick–slip transitions in PDMS-on-glass contacts [26,32]. Despite their successful application of the linear scaling, our experiments show that more sophisticated unloading models accounting for nonlinearities such as ploughing, self-healing and collective diffusion should be employed (see [45,46] for the physical basis of those nonlinearities).
Reale & Dunn [21] have studied the friction response of hydrogels experimentally, and proposed a simple model for friction of soft hydrated materials, and, therefore, their model is worth comparing with our work. The model of Reale and Dunn assumes rigid traversing of a probe over relaxed (dehydrated) and unrelaxed (hydrated) parts of soft hydrated materials, and simple areal mixing rules to estimate the friction force during unloading. Their model could not explain the pre-sliding friction results of cartilage; it overestimated the peak friction coefficients and the lateral displacement where the coefficient of friction converges (see the electronic supplementary material). The slip-based failure model, on the other hand, could explain the onset of slip and subsequent debonding better. Notwithstanding the promising fits to the experiments, the slip-based model has deficiencies in representing the decohesion (unloading) regime, which could be resolved with in situ experiments and nonlinear peeling kinematics as discussed above.
As cartilage contains a large amount of water, it is necessary to consider if the hydrodynamic effects and adhesion played a role during the application of a tangential displacement. When hydrodynamic effects are present at the interface, the viscous energy dissipation, energy release rate and the friction coefficient increase with increasing sliding velocity. The velocity employed in the friction tests was sufficiently low not to interfere with the rehydration process induced by the pressure gradient. For instance, cartilage requires sliding velocities of the order of tens of millimetres per second to restore hydration after water exudation [28]. Therefore, it is reasonable to consider that hydrodynamic effects did not significantly influence the pre-sliding friction responses reported here. In addition, the duration of each pre-sliding test was 2.5 s. Therefore, we do not anticipate any significant change in the contact relaxation and adhesion during pre-sliding tests. Substantial changes in the work of adhesion, which significantly influenced the pre-sliding friction response, were due to significant relaxation that occurred before the application of the tangential displacement.
4.3. Assumptions and limitations of the slip-based failure model
The crude assumptions and limitations of the slip-based failure model are worth revisiting. This model adopts brittle fracture initiation and assumes a small-scale process zone size. Various regularization methods with mixed-mode debonding, frictional slip with Coulomb law and plastic yielding at the interface are offered to limit infinite shear tractions at the edge of the sticking contact [47–52]. For instance, mixed-mode debonding at the interfaces between inclusions in soft matrix, fibre-reinforced composites and jointed surfaces is modelled accurately with coupled cohesion-friction models [52]. In this model, the interface obeys the cohesive constitutive law with a smooth traction–separation relation [53]. Once the tangential traction reaches its maximum, the debonding commences and frictional tractions occur between the debonded parts of the interface. After that point, the cohesive strength diminishes, while the regions under frictional slip increase until the onset of gross sliding. Although this cohesive zone model promises similar results to the slip-based failure model, the physical basis deteriorates because of the large number of input parameters required. Ongoing work by the authors considers analogies between these models, and, thus, attempts to link mechanics-based processes at the interface to the input parameters of the cohesive models. Such a model would employ observable parameters, possess the physical basis and enable relaxation of the small-scale process zone assumption.
The model also ignores the regularizing effects of crack-tip blunting and cavitation on the interfacial tractions, and therefore it is worthwhile considering their effects. As discussed thoroughly by others [54,55], an elasto-adhesive length determines the significance of blunting and cavitation of soft materials in comparison with the smallest of the other geometric features in a given failure case. The length can be estimated as . For the probe-based tangential loading, the contact radius can serve as the smallest dimension. The elasto-adhesive lengths can be estimated by using the work of adhesion and the shear modulus reported in the results section. At trelax = 200 s, the work of adhesion is 5.33 J m−2, and the elastic modulus, E, is estimated to be 33.20 ± 11.58 MPa (E = 2G(1 + v), G = 13.28 ± 4.63 MPa, and v = 0.25); this is consistent with E calculated using the load–displacement curves measured in the adhesion tests (see the electronic supplementary material). With those values, lEA at trelax = 200 s is estimated as 160.54 nm for the cartilage (89.03 nm for trelax = 5 s). As the contact radius in our experiments (≈250 µm) is significantly greater than the estimated lEA, the interfacial failure in our experiments is expected to exhibit brittle-like behaviour with negligible blunting and cavitation.
5. Conclusion
This study experimentally demonstrated the relaxation-dependent adhesion of cartilage and its effect on the pre-sliding (static) friction response of cartilage. In addition, the slip-based failure model provided the mechanistic explanation of the pre-sliding friction behaviour and the stick–slip response of cartilage. The work of adhesion of cartilage increased with a progression of relaxation. The increase in the work of adhesion linearly increased the resistance of the slip-based interface failure, resembling fast crack growth. Also, as the work of adhesion increased, the size of the critical adhered (stick) area at failure became larger, and the extension rate of the annular slip area towards its centre (crack growth) increased in the initial unloading portion. These findings fill the gap in our knowledge about the pre-sliding (static) friction response of cartilage, leading to a better understanding of the stick-induced damage on its surface. The quantitative interpretation of the friction response with the mechanics-based model can be a powerful method when the contact areas between soft-hydrated materials (e.g. cartilage) are not observable. To further our research, we are planning to investigate the effect of the tangential displacement rate on the pre-sliding friction response. In addition, further work will include the improvement of the unstable partial slip model to capture the nonlinear behaviour observed in the late stage of the unloading portion.
Supplementary Material
Acknowledgements
The authors are grateful to Prof. Corinne R. Henak for helping prepare porcine cartilage.
Data accessibility
Datasets are available from the Dryad Digital Repository (https://doi.org/10.5061/dryad.v0108) [56].
Authors' contributions
G.H. prepared the sample, performed the adhesion and friction tests, contributed to the slip-based interfacial failure model, participated in the analysis and interpretation of data, and drafted the manuscript. M.E. applied the slip-based interfacial failure model, helped the design of experiments, participated in the analysis and interpretation of data, coordinated the study and helped draft the manuscript. Both authors gave their final approval for publication.
Competing interests
We have no competing interests.
Funding
This research is partially supported by the National Science Foundation grant nos 1554146 and 1428080, and the Wisconsin Alumni Research Foundation.
References
- 1.Maroudas A, Wachtel E, Grushko G, Katz EP, Weinberg P. 1991. The effect of osmotic and mechanical pressures on water partitioning in articular cartilage. Biochim. Biophys. Acta 1073, 285–294. (doi:10.1016/0304-4165(91)90133-2) [DOI] [PubMed] [Google Scholar]
- 2.Mow VC, Ratcliffe A, Robin Poole A. 1992. Cartilage and diarthrodial joints as paradigms for hierarchical materials and structures. Biomaterials 13, 67–97. (doi:10.1016/0142-9612(92)90001-5) [DOI] [PubMed] [Google Scholar]
- 3.Nia HT, Bozchalooi IS, Li Y, Han L, Hung H-H, Frank E, Youcef-Toumi K, Ortiz C, Grodzinsky A. 2013. High-bandwidth AFM-based rheology reveals that cartilage is most sensitive to high loading rates at early stages of impairment. Biophys. J. 104, 1529–1537. (doi:10.1016/j.bpj.2013.02.048) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ateshian GA. 2009. The role of interstitial fluid pressurization in articular cartilage lubrication. J. Biomech. 42, 1163–1176. (doi:10.1016/j.jbiomech.2009.04.040) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Urueña JM, Pitenis AA, Nixon RM, Schulze KD, Angelini TE, Gregory Sawyer W. 2015. Mesh size control of polymer fluctuation lubrication in gemini hydrogels. Biotribology 1-2, 24–29. (doi:10.1016/j.biotri.2015.03.001) [Google Scholar]
- 6.MacConaill MA. 1932. The function of intra-articular fibrocartilages, with special reference to the knee and inferior radio-ulnar joints. J. Anat. 66, 210–227. [PMC free article] [PubMed] [Google Scholar]
- 7.Swann DA, Bloch KJ, Swindell D, Shore E. 1984. The lubricating activity of human synovial fluids. Arthritis Rheum. 27, 552–556. (doi:10.1002/art.1780270511) [DOI] [PubMed] [Google Scholar]
- 8.Radin EL, Swann DA, Weisser PA. 1970. Separation of a hyaluronate-free lubricating fraction from synovial fluid. Nature 228, 228377a0 (doi:10.1038/228377a0) [DOI] [PubMed] [Google Scholar]
- 9.McCutchen CW. 1962. The frictional properties of animal joints. Wear 5, 1–17. (doi:10.1016/0043-1648(62)90176-X) [Google Scholar]
- 10.Walker PS, Dowson D, Longfield MD, Wright V. 1968. ‘Boosted lubrication’ in synovial joints by fluid entrapment and enrichment. Ann. Rheum. Dis. 27, 512–520. (doi:10.1136/ard.27.6.512) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mow V, Lai W. 1980. Recent developments in synovial joint biomechanics. SIAM Rev. 22, 275–317. (doi:10.1137/1022056) [Google Scholar]
- 12.Dowson D, Jin Z-M. 1986. Micro-elastohydrodynamic lubrication of synovial joints. Eng. Med. 15, 63–65. (doi:10.1243/EMED_JOUR_1986_015_019_02) [DOI] [PubMed] [Google Scholar]
- 13.Forster H, Fisher J. 1996. The influence of loading time and lubricant on the friction of articular cartilage. Proc. Inst. Mech. Eng. 210, 109–119. (doi:10.1243/PIME_PROC_1996_210_399_02) [DOI] [PubMed] [Google Scholar]
- 14.Ateshian GA, Wang H, Lai WM. 1998. The role of interstitial fluid pressurization and surface porosities on the boundary friction of articular cartilage. J. Tribol. 120, 241–248. (doi:10.1115/1.2834416) [Google Scholar]
- 15.Caligaris M, Ateshian GA. 2008. Effects of sustained interstitial fluid pressurization under migrating contact area, and boundary lubrication by synovial fluid, on cartilage friction. Osteoarthr. Cartil. OARS Osteoarthr. Res. Soc. 16, 1220–1227. (doi:10.1016/j.joca.2008.02.020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bonnevie ED, Baro VJ, Wang L, Burris DL. 2011. In situ studies of cartilage microtribology: roles of speed and contact area. Tribol. Lett. 41, 83–95. (doi:10.1007/s11249-010-9687-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Park S, Costa KD, Ateshian GA. 2004. Microscale frictional response of bovine articular cartilage from atomic force microscopy. J. Biomech. 37, 1679–1687. (doi:10.1016/j.jbiomech.2004.02.017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schmidt TA, Sah RL. 2007. Effect of synovial fluid on boundary lubrication of articular cartilage. Osteoarthr. Cartil. 15, 35–47. (doi:10.1016/j.joca.2006.06.005) [DOI] [PubMed] [Google Scholar]
- 19.Moore AC, Schrader JL, Ulvila JJ, Burris DL. 2017. A review of methods to study hydration effects on cartilage friction. Tribol. Mater. Surf. Interf. 11, 202–214. (doi:10.1080/17515831.2017.1397329) [Google Scholar]
- 20.Lee DW, Banquy X, Israelachvili JN. 2013. Stick-slip friction and wear of articular joints. Proc. Natl Acad. Sci. USA 110, E567–E574. (doi:10.1073/pnas.1222470110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Reale ER, Dunn AC. 2017. Poroelasticity-driven lubrication in hydrogel interfaces. Soft Matter 13, 428–435. (doi:10.1039/C6SM02111E) [DOI] [PubMed] [Google Scholar]
- 22.Usta AD, Shinde S, Eriten M. 2017. Experimental investigation of energy dissipation in presliding spherical contacts under varying normal and tangential loads. J. Tribol. 139, 061 402–061 407. (doi:10.1115/1.4036183) [Google Scholar]
- 23.Yaqoob MA, Winogrodzka A, Fischer HR, Gelinck ERM, Rooij MB, Schipper DJ. 2013. Pre-sliding behaviour of single asperity contact. Tribol. Lett. 49, 553–562. (doi:10.1007/s11249-012-0096-4) [Google Scholar]
- 24.Savkoor AR. 1987. Dry adhesive friction of elastomers: a study of the fundamental mechanical aspects. Doctoral Thesis, Delft University of Technology, Delft, The Netherlands.
- 25.Singer IL, Pollock H. 1992. Fundamentals of friction: macroscopic and microscopic processes. Berlin, Germany: Springer Science & Business Media. [Google Scholar]
- 26.Brochard-Wyart F, de Gennes P-G. 2007. Naive model for stick-slip processes. Eur. Phys. J. E 23, 439–444. (doi:10.1140/epje/i2007-10215-3) [DOI] [PubMed] [Google Scholar]
- 27.Johnson KL, Kendall K, Roberts AD. 1971. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 324, 301–313. (doi:10.1098/rspa.1971.0141) [Google Scholar]
- 28.Moore AC, Burris DL. 2017. Tribological rehydration of cartilage and its potential role in preserving joint health. Osteoarthr. Cartil. 25, 99–107. (doi:10.1016/j.joca.2016.09.018) [DOI] [PubMed] [Google Scholar]
- 29.Gong JP. 2006. Friction and lubrication of hydrogels—its richness and complexity. Soft Matter 2, 544–552. (doi:10.1039/B603209P) [DOI] [PubMed] [Google Scholar]
- 30.Homola AM, Israelachvili JN, McGuiggan PM, Gee ML. 1990. Fundamental experimental studies in tribology: the transition from ‘interfacial’ friction of undamaged molecularly smooth surfaces to ‘normal’ friction with wear. Wear 136, 65–83. (doi:10.1016/0043-1648(90)90072-I) [Google Scholar]
- 31.Carpick RW, Agraït N, Ogletree DF, Salmeron M. 1996. Variation of the interfacial shear strength and adhesion of a nanometer-sized contact. Langmuir 12, 3334–3340. (doi:10.1021/la9509007) [Google Scholar]
- 32.Wu-Bavouzet F, Clain-Burckbuchler J, Buguin A, Gennes P-GD, Brochard-Wyart F. 2007. Stick-slip: wet versus dry. J. Adhes. 83, 761–784. (doi:10.1080/00218460701586178) [Google Scholar]
- 33.Greenwood JA, Johnson KL. 1981. The mechanics of adhesion of viscoelastic solids. Phil. Mag. A 43, 697–711. (doi:10.1080/01418618108240402) [Google Scholar]
- 34.Kendall K. 1971. The adhesion and surface energy of elastic solids. J. Phys. Appl. Phys. 4, 1186 (doi:10.1088/0022-3727/4/8/320) [Google Scholar]
- 35.Chan SMT, Neu CP, Komvopoulos K, Reddi AH. 2011. The role of lubricant entrapment at biological interfaces: reduction of friction and adhesion in articular cartilage. J. Biomech. 44, 2015–2020. (doi:10.1016/j.jbiomech.2011.04.015) [DOI] [PubMed] [Google Scholar]
- 36.Berteau J-P, Oyen M, Shefelbine SJ. 2016. Permeability and shear modulus of articular cartilage in growing mice. Biomech. Model. Mechanobiol. 15, 205–212. (doi:10.1007/s10237-015-0671-3) [DOI] [PubMed] [Google Scholar]
- 37.Zhu W, Mow VC, Koob TJ, Eyre DR. 1993. Viscoelastic shear properties of articular cartilage and the effects of glycosidase treatments. J. Orthop. Res. 11, 771–781. (doi:10.1002/jor.1100110602) [DOI] [PubMed] [Google Scholar]
- 38.Zemek AJ, Protsenko DE, Wong BJF. 2012. Mechanical properties of porcine cartilage after uniform RF heating. Lasers Surg. Med. 44, 572–579. (doi:10.1002/lsm.22057) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Boettcher K, Kienle S, Nachtsheim J, Burgkart R, Hugel T, Lieleg O. 2016. The structure and mechanical properties of articular cartilage are highly resilient towards transient dehydration. Acta Biomater. 29, 180–187. (doi:10.1016/j.actbio.2015.09.034) [DOI] [PubMed] [Google Scholar]
- 40.Lorenz B, Krick BA, Rodriguez N, Sawyer WG, Mangiagalli P, Persson BNJ. 2013. Static or breakloose friction for lubricated contacts: the role of surface roughness and dewetting. J. Phys. Condens. Matter 25, 445013 (doi:10.1088/0953-8984/25/44/445013) [DOI] [PubMed] [Google Scholar]
- 41.Pitenis AA, Manuel Urueña J, Cooper AC, Angelini TE, Gregory Sawyer W. 2016. Superlubricity in gemini hydrogels. J. Tribol. 138, 042103 (doi:10.1115/1.4032890) [Google Scholar]
- 42.Johnson KL. 1997. Adhesion and friction between a smooth elastic spherical asperity and a plane surface. Proc. R. Soc. Lond. Math. Phys. Eng. Sci. 453, 163–179. (doi:10.1098/rspa.1997.0010) [Google Scholar]
- 43.Maugis D, Barquins M. 1978. Fracture mechanics and the adherence of viscoelastic bodies. J. Phys. Appl. Phys. 11, 1989 (doi:10.1088/0022-3727/11/14/011) [Google Scholar]
- 44.Yin Z, Glaser KJ, Manduca A, Van Gompel JJ, Link MJ, Hughes JD, Romano A, Ehman RL, Huston J. 2015. Slip interface imaging predicts tumor-brain adhesion in vestibular schwannomas. Radiology 277, 507–517. (doi:10.1148/radiol.2015151075) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Baumberger T, Caroli C, Ronsin O. 2002. Self-healing slip pulses along a gel/glass interface. Phys. Rev. Lett. 88, 075509 (doi:10.1103/PhysRevLett.88.075509) [DOI] [PubMed] [Google Scholar]
- 46.Baumberger T, Caroli C, Ronsin O. 2003. Self-healing slip pulses and the friction of gelatin gels. Eur. Phys. J. E 11, 85–93. (doi:10.1140/epje/i2003-10009-7) [DOI] [PubMed] [Google Scholar]
- 47.Ciavarella M. 2015. Transition from stick to slip in Hertzian contact with ‘Griffith’ friction: the Cattaneo–Mindlin problem revisited. J. Mech. Phys. Solids 84, 313–324. (doi:10.1016/j.jmps.2015.08.002) [Google Scholar]
- 48.Papangelo A, Ciavarella M, Barber JR. 2015. Fracture mechanics implications for apparent static friction coefficient in contact problems involving slip-weakening laws. Proc. R. Soc. A 471, 20150271 (doi:10.1098/rspa.2015.0271) [Google Scholar]
- 49.Palmer AC, Rice JR. 1973. The growth of slip surfaces in the progressive failure of over-consolidated clay. Proc. R. Soc. Lond. A 332, 527–548. (doi:10.1098/rspa.1973.0040) [Google Scholar]
- 50.Chaboche JL, Girard R, Schaff A. 1997. Numerical analysis of composite systems by using interphase/interface models. Comput. Mech. 20, 3–11. (doi:10.1007/s004660050209) [Google Scholar]
- 51.Snozzi L, Molinari J-F. 2013. A cohesive element model for mixed mode loading with frictional contact capability. Int. J. Numer. Methods Eng. 93, 510–526. (doi:10.1002/nme.4398) [Google Scholar]
- 52.Spring DW, Paulino GH. 2015. Computational homogenization of the debonding of particle reinforced composites: the role of interphases in interfaces. Comput. Mater. Sci. 109, 209–224. (doi:10.1016/j.commatsci.2015.07.012) [Google Scholar]
- 53.Park K, Paulino GH, Roesler JR. 2009. A unified potential-based cohesive model of mixed-mode fracture. J. Mech. Phys. Solids 57, 891–908. (doi:10.1016/j.jmps.2008.10.003) [Google Scholar]
- 54.Creton C, Ciccotti M. 2016. Fracture and adhesion of soft materials: a review. Rep. Prog. Phys. 79, 046601 (doi:10.1088/0034-4885/79/4/046601) [DOI] [PubMed] [Google Scholar]
- 55.Kundu S, Crosby AJ. 2009. Cavitation and fracture behavior of polyacrylamide hydrogels. Soft Matter 5, 3963–3968. (doi:10.1039/B909237D) [Google Scholar]
- 56.Han G, Eriten M. 2018. Data from: Effect of relaxation-dependent adhesion on pre-sliding response of cartilage. Dryad Digital Repository (doi:10.5061/dryad.v0108)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Han G, Eriten M. 2018. Data from: Effect of relaxation-dependent adhesion on pre-sliding response of cartilage. Dryad Digital Repository (doi:10.5061/dryad.v0108)
Supplementary Materials
Data Availability Statement
Datasets are available from the Dryad Digital Repository (https://doi.org/10.5061/dryad.v0108) [56].