Abstract
The representation and discovery of transcription factor (TF) sequence binding specificities is critical for understanding gene regulatory networks and interpreting the impact of disease-associated noncoding genetic variants. We present a novel TF binding motif representation, the k-mer set memory (KSM), which consists of a set of aligned k-mers that are overrepresented at TF binding sites, and a new method called KMAC for de novo discovery of KSMs. We find that KSMs more accurately predict in vivo binding sites than position weight matrix (PWM) models and other more complex motif models across a large set of ChIP-seq experiments. Furthermore, KSMs outperform PWMs and more complex motif models in predicting in vitro binding sites. KMAC also identifies correct motifs in more experiments than five state-of-the-art motif discovery methods. In addition, KSM-derived features outperform both PWM and deep learning model derived sequence features in predicting differential regulatory activities of expression quantitative trait loci (eQTL) alleles. Finally, we have applied KMAC to 1600 ENCODE TF ChIP-seq data sets and created a public resource of KSM and PWM motifs. We expect that the KSM representation and KMAC method will be valuable in characterizing TF binding specificities and in interpreting the effects of noncoding genetic variations.
The binding of transcription factors (TFs) to specific short DNA sequences enables the precise control of gene expression in space and time. A TF binding motif is a short DNA sequence or sequences that a TF recognizes. We define the motif discovery task to be the identification of DNA sequences that are directly recognized by a TF and thus are located at the site of binding where they mechanistically interact with a TF. Thus, our definition of a TF binding motif excludes cofactor motifs and other sequence features that are not immediately proximal to the site of TF binding.
Motifs are often used to identify preferential genome binding locations for a TF. Computational identification of TF binding sites are essential in deciphering gene regulatory networks (Spellman et al. 1998; Lee et al. 2002; Kim and Park 2011). In addition, certain genetic variants associated with human diseases and phenotypic traits alter regulatory DNA sequences that are recognized by TFs (Maurano et al. 2012). Therefore, accurate TF binding motifs are critical to characterize TF binding differences between alleles and to identify the upstream regulators of noncoding variants (Claussnitzer et al. 2015). The advent of high-throughput technologies, such as ChIP-seq (Johnson et al. 2007) and protein binding microarrays (PBMs) (Berger et al. 2006), have made a large amount of data available for the computation of in vivo and in vitro TF binding specificities. Computational methods for TF motif discovery remains an active and important area of investigation (Zambelli et al. 2013) and continues to inspire research into new approaches (Tompa et al. 2005; Weirauch et al. 2013).
Currently, there is no single standard for TF binding motif representation (Hughes 2011). The most widely used motif model is the position weight matrix (PWM) (Stormo 2000). However, the PWM model assumes that each base position contributes independently to binding probability and thus is unable to represent inter-base dependencies. Although PWM models provide a good approximation of protein–DNA interactions for many TFs (Benos et al. 2002; Zhao and Stormo 2011), dependencies between nucleotides at different positions in TF binding sites have been observed (Man and Stormo 2001; Bulyk et al. 2002; Berger et al. 2006; Maerkl and Quake 2007). In addition, a PWM is a highly compact and lossy representation. Therefore, in practice, PWMs fail to capture the full complexity of TF binding specificities in high-throughput data. Historically, PWMs have been derived using different approaches (Stormo 2013). In this work, we use the commonly used position frequency matrix (PFM), which assigns a probability for each base occurring at each position within the binding site.
K-mer-based motif representations, which capture the exact TF-bound sequences and thus preserve positional dependencies if they exist, have been explored as alternatives to the PWM representation. Early work used individual overrepresented k-mers to represent and discover TF binding motifs (van Helden et al. 1998; Tompa 1999). MotifCut connects k-mers into a graph and represents a motif as the maximum density subgraph, which is a set of k-mers that exhibit a large number of pairwise similarities (Fratkin et al. 2006). Recently, bags of k-mers (Ghandi et al. 2014) or clusters of k-mers (Setty and Leslie 2015) were used with binary classifiers for discriminating bound versus unbound sequences. However, the k-mer-based representations of gkm-SVM (Ghandi et al. 2014) and SeqGL (Setty and Leslie 2015) represent not only the DNA binding of a particular TF, but also other aspects such as chromatin accessibility and cobinding factor motifs. Thus, gkm-SVM and SeqGL fall outside of our definition of TF motif discovery. In addition, in these recent approaches, overlapping k-mers were implicitly assumed to be independent and were combined additively to score sequences. This independent k-mer assumption does not reflect the nonadditive contributions of overlapping k-mers at a given site for binding, leading to an inaccurate representation of motifs.
More complex models accounting for positional dependencies have also been proposed, but they are rarely used in practice because they are computationally intensive and require more data to properly estimate the model's parameters and may overfit if data are limited (MacIsaac and Fraenkel 2006; Zambelli et al. 2013). For example, The TF flexible model (TFFM) uses a hidden Markov model–based framework to capture interdependencies of successive nucleotides and flexible length of the motif (Mathelier and Wasserman 2013). The sparse local inhomogeneous mixture (Slim) uses a soft feature selection approach to optimize the dependency structure and model parameters (Keilwagen and Grau 2015). Recently, deep neural network (deep learning) based approaches have been applied to predict TF binding with improved accuracy (Alipanahi et al. 2015; Zhou and Troyanskaya 2015). However, the distributed representation of deep learning models is more difficult to interpret mechanistically.
In addition, recent studies showed that proximal sequences flanking TF motifs may strongly affect the DNA shape and hence TF binding (Gordân et al. 2013; Levo and Segal 2014). Therefore, a motif model that preserves the base positional dependencies in the motif and includes proximal flanking bases may be more accurate than the PWM model and current k-mer based models.
In this paper, we present a novel motif representation that preserves the inter-position dependencies and includes the flanking k-mers, called k-mer set memory (KSM), and a de novo motif discovery method, k-mer alignment and clustering (KMAC). We compared KSM models with the PWM and more sophisticated motif models in predicting in vivo and in vitro TF binding sites. In addition, we evaluated the application of KSM motifs and other sequence features in predicting differential regulatory activities of expression quantitative trait loci (eQTL) alleles. Together, these results demonstrate that the KSM is a more accurate motif representation than the PWM and other representations for modeling TF binding and characterizing noncoding genetic variants.
Results
The KSM motif representation
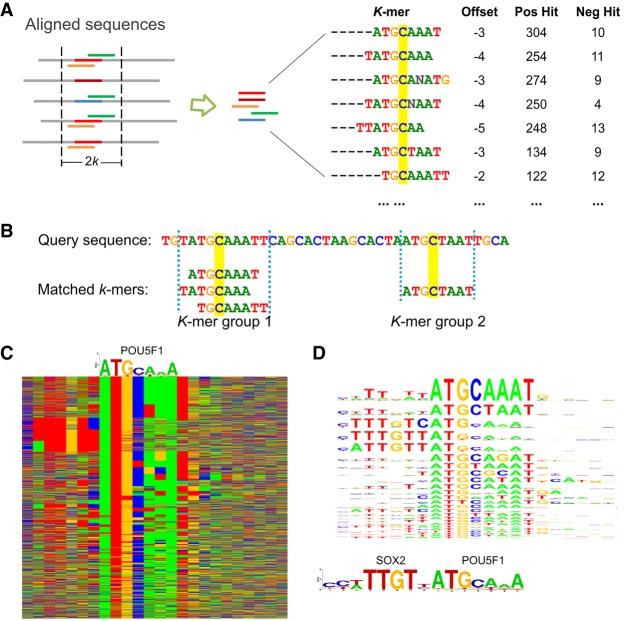
A TF's k-mer set memory (KSM) motif is the set of overrepresented k-mers (gapped and ungapped words of length k) that are contained in the binding sites for the TF and have consistent offsets relative to the center of the binding sites (Fig. 1A). The individual k-mers in a KSM are called component k-mers. A typical KSM may contain several hundred to several thousand component k-mers. The number of component k-mers in a KSM increases as the number of training sequences increases (Supplemental Table S1). The accuracy of the KSM first increases and then plateaus or drops as more training sequences are used, likely because of the saturation of overlapping k-mer information or the noise contained in weak binding sites (Supplemental Table S2).
Figure 1.
The KSM motif representation. (A) A KSM consists of a set of similar and consistently aligned component k-mers. The k-mers are extracted from a set of sequences aligned at the binding sites. Each k-mer has an offset that represents its relative position in the sequence alignment and is associated with the IDs of the positive/negative training sequences that contain the k-mer (IDs are not shown, total counts are shown). The base C, highlighted in yellow, represents the expected binding position. (B) An example of matching KSM motifs in a query sequence. (C) Color chart representation of 2183 sequences bound by POU5F1 that match the POU5F1 KSM motif. Each row represents a 23-bp sequence. Rows are sorted by the KSM motif matches. Green, blue, yellow, and red indicate A, C, G, and T, respectively. A POU5F1 PWM motif is shown above the sequences. (D) The KSM motif sequence logo of POU5F1 (corresponding to the aligned sequences in C) and the PWM logos of SOX2 and POU5F1.
Each component k-mer is annotated with a center offset and its presence/absence in each positive and negative training sequence. Unlike a PWM that assumes positional independence, KSM component k-mers are exactly matched to a query sequence being searched for a motif (Fig. 1B). By requiring exact k-mer matches, a KSM preserves dependencies among positions in the observed sequences. Long specific sequences are modeled as a group of component k-mers that overlap with each other (Fig. 1B).
Each component k-mer is required to be overrepresented in the TF-bound sequences (positive sequences) relative to the unbound sequences (negative sequences). We define the sequence hit count of a k-mer as the number of sequences containing the k-mer in the training sequence set, which is similar to the zero-or-one-per-sequence mode of MEME (Bailey and Elkan 1994). The overrepresentation of a component k-mer is evaluated by computing a hypergeometric P-value (HGP) (Barash et al. 2001) as follows:
where N is the total number of positive and negative training sequences; N+ is the number of positive training sequences; n is the number of positive and negative training sequences containing the k-mer (positive and negative hit count); and n+ is the number of positive training sequences containing the k-mer (positive hit count). In this work, the component k-mers are required to have a HGP less than 1 × 10−5.
The offset of a component k-mer is defined as the offset of the first base of the k-mer relative to the expected binding center position, which is estimated during the motif discovery process (see below). For the POU5F1 example (Fig. 1A), the expected binding position is the middle position of the binding site, i.e., base C. When searching for a KSM motif in a query sequence (discussed subsequently), the offsets of the matched component k-mers can be used to align and group the k-mers that share the same expected binding positions into KSM motif instances called k-mer groups (Fig. 1B).
A KSM's representation of a large set of overlapping k-mers allows a KSM to capture the full complexity of TF binding specificities as well as the effect of the flanking bases, leading to a richer representation than the PWM and other consensus sequence representations (Stormo and Zhao 2010). For example, the POU5F1 (also known as OCT4) bound sequences in mouse embryonic stem cells also contains a SOX2 motif, which was shown to have a strict spacing with POU5F1 motif (Chew et al. 2005; Guo et al. 2012). The PWM motif learned from these sequences does not capture the existence of the SOX2 motif, because the SOX2 motif only exists in a small subset of the sequences (Fig. 1C). In contrast, the POU5F1 KSM motif was able to capture the SOX2 motif through component k-mers, such as TTTNTCATG and TTTGTCAT, that overlap with both POU5F1 and SOX2 motifs. To elucidate the intricacies of the TF binding specificities, we graphically represent each KSM motif with a KSM sequence logo, which displays the high-scoring nonoverlapping component k-mers and their sequence contexts as a stack of PWM sequence logos (Methods). From the KSM sequence logo of POU5F1, the existence of SOX2 motif can be easily observed (Fig. 1D).
KSM motif matching and scoring
To search for KSM motif instances in a query sequence, all component k-mers of the KSM motif are simultaneously searched using the Aho-Corasick algorithm for efficient multipattern search (Aho and Corasick 1975).
The k-mer matches in a query sequence are grouped into KSM motif instances based on their expected binding locations (Fig. 1B), which are computed using the matched position of a k-mer and the offset of the k-mer specified in the KSM model. We define a k-mer group (i.e., KSM motif instance) as the subset of component k-mers in the KSM model that occur in the query sequence and that are mapped to a same expected binding position on the sequence.
The hit count for a k-mer group cannot be obtained by simply summing the hit count of all the matching component k-mers, because the component k-mers are overlapping and a simple or weighted summation will not give an accurate count that recapitulates the information in the training data. Therefore, we introduce the formulation of k-mer group hit count, which is defined as the number of all the training sequences that contain at least one of the matched k-mers in the k-mer group. A bit string is stored with each k-mer to represent its presence/absence in all the training sequences. The k-mer group hit count can then be computed efficiently by a union operation on the bit strings of all the matched k-mers (Supplemental Fig. S1). In this formulation, overlapping k-mers are not combined additively as in previous approaches (Ghandi et al. 2014; Setty and Leslie 2015), but in a nonadditive manner that more accurately recapitulates the contribution of these k-mers as a whole. Unlike the PWM motif instances, the KSM motif instances of the same motif may have different lengths because the length depends on the matched component k-mers and their relative positions.
The KSM score of a k-mer group is then defined as the odds ratio, which is a measure of association (Cornfield 1951; Edwards 1963) as follows:
where N+ and N− are the total numbers of positive and negative training sequences, respectively; n+ and n− are the k-mer group positive and negative hit counts, respectively. To avoid divided-by-zero error, a small pseudocount is added to the counts. If no component k-mer is matched in the query sequence, the KSM score of the sequence is 0.
KMAC motif discovery
The k-mer alignment and clustering (KMAC) method discovers both KSM and PWM motifs from a given set of positive (motif enriched) and negative sequences (motif depleted). If not provided, a negative sequence set is generated by randomly shuffling the positive sequences while preserving the dinucleotide frequencies. KMAC can efficiently analyze the top 10,000 sequences from an assay and thus can learn weak signals. KMAC applies to sequences from in vivo TF ChIP-seq/ChIP-chip data or sequences of predicted elements from epigenomic data. For data sets that have a weight associated with each sequence, such as the read count of a ChIP-seq binding event, KMAC by default weights the positive sequences with a factor of the natural logarithm of the input sequence weight and then normalizes the weights such that the average is equal to one. To obtain the sequence hit count for k-mers and k-mer groups, the total weights of the sequence hits are summed and rounded. Other weighting schemes such as identity, square-root, or no-weighting can be specified by the users.
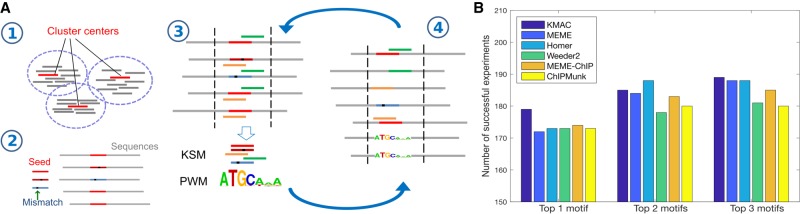
KMAC learns a KSM by aligning the positive sequences and computing the consistently aligned overrepresented k-mers. KMAC uses values of k from 5 to 13 unless otherwise directed. For each value of k, KMAC discovers both KSM and the corresponding PWM motifs as described below. All the motifs are then compared with each other, and similar motifs are merged. Thus, the final list of motifs may consist of KSMs with different values of k, allowing KMAC to capture motifs with different lengths. KMAC motif discovery consists of four steps (Fig. 2A):
Step 1: KMAC selects a set of enriched k-mers and clusters them. K-mers with k exact bases and from 0 to g gapped bases are considered. The maximum number of gaps g, which can be specified by the users, is four for all the experiments in this study. The number of positive and negative sequences that contain instances of each possible k-mer are counted, treating each k-mer and its reverse complement as one single k-mer. A HGP is computed to evaluate the significance of enrichment for each k-mer. KMAC then clusters the enriched k-mers using a density-based clustering method (Rodriguez and Laio 2014). Levenshtein distance (Levenshtein 1966) is used to quantify the distance between two k-mers. KMAC then takes each of the top ranked k-mer cluster centers as the seed k-mers for Step 2. With the density-based clustering approach, a k-mer may belong to different k-mer clusters and thus contribute to different motifs, allowing KMAC to unbiasedly discover multiple motifs. This is in contrast to the typical mask-and-discover approach used by existing methods such as MEME (Bailey and Elkan 1994) and HOMER (Heinz et al. 2010), which is biased in that the subsequently discovered motifs have a smaller sequence space.
Step 2: Each cluster center k-mer is used as a seed k-mer. This seed k-mer and similar k-mers with a one-base mismatch are used to initialize the KSM, which is then used to match and align the positive training sequences.
Step 3: With the alignment of the positive sequences, a new KSM and its corresponding PWM motif are generated from a 2 × k window around the middle of the seed k-mer. To compute the offsets of the component k-mers, a reference position in the alignment, the expected binding position, is estimated as the median of the center positions of the aligned sequences.
Step 4: The KSM and PWM motifs are used to match and align the positive sequences. The KSM motif is first used to match and align the positive sequences and then the PWM motif is used to match and align the remaining sequences. This allows KMAC to include more k-mers, especially at the initial iterations when the KSM consists of only a few component k-mers. If multiple motif matches are found in a sequence, the match with the highest score is used.
Figure 2.
KMAC motif discovery outperforms other methods when detecting motifs in ChIP-seq data. (A) KMAC motif discovery schematic. Step 1: Overrepresented k-mers with length k are clustered using density-based clustering. Bars represent the k-mers, whereas red bars represent the cluster center exemplars. Step 2: A cluster center is used as a seed k-mer. The seed k-mer and k-mers with a one-base mismatch are used to match and align the sequences. Step 3: A pair of KSM and PWM motifs are extracted from the aligned sequences. Step 4: The KSM and PWM motifs are used to match and align the sequences. Steps 3 and 4 are repeated until the significance of the motifs stops to improve. (B) The motif discovery performance of KMAC is compared to the motif discovery performance of various motif finders on 209 ENCODE ChIP-seq experiments.
Steps 3 and 4 are repeated alternately until the significance of the motifs stops to improve. The significance of a motif is evaluated as the sum of partial area under receiver operating characteristic (pAUROC) (up to a false positive rate of 0.1, FPR ≤ 0.1) scores (McClish 1989; Ma et al. 2013) of the KSM and PWM motifs in discriminating positive versus negative sequences. We choose the pAUROC because typically only the area at a false positive rate ≤0.1 is of interest for realistic motif matching.
Finally, all the discovered motifs are ranked by the KSM pAUROC scores.
Note that in the process of discovering KSM motifs, KMAC also generates corresponding PWM motifs using the same sequence alignments from which the KSMs are derived. These PWMs provide an approximation of the KSMs and can be used for matching existing PWM motifs.
KMAC outperforms other motif discovery methods in discovering known DNA-binding motifs
We tested KMAC's ability to discover biologically relevant DNA-binding motifs from in vivo binding data. We used a set of 209 TF ChIP-seq experiments comprising 78 distinct TFs that were profiled in one or more cell lines by the ENCODE project (The ENCODE Project Consortium 2012) and for which in vitro or in vivo validated DNA-binding motifs exist in the public database Cis-BP (Weirauch et al. 2014). We chose this large collection of experiments because we expected that they would be representative of the typical range of ChIP-seq data noise and sequencing depth. We used KMAC and five state-of-the-art methods, MEME (Bailey and Elkan 1994), MEME-ChIP (Machanick and Bailey 2011), HOMER (Heinz et al. 2010), Weeder2 (Zambelli et al. 2014), and ChIPMunk (Kulakovskiy et al. 2010) to train motifs from sequences derived from these ChIP-seq data. The most significant PWM motifs from each analysis were matched using STAMP (Mahony et al. 2007) to corresponding known PWM motifs of the same TFs. We found that KMAC outperforms other methods in rediscovering the known PWM motifs in Cis-BP (Fig. 2B; Weirauch et al. 2014). When allowing each method to make multiple motif predictions, KMAC performs better than or equal to the other methods. We also tested how the number of training sequences affects the performance of KMAC and found that KMAC is able to maintain good performance with 300 or more sequences and to correctly identify the primary motifs in 126 of 209 experiments with only 30 sequences (Supplemental Table S3). In addition, the running time of KMAC is similar to that of Weeder2 and is much faster (about 4–30×) than the other methods (Supplemental Table S4).
KSMs outperform PWMs in predicting in vivo TF binding
We compared the performance of KSMs versus PWMs in predicting in vivo TF binding using the ENCODE ChIP-seq data sets. We found that the KSM outperforms the PWM in discriminating TF-bound sequences (positive sequences) from randomly shuffled sequences and unbound genomic sequences near the binding sites (negative sequences).
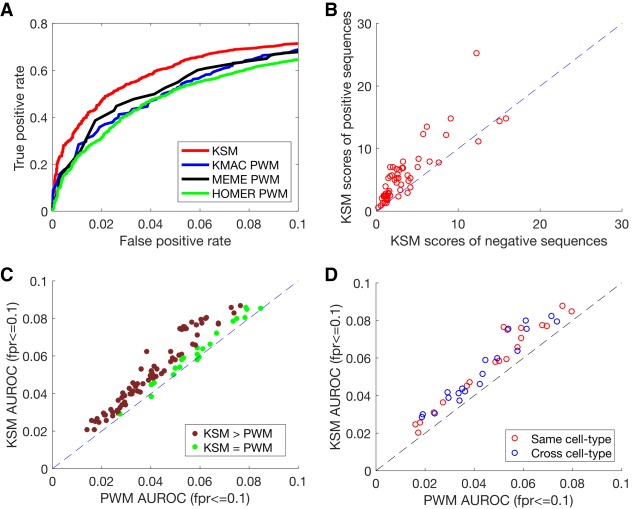
We first examined an example of a protein in which a KSM would be expected to outperform a PWM and confirmed that this is the case. We trained KSM and PWM motifs using a subset of TF GABP-bound sequences in human K562 cells and used the motif scores to discriminate held-out GABP-bound sequences from negative randomly shuffled sequences. We found that the KSM outperforms three PWMs learned by KMAC, MEME, and HOMER, respectively, from the same set of sequences (Fig. 3A). To understand why the KSM performs better than the PWM, we next studied the sequences and scores of the GABP motif matches. We found that for the same PWM motif match scores, the KSM scores of the matches in the positive sequences are generally higher than the KSM scores of those in the negative sequences (Fig. 3B). The higher KSM scores in the positive sequences are contributed by the flanking k-mers that are often present in the positive sequences but are less present in the negative sequences because the matches in the negative sequences are usually random matches of only one or very few k-mers. These results are consistent with the observation that the length of the KSM motif matches in the positive sequences are in general longer than the length in the negative sequences (Supplemental Fig. S2). Therefore, the KSM is able to use the flanking sequences to further discriminate real bound sequences from the random sequences when the PWM finds identical matches. In addition, we found cases that some sites in the negative sequences are scored highly by the PWM but not by the KSM. For example, CACTTGCGG is only one base different from the consensus sequence CACTTCCGG and has a PWM score of 6.67, which is ∼60% of the maximum PWM score for GABP motif. However, CACTTGCGG does not occur in the entire GABP-bound sequence set, suggesting that this single-base difference cannot be tolerated by GABP. The KSM score for the CACTTGCGG site is 0 because it has no exact match to the KSM. We verified this observation with in vitro binding data from a mouse GABP PBM data set (Badis et al. 2009). The enrichment scores (E-scores) of the PBM 8-mers overlapping the consensus sequence CACTTCCGG (E-score of ACTTCCGG = 0.497, and E-score of CACTTCCG = 0.486) are close to the maximum enrichment (E-score = 0.5); in contrast, the 8-mers overlapping CACTTGCGG (E-score of ACTTGCGG = −0.140, and E-score of CACTTGCG = −0.279) are not enriched at all, consistent with the KSM scores. This observation highlights the limitation of the positional independence assumption of the PWM representation and that the KSM is able to overcome this limitation. The ability of the KSM representation to accurately score the sequences with single-base differences is valuable in evaluating the impact of single-nucleotide polymorphisms (SNPs) that may alter TF binding sites.
Figure 3.
KSM outperforms PWM in predicting in vivo TF binding in held-out data. (A) The partial ROC performance of KSM, KMAC PWM, MEME PWM, and HOMER PWM for predicting ChIP-seq binding of GABP in K562 cells. (B) Scatter plot comparing the mean KSM scores of positive sequences and mean KSM scores of negative sequences that corresponds to the same PWM scores in the K562 GABP data set. Each point represents a set of sequences that have the same PWM score. (C) Scatter plot comparing the mean partial AUROC (FPR ≤ 0.1) values of KSM and PWM for predicting ChIP-seq binding for 104 experiments. (D) Similar to C, but comparing KSM and PWM in the same cell type (red) or across cell type (blue) in 19 TFs.
We then extended the comparison between the KSM and the PWM to 104 data sets for which the correct primary motifs were found for all the representations that we evaluated in this study (Methods) and that have sufficient number of binding sites. Similar to previous work (Mathelier and Wasserman 2013), we compared the performance between two methods by computing the score ratios between the methods on the same data sets. Two methods are considered performing differently if the score ratio is less than 0.95. In 102 of 104 experiments, the KSMs perform better than the PWMs in predicting TF binding in held-out data, whereas the PWMs do not perform better in any of the experiments (Fig. 3C; Supplemental Fig. S3). Across all the data sets, the KSM representation significantly outperforms the PWM representation (P = 8.53 × 10−19, paired Wilcoxon signed rank test).
Here, the KSM and PWM motifs were both learned from the same KMAC motif discovery runs to ensure that the performance differences are from the motif representation but not from the motif discovery procedures. In addition, we also compared the KSMs with PWMs that were discovered by HOMER and MEME and PWMs that were optimized by the discriminative motif optimizer (DiMO) (Patel and Stormo 2014). We found that in most cases, KSMs outperform the PWMs trained by different methods, with the exception of the MEME PWMs that outperform the KSM in 11 CTCF experiments (Supplemental Fig. S4). We reasoned that the CTCF motif is relatively long and may need more than 5000 training sequences to adequately capture the CTCF binding specificities. We therefore retrained the KSM motifs of the 11 CTCF experiments with 20,000 sequences and found that the new KSMs perform comparably to the MEME PWMs (Supplemental Fig. S4E). We also tested using flanking sequences as negative sequences and obtained similar results (P = 1.99 × 10−18, paired Wilcoxon signed rank test) (Supplemental Fig. S5). Furthermore, we compared various parameter settings for the KSM, such as the component k-mer significance cutoff and the number of the maximum gaps, and found that the differences between different parameter settings are relatively small (Supplemental Fig. S6).
In addition, we found that a KSM does not overfit the training data and is able to generalize across cell types. Because a KSM consists of hundreds to a few thousand k-mers, one legitimate concern is that it may overfit the training data. Overfitting would result in good performance on the training cell type but poor performance on a new cell type. To address this concern, we conduct a cross-cell-type analysis. For 19 unique TFs that are both profiled in different cell types by the ENCODE project, including a diverse list of CTCF, REST, YY1, USF1, SPI1, E2F6, JUN, ETS1, among others, we trained KSM and PWM motifs from one cell type (K562) and predicted binding for another cell type (GM12878 or H1-hESC). We found that KSMs also significantly outperformed PWMs in the cross-cell-type predictions (P = 0.000132, paired Wilcoxon signed rank test) (Fig. 3D). The KSM predictions across the cell types perform similarly to the KSM predictions in the same cell type (P > 0.05, paired Wilcoxon signed rank test).
Taken together, these results suggest that the KSM is a more accurate motif representation than the PWM model, and it generalizes well across cell types.
KSMs outperform complex motif models in predicting in vivo TF binding
We next compared the KSM representation with two complex motif models that have been shown to be more accurate than the PWM model. The TF flexible model (TFFM) is a hidden Markov model–based framework that captures interdependencies of successive nucleotides and flexible length of the motif (Mathelier and Wasserman 2013). The sparse local inhomogeneous mixture (Slim) uses a soft feature selection approach to optimize the dependency structure and model parameters (Keilwagen and Grau 2015). We trained TFFM and Slim models on the same subset of sequences as the KSMs and used the motif scores to predict on the remaining sequences. The KSMs perform better than the TFFMs in predicting TF binding in 53 experiments, worse in 11 experiments, and similarly in 40 experiments (Fig. 4A). Across all the data sets, the KSM significantly outperforms the TFFM representation (P = 2.85 × 10−7, paired Wilcoxon signed rank test). Similarly, the KSMs perform better than Slim in predicting TF binding in 41 experiments, worse in 12 experiments, and similarly in 51 experiments (Fig. 4B). Across all the data sets, the KSM significantly outperforms the Slim representation (P = 2.83 × 10−6, paired Wilcoxon signed rank test). In addition, the motif scanning time of KMAC is only 2–3× the PWM scanning time and is much less (about 20–80×) than that of the Slim and TFFM models (Supplemental Table S5).
Figure 4.
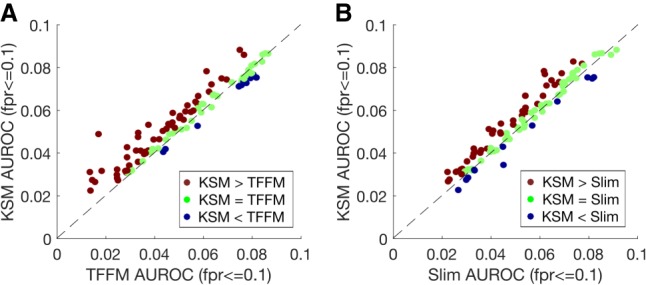
KSMs outperform complex motif models in predicting in vivo TF binding. (A) Scatter plot comparing the mean partial AUROC (FPR ≤ 0.1) values of KSM and TFFM for predicting in vivo binding in 104 TF ChIP-seq experiments. Each point represents a ChIP-seq data set. (B) Similar to A, but comparing KSM and Slim.
In summary, the KSM is more accurate at discriminating TF-bound sequences from randomly generated sequences than the conventional PWM and the more sophisticated TFFM and Slim motif representations, suggesting that the KSM is a more precise motif representation.
KSMs outperform PWMs and complex motif models in predicting in vitro TF binding
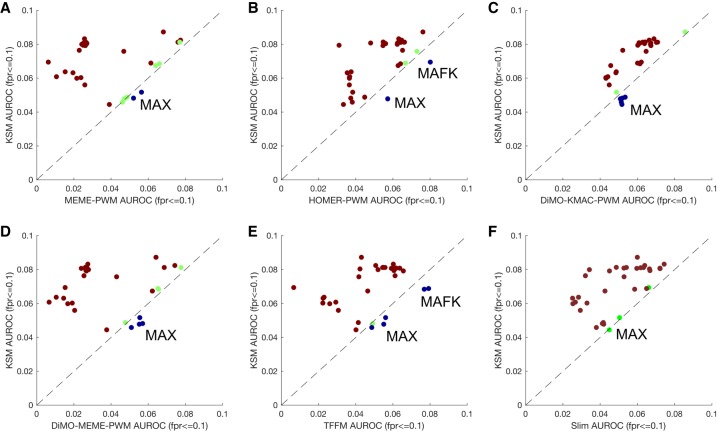
We next investigated whether the superior performance of the KSM representation holds for in vitro TF binding prediction. Motifs trained from in vivo ChIP-seq data may be confounded by factors extrinsic to binding of the profiled TF, such as local GC content, cofactors, and chromatin state. To more rigorously test various motif representations on capturing intrinsic TF binding specificities, we compared KSMs, PWMs discovered by HOMER (Heinz et al. 2010) and MEME (Bailey and Elkan 1994), PWMs optimized by DiMO (Patel and Stormo 2014), Slim (Keilwagen and Grau 2015), and TFFM (Mathelier and Wasserman 2013) motif models in predicting in vitro TF binding sites using HT-SELEX data (Jolma et al. 2013). The various motif models were trained using ChIP-seq binding data as above. For the TFs that were profiled in both HT-SELEX and ChIP-seq, we curated the sequences selected by HT-SELEX as the test sequences for the in vitro binding prediction (Methods). The list of nine TFs (33 experiments) includes CTCF, CTCFL, EBF1, SPI1, YY1, MAX, MAFK, ETS1, and POU2F2. In most cases KSMs outperform the other motif models in predicting in vitro TF binding (Fig. 5). KSMs do not perform as well on MAX and MAFK, TFs that form heterodimers in vivo and have been observed to cobind with MYC and MAFF/BACH1, respectively (Blackwood and Eisenman 1991; Kannan et al. 2012; Guo and Gifford 2017). Because the in vitro binding data for MAX and MAFK reflect the specificities of monomer or homodimer binding, the evaluation for MAX and MAFK may be confounded by the significant differences between their in vivo and in vitro binding characteristics. Across all the data sets, KSMs significantly outperform other motif representations (P < 1 × 10−5 for all comparisons, paired Wilcoxon signed rank test). These results and the in vivo binding prediction results suggest that the KSM is more accurate than the PWM and other complex motif models in representing TF binding specificities.
Figure 5.
KSMs outperform PWMs and complex motif models in predicting in vitro TF binding. Scatter plots compare the mean partial AUROC performance of KSM versus MEME PWM (A), HOMER PWM (B), DiMO-optimized KMAC PWM (C), DiMO-optimized MEME PWM (D), TFFM (E), and Slim (F) motif models for predicting HT-SELEX in vitro TF binding. Each point represents a ChIP-seq experiment of which the TF has been profiled using HT-SELEX. (Brown) KSM performs better than other motif representations; (blue) KSM performs worse; (green) both representations perform similarly.
KSM enables accurate prediction of causal regulatory variants
With the superior performance of the KSM representation on predicting in vivo TF binding, we next tested whether sequence features derived from KSM motifs would enable more accurate prediction of the effects of noncoding genetic variants on the activities of the regulatory sequences that harbor the genetic variants.
We used an ensemble model (Zeng et al. 2017) that included KSM motif features from 87 TF ChIP-seq data sets and deep learning–based features to achieve the best performance in “eQTL-causal SNPs” open challenge (Kreimer et al. 2017) in the Fourth Critical Assessment of Genome Interpretation (CAGI 4). The challenge was to predict the experimental results of thousands of regulatory elements that contains eQTL alleles (reference and alternative) from a massively parallel reporter assay in GM12878 cells (Tewhey et al. 2016).
Here, we used the same computational framework—a LASSO regression model to predict reporter expression of the reference and alternative alleles and an ensemble model to classify whether the two alleles have different regulatory activities (Zeng et al. 2017)—to evaluate the performance of different types of sequence features. We constructed KSM motif features and PWM features from motifs discovered by MEME and HOMER, respectively, from 209 TF ChIP-seq data sets (The ENCODE Project Consortium 2012). The performance of the predictions using different sets of sequence features was evaluated using AUPRC and AUROC. We found that the KSM features (AUPRC = 0.479, AUROC = 0.668) outperform HOMER PWM (AUPRC = 0.434, AUROC = 0.629) and MEME PWM (AUPRC = 0.408, AUROC = 0.619) in predicting differential reporter expression between the two alleles (Fig. 6A; Supplemental Fig. S7A). We next compared KSM motif features with the features derived from DeepBind (Alipanahi et al. 2015), a deep learning model trained on 927 TF ChIP-seq data sets, and DeepSEA (Zhou and Troyanskaya 2015), a deep learning model trained on 919 epigenomic data sets. We found that KSM features outperform DeepBind (AUPRC = 0.432, AUROC = 0.608) and DeepSEA features (AUPRC = 0.396, AUROC = 0.628) in predicting differential reporter expression between the two alleles (Fig. 6B; Supplemental Fig. S7B). In addition, the KSM features offer better interpretability than deep learning features because the predictive KSM features are directly linked to their corresponding TFs. The combined KSM and DeepBind features achieved the best AUPRC (0.483), outperforming the KSM or DeepBind features alone, although the AUROC (0.647) of the combined features is worse than that of the KSM. The combined KSM and DeepBind features or KSM features alone both outperformed all the CAGI 4 methods that use features such as PWMs, k-mers, epigenomic signals, chromatin state annotations, and evolutionary conservation (Kreimer et al. 2017). These results highlight the value of accurate motif models in the characterization of noncoding variants.
Figure 6.
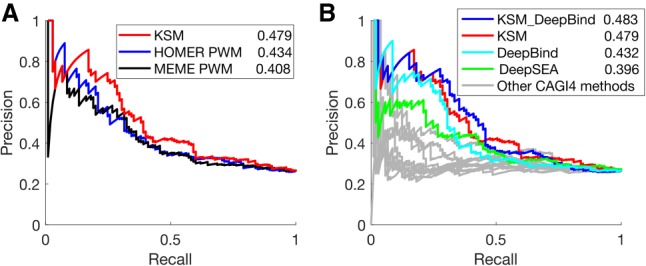
KSMs predicts allele-specific differences in regulatory activity better than PWMs and deep learning–derived features. (A) PRC performance of KSM and PWM motif representations in predicting differential regulatory activities of eQTL alleles. The numeric values in the legend are the AUPRC values. (B) Similar to A, KSM, DeepBind, and DeepSEA derived features and other CAGI 4 open challenge methods.
A new public resource of KSM and PWM motifs
Finally, we have created a public resource of KSM and PWM motifs by applying KMAC to 1600 ENCODE transcription factor ChIP-seq data sets. These motifs are available at the KMAC website (http:// groups.csail.mit.edu/cgs/gem/kmac/).
Discussion
We have demonstrated that k-mer set memory (KSM) representations are better at predicting transcription factor in vivo binding as well as in vitro binding than PWMs and the more complex TFFM and Slim models. In addition, sequence features derived from KSMs outperform those derived from PWMs and deep learning models for predicting the effect of noncoding genetic variants. In addition, the training and the motif scanning of KSM motifs are adequately efficient for large-scale analysis. Because the PWM representation is used by most computational analyses that involves TF binding motifs, the accuracy gain from replacing the PWM with the KSM will likely be widespread.
A KSM represents TF binding specificity as a set of aligned k-mers that are found to be overrepresented at factor binding sites. An important feature of the KSM is that it captures the relative positions among the k-mers, thus allowing overlapping k-mers to be assembled into k-mer groups for accurate identification and scoring of motif instances. We showed that, with contribution from the overlapping k-mers, the KSM gives TF-bound sequences higher scores than the random sequences when they have the same PWM score, highlighting the value of positional information among the k-mers for recapitulating in vivo TF binding.
The KSM is a representation for the DNA-binding motif of a single TF. To increase the probability that a KSM represents the sequence mechanistically associated with a particular TF, KMAC uses a narrow window around binding sites to extract component k-mers and requires the component k-mers to be aligned with each other. Thus, the KSM is different from and not directly comparable to methods for other tasks that use k-mers associated with multiple TF motifs in machine learning models (Ghandi et al. 2014; Setty and Leslie 2015). It will be interesting to build learning models with multiple KSM motifs learned from ChIP-seq or DNase-seq data and compare with the published k-mer-based multimotif learning methods.
Genome-wide association studies (GWAS) have made tremendous progress in linking numerous SNPs to human traits and diseases. However, finding the causal genetic variants has been challenging, because the lead GWAS SNPs are in linkage disequilibrium with nearby SNPs and the majority of GWAS loci are in noncoding regions (Maurano et al. 2012; Schaub et al. 2012). Computational approaches that identify TF binding altering genetic variants are important for meeting this challenge (Mathelier et al. 2015). The KSM motif representation and the KMAC motif discovery method enables more accurate characterization and discovery of TF binding motifs. Our results show that the KSM motif features outperform features derived from a deep learning model in predicting the effect of noncoding genetic variants, suggesting that accurate and interpretable motif features may be more appropriate for characterizing noncoding genetic variants than the deep learning features. With large-scale efforts such as the ENCODE project (The ENCODE Project Consortium 2012) profiling hundreds of TFs in diverse cellular conditions, a more comprehensive catalog of TF binding sites is now available for training new computational models. We expect that the KSM representation and KMAC method will be valuable in characterizing TF binding specificities and in interpreting the effects of noncoding genetic variations.
Methods
ChIP-seq data sets and TF binding motifs
Two hundred nine TF ChIP-seq data sets (from three ENCODE tier 1 cell types, K562, GM12878, and H1-hESC cells) that have known motifs in public databases were downloaded from the ENCODE project website (The ENCODE Project Consortium 2012). Relevant information about this data set is in Supplemental Table S6. TF binding motifs (PWMs) were downloaded from Cis-BP database (Homo_sapiens_2015_02_05) (Weirauch et al. 2014), which includes motif from the TRANSFAC (Matys et al. 2003), JASPAR (Sandelin et al. 2004), SELEX (Jolma et al. 2013), PBM UniPROBE (Berger et al. 2006), and other databases.
KSM sequence logo
We visualized a KSM sequence logo as a stack of PWM sequence logos that represent the high-scoring, nonoverlapping component k-mers and their sequence contexts. We identified the most significant k-mer in the training sequences, used this k-mer to align the sequences that contain the k-mer, and built a PWM using the sequence alignment. Thus, the top PWM represent the most significant k-mer and its sequence contexts. After removing the aligned sequences, the same process was repeated for the remaining sequences. For each KSM motif, a color chart representation of the aligned sequences and the corresponding KSM sequence logo were output by the KMAC software.
Motif discovery performance comparison
For the 209 ENCODE ChIP-seq data, KMAC and four other state-of-the-art de novo motif discovery methods—MEME v4.11 (Bailey and Elkan 1994), MEME-ChIP v4.11 (Machanick and Bailey 2011), Weeder 2.0 (Zambelli et al. 2014), and HOMER (Heinz et al. 2010)—were applied to discover motifs independently. From the top 1000 peaks of each data set, 100-bp sequences centered on the peak summits were extracted, as suggested by the MEME Suite's documentation based on the typical resolution of ChIP-seq peaks. MEME was run with options “-dna -nmotifs 9 -revcomp”; MEME-ChIP was run with options “-dna -norand -meme-nmotifs 5 -meme-maxsize 1000000 -dreme-m 5 -spamo-skip -fimo-skip”; and Weeder2 was run with options “-O HS -chipseq.” All other parameters were the defaults specified by the authors.
Discovered motifs (PWMs) were compared to known motifs in the public database Cis-BP (Weirauch et al. 2014) using STAMP (Mahony et al. 2007). For KMAC, the PWM motifs discovered were used for comparison. A motif with E-value less than 1 × 10−5 was considered a match. For each program, we counted the number of data sets that had a motif matching at least one known motif of that TF. In some cases, the correct motifs were not matched by the first motif that a method outputs, but by the second or later motifs. Therefore, we compared the motif-finding performance using the top 1, top 2, and top 3 motifs.
TF in vivo binding prediction performance comparison
We compared KSM, PWMs discovered by KMAC, HOMER (Heinz et al. 2010), and MEME (Bailey and Elkan 1994), and PWMs optimized by DiMO (Patel and Stormo 2014), Slim (Keilwagen and Grau 2015), and TFFM (Mathelier and Wasserman 2013) motif models in predicting in vivo TF ChIP-seq binding sites. For each set of bound sequences from a TF ChIP-seq experiment (positive sequences), we generated random shuffled sequences by preserving dinucleotide frequencies (shuffled negative sequences). We also generate an alternative set of negative sequences by taking the genomic sequences 200 bp away from the TF binding site (flanking negative sequences).
We first trained motifs from randomly subsampled 5000 positive sequences (training set) using KMAC, HOMER, the Jstacs library for Slim (Keilwagen and Grau 2015), and the Python TFFM framework (Mathelier and Wasserman 2013). For MEME, the running time for 5000 sequences is impractically long; therefore, we used the top 600 sequences as suggested by the MEME documentation. For Slim, additional shuffled negative sequences with signal = 0 were provided for motif discovery. For TFFM, the primary PWM motifs discovered by MEME were used to initialize the models. Two kinds of models (FIRST_ORDER and DETAILED) were constructed, and the results were similar. We reported only results from the DETAILED model. For DiMO-optimized PWM (Patel and Stormo 2014), the PWMs discovered by MEME and KMAC were used as initial inputs to optimize on the training positive and negative sequences.
For each method, the motif scores of the top ranking primary motif were then used to discriminate 5000 held-out positive and negative sequences (test set). In order to compare performance across multiple motif representations, we used 104 data sets in which all the methods/representations discover a correct primary motif that matches a known motif for the same TF in the public database Cis-BP (Weirauch et al. 2014). For the different motif representations discovered from the same set of sequences, their performance in predicting ChIP-seq TF binding sites on the held-out data was evaluated using a partial AUROC (McClish 1989) up to a false positive rate of 0.1, which typically falls in the range of realistic motif matches. We repeated this procedure five times and used the mean partial AUROC score of each ChIP-seq experiment or each TF to compare performance.
We assessed the significance for the improvement of predictive power when comparing two models using the Wilcoxon signed rank tests. The function signrank() in MATLAB software (MATLAB and Statistics Toolbox Release 2016b, The MathWorks, Inc.) was used.
TF in vitro binding prediction performance comparison
We compared KSM, PWMs discovered by HOMER (Heinz et al. 2010) and MEME (Bailey and Elkan 1994), DiMO-optimized PWM (Patel and Stormo 2014), Slim (Keilwagen and Grau 2015), and TFFM (Mathelier and Wasserman 2013) motif models in predicting in vitro TF binding sites using HT-SELEX data (Jolma et al. 2013). The motif models were trained using ChIP-seq binding data as described above. Here, we compared them in predicting in vitro TF binding sites.
For the TFs that were profiled in both HT-SELEX and ChIP-seq, we curated the sequences selected by HT-SELEX as the test sequences for the motif models. HT-SELEX FASTQ files were downloaded from https://www.ebi.ac.uk/ena/data/view/PRJEB3289. The cycle 3 and cycle 4 FASTQ sequences that have quality scores higher than 20 and that have at least four counts are selected. The data sets that contain at least 200 unique sequences are used for evaluation. In total, HT-SELEX data sets of nine TFs are curated, corresponding to 33 ChIP-seq experiments. From the positive HT-SELEX sequences, we then generated random shuffled sequences while preserving dinucleotide frequencies and used them as negative sequences.
The in vitro binding prediction comparisons were performed the same as described above for in vivo binding prediction.
Predicting the effect of regulatory variants
We used the EnsembleExpr (https://github.com/gifford-lab/EnsembleExpr/) computational framework as described in Zeng et al. (2017). Briefly, sequence features were generated by taking the maximum motif score of each motif on the training and testing sequences. LASSO regression models were trained to predict the reporter expression levels for each allele, and an ensemble of binary classification models with regularization tuned by cross-validation was trained to predict whether the two alleles have different expression levels. In this work, five sets of sequence features were derived from KSM motifs, MEME PWM motif, and HOMER PWM motifs learned from 209 ENCODE TF ChIP-seq data sets, and from the pretrained DeepBind (Alipanahi et al. 2015) and DeepSEA model (Zhou and Troyanskaya 2015).
Data access
The free software for KMAC motif discovery, for KSM motif scanning and scoring, as well as motifs discovered from ENCODE TF ChIP-seq data can be downloaded from the KMAC website (http:// groups.csail.mit.edu/cgs/gem/kmac/). The PWM motifs from ENCODE phase III TF ChIP-seq data are also provided as Supplemental Material. The source code has been deposited in GitHub (https://github.com/gifford-lab/GEM3) and is also available as Supplemental Code.
Supplementary Material
Acknowledgments
We thank Jens Keilwagen for providing suggestions and codes for training and using the Slim model. This work was supported by the National Institutes of Health (grant 1U01HG007037 and 1R01HG008363 to D.K.G.).
Author contributions: Y.G. conceived the project. Y.G. and D.K.G. designed the analysis. Y.G. developed the KSM and KMAC methods. Y.G. coordinated the analysis. Y.G., K.T., H.Z., and X.G. performed the analysis and interpreted results. Y.G. and D.K.G. wrote the manuscript.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.226852.117.
References
- Aho AV, Corasick MJ. 1975. Efficient string matching: an aid to bibliographic search. Commun ACM 18: 333–340. [Google Scholar]
- Alipanahi B, Delong A, Weirauch MT, Frey BJ. 2015. Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat Biotechnol 33: 831–838. [DOI] [PubMed] [Google Scholar]
- Badis G, Berger MF, Philippakis AA, Talukder S, Gehrke AR, Jaeger SA, Chan ET, Metzler G, Vedenko A, Chen X, et al. 2009. Diversity and complexity in DNA recognition by transcription factors. Science 324: 1720–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey TL, Elkan C. 1994. Fitting a mixture model by expectation maximization to discover motifs in biopolymers. Proc Int Conf Intell Syst Mol Biol 2: 28–36. [PubMed] [Google Scholar]
- Barash Y, Bejerano G, Friedman N. 2001. A simple hyper-geometric approach for discovering putative transcription factor binding sites. In Proceedings of the First International Workshop on Algorithms in Bioinformatics, WABI ’01, pp. 278–293, Springer-Verlag, London, UK. [Google Scholar]
- Benos PV, Bulyk ML, Stormo GD. 2002. Additivity in protein–DNA interactions: How good an approximation is it? Nucleic Acids Res 30: 4442–4451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger MF, Philippakis AA, Qureshi AM, He FS, Estep PW III, Bulyk ML. 2006. Compact, universal DNA microarrays to comprehensively determine transcription-factor binding site specificities. Nat Biotechnol 24: 1429–1435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackwood EM, Eisenman RN. 1991. Max: a helix-loop-helix zipper protein that forms a sequence-specific DNA-binding complex with Myc. Science 251: 1211–1217. [DOI] [PubMed] [Google Scholar]
- Bulyk ML, Johnson PLF, Church GM. 2002. Nucleotides of transcription factor binding sites exert interdependent effects on the binding affinities of transcription factors. Nucleic Acids Res 30: 1255–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chew JL, Loh YH, Zhang W, Chen X, Tam WL, Yeap LS, Li P, Ang YS, Lim B, Robson P, et al. 2005. Reciprocal transcriptional regulation of Pou5f1 and Sox2 via the Oct4/Sox2 complex in embryonic stem cells. Mol Cell Biol 25: 6031–6046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claussnitzer M, Dankel SN, Kim KH, Quon G, Meuleman W, Haugen C, Glunk V, Sousa IS, Beaudry JL, Puviindran V, et al. 2015. FTO obesity variant circuitry and adipocyte browning in humans. N Engl J Med 373: 895–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornfield J. 1951. A method of estimating comparative rates from clinical data; applications to cancer of the lung, breast, and cervix. J Natl Cancer Inst 11: 1269–1275. [PubMed] [Google Scholar]
- Edwards AW. 1963. The measure of association in a 2 × 2 table. J R Stat Soc Ser A 126: 109–114. [Google Scholar]
- The ENCODE Project Consortium. 2012. An integrated encyclopedia of DNA elements in the human genome. Nature 489: 57–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fratkin E, Naughton BT, Brutlag DL, Batzoglou S. 2006. MotifCut: regulatory motifs finding with maximum density subgraphs. Bioinformatics 22: e150–e157. [DOI] [PubMed] [Google Scholar]
- Ghandi M, Lee D, Mohammad-Noori M, Beer MA. 2014. Enhanced regulatory sequence prediction using gapped k-mer features. PLoS Comput Biol 10: e1003711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordân R, Shen N, Dror I, Zhou T, Horton J, Rohs R, Bulyk ML. 2013. Genomic regions flanking E-box binding sites influence DNA binding specificity of bHLH transcription factors through DNA shape. Cell Rep 3: 1093–1104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Y, Gifford DK. 2017. Modular combinatorial binding among human trans-acting factors reveals direct and indirect factor binding. BMC Genomics 18: 45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Y, Mahony S, Gifford DK. 2012. High resolution genome wide binding event finding and motif discovery reveals transcription factor spatial binding constraints. PLoS Comput Biol 8: e1002638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz S, Benner C, Spann N, Bertolino E, Lin YC, Laslo P, Cheng JX, Murre C, Singh H, Glass CK. 2010. Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and B cell identities. Mol Cell 38: 576–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes TR. 2011. Introduction to “A Handbook of Transcription Factors”. Subcell Biochem 52: 1–6. [DOI] [PubMed] [Google Scholar]
- Johnson DS, Mortazavi A, Myers RM, Wold B. 2007. Genome-wide mapping of in vivo protein-DNA interactions. Science 316: 1497–1502. [DOI] [PubMed] [Google Scholar]
- Jolma A, Yan J, Whitington T, Toivonen J, Nitta KR, Rastas P, Morgunova E, Enge M, Taipale M, Wei G, et al. 2013. DNA-binding specificities of human transcription factors. Cell 152: 327–339. [DOI] [PubMed] [Google Scholar]
- Kannan MB, Solovieva V, Blank V. 2012. The small MAF transcription factors MAFF, MAFG and MAFK: current knowledge and perspectives. Biochim Biophys Acta 1823: 1841–1846. [DOI] [PubMed] [Google Scholar]
- Keilwagen J, Grau J. 2015. Varying levels of complexity in transcription factor binding motifs. Nucleic Acids Res 43: e119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim TM, Park PJ. 2011. Advances in analysis of transcriptional regulatory networks. Wiley Interdiscip Rev Syst Biol Med 3: 21–35. [DOI] [PubMed] [Google Scholar]
- Kreimer A, Zeng H, Edwards MD, Guo Y, Tian K, Shin S, Welch R, Wainberg M, Mohan R, Sinnott-Armstrong NA, et al. 2017. Predicting gene expression in massively parallel reporter assays: a comparative study. Hum Mutat 38: 1240–1250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulakovskiy IV, Boeva VA, Favorov AV, Makeev VJ. 2010. Deep and wide digging for binding motifs in ChIP-Seq data. Bioinformatics 26: 2622–2623. [DOI] [PubMed] [Google Scholar]
- Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, et al. 2002. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science 298: 799–804. [DOI] [PubMed] [Google Scholar]
- Levenshtein VI. 1966. Binary codes capable of correcting deletions, insertions and reversals. Sov Phys Dokl 10: 707. [Google Scholar]
- Levo M, Segal E. 2014. In pursuit of design principles of regulatory sequences. Nat Rev Genet 15: 453–468. [DOI] [PubMed] [Google Scholar]
- Ma H, Bandos AI, Rockette HE, Gur D. 2013. On use of partial area under the ROC curve for evaluation of diagnostic performance. Stat Med 32: 3449–3458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machanick P, Bailey TL. 2011. MEME-ChIP: motif analysis of large DNA datasets. Bioinformatics 27: 1696–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacIsaac KD, Fraenkel E. 2006. Practical strategies for discovering regulatory DNA sequence motifs. PLoS Comput Biol 2: e36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maerkl SJ, Quake SR. 2007. A systems approach to measuring the binding energy landscapes of transcription factors. Science 315: 233–237. [DOI] [PubMed] [Google Scholar]
- Mahony S, Auron PE, Benos PV. 2007. DNA familial binding profiles made easy: comparison of various motif alignment and clustering strategies. PLoS Comput Biol 3: e61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Man TK, Stormo GD. 2001. Non-independence of Mnt repressor–operator interaction determined by a new quantitative multiple fluorescence relative affinity (QuMFRA) assay. Nucleic Acids Res 29: 2471–2478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathelier A, Wasserman WW. 2013. The next generation of transcription factor binding site prediction. PLoS Comput Biol 9: e1003214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathelier A, Shi W, Wasserman WW. 2015. Identification of altered cis-regulatory elements in human disease. Trends Genet 31: 67–76. [DOI] [PubMed] [Google Scholar]
- Matys V, Fricke E, Geffers R, Gößling E, Haubrock M, Hehl R, Hornischer K, Karas D, Kel AE, Kel-Margoulis OV, et al. 2003. TRANSFAC: transcriptional regulation, from patterns to profiles. Nucleic Acids Res 31: 374–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurano MT, Humbert R, Rynes E, Thurman RE, Haugen E, Wang H, Reynolds AP, Sandstrom R, Qu H, Brody J, et al. 2012. Systematic localization of common disease-associated variation in regulatory DNA. Science 337: 1190–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClish DK. 1989. Analyzing a portion of the ROC curve. Med Decis Making 9: 190–195. [DOI] [PubMed] [Google Scholar]
- Patel RY, Stormo GD. 2014. Discriminative motif optimization based on perceptron training. Bioinformatics 30: 941–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez A, Laio A. 2014. Clustering by fast search and find of density peaks. Science 344: 1492–1496. [DOI] [PubMed] [Google Scholar]
- Sandelin A, Alkema W, Engström P, Wasserman WW, Lenhard B. 2004. JASPAR: an open-access database for eukaryotic transcription factor binding profiles. Nucleic Acids Res 32: D91–D94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaub MA, Boyle AP, Kundaje A, Batzoglou S, Snyder M. 2012. Linking disease associations with regulatory information in the human genome. Genome Res 22: 1748–1759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setty M, Leslie CS. 2015. SeqGL identifies context-dependent binding signals in genome-wide regulatory element maps. PLoS Comput Biol 11: e1004271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B. 1998. Comprehensive identification of cell cycle–regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell 9: 3273–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stormo GD. 2000. DNA binding sites: representation and discovery. Bioinformatics 16: 16–23. [DOI] [PubMed] [Google Scholar]
- Stormo GD. 2013. Modeling the specificity of protein-DNA interactions. Quant Biol 1: 115–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stormo GD, Zhao Y. 2010. Determining the specificity of protein–DNA interactions. Nat Rev Genet 11: 751–760. [DOI] [PubMed] [Google Scholar]
- Tewhey R, Kotliar D, Park DS, Liu B, Winnicki S, Reilly SK, Andersen KG, Mikkelsen TS, Lander ES, Schaffner SF, et al. 2016. Direct identification of hundreds of expression-modulating variants using a multiplexed reporter assay. Cell 165: 1519–1529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tompa M. 1999. An exact method for finding short motifs in sequences, with application to the ribosome binding site problem. Proc Int Conf Intell Syst Mol Biol 1999: 262–271. [PubMed] [Google Scholar]
- Tompa M, Li N, Bailey TL, Church GM, De Moor B, Eskin E, Favorov AV, Frith MC, Fu Y, Kent WJ, et al. 2005. Assessing computational tools for the discovery of transcription factor binding sites. Nat Biotechnol 23: 137–144. [DOI] [PubMed] [Google Scholar]
- van Helden J, André B, Collado-Vides J. 1998. Extracting regulatory sites from the upstream region of yeast genes by computational analysis of oligonucleotide frequencies. J Mol Biol 281: 827–842. [DOI] [PubMed] [Google Scholar]
- Weirauch MT, Cote A, Norel R, Annala M, Zhao Y, Riley TR, Saez-Rodriguez J, Cokelaer T, Vedenko A, Talukder S, et al. 2013. Evaluation of methods for modeling transcription factor sequence specificity. Nat Biotechnol 31: 126–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weirauch MT, Yang A, Albu M, Cote AG, Montenegro-Montero A, Drewe P, Najafabadi HS, Lambert SA, Mann I, Cook K, et al. 2014. Determination and inference of eukaryotic transcription factor sequence specificity. Cell 158: 1431–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zambelli F, Pesole G, Pavesi G. 2013. Motif discovery and transcription factor binding sites before and after the next-generation sequencing era. Brief Bioinform 14: 225–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zambelli F, Pesole G, Pavesi G. 2014. Using Weeder, Pscan, and PscanChIP for the discovery of enriched transcription factor binding site motifs in nucleotide sequences. Curr Protoc Bioinformatics 47: 2.11.1–2.11.31. [DOI] [PubMed] [Google Scholar]
- Zeng H, Edwards MD, Guo Y, Gifford DK. 2017. Accurate eQTL prioritization with an ensemble-based framework. Hum Mutat 38: 1259–1265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Stormo GD. 2011. Quantitative analysis demonstrates most transcription factors require only simple models of specificity. Nat Biotechnol 29: 480–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J, Troyanskaya OG. 2015. Predicting effects of noncoding variants with deep learning–based sequence model. Nat Methods 12: 931–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.