Pose determination of a blade implant in three dimensions from a single two-dimensional radiograph

Abstract

The aim of the study was to introduce a mathematical method to estimate the correct pose of a blade by evaluating the radiographic features obtained from a single two-dimensional image. Blade-form implant bed preparation was performed using the piezosurgery device, and placement was attained with the use of magnetic mallet. The pose determination of the blade was described by means of three consecutive rotations defined by three angles of orientation (triplet φ, θ and ψ). Retrospective analysis on periapical radiographs was performed. This method was used to compare implant (axial length along the marker, i.e. the implant structure) vs angular correction factor (a trigonometric function of the triplet). The accuracy of the method was tested by generating two-dimensional radiographic simulations of the blades, which were then compared with the images of the implants as appearing on the real radiographs. Two patients had to be excluded from further evaluation because the values of the estimated pose angles showed a too-wide range to be effective for a good standardization of serial radiographs: intrapatient range from baseline to 1-year survey was > of a threshold determined by the clinicians (30°). The linear dependence between implant (CF°) and angular correction factor (CF^) was estimated by a robust linear regression, yielding the following coefficients: slope, 0.908; intercept, −0.092; and coefficient of determination, 0.924. The absolute error in accuracy was −0.29 ± 4.35, 0.23 ± 3.81 and 0.64 ± 1.18°, respectively, for the angles φ, θ and ψ. The present theoretical and experimental study established the possibility of determining, a posteriori, a unique triplet of angles (φ, θ and ψ) which described the pose of a blade upon a single two-dimensional radiograph, and of suggesting a method to detect cases in which the standardized geometric projection failed. The angular correction of the bone level yielded results very close to those obtained with an internal marker related to the implant length.

Introduction

Clinicians have proposed a set of criteria for implant success, describing the changes of marginal bone level (MBL) around dental implants before and after the first year of loading. Albrektsson and co-workers stated that, during radiological follow up examination, the bone loss might be less than 1.0–1.5 mm after 1 year of loading, and less than 0.2 mm per year during the following years.¹

Generally, corrections were performed considering internal markers. Even though the use of a metal marker of known dimensions as a reference during treatment planning has been suggested,² the dental implant itself has been the gold standard as a reference marker (e.g. the axial length of the implant) to compensate a measure of bone loss along an implant which appeared to be bent.^2,3

Even if a measure of bone loss along the dental implant could be compensated, errors in the alignment between pairs of radiographs could lead to a faulty evaluation of the alveolar bone levels from one radiographic examination to the next. Problems regarding the reproducibility of the relationship between the object and the radiographic detector could be resolved by the use of a rigid bite stent, whereas those arising from relationships between the detector and the X-ray beam require an extraoral apparatus which promotes the perpendicular position of the central X-ray to the film/detector plane, such as a cone paralleling device.⁴

However, a perfect parallelism between the object and the film plane is not always achievable under clinical conditions because the hard/soft tissues might be anatomical obstacles (such as hard palate in the upper jaw and tongue in the lower jaw), and could yield considerable errors in the linear measurements. So, if methods to standardize radiograph alignment fail, a loss of precision in detecting minute bone changes around structures from different vantage points can result.⁵ In the case of areas with horizontally and/or vertically atrophic alveolar ridge with insufficient bone height and/or width, which precluded the use of standard dental implants, the blade implant could represent a viable surgical option for obtaining satisfactory oral function rehabilitation. Blade implants were used for several decades, although nowadays their usage seems to be uncommon. However, with piezosurgery devices (piezoelectric bone surgery), patient rehabilitation utilizing blades could prove effective in reducing post-operative pain, swelling and patient discomfort.⁶ Moreover, a good level of primary implant stability could be achieved by the use of magnetodynamic devices, such as the Mallet.⁷

In order to set up and physically test a method for, a posteriori, determining a triplet of angles which could describe the pose of a dental implant upon a single two-dimensional radiograph, the data regarding non-conventional dental implants were retrospectively investigated. A general radiographic projection geometry which described the position of the blade as it appeared on a single two-dimensional radiograph was the multi-degrees-of-freedom (df) system; the standardization of conventional periapical radiographs removed some dfs, whereas the five dfs regarding the pose and position of the dental implant (three rotational dfs and two translational dfs) remained. The two translational dfs were irrelevant for analysis because the implant served as a reference marker. Hence, a method which allows for a posteriori evaluation of the effectiveness of standardization of serial radiographs with geometric projection to investigate the pose of the implant may be of general interest.

The present theoretical and experimental study examines whether it is possible to determine, a posteriori, a unique triplet of angles (φ , θ and ψ) describing the pose of the blade as it appears on a single two-dimensional radiograph. The secondary aim was to verify the effectiveness of the method, comparing the two measured correction factors (implant vs angular).

Methods and materials

Theory

Following general principles commonly applied in projective geometry, a quick set up of the radiographic conditions, i.e. an individualized bite record used in combination with the bite block and the long cone technique–parallel-cone technique with the use of an extension cone paralleling device (generally the XCP-ORA or the one ring and arm positioning system), increased the efficiency and the reproducibility of the examinations.

So the following requirements had to be fulfilled:

• the distance between the focal point and the image detector for each of the repeated acquisitions must be known, and they have to be identical;

• the target has to be centred to the source of energy in such a way that the X-rays are perpendicular to the midpoint of the image receptor.

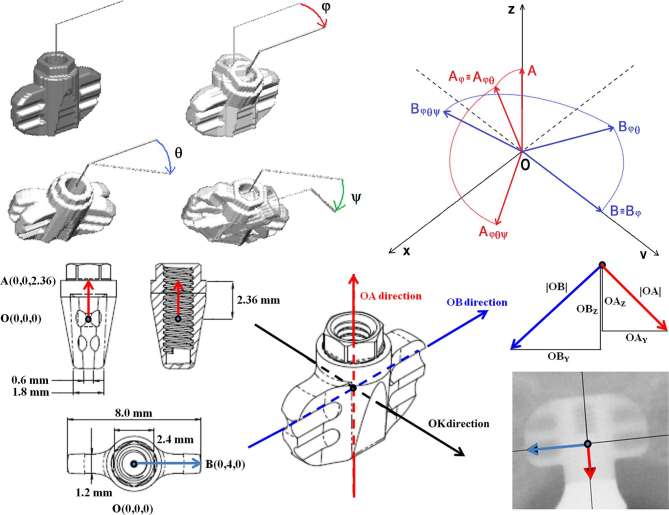
Generally, irrespective of translation movement, the theoretical position of the implant could be defined by three rotational angles (along the three principal axes of the blade), i.e. pitch φ, roll θ and yaw ψ, as reported in Figure 1. The detector could acquire the same subject with different poses.

Figure 1.

Pairwise superimposed three-dimensional renderings of the blade by using the three consecutive rotational angles φ, θ and ψ. Drawing of the projection geometry of the points O, A and B during rotations in space. The y- and z-axis of the co-ordinate system represent the horizontal and vertical axis, respectively, of the flat image receptor in which each voxel of the whole-blade phantom will be projected to generate the ghost radiographic image. Project scheme of the blade with size in mm of the body and wings. Three directions: red ${\displaystyle (\overrightarrow{\mathrm{O}\mathrm{A}})}$, blue ${\displaystyle (\overrightarrow{\mathrm{O}\mathrm{B}})}$ and black ${\displaystyle (\overrightarrow{\mathrm{O}\mathrm{K}})}$ along the three major axes of the blade. Two components of the red vectors ${\displaystyle [{\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Y}},{\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Z}}]}$ and two components of the blue vectors ${\displaystyle [{\overrightarrow{\mathrm{O}\mathrm{B}}}_Y,{\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Z}}]}$, respectively, along ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$- and ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{B}}}$-direction (respectively the red and blue arrows in the radiograph) as appearing in a two-dimensional image.

If the repeatability of the bite-block positioning was insufficient, comparative analysis of the two images generated unfitting triplets: the second triplet at Time 2 (φ ₂,θ ₂,ψ ₂) differed from the first at Time 1 (φ ₁,θ ₁,ψ ₁).

A single vector subjected in space to the rotations, as described in the Supplementary Material 1(Supplementary material available online), showed the following components in x,y,z:

$${\displaystyle \begin{array}{ll}\overrightarrow{\mathrm{X}}=& \mathrm{c}\mathrm{o}\mathrm{s}\phi \cdot \mathrm{c}\mathrm{o}\mathrm{s}\theta \cdot {\mathrm{x}}_0+(-\mathrm{c}\mathrm{o}\mathrm{s}\phi \cdot \mathrm{s}\mathrm{i}\mathrm{n}\theta \cdot \cos \psi +\sin \phi \cdot \sin \psi ){\mathrm{y}}_0\\ & +(-\sin \phi \cdot \cos \psi -\cos \phi \cdot \sin \theta \cdot \sin \psi )z_0\end{array}}$$

$${\displaystyle \overrightarrow{\mathrm{Y}}=\mathrm{s}\mathrm{i}\mathrm{n}\theta \cdot {\mathrm{x}}_0+\mathrm{c}\mathrm{o}\mathrm{s}\theta \cdot \mathrm{c}\mathrm{o}\mathrm{s}\psi \cdot {\mathrm{y}}_0+\mathrm{c}\mathrm{o}\mathrm{s}\theta \cdot \mathrm{s}\mathrm{i}\mathrm{n}\psi \cdot {\mathrm{z}}_0}$$

$${\displaystyle \begin{array}{ll}\overrightarrow{\mathrm{Z}}=& \mathrm{s}\mathrm{i}\mathrm{n}\phi \cdot \mathrm{c}\mathrm{o}\mathrm{s}\theta \cdot {\mathrm{x}}_0+(-\mathrm{c}\mathrm{o}\mathrm{s}\phi \cdot \mathrm{s}\mathrm{i}\mathrm{n}\psi -\mathrm{s}\mathrm{i}\mathrm{n}\phi \cdot \mathrm{s}\mathrm{i}\mathrm{n}\theta \cdot \mathrm{c}\mathrm{o}\mathrm{s}\psi )\cdot {\mathrm{y}}_0\\ & +(-\mathrm{s}\mathrm{i}\mathrm{n}\phi \cdot \mathrm{s}\mathrm{i}\mathrm{n}\theta \cdot \mathrm{s}\mathrm{i}\mathrm{n}\psi +\mathrm{c}\mathrm{o}\mathrm{s}\phi \cdot \mathrm{c}\mathrm{o}\mathrm{s}\psi )\cdot {\mathrm{z}}_0\end{array}}$$

For clarity, the representation of vectors generating a triplet for a blade implant could be shown by simplified equations from Equations (4) to (7). In Figures 1 and 2, the vectors from the origin O (0,0,0) to point A (lengthwise vector) and B (crosswise vector) were respectively given as (0,0,2.36) and (0,4,0). Their components were given by ${\displaystyle {\overrightarrow{\mathrm{A}\mathrm{O}}}_{\mathrm{Y}},{\overrightarrow{\mathrm{A}\mathrm{O}}}_{\mathrm{Z}}}$ and ${\displaystyle {\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Y}},{\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Z}}}$, obtained from a single two-dimensional radiograph. The system of equations describing each component in function of the rotational angles is:

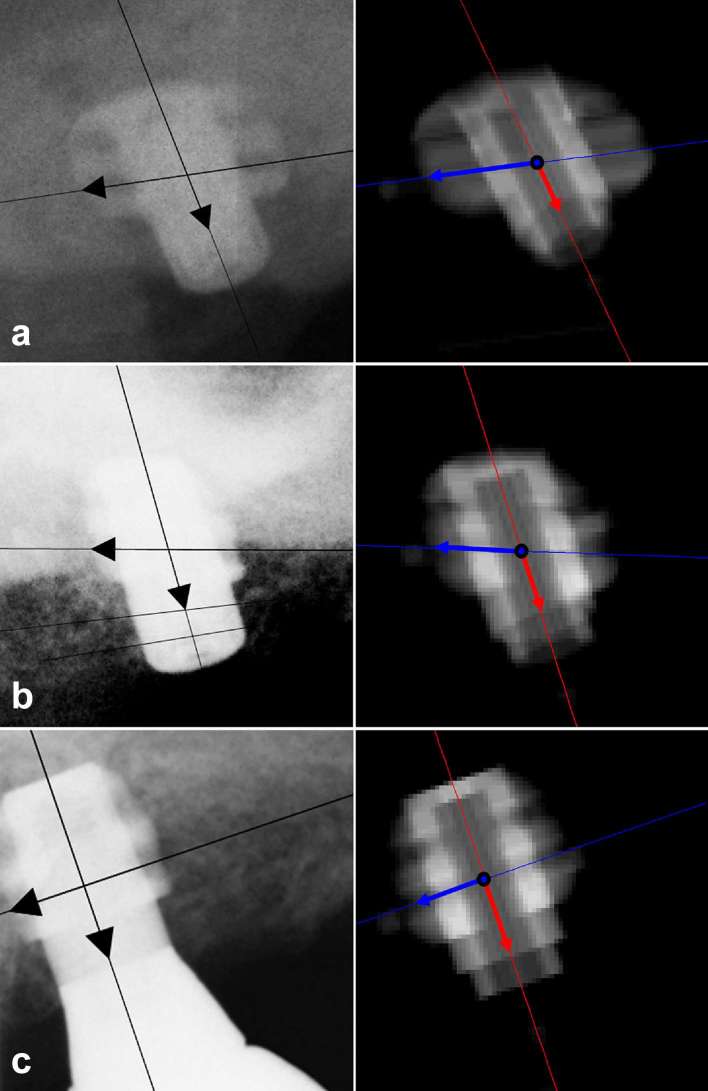
Figure 2.

Radiographs of Patient #6 (excluded from analysis of the marginal bone level) and related virtual ghosts with estimated components obtained by Measurer 1 in Session 1: (a) ${\displaystyle {\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Y}}+0.8882{\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Z}}-1.8852{\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Y}}-3.4329{\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Z}}-0.4391\mathrm{a}\mathrm{t}\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e};}$ (b) ${\displaystyle {\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Y}}+0.6824{\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Z}}-2.1852{\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Y}}-2.4088{\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Z}}+0.0855\mathrm{a}\mathrm{t}4\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{s};}$ (c) ${\displaystyle {\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Y}}+0.7540{\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Z}}-2.2363{\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Y}}-2.0650{\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Z}}+0.7180\mathrm{a}\mathrm{t}12\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{s};}$

$${\displaystyle {\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Y}}=\mathrm{c}\mathrm{o}\mathrm{s}\theta \cdot \mathrm{s}\mathrm{i}\mathrm{n}\psi \cdot 2.36}$$

$${\displaystyle {\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Z}}=(-\mathrm{s}\mathrm{i}\mathrm{n}\phi \cdot \mathrm{s}\mathrm{i}\mathrm{n}\theta \cdot \mathrm{s}\mathrm{i}\mathrm{n}\psi +\mathrm{c}\mathrm{o}\mathrm{s}\phi \cdot \mathrm{c}\mathrm{o}\mathrm{s}\psi )\cdot 2.36}$$

$${\displaystyle {\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Y}}=\cos \theta \cdot \cos \psi \cdot 4}$$

$${\displaystyle {\overrightarrow{\mathrm{O}\mathrm{B}}}_{\mathrm{Z}}=(-\cos \phi \cdot \sin \psi -\sin \phi \cdot \sin \theta \cdot \cos \psi )\cdot 4}$$

As is seen in Figure 1, ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$-direction (from the a pex to the neck of the blade, and symmetrical from left to right) and ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{B}}}$-direction (from the mesial- to the distal-aspect, and symmetrical from side to side around a central line of the most coronal groove of the blade) were represented. The ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$-direction intercepted the ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{B}}}$-direction at the central reference point, i.e. the O point. Then the ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$-direction crossed the external border of the shoulder in point A, and the ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{B}}}$-direction crossed the external border of the groove in point B.

Linear measurement along the ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$-direction could be adjusted by means of an implant correction factor (CF°), as reported by equation 8, where MBL and MBL° are, respectively, the measured and corrected values of the MBL; len and ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$ were, respectively, the real (2.36 mm) and the measured length (as appearing in a two-dimensional radiograph).

$${\displaystyle {\mathrm{M}\mathrm{B}\mathrm{L}}^{\circ }=\mathrm{M}\mathrm{B}\mathrm{L}\mathrm{C}{\mathrm{F}}^{\circ }=\mathrm{M}\mathrm{B}\mathrm{L}\frac{len}{\overrightarrow{\mathrm{O}\mathrm{A}}}}$$

The modulus of ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$ vector as appearing in a two-dimensional radiograph can also be obtained by:

$${\displaystyle \begin{array}{ll}\sqrt{{\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Y}}{}^2{\overrightarrow{\mathrm{O}\mathrm{A}}}_{\mathrm{Z}}{}^2}=& len\cdot \\ & \sqrt{{\left(\cos \theta \cdot \sin \psi \right)}^2+{\left(\cos \phi \cdot \cos \psi -\sin \phi \cdot \sin \theta \cdot sin\psi \right)}^2}\end{array}}$$

So, the linear measurement could be adjusted by means of an angular correction factor (CF^) obtained by trigonometric functions of estimated angles, as reported in equation 10, where MBL and MBL^ are, respectively, the measured and corrected values of the MBL.

$${\displaystyle \begin{array}{ll}\mathrm{M}\mathrm{B}{\mathrm{L}}^{\wedge }=& \mathrm{M}\mathrm{B}\mathrm{L}\cdot \mathrm{C}{\mathrm{F}}^{\wedge }=\mathrm{M}\mathrm{B}\mathrm{L}\cdot \\ & \frac{1}{\sqrt{(\cos \theta \cdot \sin \psi {)}^2+(\cos \phi \cdot \cos \psi -\sin \phi \cdot \sin \theta \cdot \sin \psi {)}^2}}\end{array}}$$

Experimental simulation

An experimental evaluation of the system of vector equations and of the accuracy of the method was performed by an algorithm based on the above-mentioned radiographic requirements (Figure 2 and Supplementary Material 1). Three-dimensional scans of the titanium blade implant prototype were performed (KODAK 9000 3D Extraoral Imaging System; Carestream Health, Inc., Rochester, NY); a virtual three-dimensional whole-blade phantom describing the implant prototype was voxelized from the original dicom objects, with an isotropic voxel dimension of 0.04 mm (1 full voxel, 0 empty voxel).

For each real radiograph a pose triplet (φ, θ, ψ) was estimated; then the whole-blade phantom was rotated about its orthogonal axes to simulate rotation in free space by using the system of equations 1–3 and the estimated rotational angles (φ, θ, ψ) obtained from the radiograph; all full voxels of the virtual whole-blade phantom were projected in the yz plane, obtaining a sort of two-dimensional radiographic simulation, with a resolution of 25 LP mm^–1 (Linepairs per millimetre). This was defined as a “ghost” of the virtual blade. For each real radiograph, one ghost was acquired, and the vectors representing the virtual components were measured and superimposed onto the ghost, as appears in Figure 2. These virtual components were fitted to equations 4–7, and the obtained value of the virtual triplet was compared to the real triplet, which was experimentally evaluated on the real radiograph.

Experimental evaluation

The radiological data of the subjects in the present study were retrospectively collected from the case sheets of treated patients who underwent fixed prostheses supported by blade-form implants between 2014 and 2016.

Data were included in the retrospective analysis if the patient:

1. was 18 years or older, and able to sign a consent for data analysis;

2. had at least two intraoral radiographs depicting an entire structure of the blade.

Data were excluded from the retrospective analysis if the patient:

1. had an unreadable or corrupted radiographic image which could not be recovered or restored.

The implant (Sweden & Martina s.p.a., Due Carrare, PD, Italy) had a platform with 2.4 mm external hexagon of a height of about 1 mm. The maximum height was 5.3 mm and the width was 8 mm (Figure 1). Blade implant was positioned following the manufacturer’s instructions by means of a piezosurgery (Piezosurgery, Mectron, Carasco, Italy) and a magnetic device (magnetic mallet, Sweden & Martina s.p.a., Due Carrare, PD, Italy). Implants were loaded with fully functional occlusions after soft tissue maturation; final metal–ceramic restorations were cemented on customized implant abutments.

Variables

Description of the sample

Descriptive variables were acquired, including the position and location of the blade.

Determination of numerical variables

Digital intraoral periapical radiographs were taken (70 kVp, 7 mA) using a parallel cone technique with digital sensor (Schick Technologies, Long Island City, NY). A paralleling device and individualized bite block for each subject, made of polyvinyl siloxane impression material (Flexitime, Heraeus/Kulzer, Hanu, Germany), were used for the standardization of the X-ray geometry. Calibration of the images was performed by referring to the diameter of the blade (diameter at neck = 3.3 mm). Measurements and coordinates were assessed by downloadable free software-implemented, mouse-driven measurement tools of an image-editor (Osiris 4.19 University of Genève. Switzerland); y- and z-coordinates of the points O, A and B were computed, and the distances between points were expressed in mm by using algorithms implemented in a spreadsheet software (MatLab7.13, The MathWorks, Natick, MA). Values of marginal bone level/loss were reported with an approximation to the nearest decimillimetre, whereas vector components were rounded to the nearest two decimal places.

Peri-implant marginal bone level (MBL)

MBL was evaluated on intraoral radiographs acquired before (at first or second surgery) or after prosthetic treatment, generally at 1 year after implant insertion. MBL was the distance between the fixture–abutment interface and the most apical point of the bone-to-implant contact. Changes at the mesial and distal MBLs were averaged.

Pose angles

A triplet of rotational angles φ, θ and ψ, i.e. respectively, pitch, roll and yaw (more generally employed to describe rotations around the three principal axes of aircraft), represented a sequence of three elemental rotations about the principal axes of the blade implant (height, width and depth), as appears in Figure 1.

Statistical analysis

All measurements were taken twice (repeated 1 week apart) by two independent measurers, who were not involved in the performance of the surgical treatment.

The angles were estimated by an algorithm running on a matrix elaborator that was used for all descriptive and statistical analyses (MatLab7.13, The MathWorks, Natick, MA). Correlation regarding the implant and angular correction factor was estimated by robust linear regression (giving lower weight to points that did not fit well). Normal distribution for outcome variables related to bone remodelling was checked, but not confirmed, by the Shapiro–Wilk test. A Bland–Altman analysis measured the inter- and intraobserver agreements. Accuracy was computed as absolute differences between the real and virtual estimated triplets over the entire set of angular estimations obtained from real and virtual radiographs. Patients were excluded from bone loss evaluation if the values of the estimated pose angles showed a too-wide range to be effective for a good standardization of serial radiographs. The following threshold was applied: intrapatient angles’ variation in the data set (φ, θ or ψ registered on radiographs) ≥30°.

Appropriate pairwise comparison tests were carried out. The level of statistical significance was set at 0.05 for all analyses.

Results

Data regarding 10 subjects, with a total of 28 radiographs, were enrolled in the present retrospective review analysis. All blade implants were positioned in the posterior superior sectors for fixed prosthetic rehabilitation. Table 1 shows data of all the investigated blades regarding measured components (in y- and z-direction) of the two vectors ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$ and ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{B}}}$. The measured components were input values for the non-linear fitting, which found the optimal estimated angular triplets (φ, θ, ψ) with their related estimated components and optimization metric (summarizing the excellence of the fitting process). Two patients were excluded from analysis of MBL. In Patient #5, angles of opposite signs were found when values of φ were estimated (32.5° and −26.2°, respectively immediately following, and then 1 year after, implant placement). Patient #6 showed a wide dispersion of estimated θs (ranging from 20.4° to 52.6°). This was probably owing to improper positioning of the Rinn extension cone paralleling device, with a lack-of-fit in either the longitudinal or the latitudinal direction (Figure 2 and Table 1). For the remaining blades, the mean values of the estimated φ, θ and ψ were, respectively, of 17.0 ± 18.2°, 20.9 ± 19.4° and 174.4 ± 12.9°.

Table 1.

Measured- and estimated-values of the components of vector ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$ and vector ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{B}}}$ with related values of rotational angles

			Measured components (mm)		Estimated components (mm)		Estimated angles (degree)					Optimization metric
${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$	${\displaystyle \overrightarrow{\mathrm{O}\mathrm{B}}}$	${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$	${\displaystyle \overrightarrow{\mathrm{O}\mathrm{B}}}$	φ	θ	ψ	Iterations		Residual		First-order optimality
Pats	Time		Mean	Mean	Mean	Mean	Mean	Mean	Mean	Min	Max	Min	Max	Min	Max
1	bsl	y	+0.44	−3.98	+0.19	−3.96	−3.0	5.8	175.4	7	18	<0.0001	0.0143	7.6 × 10−9	3.9 × 10−5
	z	−2.36	−0.39	−2.33	−0.36
bpl	y	+0.44	−3.95	+0.22	−3.94	−1.9	7.3	174.7	16	45	0.0216	0.0534	4.2 × 10−5	1.4 × 10−3
	z	−2.51	−0.42	−2.35	−0.39
apl	y	+0.46	−3.96	+0.20	−3.95	−1.1	6.3	175.0	7	31	<0.0001	0.0022	3.0 × 10−10	2.9 × 10−5
	z	−2.35	−0.39	−2.33	−0.39
Range							1.9	1.5	0.7
2	bsl	y	+0.21	−2.46	−0.09	−2.43	−8.7	51.8	183.6	6	6	<0.0001	0.0026	3.2 × 10−11	7.8 × 10−7
	z	−2.35	−0.23	−2.37	−0.23
bpl	y	+0.17	−2.08	−0.21	−2.08	−15.8	58.2	189.6	6	6	0.0106	0.0189	4.3 × 10−6	8.6 × 10−6
	z	−2.45	−0.28	−2.33	−0.27
apl	y	+0.13	−2.56	−0.33	−2.56	−11.6	49.2	192.2	6	7	0.0004	0.0064	7.9 × 10−8	8.7 × 10−7
	z	−2.29	+0.23	−2.34	+0.23
Range							7.1	9.0	8.6
3	bsl	y	+0.13	−3.90	−0.32	−3.95	18.5	2.0	187.9	6	31	0.0001	0.0112	7.1 × 10−8	3.9 × 10−5
	z	−2.21	+0.55	−2.21	+0.56
bpl	y	+0.15	−4.01	−0.30	−3.97	0.2	1.1	187.2	19	21	0.0376	0.0624	9.8 × 10−5	2.3 × 10−4
	z	−2.54	+0.56	−2.34	+0.50
apl	y	+0.18	−3.88	−0.31	−3.91	29.8	9.6	187.6	5	6	0.0002	0.0034	4.6 × 10−7	7.2 × 10−6
	z	−2.00	+0.78	−2.00	+0.79
Range							29.6	8.5	0.7
4	bsl	y	+0.70	−3.25	+0.54	−3.30	36.9	31.2	164.5	4	5	0.0095	0.0289	8.7 × 10−6	2.4 × 10−5
	z	−1.93	+0.30	−2.02	+0.35
bpl	y	+0.73	−3.06	+0.70	−3.20	40.5	31.4	159.6	10	10	0.2052	0.2293	1.3 × 10−4	2.3 × 10−4
	z	−1.67	+0.07	−1.96	+0.21
apl	y	+0.67	−3.47	+0.52	−3.48	13.7	26.1	165.7	7	8	0.0024	0.0121	1.2 × 10−6	9.1 × 10−6
	z	−2.21	−0.57	−2.28	−0.56
Range							26.8	5.3	6.1
5	bsl	y	0.33	−3.64	−0.04	−3.72	30.7	21.5	181.0	5	8	0.0137	0.0314	1.0 × 10−5	2.8 × 10−5
	z	−1.96	+0.75	−2.02	+0.81
bpl	y	ND	ND	ND	ND	ND	ND	ND	ND	ND	ND	ND	ND	ND
	z	ND	ND	ND	ND
apl	y	0.34	−2.97	−0.34	−3.02	−23.0	39.8	190.7	12	14	0.2143	0.2922	1.3 × 10−4	2.1 × 10−4
	z	−1.81	−0.21	−2.24	−0.30
Range							53.7	18.3	9.7
6	bsl	y	+0.86	−3.34	+0.87	−3.45	38.9	20.3	156.8	7	9	0.0420	0.0822	3.0 × 10−5	5.0 × 10−5
	z	−1.78	−0.49	−1.89	−0.42
bpl	y	+0.74	−2.42	+0.67	−2.46	33.7	47.5	155.2	8	9	0.1393	0.1692	4.2 × 10−5	1.2 × 10−4
	z	−1.84	0.03	−2.19	+0.09
apl	y	+0.84	−2.08	+0.79	−2.09	27.5	51.6	147.2	10	11	0.5040	0.6565	2.5 × 10−4	4.0 × 10−4
	z	−1.52	−0.71	−2.22	−0.71
Range							11.4	31.3	9.6
7	bsl	y	+0.71	−4.03	+0.46	−3.92	28.7	−1.4	168.8	7	17	0.0051	0.0289	1.6 × 10−5	1.6 × 10−4
	z	−2.02	−0.73	−2.03	−0.73
bpl	y	+0.70	−3.95	+0.47	−3.92	30.6	−2.6	168.6	5	7	0.0002	0.0260	1 × 10−9	7.8 × 10−6
	z	−1.98	−0.77	−1.98	−0.77
apl	y	ND	ND	ND	ND	ND	ND	ND	ND	ND	ND	ND	ND	ND
	z	ND	ND	ND	ND
Range							1.9	1.2	0.2
8	bsl	y	+0.52	−4.03	+0.19	−3.98	31.7	−2.0	175.4	5	7	0.0004	0.0086	7.2 × 10−7	2.9 × 10−5
z	−2.00	−0.35	−2.00	−0.34
bpl	y	+0.55	−3.92	+0.28	−3.96	23.7	−2.8	173.2	6	9	0.0001	0.0040	1.9 × 10−7	7.6 × 10−6
z	−2.14	−0.51	−2.14	−0.52
apl	y	+0.58	−4.00	+0.26	−3.97	33.5	−3.3	173.6	5	6	0.0000	0.0068	1.1 × 10− 8	8.1 × 10− 6
z	−1.95	−0.50	−1.95	−0.49
Range							9.8	1.3	2.2
9	bsl	y	+0.22	−3.33	−0.20	−3.35	21.4	32.6	185.8	7	8	0.0077	0.0214	5.2 × 10−6	9.3 × 10−6
z	−2.05	+1.11	−2.14	+1.15
bpl	y	+0.09	−3.97	−0.42	−3.92	26.5	4.3	190.3	5	9	<0.0001	0.0078	8.9 × 10−9	1.6 × 10−5
z	−2.06	+0.78	−2.07	+0.77
apl	y	+0.09	−3.63	−0.37	−3.65	16.3	22.3	189.8	6	7	0.0005	0.0067	3.00 × 10−7	1.3 × 10−5
z	−2.15	+1.04	−2.19	+1.07
Range							10.2	28.3	4.5
10	bsl	y	+0.79	−3.50	+0.70	−3.50	8.5	22.5	161.3	6	9	0.0001	0.0161	6.0 × 10−9	2.5 × 10−5
z	−2.17	−1.06	−2.25	−1.06
bpl	y	+0.86	−3.51	+0.73	−3.50	30.2	21.7	160.5	5	6	0.0001	0.0032	6.9 × 10−9	3.1 × 10−6
z	−2.08	−0.45	−2.07	−0.46
apl	y	+0.71	−3.13	+0.61	−3.15	20.8	34.0	162.0	8	9	0.0432	0.0839	2.7 × 10−5	5.4 × 10−5
z	−2.02	−0.44	−2.24	−0.40
Range							21.7	12.3	1.5

Angles’ ranges and results of the fitting (iterations, residual and first-order optimality). Higher intrapatient angular range resulted for patients 5 and 6. Data survey: just after surgery (baseline, bsl); before prosthetic loading (bpl), generally four months after surgery; after prosthetic loading (apl), generally 1 year after implant placement. 

apl, after prosthetic loading; bpl, before prosthetic loading; bsl, baseline; ND, not determined.

Reproducibility of the angular measurements

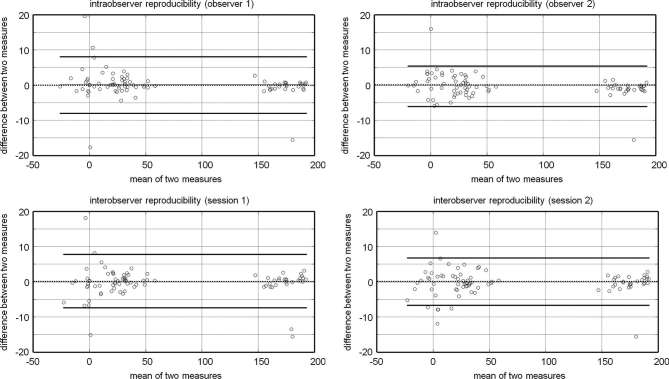
The reproducibility of the intra- and intermeasurements is described in detail in Table 2. The intraobserver differences showed a standard deviation ranging from 2.8° to 5.5° for Observer 1, and a standard deviation ranging from 1.0° to 4.1° for Observer 2, respectively. The interobserver differences showed a standard deviation ranging from 2.8° to 5.3° for Session 1, and a standard deviation ranging from 3.9° to 4.3° for Session 2, respectively. Bland and Altman plots are shown in Figure 3.

Table 2.

Intraobserver and interobserver differences and limits of agreement

	Intraobserver obs1 (ss1–ss2)			Intraobserver obs2 (ss1–ss2)			Interobserver ss1 (obs1–obs2)			Interobserver ss2 (obs1–obs2)
	φ	θ	ψ	φ	θ	ψ	φ	θ	ψ	φ	θ	ψ
Mean	0.5	0.7	−0.7	1.3	−0.1	−0.5	−0.1	−0.4	−0.3	0.7	−1.2	0.0
Standard deviation	5.5	2.8	3.1	4.1	2.8	1.0	5.3	2.8	2.9	4.3	3.9	1.4
Median	0.0	0.0	−0.2	0.7	−0.2	−0.6	0.0	−0.3	0.2	−0.4	−0.1	−0.1
25-percentile	−1.3	−0.5	−1.1	−0.8	−1.9	−1.0	−1.5	−1.5	−0.8	−1.6	−1.9	−0.9
75-percentile	2.1	0.8	0.5	3.4	2.6	0.1	1.9	0.7	0.9	3.1	1.2	1.2
Interquartile range	3.4	1.3	1.6	4.2	4.5	1.1	3.4	2.2	1.6	4.8	3.1	2.1
Minimum	−17.7	−3.0	−15.6	−4.7	−5.9	−2.5	−15.3	−6.9	−13.7	−7.9	−12.5	−2.8
Maximum	19.5	10.6	2.6	16.9	3.9	2.0	17.9	8.0	3.0	14.3	4.0	2.8
Range	37.2	13.6	18.3	21.7	9.8	4.5	33.2	14.9	16.7	22.2	16.5	5.6

Observer  1 and 2 (obs1, obs2). Session 1and 2 (ss1,ss2).

Figure 3.

Intraobserver reproducibility (Bland and Altman plots). The dashed horizontal line represents the mean difference between sessions and the straight horizontal lines represent the limits of agreements.

Accuracy of the angular measurements

The description of the input triplets for virtual whole-blade phantom analysis was of 18.0 ± 18.8°, 20.6 ± 17.6 and 173.7 ± 12.9°, respectively, for the angles φ, θ and ψ; the virtual estimated angles, as they appear in the ghosts generated from the virtual phantoms, were, for angle φ, 18.1 ± 17.4°, for angle θ, 20.8 ± 19.7° and for angle ψ, 174.3 ± 12.9°. Absolute error, as shown in Figure 4, was −0.29 ± 4.35° for angle φ, 0.23 ± 3.81° for angle θ and 0.64 ± 1.18° for angle ψ. It is worth noting that there are transcendent links among the three absolute errors owing to the fact that a mistake in the determination of an angle produces an error in the calculated values of the other two angles as well.

Figure 4.

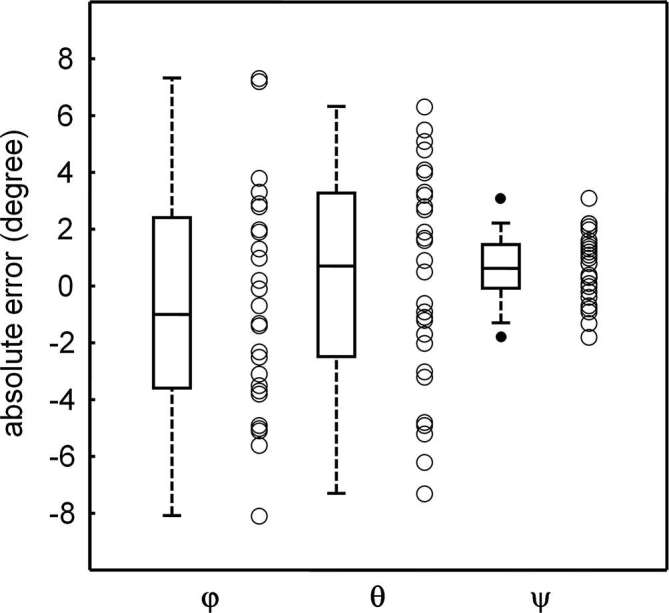
Box plots representing accuracy, expressed as difference between real and virtual estimated triplets calculated from each ghost over the entire set of angular estimations obtained from real radiographs. In box-and-whiskers plot, the box line represents the lower, median and upper quartile values, the whisker lines include the rest of the data. Outliers were data with values beyond the ends of the whiskers.

Correction factors and marginal bone levels

Radiographs of Patient #6 and the related ghost of the blades are shown in Figure 2. Data regarding radiographs of Patients #5 and #6 appeared as red points in Figure 5, and so they were excluded from the fitting tests. Implant and angular correction factors (respectively, CF° and CF^) appeared to be correlated. Such a linear dependence was verified by the results of robust linear regression: coefficients were 0.908 (slope) and −0.092° (intercept) with a coefficient of determination of 0.924. In Table 3, results regarding implant and angular correction factors with their respective values of change at the MBL are shown.

Figure 5.

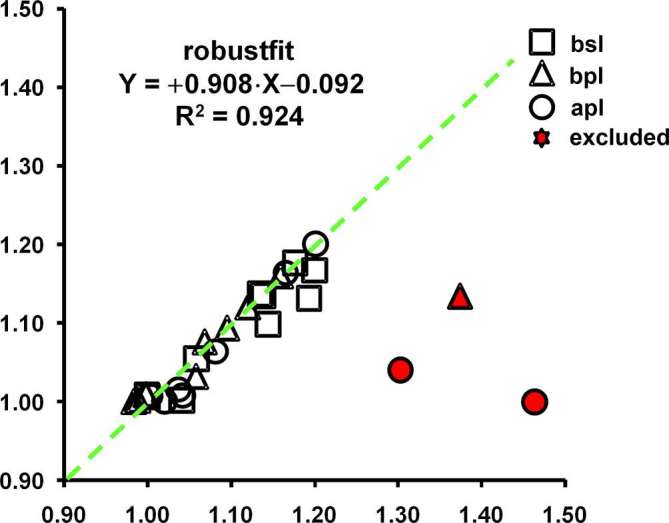
The linear relationship between implant (CF°) and angular correction factor (CF^) is depicted at baseline (bsl, square), before (bpl, triangle) and after prosthetic loading (apl, circle). Note that the two excluded data (solid triangle and circles) were related to patients #5 and 6#. The dotted line was the line tendency.

Table 3.

Implant (CF°) and angular correction factor (CF^) with related corrected measurements of the marginal bone level (MBL° and MBL^, respectively) and marginal bone loss (ΔMBL° and ΔMBL^, respectively) before and after prosthetic loading

Time	Just after surgery (bsl)				Before prosthetic loading (bpl)				After prosthetic loading (apl) —1 year after implant placement—				bsl→bpl		bsl→apl
Outcome	CF°	CF^	MBL°	MBL^	CF°	CF^	MBL°	MBL^	CF°	CF^	MBL°	MBL^	ΔMBL°	ΔMBL^	ΔMBL°	ΔMBL^
Patient
1	1.00	1.01	1.9	1.9	0.99	1.00	1.8	1.8	1.00	1.01	1.6	1.6	−0.1	−0.1	−0.3	−0.3
2	1.00	1.01	2.0	2.0	1.00	1.01	2.6	2.6	1.02	1.00	1.8	1.8	0.6	0.6	−0.1	−0.2
3	1.06	1.06	3.2	3.2	0.98	1.00	2.7	2.7	1.17	1.16	2.7	2.7	−0.5	−0.5	−0.5	−0.5
4	1.19	1.13	2.9	2.7	1.37	1.13	3.4	2.8	1.04	1.01	2.1	2.0	0.5	0.1	−0.7	−0.7
5	1.20	1.17	3.5	3.4	ND	ND	ND	ND	1.30	1.04	2.3	1.9	ND	ND	−1.1	−1.5
6	1.14	1.14	3.4	3.4	1.06	1.03	3.3	3.3	1.46	1.00	3.2	2.2	−0.1	−0.2	−0.2	−1.2
7	1.13	1.14	2.6	2.6	1.16	1.16	2.4	2.4	ND	ND	ND	ND	−0.1	−0.1	ND	ND
8	1.18	1.18	3.0	3.0	1.10	1.09	2.7	2.7	1.20	1.20	1.6	1.6	−0.3	−0.3	−1.4	−1.4
9	1.14	1.10	3.0	2.9	1.12	1.12	2.3	2.3	1.08	1.06	1.7	1.7	−0.7	−0.6	−1.3	−1.2
10	1.04	1.00	3.3	3.2	1.07	1.08	3.7	3.8	1.04	1.02	2.2	2.2	0.4	0.6	−1.1	−1.0
Mean			2.7	2.7			2.7	2.6			2.0	1.9	0.0	0.0	−0.8	−0.7
Std			0.6	0.5			0.6	0.6			0.4	0.4	0.5	0.5	0.5	0.5

Patients 5 and 6 were excluded from analysis. Data survey: just after surgery (baseline, bsl); before prosthetic loading (bpl), generally four months after surgery; after prosthetic loading (apl), generally 1 year after implant placement. 

apl, after prosthetic loading; bpl, before prosthetic loading; bsl, baseline; CF, correction factor; MBL, marginal bone level; ND, not determined.

Discussion

Fixed dental prosthesis supported by root-form osseointegrated dental implants has been one of the most common rehabilitation strategies for the treatment of a partially- or totally edentulous jaw. The placement of root-form dental implants requires a great amount of bone; if bone volume augmentation is not feasible, a blade can be positioned because it requires a lower absolute amount of bone (height and width). Treatments with blades may seem to be simple, non-invasive, to carry a very small risk of complications and to require a short time-frame for the achievement of the final objective. But blades have been used by a few expert clinicians, with unpredictable outcomes in terms of safety, efficacy and predictability regarding the rehabilitation of the posterior mandible region.⁸ Implant blades nowadays appear to be a seldom-used treatment; however, one feature of the blade, namely the absence of a cylindrical geometry (given by the wings), proved very important for the development of the present state of theory, which has led to a simplification of the system of equations. Generally, in clinical practice the measurements of alveolar bone loss surrounding implants were assessed by measuring the MBL from sequential radiographic images. As stated, differences in projection angles of radiographs could affect the assessment of the bone level owing to distorting effects and to superimpositions of various anatomical structures. Thus, the correct evaluation of bone levels was dependent on the degree to which the details of two consecutive radiographs could be superimposed.^3,9

Even if the widest source of projection errors was the misalignment between the central beam and the detector holder,¹⁰ a reproducible detector-to-sample positioning could be obtained by using bite blocks, such as unilateral or bilateral bite registration with or without rigid material.¹¹

To reduce irreversible alignment errors, several methods were proposed, even if the simplest to use was the Rinn arm device.¹¹ However, a strictly parallel geometry that could be achieved following the dictates of anatomy represented a utopia; there was an ineluctable conflict between the theoretical and the practical buccolingual inclination of the implant.

Even if advances in digital processing improved image quality, a mathematical correction of the image based on implant size as input for alignment software could not overcome all kinds of planar errors after image capture.¹²

The presence of dental implants offered an impressive feature-set for interpreting a series of radiologic examinations. In fact, the quality of the projection image could be evaluated a posteriori by means of investigating the implant (or structure) as it appeared in the radiographs. Even if the measurement of the MBL could be affected by error-in-variables ranging from 0.1 to 0.4 mm,¹³ an a posteriori method based on projection geometry which involves the determination of the three angles of implant pose had not yet been developed.

A few authors attempted to describe methods to assess the parameters of projection geometry. For example, Lehmann and Schropp provided a novel representation of sphere projection and an exhaustive analysis of the extrinsic features used²; further, great progress was made by Schulze, who developed a software providing important information for accurate image recording¹⁴ and an analytical algorithm capable of determining localization and orientation of a cylindrical dental implant in three-dimensional space from a single radiographic projection.¹⁵ The author reduced the six possible df to five (three translational and two rotational), because the one related to the implant length axis appeared hidden. In the present study, there is no interest regarding the translational movements of the blade, but an additional reference point located not collinearly with the main axis of the implant, and identifiable in a two-dimensional radiograph, such as a reference point on a blade wing, gave sufficient information to resolve the radial rotation.

In the present paper, “vector analysis” was employed to estimate the pose of the blade, evaluated by its radiographic profile on a single two-dimensional image. The present study gives a system of roles in order that the bias related to bone loss measurement can be reduced. The solutions of the system of equations were arrived at by an equation solver; explicit solutions can be easily obtained. Considerable problems were encountered with the explicit solutions owing to the multiple solutions of the inverse trigonometric functions; however, the equation solver did not find only theoretical solutions for the system of equations; quite the contrary, it provided the first real solution to the problem. The compensation given by a manual correction factor assessed bone loss which was very close to that derived by explicit trigonometric calculation of the angular correction factor.

If biases in measurements were not present, i.e. implants for which clinicians were able to prevent alignment errors, even in the presence of different poses of the implant a linear dependence between the manual and the angular correction factors was confirmed. Even if errors in the relationships established between the object and the radiographic detector were common and could not be resolved a posteriori, angular analysis could easily detect some of these misalignments. Although the divergence between the X-ray beam direction of the X-ray source and the direction of the vector perpendicular to the detector surface might generate a significant distortion of the implant contour, these could be studied in an alternative way.

Externalization of the results suggested that the full system of equations (1–-3) could be employed also for a root-form dental implant, in order to measure the differences in the projection angles between consecutive radiographs. Particularly, the cylindrical symmetry of the root-form implant implies that, even if equation of the lengthwise vector is identical to that of the ${\displaystyle \overrightarrow{\mathrm{O}\mathrm{A}}}$, the components of the crosswise vector are trigonometric functions of both the triplet and of the three-dimensional position of the crosswise reference point (an additional reference point located not collinearly with main axis of the implant and selected by the clinician). It is worth noting that the discrepancy between the implant shoulder (if chosen as origin of the axes) and the crosswise reference point must be acquired before radiographs by an alternative method, such as from a master cast or from a CAD/CAM intraoral camera.

The present results have been verified by the calculation of virtual components and virtual positional angles, which appeared to be very close to the fitted results obtained from patients’ radiographs. Accuracy in the detection of the triples was investigated. A Even though the isotropic voxels of the virtual phantom allowed the generation of a two-dimensional radiographic simulation (the ghost) with a pixel resolution of 0.04 mm, the error in the angular calculation was not homogeneous; the test revealed that dispersion of the absolute errors regarding the estimation of angles φ and θ were higher than that registered for angle ψ. However, mean errors appeared centred around 0, suggesting that there were no systematic over- or underestimation of the angles.

A limitation of the present method is that a physical determination of the degree of accuracy is very complex. Moreover, the resolution power of the sensor, i.e. the highest number of line pairs per millimetre, and the inaccurate implant boundary determination, owing to both the implant’s orientation and to the focal spot size, might highly affect the detection of the three reference points. However, implementation of the software and refinements to the method may increase the accuracy of radiological outcomes even in the case of cylindrical dental implants, although further research is required.

Conclusions

The present theoretical and experimental study has established the possibility of determining, a posteriori, a unique triplet of angles (φ, θ and ψ) which describes the pose of a blade upon a single two-dimensional radiograph, and of suggesting a method to detect cases in which the standardized geometric projection failed. The angular correction of the bone level yielded results very close to those obtained with the internal reference marker, such as implant length.

Source of funding or financial interest statement

The corresponding author, on behalf of all contributors, certifies that the present research is free of conflict of interest; moreover, none of the authors nor the authors’ institutions, that is the Universities of Pisa, Naples and Geneva, and the Tuscan Dental Institute, have any financial or personal relationships with other people or organizations which could in any way inappropriately influence their actions.

Funding

The present study was supported in part by the Tuscan Stomatologic Institute. No external funding was available for this study.