Hypothesis Testing in the Real World

Abstract

Critics of null hypothesis significance testing suggest that (a) its basic logic is invalid and (b) it addresses a question that is of no interest. In contrast to (a), I argue that the underlying logic of hypothesis testing is actually extremely straightforward and compelling. To substantiate that, I present examples showing that hypothesis testing logic is routinely used in everyday life. These same examples also refute (b) by showing circumstances in which the logic of hypothesis testing addresses a question of prime interest. Null hypothesis significance testing may sometimes be misunderstood or misapplied, but these problems should be addressed by improved education.

One important goal of statistical analysis is to find real patterns in data. This is difficult when the data are subject to random noise, because random noise can produce illusory patterns “just by chance.” Given the difficulty of separating real patterns from coincidental ones within noisy data, it is important for researchers to use all of the appropriate tools and models to make inferences from their data (e.g., Gigerenzer & Marewski, 2015).

Null hypothesis significance testing (NHST) is one of the most commonly used types of statistical analysis, but it has been criticized severely (e.g., Kline, 2004; Ziliak & McCloskey, 2008). According to Cohen (1994), for example, “NHST has not only failed to support the advance of psychology as a science but also has seriously impeded it” (p. 997). There have been calls for it to be supplemented with other types of analysis (e.g., Wilkinson & the Task Force on Statistical Inference, 1999), and at least one journal has banned its use outright (Trafimow & Marks, 2015).

This note reviews the basic logic of NHST and responds to some criticisms of it. I argue that the basic logic is straightforward and compelling—so much so that it is commonly used in everyday reasoning. It is suitable for answering certain types of research questions, and of course it can be supplemented with additional techniques to address other questions. Criticisms of NHST’s logic either distort it or implicitly deny the possibility of ever finding patterns in data. The major problem with NHST is that some aspects of the method can be misunderstood, but the solution to that problem is to improve education—not to adopt new methods that address a different set of questions but are incapable of answering the question addressed by NHST. I conclude that it would be a mistake to throw out NHST.

The Common Sense Logic of NHST

Critics of NHST assert that it uses arcane, twisted, and ultimately flawed probabilistic logic (e.g., Cohen, 1994; Hubbard & Lindsay, 2008). To the contrary, the heart of NHST is a simple, intuitive, and familiar “common sense” logic that most people routinely use when they are trying to decide whether something they observe might have happened by coincidence (a.k.a., “randomly,” “by accident,” or “by chance”).

For example, suppose that you and five colleagues attend a departmental picnic. An hour after eating, three of you start to feel queasy. It comes out in discussion that those feeling queasy ate potato salad and that those not feeling queasy did not eat the potato salad. What could be more natural than to conclude that there was something wrong with the potato salad?

It is important to realize that this nonstatistical example fully embodies the underlying logic of hypothesis testing. First, a pattern is observed. In this example, the pattern is that people who ate potato salad felt queasy. Second, it is acknowledged that the pattern might have arisen just by chance. In this example, for instance, exactly those people who ate the potato salad—and no one else—might coincidentally all have been coming down with the flu, and the flu might have caused their queasiness. Third, there is reason to believe that the observed coincidence—while possible—would be very unlikely. In the example, real-world experience suggests that coming down with flu is a rare event, so it would be quite unlikely for several people to do so at just the same time, and it would of course be even more unlikely that those were exactly the people who ate the potato salad. Fourth, it is concluded that the observed pattern did not arise by chance. In this example, the “not by chance” conclusion suggests that there was something wrong with the potato salad.

To further clarify the analogy between NHST and the potato salad example, consider how a standard coin-flipping “statistical” data analysis situation could be described in parallel terms. Suppose a coin is flipped 50 times and it comes up heads 48 of them (pattern). This quite strong pattern could happen by coincidence, but elementary probability theory says that such a coincidence would be extremely unlikely. It therefore seems reasonable to conclude that the pattern was not just a coincidence; instead, the coin appears to be biased to come up heads. This is exactly the same line of reasoning used in the potato salad example: The observed pattern would be very unlikely to occur by chance, so it is reasonable to conclude that it arose for some other reason.

There are many other nonstatistical examples of the reasoning used in NHST. For instance, if you see an unusually large number of cars parked on the street where you live (pattern), you will probably conclude that something special is going on nearby. It is logically possible for all those cars to be there at the same time just by coincidence, but you know from your experience that this would be unlikely, so you reject the “just by chance” idea. Analogously, if two statistics students make an identical series of calculation errors on a homework problem (pattern), their instructor might well conclude that they had not done the homework independently. Although it is logically possible that the two students made the same errors by chance, that would seem so unlikely—at least for some types of errors—that the instructor would reject that explanation. These and many similar examples show that people often use the logic of hypothesis testing in the real world; essentially, they do so every time they conclude “that could not just be a coincidence.” Statistical hypothesis testing differs only in that laws of probability—rather than every-day experiences with various coincidences—are used to assess the likelihood that an observed pattern would occur by chance.

Criticisms of NHST’s Logic

According to Berkson (1942), “There is no logical warrant for considering an event known to occur in a given hypothesis, even if infrequently, as disproving the hypothesis” (p. 326). In terms of our examples, Berkson is saying that it is illogical to consider 3/6 queasy friends as proving that there was something wrong with the potato salad, because it could be just a coincidence. Taken to its logical extreme, his statement implies that observing 48/50 heads should also not be regarded as disproving the hypothesis of a fair coin, because that too could happen by chance. To be sure, Berkson is mathematically correct that the suggested conclusions about the quality of the potato salad and the fairness of the coin do not follow from the observed patterns with the same 100% certainty that implications have in propositional logic (e.g., modus ponens). On the other hand, it is unrealistic to demand that level of certainty before reaching conclusions from noisy data, because such data will almost never support any interesting conclusions with 100% certainty. In practice, 48/50 heads seems like ample evidence to conclude—with no further assumptions—that a coin must be biased, and the “logical” objection that this could have happened by chance seems rather intransigent. Given that logical certainty is unattainable due to the presence of noise in the data, one can only consider the probabilities of various correct and incorrect decisions (e.g., Type I error rates, power) under various hypothesized conditions, which is exactly what NHST does.

Another long-standing objection to NHST is that its conclusions depend on the probabilities of events that did not actually occur (e.g., Cox, 1958; Wagenmakers, 2007). For example, in deciding whether 3/6 people feeling queasy was too much of a coincidence, people might be influenced by how often they had seen 4/6, 5/6, or 6/6 people in a group feel queasy by chance, even though only 3/6 had actually been observed. It is difficult to see much practical force to this objection, however. In trying to decide whether a particular pattern is too strong to be observed by chance, it seems quite relevant to consider all of the different patterns that might be observed by chance—especially the patterns that are even stronger. Proponents of this objection generally support it with artificial probability distributions in which stronger patterns are at least as likely to occur by chance as weaker patterns, but such distributions rarely if ever arise in actual research scenarios.

Critics of NHST sometimes claim that its logical form is parallel to that of the argument shown in Table 1 (e.g., Cohen, 1994; Pollard & Richardson, 1987). There is obviously something wrong with the argument in this table, and NHST must be flawed if it uses the same logic. This criticism is unfounded, however, because the logic illustrated in Table 1 is not parallel to that of NHST.

Table 1.

A Misleading Caricature of Null Hypothesis Significance Testing’s Logical Form.

1. If a person is an American, then he is probably not a member of Congress.

2. This person is a member of Congress.

3. Therefore, he is probably not an American.

The argument given in Table 1 suggests that a null hypothesis—in this case, that a person is an American—should be rejected whenever the observed results are unlikely under that hypothesis. NHST requires more than that, however. Implicitly, in order to reject a null hypothesis, NHST requires that the observed results must be more likely under an alternative hypothesis than under the null. In the potato salad example, for instance, rejecting the coincidence explanation requires not only that the observed pattern is unlikely by chance when the potato salad is good, but also that this pattern is more likely when the potato salad is bad (i.e., more likely when the null hypothesis is false than when it is true).

Figure 1 shows how this additional requirement arises within NHST using the Z test as an example. The null hypothesis predicts that the outcome is a draw from the depicted standard normal distribution, and Region A (i.e., the cross-hatched tails) of this distribution represent the Z values for which the null would be rejected at p < .05. Critically, Region B in the middle of the distribution also depicts an area of 5%. If NHST really only required that the rejection region had a probability of 5% under the null hypothesis, as implied by the argument in Table 1, then rejecting the null for an observation in Region B would be just as appropriate as rejecting it for an observation in Region A. This is not all that NHST requires, however, and in fact outcomes in Region B would not be considered evidence against the null hypothesis. The null hypothesis is rejected for outcomes in A but not for those in B, because of the requirement that an outcome in the rejection region must have higher probability when the null hypothesis is false than when it is true. Region B of Figure 1 clearly does not satisfy this additional requirement, because this area will have a higher probability when the null hypothesis is true than when it is not.

Figure 1.

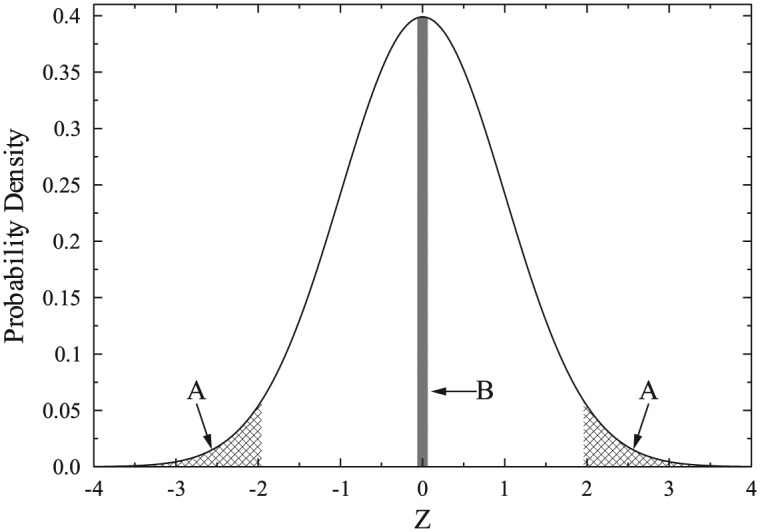
A standard normal (Z) distribution of observed scores under the null hypothesis.

Note. Region A: The two cross-hatched areas indicate the standard two-tailed rejection region—that is, the 5% of the distribution most discrepant from the mean. Region B: The dark shaded area in the middle of the distribution also represents an area of 5%. Under NHST, only observations in the tails are taken as evidence that the null hypothesis should be rejected, even though the probability of an observation in Region B is just as low (i.e., 5%).

Likewise, the example of Table 1 clearly does not satisfy the additional requirement that the observed results should be more likely under some alternative to the null hypothesis. The probability that a person is a member of Congress is lower—not higher—if the person is not an American. In fact, the logic of NHST actually requires a first premise of the form:

• 1′. If a person is an American, then he is probably not a member of Congress; on the other hand, if he is not an American, then he is more likely to be a member of Congress.

Premise 1′ is obviously false, so the conclusion (3) is obviously not supported within NHST.

Finally, critics of NHST often complain that its conclusions can depend on the sampling methods used to collect the data as well as on the data themselves (e.g., Wagenmakers, 2007). This dependence arises because NHST’s assessment of “how likely is such an extreme pattern by chance” depends on the exact probabilities of various outcomes, and these in turn depend on the details of how the sampling was carried out. This is thought to be a problem for NHST, because—according to critics—the conclusion from a data set should depend only on what the data are, but not on the sampling plan used to collect them. This argument begs the question, however. Of course, the assessment of what will happen “by chance” can only be done within a well-defined set of possible outcomes. These outcomes are necessarily determined by the sampling plan, so the plan must influence the assessment of the various patterns’ probabilities. Viewed in this manner, it seems quite reasonable that any conclusion about the presence of an unusual pattern would depend on the sampling plan as well as on the observations themselves.

Ancillary Criticisms of NHST

Additional criticisms have been directed at aspects of NHST other than its logic. For example, it is sometimes claimed that NHST does not address the question of main interest. Critics often assert that researchers “really” want to know the probability that a pattern is coincidental given the data (e.g., Berger & Berry, 1988; Cohen, 1994; Kline, 2004). Within the current examples, then, the claim is that people really want to know “the probability that these 3/6 picnic-goers feel sick by coincidence” or “the probability that the coin is biased towards heads.”

It is clear that NHST does not provide such probabilities, but it is not so clear that everyone always wants them. In many cases, people simply want to decide whether the pure chance explanation is tenable; for example, it is difficult to imagine a picnic-goer asking for a precise probability that the potato salad was bad. In any case, to obtain such probabilities requires knowing all of the other possible explanations, plus their prior probabilities (e.g., Efron, 2013). In many situations where NHST is used, the complete set of other possible explanations and their probabilities are simply unknown. In these situations, no statistical method can compute the probability that researchers supposedly want, and it seems unfair to criticize NHST for failing to provide something that cannot be determined with any other technique either.

Surely the most frequent and justified criticisms of NHST revolve around the idea that researchers do not completely understand it (e.g., Batanero, 2000; Wainer & Robinson, 2003). A number of findings suggest that one aspect of NHST in particular—the so-called “p value”—is widely misunderstood (e.g., Gelman, 2013; Haller & Kraus, 2002; Hubbard & Lindsay, 2008; Kline, 2004). Explicitly or implicitly, such findings are taken as evidence that NHST should be abandoned because it is too difficult to use properly (e.g., Cohen, 1994).

Unfortunately, similar data suggest that many other concepts in probability and statistics are also poorly understood (e.g., Campbell, 1974). If we abandon all methods based on misunderstood statistical concepts, then almost all statistically based methods will have to go, including some apparently quite practical and important ones (e.g., diagnostic testing in medicine; Gigerenzer, Gaissmaier, Kurz-Milcke, Schwartz, & Woloshin, 2008). Within this difficult context, there seems to be no reason to abandon NHST selectively, because there is “no evidence that NHST is misused any more often than any other procedure” (Wainer & Robinson, 2003, p. 22). Moreover, if one accepted the argument that all poorly understood methods should be abandoned, then some useful but poorly understood nonstatistical methods would presumably also have to go (e.g., propositional logic; Rips & Marcus, 1977; Wason, 1968). Surely it would be a mistake to abandon a valuable tool or technique simply because considerable training and effort are required to use it correctly.

The current discussion of frequent false positives and low replicability in research areas using NHST (e.g., Francis, 2012; Nosek, Spies, & Motyl, 2012; Simmons, Nelson, & Simonsohn, 2011) also suggests that there are misunderstandings and misuse of this technique. Specifically, there is evidence that researchers capitalize on flexibility in the selection of their data and in the application of their analyses (i.e., “p-hacking”) in order to obtain statistically significant and therefore publishable results (e.g., Bakker, Van Dijk, & Wicherts, 2012; John, Loewenstein, & Prelec, 2012; Tsilidis et al., 2013). Such practices are a misuse of NHST, and they inflate positive rates, especially in combination with existing biases toward publication of surprising new findings and with the relative scarcity of such findings within well-studied areas (e.g., Ferguson & Heene, 2012; Ioannidis, 2005). The false positive problem is not specific to NHST, however; it would arise analogously within any statistical framework. Whatever statistical methods are used to detect new patterns in noisy data, the rate of reporting imaginary patterns (i.e., false positives) will be inflated by flexibility in the selection of the data, flexibility in the application of the methods, and flexibility in the choice of what findings are reported.

To the extent that misunderstanding of NHST presents a problem, better education of researchers seems like the best path toward a solution (e.g., Holland, 2007; Kalinowski, Fidler, & Cumming, 2008; Leek & Peng, 2015). Although the underlying logic of NHST has considerable common sense appeal—as shown by the real-world examples described earlier—this logic is often obscured when the methods are taught to beginners. This is partly because of the specialized and unintuitive terminology that has been developed for NHST (e.g., “null hypothesis,” “Type I error,” “Type II error,” “power”). Another problem is that introductions to NHST nearly always focus primarily on the mathematical formulas used to compute the probabilities of observing various patterns by chance (i.e., “distributions under the null hypothesis”). Students can easily be so confused about the workings of these formulas that they fail to appreciate the simplicity of the underlying logic.

Conclusions

NHST is a useful heuristic for detecting nonrandom patterns, and abandoning it would be counterproductive. Its underlying logic—both in scientific research and in everyday life—is that chance can be rejected as an explanation of observed patterns that would rarely occur by coincidence. It is true that the conclusion of a biased coin does not follow with 100% certainty, and it will be wrong when an unlikely pattern really does occur by chance. Researchers should certainly keep this possibility in mind and resist the tendency to believe that every pattern documented statistically—whether by NHST or any other technique—necessarily reflects the true state of the world. As a practical strategy for detecting non-random patterns in a noisy world, however, it seems quite a reasonable heuristic to conclude tentatively that something other than chance is responsible for systematic observed patterns.

While NHST is extremely useful for deciding whether patterns might have arisen by chance, it is, of course, not the only useful statistical technique. In fact, when NHST is employed, “the answer to the significance test is rarely the only thing we should consider” (Cox, 1958, p. 367), so it is not sufficient for researchers to try to answer all research questions entirely within the NHST framework. For example, NHST is not appropriate for evaluating how strongly a data set supports a null hypothesis (e.g., Grant, 1962). For that purpose, it is better to use confidence intervals or Bayesian techniques (e.g., Cumming & Fidler, 2009; Rouder, Speckman, Sun, Morey, & Iverson, 2009; Wainer & Robinson, 2003; Wetzels, Raaijmakers, Jakab, & Wagenmakers, 2009). Fortunately, there is no fundamental limit on the number of statistical tools that researchers can use. Researchers should always use the set of tools most suitable for the questions under consideration. In many cases, that set will include NHST.