Quantitative Assessment of the Energetics of Dopamine Translocation by Human Dopamine Transporter

Abstract

Computational evaluation of the energetics of substrate binding, transport, and release events of neurotransmitter transporters at the molecular level is a challenge, as the structural transitions of these membrane proteins involve coupled global and local changes that span time scales of several orders of magnitude, from nanoseconds to seconds. Here, we provide a quantitative assessment of the energetics of dopamine (DA) translocation through the human DA transporter (hDAT), using a combination of molecular modeling, simulation, and analysis tools. DA-binding and -unbinding events, which generally involve local configurational changes, are evaluated using free-energy perturbation or adaptive biasing force methods. The global transitions between the outward-facing state and the inward-facing state, on the other hand, require a dual-boost accelerated molecular dynamics simulation. We present results on DA-binding/unbinding energetics under different conditions, as well as the conformational energy landscape of hDAT in both DA-bound and -unbound states. The study provides a tractable method of approach for quantitative evaluation of substrate-binding energetics and efficient estimation of conformational energy landscape, in general.

Graphical Abstract

INTRODUCTION

Dopamine (DA) transporter (DAT) regulates dopaminergic signaling by removing excess DA from the synapse and thus preventing the saturation of DA-gated receptors and neurotoxicity. The mechanism of DAT function is complicated: the substrate DA is transported against its electrochemical gradient from the extracellular (EC) to the intracellular (IC) domain, and the uphill energetic cost of this action is more than offset by the coupled co-transport of two sodium ions.¹ In addition to the thermodynamic coupling of substrate and Na⁺ ions co-transport, uncoupled DAT-mediated ionic fluxes^2,3 as well as inverse transport (or efflux) of the IC DA⁴ occur via channel-like pathways.^5,6 The function of DAT is modulated by addictive drugs (see refs 5–7), e.g., cocaine and amphetamine, and regulatory proteins, e.g., G-protein βγ subunits.⁸ Dysfunction of DAT results in dopaminergic dysfunction and is implicated in several neurological and psychiatric disorders, including Parkinson’s disease and schizophrenia (see refs 5, 6).

DAT belongs to the secondary active transporters family of neurotransmitter: sodium symporters (NSSs). It is generally accepted that NSSs transport their substrate via an alternating access mechanism,^9,10 in which the transporter changes its conformation from an outward-facing state (OFS), for substrate/sodium uptake from the EC environment, to inward-facing state (IFS), for their release to the IC medium, and vice versa in the apo state to resume the cycle. NSSs share the LeuT fold first resolved¹¹ for a bacterial leucine transporter, LeuT. LeuT fold is composed of 10 transmembrane (TM) helices (TM1–TM10) organized in two pseudosymmetric inverted repeats.^12,13 Bacterial LeuT has been crystallographically resolved in multiple conformers, distinguished by global (OFS or IFS) and local (open(o) or closed(c) conformations of the EC or IC gating amino acids) properties: substrate-free outward-facing open (OFo) (bound to two Na⁺ ions),¹⁴ substrate-bound outward-facing closed (OFc*; * designates the substrate-bound state),¹¹ and substrate-free inward-facing open (IFo).¹⁴ The structure and dynamics of human DAT (hDAT) at the atomic level has been originally explored using models or simulations based on LeuT.^15–21 Computations performed for LeuT-fold family members^22–29 also helped understand the conformational dynamics of NSSs. Recently, Gur et al.²⁹ have characterized the conformational energy landscape of LeuT in both substrate(Ala/Leu)-bound and apo states using conventional molecular dynamics (cMD) simulations of tens of microseconds generated with the Anton supercomputing machine³⁰ combined with a hybrid methodology, coMD,³¹ that guides cMD along collective modes of motions predicted by the anisotropic network model.^32,33 These studies revealed intermediate conformers occluded to EC and/or IC media sampled during the global transitions, as well as the differences between Ala- and Leu-bound transition pathways.²⁹

The resolution of Drosophila melanogaster DAT (dDAT) structure bound to DA, amphetamine, cocaine, and anti-depressants^34,35 has opened the way to structure-based investigations of hDAT dynamics.^36–41 Our simulations³⁷ using dual-boost accelerated MD (aMD)^42,43 and cMD provided a first description of the sequence of events and key interactions that enable DA transport by hDAT using these structural data. More recently, the kinetics of the release of the so-called Na2 sodium ion to the IC medium has been evaluated using Markov State Models.⁴¹ Yet, a comprehensive study of the energetics of all of the steps of the transport cycle has not been performed to date. Accurate prediction of ligand-binding affinity is a challenge, usually due to the conformational flexibility of the ligand and the protein⁴⁴ in addition to sensitivity to force-field parameters.^45–49 In the case of DAT, the quantitative assessment of binding and conformational energetics is further complicated by three computational challenges: (1) hDAT transport turnover time is around seconds, well beyond the reach of atomic simulations;⁵⁰ (2) the global conformational changes (OFS ↔ IFS) are coupled to local changes (o ↔ c), which necessitate the examination of global events at atomic resolution;^36,37 and (3) the substrate DA itself undergoes internal and external conformational changes, which brings another layer of complexity, not encountered in evaluating the channeling of ions, for example, through ion channels.^51–53 Single-molecule fluorescence resonance energy transfer (smFRET) imaging of LeuT⁵⁴ and glutamate transporter Glt_Ph,⁵⁵ as well as double electron–electron resonance spectroscopy measurements of spin-labeled pairs in LeuT⁵⁶ and Mhp1⁵⁷ have provided valuable insights into Na⁺- and substrate-dependent equilibrium probabilities of OFS and IFS, as well as the rates of their interconversions,^54,55 revealing different coupling reactions to Na⁺ and/or substrate gradients,^54,55,57 but no molecular-level study of energetics of DA transport by hDAT, computational or experimental, has been performed to date.

In the present study, we focus on the DA-binding and -unbinding free energies of hDAT using two rigorous methods: (i) alchemical free-energy calculations with free-energy perturbation (FEP) method⁵⁸ and (ii) potential of the mean force (PMF) calculation of the DA translocation using the adaptive biasing force (ABF) method,⁵⁹ based on all-atom cMD simulations, to achieve a high level of theoretical rigor.^45–47 We further characterize the conformational spectrum of hDAT. To this aim, we generated more than 2 μ s aMD trajectories for studying the transition of apo hDAT from OFS to IFS, and vice versa. This, together with trajectories from our previous studies of DA-loaded transitions,^36,37 permitted us to generate for the first time a first estimate of the energy landscape of hDAT.

THEORETICAL METHODS

MD Simulation Systems and Protocol

For evaluating DA-binding and -unbinding energetics, we used the DA-loaded systems of hDAT in the OFo* (Figures 1B and 2B) and OFc* (Figure 2C). In addition, three IFo* conformers with different occupancies of co-transported ions were investigated:³⁷ (1) IFo₃* bound to two Na⁺ ions and one chloride ions (Figure 3A); (2) IFo₁* bound to one Na⁺ ion (Figure 3B), sampled after the release of one Na⁺ ion and the chloride ion; and (3) the IFo₀* conformer bound to DA (Figure 3C), in which the Na⁺ ion of IFo₁* was steered to the IC solution using steered MD⁶⁰ and then the system was subjected to 10 ns cMD for equilibration. A summary of simulation methods, durations, initial conformations, observed events, and outputs is presented in Table 1. The equilibrated system containing the hDAT, 196 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) molecules, 0.15 M NaCl solution, and about 29 100 water molecules, summing up to a total of over 140 000 atoms, remained within a volume of 104 × 104 × 122 ų.

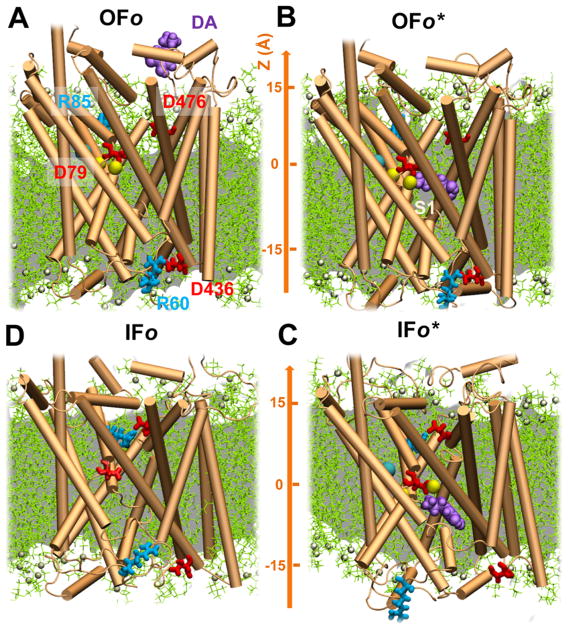
Figure 1.

Four major conformers visited during the transport cycle of hDAT, in the presence of lipid bilayer, and key residues implicated in EC gating, substrate binding, and IC gating. The panels illustrate the MD environment/snapshots for: (A) outward-facing open (OFo) state, with the substrate (DA; purple, space-filling) initially 15 Å away from substrate-binding site; (B) outward-facing open (OFo*) form with the DA bound to the S1 site; (C) DA-bound inward-facing open (IFo*), prior to translocation and release to the IC region; and (D) DA-free inward-facing open (IFo). The respective EC and IC gating pairs, R85-D476 and R60-D436, are shown in sticks. Note that the EC gates are open in (A) and (B), whereas the IC gates are closed; the opposite takes place in (C), and both gates are partially/completely closed in (D). hDAT also samples a holo occluded state,³⁷ between (B) and (C), with the gates closed to both environments, not shown here. The POPC lipids are shown in green lines with P-atoms in tan spheres. Cyan and yellow spheres represent the co-transported Cl⁻ and two Na⁺ ions, respectively.

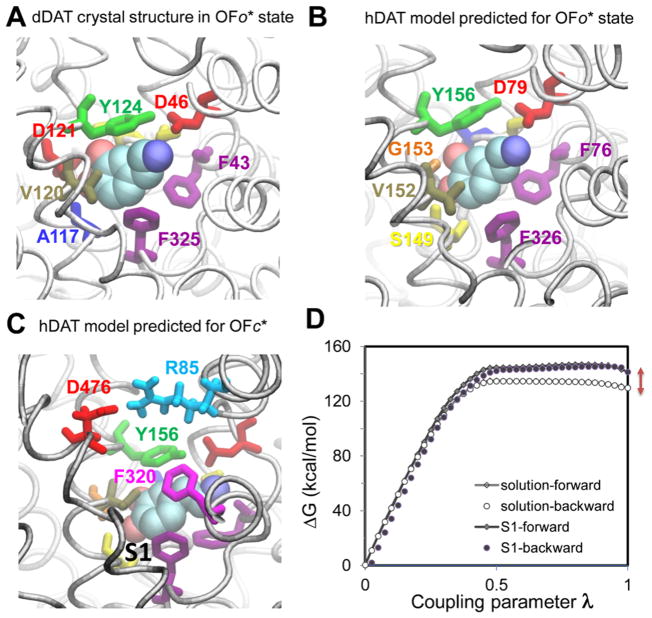
Figure 2.

DA-binding pocket from experiments and computations viewed from the EC side, and evaluation of DA-binding affinity of hDAT. (A) DA-binding site in OFo* dDAT resolved by X-ray crystallography (PDB: 4XP1); (B) counterpart of OFo* hDAT computationally predicted independently; (C) computational prediction of DA-bound hDAT in the OFc* state, where the EC gating residues³⁷ (Y156-F320 and R85-D476) are closed; and (D) free-energy change for the double annihilation of bound DA shown in (C) (black line with filled diamonds for the forward transformation; filled circles for the backward transformation), and in its free state, in a bulk aqueous environment (gray line with open diamonds for forward transformation; open circles for backward transformation). The difference at λ = 1 (red arrows) (D) between the net free-energy changes (DA–hDAT and DA–water) is –12.90 kcal/mol. The total entropy penalty due to the orientation and spatial constraints employed in the DA–hDAT system was estimated to be 5.80 kcal/mol, which leads to EC DA-binding free energy of −7.10 kcal/mol.

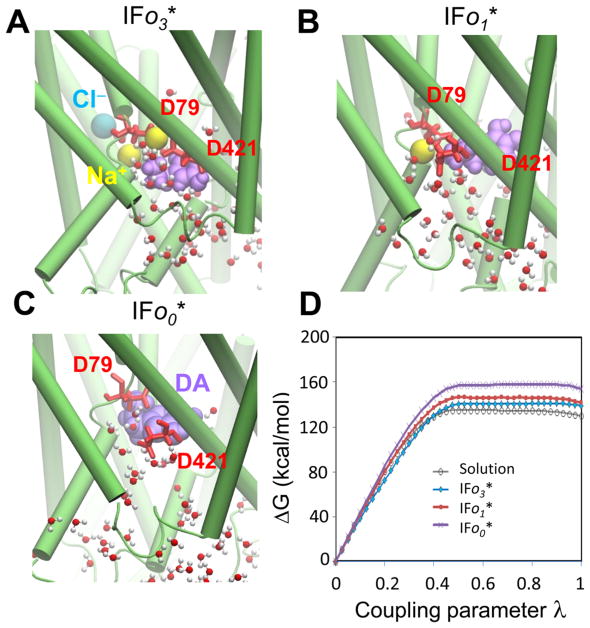
Figure 3.

Evaluation of DA-unbinding energy from hDAT in the IFS. Three conformers with different ion occupancy are shown: (A) DA-bound in the presence of two sodium ions and one chloride ion (IFo₃*); (B) DA-bound in the presence of one Na⁺ ion, after the release of Na2 and one chloride (IFo₁*); and (C) DA-bound in the absence of ions (IFo₀*). (D) Comparison of the free-energy changes for the forward annihilation of DA under the three conditions: as a free molecule in the aqueous environment (gray line with open circles), bound to IFo₃* (blue line with diamonds), bound to IFo DAT in the presence of one sodium ion, IFo₁* (red line with squares) and in the absence of other ions, IFo₀* (purple line with crosses). The respective binding affinities are listed in Table 2.

Table 1.

Summary of Simulated Systems and Events and Corresponding Outputs

run #	method	duration (ns)	initial conformation	initially bound substrate/ions	transition	output
1	aMD	200	OFo	2 Na+, 1 Cl−, and no DA binding	OFo → OFc/IFc	energy landscape Figure 6
2		200
3a	aMD	450	OFo	2 Na+, 1 Cl−, 1 DA ~15 Å away from site S1	OFo/OFo* → OFc* → occluded* → IFo*	transport events in Figure 5
4a		400	OFo*	2 Na+/1 Cl−/1 DA
5	aMD	200	IFo* D79 protonated	1 Na+/1 DA	IFo* → IFo
6	aMD	200	IFo D79 protonated	none	fluctuating near IFo	energy landscape Figure 6
7		200			IFo → IFc/OFc
8	aMD	200	IFo D79 deprotonated		fluctuating near IFo
9		200			fluctuating near IFo
10–12	FEP	2–10	OFo*	2 Na+/1 Cl−/1 DA	bound/unbound	EC DA-binding affinity Figure 2
13–15	FEP	2–10	OFc*	2 Na+/1 Cl−/1 DA
16–18	FEP	2–10	IFo3*	2 Na+/1 Cl−/1 DA		IC DA binding with different ion occupancy Figure 3
19–21	FEP	2–10	IFo1*	1 Na+/1 DA
22–23	FEP	2–10	IFo0*	1 DA
24	ABF	100	IFo1*	1 Na+/1 DA	IFo* → IFo	IC DA release Figure 4

^aTrajectory generated in earlier work,³⁷ used here for generating the outputs listed in the same column.

All MD simulations were performed using the NAMD software⁶¹ following the protocols outlined in our earlier studies of hDAT.^36,37 CHARMM36 force field with CMAP corrections was used for hDAT, water, and lipid molecules.^62,63 The DA molecule carries +1 charge, and its force-field parameters were adopted from the CHARMM General Force Field (CGenFF) v0.9.7.1beta for druglike molecules.⁶⁴ All aMD simulations were performed using dual-boost mode^42,43 and the protocols described earlier.³⁷ Briefly, in aMD, when the potential energy V(r) is lower than a threshold value E, a positive boost potential ΔV(r) is added such that the modified potential (V(r) + ΔV(r)) reduces the energy barriers separating different conformational spaces, thus enhancing conformational sampling.^42,43 The boost potential is defined as ΔV(r) = (E –V(r))²/(α + E – V(r)), where α is acceleration factor and E is a threshold energy value.^42,43 In the dual-boost aMD mode, both dihedral energy and the total potential energy are modified.^42,43 For acceleration of dihedral angle rotations, we defined the threshold energy E_dihed and the acceleration factor α_dihed as^37,43 E_dihed = 1.3V_{dihed_avg} and α_dihed = 0.3V_{dihed_avg}/5, where V_{dihed_avg} is the average dihedral energy of all bonds calculated from 20 ns cMD equilibration simulations. Likewise, for the total potential threshold E_total and its corresponding acceleration factor α_total, we adopted the relations^37,43 E_total = V_{total_avg} + 0.2N_atoms and α_total = 0.2N_atoms, where V_{total_avg} is the average total potential energy of all atoms calculated from the 20 ns cMD equilibration simulations and N_atoms is the total number of atoms in the system.

FEP Calculations of DA-Binding Affinities

Double-annihilation FEP⁶⁵ was performed to calculate DA-binding affinity of hDAT in the OFo* (Figure 2B), OFc* (Figure 2C), and multiple IFo* conformers (Figure 3A–C). DA and one chloride ion (in solution) were annihilated simultaneously in the free and bound states to maintain the electrical neutrality of the system during the FEP calculations.⁶⁶ Annihilation in the free solution was carried out in equilibrated water bath containing one DA and one chloride ion. For each DA-bound state, we performed three independent FEP calculations using slightly different snapshots taken from cMD trajectories.

The alchemical transformation was carried out in both forward (with increasing λ from 0 to 1) and backward (with decreasing λ from 1 to 0) directions. The soft-core van der Waals radius-shifting coefficient λ was chosen as 5 Å. Each FEP calculation was carried out over a reaction path stratified in 100 windows of equal width. Each stratum consisted of 10 000 equilibration steps (20 ps), followed by 40 000 (80 ps) data collection steps, hence a total simulation time of 10 ns per FEP calculation. We verified that the results from FEP runs of total duration 2–10 ns were closely reproducible.

Implementation of restraining potentials is particularly efficient for ensuring the convergence of FEP results.⁶⁷ Here, two restraints were imposed to prevent the escape of DA and maintain the salt bridge between D79 and DA during DA-bound simulations:^36,37 (1) a pseudobond was introduced between D79 and DA with an equilibrium distance of 3.2 Å between D79 Cγ-atom and DA N-atom determined from cMD runs and (2) the center-of-mass distance between DA and its binding site (residues within 3 Å of DA in the initial conformer) was restrained within 2 Å. The entropy penalty due to the confinement of DA to its binding site was −1/β ln(c₀ ΔV),⁶⁵ where ΔV is the effective volume sampled by the constrained DA; c₀ is the standard concentration (1 M; or 6.023 × 10⁻⁴/ų); and β = 1/k_BT, where k_B is the Boltzmann constant and T is the absolute temperature. This entropic penalty also takes account of the restraints imposed on the rotational mobility of DA.

ABF Calculation of the PMF for IC DA Release

We calculated the PMF for IC DA release using the ABF method⁵⁹ with the same protocol as our previous study.^68,69 The calculation started from the conformer IFo₁* (Figure 3B) and was performed using four different windows along the IC DA release path.³⁷ The width of each ABF window was 4–6 Å, along the membrane normal (see the scale in Figure 1), and 8–10 consecutive 2 ns ABF calculations were performed for each window. Within each window, the average force acting on DA was calculated for 0.2 Å-sized bins. The boundary force constant was set to be 10 kcal/mol. A total of over 100 ns ABF calculations were performed, covering the DA release from the substrate-binding site (S1) to the IC solution (see Figure 4). The convergence of PMFs was verified by the minimal (<2 kJ/ mol) variation between the last two consecutive runs.

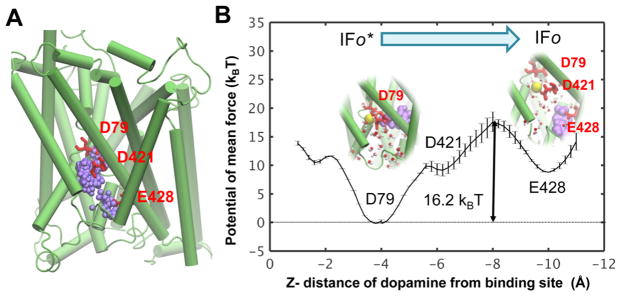
Figure 4.

Intracellular release of DA from hDAT in IFo₁* state. (A) IC release pathway of DA identified in our previous study.³⁷ Purple spheres represent successive positions of DA centroid. (B) Potential of the mean force (PMF) for the IC release of DA. The interactions with D79 plays a major role in stabilizing the bound state. Transient interactions with D421 and E428 are noted during the dislocation and release of DA from its binding site to the IC region.

Trajectory Analysis

VMD⁷⁰ with in-house scripts was used for visualization and trajectory analysis. FEP outputs were assessed using the ParseFEP⁷¹ module implemented in VMD by means of the Bennett acceptance ratio (BAR)⁷¹ based on forward and backward annihilations. To estimate the effective volume ΔV sampled by the constrained DA, first the simulation trajectories were aligned; then the distances between D79 Cγ-and DA N-atoms were calculated; and the deviation around the average value was taken as the effective radius sampled by DA. The effective radius was estimated to be 0.3 ± 0.1 Å.

Generation of Conformational Landscape

Snapshots from aMD simulations were used to generate conformational energy landscapes, similar to a recent study²⁹ performed for LeuT. The reweighted energy landscapes were constructed from aMD snapshots following the procedure described earlier,^72,73 and the ensemble-averaged Boltzmann factor of the boost potential was approximated by summation over the Maclaurin series.^72,73 Interhelical distances between the EC-exposed TM1b (L80–Q93)–TM10 (G467–G481) and IC-exposed TM1a (K66–V78)–TM6b (F326–Y335) were chosen as reaction coordinates to characterize the opening/ closure of the respective EC and IC vestibules.^36,37

RESULTS AND DISCUSSION

DA-Binding Affinity of DAT and Comparison with Experimental Data

The binding geometry of DA in the crystal structure of dDAT bound to DA in the OFo* state (PDB: 4XP1)³⁵ shows significant similarity to that we independently predicted³⁶ by our docking simulations for DA-bound hDAT (Figure 2A,B). Moreover, our MD simulations^36,37 further revealed that binding of DA promoted the closure of EC gates, leading to a new occluded state, OFc* (Figure 2C),³⁶ which has not yet been resolved for DAT but closely resembles the OFc* state resolved for Leu-bound LeuT.¹¹

To estimate the EC DA-binding affinity to hDAT OFo* and OFc* states, we performed FEP calculations as described in Theoretical Methods. Results are illustrated in Figure 2D for the initial binding pose shown in Figure 2C. The EC DA-binding free energy of OFc* DAT is calculated to be −7.10 kcal/mol. FEP calculations repeated for three slightly different initial OFc* conformers yielded an average binding affinity of −7.8 ± 1.5 kcal/mol. This value is close to the estimated −7.4 kcal/mol²⁰ derived from experimental data.⁷⁴ On the basis of this free-energy change, ΔG_bind, the dissociation constant (K_d) for the DAT–DA complex is estimated to be 2.2 μM. Early computational study using the molecular mechanics-Poisson–Boltzmann surface area (MM-PBSA) on hDAT, prior to the elucidation of dDAT structure, reported a binding free energy of −6.4 ± 1.0 kcal/mol,²⁰ which underestimated the binding free energy perhaps due to the approximate structural model constructed therein using the OFc* LeuT crystal structure.

For DA bound to the OFc* hDAT, we noted that both forward (filled diamonds) and backward (filled circles) calculations yielded data that reproduced almost the same curve with very minor variations (Figure 2D) in all three independent calculations. However, the forward and backward calculations for DA binding to OFo* hDAT (Figure 2B) exhibited a significant difference (5–10 kcal/mol) using the same protocol as that used for the OFc* state. FEP calculations benefit from the stabilization of buried ligands⁷⁵ and hence the more stable and accurate results obtained with the OFc*, where the substrate is completely sequestered upon closure of the EC gates (Figure 2C). These observations suggest that additional constraints may be necessary to ensure convergence of FEP results generated for the OFo conformer.

Significance of Co-transported Ions for Facilitating Intracellular DA Release

To assess the impact of co-transported ions on DA IC release, we performed FEP calculations on three IFo* conformers with different ion occupancies (Figure 3). The corresponding free-energy changes calculated using the forward annihilation are compared in Figure 3D. The DA-binding affinities assessed using the BAR method⁷¹ based on both forward and backward annihilations are listed in Table 2. Although the DA-binding affinity was roughly similar in IFo₁* and IFo₃*, the absence of co-transported sodium ions significantly increased DA-binding affinity in the IF state, presumably due to strong electrostatic attractions from two acidic residues D79 and D421, which coordinate the binding of the positively charged DA molecule (see Figure 3C). The presence of positively charged ion(s) (i.e., Na⁺) weakens these attractions, thus facilitating the intracellular release of DA.

Table 2.

DA-Binding Affinity of hDAT in the IFo* State

binding affinity	IFo3* 2Na+/1Cl−	IFo1*1Na+	IFo0* none
ΔG (kcal/mol)	−6.9 ± 2.5	−9.4 ± 2.5	−21.1 ± 5.0

NSSs are able to transport substrate against a 10⁶-fold concentration increase in the IC compared to EC environment, which is enabled by co-transport of Na⁺ ions down their electrochemical gradient.⁷⁶ The co-transported sodium ions have been suggested to stabilize the OFo state for substrate EC binding (reviewed in ref 77) and to facilitate the hydration of the IC vestibule (contributed by the Na2 dislodging).^37,39,41,78 The present analysis provides a quantitative explanation for the role of Na⁺ co-transport in promoting the intracellular release of DA.

Potential of the Mean Force for Substrate Binding/ Release

We have further evaluated the energetics for DA binding/release using PMF-based calculations (Figure 4) with ABF method.⁵⁹ The calculation of substrate-binding affinity using this method requires to know the translocation pathways.⁶⁷ We took advantage of the DA release pathway identified in our recent study (Figure 4A).³⁷ We defined four consecutive windows, as described in Theoretical Methods, and calculated the PMF of DA release from hDAT IFo₁* (Figure 3B). The result is presented in Figure 4B. Remarkably, the binding affinity (−16.2 k_BT or −9.7 kcal/mol at T = 300 K) deduced from this calculation is in excellent agreement with that obtained by FEP (−9.4 kcal/mol).

However, we did not obtain a well-converged PMF for the EC DA binding because the binding of DA to the EC vestibule induced reconfiguration of the EC-exposed residues, i.e., inducing intermittent closure of the EC gate residues during the calculations. Such conformational variations significantly impeded the convergence of the output from the calculations.

Implication of D79 in the Reverse Transition from the IFS to OFS

In our previous study,³⁷ we performed a total of 3.6 μ s aMD simulations starting from OFo/OFo* and visualized the local change OFo* → OFc* (i.e., EC gate closing) shortly after substrate/ion binding, the global OFc* → IFo* transition through an intermediate state (referred to as occluded or IFc*), and subsequent release of DA and co-transported ions upon protonating D79. Here, we extended these simulations to sample the transition of hDAT from IFo back to OFS (and the intermediate on-pathway conformers) to complete the transport cycle. To this aim, we started from our in silico resolved IFo conformer³⁷ and performed four aMD runs of 200 ns each, two with protonated D79 and two in the absence of protonation. Among these, only one (with protonated D79) proceeded to OFS, with minimum hydration of EC and IC vestibule. Figure 5 illustrates the time evolution of DA and accompanying changes in interhelical packing during a complete cycle obtained by stitching together earlier and current simulations. As noted along the upper abscissa of Figure 5C, the transporter successively visits a series of conformers, which can be approximated by the reaction

Figure 5.

Successive events during DA transport cycle observed in aMD. (A) Initial OFo hDAT, with DA (purple spheres) located 15 Å away from site S1. (B) Trajectory of DA along the z axis (Figure 1) as it binds gradually moves toward the substrate-binding pocket (around 0 < z < −5 Å) and is released to the IC region after hundreds of nanoseconds. The y axis shows the position of its center of mass. (C) Time evolution of interhelical distances for EC-exposed TM1b–TM10 (blue) and IC-exposed TM1a–TM6b (green). These curves provide a measure of exposure to the respective EC and IC media. The trajectory is composed of the first 450 ns of run 3 (OFo → IFo*; see Table 1), followed by run 5 (200 ns; IFo* → IFo with protonated D79) and run 7 (180 ns; IFo → IFc → OFc).

$$\text{OF}o\to \text{OF}o\ast \to \text{OF}c\ast \to \text{IF}c\ast \to \text{IF}o\ast \to \text{IF}o\to \text{IF}c\to \text{OF}c(\to \text{OF}o)$$ (I)

Here, we indicated the binding/unbinding events and global changes (between OF and IF) by black arrows and local changes (between o and c) by gray arrows. If local changes are not considered, Reaction I may be reduced to

$$\text{OF}\to \text{OF}\ast \to \text{IF}\ast \to \text{IF}(\to \text{OF})$$ (II)

However, partially or fully closed/occluded conformers occupy an important subspace of the conformational space, in both DA-bound and -unbound forms of hDAT, and a six-state reaction, Reaction III, will be shown below to be a better approximation to the ensemble of states that are visited during the transport cycle.

The new simulations reveal a few important features. First, the driving potential for the reverse transition IF→OF in the apo state appears to be much weaker than the forward (OF*→IF*) transition in the bound form. The latter occurred within 200 ns in all four simulations,³⁷ whereas the IF → OF transition took place only in one run out of four. This suggests that binding of substrate and ions cooperatively triggers an allosteric reconfiguration toward IFS, whereas in the absence of substrate/ions, the transporter is less committed to move in one direction. Second, one Na⁺ from the IC solution was observed to bind near D79 in two runs in the absence of D79 protonation, indicating the strong driving potential to have a countercharge near D79. Third, D79 side-chain isomerization appeared to play a role in directing the IF → OF transition. Its rotation toward the EC vestibule reduced the hydration of the IC vestibule, which would then assist in the transition from IF to OF transition.

D79 has been observed to play an important role in coordinating the substrate bound to site S1.^{16,17,20,21,36,37} This aspartate is conserved among NSS family members, including DAT, and serotonine transporter. Mutations of D79 to alanine, glycine, or glutamate significantly reduced DA uptake, presumably due to the reduced ability to recognize DA or to efficiently modulate its transport after recognition.⁷⁹ Here, we noted that the empty IC vestibule may favor the binding of one positively charged ion if D79 is deprotonated. Interestingly, efflux of one K⁺ directs the IF → OF transition of another neurotransmitter transporter, glutamate transporter, to complete its transport cycle.⁸⁰ It remains to be determined whether the efflux of IC ions, such as K⁺, or the involvement of a proton, even if not required, may also help resume the hDAT cycle.

Conformational Energy Landscape of hDAT in DA-Loaded and DA-Free Forms

We explored the conformational landscape accessed by hDAT in DA-loaded and DA-free states (Figure 6) using the reweighting procedure for evaluating free energies from aMD trajectories, established in a recent study.⁷² For constructing the energy landscape for DA-loaded hDAT, two 400 ns aMD runs starting from OFo* hDAT were chosen, both of which independently sampled the OFo*→IFo* transition. For DA-free hDAT, four aMD simulations of total duration 800 ns were utilized, including conformers sampled in the presence/absence of Na⁺ and Cl⁻ ions. The distances TM1b–TM10 and TM1a–TM6b were adopted again as reaction coordinates for the extent of opening of the respective EC and IC vestibules.^36,37

Figure 6.

Conformational energy landscape of hDAT in substrate-bound and -unbound forms. The maps are generated for (A) DA-bound and (B) DA-free states of hDAT. The energy map for DA-bound hDAT (A) is generated using ~170 000 snapshots from two 400 ns aMD simulations (runs 3 and 4 in Table 1) starting from OFo*. That of DA-free hDAT results from an equal number of snapshots taken from a total of 800 ns simulations (runs 1, 2 and 7, 8) initiated from both ends, IFo and OFo. Regions colored blue are the most populated regions; brown regions are not practically visited. The scale bar represents the potential of mean force, in kcal/mol.

The low probability of OFo* in Figure 6A is consistent with the closure of the EC gate triggered shortly after substrate binding, with negligible (if any) reverse transition from OFc* to OFo*. Likewise, the states IFc and OFc merge into a broad energy minimum in Figure 6B. This leads to three substates in both bound and unbound forms: OFc*, occluded* (in lieu of IFc*), and IFo* in the DA-bound form (Figure 6A), and IFo, IFc/OFc, and OFo in DA-free hDAT (Figure 6B). These observations lead to the refined reaction of six states

$$\text{OF}o\to \text{OF}c\ast \to \text{occluded}\ast \to \text{IF}o\ast \to \text{IF}o\to \text{IF}c/\text{OF}c(\to \text{OF}o)$$ (III)

We also note that two transitions along this reaction, OFc* → occluded* and OFo → OFc/IFc, involve relatively low energy barriers, whereas the state IFc/OFc is a broad sink, where the transporter samples a broad range of fluctuations between OFc and IFc conformers. The barriers (1.5–3.5 kcal/mol) in those maps might be underestimated as discussed in earlier work;⁷² nevertheless, the map provides an accurate description of the distribution of states and accessible interconversion paths.

Finally, we note that hDAT is able to sample relatively closed conformers (IFc/OFc) even in the absence of DA, but the EC and IC gates therein were not as tightly closed as in the occluded DA-bound form. These conformers occasionally gave rise to open states of both EC and IC gates such that an intermittent formation of a water channel was detected (Figure 6B).

CONCLUSIONS

In the present study, we performed a detailed investigation of the energetics for DA translocation through hDAT. We employed two distinct approaches for evaluating DA-binding or -unbinding energetics under different conditions (Figures 2–4): FEP⁵⁸ and PMF calculations using the ABF method,⁵⁹ which confirmed the reproducibility of the results. DA binding/ unbinding generally involves local conformational changes, and its energetics may be estimated to a good approximation using these methods. Notably, both approaches proved to compute the substrate-binding free energy with high consistency, if substrate translocation path is well defined. FEP calculations yielded a binding free-energy change of ΔG_bind = −7.8 ± 1.5 kcal/mol in agreement with the value of −7.4 kcal/mol²⁰ derived from experiments.⁷⁴ However, we note that both free-energy calculation methods have limitations. Maintaining equilibrium conformation during calculations is essential.⁶⁷ FEP yields more accurate results for buried substrates, and PMF-based method is more suitable for pulling a charged substrate along an open pathway.⁷⁵ We did not obtain convergent outputs for DA binding to OFo hDAT, as the latter conformation exhibited significant variations upon DA binding.

We investigated the global OF ⇔ IF transition with dual-boost aMD simulations,^42,43 which have been shown to successfully sample long-time events beyond the scope of cMD.⁷³ Strikingly, without a priori definition of the targeted transitions, aMD trajectories sample not only local rearrangements and side-chain rotations efficiently but also the global transitions of hDAT.³⁷ Yet, the reweighting of the energies and/or rescaling of computing time to yield the effective time scales and energetics remains challenging (Figure 6). Simulations yield insights into the time-resolved mechanisms of DA translocation and accompanying global changes during a complete transport cycle (Figure 5) and provide good estimates of the relative populations of different conformational states (Figure 6) but not the absolute rates of transitions between those states.

Our MD simulations show that hDAT is able to fluctuate between OFS and IFS, regardless of the bound state of substrate (Figure 6); binding of DA preferentially facilitates transition, leading to the IC release of DA. This is consistent with the intrinsic dynamics of transporters encoded by their 3D architecture (or topology of inter-residue contacts). In this case, the architecture favors these global transitions, as well as the local transitions between open and closed forms of the gates, irrespective of substrate/ion binding state.⁸¹

Notably, in the substrate-bound state, both the EC and IC vestibules are fully occluded, thus ensuring complete sealing of the cargo, whereas in the apo state, the structure is less tightly packed (Figure 6), similar to the observations reported for LeuT.²⁹ Furthermore, a continuous water channel was intermittently formed in DA-free hDAT (see Figure 6B). Spontaneous formation of water-conducting (channel-like) states along the transport cycle has been reported for other transporters.⁸² In a recent study, such a water-conducting channel was shown to be involved in chloride channeling⁶⁸ for mammalian and archaeal glutamate transporters. It would be interesting to investigate whether the channel-like states observed in our simulations are associated with multiple DAT-mediated ionic fluxes.^2,3 Finally, our study showed the significant role of co-transported Na⁺ ions (Table 2). It also reveals that D79 protonation (or coordination with a cation), or at a minimum its reorientation away from the IC medium, is a major determinant of the release of DA and progress of hDAT toward resuming a new transport cycle.

DA transport by hDAT is much faster than Leu transport by LeuT. The latter takes ~60 s,⁵⁴ which is 60 times slower than the turnover time of ~1 DA/s per hDAT.⁵⁰ Sodium and substrate were found to shift equilibrium toward the OF state in LeuT⁵⁴ but toward the IF state in Glt_Ph.⁵⁵ Our simulations, performed under physiological NaCl levels (0.15 M), showed that binding of DA and Na⁺ triggered cooperative changes toward the IFS (Figure 6), consistent with the higher intrinsic disposition of hDAT to translocate DA, compared to LeuT. Differences in the response to substrate binding between transporters sharing the same (LeuT) fold may be associated with specific interactions and translocation events,⁵⁷ presumably endowed by the conformational adaptability of the LeuT fold.