Kinetics and mechanical stability of the fibril state control fibril formation time of polypeptide chains: A computational study

Abstract

Fibril formation resulting from protein misfolding and aggregation is a hallmark of several neurodegenerative diseases such as Alzheimer’s and Parkinson’s diseases. Despite much progress in the understanding of the protein aggregation process, the factors governing fibril formation rates and fibril stability have not been fully understood. Using lattice models, we have shown that the fibril formation time is controlled by the kinetic stability of the fibril state but not by its energy. Having performed all-atom explicit solvent molecular dynamics simulations with the GROMOS43a1 force field for full-length amyloid beta peptides Aβ₄₀ and Aβ₄₂ and truncated peptides, we demonstrated that kinetic stability can be accessed via mechanical stability in such a way that the higher the mechanical stability or the kinetic stability, the faster the fibril formation. This result opens up a new way for predicting fibril formation rates based on mechanical stability that may be easily estimated by steered molecular dynamics.

INTRODUCTION

Neurodegenerative diseases are believed to be associated with the aggregation of amyloid proteins.^1,2 For example, according to the amyloid cascade hypothesis, Alzheimer’s disease (AD) is caused by the fibrillation of amyloid beta peptides (Aβ) as amyloid plaques.³ Aβ peptides, which are cleaved from the amyloid precursor protein (APP) by β- and γ-secretases, have 36-43 residues, but Aβ40 (40 amino acids) and Aβ42 (42 amino acids) are the most abundant. Aβ42 is more neurotoxic than Aβ40 and is the main component of amyloid plaques in the human brain because Aβ42 self-aggregates faster.⁴ Because understanding the key factors that govern protein aggregation is important for designing efficient drugs for many diseases, this problem has attracted a lot of attention from researchers over the last few decades.

In addition to the external factors such as temperature, pH, salt concentration, crowders, etc., the intrinsic factors, which are ultimately sequence-dependent, influence not only fibril formation rates but also pathways. Accumulated experimental and theoretical evidence has demonstrated that hydrophobicity, net charge, and secondary structure are important driving forces in protein self-assembly.^5–7 The aggregation rate of polypeptide chains was shown to exponentially depend on the population of the so-called fibril-prone state N^* in the monomeric state.⁶ An accurate estimation of hydrophobicity,⁷ beta content,^8,9 and population of N^*10 using all-atom molecular dynamics (MD) simulations is time-consuming and thus difficult to use. The criterion based on net charge is simple, but it fails to distinguish aggregation propensities of the sequences that have the same net charge. Therefore, a more efficient criterion is necessary for predicting protein self-aggregation propensity.

In this paper, we have shown using a lattice model¹¹ that the fibril formation rate depends on the kinetics stability of the fibril state. Because the kinetics stability may be accessed through the mechanical stability of the fibril state, we suggest using this quantity as a measure for propensity to fibrillization that the more kinetically stable is the fibril state, the faster is the fibril formation. On the other hand, mechanical stability may be probed by the steered molecular dynamics (SMD) simulation, which is computationally much less demanding than conventional molecular dynamics (MD), and our novel criterion is more efficient compared with the previous ones. The new proposal is fully supported by our results on fibril formation rates and mechanical stability, obtained for two short peptides KLVFF and FVFLM, using all-atom MD simulation in explicit water. For full-length Aβ peptides, we have shown that the Aβ₄₂ fibril is more stable than the Aβ₄₀ fibril, and this is also consistent with the experimental fact that Aβ₄₂ aggregates faster than Aβ₄₀.

METHODS

Lattice models

The lattice model¹¹ based on Monte Carlo (MC) algorithm was designed with the aim of studying aggregation of simple polypeptide chains. The model focuses on enhancing the sampling of simulation process considering a set of toy chains that are composed of M-connected beads per monomer. We conduct our simulation with N identical 8-bead chains characterized by connected beads +HHPPHH− as primary sequence structure, where H and P describe hydrophobic and hydrophilic residues, while + and − represent charge beads of opposite sign. Once the distance of two beads equals the lattice site a, they form one contact, and summation of all intra- and inter-chain contacts determine the total energy of the simulation system. The energy of N chains is

$$\begin{array}{ccc}\hfill E& =\hfill & \sum _{l=1}^N\sum _{i<j}^M{e}_{sl\left(i\right)sl\left(j\right)}\delta \left(r_{ij}-a\right)\hfill \\ \hfill & \hfill & +\sum _{m<l}^N\sum _{i,j}^M{e}_{sl\left(i\right)sm\left(j\right)}\delta \left(r_{ij}-a\right),\hfill \end{array}$$ (1)

where r_ij is the distance between residues i and j, a is a lattice spacing, sm(i) indicates the type of residue i from m-th peptide, and δ(0) = 1 and zero, otherwise. The first and second terms in Eq. (1) represent intrapeptide and interpeptide interactions, respectively. The contact energies are measured in the unit of the hydrogen bond energy ϵ_H. The interaction energies between H beads are denoted as e_HH. The propensity of polar (including charged) residues to be “solvated” is mimicked using e_Pα = −0.2, where α = P, +, or −. “Salt-bridge” formation between oppositely charged beads is accounted for by a favorable contact energy e₊₋. All other contact interactions are repulsive. The generic value for repulsion e_αβ is 0.2. For a pair of like-charged beads, the repulsion is stronger, i.e., e₊₊ = e₋₋ = −e₊₋/2. We varied e_HH and e₊₋ to obtain different systems. Overall, our toy force field roughly mimics the interactions between amino acids.

Each bead of a polypeptide chain occupies vertex of a three-dimensional hypercube, and to minimize the finite size effect, periodic boundary conditions have been implemented. Random movements of the monomers are enabled by MC moves, including local and global moves. The local moves involve corner flip, crankshaft, and tail rotation, while the global moves represent either translation of a chain by a in a random direction or rotation by 90° around one of randomly chosen coordinate axes. The acceptance rates of global and local moves are 0.2 and 0.8, respectively (see Ref. 11 for more details). Simulation time is counted in units of Monte Carlo steps (MCS) determined by the combination of local and global moves. The value of the concentration of chains in each system was set around 57 μM (the cubic sizes are 113, 135, and 151a for N = 6, 10, and 14 monomers with a, lattice space, set equal to 1). This concentration is compatible with that from real experiments.

All-atom molecular dynamics simulations

We used the GROMOS43a1 force field¹² to describe the peptides and the simple point charge (SPC)¹³ water model for the solvent for studying pentapeptide systems. To avoid potential bias due to the use of a particular force field and water model, we choose Optimized Potential for Liquid Simulations (OPLS) force field¹⁴ to describe interactions between atoms in Aβ₄₀ and Aβ₄₂ fibril structures and TIP4P to describe a solvent.¹⁵ All-atom MD simulations were carried out using the Gromacs program suite¹⁶ that was previously employed successfully by our group for studying protein folding, unfolding, aggregation, and protein-peptide interactions.^17–19 We use periodic boundary conditions and calculate the electrostatic interactions by the particle mesh Ewald method.²⁰ The non-bonded interaction pair-lists are updated every 10 fs, using a cutoff of 1.5 nm. All bond lengths are constrained with the LINCS²¹ linear constraint solver to integrate the equations of motion with a time step of 2 fs.

To avoid improper structures, the whole system was minimized with the steepest-descent method before being equilibrated at 300 K with two successive molecular dynamics runs of 1 ns each: the first one at constant volume and the second one at constant pressure (1 atm). Initial velocities of the atoms were generated from Maxwell distribution at 300 K. The temperature was kept close to 300 K using the v-rescale thermostat. Data analysis was done using the corresponding Gromacs programs, and snapshots of all peptides were created with VMD software.²²

Steered molecular dynamics simulation

The system we considered for oligomer formed by pentapeptides was a trimer [Fig. 3(c)]. Initial structures of the trimer in our simulation were obtained by molecular dynamics simulation with the GROMOS43a1 force field and explicit water in our previous work.²³ Initial structures for fibril structures of Aβ₄₀ and Aβ₄₂ amyloid fibrils were taken from the Protein Data Bank (PDB) under identifiers 2M4J²⁴ and 2NAO.²⁵ Note that in order to avoid potential bias due to the use of a particular force field and water model, we choose OPLS force field¹⁴ to describe interactions between atoms in fibril structures and TIP4P to describe a solvent¹⁵ (the GROMOS force field¹² and SPC water model¹³ were implemented in the modeling of short KLVFF and FVFLM peptides).

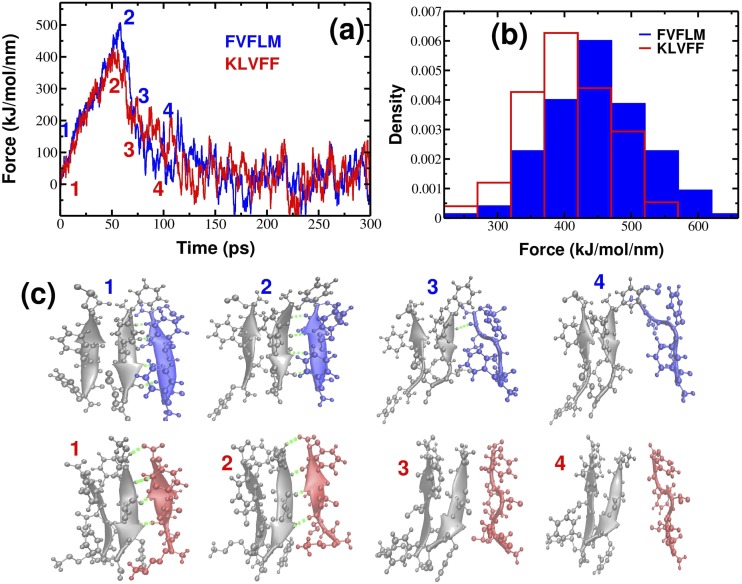
FIG. 3.

(a) Typical force-time profiles for FVFLM (blue) and KLVFF (red) peptides at v = 0.01 nm/ps. (b) Histograms of unbinding/rupture forces for FVFLM and KLVFF peptides. The histograms clearly show that the force peak moves toward higher values for FVFLM compared with KLVFF. (c) Details of the mechanical unfolding pathway of FVFLM are shown in blue (upper row) and of KLVFF are shown in red (bottom row). Hydrogen bonds between the pulled peptide and the template are indicated as dashed green lines.

We applied an external force to one end of a spring that is attached to the center of mass (COM) of one of the monomers and pulled it along the vector drawn between the COM of the pulled peptide and the COM of the neighboring peptide. In all the SMD simulations, the spring constant was chosen as k = 1000 kJ/(mol/nm²) ≈ 1700 pN/nm, which corresponds to the upper limit of k of the cantilever used in Atomic Force Microscopy (AFM) experiments.

The movement of a pulled peptide under an external force caused its dissociation from the template, and the total force needed to bring about this dissociation was measured by $F=k\left(vt-x\right)$, where x denotes the displacement of the pulled peptide from its initial position. The resulting force was computed for each time step to generate a force-extension profile that recorded a single peak showing the most mechanically resisting conformation in our system. Once the critical interactions were disrupted, the pulled peptide was found to no longer resist the applied force. Overall, the simulation procedure could be described as one similar to that followed during the AFM experiments, except that the pulling speeds in our SMD simulations were fixed at several orders of magnitude higher than those used in AFM experiments.^26–29

We conducted SMD simulations at room temperature (T = 300 K) at pulling speeds $v$ = 0.001 nm/ps and $v$ = 0.01 nm/ps. Because the most probable rupture force might vary considerably from trajectory to trajectory, we generated 55 and 200 trajectories for each pentapeptide system at $v$ = 0.001 nm/ps and $v$ = 0.01 nm/ps, respectively. For Aβ₄₀ and Aβ₄₂ systems, we generated 55 and 200 trajectories at $v$ = 0.001 nm/ps and $v$ = 0.01 nm/ps, respectively. Extracted peak forces were subsequently used to construct a histogram of the most probable rupture forces. Sturges’ formula was used for the optimal bin size (k = log₂ N + 1, where N is the number of trajectories).

RESULTS AND DISCUSSION

Fibril formation time does not correlate with energy of the fibril state

Because the computation of the fibril formation time is too time-consuming not only in all-atom models but also in off-lattice coarse-grained models, we will use the toy lattice model,¹¹ the details of which are available in the Methods section. Although this model is simple, it has been successfully applied to reveal the hydrophobicity, net charge, and population of the N^* state as crucial factors for the aggregation propensity of polypeptide chains.⁶ The lattice model is also reliable for describing aggregation in a crowded environment³⁰ and predicting the size of the critical nucleus of fibril formation.³¹

A polypeptide chain in the lattice model has 8 beads +HHPPHH−, where H and P describe hydrophobic and hydrophilic residues, while + and − represent charge beads of opposite sign. To obtain different systems, we varied the contact energies between H beads e_HH and “salt-bridge” formation energy between oppositely charged e₊₋, keeping e₊₊ = e₋₋ = −e₊₋/2. We fixed e_Pα = −0.2, where α = P, +, or − and all other repulsive contact interactions equal to 0.2 (see the supplementary material). The morphology of the fibril state depends not only on energy interactions but also on the number of chains.⁶ Here, we choose contact energies in such a way that the fibril structures of all studied systems had one layer with antiparallel U-shape chains confined to the vertices of the three-dimensional hypercube (Fig. 2). The fibril structures had the lowest energy denoted as E_fib.

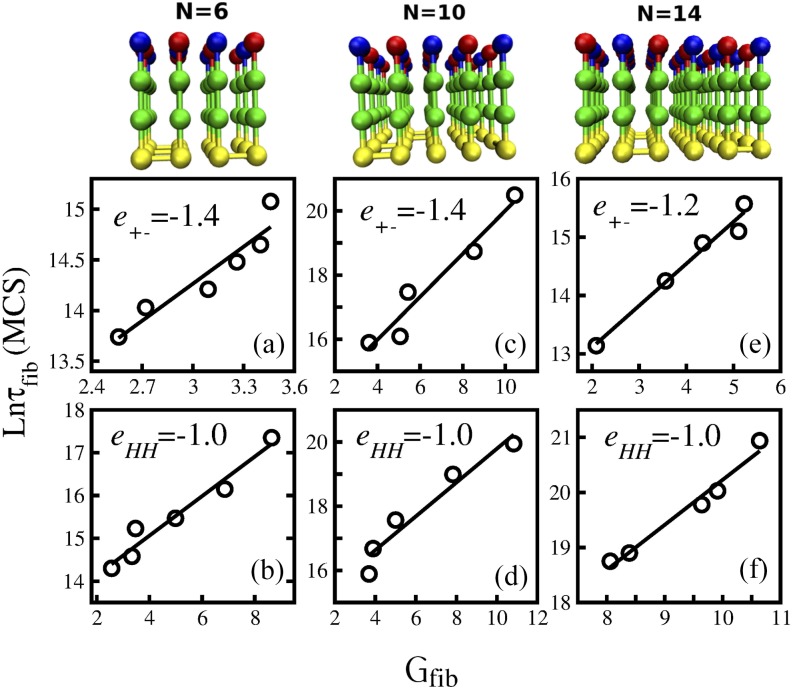
FIG. 2.

Correlation between the formation of polypeptide chains and kinetics stability of the fibril state G_fib. The first row represents fibril structures for N = 6, 10, and 14. The second row shows the dependence of ln τ_fib on G_fib in the case when the electrostatic interaction e₊₋ is kept fixed but the hydrophobic interaction e_HH is varied. The third row is the same as the second row but e_HH is fixed, while e₊₋ is varied. (a) N = 6, e₊₋ = −1.4, and the linear fit y = 1.21x + 10.61. (b) N = 6, e_HH = −1.0, and y = 0.46x + 13.21. (c) N = 10, e₊₋ = −1.4, and y = 0.67x + 13.3. (d) N = 10, e_HH = −1.0, and y = 0.52 + 14.52. (e) N = 14, e₊₋ = −1.2, and y = 0.71x + 11.6. (f) N = 14, e_HH = −1.0, and y = 0.81x + 12.0.

The fibril formation time, τ_fib, is the first passage time for acquisition of the fibril state starting from random configurations. For comparison between different systems, τ_fib is computed at T_min where fibril formation is fastest. For the number of chains of N = 6 or 10, fibril formation becomes slower as the energy of the fibril state E_fib increases (Fig. S1 of the supplementary material). This is also valid for N = 14 if we keep the hydrophobic interaction constant (e_HH = −1.4) but vary electrostatic interactions (Fig. S1F of the supplementary material). If we fix e₊₋ = −1.2 and vary e_HH, the situation will greatly change (Fig. S1E of the supplementary material) in such a way that τ_fib grows as hydrophobic interaction gets stronger (the absolute value of e_HH becomes larger). This result contradicts the common belief that hydrophobic interactions should promote aggregation. However, this controversy can be resolved because at strong inter-chain interactions kinetic traps are deep and thus difficult to escape from resulting in slow fibril growth. In other words, to have fast fibril formation, the fibril state should be not only stable but also kinetically accessible. Thus, in general, τ_fib does not correlate with the energy of the fibril state E_fib.

Fibril formation time does not correlate with the free energy

The free energy is defined in the following standard way:

$$F=-k_{B}T\ln \left(Z\right),$$ (2)

where Z is the participation function computed at equilibrium. With this definition, F characterizes the thermodynamic stability of the system but not the fibril state itself. Similar to the case of energy of the fibril structure, τ_fib correlates with the free energy for N = 6 and 10 but not for N = 14 (Fig. S2 of the supplementary material). This is because the fibril formation is a barrier crossing event and, in general, its rate does not depend on the free energy but on the barrier separating the fibril state from the transition state, as known from the simple two-state scenario. Thus, as expected, the free energy cannot be used as an indicator for fibril formation rates.

Fibril formation time correlates with kinetic stability of the fibril state

To explore the kinetics of fibril formation, we studied the free energy G as a function of the multi-dimentional reaction coordinate V:

$$G\left(V\right)=-k_{B}T\ln P\left(V\right),$$ (3)

where P(V) is the probability distribution obtained from a histogram of the simulated data. k_B is Boltzmann’s constant (set equal to 1 in the lattice model) and T represents simulation temperature. In difference from F, defined in Eq. (2), G(V) was computed using not only data collected at equilibrium but also out of equilibrium, implying that G(V) can be used to characterize the kinetic stability.

For the fibril state, Eq. (3) is rewritten as follows:

$$G_{\mathrm{fib}}=-k_{B}T\ln P_{\mathrm{fib}}.$$ (4)

Here P_fib is the probability of observing the fibril state during simulation, P_fib = n_fib/n_total, where n_fib counts how many times the fibril structure occurred during simulation, whereas n_fib is the total number of simulation steps. Thus, by definition [Eq. (4)], the correlation of fibril formation time with the kinetic stability is obvious as for a given amount of simulation time (MCs in MC dynamics), the larger number of times the N^* state occurs (or higher kinetics stability), the shorter the fibril formation time.

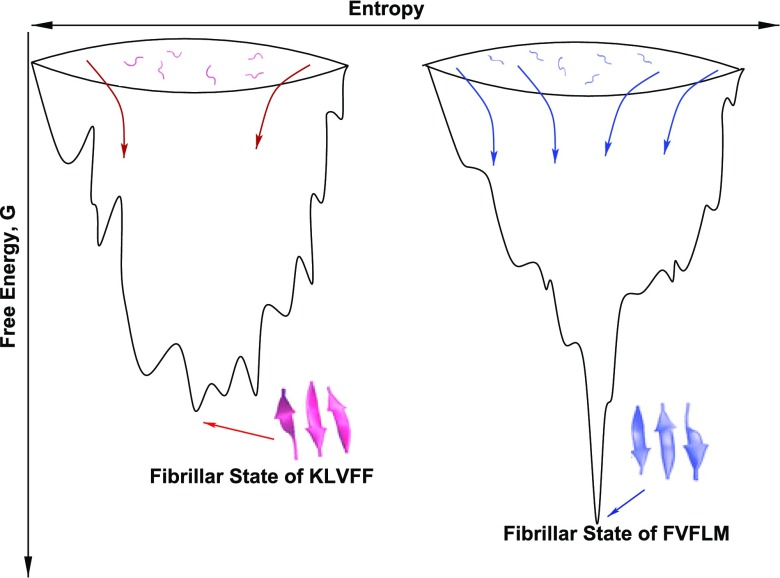
To make this point more transparent, we present schematic free energy landscapes of two sequences with different fibril formation rates (Fig. 1). The sequence in the right has more routes to the fibril state (higher P_fib) resulting in faster aggregation. As follows from Eq. (4), this sequence has lower G_fib or higher kinetic stability.

FIG. 1.

Schematic free energy landscapes for two sequences with different G_fib. The fibrillar state of the sequencein the left is kinetically less stable having the shallower minimum than the sequence in the right. Arrows refer to pathways to the fibril state. Peptides KLVFF and FVFLM are detailed in the next.

To demonstrate the correlation between τ_fib and G_fib, we have carried out lattice simulations. Here, the number of Monte Carlo steps (MCs) was set to 10⁸, 1.5 × 10⁹, and 2 × 10⁹ in each trajectory for the system with N = 6, 10, and 14 monomers, respectively. To obtain reliable results, we applied 50-100 MC trajectories for each system. As evident from Fig. 2, for all the studied systems including N = 14, τ_fib exponentially depends on G_fib, i.e.,

$${\tau }_{fib}\sim \exp \left(\alpha *G_{\mathrm{fib}}\right).$$ (5)

The α constant is not universal but rather depends on the number of chains and interaction energies. For N = 6, we have α = 1.21 and 0.46 for fixed e₊₋ = −1.4 and e_HH = −1, respectively. For N = 10, the corresponding values are α = 0.67 and 0.52. For N = 14, we obtained α = 0.71 and 0.81 for fixed e₊₋ = −1.2 and e_HH = −1, respectively. These results confirmed the fact that the higher the kinetic stability of the fibril state, the faster the fibril formation.

Correlation between kinetic stability and fibril formation time

Because the estimation of kinetic stability G_fib is time-consuming, in particular, in simulation with all-atom models, we propose to probe G_fib or the propensity of polypeptide chains to fibril formation through mechanical stability of the fibril state in such a way that the faster the fibril formation, the higher the mechanical stability of the fibril state. Rationale for our assumption is based on the free energy landscapes shown in Fig. 1 that the higher the kinetic stability, which corresponds to the deeper minimum of G_fib and faster aggregation, the higher the mechanical stability. In other words, the more stable is the fibril state, the higher is the external force needed to degradate it as happens in the mechanical unfolding of protein.²⁷

The mechanical stability of the fibril state can be characterized by the rupture force to pull out a chain from the fibril structure. The rupture force can be obtained in the AFM experiment as well as in simulation when the external force is applied. Since pulling simulation with a constant velocity in lattice models is ambiguous, we use off-lattice all-atom models.

Assessing the mechanical stability of FVFLM and KLVFF trimers using SMD and correlation of rupture force with oligomerization time

Recent experiments have demonstrated that short KLVFF-containing peptides form amyloid fibrils similar to those formed by their full-length parent proteins.^32,33 The KLVFF peptide is a fragment of the 42 amino acid form of β-amyloid protein linked to Alzheimer’s disease, while FVFLM peptide derived from SERPINA1 protein is suspected to be involved in the pathogenesis of preeclampsia (PE).^23,34 The fibril-like structures of FVFLM and KLVFF trimers were obtained in a previous work²³ and are shown in Fig. 3. To probe their stability, we used SMD with a constant pulling speed and performed all-atom MD simulation (see the supplementary material for more details). We applied an external force to the center of mass (COM) of one of the monomers and pulled it along the vector drawn between the COM of the pulled peptide and the COM of the neighboring peptide.

Figure 3(a) shows the typical force-extension curves for a pulling speed of $v$ = 0.01 nm/ps for KLVFF and FVFLM trimers. In all MD runs, one distinct peak was consistently observed, which corresponded to the detachment of one monomer from the core of the preformed template. The nature of this peak furnished some insights about the network of backbone hydrogen bonds between monomers. Typical conformations found before and after the occurrence of this peak are shown as snapshots in Fig. 3(c). The separating force was found to drop drastically, though expectedly, once the backbone hydrogen bonds between the monomer and the rest of the core were ruptured; that was because the monomer could no longer resist the applied force after detachment from the core.

Evaluation of 150 unbinding events revealed the distribution of rupture forces shown in Fig. 3(b). The distributions appeared to be symmetrical around the value of the most probable rupture force, F_max. As is evident from the plot, the position of the peak corresponding to the most probable rupture force moves toward higher values for the 3FVFLM compared with the 3KLVFF system. The difference between F_max for FVFLM and KLVFF of ∼50 kJ/(mol/nm) (or ∼83 pN) indicates that 3FVFLM is more mechanically stable than 3KLVFF.

Interesting is a comparison of oligomer stability with aggregation kinetics of pentapeptides. Using all-atom MD simulation, it is found that the oligomer formation of FVFLM is much faster than of Aβ₁₆₋₂₀ (KLVFF) and Aβ₁₆₋₂₂ (KLVFFAE) sequences.²³ The time required to form the FVFLM dimer and trimer is ${\tau }_{dimer}^{FVFLM}\approx 17$ ns and ${\tau }_{trimer}^{FVFLM}\approx 46$ ns, respectively, which is shorter than that of KLVFF, ${\tau }_{dimer}^{KLVFF}\approx 23$ ns and ${\tau }_{trimer}^{KLVFF}\approx 100$ ns. Thus, the faster aggregation kinetics result in higher mechanical stability, implying that mechanical stability can be used to accurately predict aggregation rates. Though we obtained this trend by observing the aggregation profiles for KLVFF and FVFLM oligomers, we can expect it to hold for other systems (see below) because the mechanical stability and kinetics stability of the fibril state are equivalent.

Mechanical stability of Aβ₄₀ and Aβ₄₂ fibrils

The next question we ask is whether a relationship between a fibril’s mechanical stability and aggregation kinetics of its monomers observed for short KLVFF and FVFLM peptides is also valid for larger structures. To answer this question, we studied mechanical stability of two recently found Aβ₄₀ and Aβ₄₂ fibrils using the SMD method. It is well established that Aβ₄₂ aggregates much more rapidly than Aβ₄₀^35,36 due to the difference in the last two hydrophobic residues. Such a small difference in sequence leads not only to very different τ_fib but also to different pathways toward the fibril state. Recent fibril structures of Aβ₄₀ and Aβ₄₂ are surprisingly different^24,25 as evident from Figs. 4(a) and 4(b).

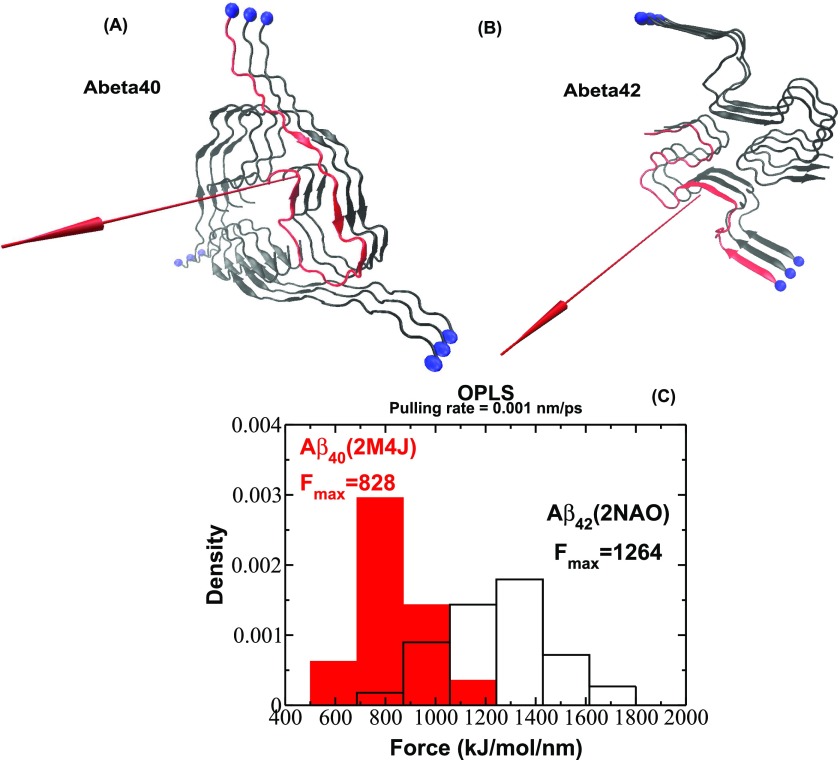
FIG. 4.

Fibril structure of Aβ₄₀ (a) and Aβ₄₂ (b) fibrils as deposited in PDB under identifiers 2M4J²⁴ and 2NAO.²⁵ The red arrow represents the direction of pulling. (c) Histograms of unbinding forces obtained from force-extension profiles at a pulling rate of $v$ = 0.001 nm/ps for Aβ₄₀ and Aβ₄₂ fibrils. The histograms clearly show that the force peak moves toward higher values for Aβ₄₂ compared with Aβ₄₀.

Evaluation of unbinding events for Aβ₄₀ and Aβ₄₂ at a pulling speed of $v$ = 0.001 nm/ps revealed the distributions of rupture forces shown in Fig. 4(c). The position of the peak corresponding to the most probable rupture force moves toward higher values for Aβ₄₂ compared with Aβ₄₀. Because the difference in the most probable rupture forces between Aβ₄₂ and Aβ₄₀ remains also noticeable at higher pulling rates (Figs. S3 and S4 of the supplementary material), we conclude that it is robust against different pulling rates and expect it to hold for slower pulling rates. We want to stress that an investigation of mechanical unfolding at lower pulling rates by explicit solvent all-atom MD simulations is still a challenge due to the enormous computation time required. However, the knowledge gathered from a two-decade-long spectrum of protein unfolding studies provides evidence to support the claim that the difference in mechanical stability observed in a high-force regime will remain robust in a low-force regime.

Thus, we obtained a very interesting result that, as with pentapeptides, the mechanical stability of β-amyloid fibrils correlates with the aggregation rate in such a way that Aβ₄₂ fibrils are more stable and are formed faster than the Aβ₄₀ fibrils. Taken together, the overall picture of relationships between aggregation rates and mechanical stability remains the same as for short pentapeptides. For lattice models, we have shown that τ_fib does not correlate with the energy of the fibril state. We wanted to check this conclusion for full-length Aβ fibrils. To address this question, we studied the contact energies of two recently solved Aβ₄₀²⁴ and Aβ₄₂²⁵ fibril structures using all-atom MD simulations in an explicit solvent with four different force fields (OPLS,¹⁴ CHARMM,³⁷ AMBER99SB,³⁸ and GROMOS43a1¹²) and two water models (SPC¹³ and TIP4P¹⁵).

Each system was subjected to energy minimization and constant number, volume, and temperature (NVT) and constant number, pressure, and temperature (NPT) equilibration followed by a short production run.³⁹ All-atom interaction energies calculated as a sum of Coulomb and Lennard-Jones interaction energies in the fibril structure and averaged over all saved configurations of a production run are summarized in Table S1 of the supplementary material. Results from four all-atom force fields show that the contact energy per chain of fibril conformation of the Aβ₄₀ and Aβ₄₂ fibrils is nearly the same, implying that, in agreement with the results based on lattice models, the energy of the fibril state does not control the fibril formation rate.

Robustness of results against potential force field bias and different Aβ₄₂ fibril structures

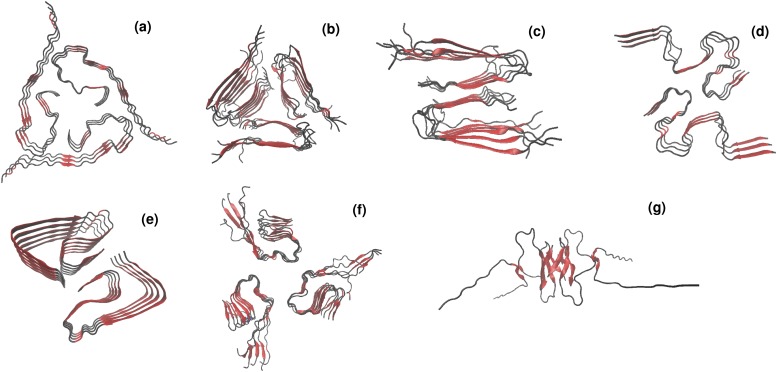
So far we have carried SMD simulations for the fibril structures of Aβ₄₀ and Aβ₄₂ [Figs. 4(a) and 4(b)]. However, it should be noted that a significant challenge for drug design is to understand which fibril structures and pathways are more directly related to diseases. While experimentally resolved structures of Aβ₁₋₄₂ fibrils relate to the S-shaped motif,²⁵ the previously found structures of Aβ₁₋₄₀ and Aβ₁₁₋₄₀ fibrils suggested U-shaped motif of the fibril conformation.^24,40 Interestingly, the most recently resolved structure of Aβ₁₋₄₂ fibrils by cryo–electron microscopy demonstrates the “L-S”-shaped polymorph that differs significantly from the previously reported models (shown in Fig. 5). Moreover, using MD simulations, the new variants of plausible models of β-amyloids fibrils have been proposed recently.^41,42 The problem of structural polymorphism of β-amyloid fibrils becomes even more challenging as recent studies have claimed that a mixture of different amyloid polymorphs can coexist and possibly interconvert.^43,44

FIG. 5.

Polymorphism in β-amyloid fibrils. Experimentally resolved U-shaped Aβ₁₋₄₀ (a), Aβ₉₋₄₀ [(b) and (c)] fibril structures as well as the new S-shaped (d) and LS-shaped (e) fibril structures of Aβ₁₋₄₂ deposited in PDB under codes 2M4J,²⁴ 2LMP,⁴⁵ 2LMO,⁴⁵ 2NAO,²⁵ and 5OQV,⁴⁶ respectively. Representative structures of the proposed out-of-register model (f) and ring-like model (g) of Aβ₁₋₄₂ fibrils reported in Refs. 41 and 42.

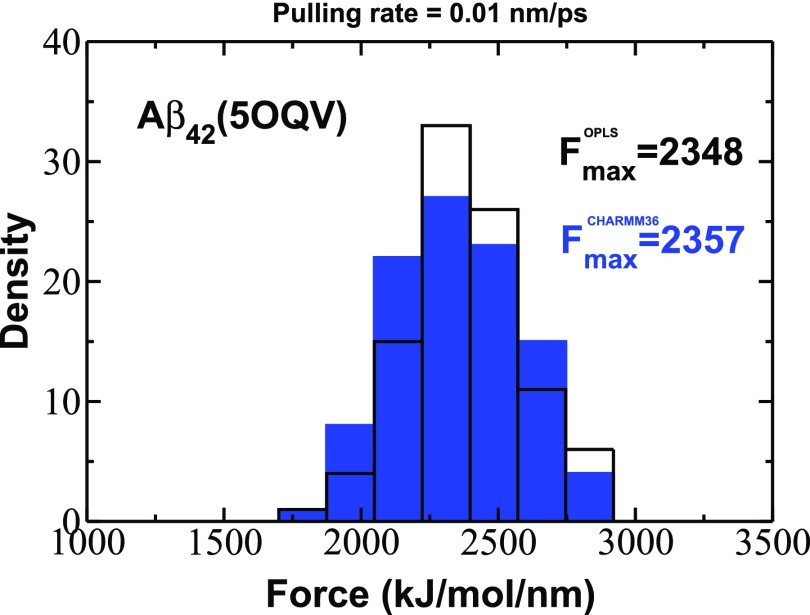
In order to check the robustness of our results against different Aβ₄₂ fibril structures and different force fields, we performed the additional SMD simulations for the new structure of Aβ₁₋₄₂ (5OQV) using OPLS and CHARMM36⁴⁷ force fields. Note that the CHARMM36 force field is one of the best force fields for describing intrinsically disordered proteins including Aβ peptides. We generated 100 trajectories for each force field at $v$ = 0.01 nm/ps. Figure 6 shows the distributions of rupture forces that are nearly the same, although they were obtained by applying different force fields. We obtained the value of F_max = 2348 and 2357 kJ/(mol/nm) for OPLS and CHARMM36 force fields, respectively. Those values are higher than F_max = 2060 kJ/(mol/nm) obtained for Aβ₁₋₄₀ (2M4J) using OPLS force field (Fig. S4 of the supplementary material). Thus, we conclude that the difference in mechanical stabilities of Aβ₁₋₄₂ and Aβ₁₋₄₀ is robust against not only different force fields but also different fibril structures, and we expect that this effect is universal and holds for other β-amyloid fibril structures.

FIG. 6.

Histograms of rupture forces obtained from force-extension profiles at the pulling rate $v$ = 0.01 nm/ps for Aβ₄₂ fibrils (PDB code 5OQV) using OPLS and CHARMM36 force fields.

CONCLUSIONS

It is natural that the kinetic stability of the fibril state controls the fibril formation rate, and this fact has been further ascertained by the results obtained in lattice models. Because the kinetic stability can be accessed through mechanical stability, we have come up for the first time with a novel criterion that the higher the mechanical stability, the faster the fibril formation of proteins. This factor is very valuable because the estimation of the fibril formation time of biomolecules is practically impossible using all-atom models. Using the relationship between τ_fib and mechanical stability, we can easily predict the aggregation propensity based just on fibril structures that are available in PDB. Our finding may also be utilized as a predictive tool for revealing neurotoxicity that is very likely associated with the rate of amyloid fibril/oligomer formation.

Finally, it should be noted that the relationship between the foldability and the stability of the native state of the protein has been explored previously.^48–50 In particular, using lattice models, it has been found that⁴⁹ the folding rate of two-state proteins grows exponentially with the free energy of stability of the native basin with respect to denatured states. In some sense, this finding is similar to our result on the relationship between the fibril formation time and the mechanical stability.

SUPPLEMENTARY MATERIAL

See supplementary material for the correlation of the natural logarithm of the fibril formation time ln τ_fib of polypeptide chains and the lowest energy of the fibril state E_fib per one chain; correlation of ln τ_fib of polypeptide chains and free energy of the system F per one chain; force-time profiles for Aβ₄₀ and Aβ₄₂ at $v$ = 0.01 nm/ps; histograms of unbinding forces obtained from force-extension profiles at the pulling rate, $v$ = 0.01 nm/ps, for Aβ₄₀ and Aβ₄₂ fibrils; and the contact energy calculated as a sum of Coulomb and Lennard-Jones interaction energies in fibril structures using different force fields.