Survival of the most transferable at the top of Jacob’s ladder: Defining and testing the ωB97M(2) double hybrid density functional

Abstract

A meta-generalized gradient approximation, range-separated double hybrid (DH) density functional with VV10 non-local correlation is presented. The final 14-parameter functional form is determined by screening trillions of candidate fits through a combination of best subset selection, forward stepwise selection, and random sample consensus (RANSAC) outlier detection. The MGCDB84 database of 4986 data points is employed in this work, containing a training set of 870 data points, a validation set of 2964 data points, and a test set of 1152 data points. Following an xDH approach, orbitals from the ωB97M-V density functional are used to compute the second-order perturbation theory correction. The resulting functional, ωB97M(2), is benchmarked against a variety of leading double hybrid density functionals, including B2PLYP-D3(BJ), B2GPPLYP-D3(BJ), ωB97X-2(TQZ), XYG3, PTPSS-D3(0), XYGJ-OS, DSD-PBEP86-D3(BJ), and DSD-PBEPBE-D3(BJ). Encouragingly, the overall performance of ωB97M(2) on nearly 5000 data points clearly surpasses that of all of the tested density functionals. As a Rung 5 density functional, ωB97M(2) completes our family of combinatorially optimized functionals, complementing B97M-V on Rung 3, and ωB97X-V and ωB97M-V on Rung 4. The results suggest that ωB97M(2) has the potential to serve as a powerful predictive tool for accurate and efficient electronic structure calculations of main-group chemistry.

I. INTRODUCTION

Kohn-Sham density functional theory (DFT) is nowadays the predominant form of electronic structure theory^1–3 because relatively simple and computationally efficient functionals, while approximate, are accurate enough to be useful for simulating chemical structures, properties, and reactivity in systems ranging from molecules to materials. In DFT, all energy terms are evaluated exactly, apart from non-classical exchange and correlation (XC) which must be modeled via approximate XC functionals. Unfortunately, such functionals are not systematically improvable in the same sense as wavefunction-based electronic structure theory, where the addition of more terms to a trial function guarantees a lower energy. However, functionals can nonetheless be categorized onto the five rungs of Perdew’s metaphorical “Jacob’s ladder” according to the sophistication of the components used for their construction.⁴ This classification has proven to be useful because the best functional at each rung typically improves over the best functional from the rung below, as demonstrated by recent comprehensive assessments of accuracy.^3,5 In order to account for long-range dispersion forces, damped atom-pairwise corrections⁶ or non-local density-density correlation functionals⁷ are typically appended to functionals at each rung.

The functionals on the highest rung (Rung 5) are called “double hybrids” because they include a dependence on occupied orbitals (which is sufficient to characterize exact or wavefunction exchange) as well as a dependence on virtual orbitals (to describe wavefunction correlation). Within the generalized Kohn-Sham theory, such functionals are potentially exact.⁸ In practice, the inclusion of some fraction of second-order perturbation theory (PT2) can be justified based on the Görling-Levy perturbation theory.⁹ The simplest form that a double hybrid can take is given in the following equation:

$$E_{DH}=c_x{E}_x^{exact}+c_{x,DFT}{E}_x^{DFT}+c_c{E}_c^{PT2}+c_{c,DFT}{E}_c^{DFT}.$$ (1)

The fraction of exact exchange is determined by the coefficient, c_x, while the fraction of the PT2 energy is controlled by the coefficient, c_c. It is straightforward to satisfy the uniform electron gas constraints, namely, c_x + c_x,DFT = 1 and c_c + c_c,DFT = 1. The first modern double hybrid functional that used Kohn-Sham orbitals to compute the PT2 contribution was developed by Grimme in 2006 and termed B2PLYP.¹⁰ This functional is perhaps the most widely used double hybrid today, especially when combined with dispersion corrections¹¹ such as DFT-D3(0)¹² and DFT-D3(BJ).¹³ B2PLYP is defined with c_x = 0.53, c_x,DFT = 0.47, c_c = 0.27, and c_c,DFT = 0.73, where the DFT exchange functional is B88 and the DFT correlation functional is LYP. Another early approach was taken by Ángyán and co-workers with the RSH+MP2 method.¹⁴

Since 2006, around 75 double hybrids have been proposed—most of them containing a few empirical parameters, but a few containing theoretically justified parameters. Some of the more widely used empirical double hybrid functionals are B2PLYP,¹⁰ B2GPPLYP,¹⁵ ωB97X-2(TQZ),¹⁶ XYG3,⁹ DSD-BLYP-D3,¹⁷ PTPSS-D3(0),¹⁸ PWPB95-D3(BJ),¹⁸ XYGJ-OS,¹⁹ DSD-PBEP86-D3(BJ),²⁰ and DSD-PBEPBE-D3(BJ).²⁰ Some non-empirical functionals include PBE0-DH, ²¹ PBE0-2,²² 1DH-BLYP,²³ LS1DH-PBE,²⁴ and PBE-QIDH.²⁵ It is beyond the scope of this paper to review these functionals,¹⁸ but a few key points should be noted. First, based on statistics gathered from more than 50 existing double hybrid density functionals, the average percentage of exact exchange is 64%, while the average percentage of PT2 correlation is 32%. It is evident that the non-local PT2 correlation in double hybrids enables a significantly higher fraction of exact exchange than is found in the standard Rung 4 hybrids (typically around 20%). B2PLYP and its descendants remain very widely used²⁶ and involve optimizing orbitals based on neglecting the PT2 component of the functional (orbital-optimized double hybrids²⁷ use the entire functional, at a significantly greater cost). However, a very successful double hybrid, the XYG3 functional,⁹ introduced a modified approach (called xDH), which involves using fixed orbitals from a successful lower rung functional (B3LYP in the case of XYG3), performing a single shot correction for non-local correlation using these orbitals, as well as a repartitioning of the semi-local DFT energy. A number of other double hybrids have subsequently followed this approach.²⁸

A vast amount of literature is dedicated to the determination of effective density functional forms, and, broadly, this can be done in one of two ways: non-empirically (via constraint satisfaction) or empirically (via fitting). It is also possible to combine aspects of both approaches. The training of density functional parameters has historically been carried out via a least-squares procedure. A handful of linear functional forms are optimized on a training set and the optimal form (based on a goodness-of-fit or related measure) is selected for publication. Recently, we introduced an approach to screen up to billions of potential functional forms in order to select the most transferable fit.^29–31 A vast number of functional forms are trained on a training set and ranked based on their performance on a validation set (a test of transferability). Finally, a small fraction of the best performers are further tested on a test set in order to determine the best candidate for publication. Initially, this approach was applied³² to generalized gradient approximation (GGA) functionals on Rung 2, but no significant advantage was gained over the best existing functionals in the same class (e.g., B97-D). However, a very effective Rung 4 hybrid GGA was achieved, termed ωB97X-V.²⁹ By contrast, because of the huge dimensionality of the space of Rung 3 meta-GGAs, a considerable improvement in predictive power was achieved via this approach to define the B97M-V functional³⁰ and, subsequently, the Rung 4 hybrid meta-GGA, ωB97M-V.³¹ The Rung 4 functionals both employ a range-separated treatment of exact exchange,³³ treating long-range exchange exactly, where semi-local DFT is expected to be poorest. ωB97M-V may be the most accurate Rung 4 functional proposed to date.

The objective of this work is to adapt the combinatorial training procedure to develop a Rung 5 functional which combines the richness of the meta-GGA space with non-local PT2 correlation and range-separated exact exchange. Additionally, the “-V” component of the functionals mentioned above, namely, the VV10 dispersion functional,⁷ will be included as it proved essential to achieving high accuracy for non-covalent interactions.^7,34,35 The overall strategy is outlined in the remainder of this section. To ensure a good starting point, the orbitals from a self-consistent ωB97M-V calculation will be used to evaluate the double hybrid XC energy,

$$E_{xc}=E_x+E_c.$$ (2)

The exchange component, Eq. (3), contains a semi-local meta-GGA contribution, a fraction, c_x, of short-range (sr) exact exchange, and full (100%) long-range (lr) exact exchange,

$$E_x=E_{x,sr}^{mGGA}+c_x{E}_{x,sr}^{exact}+E_{x,lr}^{exact}.$$ (3)

The correlation component contains same-spin (ss) and opposite-spin (os) semi-local meta-GGA contributions as well as a fraction, c_VV10, of non-local VV10 dispersion and a fraction, c_PT2, of non-local PT2 energy,

$$E_c=E_{c,ss}^{mGGA}+E_{c,os}^{mGGA}+c_{VV10}{E}_{c,nl}^{VV10}+c_{PT2}{E}_{c,nl}^{PT2}.$$ (4)

Definitions for the terms in the equations above can be found in Sec. V of Ref. 31.

The main results of this paper are the chosen functional form, selected for optimal transferability using an adaptation of the combinatorial approach briefly mentioned above, the resulting parameters, and an assessment of the final functional against existing hybrids and double hybrids. The rest of the paper is organized as follows. The approach to combinatorial training and testing is reviewed in Sec. II in order to place it in the context of other machine learning and statistical approaches. The computational details regarding the database as well as calculation settings are given in Sec. III, while a thorough account of the design procedure followed to obtain ωB97M(2) is given in Sec. IV. This is followed by a brief comparison to other existing density functionals in Sec. V and a summary of the now-complete family of combinatorially optimized density functionals in Sec. VI.

II. COMBINATORIAL SELECTION: SURVIVAL OF THE MOST TRANSFERABLE

The combinatorial approach used previously³¹ combines statistical tools known as best subset selection (BSS), also known as least-squares optimization with L0-norm regularization, and forward stepwise selection (FSS) to explore the vast space of potential functionals. A very large number of candidate functional forms are trained using a training set and ranked based on their performance on a validation set (a test of transferability). Finally, a small fraction of the best performers are further tested on a test set in order to determine the best final candidate.

The idea of best subset selection³⁶ is fundamentally very simple. Given a set of n features (or coefficients), all 2ⁿ − 1 combinations are trained in order to determine the optimal choice based on predetermined criteria. For example, given a total of n = 3 linear features (e.g., {x₁, x₂, x₃}), all 2³ − 1 = 7 combinations would be fit ({x₁}, {x₂}, {x₃}, {x₁, x₂}, {x₁, x₃}, {x₂, x₃}, {x₁, x₂, x₃}). If the number of features is not excessively large, it is possible to comprehensively explore the entire space of parameters without approximations. For example, in 1997, Becke introduced the semi-empirical B97 functional³⁷ which contains three separate power series [Eq. (5)] enhancing the corresponding uniform electron gas (UEG) energy density for exchange, same-spin correlation, and opposite-spin correlation,

$$f\left(u\right)=\sum _{j=0}^N{c}_j{u}^j.$$ (5)

In Eq. (5), the variable $u\approx \frac{\gamma s^2}{1+\gamma s^2}$ is a finite domain transformation of the dimensionless spin-density gradient, $s\approx \frac{|\nabla \rho |}{{\rho }^{4/3}}$, where γ is an empirical nonlinear parameter.

Assuming the same value of N across all three components, applying BSS to the optimization of the B97 density functional involves n = 3(N + 1) features and 2^3(N+1) − 1 total combinations. For a typical value of N = 4, this equates to 32 767 least squares fits which is indeed manageable³² (and was carried out during the optimization of the ωB97X-V functional²⁹).

For sufficiently large N, however, performing all 2ⁿ − 1 least squares fits becomes intractable. The meta-GGA parameter space that was recently explored for both B97M-V and ωB97M-V is a prominent example of when this limit can be exceeded. A typical power series enhancement factor for a meta-GGA density functional is two-dimensional, as given in the following equation:

$$f\left(w,u\right)=\sum _{i=0}^{N^{\prime }}\sum _{j=0}^N{c}_{ij}{w}^i{u}^j.$$ (6)

In Eq. (6), the variable $w\approx \frac{t-1}{t+1}$ is a finite domain transformation of the dimensionless ratio of the UEG kinetic energy density to the exact kinetic energy density, $t=\frac{{\tau }^{UEG}}{\tau }$, where ${\tau }^{UEG}=\frac{3}{5}{\left(6{\pi }^2\right)}^{2/3}{\rho }^{5/3}$.

The number of features increases to n = 3(N′ + 1)(N + 1), for a total of 2^{3(N′+1)(N+1)} − 1 possibilities. Therefore, even for N′ = N = 4, the total number of fits exceeds 10²². During the development of B97M-V and ωB97M-V, values of N′ = 8 and N = 4 were explored, for a total of more than 10⁴⁰ candidate fits. Clearly, performing 10⁴⁰ or even 10²² least-squares fits is entirely impractical.

A way to circumvent this bottleneck is to use forward stepwise selection.³⁸ With FSS, all $\left(\genfrac{}{}{0.0pt}{}{n}{1}\right)$ one-parameter fits are generated, and the most influential feature based on predetermined criteria is identified. This feature is then frozen, $\left(\genfrac{}{}{0.0pt}{}{n-1}{1}\right)$ two-parameter fits (one fixed variable and one free variable) are performed, and so on. A third option, which was used to develop B97M-V and ωB97M-V (and the present functional), involves a combination of BSS and FSS. BSS is applied up to the largest manageable number of parameters, p, and then, the FSS procedure takes over in order to sample fits with more parameters. For example, given n = 50 features and the ability to perform a maximum of a billion fits, one can begin with $\left(\genfrac{}{}{0.0pt}{}{50}{1}\right)=50$ one-parameter fits and continue through $\left(\genfrac{}{}{0.0pt}{}{50}{8}\right)=\mathrm{536,878,650}$ 8-parameter fits. At this point, since $\left(\genfrac{}{}{0.0pt}{}{50}{9}\right)$ is larger than a billion, the FSS procedure takes over and $\left(\genfrac{}{}{0.0pt}{}{50-1}{8}\right)=\mathrm{450,978,066}$ 9-parameter fits are performed with the most significant feature from the previous optimization fixed. Another way to represent the total number of fits given a certain number of features, n, is ${\sum }_p^n\left(\genfrac{}{}{0.0pt}{}{n}{p}\right)$, which makes it easier to see that there are $\left(\genfrac{}{}{0.0pt}{}{n}{1}\right)$ 1-parameter fits, $\left(\genfrac{}{}{0.0pt}{}{n}{2}\right)$ 2-parameter fits, $\left(\genfrac{}{}{0.0pt}{}{n}{3}\right)$ 3-parameter fits, and so on.

In this work, N′ and N are both set to 4, for a total of 75 features coming from the semi-local DFT components (exchange, same-spin correlation, and opposite-spin correlation). Additionally, exact exchange, VV10, and PT2 each contribute a single parameter, for a total of 78 features. Two constraints are permanently applied. First, in the exchange energy, Eq. (3), the uniform electron gas limit is satisfied via

$$c_x+c_{x,00}=1.$$ (7)

Second, in the correlation energy, Eq. (4), we constrain the total contribution of the two types of non-local correlation to be unity,

$$c_{PT2}+c_{VV10}=1.$$ (8)

Finally, two features, c_x and c_PT2, are invariably included in all of the fits (their values are not frozen). This is to uphold the definition of a double hybrid which is a functional that depends on both occupied and virtual orbitals.

With these constraints in place, the total number of fits with a fixed number of parameters, p + 2, is $\left(\genfrac{}{}{0.0pt}{}{76-2}{p}\right)$. The current implementation that carries out this procedure is capable of performing (on average) 1000 fits per second per core on a 64-core node, assuming that all 64-cores are utilized. Recursion relations are used to break down the full set of requested fits into a number that is manageable per core (≈10⁸–10⁹). Given the total number of available features (74), the largest optimization attempted here is $\left(\genfrac{}{}{0.0pt}{}{74}{10}\right)=\mathrm{718,406,958,841}$, with recursion relations applied to break the task into no more than 10⁹ fits per core. This results in 1786 separate processes that perform between 10⁸ and 10⁹ fits each and take at most a week of elapsed time to complete. Therefore, performing on the order of a trillion fits is manageable in the span of a week, given the full use of a cluster with around 2000 cores.

In this work, a combination of BSS, FSS, and the random sample consensus (RANSAC) outlier detection method³⁹ is used in order to determine an optimal choice of features for a double hybrid functional, as well as their values, given the limitation of a relatively small number (10³–10⁴) of high-quality data points that can be used for training, validation, and testing. This limitation arises due to the fact that the computation of reference values [typically coupled cluster with singles, doubles, and perturbative triples at the complete basis set limit (CCSD(T)/CBS) or better] is very costly, and chemical space is intractably vast. Therefore, any database used for such purposes will certainly not fully characterize (and may even misrepresent) the diversity of chemical space. In past work, it became evident that when working in the space of meta-GGA functionals, the least-squares residuals from the initial guess are unreliable predictors for the performance of the final, self-consistently optimized functional, and therefore, it was necessary to update the feature matrix with a guess that more closely resembled the final functional form. Naturally, this is an inconvenience that would ideally be avoided. The xDH approach we will follow (using fixed ωB97M-V orbitals) does not have this issue, since the orbitals are pre-defined and thus fixed throughout the optimization of the parameters. The parameter optimization procedure simply determines the partitioning of the SCF and PT2 energies. As a result of this simplification, it is also possible to utilize other supervised machine learning tools such as Lasso (L1-norm regularization) and Ridge Regression (L2-norm regularization). The former approach attempts to return a sparse vector from the original feature matrix, while the latter penalizes large parameter values and thus results in a model with many well-behaved coefficients. Finally, the RANSAC outlier detection method mentioned above is applied to identify outliers in the training data. Such data points may include those that are multi-reference in nature or those with very large magnitudes (i.e., absolute atomic energies).

III. COMPUTATIONAL DETAILS

The database used in this work contains 84 datasets (Table I) and 4986 data points and is named the Main-Group Chemistry DataBase (MGCDB84).³ These datasets have been compiled from the benchmarking activities of numerous groups, including Grimme, Herbert, Hobza, Karton, Martin, Sherrill, and Truhlar. The reference data are typically estimated to be at least 10 times more accurate than the very best available density functionals so that robust and meaningful conclusions can be drawn. Of the 84 datasets, 82 are categorized into eight datatypes: NCED, NCEC, NCD, IE, ID, TCE, TCD, and BH. The two datasets that are excluded from the datatype categorization are AE18 (absolute atomic energies) and RG10 (rare-gas dimer potential energy curves). The first three datatypes (NCED, NCEC, and NCD) pertain to non-covalent interactions (NC), the next two datatypes (IE and ID) pertain to isomerization energies (I), the next two datatypes (TCE and TCD) pertain to thermochemistry (TC), and the last datatype pertains to barrier heights (BH). Since the eight datatypes will be heavily referenced in this work, we specify the types of interactions that belong to each category, as well as the origin of the abbreviations. The datatype abbreviations begin with letters corresponding to one of the four main categories: NC, I, TC, or BH. Appending one of the four main categories with the letter “E’” indicates that the interactions within are considered to be “easy” cases (not very sensitive to self-interaction error or strong correlation), while the letter “D’” indicates that the interactions are considered to be “difficult.” Finally, for the non-covalent interactions only, the presence of a fourth letter, either “D’” or “C’” indicates the presence of dimers or clusters, respectively. Regarding the datatypes, NCED contains 18 datasets and 1744 data points, NCEC contains 12 datasets and 243 data points, NCD contains 5 datasets and 91 data points, IE contains 12 datasets and 755 data points, ID contains 5 datasets and 155 data points, TCE contains 51 datasets and 947 data points, TCD contains 7 datasets and 258 data points, while BH contains 8 datasets and 206 data points. Overall, the training set contains 870 data points, the validation set contains 2964 data points, and the test set contains 1152 data points.

TABLE I.

Summary of the 84 datasets that comprise MGCDB84.³ The datatypes are explained in Sec. III. The sixth column contains the root-mean-squares of the dataset reaction energies. PEC stands for potential energy curve, SR stands for single-reference, MR stands for multi-reference, Bz stands for benzene, Me stands for methane, and Py stands for pyridine.

Name	Set	Datatype	#	Description	ΔE (kcal/mol)	References
A24	Training	NCED	24	Binding energies of small non-covalent complexes	2.65	40
DS14	Training	NCED	14	Binding energies of complexes containing divalent sulfur	3.70	41
HB15	Training	NCED	15	Binding energies of hydrogen-bonded dimers featuring ionic groups common in biomolecules	19.91	42
HSG	Training	NCED	21	Binding energies of small ligands interacting with protein receptors	6.63	43 and 44
NBC10	Training	NCED	184	PECs for BzBz (5), BzMe (1), MeMe (1), BzH2S (1), and PyPy (2)	1.91	44–47
S22	Training	NCED	22	Binding energies of hydrogen-bonded and dispersion-bound non-covalent complexes	9.65	44 and 48
X40	Training	NCED	31	Binding energies of non-covalent interactions involving halogenated molecules	5.26	49
A21x12	Validation	NCED	252	PECs for the 21 equilibrium complexes from A24	1.43	50
BzDC215	Validation	NCED	215	PECs for benzene interacting with two rare-gas atoms and eight first- and second-row hydrides	1.81	51
HW30	Validation	NCED	30	Binding energies of hydrocarbon-water dimers	2.34	52
NC15	Validation	NCED	15	Binding energies of very small non-covalent complexes	0.95	53
S66	Validation	NCED	66	Binding energies of non-covalent interactions found in organic molecules and biomolecules	6.88	54 and 55
S66x8	Validation	NCED	528	PECs for the 66 complexes from S66 × 8	5.57	54
3B-69-DIM	Test	NCED	207	Binding energies of all relevant pairs of monomers from 3B-69-TRIM	5.87	56
AlkBind12	Test	NCED	12	Binding energies of saturated and unsaturated hydrocarbon dimers	3.14	57
CO2Nitrogen16	Test	NCED	16	Binding energies of CO2 to molecular models of pyridinic N-doped graphene	3.84	58
HB49	Test	NCED	49	Binding energies of small- and medium-sized hydrogen-bonded systems	14.12	59–61
Ionic43	Test	NCED	43	Binding energies of anion-neutral, cation-neutral, and anion-cation dimers	69.94	62
H2O6Bind8	Training	NCEC	8	Binding energies of isomers of (H2O)6	46.96	63 and 64
HW6Cl	Training	NCEC	6	Binding energies of Cl−(H2O)n (n = 1–6)	57.71	63 and 64
HW6F	Training	NCEC	6	Binding energies of F−(H2O)n (n = 1–6)	81.42	63 and 64
FmH2O10	Validation	NCEC	10	Binding energies of isomers of F−(H2O)10	168.50	63 and 64
Shields38	Validation	NCEC	38	Binding energies of (H2O)n (n = 2–10)	51.54	65
SW49Bind345	Validation	NCEC	31	Binding energies of isomers of ${{\mathrm{S}\mathrm{O}}_4}^{2-}$(H2O)n (n = 3–5)	28.83	66
SW49Bind6	Validation	NCEC	18	Binding energies of isomers of ${{\mathrm{S}\mathrm{O}}_4}^{2-}$(H2O)6	62.11	66
WATER27	Validation	NCEC	23	Binding energies of neutral and charged water clusters	67.48	67 and 68
3B-69-TRIM	Test	NCEC	69	Binding energies of trimers, with three different orientations of 23 distinct molecular crystals	14.36	56
CE20	Test	NCEC	20	Binding energies of water, ammonia, and hydrogen fluoride clusters	30.21	69 and 70
H2O20Bind10	Test	NCEC	10	Binding energies of isomers of (H2O)20 (low-energy structures)	198.16	64
H2O20Bind4	Test	NCEC	4	Binding energies of isomers of (H2O)20 (dod, fc, fs, and es)	206.12	67, 68, 71, and 72
TA13	Training	NCD	13	Binding energies of dimers involving radicals	22.00	73
XB18	Training	NCD	8	Binding energies of small halogen-bonded dimers	5.23	74
Bauza30	Validation	NCD	30	Binding energies of halogen-, chalcogen-, and pnicogen-bonded dimers	23.65	75 and 76
CT20	Validation	NCD	20	Binding energies of charge-transfer complexes	1.07	77
XB51	Validation	NCD	20	Binding energies of large halogen-bonded dimers	6.06	74
AlkIsomer11	Training	IE	11	Isomerization energies of n = 4–8 alkanes	1.81	78
Butanediol65	Training	IE	65	Isomerization energies of butane-1,4-diol	2.89	79
ACONF	Validation	IE	15	Isomerization energies of alkane conformers	2.23	68 and 80
CYCONF	Validation	IE	11	Isomerization energies of cysteine conformers	2.00	68 and 81
Pentane14	Validation	IE	14	Isomerization energies of stationary points on the n-pentane torsional surface	6.53	82
SW49Rel345	Validation	IE	31	Isomerization energies of ${{\mathrm{S}\mathrm{O}}_4}^{2-}$(H2O)n (n = 3–5)	1.47	66
SW49Rel6	Validation	IE	18	Isomerization energies of ${{\mathrm{S}\mathrm{O}}_4}^{2-}$(H2O)6	1.22	66
H2O16Rel5	Test	IE	5	Isomerization energies of (H2O)16 (boat and fused cube structures)	0.40	83
H2O20Rel10	Test	IE	10	Isomerization energies of (H2O)20 (low-energy structures)	2.62	64
H2O20Rel4	Test	IE	4	Isomerization energies of (H2O)20 (dod, fc, fs, and es)	5.68	67, 68, 71, and 72
Melatonin52	Test	IE	52	Isomerization energies of melatonin	5.54	84
YMPJ519	Test	IE	519	Isomerization energies of the proteinogenic amino acids	8.33	85
EIE22	Training	ID	22	Isomerization energies of enecarbonyls	4.97	86
Styrene45	Training	ID	45	Isomerization energies of C8H8	68.69	87
DIE60	Validation	ID	60	Isomerization energies of reactions involving double-bond migration in conjugated dienes	5.06	88
ISOMERIZATION20	Validation	ID	20	Isomerization energies	44.05	89
C20C24	Test	ID	8	Isomerization energies of the ground state structures of C20 and C24	36.12	90
AlkAtom19	Training	TCE	19	n = 1–8 alkane atomization energies	1 829.31	78
BDE99nonMR	Training	TCE	83	Bond dissociation energies (SR)	114.98	89
G21EA	Training	TCE	25	Adiabatic electron affinities of atoms and small molecules	40.86	68 and 91
G21IP	Training	TCE	36	Adiabatic ionization potentials of atoms and small molecules	265.35	68 and 91
TAE140nonMR	Training	TCE	124	Total atomization energies (SR)	381.05	89
AlkIsod14	Validation	TCE	14	n = 3–8 alkane isodesmic reaction energies	10.35	78
BH76RC	Validation	TCE	30	Reaction energies from HTBH38 and NHTBH38	30.44	68, 92, and 93
EA13	Validation	TCE	13	Adiabatic electron affinities	42.51	94
HAT707nonMR	Validation	TCE	505	Heavy-atom transfer energies (SR)	74.79	89
IP13	Validation	TCE	13	Adiabatic ionization potentials	256.24	94
NBPRC	Validation	TCE	12	Reactions involving NH3/BH3 and PH3/BH3	30.52	18, 68, and 95
SN13	Validation	TCE	13	Nucleophilic substitution energies	25.67	89
BSR36	Test	TCE	36	Hydrocarbon bond separation reaction energies	20.06	18 and 96
HNBrBDE18	Test	TCE	18	Homolytic N–Br bond dissociation energies	56.95	97
WCPT6	Test	TCE	6	Tautomerization energies for water-catalyzed proton-transfer reactions	7.53	98
BDE99MR	Validation	TCD	16	Bond dissociation energies (MR)	54.51	89
HAT707MR	Validation	TCD	202	Heavy-atom transfer energies (MR)	83.41	89
TAE140MR	Validation	TCD	16	Total atomization energies (MR)	147.20	89
PlatonicHD6	Test	TCD	6	Homodesmotic reactions involving platonic hydrocarbon cages, CnHn (n = 4, 6, 8, 10, 12, 20)	136.71	99
PlatonicID6	Test	TCD	6	Isodesmic reactions involving platonic hydrocarbon cages, CnHn (n = 4, 6, 8, 10, 12, 20)	96.19	99
PlatonicIG6	Test	TCD	6	Isogyric reactions involving platonic hydrocarbon cages, CnHn (n = 4, 6, 8, 10, 12, 20)	356.33	99
PlatonicTAE6	Test	TCD	6	Total atomization energies of platonic hydrocarbon cages, CnHn (n = 4, 6, 8, 10, 12, 20)	2539.27	99
BHPERI26	Training	BH	26	Barrier heights of pericyclic reactions	23.15	68 and 100
CRBH20	Training	BH	20	Barrier heights for cycloreversion of heterocyclic rings	46.40	101
DBH24	Training	BH	24	Diverse barrier heights	28.34	15 and 102
CR20	Validation	BH	20	Cycloreversion reaction energies	22.31	103
HTBH38	Validation	BH	38	Hydrogen transfer barrier heights	16.05	93
NHTBH38	Validation	BH	38	Non-hydrogen transfer barrier heights	33.48	92
PX13	Test	BH	13	Barrier heights for proton exchange in water, ammonia, and hydrogen fluoride clusters	28.83	69 and 70
WCPT27	Test	BH	27	Barrier heights of water-catalyzed proton-transfer reactions	38.73	98
AE18	Training	…	18	Absolute atomic energies of hydrogen through argon	148 739.00	104
RG10	Validation	…	569	PECs for the 10 rare-gas dimers involving helium through krypton	1.21	105

The def2-QZVPPD basis set¹⁰⁶ is used without counterpoise corrections throughout. A (99,590) grid (99 radial shells with 590 grid points per shell) is used throughout, except for AE18 and RG10, where a (500,974) grid is used. The SG-1 grid¹⁰⁷ is used to calculate the contribution from the VV10 non-local correlation functional⁷ throughout, except for AE18 and RG10, where a (75,302) grid is used. All of the calculations were performed with a development version of the Q-Chem 4 software package.¹⁰⁸ For the MP2 calculations, the frozen core approximation is utilized, along with the resolution-of-the-identity (RI) approximation and the appropriate auxiliary basis set for def2-QZVPPD.

An in-house Python implementation of BSS and FSS is used, while RANSAC is used as implemented in sci-kit learn.¹⁰⁹ For all RANSAC applications in this work, a minimum sample size of 75% is utilized, the outlier threshold is 10 kcal/mol, and the maximum number of random trials is set to 10 000.

IV. DESIGN OF ωB97M(2) AND INTERNAL ASSESSMENT

As mentioned previously, the orbitals from an ωB97M-V calculation serve as the foundation upon which the ωB97M(2) functional is built. In order to begin the optimization procedure, a series of decisions regarding the functional form must be made. For the range-separation parameter, ω, a value of 0.3 is used (as in the ωB97X-V and ωB97M-V functionals). For the VV10 damping parameter, b, an analysis¹¹⁰ of past double hybrids with VV10 indicated that on average the parameter is valued at 10. Therefore, b = 10 is used without further optimization (since b is a nonlinear parameter). Similarly, the parameter that controls the C₆ coefficients in VV10, C, is set to 0.01 as in ωB97X-V and ωB97M-V. The ωB97M-V orbitals are used to compute the PT2 contribution, the semi-local contributions (or features), and the VV10 energy. The lattermost is computed non-self-consistently. There are two nearly equivalent options for defining the energy of such a functional. The first is as a perturbation to the ωB97M-V energy, while the second is as a combination of VV10, PT2, exact exchange, and a reparameterization of the semi-local space. The former option provides slightly less flexibility because ωB97M-V may contain variables that are not optimal for the double hybrid functional. For example, ωB97M-V contains the coefficient, c_x,10, with a value of 0.259. Any perturbation to the ωB97M-V energy would necessarily contain that feature either with the original coefficient of 0.259 or an updated value if the combinatorial approach selects c_x,10 as an optimizable parameter. Unless the value of c_x,10 is constrained to be −0.259, the final energy will directly involve a contribution from c_x,10. Since starting from a complete repartitioning of the semi-local space avoids this issue, the latter option is chosen for this work.

The weighting scheme used for ωB97M(2) is similar to that used for ωB97M-V. Initially, each data point is given a weight that corresponds to the inverse of the product of the number of data points in the associated dataset and the root-mean-square of the reaction energies in the associated dataset. These values can be found in the fourth and sixth columns of Table I, respectively. Within each of the datatypes, the weights are normalized by dividing by the smallest weight and then exponentiated such that they lie between 1 and 2. For the determination of the weights only, AE18 is included in the TCE datatype. Finally, the eight datatypes get a multiplicative weight based on intuition: 0.1 for TCD, 1 for TCE, 10 for NCD, ID, and BH, 100 for NCED and NCEC, and 1000 for IE. As RG10 does not belong to a datatype, the bound (attractive) data points receive a weight of 10 000, while the unbound (repulsive) data points receive a weight of 1. These weights are used to define the weighted root-mean-square deviations (RMSD) for the training, validation, and test sets.

A series of BSS optimizations are performed within the aforementioned space of 74 available features, up to 10 features. The training set is used for the fits, and transferability assessment is performed on the validation set. Since the exact exchange and PT2 coefficients are mandatory, this results in 3- through 12-parameter unbiased fits. Within each run (e.g., all 1 799 579 064 $\left(\genfrac{}{}{0.0pt}{}{74}{7}\right)$ fits), the top 10 000 fits (based on the weighted validation error) are saved. At $\left(\genfrac{}{}{0.0pt}{}{74}{10}\right)$, it is necessary to start freezing parameters, and the freezing is done based on the effectiveness of the parameter in reducing the validation error, since transferability is the most important aspect of these fits. In order, the following features are frozen to arrive at up to 17-parameter fits: c_cos,00, c_css,20, c_cos,20, c_cos,01, c_x,20. At this point, we have the top 10 000 (based on weighted validation error) 1- through 17-parameter fits.

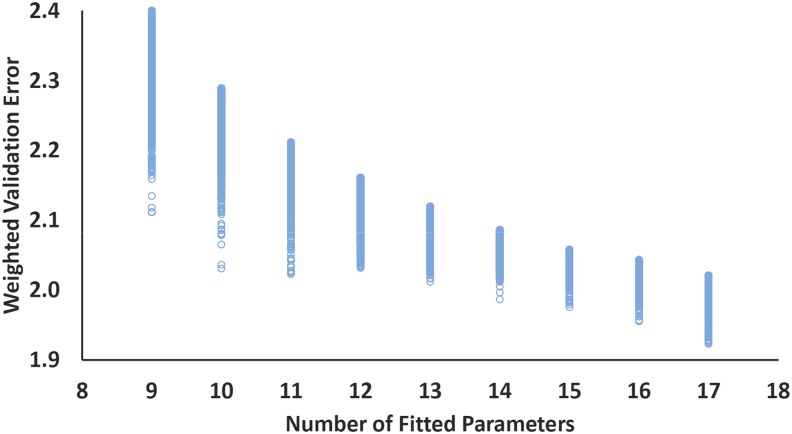
This procedure produces the data shown in Fig. 1, where the weighted validation error is plotted for the top 10 000 9- through 17-parameter fits. These results represent the double hybrid analog of the way in which our Rung 3 (B97M-V) and Rung 4 (ωB97M-V) functionals were developed. The relevant information contained in this figure is the curve defined by the best functional (lowest weighted validation error) with a fixed number of parameters. This is a basis for selecting a functional that exhibits greatest transferability. Either 10- or 11-parameter choices represent minimally parameterized functionals that are promising candidates. However, the weighted validation error continues to decline even with 16- and 17-parameter fits, and despite the additional parameters, there is some argument that the best such functionals offer significantly improved overall results. However, caution is needed because when the number of parameters is greater, it is more likely that the best functional on the validation set will not perform comparably well on the independent test set. In addition, it is possible that outlier data in the training set have biased the parameters.

FIG. 1.

Weighted validation error (in kcal/mol) plotted against the number of fitted parameters for the top 10 000 fits for each number of parameters considered (up to 17). All training data are included in the fitting process, and the resulting parameters are subsequently applied to the validation set, as described in detail in the text. Improvement in the validation performance of the best functional is not monotonic with the number of parameters. However, improvements are still occurring up to 17 parameters.

To explore these issues, these best fits are then refit on the training set using the RANSAC outlier detection method. The RANSAC method takes each set of variables and performs the fitting procedure a number of times in order to identify outliers based on the criteria specified in Sec. III. For a given set of features, once the RANSAC procedure is complete, a new set of coefficients is the result, along with a list of the data points that were deemed outliers. The new coefficients are a result of simply fitting to the training set with the original weights, with these outliers removed. Because the outlier detection is performed using the fits that performed best on the validation set, the weighted validation set error can no longer be meaningfully used to assess the modified fits. Instead, the resulting fits are ranked using the (completely independent) weighted test set error. The fit with the best test set performance is what we finally select as the ωB97M(2) density functional.

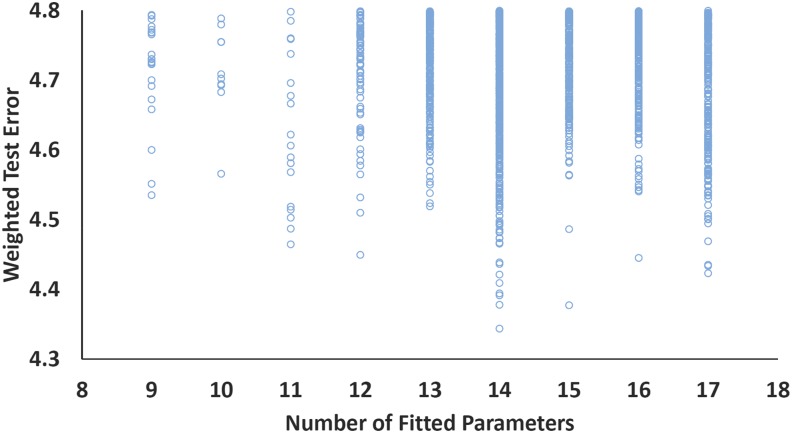
For the 90 000 fits pictured in Fig. 1, RANSAC is individually applied to redetermine the values of the coefficients with the outliers removed. This procedure produces the data shown in Fig. 2, where the weighted test error is plotted. Since the test set is indeed an independent assessment, there is a minimum in the weighted test error at 14 parameters, and this fit corresponds to the ωB97M(2) density functional. The RANSAC procedure removes 11 data points from the training set (of 870), and these specific data points are the absolute atomic energies of nitrogen, oxygen, fluorine, neon, sodium, magnesium, and aluminum, the ionization potential of beryllium, two isomers from the Styrene45 dataset (isomers 38 and 40), and the binding energy of HF–CO⁺. Inspecting Fig. 2 shows that while our chosen form is optimal, its margin of superiority against other contenders is small. There are roughly half a dozen other contenders whose overall performance is within 2% of our choice and hundreds within 10%, so the optimal choice is certainly dependent upon the composition of the test set as well as the chosen optimization procedure. Our view is that ωB97M(2) is one representative of the best candidates, balanced across the different datatypes by the weights and constraints that we have imposed.

FIG. 2.

Weighted test error (in kcal/mol) plotted against the number of fitted parameters, where the parameters are obtained after application of the RANSAC procedure to the training set, as described in the text. The independent test set results show a minimum at the best 14-parameter functional, which is selected to define the ωB97M(2) double hybrid functional.

The ωB97M(2) functional contains approximately 62% short-range exact exchange and 34% PT2 correlation. Relative to the parent ωB97M-V functional, the fraction of short-range exact exchange is about 4 times higher, which will reduce self-interaction error. All of the optimized parameters are given in Table II. The parameters are numerically very well-behaved, all of them smaller than 5 in magnitude. The inhomogeneity correction factors (ICFs) are also very well-behaved. For exchange, the ICFs are bound by 0.37 and 1.73, clearly obeying the Lieb-Oxford bound of 2.273. For same-spin correlation, the ICF is bound by −4.31 and 0.65, while for opposite-spin correlation, the ICF is bound by 0.16 and 2.77. Therefore, the resulting functional is very smoothly varying. Since both zeroth order contributions for correlation (c_css,00 and c_cos,00) end up in the parameterization, it is interesting to see their values. The value of c_css,00 is 0.548, while the value of c_cos,00 is 0.462, which are each much less than 1 (the value for a meta-GGA that obeys the uniform electron gas limit). This result shows how the presence of PT2 correlation reduces the need for semi-local DFT correlation.

TABLE II.

The optimized parameters that define the ωB97M(2) density functional. The first two columns correspond to semi-local meta-GGA exchange, the next two columns correspond to semi-local meta-GGA same-spin correlation, the next two columns correspond to semi-local meta-GGA opposite-spin correlation, and the final two columns correspond to the short-range exact exchange contribution, the VV10 non-local correlation contribution, and the PT2 contribution.

cx,00	0.378 06	ccss,00	0.548 46	ccos,00	0.461 52	cx	0.621 94
cx,20	0.281 93	ccss,10	−1.177 24	ccos,20	2.304 90	cVV10	0.659 04
cx,30	−0.218 86	ccss,20	−3.672 67	ccos,01	−1.947 94	cPT2	0.340 96
cx,01	0.136 42			ccos,02	3.249 10
cx,41	0.707 67			ccos,22	−2.262 80

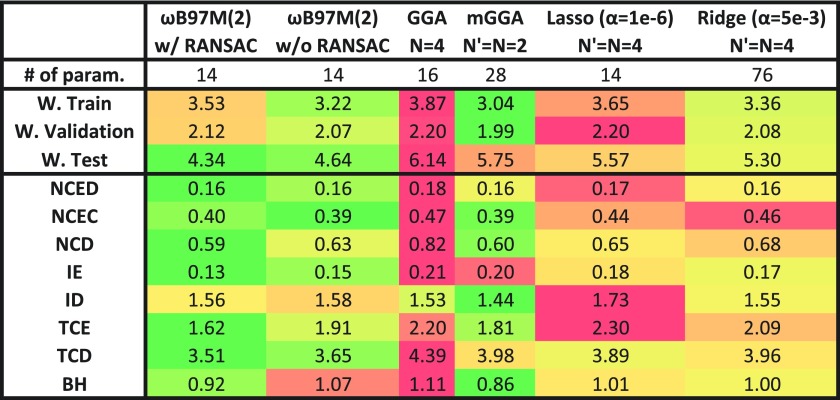
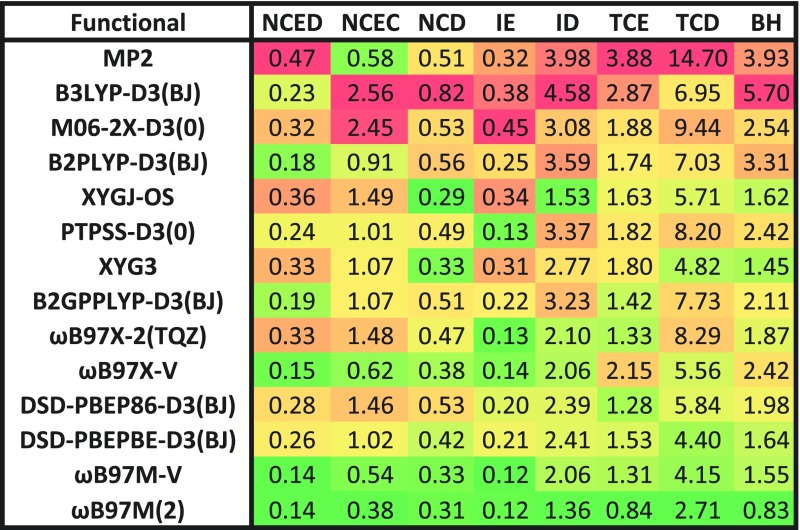
The first tests of ωB97M(2) are against other design alternatives, as summarized in Fig. 3. This testing constitutes an internal assessment of the effectiveness of our chosen design strategy. The first column, ωB97M(2) w/ RANSAC, corresponds to our chosen functional form. The first interesting comparison is to compare this to the same fit, except without the use of RANSAC. This is shown in the adjacent column. For the most part, the two models perform comparably; however, for thermochemistry, the model with RANSAC performs significantly better, since the removal of a handful of absolute atomic energies leads to much better performance overall on relevant bonded energy differences. As a reminder, the TCE datatype does not contain the AE18 dataset of absolute atomic energies. Furthermore, the performance for barrier heights is also improved. Perhaps most importantly, the weighted test error is significantly smaller, indicating better transferability.

FIG. 3.

Performance of the 14-parameter RANSAC-derived fit for ωB97M(2) (first column) against the same fit without RANSAC (second column), non-combinatorial GGA and meta-GGA double hybrids fitted to both training and validation sets (third and fourth columns), and results from the Lasso and Ridge Regression machine learning procedures (see the text for details). The first row gives the number of parameters in each functional. Subsequent rows show the weighted RMS errors for the training, validation, and test sets (kcal/mol), and RMS errors (kcal/mol) for each of the datatypes across the entire database (see Sec. III for the meaning of the acronyms).

The third and fourth columns of Fig. 3 (GGA and mGGA) employ the standard linear regression corresponding to the specified expansion of the power series. These two double hybrid models are fit to both the training and validation sets. The GGA model contains more fitted parameters than ωB97M(2), yet no dependence on the kinetic energy density. As expected, this model is almost always worse than ωB97M(2), particularly for the independent test set. The meta-GGA model shown is a functional that is expanded up to quadratic order in both the density gradient and the kinetic energy density. This results in a functional with twice as many parameters as ωB97M(2). Since it is trained on the training and validation sets, it performs better for these two datasets, but its weighted test error is more than 30% larger than that of ωB97M(2), indicating significantly poorer transferability. Across the full dataset, it is also significantly worse for the IE, TCE, and TCD datatypes.

Finally, it is interesting to compare the Lasso and Ridge Regression machine learning models. These models were applied in the same space as the combinatorial search, namely, up to quartic power contributions (N′ = N = 4). The hyperparameter, α, is minimized on the validation set, and then, the model is trained on both the training and validation set using the optimal hyperparameter. The Lasso result is particularly interesting because the number of resulting non-zero parameters is fortuitously 14 which is the same number of parameters as in the final model. Therefore, comparing ωB97M(2) with the Lasso result is relevant. For all of the datatypes, ωB97M(2) performs better, particularly for IE, TCE, and TCD. Comparing Lasso and Ridge Regression is also interesting, since the latter retains all 76 parameters in the feature matrix. For this specific application, Ridge Regression performs slightly better than Lasso, but its thermochemistry performance is still subpar relative to ωB97M(2). Overall, both machine learning models perform more than 20% worse on the independent test set relative to ωB97M(2), although they do outperform the meta-GGA model on the test set. It is evident that our design approach has yielded better results than are possible from either fitting with an assumed form (e.g., the GGA or meta-GGA model) or using the standard machine learning methods.

It is worth mentioning that a variety of different approaches were considered during the development of ωB97M(2)—approaches that were ultimately abandoned in favor of the final functional form. One such endeavor was the exploration of attenuated MP2¹¹¹ instead of canonical MP2. However, the results indicated that little to no attenuation performed better than any attenuated form, despite the known limitations of MP2 for long-range correlation and the presence of VV10. Furthermore, we also attempted to train a regularized form of MP2, with a level shift in the denominator, which would make the method more robust in the limit of small HOMO-LUMO gaps. We also tried relaxing the constraint that c_PT2+c_VV10 = 1, but this produced fits that tested 5%-10% worse than their constrained counterparts. Finally, it is worth noting that at the beginning of this project, we had intended to develop a non-xDH functional, but realized early on that this approach was not amenable to the combinatorial design methodology because the resulting fits were highly sensitive to the choice of initial orbitals.

V. EXTERNAL ASSESSMENT AGAINST EXISTING HYBRIDS AND DOUBLE HYBRIDS

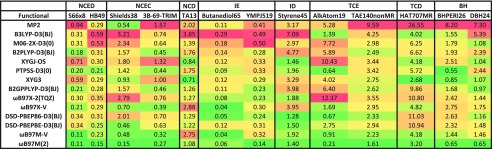
The next stage of assessment is to compare the performance of the ωB97M(2) density functional against existing double hybrids, as well as hybrid density functionals. For this purpose, we have selected 8 well-recognized double hybrid functionals and 4 existing hybrids, as summarized in Table III. Additionally, we compare against the performance of the standard MP2 method. Instead of showing vast tables that contain RMSDs for all 84 datasets, we summarize the data into two simple figures. The first figure (Fig. 4) summarizes the results based on the datatypes described in Sec. III. The second figure (Fig. 5) contains RMSDs for a selection of specific datasets from the total of 84 that comprise the database.

TABLE III.

Details for the 12 density functionals chosen for comparison to ωB97M(2). The second column indicates the percentage of exact exchange: a single value indicates that the hybridization is global, while a range (e.g., 15–100) indicates that the hybridization is range-separated, with the first value being the percentage of short-range exact exchange and the second value being the percentage of long-range exact exchange (the value in parentheses is ω). The third and fourth columns indicate the percentage of same-spin and opposite-spin MP2 correlation energy. The fifth column indicates the type of hybridization (GH stands for global hybrid, RSH stands for range-separated hybrid, GDH stands for global double hybrid, and RSDH stands for range-separated double hybrid). The sixth column indicates the ingredients contained in the functional. The seventh column indicates the type of dispersion correction, with D3(0) and D3(BJ) referring to Grimme’s D3 method using the original damping function and the Becke-Johnson damping function, respectively, and VV10 referring to the Vydrov and van Voorhis non-local correlation functional.

Functional	cx·100 (ω)	ccss·100	ccos·100	Hyb.	Ing.	Disp.	Year	References
B3LYP-D3(BJ)	20	0	0	GH	GGA	D3(BJ)	1993/2011	13 and 112
M06-2X-D3(0)	54	0	0	GH	meta-GGA	D3(0)	2006	113
ωB97X-V	16.7-100 (0.3)	0	0	RSH	GGA	VV10	2014	29
ωB97M-V	15-100 (0.3)	0	0	RSH	meta-GGA	VV10	2016	31
B2PLYP-D3(BJ)	53	27	27	GDH	GGA	D3(BJ)	2006/2011	10 and 13
B2GPPLYP-D3(BJ)	65	36	36	GDH	GGA	D3(BJ)	2008/2011	13 and 15
ωB97X-2(TQZ)	63.62-100 (0.3)	52.93	44.71	RSDH	GGA	None	2009	16
XYG3	80.33	32.11	32.11	GDH	GGA	None	2009	9
PTPSS-D3(0)	50	37.5	37.5	GH	meta-GGA	D3(0)	2011	18
XYGJ-OS	77.31	0	43.64	GDH	GGA	None	2011	19
DSD-PBEP86-D3(BJ)	69	22	52	GDH	GGA	D3(BJ)	2013	20
DSD-PBEPBE-D3(BJ)	68	13	55	GDH	GGA	D3(BJ)	2013	20
ωB97M(2)	62-100 (0.3)	34	34	RSDH	meta-GGA	VV10	2018	P.W.

FIG. 4.

Performance of 9 double hybrid density functionals, 4 hybrid density functionals, and MP2 for the datatypes in the MGCDB84 database. The errors are geometric means of the RMSDs (in kcal/mol) for each individual dataset belonging to a given datatype.

FIG. 5.

Performance of 9 double hybrid density functionals, 4 hybrid density functionals, and MP2 for a selection of datasets from the MGCDB84 database. The errors are the standard RMSDs (in kcal/mol) across the data points in the corresponding dataset.

The errors contained in Fig. 4 are geometric means of the RMSDs for each individual dataset belonging to a given datatype (these will be referred to as GM-RMSDs). For instance, the value for NCED is the geometric mean across all 18 NCED dataset RMSDs. We use this measure instead of an RMSD across all 1744 NCED data points (for example) so that datasets that have an overwhelming number of data points do not have too much influence on the statistics. The last two columns are extracted from 81 potential energy curves (PECs) from the BzDC215, S66x8, and NBC10 datasets. EBL contains interpolated equilibrium bond lengths for these 81 PECs, while EBE contains interpolated equilibrium binding energies for these 81 PECs. As with the other columns, these values are geometric means across the appropriate RMSDs for the three included datasets. Finally, the “Overall” column is an attempt at devising a single metric to portray the performance of a functional. Essentially, it is a geometric mean of four geometric means, where each of the four geometric means corresponds to a type of chemical interaction. The first type is non-covalent interactions, and includes the NCED, NCEC, NCD, EBL, and EBE values from Fig. 4, the second type is isomerization energies and includes the IE and ID values from Fig. 4, the third type is thermochemistry and includes the TCE and TCD values from Fig. 4, and finally the last type is barrier heights and is simply the BH value. For the datatypes NCED through BH, as well as EBE, the units are in kcal/mol. EBL is in Angstrom, and the “Overall” metric uses mixed units.

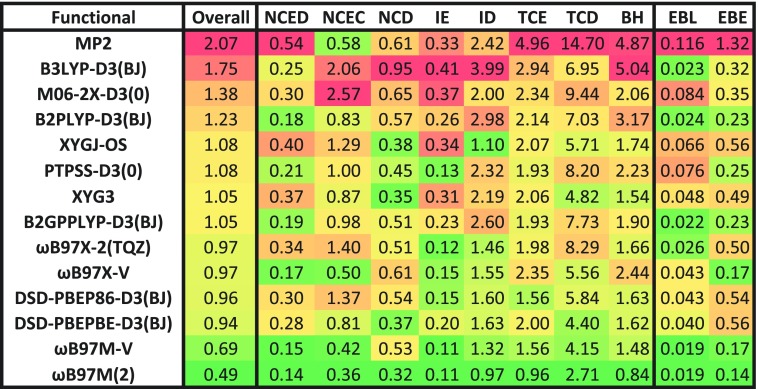
Considering the data in Fig. 4, it is evident that there are many interesting aspects to consider in the comparison of ωB97M(2) against the existing functionals. The most apples-to-apples comparison is between ωB97M(2) (Rung 5) and ωB97M-V (Rung 4) because we have developed them both using very similar approaches, and the former is a correction to the latter. It is therefore significant that ωB97M(2) matches or reduces the errors of ωB97M-V across every category that we have examined, with the overall reduction being more than 28%. While the double hybrid is computationally more costly, this is a very significant narrowing of the error distribution, particularly as ωB97M-V is the best existing Rung 4 functional based on our recent assessment.³ Based on this statistical assessment, there is no downside to using ωB97M(2) relative to ωB97M-V.

The largest improvements in ωB97M(2) relative to ωB97M-V are for thermochemistry (both TCE and TCD), barrier heights (BH), difficult non-covalent interactions (NCD), and isomerization energies (ID). These are ascribable to improvements in the correlation functional as well as to reductions in self-interaction error (particularly for the difficult categories). The improved TCD performance relative to ωB97M-V is worthy of comment because its difficult designation is due to its mostly multi-reference data and one might expect higher exact exchange to lead to poorer performance. We believe that the key reason is the use of ωB97M-V orbitals to compute the PT2 contribution, which is further reinforced by the fact that XYGJ-OS and XYG3 (both xDH-type functionals that use B3LYP orbitals) also perform reasonably well, whereas the standard double hybrids like PTPSS-D3(0) and ωB97X-2(TQZ) perform poorly. Finally we observe that there is virtually no improvement in ωB97M(2) relative to ωB97M-V for easy non-covalent interaction energies and isomerization energies, perhaps consistent with the fact that PT2 correlation offers no advantage over the VV10 non-local correlation functional for dispersion interactions.

An alternate view of the relative success of xDH functionals is offered by Grimme in Ref. 18. In this work, it is concluded that the improved performance of xDH double hybrids is not due to “better orbitals” but rather the small fraction of exact exchange in the initial orbitals, which yields a smaller occupied–virtual orbital gap and thus results in a larger amount of “effective” PT2 correlation.

Comparisons of ωB97M(2) against other double hybrids are also very interesting. This is not strictly an apples-to-apples comparison because ωB97M(2) was trained on part of these data, but since only 14 parameters are involved, and the dataset contains almost 5000 data points, we expect this influence to be minor. However, to provide full transparency, we provide a similar figure of GM-RMSDs (Fig. 6) that involves only the datasets in the validation and test sets. Relative to other double hybrids, ωB97M(2) is the best performer by a wide margin. The second and third best double hybrids are DSD-PBEPBE-D3(BJ) (92% larger overall GM-RMSD) and ωB97X-2(TQZ) (98% larger overall GM-RMSD), followed closely by three other functionals that have roughly 114% larger overall GM-RMSD. This very large gap has four main origins which contribute multiplicatively. First is the fact that ωB97M(2) is a correction to the already very accurate ωB97M-V hybrid meta-GGA which itself outperforms all other tested double hybrids. A zero correction would already be superior. Second is the fact that this is the first double hybrid functional that is semi-empirically designed using full semi-local meta-GGA functionality—our own tests in Fig. 3 (e.g., column 3 vs column 4) already show the clear advantage relative to semi-local GGA functionality. Third is the fact that combinatorial design (including the RANSAC refinement) has not previously been applied to double hybrid functionals (one measure of improvement is comparing columns 1 and 4 of Fig. 3). Finally, the use of VV10 and PT2 correlation together is likely to be important for accurately evaluating weak interactions.

FIG. 6.

Performance of 9 double hybrid density functionals, 4 hybrid density functionals, and MP2 for the validation and test components of the MGCDB84 database. The errors are geometric means (in kcal/mol) of the RMSDs for each individual dataset belonging to a given datatype.

Finally, it is interesting that based on the overall measure, MP2 is the worst-performing method considered. However, MP2 does have its strong points, namely, the NCD and ID categories, where the inclusion of 100% exact exchange is advantageous. It is also worth noting that these calculations are performed without counterpoise (CP) corrections, so it is likely that CP-corrected MP2 will perform slightly better for the NCED and NCEC datatypes. Given how crude MP2 itself is, it is therefore likely that the use of better non-local wavefunction correlation corrections could lead to potentially significant further improvements in future double hybrid functionals.

Turning to Fig. 5, there is also much that can be said, but we shall limit ourselves to a few comments. By examining the results for the select datasets, it is evident that while they mostly support the overall conclusions reported in Fig. 4, there are a few noteworthy deviations. Two datasets where ωB97M(2) is most impressive are the Shields38 dataset from the NCEC category and the AlkAtom19 dataset from the TCE category (the second best functional has more than 300% larger error in both cases). At the other extreme, for example, in the (self-interaction sensitive) TA13 dataset from the NCD category, the best overall result belongs to XYG3, and all tested double hybrids outperform ωB97M-V! The major purpose of presenting these results is to remind the reader that the overall statistics that we have mainly focused on represent the typical cases, but individual results will vary, as reflected in the outcomes for sample datasets.

VI. RECOMMENDATIONS AND SUMMARY

The ωB97M(2) double hybrid (Rung 5) density functional presented in this work completes our family of combinatorially optimized functionals, complementing B97M-V on Rung 3 and ωB97X-V and ωB97M-V on Rung 4. Regarding proper use of the functional, ωB97M(2) should be used with the def2-QZVPPD basis set without counterpoise corrections, and its grid requirements are as follows: the (75,302)/SG-0 grid is recommended as a viable coarse option (particularly for quick calculations), the (99,590)/SG-1 grid is recommended as the fine option if results near the integration grid limit are required, while for most applications, the medium-sized (75,590)/SG-1 grid can serve as a compromise between these two limits.

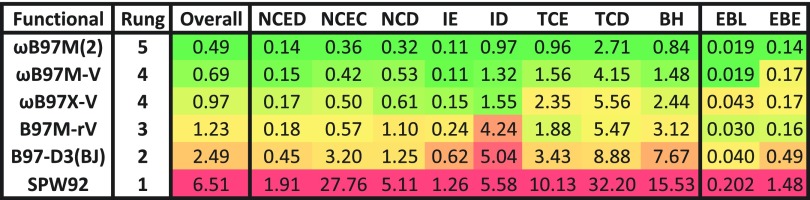
The data presented here establish that ωB97M(2) is perhaps the most accurate density functional yet defined for main-group chemistry and that ωB97M(2) is significantly more accurate than the ωB97M-V functional which it corrects. While still not a viable solution for problems with genuinely strong correlations or as accurate as high-level wavefunction-based quantum chemistry¹¹⁴ such as complete basis set limit CCSD(T), ωB97M(2) is a very promising tool for a wide spectrum of chemical applications. One way of seeing the improvements that have been obtained is via the best results yet reported at each rung of Jacob’s ladder of density functionals across the MGCDB84 database, as shown in Fig. 7. There are statistically significant reductions in RMSD upon ascending each additional rung of the ladder, with ωB97M(2) sitting at the highest level yet achieved for DFT, to our knowledge. However, these statistical improvements come with a high computational price, in the form of the need to evaluate exact exchange at Rung 4 and non-local PT2 correlation at Rung 5. The latter changes the formal computational scaling of the calculation to fifth order in molecular size from no worse than cubic at Rung 4.

FIG. 7.

A realization of Jacob’s ladder as determined by the performance of several functionals on the MGCDB84 database of nearly 5000 data points. SPW92 represents the local spin-density approximation (LSDA) on Rung 1, B97-D3(BJ) represents the generalized gradient approximation (GGA) on Rung 2, B97M-rV represents the meta-generalized gradient approximation (meta-GGA) on Rung 3, ωB97X-V and ωB97M-V represent GGA and meta-GGA hybrids, respectively, on Rung 4, and ωB97M(2) represents the double hybrids on Rung 5. The datatypes are described in Sec. III, and the statistical measure is described in Sec. V.

Due to the increased computational cost of a double hybrid, it is interesting to compare timings between B97M-V, ωB97M-V, and ωB97M(2) in order to determine the extent to which the addition of exact exchange and PT2 affect the efficacy of calculations. For this purpose, we selected three model systems: (1) hexane from AlkAtom19, (2) adenine-thymine (Watson-Crick geometry) from S22, and (3) the dodecahedron water 20-mer from H2O20Bind4. The calculations are performed in Q-Chem 5.0 with four threads. The def2-QZVPPD AO basis set and the accompanying RI-MP2 basis set is utilized, and the SCF timings are averaged across two iterations and multiplied by 10 in order to represent a full SCF calculation consisting of 10 iterations.

The timings displayed in Table IV are encouraging, since they demonstrate that at least up to 3000 basis functions, the PT2 component is not a bottleneck. For the water 20-mer, even a semi-local functional like B97M-V is more expensive to evaluate than the PT2 component, with the former requiring 3243 s per SCF iteration (9 h for 10 iterations) and the latter requiring less than 2 h to complete. With exact exchange included, 10 SCF iterations will take more than 2 days, compared to the PT2 computation time of only 2 h. Therefore, if one can afford to run a hybrid functional such as ωB97M-V, it is very likely that ωB97M(2) using the RI approximation is plausible.

TABLE IV.

Timings (in seconds) for B97M-V, ωB97M-V, and the PT2 component of ωB97M(2) for three systems: (1) hexane from AlkAtom19, (2) adenine-thymine (Watson-Crick geometry) from S22, and (3) the dodecahedron water 20-mer from H2O20Bind4. The number of atomic orbital (AO) basis functions (def2-QZVPPD) is given in the second column, while the number of auxiliary basis functions used for the resolution-of-the-identity (RI) expansions is given in the third column. The calculations are performed in Q-Chem 5.0 with four threads, and the SCF timings are averaged across two iterations and multiplied by 10 in order to represent a full SCF calculation consisting of 10 iterations.

Empty	AO BF	RI BF	B97M-V	ωB97M-V	ωB97M(2)//PT2 only
C6H6	840	1852	2 020	8 840	66
AT-WC	1566	3698	10 770	61 630	729
H2O20	2640	5740	32 430	179 220	6372

Knowledge of the relative accuracy and costs of functionals at Rungs 2-5 can facilitate their effective use in workflows to solve computational chemistry problems. In the first instance, for example, a suitably accurate Rung 5 functional such as ωB97M(2) might be applied to refine the relative energies at stationary points along a chemical reaction mechanism via single point calculations. Such calculations are very small in number relative to the hundreds or even thousands of calculations necessary to refine the geometry at all relevant stationary points or the evaluation of vibrational frequencies to obtain zero point energies and vibrational partition functions. For smaller systems where geometry optimizations are feasible with double hybrids, it will be very interesting to assess whether there are useful improvements with ωB97M(2) relative to other hybrids and double hybrids in the future. Finally, the very encouraging results reported here provide a strong incentive for the future development of more efficient methods to evaluate double hybrid DFT energies as well as analytic derivatives.