Encoding of articulatory kinematic trajectories in human speech sensorimotor cortex

Summary

When speaking, we dynamically coordinate movements of our jaw, tongue, lips, and larynx. To investigate the neural mechanisms underlying articulation, we used direct cortical recordings from human sensorimotor cortex while participants spoke natural sentences that included sounds spanning the entire English phonetic inventory. We used deep neural networks to infer speakers’ articulator movements from produced speech acoustics. Individual electrodes encoded a diversity of articulatory kinematic trajectories (AKTs), each revealing coordinated articulator movements toward specific vocal tract shapes. AKTs captured a wide range of movement types, yet they could be differentiated by the place of vocal tract constriction. Additionally, AKTs manifested out-and-back trajectories with harmonic oscillator dynamics. While AKTs were functionally stereotyped across different sentences, context-dependent encoding of preceding and following movements during production of the same phoneme demonstrated the cortical representation of coarticulation. Articulatory movements encoded in sensorimotor cortex give rise to the complex kinematics underlying continuous speech production.

Introduction

To speak fluently, we perform an extraordinary movement control task by engaging nearly 100 muscles to rapidly shape and reshape our vocal tract to produce successive speech segments to form words and phrases. The movements of the articulators—lips, jaw, tongue, and larynx—are precisely coordinated to produce particular vocal tract patterns (Fowler et al., 1980; Bernstein, 1967). Previous research that has coded these movements by linguistic features (e.g. phonemes—well studied units of sound) has found evidence that the neural encoding in the ventral sensorimotor cortex (vSMC) is related to the presumed kinematics underlying speech sounds (Bouchard, et al., 2013, Lotte et al., 2015, Carey et al., 2017). However, there are two key challenges that have precluded a complete understanding of how vSMC neural populations represent the actual articulatory movements underlying speech production.

The first challenge is to move beyond the experimentally convenient approach, taken in most studies, of studying the vSMC during isolated speech segments (Grabski et al., 2012, Bouchard, et al., 2013, Carey et al., 2017), towards studying the richer, complex movement dynamics in natural, continuous speech production. The second challenge is to go beyond categorical linguistic features (e.g. phonemes or syllables), towards describing the precise representations of movement, that is, the actual speech kinematics. Overcoming these challenges is critical to understanding the fluid nature of speech production. While speech is often described as the combination of discrete components with local invariances (i.e. vocal tract gestures (Browman & Goldstein, 1989) or phonemes), at any given time, the articulatory movements underlying the production of a speech segment may be influenced by previous and upcoming speech segments (known as coarticulation) (Hardcastle & Hewitt, 1999). For example, in “cool,” lip rounding necessary for /u/ is also present in /k/ while in “keep” /k/ is palatalized in anticipation of /i/. A central question remains as to whether cortical control invokes combinations of these primitive movement patterns to perform more complicated tasks (Bernstein, 1967, Bizzi et al., 1991, Bizzi & Cheung, 2013).

To address these challenges, we recorded high-density intracranial electrocorticography (ECoG) signals while participants spoke aloud full sentences. Our focus on continuous speech production allowed us to study the dynamics and coordination of articulatory movements not well captured during isolated syllable production. Furthermore, since a wide range of articulatory movements is possible in natural speech, we used sentences to cover nearly all phonetic and articulatory contexts in American English. Our approach allowed us to characterize sensorimotor cortical activity during speech production in terms of vocal tract movements.

A major obstacle to studying natural speech mechanisms is that the inner vocal tract movements can only be monitored for extended durations with specialized tools for tracking tongue movements with high spatial and temporal resolution, most of which are not practically compatible with intracranial recordings nor suitable for capturing naturalistic speech patterns. We overcame this obstacle by developing a statistical approach to derive the vocal tract movements from the produced acoustics. Then, we used the inferred articulatory kinematics to determine the neural encoding of articulatory movements, in a manner that was model independent and agnostic to pre-defined articulatory and acoustic patterns used in speech production (e.g. phonemes, gestures, etc.). By learning how combinations of articulator movements mapped to electrode activity, we estimated articulatory kinematic trajectories (AKTs) for single electrodes, and characterized the heterogeneity of movements that were represented through the speech vSMC.

Results

Inferring articulatory kinematics

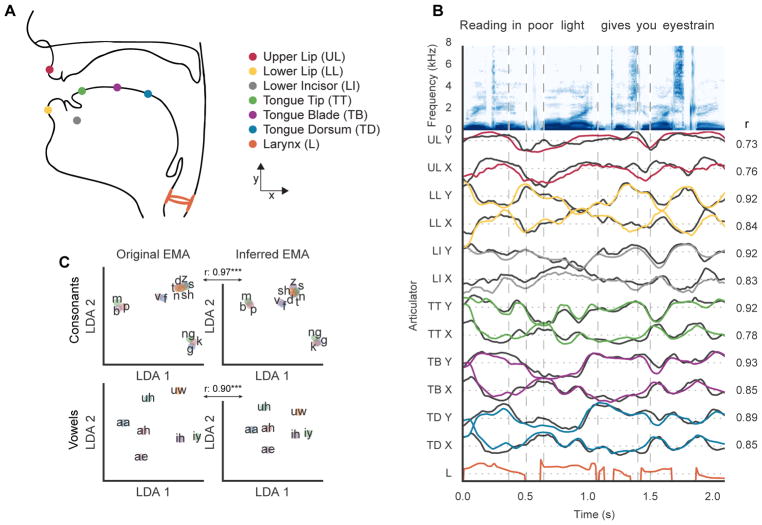
To estimate the articulatory kinematics during natural speech production, we built upon recent advances in acoustic-to-articulatory inversion (AAI) to obtain reliable estimates of vocal tract movements from only the produced speech acoustics (Richmond, 2001; Afshan et al., 2015, Mitra et. al., 2017). While existing methods for AAI work well in situations where simultaneously recorded acoustic and articulatory data are available to train for the target speaker, there are few successful attempts for AAI in which no articulatory data is available from the target speaker. Specifically for this purpose, we developed an approach for Speaker-Independent Acoustic-to-Articulatory Inversion (AAI). We trained the AAI model using publicly available multi-speaker articulatory data recorded via Electromagnetic Midsagittal Articulography (EMA), a reliable vocal tract imaging technique well suited to study articulation during continuous speech production (Berry, 2011). The training dataset comprised simultaneous recordings of speech acoustics and EMA data from 8 participants reading aloud sentences from the MOCHA-TIMIT dataset (Wrench, 1999; Richmond, et. al., 2011). EMA data for a speech utterance consisted of six sensors that tracked the displacement of articulators, critical to speech articulation (Figure 1A) in the caudo-rostral (x) and dorso-ventral (y) directions. We approximated laryngeal function by using the fundamental frequency (f0) of produced acoustics and whether or not the vocal folds were vibrating (voicing) during the production of any given segment of speech. In all, a 13 dimensional feature vector described articulatory kinematics at each time point (Figure 1B).

Figure 1. Inferred articulator kinematics.

A, Approximate sensor locations for each articulator during EMA recordings. Midsagittal movements represented as Cartesian X and Y coordinates. B, Midsagittal articulator movements inferred from both acoustic and phonetic features (in color), the trace of each reference sensor coordinate is also shown (in black). The larynx was approximated by fundamental frequency (f0) modulated by whether the segment of speech was voiced. C, Recorded articulator movements (EMA) representing consonants and vowels projected into a low dimensional (LDA) space. Inferred articulator movements projected into the same space were highly correlated with the original EMA. Correlations were pairwise distances between phonemes (consonants: r = 0.97, p<.001, vowels: r = 0.90, p<.001).

We modified the deep learning approach by Liu et. al., 2015 by incorporating phonological context to capture context dependent variance. Additionally, we spectrally warped training speakers to sound like the target (or test) speaker to improve cross-speaker generalizability (Toda et al., 2007). With these modifications, our AAI method performed markedly better than the current state-of-the-art methods within the speaker independent condition, and proved to be a reliable method to estimate articulatory kinematics. Using leave-one-participant-out cross validation, the mean correlation of inferred trajectories with ground truth EMA for a held out test participant was 0.68 ± 0.11 across all articulators and participants (0.53 correlation reported by Afshan et al., 2015). Figure 1B shows the inferred and ground truth EMA traces for each articulator during an example utterance for an unseen test speaker. There was a high degree of correlation across all articulators between the reference and inferred movements. Figure S1A shows a detailed breakdown of performance across each of the 12 articulators.

To investigate the ability of our AAI method to infer acoustically relevant articulatory movements, we trained identical deep recurrent networks to perform articulatory synthesis, i.e., predicting the acoustic spectrum (coded as 24 dimensional mel-cepstral coefficients and energy) from articulatory kinematics, for both the real and inferred EMA. We found on average that there was no significant difference (p=.4, Figures S1B and C) in the resulting acoustic spectrum of unseen utterances when using either the target speaker’s real EMA or those inferred via from the AAI method. This suggests that the difference between inferred and real EMA may largely be attributed to kinematic excursions that do not have significant acoustic effects. Other factors may also include differences in sensor placement, acquisition noise, and other speaker/recording specific artifacts that may not have acoustic relevance.

To further validate the AAI method, we examined how well the inferred kinematics preserved phonetic structure. To do so, we analyzed the phonetic clustering resulting from both real and inferred kinematic descriptions of phonemes. For one participant’s real and inferred EMA, a 200 millisecond window of analysis was constructed around the kinematics for each phoneme onset. We then used linear discriminant analysis (LDA) to model the kinematic differences between phonemes from the real EMA data. We projected the both real and inferred EMA data for phonemes into this two dimensional LDA space to observe the relative differences in phonetic structure between real and inferred EMA. We found that the phonetic clustering and relative distances between phonemes centroids were largely preserved (Figure 1C) between inferred and real kinematic data (correlation r = 0.97 for consonants and 0.9 for vowels, p<.001). Together, these results demonstrate that using kinematic, acoustic, and linguistic metrics, it is possible to obtain high-resolution descriptions of vocal tract movements from easy-to-record acoustic data.

Encoding of articulatory kinematic trajectories at single vSMC electrodes

Using AAI, we inferred vocal tract movements as traces from EMA sensor locations (Figure 1A) while participants read aloud full sentences during simultaneous recording of acoustic and high-density intracranial electrocorticography signals. To describe the relationship between vocal tract dynamics and sensorimotor cortical activity, we used a trajectory encoding model (Saleh et al., 2012) to predict each electrode’s high gamma (70 – 150 Hz) activity (z-scored analytic amplitude) (Crone et al., 2001) as a weighted sum of articulator kinematics over time. Similar to models describing spectro-temporal receptive fields (Theunissen et al., 2001), a widely used tool to describe acoustic selectivity, we used ridge regression to model high gamma activity for a given electrode from time-varying estimated EMA sensor positions. In Figure 2, we show for an example electrode (Figure 2A), the weights learned (Figure 2C) from the linear model act as a spatio-temporal filter that we then convolved with articulator kinematics (Figure 2B) to predict electrode activity (Figure 2D).

Figure 2. Neural encoding of articulatory kinematic trajectories.

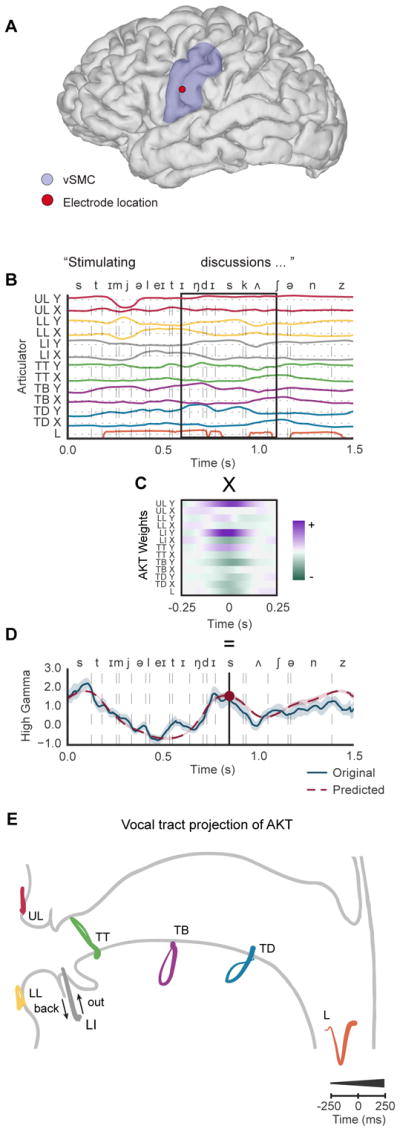
A, Magnetic resonance imaging (MRI) reconstruction of single participant brain where an example electrode is shown in the ventral sensorimotor cortex (vSMC). B, Inferred articulator movements during the production of the phrase “stimulating discussions.” Movement directions differentiated by color; positive X and Y (purple), negative X and Y (green) directions as shown in Figure 1A. C, Spatiotemporal filter resulting from fitting articulator movements to explain high gamma activity for an example electrode. Time 0 represents the alignment to the predicted sample of neural activity. Convolving the spatiotemporal filter with articulator kinematics explains high gamma activity D as shown by example electrode. High gamma from ten trials of speaking “stimulation discussions” were dynamically time warped based on the recorded acoustics and averaged together to emphasize peak high gamma activity throughout the course of a spoken phrase. E, Example electrode encoded filter weights projected onto midsagittal view of vocal tract exhibits speech-relevant articulatory kinematic trajectories (AKT). Time course of trajectories is represented by thin-to-thick lines. Larynx (pitch modulated by voicing) is one dimensional along y-axis with x-axis showing time course.

The resulting filters described specific patterns of articulatory kinematic trajectories (AKTs) (Figure 2C), which are the vocal tract dynamics that best explain each electrode’s activity. By validating on held-out data, we found that the AKT model significantly explained neural activity for electrodes active during speech in the vSMC (108 electrodes across 5 participants, mean r = 0.25 ± 0.08 up to 0.5, p<.001) compared to AKT models constructed for electrodes in other anatomical regions (p<.001, Wilcoxon signed rank tests, Figure S7).

To provide a more intuitive understanding of these filters, we projected the X and Y coordinates of each trajectory onto a midsagittal schematic view of the vocal tract (Figure 2E). Each trace represents a kinematic trajectory of an articulator with a line that thickens with time to illustrate the time course of the filter. For the special case of the larynx, we did not estimate actual movements because they are not measured with EMA, and therefore used voicing-related pitch modulations that were represented along the y-axis with the x-axis providing a time course for visualization.

We observed a consistent pattern across articulators where each exhibited a trajectory that moved away from the starting point in a directed fashion before returning to the starting point. The points of maximal movement describe a specific functional vocal tract shape involving the coordination of multiple articulators. For example, the AKT (Figure 2E) for the electrode in Figure 2A exhibits a clear coordinated movement of the lower incisor and the tongue tip in making a constriction at the alveolar ridge. Additionally, the tongue blade and dorsum move frontward to facilitate the movement of the tongue tip. The upper and lower lips remain open and the larynx is unvoiced. The vocal tract configuration corresponds to the classical description of an alveolar constriction (e.g., production of /t/, /d/, /s/, /z/, etc.). The tuning of this electrode to this particular phonetic category is apparent in Figure 2D, where both the measured and predicted high gamma activity increased during the productions /st/, /dɪs/, and /nz/, all of which require an alveolar constriction of the vocal tract.

While vocal tract constrictions have typically been described as the action of one primary articulator, the coordination among multiple articulators is critical for achieving the intended vocal tract shape (Kelso, et al., 1984). For example, in producing a /p/, if the lower lip moves less than it usually does (randomly, or because of an obstruction) the upper lip compensates and the lip closure is accomplished (Abbs & Gracco, 1984). This coordination may arise from the complex and highly overlapping topographical organization of articulator representation in the vSMC (Meier et al., 2008, Grabski et al., 2012). We asked whether, like the coordinated limb movements encoded motor cortex (Aflalo & Graziano, 2006; Saleh et al., 2012), the encoded AKTs were the result of coordinated articulator movements. Alternatively, high gamma activity could be related to a single articulator trajectory with the rest of articulators representing irrelevant correlated movements. To evaluate these hypotheses, we used a cross-validated, nested regression model to compare the neural encoding of a single articulator trajectory with the AKT model. Here, we refer to one articulator as one EMA sensor. The models were trained on 80% of the data and tested on the remaining 20% data. For each electrode, we fit single articulatory trajectory models using both X and Y directions for each estimated EMA sensor and chose the single articulator model that performed best for our comparison with the AKT model. Since each single articulator model is nested in the full AKT model, we used a general linear F-test to determine whether the additional variance explained by adding the rest of the articulators at the cost of increasing the number of parameters was significant. After testing each electrode on the data held-out from the training set, we found that the multi-articulatory patterns described by the AKT model explained significantly more variance compared to the single articulator trajectory model (F(280, 1820)>1.31, p <.001 for 96 of 108 electrodes, mean F-statistic=6.68, p<.001, Wilcoxon signed rank tests, Figure S3, mean change in R²: 99.55% ± 8.63%, Figure S4). This means that activity of single electrodes is more related to vocal tract movement patterns involving multiple articulators than those of a single articulator.

One potential explanation for this result is that single electrode neural activity in fact encodes the trajectory of a single articulator, but could appear to be multi-articulatory because of the correlated movements of other articulators due to the biomechanical properties of the vocal tract. While we would expect some coordination among articulator movements due to the intrinsic dynamics of the vocal tract, it is possible that further coordination could be cortically encoded. To evaluate these hypotheses, we examined the structure of correlations among articulators during periods of high and low neural activity for each speech-active electrode. If the articulator correlation structures were same regardless of electrode activity, the additional articulator movements were solely the result of governing biomechanical properties of the vocal tract. However, we found that articulator correlation structures differed according to whether high gamma activity was high or low (threshold at 1.5 standard deviations) (p<.001 for 108 electrodes, Bonferroni corrected) indicating that, in addition to coordination due to biomechanical properties of the vocal tract, coordination among articulators was reflected in changes of neural activity. Contrary to popular assumptions of a one-to-one relationship between a given cortical site and articulator in the homunculus, these results demonstrate that, similar to cortical encoding of coordinated movements in limb control (Saleh, et al., 2012), neural activity at a single electrode encodes the specific, coordinated trajectory of multiple articulators.

Kinematic organization of vSMC

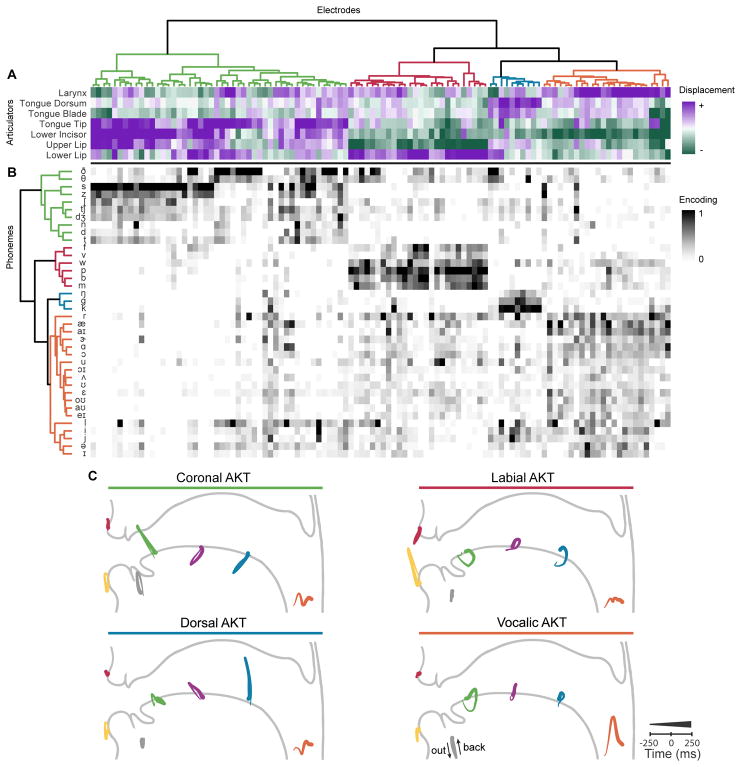
In our previous work, we used hierarchical clustering of electrode selectivity patterns to reveal the phonetic organization of the vSMC (Bouchard et al., 2013). We next wanted to examine whether clustering based upon all encoded movement trajectories, i.e. grouping of kinematically similar AKTs, yielded similar organization. Because the AKTs were mostly out-and-back in nature, we extracted the point of maximal displacement for each articulator along their principal axis of movement (see methods) to concisely summarize the kinematics of each AKT. We used hierarchical clustering to organize electrodes by their condensed kinematic descriptions (Figure 3A). To interpret the clusters in terms of phonetics, we fit a phoneme encoding model for each electrode. Similar to the AKT model, electrode activity was explained as a weighted sum of phonemes in which the value each phoneme was either 1 or 0 depending on whether it was being uttered at a given time. For each electrode, we extracted the maximum encoding weight for each phoneme. The encoded phonemes for each electrode were shown in the same order as the kinematically clustered electrodes (Figure 3B).

Figure 3. Clustered articulatory kinematic trajectories and phonetic outcomes.

A, Hierarchical clustering of encoded articulatory kinematic trajectories (AKTs) for all 108 electrodes across 5 participants. Each column represents one electrode. Kinematics of AKTs were described as a 7 dimensional vector by the points of maximal displacement along the principal movement axis of each articulator. Electrodes were hierarchically clustered by their kinematic descriptions resulting in four primary clusters. B, A phoneme encoding model was fit for each electrode. Kinematically clustered electrodes also encoded four clusters of encoded phonemes differentiated by place of articulation (alveolar, bilabial, velar, and vowels). C, Average AKTs across all electrodes in a cluster. Four distinct vocal tract configurations encompassed coronal, labial, and dorsal constrictions in addition to vocalic control.

There was a clear organizational structure that revealed shared articulatory patterns among AKTs. The first level organized AKTs by their direction of jaw movement (lower incisor goes up or down). Sub-levels manifested four main clusters of AKTs with distinct coordinative articulatory patterns. The AKTs in each cluster were averaged together yielding a representative AKT for each cluster (Figure 3C). Three of the clusters described constrictions of the vocal tract: coronal, labial, and dorsal, which broadly cover all consonants in English. The other cluster described a vocalic (vowel) AKT involving laryngeal activation and a jaw opening motion.

Instead of distributed patterns of electrode activity representing individual phonemes, we found that electrodes exhibited a high degree of specificity towards a particular group of phonemes. Electrodes within each AKT cluster also primarily encoded phonemes that had the same canonically defined place of articulation. For example, an electrode within the coronal AKT cluster was selective for /t/, /d/, /n/, /ʃ/, /s/, and /z/, all of which have a similar place of articulation. However, there were differences within clusters. For instance, within the coronal AKT cluster (Figures 3A and B, green), electrodes that exhibited a comparatively weaker tongue tip movement (less purple) had phonetic outcomes less constrained to phonemes with alveolar places of constriction (less black for phonemes in green cluster).

Hierarchical clustering was also performed on the phoneme encoding weights to identify phoneme organization to both compare with and help interpret the clustering of AKTs. These results confirm our previous description of phonetic organization of the vSMC (Bouchard, et al., 2013), as phonetic features defined by place-of-articulation were dominant. We found a strong similarity in clustering when electrodes were described by their AKTs and phonemes (Figures 3A and B), which is not surprising given that AKTs reflected specific locations of vocal tract constrictions (Figure 3C).

We observed broad groupings of electrodes that were sensitive to place-of-articulation, but within those groupings, we found differences in encoding for manner and voicing in consonant production. Within the coronal cluster, electrode encoding weights were highest for fricatives, then affricates, and followed by stops (F(3) = 36.01, p < .001, ANOVA). Conversely, bilabial stops were more strongly encoded than labiodental fricatives (p < .001, Wilcoxon signed rank tests). Additionally, we found that consonants (excluding liquids) were clustered entirely separately from vowels. This is an important distinction from our previous work (Bouchard et al., 2013), where clustering was performed independently for the consonants and vowels in a CV syllable. Again, the vocalic AKTs were defined by both laryngeal action (voicing) and jaw opening configuration. Vowels were organized by three primary clusters which correspond to low vowels, mid/high vowels, and high front vowels.

To understand how kinematically and phonetically distinct each AKT cluster was from one another, we quantified the relationship between within-cluster and between-cluster similarities for each AKT cluster using the silhouette index as a measure of clustering strength (Figure S5). The degrees of clustering strength of AKT clusters for kinematic and phonetic descriptions were significantly higher compared to shuffled distributions indicating that clusters had both similar kinematic and phonetic outcomes (p < .01, Wilcoxon signed rank tests).

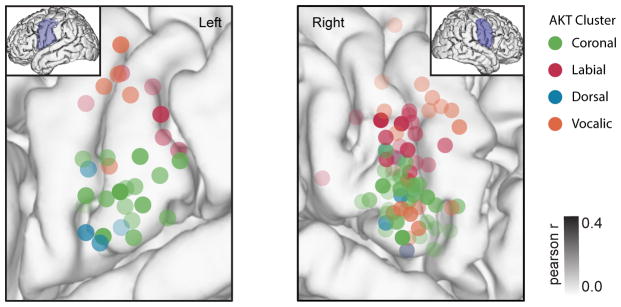
We also examined the anatomical clustering of AKTs across vSMC for each participant. While the anatomical clusterings for coronal and labial AKTs were significant (p < .01, Wilcoxon signed rank tests), clusterings for dorsal and vocalic AKTs were not. We found that only one participant had more than two dorsal AKT electrodes so we could not justly quantify the clustering strength of this cluster. Furthermore, vocalic AKTs were not well clustered because two spatial locations (dorsal and ventral LMC) were found, as previously seen in Bouchard et al., 2013. To further investigate the anatomical locations of AKT clusters, we projected electrode locations from all participants onto a common brain (Figure 4). Previous research has suggested that somatomotor maps of place of articulation are organized along the dorsal-ventral axis of the vSMC with labial constrictions were more dorsal and velar constrictions more ventral (Bouchard et al., 2013, Carey et al., 2017). We found that this coarse somatotopic organization was present for AKTs, which were spatially localized according to kinematic function and place of articulation. Since AKTs encoded coordinated articulatory movements, we did not find single articulator localization. For example, with detailed descriptions of articulator movements, we found lower incisor movements were not localized to a single region, but rather opening and closing movements were represented separately as seen in vocalic and coronal AKTs, respectively.

Figure 4. Spatial organization of vocal tract gestures.

Electrodes from 5 participants (2 left, 3 right hemisphere) colored by kinematic cluster warped to vSMC location on common MRI reconstructed brain. Opacity of electrode varies with Pearson’s correlation coefficient from kinematic trajectory encoding model.

Damped oscillatory dynamics of trajectories

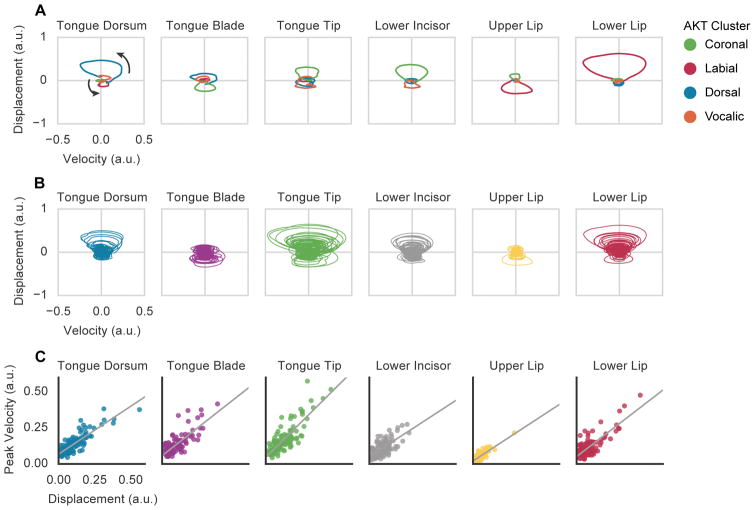
Similar to motor cortical neurons involved in limb control, we found that the encoded kinematic properties were time-varying trajectories (Hatsopoulos et al., 2007). However, in contrast to the variety of trajectory patterns found during limb control from single neurons, we observed that each AKT exhibited an out-and-back trajectory from single ECoG electrode recordings. To further investigate the trajectory dynamics of every AKT, we analyzed phase portraits (velocity and displacement relationships) for each articulator. In Figure 5A, we show the encoded position and velocity of trajectories of each articulator, along its principal axis of displacement, for AKTs of 4 example electrodes, each representative of a main AKT cluster. The trajectory of each articulator was determined by the encoding weights from each AKT. All trajectories moved outwards and then returned to the same position as the starting point with corresponding increases and decreases in velocity forming a loop. This was true even for articulators that only made relatively small movements. In Figure 5B, we show the trajectories for each articulator from all 108 AKTs, which again illustrate the out-and-back trajectory patterns. Trajectories for a given articulator did not exhibit the same degree of displacement, indicating a level of specificity for AKTs within a particular cluster. Qualitatively, we observed that trajectories with more displacement also tended to correspond with high velocities.

Figure 5. Damped oscillatory dynamics of kinematic trajectories.

A, Articulator trajectories from encoded AKTs along the principal movement axes for example electrodes from each kinematic cluster. Positive values indicate a combination of upward and frontward movements. B, Articulator trajectories for all 108 encoded kinematic trajectories across 5 participants. C, Linear relationship between peak velocity and articulator displacement (r: 0.85, 0.77. 0.83, 0.69, 0.79, 0.83 in respective order, p <.001). Each point represents the peak velocity and associated displacement of an articulator from the AKT for an electrode.

While each AKT specifies time-varying articulator movements, the governing dynamics dictating how each articulator moves, may be time-invariant. In articulator movement studies, the time-invariant properties of vocal tract gestures have been described by damped oscillatory dynamics (Saltzman & Munhall, 1989). Just like a pendulum, descriptors of movement (i.e. velocity and position) are related to one another independent of time. We found that there was a linear relationship between peak velocity and displacement for every articulator described by the AKTs (Figure 5C, r: 0.85, 0.77. 0.83, 0.69, 0.79, 0.83 in respective order, p < .001), demonstrating that AKTs also exhibited damped oscillatory dynamics. Furthermore, the slope associated with each articulator revealed the relative speed of that articulator. The lower incisor and upper lip moved the slowest (0.65 and 0.65 slopes) and the tongue varied in speed along the body with the tip moving fastest (0.66, 0.78, 0.99 slopes, respectively). These dynamics indicate that an AKT makes a stereotyped trajectory to form a single vocal tract configuration, a sub-syllabic speech component, acting as a building block for the multiple vocal tract configurations required to produce single syllables. While we were unable to dissociate whether the dynamical properties of single articulators were centrally planned or resulted from biomechanical properties of the vocal tract (Fuchs & Perrier, 2005), the velocity-position relationship strongly indicates that the AKT model encoded movements for each articulator corresponding to the intrinsic dynamics of continuous speech production.

Coarticulated kinematic trajectories

Some of the patterns observed in the detailed kinematics of speech result from interactions between successive vocal tract constrictions, a phenomenon known as coarticulation (Farnetani, 1997). Depending on the kinematic constraints of upcoming or previous vocal tract constrictions, some vocal tract constrictions may require anticipatory or carryover modifications to be optimally produced. Despite these modifications, each vocal tract constriction is often thought of as an invariant articulatory unit of speech production in which context-dependent kinematic variability results from the co-activation (i.e. temporal overlap) of vocal tract constrictions (Fowler, 1980; Browman & Goldstein, 1989; Saltzman & Munhall, 1989). We investigated whether the vSMC shared similar invariant properties by studying how vSMC representations of vocal tract AKTs interacted with one another during varying degrees of anticipatory and carryover coarticulation.

During anticipatory coarticulation, kinematic effects of upcoming phonemes may be observed during the production of the present phoneme. For example, consider the differences in jaw opening (lower incisor goes down) during the productions of /æz/ (as in ‘has’) and /æp/ (as in ‘tap’) (Figure 6A). The production of /æ/ requires a jaw opening but the degree of opening is modulated by the upcoming phoneme. Since /z/ requires a jaw closure to be produced, the jaw opens less during /æz/ to compensate for the requirements of /z/. On the other hand, /p/ does not require a jaw closure and the jaw opens more during /æp/. In each context, the jaw opens during /æ/, but to differing degrees based the compatibility of the upcoming movement.

Figure 6. Neural representation of coarticulated kinematics.

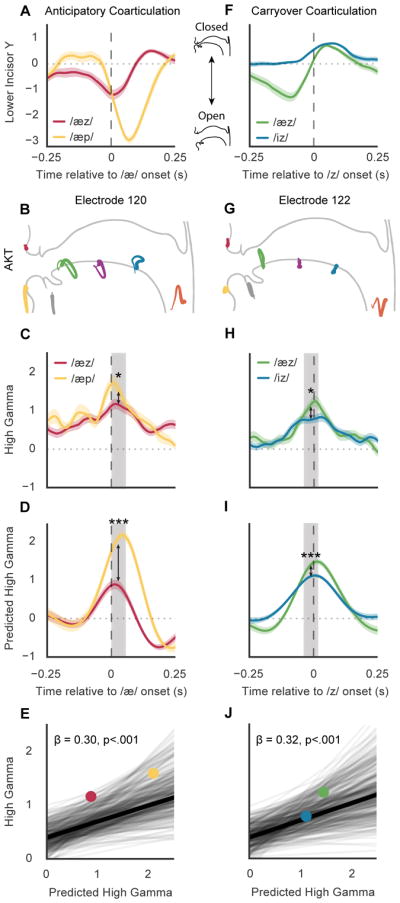
A, Example of different degrees of anticipatory coarticulation for the lower incisor. Average traces for the lower incisor (y-direction) are shown for /æz/ and /æp/ aligned to the acoustic onset of /æ/. B, Electrode 120 is crucially involved in the production of /æ/ with a vocalic AKT (jaw opening and laryngeal control), and has a high phonetic selectivity index for /æ/. C, Average high gamma activity for electrode 120 during the productions of /æz/ and /æp/. Median high gamma during 50 ms centered at the electrode’s point of peak phoneme discriminability (grey box) is significantly higher for /æp/ than /æz/ (p<.05, Wilcoxon signed ranks tests). D, Average predicted high gamma activity predicted by AKT in B. Median predicted high gamma is significantly higher for /æp/ than /æz/ (p<.001, Wilcoxon signed ranks tests). E, Mixed-effect model shows relationship of high gamma with kinematic variability due to anticipatory coarticulatory effects of following phonemes for all electrodes and phonemes (β = 0.30, SE = 0.04, χ²(1) = 38.96, p = 4e–10). Each line shows the relationship between high gamma and coarticulated kinematic variability for a given phoneme and electrode in all following phonetic contexts with at least 25 instances. Relationships from C and D for /æz/ (red) and /æp/ (yellow) are shown as points. Electrodes in all participants were used to construct the model. F, Example of different degrees of carryover coarticulation for the lower incisor. Average traces for the lower incisor (y-direction) are shown for /æz/ and /iz/ aligned to the acoustic onset of /z/. G, Electrode 122 is crucially involved in the production of /z/ with a coronal AKT, and has a high phonetic selectivity index for /z/. H, Average high gamma activity for electrode 122 during the productions of /æz/ and /iz/. Median high gamma is significantly higher for /æz/ than /iz/ (p<.05, Wilcoxon signed ranks tests). I, Average predicted high gamma activity predicted by AKT in G. Median predicted high gamma is significantly higher for /æz/ than /iz/ (p<.001, Wilcoxon signed ranks tests). J, Mixed-effect model shows relationship of high gamma with kinematic variability due to carryover coarticulatory effects of preceding phonemes for all electrodes (in all participants) and phonemes (β = 0.32, SE = 0.04, χ²(1) = 42.58, p = 6e–11). Relationships from H and I for /æz/ (green) and /iz/ (blue) are shown as points.

To investigate whether anticipatory coarticulation is neurally represented, we investigated the change in neural activity during the production /æz/ and /æp/, two contexts with differing degrees of coarticulation. While vSMC activity at the electrode population level is biased towards surrounding contextual phonemes (Bouchard & Chang, 2014), we investigated the representation of coarticulation at single electrodes. We studied high gamma of an electrode that encoded a vocalic AKT, crucial for the production of /æ/ (high phonetic selectivity index for /æ/, see methods). In Figure 6B, the AKT for electrode 120, describes a jaw opening and laryngeal vocal tract configuration. Time locked to the acoustic onset of /æ/, high gamma for electrode 120 was higher during /æp/ than /æz/ (Figure 6C). To quantify this difference, we compared the median high gamma activity during 50 ms centered at point of peak discriminability for all phonemes (p<.05, Wilcoxon signed rank tests). We also found that the predicted high gamma from the AKT was similarly higher during /æp/ than /æz/ (p<.001, Wilcoxon signed rank tests) (Figure 6D). For this electrode, we found that high gamma activity reflected changes in kinematics, as predicted by the AKT, due to anticipatory coarticulation effects.

We then examined whether coarticulatory effects were present in all vSMC electrodes during all the anticipatory contexts of every phoneme. To quantify this effect, we fit a mixed-effects model to study how high gamma for a given electrode changed during the production of a phoneme with different following phonemes. In particular, we expected that for an electrode with an AKT heavily involved in producing a given phoneme, the kinematic compatibility of the following phoneme would be reflected in its peak high gamma. The model used cross-random effects to control for differences across electrodes and phonemes and a fixed effect of predicted high gamma from the AKT to describe the kinematic variability to which each electrode is sensitive. In Figure 6E, each line shows the relationship between high gamma and coarticulated kinematic variability for a given phoneme and electrode in all following phonetic contexts with at least 25 instances. For example, one line indicates how high gamma varied with the kinematic differences during /tæ/, /tɑ/, …, /ts/, etc. Kinematic variability due to following phonemes was a significant effect of the model indicating that neural activity associated with particular articulatory movements is modulated by the kinematic constraints of the following articulatory context (β = 0.30, SE = 0.04, χ²(1) = 38.96, p = 4e–10).

In a similar fashion, we also investigated the neural representation of carryover articulation, in which kinematic effects of previously produced phonemes are observed. In Figure 6F, we again show two coarticulated contexts with varying degrees of compatibility: /æz/ (as in ‘has’) and /iz/ (as in ‘ease’). /æ/ involves a large jaw opening while /i/ does not. However, in both contexts the jaw is equally closed for /z/ and the major difference between /æz/ and /iz/ is how much the jaw must move to make the closure. While the target jaw position for /z/ was achieved in both contexts, we found that for an electrode with a coronal AKT involved in producing /z/ (Figure 6G), the difference in high gamma reflected the kinematic differences between the two preceding phonemes (Figures 6H and I). Again, we used a mixed-effects model to examine the effects of carryover coarticulation in all vSMC electrodes to find that neural activity reflected carried-over kinematic differences in electrodes with AKTs for making the present phoneme (β = 0.32, SE = 0.04, χ²(1) = 42.58, p = 6e–11) (Figure 6J). These results indicate that electrodes involved in producing a particular vocal tract configuration reflect kinematic variability due to anticipatory and carryover coarticulation.

Comparison with other encoding models

To evaluate how well AKTs are encoded in the vSMC, we compared i) the AKT model’s encoding performance with respect to other cortical regions, and ii) vSMC encoding models for alternative representations of speech.

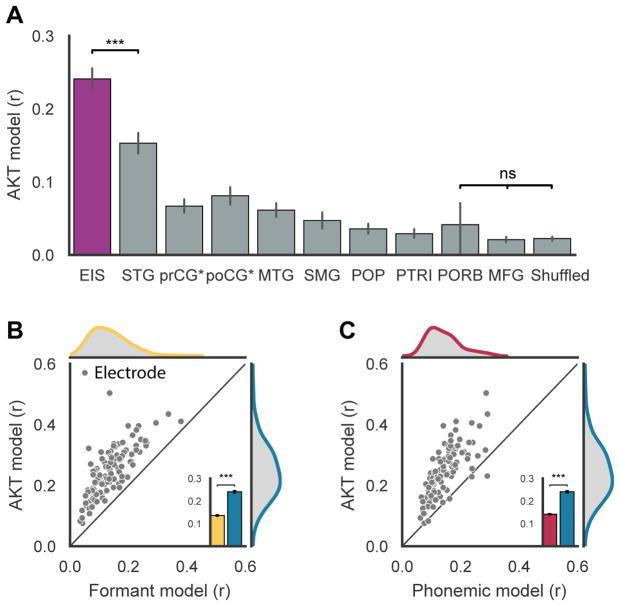
To determine how specific AKTs are to the vSMC, we compared AKT model performance (Pearson’s r on held-out data) of every cortical region recorded from across participants (Figure 7A). Besides electrodes from middle frontal gyrus (MFG) and pars orbitalis (n = 4), the AKT model significantly explained some of the variance for all recorded cortical regions above chance level (p<.001, Wilcoxon rank-sum test). However, for the considered electrodes in this study (EIS)—i.e., the speech active electrodes in the vSMC—the AKT model explained neural activity markedly better than in other cortical areas (p<1e–15, Wilcoxon rank-sum test). The other cortical areas we examined were all previously shown to be involved in different aspects of speech processing: acoustic and phonological processing (STG & MTG) (Mesgarani et al., 2013), and articulatory planning (IFG) (Flinker et al., 2015). Therefore, it was expected that cortical activity in these regions would have some correlation to the produced kinematics. The higher performance of the AKT model for EIS indicates that studying the neural correlates of kinematics may best focused in the vSMC.

Figure 7. Neural encoding model evaluation.

A Comparison of AKT encoding performance across electrodes in different anatomical regions. Anatomical regions compared: electrodes in study (EIS), superior temporal gyrus (STG), precentral gyrus* (preCG*), postcentral gyrus* (postCG*), middle temporal gyrus (MTG), supramarginal gyrus (SMG), pars opercularis (POP), pars triangularis (PTRI), pars orbitalis (PORB), middle frontal gyrus (MFG). Electrodes in study were speech selective electrodes from pre and post central gyri while preCG* and postCG* only included electrodes that were not speech selective. EIS encoding performance was significantly higher than all other regions (p<1e–15, Wilcoxon signed rank-test). B Comparison of AKT and formant encoding models for electrodes in the study. Using F1, F2, and F3, the formant encoding model was fit in the same manner as the AKT model. Each point represents the performance of both models for one electrode. C Comparison of AKT and phonemic encoding models. The phonemic model was fit in the manner as the AKT model except with phonemes described as one hot vectors. The best single phoneme predicting electrode activity was said to be the encoded phoneme of that particular electrode and that r-value was reported along with the r-value of the AKT model. Pearson’s r was computed on held-out data from training for all models. In both comparisons, the AKT performed significantly higher (p<1e–20, Wilcoxon signed rank-test)

While AKTs were best encoded in vSMC, there may be alternative representations of speech that may better explain vSMC activity. We evaluated vSMC encoding of both acoustics (described here by using the first three formants: F1, F2, and F3) and phonemes with respect to the AKT model. Each model was fit in the same manner as the AKT model and performance compared on held-out data from training. If each vSMC electrode represented acoustics or phonemes, we would expect a higher model fit for that representation than the AKT model. Due to the similarity of these representations, we expected the encoding models to be highly correlated. It is worth noting that the inferred articulator movements are unable to provide an account of movements without correlations to acoustically significant events, a key property that would be invaluable for differentiating between models. Furthermore, while acoustics and phonemes are both complete representations of speech, the midsagittal movements of a few vocal tract locations captured by EMA are a partial description of speech relevant movements of the vocal tract in that we are missing palate, lateral and oropharyngeal movements. Even so, we found that articulator movements were encoded markedly better than both the acoustic and phoneme encoding models despite the limitations of the AKT model (Figure 7B & C, p<1e–20, Wilcoxon rank-sum test).

These comparisons were consistent with previous findings that vSMC encoding is tuned to articulatory features (Bouchard et al., 2013; Cheung et al., 2015). During single vowel production, vSMC showed encoding of directly measured kinematics over phonemes and acoustics (Conant et al., 2018). Furthermore, vSMC is also responsible for non-speech voluntary movements of the lips, tongue, and jaw, in behaviors such as swallowing, kissing, oral gestures. While vSMC is critical for speech production, it is not the only vSMC function. Indeed, when vSMC is injured, patients have facial and tongue weakness, in addition to dysarthria. When vSMC is electrically stimulated, we observe movements -- not speech sounds, phonemes, or auditory sensations (Penfield & Boldrey, 1937; Breshears et al., 2015).

Decoding articulator movements

Given that we could determine encoding of AKTs at single electrodes, we next wanted to understand how well we could decode vocal tract movements from the population of electrodes. We decoded articulatory movements during sentence production with a long short-term memory recurrent neural network (LSTM), an algorithm well suited for time series regression (Hochreiter & Schmidhuber, 1997). The performance of the decoder was high, especially in light of the articulatory variance lost due to process of inferring kinematics and the neural variance unrecorded by the ECoG grid (i.e. within the central sulcus or at a resolution finer than the capability of the electrodes). For an example sentence (Figure 8A), the predicted articulator movements from the decoder closely matched with the inferred articulator movements from the acoustics. All of the articulator movements were well predicted across 100 held-out sentences significantly above chance (mean r: 0.43, p<.001) (Figure 8B). Prior work has demonstrated the possibility of decoding phonemes from ECoG recordings (Mugler et al., 2014) with automatic speech recognition techniques to decode full sentences (Herff et al., 2015) in addition to phrase classification with non-invasive recordings (Wang et al. 2017). Here, we show that decoding articulator movements directly from neural signals may be an additional approach for decoding speech.

Figure 8. Decoded articulator movements from vSMC activity.

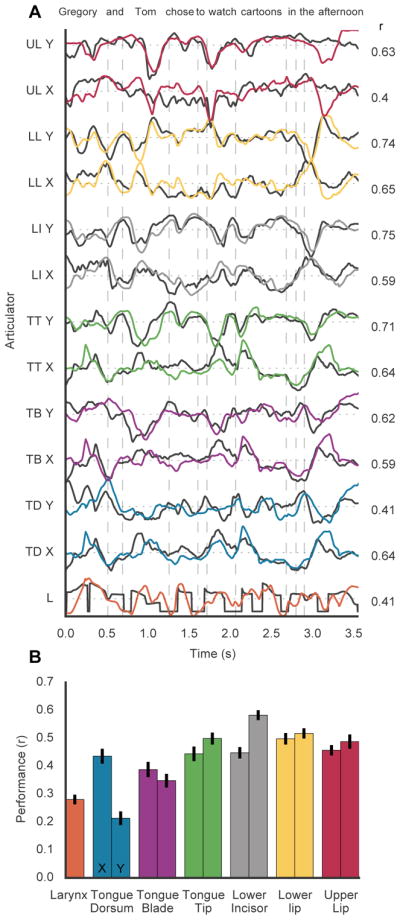
A, Original (black) and predicted (colored) X and Y coordinates of articulation movements during the production of an example held-out sentence. Pearson’s correlation coefficient (r) for each articulator trace. B, Average performance (correlation) for each articulator for 100 sentences held out from training set.

Discussion

Our goal was to demonstrate how neural activity in human sensorimotor cortex represents the movements of vocal tract articulators during continuous speech production. We used a novel acoustic-to-articulatory inversion (AAI) method to infer vocal tract movements, which we then related directly to high-resolution neural recordings. By describing vSMC activity with respect to detailed articulatory movements, we demonstrate that discrete neural populations encode articulatory kinematic trajectories (AKTs), a level of complexity that has not been observed using simpler syllable-level speech tasks in our previous work.

There are two important features of the AKTs that are encoded in the vSMC. First, encoded articulator movements are coordinated to make a specific vocal tract configuration. While the structure of coordination across articulators has been shown shown to be task-specific (e.g. different coordinative patterns during /p/ versus /z/) (Kelso et al., 1984), cortical control of this coordination has not been previously studied. However, studies in limb control have discovered single motor cortical neurons that encode complex coordinated movements involving both the arm and hand with specific functions (Aflalo & Graziano, 2006; Saleh et al., 2012). While previous studies have investigated vSMC activity on the basis of whether or not a given articulator is involved (Bouchard et al., 2013), we studied vSMC activity using detailed articulatory trajectories that suggest, similar to limb control, coordinated movements across articulators for specialized vocal tract configurations are encoded at the single electrode level. For example, the coordinated movement to close the lips is encoded rather than individual lip movements. This finding is consistent with studies where stimulation of localized neural populations in non-human primates has revealed functional action maps of complex arm and hand movements (Graziano et al., 2002). For speech, we found four major clusters of AKTs that were differentiated by place of articulation and covered the main vocal tract configurations that comprise American English. At the sampling level of ECoG, cortical populations encode sub-syllabic coordinative movements of the vocal tract.

The second important feature of AKTs is the trajectory profile itself. Encoded articulators moved in out-and-back trajectories with damped oscillatory dynamics. During limb control, single motor cortical neurons have been also found to encode time-dependent kinematic trajectories, but the patterns were very heterogeneous and did not show clear spatial organization (Hatsopoulos et al., 2007). It is possible that individual neurons encode highly specific movement fragments that combine together to form larger movements represented by ensemble activity at the ECoG scale of resolution. For speech, these larger movements correspond to canonical vocal tract configurations. While motor cortical neurons encoded a variety of trajectory patterns, we found that AKTs only exhibited out-and-back profiles which may be a fundamental movement motif in continuous speech production.

With both coordinative and dynamical properties, each AKT appeared to encode the movement necessary to make a specific vocal tract configuration and return to a neutral position. Although we have described neural activity associated with articulatory movements without regard to any particular theory of speech production, the AKTs discovered here bear a striking resemblance to the vocal tract gestures theorized to be the articulatory units of speech production (Fowler et al., 1980; Browman & Goldstein, 1989). Each vocal tract gesture is described as a coordinated articulatory pattern to make a vocal tract constriction. Like the AKTs, each vocal tract gesture has been characterized as a time-invariant system with damped oscillatory dynamics (Saltzman and Munhall, 1989).

Articulatory theories suggest that each vocal tract gesture is an invariant unit and that the variability in the kinematics of continuous speech directly results from the temporal overlapping of successive gestures (Saltzman and Munhall, 1989). A particularly interesting phenomenon is that some vocal tract gestures are incompatible with one another in that the two vocal tract patterns require opposing movements of the articulators. This incompatibility results in a coarticulated compromise of target vocal tract patterns while compatible gestures are able to combine without inhibiting any necessary articulator movements (Farnetani, 1991; Farnetani & Faber, 1992). Despite the theorized invariance of vocal tract gestures, we found that AKTs encoded in vSMC neural activity reflected kinematic differences due to constraints of the phonetic or articulatory context. While the invariant properties of vocal tract gestures may be represented elsewhere in higher order speech processes, the AKTs encoded in the vSMC represent coarticulation of successive AKTs.

The neural encoding of coarticulation also suggests that the vSMC does not locally encode phonemes. Phonemes by definition are segmental, perceptually defined, discrete units of sound. We would expect that an electrode encoding a particular set of phonemes as features would exhibit the same patterns of activation during the production of the same phoneme regardless of preceding or following phonemes and the accompanying kinematic constraints. However, we found that not only was there a difference in neural activity between productions of the same phoneme in different contexts, but also that the differences in kinematics partially explained the changes in neural activity. Furthermore, a direct comparison showed that AKTs were better encoded than both phoneme and acoustic models at single electrodes. We find the neural encoding of coarticulation to offer compelling support for AKTs as dominant features encoded in the speech sensorimotor cortex.

In summary, we described the cortical encoding of the movements underlying the rich dynamics of continuous speech production. These findings paint a new picture about the cortical basis of speech, and perhaps other sequential motor tasks. Coordinated articulator trajectories are locally encoded and fluidly combine while taking into account the surrounding movement context to produce the wide range of vocal tract movements we require to communicate. The insights gained by understanding the vSMC in terms of articulatory movements will help frame new questions of higher order planning and its realization as speech, or more broadly, movement.

STAR Methods

CONTACT FOR RESOURCE SHARING

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Edward Chang (Edward.Chang@ucsf.edu).

EXPERIMENTAL MODEL AND PARTICIPANT DETAILS

Participants

Five human participants (Female, ages: 30, 31, 43, 46, 47) underwent chronic implantation of high-density, subdural electrode array over the lateral surface of the brain as part of their clinical treatment of epilepsy (2 left hemisphere grids, 3 right hemisphere grids). Participants gave their written informed consent before the day of the surgery. No participants had a history of any cognitive deficits that were relevant to the aims of the present study. All participants were fluent in English. All procedures were approved by the University of California, San Francisco Institutional Review Board.

METHOD DEAILS

Experimental Task

Participants read aloud 460 sentences from the MOCHA-TIMIT database (Wrench, 1999). Sentences were recorded in 9 blocks (8 of 50, and 1 of 60 sentences) spread across several days of patients’ stay. Within each block, sentences are presented on a screen, one at a time, for the participant to read out. The order was random and participants were given a few seconds of rest in between. MOCHA-TIMIT is a sentence-level database, a subset of the TIMIT corpus designed to cover all phonetic contexts in American English. Each participant read each sentence 1–10 times. Microphone recordings were obtained synchronously with the ECoG recordings.

Data acquisition and signal processing

Electrocorticography was recorded with a multi-channel amplifier optically connected to a digital signal processor (Tucker-Davis Technologies). Speech was amplified digitally and recorded with a microphone simultaneously with the cortical recordings. ECoG electrodes were arranged in a 16 × 16 grid with 4 mm pitch. The grid placements were decided upon purely by clinical considerations. ECoG signals were recorded at a sampling rate of 3,052 Hz. Each channel was visually and quantitatively inspected for artifacts or excessive noise (typically 60 Hz line noise). The analytic amplitude of the high-gamma frequency component of the local field potentials (70 – 150 Hz) was extracted with the Hilbert transform and down-sampled to 200 Hz. Finally, the signal was z-scored relative to a 30 second window of running mean and standard deviation, so as to normalize the data across different recording sessions. We studied high-gamma amplitude because it has been shown to correlate well with multi-unit firing rates and has the temporal resolution to resolve fine articulatory movements (Crone et al., 2006).

Phonetic and phonological transcription

For the collected speech acoustic recordings, transcriptions were corrected manually at the word level so that the transcript reflected the vocalization that the participant actually produced. Given sentence level transcriptions and acoustic utterances chunked at the sentence level, hidden Markov model based acoustic models were built for each participant so as to perform sub-phonetic alignment (Prahallad et. al., 2006). Phonological context features were also generated from the phonetic labels, given their phonetic, syllabic and word contexts.

Speaker-Independent Acoustic-to-Articulatory Inversion (AAI)

To perform articulatory inversion for a target participant for whom only acoustic data is available, we developed a method, we refer to as “Speaker-Independent AAI”, where parallel EMA and speech data were simulated for the target speaker. In contrast to earlier approaches for speaker-independent AAI, where normalization is performed to remove speaker identity from acoustics, we accomplished the opposite goal of transforming the 8 EMA participants’ spectral properties to match those of the target speaker for whom we want to estimate vocal tract kinematics. To transform the acoustics of all data to the target speaker, we applied voice conversion (as proposed in Toda et al., 2007) to transform the spectral properties of each EMA speaker to match those of the target participant. This method assumes acoustic data corresponding to the same sentences for the two participants. When parallel acoustic data was not available across participants in our case (the mngu0 corpus uses a different set of sentences than the MOCHA-TIMIT corpus), concatenative speech synthesis were used to synthesize comparable data across participants (Hunt and Black ‘94).

Since there was no information about the target speaker’s kinematics, we back off to using a participant and articulator normalized average of the 8 speakers’ articulatory space. For cross-participant utilization of kinematic data, for each of the training speakers, we use an articulator specific z-scoring across each participant’s EMA data. This ensured that the target speaker’s kinematics were an unbiased average across all available EMA participants. The kinematics were described by 13 dimensional feature vectors (12 dimensions to represent X and Y coordinates of 6 vocal tract points and fundamental frequency, F0, representing the Laryngeal function).

We used 24 dimensional mel-cepstral coefficients as the spectral features. Both kinematics and acoustics were sampled at a frequency 200 Hz (each feature vector represented a 5 ms segment of speech). Additionally, phonetic and phonological information corresponding to each frame of speech was coded as one-hot vectors and padded onto the acoustic features. These features included phoneme identity, syllable position, word part of speech, positional features of the current and of the neighboring phoneme and syllable states. We found that contextual data provided complementary information to acoustics and improved inversion accuracies.

Using these methods for each EMA participant-to-target participant pair, we were able to create a simulated dataset of parallel speech and EMA data, that were both customized for the target participant. For training the inversion model itself, we used a deep recurrent neural network based articulatory inversion technique (replicating Liu. et al., 2015) to learn a mapping from spectral and phonological context to a speaker generic articulatory space. Following (Liu., et. al., 2015) an optimal network architecture with a 4 layer deep recurrent network with two feedforward layers (200 hidden nodes) and two bidirectional LSTM layers (with 100 LSTM cells) was chosen. The trained inversion model was then applied to all speech produced by the target participant to infer articulatory kinematics in the form of Cartesian X and Y coordinates of articulator movements. The network was implemented using Keras (Chollet et. al., 2015), a deep learning library running on top of a Tensorflow backend.

Electrode selection

We selected electrodes located on either the precentral and postcentral gyri that had distinguishable high gamma activity during speech production. We measured the separability of phonemes using the ratio of between-class to within-class variability (F statistic) for a given electrode across time. We chose electrodes with a maximum F statistic of 8 or greater. This resulted in a total of 108 electrodes across the 5 participants with robust activity during speech production.

Encoding models

To uncover the kinematic trajectories represented in electrodes, we used linear encoding models to describe the high gamma activity recorded at each electrode as a weighted sum of articulator kinematics over time. This model is similar to the spectrotemporal receptive field, a model widely used to describe selectivity for natural acoustic stimuli (Theunissen et al., 2001). However, in our model, articulator X and Y coordinates are used instead spectral components. The model estimates the time series x_i(t) for each electrode i as the convolution of the articulator kinematics A, comprised of kinematic parameters k, and a filter H, which we refer to as the articulatory kinematic trajectory (AKT) encoding of an electrode.

$${\widehat{x}}_i(t)=\sum _k^K\sum _{\tau }^T{H}_i(k,\tau )A(k,t-\tau )$$

Since our task was not designed to differentiate between motor commands and somatosensory feedback, we designed our filter to use a 500 ms window of articulator movements centered about the high gamma sample to be predicted. Movements occurring before the sample of high gamma are indicated by a negative lag while movements occurring after the high gamma sample are indicated by a positive lag. The 500 ms window was chosen to both maximize the performance of the AKT model (Figure S6) and allow full visualization of the AKTs. While Figure S6, indicates the filters need only be 200 ms long for optimal performance, we found that extending filters to 500 ms with appropriate regularization ensured that we could visualize every AKT in its entirety. Some AKTs encoded movements occurring well before or after the corresponding neural activity resulting AKTs cutoff using a 200 ms window. L2 regularization ensured that weights from time points not encoding an articulatory trajectory (e.g. at 250 ms before the neural sample) had no weighting and did not affect interpretability of the AKTs.

Additionally, we fit acoustic and phoneme encoding models to electrode activity. Instead of articulator X and Y coordinates, we used formants (F1, F2, and F3) as a description of acoustics and a binary description of the phonemes produced during a sentence. Each feature indicated whether a particular phoneme was being produced or not with a 1 or 0, respectively.

The encoding models were fit using ridge regression and trained using cross-validation with 70% of the data used for training, 10% of the data held-out for estimating the ridge parameter, and 20% held out as a final test set. The final test set consisted of sentences produced during entirely separate recording sessions from the training sentences. Performance was measured as the correlation between the predicted response of the model and the actual high gamma measured in the final test set.

Hierarchical clustering

We used Ward’s method for agglomerative hierarchical clustering. Clustering of the electrodes was carried out solely on the kinematic descriptions for encoded kinematic trajectory of each electrode. To develop concise kinematic descriptions for each kinematic trajectory, we extracted the point of maximal displacement for each articulation. We used principal components analysis on each articulator to extract the direction of each articulator that explained the most variance. We then projected the filter weights onto each articulator’s first principal component and chose the point with the highest magnitude. This resulted in length 7 vector with each articulator described by the maximum value of the first principal component. Phonemes were clustered based on the phoneme encoding weights for each electrode. For a given electrode, we extracted the maximum encoding weight for each phoneme during a 100 ms window centered at the point of maximum phoneme discriminability (peak F statistic) for the given electrode.

Cortical surface extraction and electrode visualization

To visualize electrodes on the cortical surface of a participant’s brain, we used a normalized mutual information routine in SPM12 to co-register the preoperative T1 MRI with a postoperative CT scan containing electrode locations. We used Freesurfer to make pial surface reconstructions. To visualize electrodes across participants on a common MNI brain, we performed nonlinear surface registration using a spherical sulcal-based alignment in Freesurfer, aligned to the cvs avg35 inMNI152 template (Fischl et al., 1999). While the geometry of the grid is not maintained, the nonlinear alignment ensures that electrodes on a gyrus in the participant’s native space will remain on the same gyrus in the atlas space.

Decoding model

To decode articulatory movements, we trained a long short-term memory (LSTM) recurrent neural network to learn the mapping from high gamma activity to articulatory movements. LSTM are particularly well suited for learning mappings with time-dependent information (Hochreiter & Urgen Schmidhuber, 1997). Each sample of articulator position was predicted by the LSTM using a window of 500 ms of high gamma activity, centered about the decoded sample, from all vSMC electrodes. The decoder architecture was a 4 layer deep recurrent network with two feedforward layers (100 hidden nodes each) and two bidirectional LSTM layers (100 cells). Using Adam optimization and dropout (40% of nodes), we trained the network to reduce mean squared error of the decoded and actual output. The network was implemented using Keras (Chollet et. al., 2015), a deep learning library running on top of a Tensorflow backend.

QUANTIFICATION AND STATISTICAL ANALYSIS

Nested encoding model comparison

We used a nested regression model to compare the neural encoding of a single articulator trajectory with the AKT model (Allen, 1997). For each electrode, we fit single articulatory trajectories models using both X and Y directions for each EMA sensor and chose the single articulator model that with the lowest residual sum of squares (RSS) on held-out data. From RSS values for the full (2) and nested (1) models, we compared the significance of the explained variance by calculating an F statistic for each electrode.

$$F=\frac{\left(\frac{{\mathit{RSS}}_1-{\mathit{RSS}}_2}{p_2-p_1}\right)}{\frac{{\mathit{RSS}}_2}{n-p_2}}$$

p and n are the number of model parameters and samples used in RSS computation, respectively. An F statistic greater than the critical value defined by the number of parameters in both models and confidence interval indicates that the full model (AKT) explains statistically significantly explains more variance than the nested model (single articulator) after accounting for difference in parameter numbers.

Correlation structure comparison

To test whether the correlational structure of articulators (EMA points) was different between periods of low and high gamma activity for a speech responsive electrode, we split the inferred articulator movements into two data sets based on whether the z-scored high gamma activity of given electrode for that sample was above the threshold (1.5). We then randomly sampled 1000 points of articulator movement from each data set to construct two cross-correlational structures between articulators. To quantify the difference between the correlational structures, we computed the Euclidean distance between the two structures. We then sampled an additional 1000 points from the below threshold data set to quantify the difference between correlational structures within the sub-threshold data. We repeated this process 1000 times for each electrode and compared the two distributions of Euclidean distances with a Wilcoxon rank sum test (Bonferroni corrected for multiple comparisons) to determine whether correlational structures of articulators differed in relation to high or low high gamma activity of an electrode.

Silhouette analysis

To assess cluster separability, we computed the silhouette index for each electrode to compare how well each electrode matched its own cluster based on the given feature representation. The silhouette index for an electrode is calculated by taking the difference between the average dissimilarity with all electrodes within the same cluster and the average dissimilarity with electrodes from the nearest cluster. This value is then normalized by taking the maximum value of the previous two dissimilarity measures. A silhouette index close to 1 indicates that the electrode is highly matched to its own cluster. 0 indicates that that the clusters may be overlapping, while −1 indicates that the electrode may be assigned to the wrong cluster.

Phoneme Selectivity Index (PSI)

To determine the phoneme selectivity of each electrode, we use the statistical framework as described in Mesgarani et al., 2014 to test whether the high gamma activity of an electrode is significantly different during the productions of two different phonemes. For a phoneme pair and a given electrode, we created two distributions of high gamma activity from data acoustically aligned to each phoneme. We used a 50 ms window of activity centered on the time point with the peak F statistic for that electrode. We used a non-parametric statistical hypothesis test (Wilcox rank-sum test) to assess whether these distributions have different medians (p<0.001). The PSI is the number of phonemes that have statistically distinguishable high gamma activity for a given electrode. A PSI of 0 indicates that no other phonemes have a distinguishable high gamma activity. Whereas, a PSI of 40 indicates that all other phonemes have distinguishable high gamma activity.

Mixed effects model

To examine the relationship between high gamma and coarticulated kinematics, we used a mixed-effects model with several crossed random effects. In particular, for a given electrode, we computed the “peak activity” by taking the median high gamma activity during a 50 ms window centered about the peak F statistic for that electrode (see PSI method) during the production of a target phoneme. We then took the mean peak activity for each unique phoneme pair (target phoneme preceded by context phoneme). For each electrode, we only considered phoneme pairs with at least 25 instances and a target PSI > 25. This helped stabilize the means and targeted electrodes that presumably encoded the AKT necessary to produce the target phoneme. In Figure 6C,D,H,I, we extended /z/ to include /z/ and /s/, and /p/ to include /p/ and /b/ since, from an EMA standpoint, the articulation is nearly identical and it increased the number of coarticulated instances we could analyze, thus decreasing biases from other contextual effects and variability from noise. In a similar fashion to high gamma, we computed high gamma activity predicted by the AKT model to provide insight into the kinematics during the production of a particular phoneme pair. Our mixed-effects model described high gamma from a fixed effect of kinematically predicted high gamma with crossed random effects (random slopes and intercepts) controlling for difference in electrodes, and target and context phonemes (Barr et al., 2013). To determine model goodness, we used ANOVA to compare the model with a nested model that retained the crossed random effects but removed the fixed effect. The mixed-effects model was fit using the lme4 package in R (Baayen et al., 2008).

DATA AND SOFTWARE AVAILABILITY

All analyses were conducted in Python using NumPy, SciPy, Pandas, and scikit-learn unless otherwise specified. Code and data are available upon request.

Highlights.

• Sensorimotor cortex encodes articulatory kinematic trajectories (AKTs) in speech

• AKTs reveal coordinated movements of the tongue, lips, jaw, and larynx

• AKTs manifest stereotyped trajectory profiles of vocal tract articulators

• AKTs show context-dependent encoding of movements due to coarticulation