Abstract
A block copolymer self-consistent field theory (SCFT) model is used for direct analysis of experimental X-ray scattering data obtained from thin films of polystyrene-b-poly(methyl methacrylate) (PS-b-PMMA) made from directed self-assembly. In a departure from traditional approaches, which reconstruct the real space structure using simple geometric shapes, we build on recent work that has relied on physics-based models to determine shape profiles and extract thermodynamic processing information from the scattering data. More specifically, an SCFT model, coupled to a covariance matrix adaptation evolutionary strategy (CMAES), is used to find the set of simulation parameters for the model that best reproduces the scattering data. The SCFT model is detailed enough to capture the essential physics of the copolymer self-assembly, but sufficiently simple to rapidly produce structure profiles needed for interpreting the scattering data. The ability of the model to produce a matching scattering profile is assessed, and several improvements are proposed in order to more accurately recreate the experimental observations. The predicted parameters are compared to those extracted from model fits via additional experimental methods and with predicted parameters from direct particle-based simulations of the same model, which incorporate the effects of fluctuations. The Flory–Huggins interaction parameter for PS-b-PMMA is found to be in agreement with reported ranges for this material. These results serve to strengthen the case for relying on physics-based models for direct analysis of scattering and light signal based experiments.
Introduction
Scattering based metrologies have become an important characterization method for nanoscale structures for integrated circuit and memory storage device applications. The need to fabricate small, nanoscale structures for these applications has led to enormous advances in non-traditional nanolithographic techniques1–4 that require non-invasive metrology in order to understand how to best optimize the processing methods. Development of such metrologies is an integral part of the design process for advanced nanofabrication technologies that rely on molecular assembly processes. Interpretation of scattering data has traditionally relied on simple shape models (e.g., stacks of trapezoids) that do not account for material properties and thermodynamic processing information. Of the alternative nanomanufacturing methods, block copolymer (BCP) directed self-assembly (DSA)5–10 offers one of the least expensive and highest throughput routes.11 As with all lithographic patterning techniques, one of the central challenges in having DSA become the method of choice for next-generation nanolithography is achieving complete control over defectivity in the system.12 In this regard, it is important to note that if a given BCP morphology is not perfectly commensurate with the underlying DSA template, undesired metastable periodic structures may arise, with features that are not observable from surface measurements. 13 It is therefore important that non-invasive measurement techniques, capable of providing high-throughput, cross-sectional information be developed to supplement traditional top-down microscopy methods.
An extensive body of work has established that theoretical approaches, most notably self-consistent field theory (SCFT)14 and theoretically informed coarse-grained (TICG)15 models, are capable of identifying stable and metastable BCP structures with considerable fidelity. The predictive nature of such approaches raises the tantalizing prospect of integrating such models directly into the characterization process, in lieu of simple shape fitting techniques, thereby greatly enhancing the underlying metrology and extracting additional information from the experimental data that cannot be accessed by other means. Our recent work has shown that this is indeed possible with fully three-dimensional particle-based simulations; 16 here we expand on that context and demonstrate that it is also possible with SCFT.
DSA has been a successful method for producing large arrays of periodic structures17–19 with feature sizes on the order of 10 nm. In particular, for BCP DSA, two main processes have been used to template the BCP. Graphoepitaxy (aka topographical DSA) uses physical modifications of the substrate via trenches and post patterns with a commensurate period of the BCP to direct the self-assembly.20 Graphoepitaxy is generally used for templating cylindrical or sphere forming BCPs, such that the patterned features exist in a monolayer17,20–24 or controlled number of multilayers25 and uses a supplemental lithography technique such as electron beam lithography26 or nanoimprint lithography27 to fabricate the DSA template. Chemoepitaxy (aka chemical DSA) uses modified surface chemistry of the substrate via self-assembled monolayers, polymer brushes, and other surface alterations in a manner that creates controlled patterns for assembly of the BCP.28 Chemoepitaxy has been used to direct the assembly of lamellae forming BCPs, such that the desired morphology goes through the entire film thickness,28–33 and it has also been applied to cylinder and sphere-forming materials.34–37 For applications that require pattern transfer by etching, chemoepitaxy might offer advantages; as such, but without loss of generality, in this study we focus on DSA of block copolymers on chemical patterns.
Polymer thin films are difficult to characterize. While there has been some success utilizing real space methods such as 3D transmission electron microscopy,38,39 sensitivity to the electron beam and a lack of contrast can limit the range of materials that can be probed. More importantly, characterization by 3D TEM is limited to relatively small areas. X-ray scattering methods have been used extensively to characterize the structure and thermodynamics of BCPs.40–43 Grazing incidence small angle X-ray scattering (GISAXS) can be used to examine such samples (both with hard and soft X-rays), but requires that complex structure models be used to interpret the data, leading to considerable uncertainty regarding the uniqueness of the corresponding solutions,44 and placing limits on the overall approach.45–47 Critical dimension small angle X-ray scattering (CDSAXS),48–50 a transmission X-ray scattering technique, is much simpler to model than GISAXS. However, for polymeric samples, the contrast between the different organic polymer species is limited when high energy X-rays are used, and little scattering between domains occurs. In contrast, soft X-rays are well suited for characterization of sub-100 nm thick films.51,52 Soft X-rays utilize the sensitivity to the atomic absorption edge to significantly enhance the contrast between components as a function of the specific film chemistry.51,53–56 The contrast enhancement between components afforded by soft X-rays is important, as most organic materials have a difference in electron density (that produces contrast for higher energy X-rays) of less than 10%. The advantages of CDSAXS and resonant soft X-rays (res-CDSAXS) therefore enable reconstruction of the three-dimensional morphology of thin polymer films.55,57,58
Both SCFT14,17,23–25,59–67 and TICG15,33,68 simulations can provide important insights into the thermodynamic and template conditions under which various periodic morphologies arise. Importantly, they have been able to identify conditions under which defects are more prone to appear, and interfere with the formation of “ideal” structures. Theory and simulations have also been able to identify the pathways for annihilation of such defects.69–71
Recent work has shown how theory and simulations can be coupled to inverse algorithms in order to identify optimal conditions for assembly of sought after morphologies in DSA.72–79 Such an approach allows a user to determine what parameters to use in order to arrive at a “target” morphology. Building on that concept, one can turn “inverse design” on its head, and define experimental data from CDSAXS measurements as the “target structure”; it is then possible to rely on inverse algorithms to determine the set of model parameters needed to obtain that scattering intensity profile. Indeed, such an approach was introduced in a recent study where TICG simulations were used to extract model parameters from CDSAXS and GISAXS experiments.16 More specifically, as many as 15 process variables and materials characteristics were inferred from measurements of the structure of symmetric block copolymers assembled in sparse patterns of lines. In that work, TICG simulations were coupled to a covariance matrix adaptation evolutionary strategy (CMAES) for inverse design, and the validity of the structures determined through that approach were compared to those determined from 3D TEM images, serving to establish the merits and potential of the proposed strategy.16 Building on that concept, in this study we implement a similar approach, but we do so by relying on SCFT calculations, as opposed to TICG simulations. In principle, the two approaches rely on the same level of description of the material, but SCFT methods can in some cases be more computationally efficient. A disadvantage of SCFT, however, is that thermal fluctuations are neglected and, strictly speaking, the model is exact only in the limit of infinite molecular weight. Furthermore, to improve the efficiency of SCFT calculations, a 2-dimensional implementation is adopted here. One of the questions that we therefore address here is how fluctuations, intermediate molecular weights, and discretization effects might alter the interpretation of scattering measurements. With that goal in mind, in what follows, we compare the parameters identified in the original TICG study to those obtained here, and any differences are discussed in the context of the underlying model and theories.
As pointed out earlier, previous CDSAXS work54,55,57,58 used a trapezoid stack shape model to represent the periodic structure and extract geometric details about the morphology of the materials. Physics-based models, on the other hand, can also give insight into thermodynamic parameters like the Flory–Huggins parameter quantitatively and other parameters such as surface chemical potentials that are less sensitive to the geometric structure qualitatively. We therefore compare our results to those obtained from a trapezoid analysis, and present a discussion of the types of morphologies that are particularly difficult to characterize without relying on a physics-based approach.
Methods
a. Sample materials and preparation
Samples were prepared similarly to previous work that examined the samples via scanning electron microscopy (SEM)80 and X-ray scattering with analysis via the TICG model. Synthesis of polymers was performed by Merck EMD¶ including a hydroxyl-terminated poly(styrene-random-methyl methacrylate) (P(S-r-MMA)–OH) brush (AZEMBLY NLD127), a cross-linked poly(styrene) (X-PS, AZEMBLY NLD128), and a poly(styrene-block-methyl methacrylate) (PS-b-PMMA, AZEMBLY PME312) BCP with natural period L0 ≅ 28 nm. These materials were used as received. Organic solvent RER600 (Fujifilm) was used. Orgasolv STR 301 (BASF) was also used. ArF immersion photoresist, AIM5484 (JSR Micro), was used. The imec TEL CLEAN TRACK ACT™ 12 system was used for all processing. The 3× feature multiplication process used a pre-patterned pitch of 84 nm by exposing the photoresist with an ASML XT:1950Gi scanner at 1.35NA (numerical aperture) at quadrupole illumination (XY polarized, NA = 1.35, σo = 0.87, σi = 0.72). Chemical vapor deposition (CVD) was used to deposit a 14 nm thin antireflective coating (ARC) film of SiN on the 300 mm Si wafers. A 7 nm to 8 nm thin film of X-PS was spun coat and annealed in an N2 atmosphere at a temperature of ≈250 °C for 5 min. Vendor recommended settings were used to coat and expose the photoresist for post-apply bake (PAB), post-exposure bake (PEB), and development. At this point in the processing, 84 nm pitch lines and spaces with critical dimensions (CDs) varying for a given sample from ≈L0/2 to ≈L0 were produced. Plasma etching using O2 and Cl2 was performed to trim the resist and X-PS to the target CDs. Orgasolv STR 301 was used to strip the remaining resist at room temperature. Spin coating of the P(S-r-MMA)–OH random brush was performed and the sample was annealed at 250 °C in an N2 atmosphere for 5 min to react the brush with the substrate. Any remaining non-reacted brush was rinsed away with the RER600 solvent. Spin coating of the PS-b-PMMA BCP was performed and the sample annealed at 250 °C in an N2 atmosphere for 5 min producing the final self-assembled periodic morphologies examined. To examine the structures, the films were transferred to a silicon nitride membrane that were back etched with areas patterned by a diamond scribe to create a thin enough window to shine the X-ray source through.
b. Res-CDSAXS experimental procedure and intensity calculations
Soft X-ray measurements were conducted at the 11.0.1.2 beamline at the advanced light source (ALS) at Lawrence Berkeley National Laboratory. Measurements were conducted at 282 eV, below the carbon absorption edge to enhance contrast while minimizing beam damage. The sample chamber was maintained under high vacuum (10−5 Pa). The beam was circular and had a spot size of approximately 200 μm full width half maximum. Collection time varied from 0.1 s to 60 s depending on the sample and detector angles to maximize signal to noise. The DSA sample was placed on a rotation stage such that the line gratings were parallel to the axis of rotation, which was aligned to coincide with the beam center.
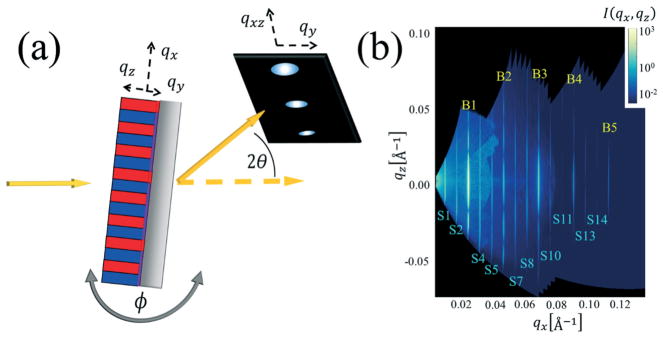
The CDSAXS geometry is depicted in Fig. 1a at normal incidence (X-ray beam perpendicular to the sample plane); the scattering contains information primarily on the in-plane structure (pitch and linewidth). As the sample is rotated, there are increasingly large contributions from the out-of-plane structure. The individual diffraction spots are converted to an intensity I(qx, qz), shown in Fig. 1b, where qx and qz are reciprocal space positions. The diffraction spots are present at intervals along the qx direction, where the spacing is inversely proportional to the lamella and template pitch. The variation in intensity along the qz direction originates from variations in the vertical lamella profile.
Fig. 1.
(a) Schematic of the experimental setup for res-CDSAXS experiment. Reciprocal space axes are shown. (b) Example 2D reciprocal space map of the intensity I(qx, qz) used to extract the peak slices along qx direction for inversely fitting the structure profile. Peak slice types are labeled as yellow Bn for Bragg peaks (that contain more information about the BCP periodic structure) and Sn for satellite peaks (that contain more information about the DSA template structure).
Scattering from the three-dimensional sample (with the scattering vector q⃗ defined as [qx, qy, qz] as shown in Fig. 1a) is then projected onto the 2D detector (with q⃗ vectors of [qxz, qy]). qxz is transformed to qx and qz using eqn (1a) and (1b). The individual images from all angles are then reconstructed into a 2D reciprocal space intensity map (example shown in Fig. 1b). This reciprocal space map shows peak slices at different qx values that are used in the structure reconstruction inverse fitting algorithm. The qx values from which the peak slices are taken are noted as qx,Cn, where C can be S for satellite or B for Bragg and n represents the order of the Bragg peaks or the numerator of the fraction the given peak equals of qx,B1 for the satellite peaks (e.g., qx,S2 = 2qx,B1/3 since the template is three times the BCP periodicity).
| (1a) |
| (1b) |
The simulated scattering intensity from the proposed model structure is calculated from eqn (2) through (4) where I0, the square magnitude of the form factor, is found using eqn (2) where r⃗ is the position vector, SLD (r⃗) is the shape function including scattering length density contrast, * represents a convolution, σ(x) is the periodic shift factor (aka structure factor) given by eqn 3, and i is the imaginary number. In eqn (3), PTemp is the template periodicity, n is the summation index over all repeat units, and δ(x) is the Dirac delta function. The final simulated scattering intensity ISim is given in eqn (4) where IS is a scaling constant, IBk is a constant that shifts the background intensity, and DW is the Debye– Waller factor which accounts for interfacial roughness.
| (2) |
| (3) |
| (4) |
In practice, n is set to 0 and σ(x) = δ(x). This assumption does not affect the shape of the scattered intensity peaks as a function of qz, only the magnitude scaling of the scattered intensity as a function of qx which is rescaled in the fitting procedure through IS. Since data is fit along the qz direction such an assumption is valid. The SLD describes the strength of interaction of the X-rays at a given energy with a material which is used in calculating the scattering contrast between materials. Thus, the SLD is not simply proportional to the composition density profile, but related in a non-linear fashion as well as being a function of the incident X-ray beam energy. Thus, the simplest approach to model the system is a binary SLD (which will be described shortly) coupled to a Debye–Waller parameter that accounts for the interfacial change in the composition density between different species domains. This model assumption will affect the fits of the scattering profile by requiring the Debye–Waller parameter be fit explicitly. Additionally, the intensity scaling parameter IS accounts for the absolute magnitude of the SLD as the model used assumes a relative SLD value rather than an absolute value.
c. BCP model: self-consistent field theory
SCFT describes the equilibrium phase behavior of BCP systems in the moderate to high χN regimes; details about SCFT can be found in the literature.14,59–61,67 Additional considerations, like complex Langevin dynamics, are necessary when fluctuation effects become important, for example in the low χN limit.81,82 Following our previous work with TICG simulations, for the system considered in this study up to 12 independent model parameters were either fixed or allowed to vary freely in any given inverse structure calculation. The model parameters depicted in Fig. 2 correspond to the geometric boundary conditions for the DSA template and thin film conditions as well as the thermodynamic control parameters for the thermal annealing of the samples in experiment. Additionally, DW (in terms of the statistical segment Kuhn segment length b through the interface width (see ESI1‡)), IS (in terms of the parameter IExp = log10 IS), and IBk used in calculating ISim are also varied freely for a total of 15 optimizable parameters.
Fig. 2.
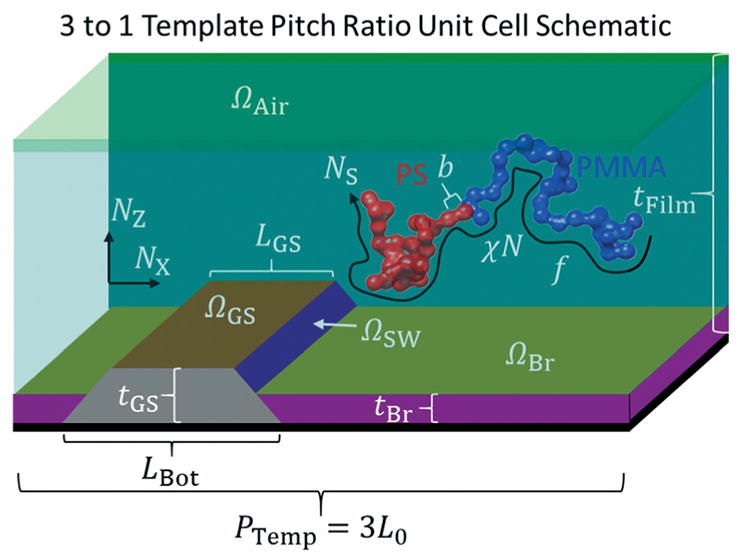
Schematic diagram of the boundary conditions used with all possible physical parameters that can be varied in the evolutionary strategy determination of the BCP structure from the CDSAXS measurements. Schematic of unit cell used for DSA templates with a 3 to 1 BCP L0 to template pitch ratio is shown as a 3D cut through for clarity while actual simulations are 2D. Red polymer is PS, blue polymer is PMMA, green top area is the air interface, teal area is where the BCP thin film density fields evolve in the SCFT simulations, olive area is the brush interface, purple area is the brush region, dark orange area is the guide stripe top interface, dark purple area is the guide stripe sidewall, grey area is the guide stripe region, and black area is the substrate. Axes are shown with directions corresponding to the 2D grid discretization.
The SCFT model parameters considered here include the volume fraction f, the product of the Flory–Huggins interaction parameter and the degree of polymerization χN (with N fixed to avoid parameter correlation), the assigned length of the unit cell in the plane direction PTemp (in terms of a varied L0 parameter such that PTemp = nL0 where n is the number of BCP domains per template domain), film thickness tFilm, the strength of the guide stripe interaction ΩGS, the strength of the guide stripe sidewall ΩSW, the strength of the neutral brush interaction ΩBr for an implicit brush, the strength of the air interaction ΩAir, the length of the top of the guide stripe LGS, the length of the bottom of the guide stripe LBot (which determines the slope of the guide stripe and brush sidewalls), the thickness of the guide stripe tGS, and the thickness of the neutral brush (see Fig. 2). The number of grid points used for coarse-graining the unit cell space was such that 30 points were assigned to each L0 region (i.e., a 3 to 1 template had NX = 90 grid points in the X-direction and an NZ (number of grid points in the Z-direction) that changed depending on what tFilm was). The polymer chains were coarse-grained to have NS = 51 statistical chain segments, a number less than the chemical repeat unit degree of polymerization N ≅ 489 that is large enough to exhibit the chain statistics of the BCP chain but small enough to be computationally efficient at calculating the density fields to relevant accuracy (the assigned N value was input in the full χN parameter while NS only affects the calculation of the chain partition function in the SCFT such that a smaller NS is less accurate but computationally more efficient, thus a value of 51 was chosen as a compromise between these effects). For the Ω parameters, negative values correspond to an affinity for PS and positive for PMMA. Complex Langevin dynamics were used during the first half of the simulations to perturb the system to prevent it from getting stuck in the initial seeded field state and to relax to a true equilibrium structure. The resulting fields still had to be relaxed to a mean field solution in order to calculate the SLD, so complex Langevin dynamics noise was turned off in the second half of the simulation.
The L0 parameter is varied based on a multiplication factor of the expected strong segregation limit value L0,SSL, such that L0,SSL = bχ1/6N2/3, where b is the Kuhn segment length. All lengths are varied in ratios of L0 calculated from L0,SSL times a varied pre-factor in the range of ≈0.6 to 1.2. This variable allows the system to select the appropriate L0 value that matches the templating conditions under the non-strong segregation limit χN values encountered. Since L0 is a function of χ and N, to avoid parameter correlation issues N was fixed to the experimentally known value of ≈489 and χ allowed to vary freely. By correlation issues, we mean when two or more parameters together affect the overall goodness of fit such that more than one combination of those parameters can give a similar overall fitness. This is different from dependent parameters that have already been accounted for in selecting the model parameters. Constraining one parameter in a pair that is correlated is necessary to ensure a unique solution. To calculate the scattering intensities, the dimensions of the system are converted to real units assigning values based on the primary qx,B1 Bragg peak slice value such that PTemp = 2π/qx,B1 where PTemp is the template period. For the samples examined this gave PTemp ≅ 84 nm.
The interfacial thickness effect on the scattering is captured in the DW parameter where
| (5) |
DW here corresponds to the average interface width and the local interface width can still vary locally along the PS/PMMA interface. Many previous studies have looked at modeling the interface width as a function of χN.83,84 Discussion of how the average interface width wInterface for eqn (5) is calculated is in the ESI;‡ (see ESI1).
d. Shape models
To compare the accuracy of the solutions found using the SCFT model, both a trapezoid stack shape model (discussed in prior work)54,55,57,58 and a grid based shape model were used. Discussion of these fits and the grid model are found in the ESI‡ (see ESI1 for discussion of these models and fits).
e. Evolutionary strategy and inverse methodology summary
In order to compare the experimental X-ray scattering intensity profiles with simulated data from different models, a fast optimization technique is necessary to find the set of parameters from which the simulated intensity profile best matches the experimental profile. The CMAES algorithm has been used in prior work to find inverse solutions to various problems fast and efficiently.57,74,75,77,85–87 A description of the algorithm can be found in previous work.16,57,74,75,85 Here we use the method to find the set of model parameters that lead to the self-assembly in simulation of a BCP density profile that when transformed into a scattered intensity pattern has the best match with an experimental data set. In the model, the density fields ϕ are defined on a 2D grid of size NZ by NX. Since the system considered is a diblock system with two species, there are two distinct density fields ϕPS and ϕPMMA for the polystyrene (PS) and poly(methyl methacrylate) (PMMA) species, respectively, corresponding to the physical location of the polymer chain segments in the experimental PS-b-PMMA thin films. To convert these densities to a relative electron scattering length density SLD needed for simulating the intensity profile ISim, the density difference Δϕ = ϕPS − ϕPMMA is first calculated and renormalized to a reference SLD’ value such that.
| (6) |
where min(*) is the minimum value function and max(*) is the maximum value function. SLD’ is then converted to a discrete SLD denoted SLDH or ϕH such that
| (7) |
This binary conversion is performed so that the intensity calculation model is comparable to previous work that used the same approach.16,54,55,57 Eqn (6) and (7) implicitly assume evaluation at every grid point in the unit cell. SLDH requires the use of either a Debye–Waller parameter or interfacial convolution to model the interface width that has to be fit with model parameters. SLDH is then related to SLD(r⃗) in eqn (2) so ISim can be calculated in eqn (4). The template regions are set such that the brush region has SLDH = 0.5 (halfway between the PS and PMMA values) and the X-PS mat region has SLDH = 0 to match the native BCP PS SLD.
In order to compare the simulated intensities ISim with the experimental target intensities ITar, an objective function that properly measures the goodness of fit of the simulated intensities to the actual data is necessary. Since the intensity data is dynamic in range over several orders of magnitude, a logarithmic based objective function is a natural choice. A reduced χ2 statistic might seem reasonable, but previous work has shown that such a metric is still inherently biased towards fitting mostly the primary peak.57 We choose the mean absolute error logarithmic objective function88 Ξ in base 10, where for Nq data points
| (8) |
In comparing ISim with ITar, data for ITar was processed such that values at constant qx slices were extracted and fits performed for these slices as a function of qz. These slices correspond to either Bragg peaks or satellite peaks of the scattered intensity.
Here we briefly present how the inverse methodology using the CMAES algorithm with the SCFT model was performed. The algorithm is initialized by the experimental target intensities ITar and model parameters to be varied with lower and upper bounds being inputs. A population of SCFT simulations are then performed (a size of 64 was used in all runs) in parallel with parameters randomly initiated over the range of the defined upper and lower bounds. An initial parameter step size σ = 5 was used based on an estimate of the average standard deviation of the different parameters varied. The parameters of the CMAES, including σ, are auto-tuned by the algorithm as discussed in previous work.57 These simulations are seeded with field solutions close to the final solution (found using a set of initial simulations at nominal parameters) for enhanced speed as well as to avoid the tendency of SCFT to get trapped in metastable solutions.14 Once the SCFT fields have relaxed, the goodness of fit Ξ using eqn (8) is calculated for each resulting density field map after converting the densities to SLD according to eqn (6) through (7) and calculating ISim according to eqn (4). These goodness of fit values are compared amongst each other as well as the best-found value thus far to see if there is a new best fit candidate in matching the experimental data. If a new best fit is found, the corresponding simulation result and parameter set are stored as the candidate solution. Regardless if a new best fit is found, the set of simulation parameters are updated according to the CMAES algorithm based on a ranking of the best half of the population by goodness of fit through a random distribution update with the step size as detailed in the previous work57 and the overall inverse methodology repeated with the new updated population set until successive generations of simulation parameters no longer produce better fits to the data. This typically took on the order of 50 to 100 generations for convergence for the most complex template model used.
Results & discussion
Here we examine the CDSAXS metrology applied to a set of BCP DSA samples. As a preliminary test of the methodology, a candidate simulated intensity was produced from a known set of SCFT parameters and used to test the ability of the algorithm to find an appropriate solution to the data with various amounts of noise added to the intensity. Details of this test are in the ESI‡ (see ESI2). To determine the appropriate complexity needed in the boundary conditions to model the DSA template, an increasingly complex template model was used to see how the accuracy of the solutions found increase with a more accurate template model in the SCFT framework for a given sample. The DSA conditions found from this sample that best recreated both the template structure and the polymer structure were then used to set the parameter search bounds in finding the best structure fits for other samples with templates that had varying guide stripe dimensions. These results for five different samples are then compared, both with known parameter values and values found using the TICG model in the other study.79
a. Model complexity study
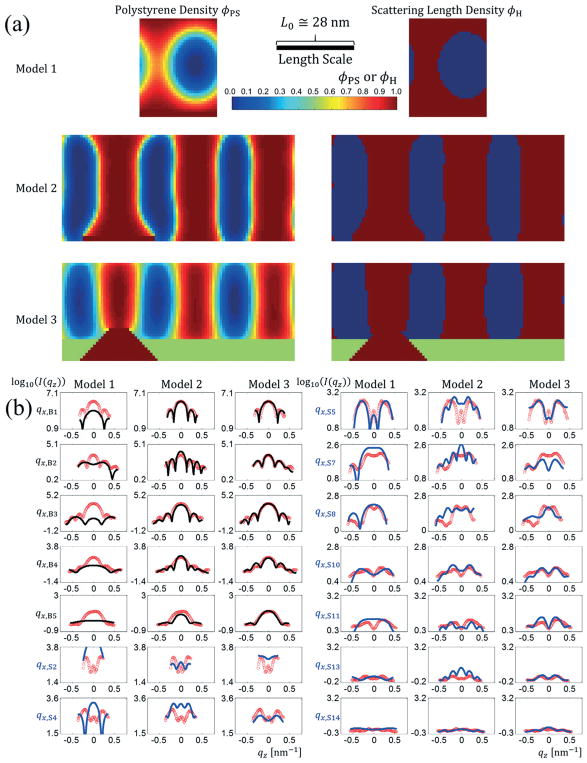
As an experimental demonstration of the CDSAXS methodology with the SCFT model, a set of samples of PS-b-PMMA templated by an X-PS guide stripe region alternating with a neutral brush region (P(S-r-MMA)–OH) were examined. To calibrate the model, three different template models were checked using the experimental data of one sample. Each template model had increasing complexity in terms of parameter constraints and how the template region was modeled. Model 1 assumed only a single lamellae period repeated structure with no constraint on a guiding stripe or brush region (surface energies for the top and bottom regions were uniform over the entire unit cell). Model 2 extended the unit cell to 3 BCP lengths adding a flat preferential guiding stripe region with variable width and the other region having a different surface affinity. Model 3 allowed the guiding stripe and brush regions to have full 2D shapes with a trapezoidal structure as described in Fig. 2. Model 3 is based on the one used in the previous TICG study where the guide stripe is also modeled as a trapezoid but has a variable sidewall angle θSW instead of varying LBot.16
The density profiles for the best fits to the data are shown in Fig. 3a and the intensity profile fits in Fig. 3b. The best fit parameters for each model with their bounded values along with goodness of fit values Ξ are given in Table 1. In interpreting the values for Ξ, a perfect fit would be such that the value represented the variance in the data due to Poisson noise. For the samples presented, this would correspond to an upper limit of Ξ ≅ 0.167 based on the noise levels examined in the ESI‡ for completely simulated structures where the Poison noise is known (see ESI2). Thus, the smaller and closer to that value Ξ is, the more accurate the fit. As seen visually from the fits in Fig. 3b and quantitatively in Table 1, the goodness of fit with the experimental data became better with increasing model complexity. Model 1, the simplest template model, was a very poor fit with many Bragg peak slices mismatching (Ξ = 0.508). Model 2 had better agreement with the Bragg peak slices and most of the difference in the goodness of fit came from the satellite peak slices (Ξ = 0.304). The addition of the realistic template structure in Model 3 resulted in the best overall fit by far (Ξ = 0.206), serving to highlight that the approach provides critical information to the template structure. Runs with model 1 and 2 and preliminary runs using model 3 showed correlation between parameters f as well as χN, so f was fixed based on the known volume fraction of 0.47 for the PMMA in the PS-b-PMMA used. Fitting f separately would have been informative to confirm that the results were converging towards a known parameter, but since there were parameter correlations, this was not feasible. From these different results, we can see that the most complex structure model, the one most like the expected template shape, gave the best fit. This fact shows the considerable influence of template shape in fitting of the data appropriately. This aspect of the approach in including the complex template details was originally identified in our recent TICG-scattering study,16 and the fact that it emerges here again serves to reinforce that it is not an artifact of the models, but rather a true feature of the samples.
Fig. 3.
(a) Resulting PS SCFT density profiles (left) and scattering length density profiles (right) for the best fits found to a set of experimental BCP DSA data with a template period to BCP period ratio of 3 to 1. Model 1 (top) uses no guiding stripe and lets the surface energies vary freely (corresponds to only a single repeating lamellae feature). Model 2 (middle) uses a flat guiding stripe with no height difference in the guiding stripe and brush regions. Model 3 (bottom) uses a trapezoidal shape profile to model the guiding stripe region (crimson red) and the brush region (green). (b) Best fit scattered intensity profiles for the three different template models for 14 different qx slice values with Bragg peak slices in black and satellite peak slices in blue plotted over the experimental data (red circles) against qz. The left column contains the Bragg peak slices and first two satellite peak slices and the right column the last seven satellite peak slices. In each column from left to right are fits using template model 1, model 2, and model 3. The length scale bar is for both horizontal and vertical directions (i.e., the aspect ratio as shown is unity).
Table 1.
(Top) Parameter values and their bounds for the three different template models for the best fit found to the set of experimental data shown in Fig. 3b. “Not applicable” denotes a parameter not being part of the given template model. (Bottom) The corresponding Ξ goodness of fit values for the three different template models. Uncertainty values for model 3 are averaged from the 5 best fits of that model. Only a single fit was performed with the other models so no uncertainty is presented in those cases
| Parameter | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|
|
|
|
|
||||
| Value | Bounds | Value | Bounds | Value | Bounds | |
| f | 0.42 | 0.35 : 0.52 | 0.42 | 0.35 : 0.52 | 0.47 | Fixed |
| χN | 16.3 | 12.0 : 35.0 | 28.6 | 12.0 : 35.0 | 16.5 ± 0.7 | 12.0 : 30.0 |
| L0/L0,SSL | 0.74 | 0.65 : 1.10 | 1.04 | 0.65 : 1.10 | 0.76 ± 0.07 | 0.60 : 1.10 |
| tFilm/L0 | 1.27 | 1.20 : 1.70 | 1.37 | 1.20 : 1.70 | 1.26 ± 0.12 | 1.20 : 1.60 |
| ΩGS | −14.2 | −15.0 : −2.0 | −14.0 | −15.0 : −2.0 | −9.9 ± 1.8 | −15.0 : −2.0 |
| ΩAir | −14.5 | −15.0 : −0.5 | −4.8 | −15.0 : −0.5 | −1.20 ± 0.12 | −8.0 : −0.5 |
| ΩBr | Not applicable | −10.7 | −15.0 : −0.5 | −1.55 ± 0.12 | −8.0 : −0.5 | |
| ΩSW | Not applicable | Not applicable | 6.2 ± 0.2 | 2.0 : 15.0 | ||
| LGS/L0 | Not applicable | 0.96 | 0.05 : 1.50 | 0.27 ± 0.04 | 0.20 : 0.70 | |
| LBot/L0 | Not applicable | Not applicable | 1.00 ± 0.04 | 0.20 : 1.60 | ||
| tGS/L0 | Not applicable | Not applicable | 0.40 ± 0.03 | 0.05 : 0.50 | ||
| tBr/L0 | Not applicable | Not applicable | 0.27 ± 0.03 | 0:05 : 0.40 | ||
| b [nm] | 0.69 | 0.5 : 2.0 | 1.16 | 0.5 : 2.0 | 0.81 ± 0.01 | 0.5 : 2.0 |
| DW [nm] | 1.89 | 0.02 : 9.90 | 2.24 | 0.02 : 9.90 | 2.20 ± 0.03 | 0.03 : 9.90 |
| IExp | −1.34 | −1.57 : −0.57 | −1.09 | −1.57 : −0.57 | −0.87 ± 0.04 | −1.57 : −0.57 |
| IBk | 0.88 | 0.11 : 0.90 | 0.65 | 0.11 : 0.90 | 0.62 ± 0.02 | 0.11 : 0.90 |
| Goodness of fit | ||||||
| Ξ | 0.508 | 0.304 | 0.206 ± 0.027 | |||
From the various parameter values for the best fit, the L0/L0,SSL values were usually less than 1.0 (an exception being model 2) indicating the samples did not follow strong segregation scaling. The magnitude of ΩGS for both model 2 and model 3 was much larger than |ΩBr| which was still larger than |ΩAir|, indicating that the guide stripe region was most preferential to PS as would be expected for a X-PS surface, the neutral brush was slightly preferential to PS, and the air interface was also slightly preferential to PS but not nearly as much as the brush layer. ΩSW was large and positive, indicating a strong preference for PMMA at the sidewalls. The TICG study arrived at similar results, with the sidewalls being PMMA preferential. In combination with TEM images, it was concluded that the templates are indeed three-toned with PS preferential stripes, PMMA preferential sidewalls, and neutral to slightly PS preferential brush regions.75 Other recent studies using SEM, cross-sectional transmission electron microscopy, GISAXS, and water contact angles to characterize the templates show additional evidence for this PMMA preference at the sidewalls.89,90 The experimental reasoning for the three-toned surface chemistry is that the photoresist used to pattern the guide stripes protects the top surface from the plasma etch while the sidewalls of the guide stripe are oxidized by the plasma, resulting in different surface chemistries. The guide stripe thickness was more than the brush which makes sense from the processing conditions where the brush back fills the regions made from the guide stripes. The DW parameter had a value around 2.20 nm which corresponds to an interfacial width of . These parameters thus generally agree with what one would expect from PS-b-PMMA at this molecular mass. Both the TICG model in the previous study and the SCFT model here showed values very close to 5 nm, a value previously reported for the bulk PS-b-PMMA systems91–94 with the SCFT model slightly larger than the TICG model. The binary SLD model used loses information on how χ affects the interfacial density profile within the SCFT model and instead that information gets incorporated in the calculation of DW. Thus, the best fit structure is less sensitive to χ than if the scattering model could incorporate the polymer density shape explicitly rather than having to convert to the binary SLD. Future work should consider developing an SLD model that can relate the continuous polymer density profile produced by the SCFT model to the SLD directly to avoid this issue.
b. Study of samples with varying guide stripe width
The previous section focused on one particular sample with a fixed guide stripe width (measured to be ≈0.47 L0 from SEM). In total, five different guide stripe widths were produced and examined. These samples in expected increasing guide stripe width order are labeled as sample 1, 2, 3, 4, and 5, respectively. All the results so far focused on sample 1.
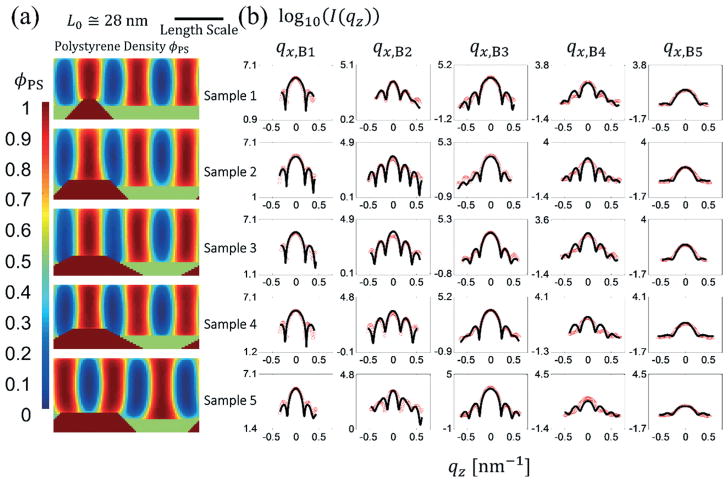
Fig. 4a shows the resulting SCFT density profiles and SLD profiles for the best fits for each sample using the SCFT model. Fig. 4b shows the intensity profile fits for each sample for the Bragg peak slices; satellite peak slice data fits are shown in the ESI‡ (see ESI3). The best fit model parameters for all 5 samples are also given in a table in the ESI‡ (see ESI3).
Fig. 4.
(a) From top to bottom, the PS densities from SCFT simulations are shown for the best fit solutions from a different sample with an expected increasing guide stripe width. (b) Intensity profiles for the five samples whose structure profile solutions are shown in (a) where the red circles are the experimental data and the black lines are the Bragg peak slice fits. The satellite peak slice fits are presented in the ESI.‡ The length scale bar is for both horizontal and vertical directions (i.e., the aspect ratio as shown is unity).
In terms of parameters varied for the SCFT model, the same bounds used for sample 1 given in Table 1 for model 3 were used but fixing tGS and tBr to the values found for sample 1 and constraining the bounds for LGS based on the expected value from supplemental SEM measurements. These values should not be taken as an absolute comparison value since they are top-down measurements of carbon based lines that weakly scatter, meaning the actual line width sizes are likely smaller than those reported, and Monte Carlo trajectory modeling would be necessary to accurately interpret the SEM results.95
For samples 4 and 5, two different SCFT field seeds were tested that would favor the convergence of a PS lamellae centered over the guide stripe or a U-type structure where two PS lamellae were off center relative to the guide stripe with PS wetting the top of the guide stripe. Such a structure was shown possible in preliminary SCFT simulations being stable for larger guide stripe widths. (i.e., the free energy of the structures for LGS ≳ L0 were lower for the U-based seeded simulations than those seeded with the PS stripe centered over the guide stripe). The resulting fits showed the U-type structure had the better goodness of fit Ξ for the final relaxed structure solution to the experimental data for the largest stripe sample only, sample 5, usually with Ξ of the U-seed being ≈20% lower than the guide stripe centered seed.
Table 2 shows the expected guide stripe widths for the samples found from SEM measurements against the values found in the best fits with uncertainty found considering the increasing width along the guide stripe going toward the substrate. Additionally, the table lists the interface width wInterface for the best solution with uncertainty calculated from five separate fits, χN for the best solution with uncertainty, and the best fit Ξ values for each sample.
Table 2.
Measured normalized guide stripe widths LGS/L0 compared with the values obtained from the best fits for each sample for the SCFT model. The SEM uncertainty is based on the minimum resolution of the measurement. The simulation uncertainty shown is found by projecting the guide stripe length where the guide stripe meets the top of the brush layer and computing a standard deviation for that value and the top value. The wInterface, χN, and goodness of fit Ξ for the best fit for each sample are also noted. Sample 3 and 4 just happened to have the same best fitting LGS/L0 with uncertainty
| Sample | SEM measurement | SCFT model | |||
|---|---|---|---|---|---|
|
|
|
||||
| LGS/L0 | LGS/L0 | wInterface [nm] | χN | Ξ | |
| 1 | 0.47 ± 0.04 | 0.27 ± 0.19 | 5.52 ± 0.09 | 16.5 ± 0.7 | 0.207 |
| 2 | 0.66 ± 0.04 | 0.87 ± 0.19 | 5.31 ± 0.16 | 13.6 ± 1.1 | 0.223 |
| 3 | 0.73 ± 0.04 | 0.73 ± 0.38 | 5.55 ± 0.04 | 15.0 ± 0.8 | 0.167 |
| 4 | 0.93 ± 0.04 | 0.73 ± 0.38 | 5.57 ± 0.06 | 17.6 ± 0.4 | 0.209 |
| 5 | 1.14 ± 0.04 | 1.20 ± 0.19 | 5.76 ± 0.05 | 17.9 ± 0.4 | 0.194 |
A comparison plot of the best fit structures found from the previous TICG study with the SCFT results are shown in Fig. 5 for all five samples. Qualitatively all five structures appear similar, with the size of the template guide stripe increasing from sample 1 to 5 as expected. Some minor differences are observed in the slope of the guide stripe, and the centering of the stripe around the guide stripe being the same. One noticeable difference is the top layer having PS wet more in the SCFT model than the TICG. Also shown in Fig. 5 is a cross-section scanning transmission electron microscopy (STEM) image of sample 4 from the previous study. The STEM qualitatively agrees with the symmetry of the line structures as observed, but structural details are difficult to discern from the resolution of the STEM.
Fig. 5.

Comparison of the best structure profiles from the TICG model in the previous study with the SCFT model in the present study. The TICG structures are on top and the SCFT structures on the bottom for each labeled sample. Color maps used for the density values going from 100% PS in red to 100% PMMA in blue are shown inset for each model with the TICG going from shades of red to white to blue and the SCFT using a color map that goes from red to orange to yellow to green to cyan to blue. Inset in the lower left corner is a STEM cross-sectional image where the dark regions are PS and the light regions are PMMA. The length scale bar is for both horizontal and vertical directions (i.e., the aspect ratio as shown is unity).
A detailed quantitative discussion of the all best fit parameters observed in the SCFT and TICG models can be found in the ESI‡ (see ESI4). The general trends for the parameters found agree with the sidewalls being preferential for PMMA, the guide stripe top being preferential for PS, and the brush layer being slightly preferential to PS. These similar qualitative features found from the fits for both models give credence to the SCFT model being appropriate for capturing the essential details of the average periodic structure of the thin films.
The inverse methodology provided shows the potential for a physics-based model like SCFT to be incorporated into CDSAXS metrology as appropriate fits to the scattered intensity profiles were found for the samples examined. The model as presented works well, though one can always consider model enhancements and such considerations are discussed in the ESI‡ (see ESI5).
In light of the results, many aspects of the DSA process as well as information on the polymers used can be gleaned. In terms of the surface energies, the chemical potentials were observed to generally be from most PMMA preferential to most PS preferential (i.e., least PMMA preferential) ΩSW > ΩAir > ΩBr > ΩGS. An exception was sample 5 that had ΩGS > ΩBr, likely because under the assumed template conditions some of the top of the guide stripe would actually be PS in the BCP. Another exception was sample 4 that had ΩBr > ΩAir, though the values are still relatively close to zero implying those regions are close to neutral but still slightly preferential to PS. The absolute magnitude of assigned chemical potentials had great variance due to the fact the SCFT field conditions are such that similar shape profiles can be produced from chemical potential wetting conditions over a large range of Ω values. This variance was much larger than the measured uncertainty from the best fits across the samples for the Ω parameters, thus the fits are not very sensitive to the exact value of the Ω parameters and only qualitative trend information for the surface energies can be obtained from these results. However, the qualitative picture supports the idea of a three-toned template seeing that ΩSW was always strongly preferential to PMMA, the brush was approximately neutral with a slight preference to PS, and guide stripe usually strongly preferential to PS. The general trend of increasing guide stripe width was observed with the samples as expected, although strict quantitative agreement was lacking due to the uncertainty in where the BCP PS region ends and the X-PS regions begins. Since a goal of DSA is to produce lamellae well aligned with the underlying template with as little interfacial roughness as possible for the pattern, sample 1 shows the best potential to fill this role as the side profile view shows the least amount of widening of the shape profile at the bottom of the template.
Comparing the average fitted values of χN to what would be expected from previous work,96,97 the value found for χ falls well within the expected range of 0.02 to 0.04 with a value of χ ≅ 0.033 ± 0.004 in the SCFT model. The previous TICG study16 found an effective χ value of χeff ≅ 0.046 ± 0.002 amongst the samples which is larger compared with previously reported experimental range due to the effects of fluctuations on the effective χ in the model. The variance in the χ parameter observed is likely due to fluctuation effects not being included, which strongly suggests that the actual structures are composed of non-uniform periodic patterns (i.e., no single unique unit cell). The overall variance of the χ parameter across samples is slightly larger than the measured uncertainties for each sample across the best fits, but not nearly as large a difference compared to the less sensitive Ω parameters meaning the χN parameters found can be considered a more quantitatively sound parameter than the Ω parameters. Taken together, the structure profiles found here only represent the best mean field solution of what one would expect to observe on average in these samples. These results show that the use of the physics-based models, such as SCFT, does indeed allow one to extract additional insights from the BCP DSA process, thereby enhancing the characterization of thin films of periodic structure forming BCPs. Our proposed strategy can also be used to validate the SCFT model when comparing the parameters found from known parameters. Both the SCFT and TICG models can reproduce the X-ray scattering profiles measured in experiment. If one just wants the average shape profile information, then a SCFT model is sufficient. If one wants more specific local fluctuation details, the TICG model should be used with the positional fluctuations of the structure being used to gauge how non-uniform the sample structure is across the film.
Summary & Conclusion
Here we showed the potential of CDSAXS with a physics-based shape model in SCFT to be used as a direct measurement and model validation technique for thin films of BCPs. Both quantitative thermodynamic and physical information in terms of χ (the ≈0.033 value found is quantitatively in agreement with previous reported values for PS and PMMA), f, interfacial width, film thickness, and template dimensions and qualitative information in terms of surface energies and morphological details are extracted from the X-ray data. The resulting SCFT density field maps found show good reproducibility of the scattered intensity profiles. Increasing the complexity of the boundary conditions and number of parameters varied in the SCFT model allows for better fits to be found. The relative surface energies of the different components of the template suggest that a three-toned template is indeed being used in the DSA process. The SCFT fits are in good agreement with the more detailed TICG model previously studied which means the simpler SCFT model is sufficient in capturing the necessary physics to interpret the scattering data.16 Using simpler physics-based models for such work is important since doing so increases calculation speeds, an important aspect of X-ray scattering data analysis as solving the inverse fitting problem can take many generations to converge even with advanced search algorithms like the CMAES. By examining different physics-based models with the res-CDSAXS methodology, a direct comparison with experiments is possible that can then either validate the models or give insight into model limitations that need to be addressed (e.g., fluctuation effects, which are naturally included in the TICG models, can be compared with the SCFT model, which did not incorporate such effects). In future work, systems other than periodic lamellae will be examined, such as periodic cylinders and spheres that require more complicated shape models but whose structure would arise naturally from the physics-based simulations.
Design, System, Application.
The molecular design strategy employed in this study can be used for examining the thermodynamic and structural properties of different polymer systems and thus be used to optimize the polymers used in directed self-assembly applications. The desired system will function to give small sub-10 nm size features with great etch selectivity for nanolithographic patterning applications. The work will enable a variety of next generation computer and memory storage device applications.
Acknowledgments
This research was performed while the author held a National Research Council Research Associateship Program award at the National Institute of Standards and Technology. The author also acknowledges financial support in the form of a Cooperative Agreement Grant (award number 70NANB16H005) through Georgetown University in the Professional Research Experience Program. The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We thank Anthony Young and Cheng Wang for assistance at BL 11.0.1.2.
Footnotes
Official contribution of the National Institute of Standards and Technology; not subject to copyright in the United States.
Electronic supplementary information (ESI) available. See DOI: 10.1039/c7me00098g
Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
Conflicts of interest
There are no conflicts of interest to declare.
References
- 1.Ito T, Okazaki S. Nature. 2000;406:1027–1031. doi: 10.1038/35023233. [DOI] [PubMed] [Google Scholar]
- 2.Acikgoz C, Hempenius MA, Huskens J, Vancso GJ. Eur Polym J. 2011;47:2033–2052. [Google Scholar]
- 3.Liddle JA, Gallatin GM. ACS Nano. 2016;10:2995–3014. doi: 10.1021/acsnano.5b03299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bai W, Ross CA. MRS Bull. 2016;41:100–107. [Google Scholar]
- 5.Herr DJC. J Mater Res. 2011;26:122–139. [Google Scholar]
- 6.Kim SO, Solak HH, Stoykovich MP, Ferrier NJ, De Pablo JJ, Nealey PF. Nature. 2003;424:411–414. doi: 10.1038/nature01775. [DOI] [PubMed] [Google Scholar]
- 7.Stoykovich MP, Müller M, Kim SO, Solak HH, Edwards EW, de Pablo JJ, Nealey PF. Science. 2005;308:1442–1446. doi: 10.1126/science.1111041. [DOI] [PubMed] [Google Scholar]
- 8.Ruiz R, Kang H, Detcheverry FA, Dobisz E, Kercher DS, Albrecht TR, de Pablo JJ, Nealey PF. Science. 2008;321:936–939. doi: 10.1126/science.1157626. [DOI] [PubMed] [Google Scholar]
- 9.Bita I, Yang JKW, Jung YS, Ross CA, Thomas EL, Berggren KK. Science. 2008;321:939–943. doi: 10.1126/science.1159352. [DOI] [PubMed] [Google Scholar]
- 10.Yang JKW, Jung YS, Chang JB, Mickiewicz RA, Alexander-Katz A, Ross CA, Berggren KK. Nat Nanotechnol. 2010;5:256–260. doi: 10.1038/nnano.2010.30. [DOI] [PubMed] [Google Scholar]
- 11.Luo M, Epps TH. Macromolecules. 2013;46:7567–7579. [Google Scholar]
- 12.Bencher C, Yi H, Zhou J, Cai M, Smith J, Miao L, Montal O, Blitshtein S, Lavi A, Dotan K, Dai H, Cheng JY, Sanders DP, Tjio M, Holmes S. Proc SPIE. 2012;8323:83230N. [Google Scholar]
- 13.Liu CC, Ramirez-Hernandez A, Han E, Craig GSW, Tada Y, Yoshida H, Kang H, Ji S, Gopalan P, De Pablo JJ, Nealey PF. Macromolecules. 2013;46:1415–1424. [Google Scholar]
- 14.Fredrickson G. The Equilibrium Theory of Inhomogeneous Polymers. Oxford University Press; Oxford, New York: 2005. [Google Scholar]
- 15.Detcheverry FA, Pike DQ, Nagpal U, Nealey PF, de Pablo JJ. Soft Matter. 2009;5:4858. [Google Scholar]
- 16.Khaira G, Doxastakis M, Bowen A, Ren J, Suh HS, Segal-Peretz T, Chen X, Zhou C, Hannon AF, Ferrier NJ, Vishwanath V, Sunday DF, Gronheid R, Kline RJ, de Pablo JJ, Nealey PF. Macromolecules. 2017;50:7783–7793. [Google Scholar]
- 17.Chang JB, Son JG, Hannon AF, Alexander-Katz A, Ross CA, Berggren KK. ACS Nano. 2012;6:2071–2077. doi: 10.1021/nn203767s. [DOI] [PubMed] [Google Scholar]
- 18.Park SM, Stoykovich MP, Ruiz R, Zhang Y, Black CT, Nealey PF. Adv Mater. 2007;19:607–611. [Google Scholar]
- 19.Stoykovich MP. Science. 2005;308:1442–1446. doi: 10.1126/science.1111041. [DOI] [PubMed] [Google Scholar]
- 20.Bita I, Yang JKW, Jung YS, Ross CA, Thomas EL, Berggren KK. Science. 2008;321:939–943. doi: 10.1126/science.1159352. [DOI] [PubMed] [Google Scholar]
- 21.Yang JKW, Jung YS, Chang JB, Mickiewicz RA, Alexander-Katz A, Ross CA, Berggren KK. Nat Nanotechnol. 2010;5:256–260. doi: 10.1038/nnano.2010.30. [DOI] [PubMed] [Google Scholar]
- 22.Xiao S, Yang X, Edwards EW, La Y-H, Nealey PF. Nanotechnology. 2005;16:S324–S329. doi: 10.1088/0957-4484/16/7/003. [DOI] [PubMed] [Google Scholar]
- 23.Tavakkoli AKG, Hannon AF, Gotrik KW, Alexander-Katz A, Ross CA, Berggren KK. Adv Mater. 2012;24:4249–4254. doi: 10.1002/adma.201104895. [DOI] [PubMed] [Google Scholar]
- 24.Chang JB, Choi HK, Hannon AF, Alexander-Katz A, Ross CA, Berggren KK. Nat Commun. 2014;5:3305. doi: 10.1038/ncomms4305. [DOI] [PubMed] [Google Scholar]
- 25.Tavakkoli KGA, Gotrik KW, Hannon AF, Alexander-Katz A, Ross CA, Berggren KK. Science. 2012;336:1294–1298. doi: 10.1126/science.1218437. [DOI] [PubMed] [Google Scholar]
- 26.Yang JKW, Berggren KK. J Vac Sci Technol, B: Microelectron Nanometer Struct–Process, Meas, Phenom. 2007;25:2025. [Google Scholar]
- 27.Park SM, Liang X, Harteneck BD, Pick TE, Hiroshiba N, Wu Y, Helms BA, Olynick DL. ACS Nano. 2011;5:8523–8531. doi: 10.1021/nn201391d. [DOI] [PubMed] [Google Scholar]
- 28.Doerk GS, Liu CC, Cheng JY, Rettner CT, Pitera JW, Krupp LE, Topuria T, Arellano N, Sanders DP. ACS Nano. 2013;7:276–285. doi: 10.1021/nn303974j. [DOI] [PubMed] [Google Scholar]
- 29.Rockford L, Liu Y, Mansky P, Russell T, Yoon M, Mochrie S. Phys Rev Lett. 1999;82:2602–2605. [Google Scholar]
- 30.Cheng JK, Rettner CT, Sanders DP, Kim HC, Hinsberg WD. Adv Mater. 2008;20:3155–3158. [Google Scholar]
- 31.Edwards EW, Montague MF, Solak HH, Hawker CJ, Nealey PF. Adv Mater. 2004;16:1315–1319. [Google Scholar]
- 32.Daoulas KC, Müeller M, Stoykovich MP, Park SM, Papakonstantopoulos YJ, De Pablo JJ, Nealey PF, Solak HH. Phys Rev Lett. 2006;96:036104. doi: 10.1103/PhysRevLett.96.036104. [DOI] [PubMed] [Google Scholar]
- 33.Detcheverry FA, Liu G, Nealey PF, De Pablo JJ. Macromolecules. 2010;43:3446–3454. [Google Scholar]
- 34.Detcheverry FA, Nealey PF, De Pablo JJ. Macromolecules. 2010;43:6495–6504. [Google Scholar]
- 35.Park SM, Craig GSW, La YH, Solak HH, Nealey PF. Macromolecules. 2007;40:5084–5094. [Google Scholar]
- 36.Tada Y, Yoshida H, Ishida Y, Hirai T, Bosworth JK, Dobisz E, Ruiz R, Takenaka M, Hayakawa T, Hasegawa H. Macromolecules. 2012;45:292–304. [Google Scholar]
- 37.Park SM, Craig GSW, La YH, Nealey PF. Macromolecules. 2008;41:9124–9129. [Google Scholar]
- 38.Gotrik KW, Lam T, Hannon AF, Bai W, Ding Y, Winterstein J, Alexander-Katz A, Liddle JA, Ross CA. Adv Funct Mater. 2014;24:7689–7697. [Google Scholar]
- 39.Segal-Peretz T, Winterstein J, Doxastakis M, Ramirez-Hernandez A, Biswas M, Ren J, Suh HS, Darling SB, Liddle JA, Elam JW, De Pablo JJ, Zaluzec NJ, Nealey PF. ACS Nano. 2015;9:5333–5347. doi: 10.1021/acsnano.5b01013. [DOI] [PubMed] [Google Scholar]
- 40.Hashimoto T, Nagatoshi K, Todo A, Hasegawa H, Kawai H. Macromolecules. 1974;7:364–373. [Google Scholar]
- 41.Todo A, Hashimoto T, Kawai H. J Appl Crystallogr. 1978;11:558–563. [Google Scholar]
- 42.Mori K, Hasegawa H, Hashimoto T. Polym J. 1985;17:799–806. [Google Scholar]
- 43.Bates FS, Fredrickson GH. Annu Rev Phys Chem. 1990;41:525–557. doi: 10.1146/annurev.pc.41.100190.002521. [DOI] [PubMed] [Google Scholar]
- 44.Müller-Buschbaum P. Eur Polym J. 2016;81:470–493. [Google Scholar]
- 45.Müller-Buschbaum P. Anal Bioanal Chem. 2003;376:3–10. doi: 10.1007/s00216-003-1869-2. [DOI] [PubMed] [Google Scholar]
- 46.Gunkel I, Gu X, Sun Z, Schaible E, Hexemer A, Russell TP. J Polym Sci, Part B: Polym Phys. 2016;54:331–338. [Google Scholar]
- 47.Bai W, Yager KG, Ross CA. Macromolecules. 2015;48:8574–8584. [Google Scholar]
- 48.Jones RL, Hu T, Lin EK, Wu WL, Kolb R, Casa DM, Bolton PJ, Barclay GG. Appl Phys Lett. 2003;83:4059–4061. [Google Scholar]
- 49.Jones RL, Soles CL, Lin EK, Hu W, Reano RM, Pang SW, Weigand SJ, Keane DT, Quintana JP. J Microlithogr, Microfabr, Microsyst. 2006;5:013001. [Google Scholar]
- 50.Wang C, Fu WE, Li B, Huang H, Soles C, Lin EK, Wu WL, Ho PS, Cresswell MW. Thin Solid Films. 2009;517:5844–5847. [Google Scholar]
- 51.Virgili JM, Tao YF, Kortright JB, Balsara NP, Segalman RA. Macromolecules. 2007;40:2092–2099. [Google Scholar]
- 52.Wang C, Araki T, Ade H. Appl Phys Lett. 2005;87:214109. [Google Scholar]
- 53.Wang C, Lee DH, Hexemer A, Kim MI, Zhao W, Hasegawa H, Ade H, Russell TP. Nano Lett. 2011;11:3906–3911. doi: 10.1021/nl2020526. [DOI] [PubMed] [Google Scholar]
- 54.Sunday DF, Hammond MR, Wang C, Wu W, Kline RJ, Stein GE. J Micro/Nanolithogr, MEMS, MOEMS. 2013;12:031103. [Google Scholar]
- 55.Sunday DF, Hammond MR, Wang C, Wu WL, Delongchamp DM, Tjio M, Cheng JY, Pitera JW, Kline RJ. ACS Nano. 2014;8:8426–8437. doi: 10.1021/nn5029289. [DOI] [PubMed] [Google Scholar]
- 56.Sunday DF, Ashley E, Wan L, Patel KC, Ruiz R, Kline RJ. J Polym Sci, Part B: Polym Phys. 2015;53:595–603. [Google Scholar]
- 57.Hannon AF, Sunday DF, Windover D, Joseph Kline R. J Micro/Nanolithogr, MEMS, MOEMS. 2016;15:034001. doi: 10.1117/1.JMM.15.3.034001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sunday DF, Ren J, Liman CD, Williamson LD, Gronheid R, Nealey PF, Kline RJ. ACS Appl Mater Interfaces. 2017;9:31325–31334. doi: 10.1021/acsami.7b02791. [DOI] [PubMed] [Google Scholar]
- 59.Mickiewicz RA, Yang JKW, Hannon AF, Jung YS, Alexander-Katz A, Berggren KK, Ross CA. Macromolecules. 2010;43:8290–8295. [Google Scholar]
- 60.Alexander-Katz A, Moreira AG, Fredrickson GH. J Chem Phys. 2003;118:9030–9036. doi: 10.1063/1.1827211. [DOI] [PubMed] [Google Scholar]
- 61.Fredrickson GH, Ganesan V, Drolet F. Macromolecules. 2002;35:16–39. [Google Scholar]
- 62.Son JG, Hannon AF, Gotrik KW, Alexander-Katz A, Ross CA. Adv Mater. 2011;23:634–639. doi: 10.1002/adma.201002999. [DOI] [PubMed] [Google Scholar]
- 63.Tavakkoli AKG, Nicaise SM, Gadelrab KR, Alexander-Katz A, Ross CA, Berggren KK. Nat Commun. 2016;7:10518. doi: 10.1038/ncomms10518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Bai W, Gadelrab K, Alexander-Katz A, Ross CA. Nano Lett. 2015;15:6901–6908. doi: 10.1021/acs.nanolett.5b02815. [DOI] [PubMed] [Google Scholar]
- 65.Gotrik KW, Hannon AF, Son JG, Keller B, Alexander-Katz A, Ross CA. ACS Nano. 2012;6:8052–8059. doi: 10.1021/nn302641z. [DOI] [PubMed] [Google Scholar]
- 66.Bai W, Hannon AF, Gotrik KW, Choi HK, Aissou K, Liontos G, Ntetsikas K, Alexander-Katz A, Avgeropoulos A, Ross CA. Macromolecules. 2014;47:6000–6008. [Google Scholar]
- 67.Hannon AF, Bai W, Alexander-Katz A, Ross CA. Soft Matter. 2015;11:3794–3805. doi: 10.1039/c5sm00324e. [DOI] [PubMed] [Google Scholar]
- 68.Nagpal U, Mueller M, Nealey PF, De Pablo JJ. ACS Macro Lett. 2012;1:418–422. doi: 10.1021/mz200245s. [DOI] [PubMed] [Google Scholar]
- 69.Li W, Nealey PF, De Pablo JJ, Müeller M. Phys Rev Lett. 2014;113:168301. doi: 10.1103/PhysRevLett.113.168301. [DOI] [PubMed] [Google Scholar]
- 70.Hur SM, Thapar V, Ramírez-Hernández A, Khaira G, Segal-Peretz T, Rincon-Delgadillo PA, Li W, Müller M, Nealey PF, de Pablo JJ. Proc Natl Acad Sci. 2015;112:14144–14149. doi: 10.1073/pnas.1508225112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Izumi K, Kim B, Laachi N, Delaney KT, Carilli MF, Fredrickson GH. SPIE Adv Lithogr. 2015;9423:94232C. [Google Scholar]
- 72.Hannon AF, Gotrik KW, Ross CA, Alexander-Katz A. ACS Macro Lett. 2013;2:251–255. doi: 10.1021/mz400038b. [DOI] [PubMed] [Google Scholar]
- 73.Hannon AF, Ding Y, Bai W, Ross CA, Alexander-Katz A. Nano Lett. 2014;14:318–325. doi: 10.1021/nl404067s. [DOI] [PubMed] [Google Scholar]
- 74.Qin J, Khaira GS, Su Y, Garner GP, Miskin M, Jaeger HM, de Pablo JJ. Soft Matter. 2013;9:11467. [Google Scholar]
- 75.Khaira GS, Qin J, Garner GP, Xiong S, Wan L, Ruiz R, Jaeger HM, Nealey PF, De Pablo JJ. ACS Macro Lett. 2014;3:747–752. doi: 10.1021/mz5002349. [DOI] [PubMed] [Google Scholar]
- 76.Xu D, Liu H, Zhu YL, Lu ZY. Nanoscale. 2016;8:5235–5244. doi: 10.1039/c5nr07497e. [DOI] [PubMed] [Google Scholar]
- 77.Jaeger HM, de Pablo JJ. APL Mater. 2016;4:053209. [Google Scholar]
- 78.Tsai CL, Delaney KT, Fredrickson GH. Macromolecules. 2016;49:6558–6567. [Google Scholar]
- 79.Miskin MZ, Khaira G, de Pablo JJ, Jaeger HM. Proc Natl Acad Sci U S A. 2016;113:34–39. doi: 10.1073/pnas.1509316112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Gronheid R, Rincon Delgadillo P, Pathangi H, Van den Heuvel D, Parnell D, Chan BT, Lee Y-T, Van Look L, Cao Y, Her Y, Lin G, Harukawa R, Nagaswami V, D’Urzo L, Somervell M, Nealey P. Proc SPIE. 2014;9049:904905. [Google Scholar]
- 81.Müller M, Schmid F. Adv Polym Sci. 2005;185:1–58. [Google Scholar]
- 82.Ganesan V, Fredrickson GH. Europhys Lett. 2007;55:814–820. [Google Scholar]
- 83.Semenov AN. Macromolecules. 1993;26:6617–6621. [Google Scholar]
- 84.Matsen MW, Bates FS. Macromolecules. 1996;29:1091–1098. [Google Scholar]
- 85.Hansen N, Ostermeier A. Evol Comput. 2001;9:159–195. doi: 10.1162/106365601750190398. [DOI] [PubMed] [Google Scholar]
- 86.Hansen N, Müller SD, Koumoutsakos P. Evol Comput. 2003;11:1–18. doi: 10.1162/106365603321828970. [DOI] [PubMed] [Google Scholar]
- 87.Hansen N, Kern S. Proc 8th Int. Conf. Parallel Probl. Solving from Nat. - PPSN VIII; 2004. pp. 282–291. [Google Scholar]
- 88.Wormington M, Panaccione C, Matney KM, Bowen DK. Philos Trans R Soc, A. 1999;357:2827–2848. [Google Scholar]
- 89.Williamson LD, Seidel RN, Chen X, Suh HS, Delgadillo PR, Gronheid R, Nealey PF. ACS Appl Mater Interfaces. 2016;8:2704–2712. doi: 10.1021/acsami.5b10562. [DOI] [PubMed] [Google Scholar]
- 90.Cushen J, Wan L, Blachut G, Maher MJ, Albrecht TR, Ellison CJ, Willson CG, Ruiz R. ACS Appl Mater Interfaces. 2015;7:13476–13483. doi: 10.1021/acsami.5b02481. [DOI] [PubMed] [Google Scholar]
- 91.Anastasiadis SH, Russell TP, Satija SK, Majkrzak CF. J Chem Phys. 1990;92:5677–5691. [Google Scholar]
- 92.Russell TP, Menelle A, Hamilton WA, Smith GS, Satija SK, Majkrzak CF. Macromolecules. 1991;24:5721–5726. [Google Scholar]
- 93.Ramya P, Ranganathaiah C, Williams JF. Polymer. 2012;53:4539–4546. [Google Scholar]
- 94.Sunday DF, Kline RJ. Macromolecules. 2015;48:679–686. [Google Scholar]
- 95.Shimizu R, Ze-Jun D. Rep Prog Phys. 1992;55:487–531. [Google Scholar]
- 96.Sweat DP, Kim M, Schmitt AK, Perroni DV, Fry CG, Mahanthappa MK, Gopalan P. Macromolecules. 2014;47:6302–6310. [Google Scholar]
- 97.Sunday DF, Hannon AF, Tein S, Kline RJ. Macromolecules. 2016;49:4898–4908. [Google Scholar]